1 Introduction

The support vector machine (SVM) proposed by Vapnik et al. [1] is a machine learning method that is based on the principle of the Vapnik-Chervonekis (VC) dimension and structural risk minimization in statistical learning. It has been widely used in many fields, such as text recognition [2], feature extraction [3], multiview learning [4, 5], and sample screening [6]. This method uses the margin maximization strategy to find the optimal classification hyperplane that classifies the training datasets correctly with a sufficiently large certainty factor. This means that the hyperplane not only classifies positive and negative samples, but also has a sufficiently large certainty factor for classifying samples that are close to the hyperplane. Therefore, SVM has many advantages in terms of classification and prediction of unknown samples. In addition, SVM is formalized to solve a convex quadratic programming problem. However, with the continuous growth of the scale of data, some problems with SVM have been exposed. For example, SVM has high complexity with O (m3), where m is the number of training samples. It has difficulty coping with the processing requirements of large-scale data, and its anti-noise performance is weak. To this end, researchers have proposed some improved methods. Mangasarian et al. [7] proposed the proximal support vector machine (PSVM). This algorithm uses equation constraints to transform a quadratic programming problem into a problem of solving linear equations, and this improves the training speed of the algorithm. On this basis, they further proposed a generalized eigenvalue ​​proximal support vector machine GEPSVM [8]. In their proposed algorithm, by relaxing the parallel constraints of the hyperplane, the original problem is transformed into solving two generalized eigen equations.

Inspired by the PSVM and GEPSVM, Jayadeva et al. [9] proposed the twin support vector machine (TWSVM) by minimizing the empirical risk, turning the single large quadratic programming problem into a pair of smaller quadratic programming problems. Unlike the GEPSVM, the TWSVM requires one hyperplane at least one unit distance away from other class. The complexity of the algorithm becomes 1/4 that of the SVM, and this further saves computation time. It has been shown that the TWSVM has more favorable properties than the SVM in terms of computing complexity and classification accuracy. Since TWSVM has excellent classification performance, it has attracted increasing attention. Therefore, many variants of the TWSVM have been proposed. For example, the twin bounded support vector machine (TBSVM) proposed by Shao et al. [10] is implemented by adding a regularization term to the objective function. It further improves the generalization performance of the TWSVM. In addition, researchers have proposed different twin support vector machines by exploring the structures of datasets and the different roles of samples [11,12,13,14,15,16,17,18].

From the above, to establish a support vector machine model, researchers mainly use a hinge loss function, which is sensitive to noise and unstable for resampling. To cope with these problems, Huang et al. [19] introduced the pinball loss into the support vector machine and proposed the Pin-SVM, which better solved the problems of noise sensitivity and resampling instability than previous SVMs. After that, researchers introduced the pinball loss into twin support vector machines and proposed different versions [20,21,22]. However, these models still need to solve two quadratic programming problems in the dual space. In fact, for the solution of the model in the original space, Mangasarian et al. [23] studied the support vector machine using smoothing technique and proposed a smooth support vector machine (SSVM). Moreover, researchers applied the smoothing technique to the twin support vector machines and proposed different algorithms for such twin support vector machines [24,25,26,27]. To obtain the required decision surface, the corresponding models of the twin support vector machines mentioned above are mainly solved in the dual space. Even if the researchers proposed a twin support vector machine solved in the original space, the model is still based on the hinge loss function.

The contributions of this paper are as follows:

  1. 1.

    We introduce the pinball loss into the twin bounded support vector machine to construct a twin bounded support vector machine model with pinball loss, which overcomes noise sensitivity and resampling instability in the hinge loss function.

  2. 2.

    To solve the nondifferentiable term in the objective function of the model, we construct a smooth approximation function for the pinball loss function so that the model in the original space can be solved directly. At the same time, the smooth twin bounded support vector machine with pinball loss is proposed.

  3. 3.

    A proof of the convergence of the algorithm is given theoretically.

  4. 4.

    We select UCI datasets and artificially generated datasets to validate the presented algorithm and compare its performance with the representative algorithms.

The remainder of this paper is organized as follows. Section 2 recalls three kinds of support vector machine models and analyzes the pinball loss function. Moreover, the corresponding smooth approximation function for the pinball loss function is constructed. Section 3 introduces the smooth twin bounded support vector machine model with pinball loss. The Newton-Armijo method is used to solve the model. Based on this, a smooth twin bounded support vector machine algorithm with pinball loss is proposed. Section 4 provides the theoretical analysis and proof of convergence for the presented algorithm. Experiments are conducted on UCI datasets and artificially generated datasets in section 5. In addition, we also discuss the other approximation function based on the integral of sigmoid function for the pinball loss function and experiments on the toy dataset. The detailed derivations are provided in the appendix. Finally, the conclusion is given.

2 Related works

In this section, we briefly review the formulations of the smooth support vector machine (SSVM), twin support vector machine (TWSVM), twin bounded support vector machine (TBSVM) and a smooth approximation function for the pinball loss function.

2.1 SSVM

Lee et al. [23] introduced a smooth method into the SVM and conducted a new formulation of SVM.

The standard support vector machine is

$$ {\displaystyle \begin{array}{c}\kern0.3em \underset{\left(w,b,\xi \right)\in {\mathfrak{R}}^{n+1+m}}{\min}\kern0.9300001em v{e}^T\xi +\frac{1}{2}\parallel w{\parallel}^2\\ {}\kern1.65em s.t.\kern1.98em D\left( Aw- eb\right)+\xi \ge e,\\ {}\kern4.95em \xi \ge 0.\end{array}} $$
(1)

The matrix A contains m points in n-dimensional place, v > 0, w ∈ Rn, b ∈ R.ξ is the slack variable and e is a column vector of ones that is of arbitrary dimension and D is an m × m order matrix with ones or minus ones on its diagonal. In the smooth approach, using twice the reciprocal squared of the margin instead, the modified SVM problem is as follows:

$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{\left(w,b,\xi \right)\in {\mathfrak{R}}^{n+1+m}}{\min}\kern0.9300001em \frac{v}{2}{\xi}^T\xi +\frac{1}{2}\left(\parallel w{\parallel}^2+{b}^2\right)\\ {}\kern1.65em s.t.\kern1.98em D\left( Aw- eb\right)+\xi \ge e,\\ {}\kern4.95em \xi \ge 0.\end{array}} $$
(2)

According to [28], the plus function is defined as

$$ {(u)}_{+}=\mathit{\max}\left\{u,0\right\}, $$
(3)

and ξ is given by

$$ \xi =\kern0.66em {\left(e-D\left( Aw- eb\right)\right)}_{+} $$
(4)

Furthermore, the equivalent unconstrained problem is formulated as

$$ \kern0.50em \underset{w,b}{\mathit{\min}}\kern0.30em \;\frac{v}{2}\parallel {\left(e-D\left( Aw- eb\right)\right)}_{+}{\parallel}_2^2+\frac{1}{2}\left(\parallel w{\parallel}^2+{b}^2\right). $$
(5)

It is clear that (5) is strongly convex and has a unique solution. However, it is not twice differentiable at zero. Therefore, the integral of the sigmoid function

$$ \kern0.1em p\left(x,\alpha \right)=x+\frac{1}{\alpha}\log \left(1+{e}^{-\alpha x}\right),\alpha >0, $$
(6)

is used here to replace the first term in (5), and a smooth support vector machine can be obtained:

$$ \kern0.50em \underset{w,b}{\mathit{\min}}\kern0.60em {\varPhi}_{\alpha}\left(w,b\right):= \underset{w,b}{\mathit{\min}}\kern0.1em \;\;\frac{v}{2}\parallel p\left(e-D\left( Aw- eb\right),\alpha \right){\parallel}_2^2+\frac{1}{2}\left(\parallel w{\parallel}^2+{b}^2\right). $$
(7)

It can be seen that (7) is smooth and twice differentiable, so it can be solved by using the Newton-Armijo method [29,30,31].

2.2 TWSVM

Consider a binary classification dataset X = {(xi, yi)| i = 1, 2, …, m}, xi ∈ Rn, yi ∈ {+1, −1}. It contains m1 positive samples and m2 negative samples, which are represented by the matrices A and B, respectively, with m1 + m2 = m. Jayadeva et al. [9] proposed the twin support vector machine (TWSVM) using the hinge loss function, turning the optimization problem into a pair of smaller quadratic programming problems. Two nonparallel classification hyperplanes \( {f}_1(x)={w}_1^Tx+{b}_1=0 \) and \( {f}_2(x)={w}_2^Tx+{b}_2=0 \) need to be found to separate the samples correctly.

The primal problems of the TWSVM can be expressed as follows:

$$ {\displaystyle \begin{array}{c}\kern0.1em \underset{w_1,{b}_1,{\xi}_1}{\min}\kern1.1em \frac{1}{2}{\left\Vert A{w}_1+{e}_1{b}_1\right\Vert}^2+{c}_1{e_2}^T{\xi}_1\\ {}\kern0.9000001em s.t.\kern1.2em -\left(B{w}_1+{e}_2{b}_1\right)+{\xi}_1\ge {e}_2,\kern0.3em \end{array}} $$
(8)
$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{w_2,{b}_2,{\xi}_2}{\min}\kern1.1em \frac{1}{2}{\left\Vert B{w}_2+{e}_2{b}_2\right\Vert}^2+{c}_2{e_1}^T{\xi}_2\\ {}\kern0.9000001em s.t.\kern1.2em \left(A{w}_2+{e}_1{b}_2\right)+{\xi}_2\ge {e}_1,\kern0.3em \end{array}} $$
(9)

where c1,c2 > 0, ξ1 and ξ2 are slack variables, e1 and e2 are column vectors of ones those are of arbitrary dimension. For optimization problems (8) and (9), the Lagrange method and K.K.T. optimality conditions are used to obtain their dual problems:

$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{\alpha }{\max}\kern1.1em {e_2}^T\alpha -\frac{1}{2}{\alpha}^TG{\left({H}^TH\right)}^{-1}{G}^T\alpha \\ {}\kern0.9000001em s.t.\kern1.2em 0\le \alpha \le {c}_1,\end{array}} $$
(10)
$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{\alpha }{\max}\kern1.1em {e_1}^T\gamma -\frac{1}{2}{\gamma}^TP{\left({Q}^TQ\right)}^{-1}{P}^T\gamma \\ {}\kern0.9000001em s.t.\kern1.2em 0\le \gamma \le {c}_2,\end{array}} $$
(11)

where α ≥ 0, γ ≥ 0.

2.3 TBSVM

Shao et al. [10] introduced a regularization term into the TWSVM and proposed a twin bounded support vector machine (TBSVM). The primal problems of the TBSVM can be expressed as follows:

$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{w_1,{b}_1,{\xi}_1}{\min}\kern1.1em \frac{1}{2}{\left\Vert A{w}_1+{e}_1{b}_1\right\Vert}^2+\frac{1}{2}{c}_3\left({\left\Vert {w}_1\right\Vert}^2+{b_1}^2\right)+{c}_1{e_2}^T{\xi}_1\\ {}\kern0.9000001em s.t.\kern1.2em -\left(B{w}_1+{e}_2{b}_1\right)+{\xi}_1\ge {e}_2,\kern0.3em \end{array}} $$
(12)
$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{w_2,{b}_2,{\xi}_2}{\min}\kern1.1em \frac{1}{2}{\left\Vert B{w}_2+{e}_2{b}_2\right\Vert}^2+\frac{1}{2}{c}_4\left({\left\Vert {w}_2\right\Vert}^2+{b_2}^2\right)+{c}_2{e_1}^T{\xi}_2\\ {}\kern0.9000001em s.t.\kern1.2em \left(A{w}_2+{e}_1{b}_2\right)+{\xi}_2\ge {e}_1,\kern0.3em \end{array}} $$
(13)

where c1,c2,c3,c4 > 0, ξ1 and ξ2 are slack variables, e1 and e2 are column vectors of ones those are of arbitrary. For optimization problems (12) and (13), the Lagrange method and K.K.T. optimality conditions are used to obtain their dual problems:

$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{\alpha }{\max}\kern1.1em {e_2}^T\alpha -\frac{1}{2}{\alpha}^TG{\left({H}^TH+{c}_3I\right)}^{-1}{G}^T\alpha \\ {}\kern0.9000001em s.t.\kern1.2em 0\le \alpha \le {c}_1,\end{array}} $$
(14)
$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{\upalpha}{\max}\kern1.1em {e_1}^T\gamma -\frac{1}{2}{\gamma}^TP{\left({Q}^TQ+{c}_4I\right)}^{-1}{P}^T\gamma \\ {}\kern0.9000001em s.t.\kern1.2em 0\le \gamma \le {c}_2,\end{array}} $$
(15)

where α ≥ 0, γ ≥ 0.

2.4 Pinball loss and its smooth approximation function

In support vector machines or twin support vector machines, the hinge loss function is typically used to measure the correctness and error of classification. However, this function has strong sensitivity to noise and instability of resampling. Therefore, this paper uses the pinball loss function to study the twin bounded support vector machine.

We know that the Chen-Harker-Kanzow-Smale function [28] is one of the approximations of the plus function, and it is denoted by

$$ \frac{u+\sqrt{u^2+4{\varepsilon}^2}}{2}, $$
(16)

where ε > 0.

The pinball loss function can be rewritten as

$$ {L}_{\tau }(u)={(u)}_{+}+{\left(-\tau u\right)}_{+},\kern0.75em \tau \in \left[0,1\right]. $$
(17)

From (17), we know that the left and right derivatives of the function at zero are

$$ \underset{\varDelta u\to {0}^{-}}{\lim}\frac{L_{\tau}\left(0+\varDelta u\right)-{L}_{\tau }(0)}{\varDelta u}=\frac{-\tau \left(0+\varDelta u\right)-0}{\varDelta u}=-\tau \kern0.9000001em \mathrm{and} $$
$$ \underset{\varDelta u\to {0}^{+}}{\lim}\frac{L_{\tau}\left(0+\varDelta u\right)-{L}_{\tau }(0)}{\varDelta u}=\frac{0+\varDelta u-0}{\varDelta u}=1 $$

It can be seen that the left and right derivatives of the pinball loss function at zero are not equal, that is, the function is not differentiable at zero. To this end, a smooth function ϕτ(u, ε) is used to approximate it by using (16) and (17), where ε is a sufficiently small parameter, and the function ϕτ(u, ε) is shown in (18):

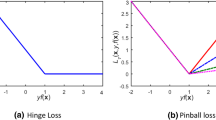
$$ \kern0.1em {\phi}_{\tau}\left(u,\varepsilon \right)=\frac{u+\sqrt{u^2+4{\varepsilon}^2}}{2}+\frac{-\tau u+\sqrt{\tau^2{u}^2+4{\varepsilon}^2}}{2}. $$
(18)

From (18), it is known that this function has arbitrary-order derivatives. Figure 1 provides a graph with the pinball loss function and its approximation function ϕτ(u, ε) at τ = 0.5 and ε = 10−6. It can be intuitively seen that the approximation function ϕτ(u, ε) is smooth everywhere when ε is small enough.

Fig. 1
figure 1

Pinball loss function and its smooth approximation function

Full size image

Moreover, we also study another approximation function for the pinball loss function that is defined as follows:

$$ \kern0.1em {p}_{\tau}\left(x,\alpha \right)=p\left(x,\alpha \right)+p\left(-\tau x,\alpha \right)=x+\frac{1}{\alpha}\mathit{\log}\left(1+{e}^{-\alpha x}\right)+\left[-\tau x+\frac{1}{\alpha}\mathit{\log}\left(1+{e}^{\alpha \tau x}\right)\right], $$

where α > 0.

Below, we introduce a smooth twin bounded support vector machine with pinball loss based on the approximation function ϕτ(u, ε). For the other approximation function pτ(x, α), the detailed process is presented in the appendix.

3 Smooth twin bounded support vector machine with pinball loss

3.1 Linear case

To overcome the shortcomings of the hinge loss function, pinball loss is introduced into the twin bounded support vector machine in this paper, and the optimization problems are obtained as follows:

$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{w_1,{b}_1,\xi }{\min}\kern.5em \frac{1}{2}\sum \limits_{i=1}^{m_1}{\left({w}_1^T{x}_i^{(1)}+{b}_1\right)}^2+\frac{1}{2}{c}_3\left(\parallel {w}_1{\parallel}^2+{b}_1^2\right)+{c}_1\sum \limits_{j=1}^{m_2}{\xi}_j\\ {}s.t.\kern.5em -\left({w}_1^T{x}_j^{(2)}+{b}_1\right)+{\xi}_j\ge 1,\kern0.3em \\ {}\kern.5em -\left({w}_1^T{x}_j^{(2)}+{b}_1\right)-\frac{\xi_j}{\tau_2}\le 1,\end{array}} $$
(19)
$$ {\displaystyle \begin{array}{c}\kern0.5em \underset{w_2,{b}_2,\eta }{\min}\kern.3em \frac{1}{2}\sum \limits_{q=1}^{m_2}{\left({w}_2^T{x}_q^{(2)}+{b}_2\right)}^2+\frac{1}{2}{c}_4\left(\parallel {w}_2{\parallel}^2+{b}_2^2\right)+{c}_2\sum \limits_{p=1}^{m_1}{\eta}_p\\ {}\kern0.9000001em s.t.\kern.5em \left({w}_2^T{x}_p^{(1)}+{b}_2\right)+{\eta}_p\ge 1,\\ {}\kern2.2em \left({w}_2^T{x}_p^{(1)}+{b}_2\right)-\frac{\eta_p}{\tau_1}\le 1.\end{array}} $$
(20)

For (19) and (20), the solutions can be obtained by solving the quadratic programming problems in the dual space. The required classification surfaces are further obtained. This method is referred to as Pin-GTBSVM. In the following, we mainly introduce the iterative solutions of (19) and (20) in the original space.

First, we convert (19) and (20) into unconstrained optimization problems and obtain the following model:

$$ \kern0.40em \underset{w_1,{b}_1}{\mathit{\min}}\kern0.20em \;{\varPhi}_1\left({w}_1,{b}_1;{\tau}_2\right)=\underset{w_1,{b}_1}{\mathit{\min}}\kern0.60em \frac{1}{2}\sum \limits_{i=1}^{m_1}{\left({w}_1^T{x}_i^{(1)}+{b}_1\right)}^2+\frac{1}{2}{c}_3\left({\left\Vert {w}_1\right\Vert}^2+{b_1}^2\right)+{c}_1\sum \limits_{j=1}^{m_2}{L}_{\tau_2}\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right) $$
(21)
$$ \kern0.40em \underset{w_2,{b}_2}{\mathit{\min}}\;{\varPhi}_1\left({w}_2,{b}_2;{\tau}_1\right)=\underset{w_2,{b}_2}{\mathit{\min}}\kern0.80em \frac{1}{2}\sum \limits_{q=1}^{m_2}{\left({w}_2^T{x}_q^{(2)}+{b}_2\right)}^2+\frac{1}{2}{c}_4\left(\parallel {w}_2{\parallel}^2+{b}_2^2\right)+{c}_2\sum \limits_{p=1}^{m_1}{L}_{\tau_1}\left(1-{w}_2^T{x}_p^{(1)}-{b}_2\right) $$
(22)

It can be seen that the objective functions of optimization problems (21) and (22) are continuous but not smooth. For this reason, we use the smooth function ϕ(⋅, ⋅) to approximate\( {L}_{\tau_2}\left(\cdot \right) \), namely,

$$ {\phi}_{\tau_2}\left({w}_1^T{x}_j^{(2)}+{b}_1+1,\varepsilon \right)\approx {L}_{\tau_2}\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right), $$
(23)
$$ {\phi}_{\tau_1}\left(1-{w}_2^T{x}_p^{(1)}-{b}_2,\varepsilon \right)\approx {L}_{\tau_1}\left(1-{w}_2^T{x}_p^{(1)}-{b}_2\right). $$
(24)

Here, we rewrite

$$ {\phi}_1\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)={\phi}_{\tau_2}\left({w}_1^T{x}_j^{(2)}+{b}_1+1,\varepsilon \right), $$
(25)
$$ {\phi}_2\left({w}_2,{b}_2;{\tau}_1,\varepsilon \right)={\phi}_{\tau_1}\left(1-{w}_2^T{x}_p^{(1)}-{b}_2,\varepsilon \right). $$
(26)

We replace the last terms of (21) and (22) with (25) and (26), respectively, to obtain the following model:

$$ \kern0.1em \underset{w_1,{b}_1}{\mathit{\min}}\kern0.30em \varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)=\underset{w_1,{b}_1}{\mathit{\min}}\kern0.40em {c}_1\sum \limits_{j=1}^{m_2}{\phi}_1\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+\frac{1}{2}\sum \limits_{i=1}^{m_1}{\left({w}_1^T{x}_i^{(1)}+{b}_1\right)}^2+\frac{1}{2}{c}_3\left(\parallel {w}_1{\parallel}^2+{b}_1^2\right) $$
(27)
$$ \underset{w_2,{b}_2}{\mathit{\min}}\kern0.30em \varPhi \left({w}_2,{b}_2;{\tau}_1,\varepsilon \right)=\underset{w_2,{b}_2}{\mathit{\min}}\kern0.30em {c}_2\sum \limits_{p=1}^{m_1}{\phi}_2\left({w}_2,{b}_2;{\tau}_1,\varepsilon \right)+\frac{1}{2}\sum \limits_{q=1}^{m_2}{\left({w}_2^T{x}_q^{(2)}+{b}_2\right)}^2+\frac{1}{2}{c}_4\left(\parallel {w}_2{\parallel}^2+{b}_2^2\right) $$
(28)

where ci > 0(i = 1,2,3,4).

3.2 Nonlinear case

In the nonlinear case, by introducing a kernel function that map the input space to the feature space, a nonlinear problem can be converted into a linear problem in the feature space. In the feature space, the two nonparallel classification hyperplanes to be found are K(xT, CT)u1 + b1 = 0 and K(xT, CT)u2 + b2 = 0, where CT = [X(1)TX(2)T]T, \( {X}^{(1)}=\left[{x}_1^{(1)},{x}_2^{(1)},\dots, {x}_{m1}^{(1)}\right] \), and \( {X}^{(2)}=\left[{x}_1^{(2)},{x}_2^{(2)},\dots, {x}_{m2}^{(2)}\right] \) . The corresponding optimization problems are as follows:

$$ {\displaystyle \begin{array}{c}\kern0.1em \underset{u_1,{b}_1,\xi }{\min}\kern.2em \frac{1}{2}\sum \limits_{i=1}^{m_1}{\left(K\left({x}_i^{(1)T},{C}^T\right){u}_1+{b}_1\right)}^2+\frac{1}{2}{c}_3\left(\parallel {u}_1{\parallel}^2+{b}_1^2\right)+{c}_1\sum \limits_{j=1}^{m_2}{\xi}_j\\ {}\kern0.9000001em s.t.\kern1.2em -\left(K\left({x}_j^{(1)T},{C}^T\right){u}_1+{b}_1\right)+{\xi}_j\ge 1,\kern0.3em \\ {}\kern2.6em -\left(K\left({x}_j^{(1)T},{C}^T\right){u}_1+{b}_1\right)-\frac{\xi_j}{\tau_2}\le 1,\end{array}} $$
(29)
$$ {\displaystyle \begin{array}{c}\kern0.1em \underset{u_2,{b}_2,\eta }{\min}\kern.3em \frac{1}{2}\sum \limits_{q=1}^{m_2}{\left(K\left({x}_q^{(2)T},{C}^T\right){u}_2+{b}_2\right)}^2+\frac{1}{2}{c}_4\left({\left\Vert {u}_2\right\Vert}^2+{b_2}^2\right)+{c}_2\sum \limits_{p=1}^{m_1}{\eta}_p\\ {}\kern0.9000001em s.t.\kern1.2em \left(K\left({x_p^{(1)}}^T,{C}^T\right){u}_2+{b}_2\right)+{\eta}_p\ge 1,\\ {}\kern1.6em \left(K\left({x_p^{(1)}}^T,{C}^T\right){u}_2+{b}_2\right)-\frac{\eta_p}{\tau_1}\le 1.\end{array}} $$
(30)

Similar to the linear case, the following model is obtained after the smooth and unconstrained processing of (29) and (30):

$$ \kern0.1em \underset{u_1,{b}_1}{\mathit{\min}}\kern0.30em \varPhi \left({u}_1,{b}_1;{\tau}_2,\varepsilon \right)=\underset{u_1,{b}_1}{\mathit{\min}}\kern0.30em {c}_1\sum \limits_{j=1}^{m_2}{\phi}_1\left({u}_1,{b}_1;{\tau}_2,\varepsilon \right)+\frac{1}{2}\sum \limits_{i=1}^{m_1}{\left(K\left({x_i^{(1)}}^T,{C}^T\right){u}_1+{b}_1\right)}^2+\frac{1}{2}{c}_3\left({\left\Vert {u}_1\right\Vert}^2+{b_1}^2\right) $$
(31)
$$ \underset{u_2,{b}_2}{\mathit{\min}}\kern0.30em \varPhi \left({u}_2,{b}_2;{\tau}_1,\varepsilon \right)=\underset{u_2,{b}_2}{\mathit{\min}}\kern0.30em {c}_2\sum \limits_{p=1}^{m_1}{\phi}_2\left({u}_2,{b}_2;{\tau}_1,\varepsilon \right)+\frac{1}{2}\sum \limits_{q=1}^{m_2}{\left(K\left({x_q^{(2)}}^T,{C}^T\right){u}_2+{b}_2\right)}^2+\frac{1}{2}{c}_4\left({\left\Vert {u}_2\right\Vert}^2+{b_2}^2\right) $$
(32)

where ci > 0(i = 1,2,3,4).

From Eqs. (27)–(28) and (31)–(32), although the objective functions are different, the solutions are similar. Therefore, for optimization problem (27), the Newton-Armijo iteration method is used below to provide an algorithm for solving the nonparallel hyperplane, and it is denoted as Pin-SGTBSVM.

Pin-SGTBSVM Algorithm:

  1. Step 1:

    Given the initial point \( \left({w}_1^0,{b}_1^0\right)\in {R}^{n+1} \) and error η;

  2. Step 2:

    If \( \left\Vert \nabla \varPhi \left({w}_1^i,{b}_1^i;{\tau}_2,\varepsilon \right)\right\Vert <\eta \) or the required number of iterations is satisfied, then (w1i, b1i) is considered to be the solution, and the algorithm ends; otherwise, the Newton direction di should be recalculated by solving the equations ∇2Φ(w1i, b1i; τ2, ε)di =  −  ∇ Φ(w1i, b1i; τ2, ε);

  3. Step 3:

    w1i + 1, b1i + 1 can be calculated by choosing an appropriate step size \( {\lambda}_i=\mathit{\max}\left\{1,\frac{1}{2},\frac{1}{4}\dots \right\} \) according to(w1i + 1, b1i + 1) = (w1i, b1i) + λidi, where the constraints \( \varPhi \left({w_1}^i,{b_1}^i;{\tau}_2,\varepsilon \right)-\varPhi \left(\left({w_1}^i,{b_1}^i\right)+{\lambda}_i{d}^i;{\tau}_2,\varepsilon \right)\ge -\delta {\lambda}_i\nabla \varPhi \left({w_1}^i,{b_1}^i;{\tau}_2,\varepsilon \right){d}^i,\delta \in \left[0,\frac{1}{2}\right] \) should be met and δ is fixed at 1/2 here.

For an unknown sample x, it is assigned to class i (i = +1,-1) by using the following method:

$$ {\displaystyle \begin{array}{c} class(x)=\mathit{\operatorname{sgn}}\left(\frac{w_1^Tx+{b}_1}{\left\Vert {w}_1\right\Vert }+\frac{w_2^Tx+{b}_2}{\left\Vert {w}_2\right\Vert}\right)\ \mathrm{or}\\ {} class(x)=\mathit{\operatorname{sgn}}\left(\frac{K\left({x}^T,{C}^T\right){u}_1+{b}_1}{\left\Vert {u}_1\right\Vert }+\frac{K\left({x}^T,{C}^T\right){u}_2+{b}_2}{\left\Vert {u}_2\right\Vert}\right),\end{array}} $$

where sgn denotes the sign function.

4 Convergence of the algorithm

In section 3, the Pin-SGTBSVM algorithm is used to obtain the solution sequences\( \left\{\left({w}_1^i,{b}_1^i\right)\right\}\ and\ \left\{\left({w}_2^i,{b}_2^i\right)\right\} \). This section mainly studies the convergence of the sequence.

Theorem 1 Given the functions Φ(w1, b1; τ2, ε), Φ(w2, b2; τ1, ε), Φ1(w1, b1; τ2), and Φ1(w2, b2; τ1) respectively, the following conclusions are established:

  1. (1)

    Φ(w1, b1; τ2, ε) and Φ(w2, b2; τ1, ε) are arbitrary, continuous and smooth functions with respect to w1, b1 and w2, b2 for arbitrary (w1, b1) ∈ Rn + 1 and (w2, b2) ∈ Rn + 1.

  2. (2)

    For arbitrary (w1, b1) ∈ Rn + 1 and(w2, b2) ∈ Rn + 1, when ε > 0, we have

    $$ {\displaystyle \begin{array}{c}{\varPhi}_1\left({w}_1,{b}_1;{\tau}_2\right)\le \varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)\le {\varPhi}_1\left({w}_1,{b}_1;{\tau}_2\right)+2{c}_1{m}_2\varepsilon, \\ {}{\varPhi}_1\left({w}_2,{b}_2;{\tau}_1\right)\le \varPhi \left({w}_2,{b}_2;{\tau}_1,\varepsilon \right)\le {\varPhi}_1\left({w}_2,{b}_2;{\tau}_1\right)+2{c}_2{m}_1\varepsilon .\end{array}} $$
  3. (3)

    Φ(w1, b1; τ2, ε) and Φ(w2, b2; τ1, ε) are continuously differentiable and strictly convex functions for any arbitrary ε > 0.

Proof:

  1. (1)

    According to the smoothness of the constructed function, conclusion (1) is obviously true.

  2. (2)

    We bound the difference between the smooth function and pinball loss function:

    $$ \kern0.1em {\phi}_{\tau}\left(u,\varepsilon \right)-{L}_{\tau }(u)=\left\{\begin{array}{c}\frac{u+\sqrt{u^2+4{\varepsilon}^2}}{2}+\frac{-\tau u+\sqrt{\tau^2{u}^2+4{\varepsilon}^2}}{2}-u\kern0.96em ,u\ge 0,\\ {}\frac{u+\sqrt{u^2+4{\varepsilon}^2}}{2}+\frac{-\tau u+\sqrt{\tau^2{u}^2+4{\varepsilon}^2}}{2}-\left(-\tau u\right),u<0.\end{array}\right. $$

Then, we can obtain

$$ {\displaystyle \begin{array}{c}\kern0.1em \\ {}{\phi}_{\tau}\left(u,\varepsilon \right)-{L}_{\tau }(u)=\left\{\begin{array}{c}\frac{\sqrt{u^2+4{\varepsilon}^2}-u}{2}+\frac{\sqrt{\tau^2{u}^2+4{\varepsilon}^2}-\tau u}{2}\kern1.8em ,u\ge 0,\\ {}\frac{\sqrt{u^2+4{\varepsilon}^2}+u}{2}+\frac{\sqrt{\tau^2{u}^2+4{\varepsilon}^2}+\tau u}{2}\kern1.68em ,u<0,\end{array}\right.\end{array}} $$

so 0 ≤ ϕτ(u, ε) − Lτ(u) ≤ 2ε.

As a result, Φ1(w1, b1; τ2) ≤ Φ(w1, b1; τ2, ε) ≤ Φ1(w1, b1; τ2) + 2c1m2ε.

In the same way, we can obtain

$$ {\varPhi}_1\left({w}_2,{b}_2;{\tau}_1\right)\le \varPhi \left({w}_2,{b}_2;{\tau}_1,\varepsilon \right)\le {\varPhi}_1\left({w}_2,{b}_2;{\tau}_1\right)+2{c}_2{m}_1\varepsilon $$

(3) From (1), Φ(w1, b1; τ2, ε) is a continuous and smooth function, so we see that

$$ \nabla \Phi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)=\left(\begin{array}{c}\frac{\partial \varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{\partial {w}_1}\\ {}\frac{\partial \varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{\partial {b}_1}\end{array}\right). $$

For Φ(w1, b1; τ2, ε), its first-order partial derivatives with respect to w1 and b1 are as follows:

$$ {\displaystyle \begin{array}{l}\frac{\partial \varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{\partial {w}_1}=\frac{c_1}{2}\sum \limits_{j=1}^{m_2}\left({x}_j^{(2)}+\frac{x_j^{(2)}\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}{\sqrt{{\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}^2+4{\varepsilon}^2}}+\left(-{\tau}_2{x}_j^{(2)}+\frac{\tau_2^2{x}_j^{(2)}\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}{\sqrt{\tau_2^2{\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}^2+4{\varepsilon}^2}}\right)\right)\\ {}+\sum \limits_{i=1}^{m_1}{x}_i^{(1)}\left({w}_1^T{x}_i^{(1)}+{b}_1\right)+{c}_3{w}_1,\\ {}\begin{array}{l}\frac{\partial \varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{\partial {b}_1}=\frac{c_1}{2}\sum \limits_{j=1}^{m_2}\left(1+\frac{\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}{\sqrt{{\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}^2+4{\varepsilon}^2}}+\left(-{\tau}_2+\frac{\tau_2^2\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}{\sqrt{\tau_2^2{\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}^2+4{\varepsilon}^2}}\right)\right)\\ {}+\sum \limits_{i=1}^{m_1}\left({w}_1^T{x}_i^{(1)}+{b}_1\right)+{c}_3{b}_1.\end{array}\end{array}} $$

We further obtain

$$ {\nabla}^2\varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)=\left(\begin{array}{cc}\frac{\partial^2\varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{{\partial w}_1^2}& \frac{\partial^2\varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{\partial {b}_1\partial {w}_1}\\ {}\frac{\partial^2\varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{\partial {w}_1\partial {b}_1}& \frac{\partial^2\varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)}{{\partial b}_1^2}\end{array}\right). $$

The second-order partial derivatives of the function Φ(w1, b1; τ2, ε) with respect to w1 and b1 are

$$ {\nabla}^2\varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)=\left[\begin{array}{c}\sum \limits_{j=1}^{m_2}{x}_j^{(2)}{x}_j^{(2)T}{\lambda}_1\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+\sum \limits_{i=1}^{m_1}{x}_i^{(1)}{x}_i^{(1)T}+{c}_3{I}_n\kern0.24em \sum \limits_{j=1}^{m_2}{x}_j^{(2)}{\lambda}_1\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+\sum \limits_{i=1}^{m_1}{x}_i^{(1)}\\ {}\sum \limits_{j=1}^{m_2}{x}_j^{(2)T}{\lambda}_1\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+\sum \limits_{i=1}^{m_1}{x}_i^{(1)T}\kern2.4em \sum \limits_{j=1}^{m_2}{\lambda}_1\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+{m}_1+{c}_3\end{array}\right] $$

where

$$ {\lambda}_1\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)=\frac{c_1}{2}\left(\frac{4{\varepsilon}^2}{{\left({\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}^2+4{\varepsilon}^2\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\tau_2^24{\varepsilon}^2}{{\left({\tau}_2^2{\left({w}_1^T{x}_j^{(2)}+{b}_1+1\right)}^2+4{\varepsilon}^2\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right). $$

It can be seen thatλ1(w1, b1; τ2, ε) > 0. For arbitrary \( {\xi}_1^T=\left({\xi}^T,{\xi}_0\right)\in {R}^{n+1} \) and ξ1 ≠ 0, ξ ∈ Rn, we have

$$ {\displaystyle \begin{array}{l}{\xi}_1^T{\nabla}^2\varPhi \left({w}_1,{b}_1;{\tau}_2,\varepsilon \right){\xi}_1={\xi}^T\left(\sum \limits_{j=1}^{m_2}{x}_j^{(2)}{x}_j^{(2)T}{\lambda}_{\mathsf{1}}\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+\sum \limits_{i=1}^{m_1}{x}_i^{(1)}{x}_i^{(1)T}+{c}_3{I}_n\right)\xi \\ {}+{\xi}_0\left(\sum \limits_{j=1}^{m_2}{x}_j^{(2)T}{\lambda}_{\mathsf{1}}\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+\sum \limits_{i=1}^{m_1}{x}_i^{(1)T}\right)\xi \\ {}\begin{array}{l}+{\xi}^T\left(\sum \limits_{j=1}^{m_2}{x}_j^{(2)}{\lambda}_{\mathsf{1}}\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+\sum \limits_{i=1}^{m_1}{x}_i^{(1)}\right){\xi}_0\\ {}+{\xi}_0\left(\sum \limits_{j=1}^{m_2}{\lambda}_{\mathsf{1}}\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)+{m}_1+{c}_3\right){\xi}_0\\ {}={\lambda}_{\mathsf{1}}\left({w}_1,{b}_1;{\tau}_2,\varepsilon \right)\sum \limits_{j=1}^{m_2}{\left({x}_j^{(2)T}\xi +{\xi}_0\right)}^2+\sum \limits_{i=1}^{m_1}{\left({x}_i^{(1)T}\xi +{\xi}_0\right)}^2+{c}_3{\xi}_1^T{\xi}_1>0.\end{array}\end{array}} $$

This shows that∇2Φ(w1, b1; τ2, ε) is a positive definite matrix. Therefore, we can obtain Φ(w1, b1; τ2, ε)is a continuously differentiable and strictly convex function. For the functionΦ(w2, b2; τ1, ε), we can obtain the same conclusion.

Theorem 2 The Pin-SGTBSVM algorithm converges to the solutions of problems (21) and (22), that is, when \( \left\{\left({w}_1^i,{b}_1^i\right)\right\} \)and \( \left\{\left({w}_2^i,{b}_2^i\right)\right\} \)are the solution sequences of (27) and (28), respectively, the minimum points of (27) and (28),which are (w1∗, b1∗) and (w2∗, b2∗), yield \( \underset{k\to \infty }{\lim}\left({w_1}^i,{b_1}^i\right)=\left({w_1}^{\ast },{b_1}^{\ast}\right) \) and \( \underset{k\to \infty }{\lim}\left({w_2}^i,{b_2}^i\right)=\left({w_2}^{\ast },{b_2}^{\ast}\right) \).

Proof:

According to Theorem 1, Φ(w1, b1; τ2, ε) and Φ(w2, b2; τ1, ε) are continuous and differentiable, strictly convex functions; therefore, there is a unique minimum because0 ≤ Φ(w1, b1; τ2, ε) − Φ1(w1, b1; τ2) ≤ 2c1m2ε and0 ≤ Φ(w2, b2; τ1, ε) − Φ1(w2, b2; τ1) ≤ 2c2m1ε, so the sequences{(w1i, b1i)} and {(w2i, b2i)}converge to (w1∗, b1∗) and(w2∗, b2∗), respectively.

5 Experimental results and analysis

To validate the performance of the proposed Pin-SGTBSVM algorithm, we selects German, Haberman, CMC, Fertility, WPBC, Ionosphere, and Live-disorders from the UCI database [32] for experimentation. For a convenient comparison, some representative algorithms, including the TWSVM [9], TBSVM [10], Pin-GTWSVM [21] (TWSVM based on pinball loss and solved in the dual space), Pin-GTBSVM (TBSVM based on pinball loss and solved in the dual space), and Pin-SGTWSVM (TWSVM based on pinball loss and solved in the original space), are selected. The kernel function used in the experiments is K(x, y) = exp(−θ × ‖x − y‖2), where θ is a parameter in the kernel function. A tenfold cross-validation method is used to find the optimal parameter value in the range of [10−6,105]. The values of τ1 and τ2 are 0.5, 0.8, 1, and the value range of ci > 0 (i = 1, 2, 3, 4) is [2−10, 210]. The value of ε in the experiments is 10−6, the value of η in the algorithm is 10−4, and the experimental results are the average accuracy and standard deviation. All experiments in this paper are run on an Intel (R) Core (TM) i7-5500U CPU @ 2.40 GHz with 4 GB of memory and MATLAB R2016a.

5.1 UCI datasets

In this subsection, we compare the performance of the presented TWSVM,TBSVM, and Pin-GTWSVM algorithms with those of the traditional solving method and the Pin-GTBSVM, Pin-SGTWSVM and Pin-SGTBSVM solved by the iterative method. The experimental results are shown in Table 1. The accuracy (%) and standard deviation are used for evaluation, abbreviated as Acc and sd, respectively. It can be seen that the Pin-SGTBSVM algorithm is superior to the other five methods on five of the seven datasets. It obtains the same result as Pin-SGTWSVM on the Haberman dataset. And on the Fertility dataset, it obtains the same result as those of the other five algorithms. In addition, the Pin-SGTWSVM algorithm achieves the higher accuracy on six of the seven datasets, but its accuracy on the German dataset is inferior to that of the TWSVM algorithm.

Table 1 Performance of different algorithms on UCI datasets with nonlinear kernel
Full size table

To further analyze the influence of parameters on the algorithms, we selected 6 datasets to conduct experiments with the Pin-GTWSVM, Pin-GTBSVM, Pin-SGTWSVM algorithms for different values of τ. As shown in Fig. 2, although these algorithms use the pinball loss function, for the Pin-SGTBSVM and Pin-SGTWSVM algorithms, when the parameters take different values, there exist certain impacts on the classification accuracy; for the Pin-GTBSVM and Pin-GTWSVM algorithms, the influence of the parameter values on the classification accuracy is small.

Fig. 2
figure 2

Influence of different parameter values on the algorithms, (a) CMC, (b) Ionosphere, (c) German, (d) WPBC, (e) Haberman, (f) Live-disorders

Full size image

Moreover, Gaussian characteristic noise with mean value 0 and variance σ2 are added to the selected UCI datasets according to the ratio r = 5% and 10% to test the noise sensitivity of the algorithms, and σ2 is obtained as the variance of different features multiplied by the ratio r. The experimental results are shown in Table 2, where Acc and sd are the accuracy (%) and standard deviation, respectively. When the noise ratio is 5%, the proposed algorithm achieves the best classification performance on five of the seven datasets. However, its classification performance on the German dataset is worse than the TWSVM algorithm but better than that of the TBSVM algorithm. A similar conclusion can be reached when the noise ratio is 10%.

Table 2 Performance of different algorithms on datasets with noise
Full size table

To further validate the anti-noise performance of the proposed algorithm, the real-world dataset Waveform (with noise) from UCI is selected for the experiment. It includes Waveform (v1) and Waveform (v2). The number of samples is 5000, where each contains 21(v1) or 40(v2) features that take real numbers and belong to three categories. For the Waveform (v1) dataset, Gaussian noise is added to each feature with a mean of 0 and variance of 1. For the Waveform (v2) dataset, 19 features of Gaussian noise with a mean of 0 and variance of 1 are added to the Waveform (v1) dataset. As the dataset is a triple-class problem, two categories of samples are taken from the dataset each time, and ten experiments are averaged in three combinations. The experimental results are shown in Table 3.

Table 3 Classification performance of different algorithms on Waveform datasets with noise
Full size table

From Table 3, it can be seen that the proposed algorithms achieve the best classification performance on both the Waveform (v1) and Waveform (v2) datasets. It is worth mentioning that these algorithms take much different amounts of time to classify the datasets. For the proposed algorithm and the Pin-SGTWSVM algorithm using the iterative technique, on the two datasets, the time spent is 28.4918 s / 31.0971 s, and 35.8810 s / 35.0951 s, respectively. The main reason for this is that the proposed algorithm solves linear equations instead of solving the quadratic programming problems.

5.2 Friedman test

In the following, we mainly use the Friedman test to evaluate the classification performance of the proposed Pin-SGTBSVM algorithm on the UCI datasets. The Friedman test is a statistical test method, and it is a nonparametric test method that uses ranks to determine whether there are significant differences between multiple population distributions. This method can make full use of the information in the samples and is suitable for comparisons of different classifiers on many datasets.

First, the null hypothesis and the opposite hypothesis are given:

  • H0: There is no significant difference among the 6 classifiers;

  • H1: There are significant differences among the 6 classifiers.

We discuss k classifiers (k = 6) on N datasets (N = 7) for comparison purposes. The corresponding classifiers are sorted according to their accuracy on each dataset, and the classifier corresponding to the highest accuracy has the smallest rank ri. Table 4 shows the average ranks of different algorithms on the UCI datasets.

Table 4 Average ranks of different algorithms on UCI datasets
Full size table

In the Friedman test, the chi-square distribution is

$$ {\chi}_F^2=\frac{12N}{k\left(k+1\right)}\left[\sum \limits_{j=1}^k{R}_j^2-\frac{k{\left(k+1\right)}^2}{4}\right], $$

where \( {R}_j=\frac{1}{N}\sum \limits_{i=1}^N{r}_i \). Its degree of freedom is (k-1). In addition, on the basis of the Friedman test, the F distribution is further used for testing, where the F distribution is

$$ {F}_F=\frac{\left(N-1\right){\chi}_F^2}{N\left(k-1\right)-{\chi}_F^2}. $$

And its degrees of freedom are (k-1) and (k-1) × (N-1). According to the data in Table 4, we obtain \( {\chi}_F^2=16.8556 \) and FF = 5.5739. After looking up the table, we know that the critical value of F(5,30) at the confidence level of 0.05 is 2.53, and 5.5739 > 2.53, so the null hypothesis H0 is rejected. That is, there are significant differences among the 6 classifiers. The classification performance of Pin-SGTBSVM algorithm on the above 7 datasets is better than those of the other five algorithms.

According to the same method, the corresponding average ranks are calculated by using the classification results with different noise ratios from Table 2, as shown in Table 5.

Table 5 Average ranks of different algorithms on UCI datasets with noise
Full size table

In the same way, two sets of null hypotheses and opposite hypotheses are given as follows:

  • H0(r = 0.05): There is no significant difference among the 6 classifiers on the datasets with 5% noise added;

  • H1(r = 0.05): There are significant differences among the 6 classifiers on the datasets with 5% noise added.

  • H0(r = 0.1): There is no significant difference among the 6 classifiers on the datasets with 10% noise added;

  • H1(r = 0.1): There are significant differences among the 6 classifiers on the datasets with 10% noise added.

The test values are calculated according to Table 5 as follows: \( {\chi}_{F\left(r=0.05\right)}^2=14.2857 \), FF(r = 0.05) = 4.1379, \( {\chi}_{F\left(r=0.1\right)}^2=15.5886 \), FF(r = 0.1) = 4.8184. Since the test values 4.1379 and 4.8184 at both noise levels are greater than 2.53, the H0 (r = 0.05) and H0 (r = 0.1) hypotheses are rejected. That is, there are significant differences among the 6 classifiers. The classification performance of Pin-SGTBSVM on the selected datasets with different noise is better than those of the other five algorithms.

In addition, we compare the proposed Pin-SGTBSVM and Pin-SGTWSVM algorithms with the TWSVM, TBSVM, Pin-GTWSVM, and Pin-GTBSVM algorithms on 7 datasets, as shown in Fig. 3. It can be seen that the algorithms using the iterative method perform significantly better on 6 noise-free datasets and 5 datasets with noise, where r = 0, 0.05 and 0.1 represent no noise, the 5% noise ratio and the 10% noise ratio, respectively.

Fig. 3
figure 3

Comparisons of different algorithms on 7 datasets

Full size image

5.3 Artificial datasets

In this section, six algorithms are tested on two datasets Art1 and Halfmoons [27]. The samples of each class follow a Gaussian distribution. Each class consists of two clusters, each cluster contains 100 samples, where positive samples xi(yi = 1, i = 1, 2, …, 100)~N(μ1, Σ1), xi(yi = 1, i = 101,102, …, 200)~N(μ2, Σ1), and negative samples xj(yj =  − 1, j = 1, 2, …, 100)~N(μ3, Σ2), xj(yj =  − 1, j = 101,102, …, 200)~N(μ4, Σ2). Among them, μ1 = [5, 1], μ2 = [1, 0], μ3 = [0, 5], μ4 = [4, 7], Σ1 = [0.5, 0; 0, 4], Σ2 = [1, 0; 0, 1]. The two types of samples in the Halfmoons dataset consist of two half months, and each half month contains 250 samples. The experimental results are shown in Fig. 4. It can be seen that the computational time of the algorithms that use the iterative method is lower on both datasets than those of the other algorithms for the linear case.

Fig. 4
figure 4

Performance of different algorithms with linear kernel on artificial datasets

Full size image

At the same time, we also add 5% and 10% Gaussian characteristic noise to the above two datasets, respectively. The experimental results are shown in Fig. 5. It can be seen that the accuracy of the proposed algorithm on both datasets is higher than those of the other five algorithms.

Fig. 5
figure 5

Performance of different algorithms with Gaussian kernel on artificial datasets, (a) Art1, (b) Halfmoons

Full size image

5.4 NDC datasets

To further study the classification performance of the proposed algorithm on large-scale datasets, experiments are carried out on the NDC [33] datasets, and 5% characteristic noise is added to the generated datasets. Detailed information about the datasets is shown in Table 6. The experimental results are shown in Fig. 6.

Table 6 Information about the NDC datasets
Full size table
Fig. 6
figure 6

Classification performance of different algorithms on the NDC datasets, a Noise free, b With noise

Full size image

It can be seen that the Pin-SGTBSVM algorithm has higher classification accuracy on the NDC datasets than those of the other five algorithms. At the same time, we also analyze the execution time of the algorithms. Experiments show that the running time of the Pin-SGTBSVM and Pin-SGTWSVM algorithms become much lower than those of the other four algorithms as the sizes of the NDC datasets continues to grow. Their time complexity is better than that of the algorithms without using the iterative method, for which the execution time of the Pin-SGTBSVM algorithm is slightly lower than that of the Pin-SGTWSVM algorithm. To clarify the comparison of the time consumed by the six algorithms on the NDC datasets, the logarithms of the execution time for the six algorithms are calculated here, and the experimental results are shown in Fig. 7.

Fig. 7
figure 7

Comparisons of time performance of different algorithms on NDC datasets, a Noise free b With noise

Full size image

5.5 Toy dataset

In this subsection, we discuss a smooth twin bounded support vector machine model with approximate pinball loss ϕτ(u, α) and pτ(u, α). The corresponding algorithms using the function pτ(u, α) are denoted as Pin-PSGTWSVM (α = 5), Pin-PSGTWSVM (α = 1000), Pin-PSGTBSVM (α = 5), and Pin-PSGTBSVM (α = 1000). In the following, experiments are carried out on the toy dataset (named “crossplane”), which is seen in Fig. 8, and the experimental results are shown in Table 7.

Fig. 8
figure 8

Toy dataset

Full size image
Table 7 Comparison of performance achieved by different algorithms
Full size table

From Table 7, it can be seen that the accuracy of the Pin-SGTBSVM algorithm is the highest in the linear case, followed by Pin-PSGTWSVM (α = 5). In the nonlinear case, the accuracy rates of the Pin-SGTBSVM and Pin-SGTWSVM algorithms are higher than those of the other algorithms. The experimental results show that ϕτ(u, α) is better than pτ(u, α).

6 Conclusion

Aiming at the shortcomings of the twin support vector machine, we introduce the pinball loss function into the twin bounded support vector machine. By constructing a smooth approximation function, a smooth twin bounded support vector machine model with pinball loss is obtained. On this basis, a twin bounded support vector machine algorithm with pinball loss is proposed, and the convergence of the algorithm is theoretically proven. We compare the proposed algorithms with other representative algorithms on the UCI datasets and artificial datasets. Under the premise of ensuring the accuracy, the defects of the twin support vector machine with regard to noise sensitivity and resampling instability are solved, and the time complexity is improved as well, thereby demonstrating the effectiveness of the proposed algorithm.