Symmetries and configurations of hydraulic fracturing electromagnetic monitoring: a 2D anisotropic approach

Abstract

A simulation was performed of the electromagnetic fields response to different unconventional reservoir scenarios and transmitter to receiver configuration, including strong anisotropy, combination of anisotropies and geometries, and larger monitoring times than conventional ones. The approximate solution of the anisotropic Maxwell equations was obtained using a mixed finite element method, discretized in space through the Nédélec spaces, combined with a leapfrog time stepping procedure. The results indicate: first, the signals have a long period; second, the magnetic field is the most sensitive field when discriminating different types of anisotropy for all receiver positions, the horizontal electric field does in the top and above the anisotropic layer and the vertical electric field does inside it; third, in both stratified and fractured medium the vertical electric field have higher total amplitudes inside the layer, the magnetic field in the top and inside it, and the horizontal electric field does in the top and above it, so, a receiver in the top of the formation could be advantageous; fourth, independently of the symmetry, the horizontal electric field is one order of magnitude higher than the vertical electric field above the anisotropic layer and this relation changes inside the layer; fifth, the conservation of currents in combination of anisotropies is preserved. Finally, in a horizontal well hydraulically fractured, the relative percent difference of the vertical electric field is higher than the other fields, but this relation can change when moving to other geometries like a T-shape fracture where the three fields have closer relative differences.

1 Highlights

• Hydraulic fracturing monitoring with electromagnetics is crucial for stimulated reservoir volume determination. This study analyzes the EM response when strong anisotropy, combination of anisotropies, geometries, and larger time than conventional monitoring are considered.

• Surface to surface configuration is not as meaningful as the surface to borehole configuration to discriminate the type of anisotropy and the percentage of relative difference of the fields.

• Independently of the symmetry, the horizontal electric field is one order of magnitude higher than the vertical electric field above the anisotropic layer and this relation changes inside the layer.

• The magnetic field is the most sensitive field when discriminating different types of anisotropy for all receiver positions, the horizontal electric field does in the top and above the anisotropic layer and the vertical electric field does inside it. In both stratified and fractured medium the vertical electric field have higher total amplitude inside the layer, the magnetic field in the top and inside it whereas the horizontal electric field does in the top and above it, so, a receiver in the top of the formation could be advantageous.

2 Introduction

Characterizing different geological scenarios in unconventional reservoirs and monitoring the evolution of the hydraulic fracturing geometry are very important for the engineering diagnosis of the effectiveness of the completion, for the well placement strategy and for the geoscientific understanding of the reservoir. Although the microseismic technology is a useful tool that contributes to the geological knowledge of the fault systems, of the natural fractures, of the connectivity between wells and of geomechanics, reliable location of microseismic events depends on several factors, hypotheses and constraints related to the acquisition design, processing and interpretation, that many times are not satisfied, originating significant economic repercussions (Taylor and Curcio 2014).

One of the most critical points is the determination of the stimulated reservoir volume (SRV): not only these uncertainties influence its calculation, but also the determination does not identify the type of rock movement or geomechanical deformation that created it; therefore, valuable information regarding the hydraulic fracture area and the fracking conductivity is lost (Cipolla and Wallace 2014; Zimmer 2011). There are several case studies in which the microseismic technique fails to determine the proppant location (Cipolla and Wallace 2014; Taylor and Curcio 2014; Zimmer 2011), and it is here where electromagnetic (EM) techniques might play an important role (Curcio and Macias 2019; Strack and Aziz 2012; Wirianto 2012). During the hydraulic fracturing procedure the formation changes from hydrocarbon saturated to water saturated, due to the abrupt fluid flow at high pressures and discharges, which in turn induces an electrical conductivity anomaly that is space-time dependent. The idea of monitoring the fluid flow with electromagnetics for waterflooding purposes is technologically viable and the numerical aspects of fluid flow of a single or multiphase fluid in a porous medium with anisotropic permeability is well understood (Jacovkis et al. 1999; Savioli and Bidner 2005).

Recently, in Curcio and Macias (2019), a description of the state of the art in hydraulic fracturing applications was carried out, highlighting a microseismic and magnetotellurics (MT) monitoring of shale gas (Rees et al. 2016); MT applied to monitoring of hydraulic fracturing of enhanced geothermal systems (EGS) and hydrocarbon gas (Peacock et al. 2013); CSEM monitoring of reservoir oil saturation and CO₂-sequestration scenario (Thiel 2017) and a shale fracking monitoring using Depth to Surface (DSR) configuration (Nieuwenhuis et al. 2016). In all cases, although both academia and industry uses proven microseismic algorithms and modeling codes based on static and isotropic Maxwell equations, a dynamic model which joins electromagnetic and elasticity needed to be explored. In consequence, in Curcio and Macias (2019), it was constructed a dynamic concept that joined CSEM with seismic modeling, including VTI anisotropy caused by differences in horizontal and vertical permeability which provides three added values to conventional technology: first, the numerical experiment comprises the time-space evolution of pressure, saturation, electric field, magnetic field, electrical current and electrical resistivity and, although all of them present a geometric correlation, from a given time the saturation and the consequent electric and magnetic fields grow less than the pressure anomaly; that could be a useful tool for real time fracking rescheduling purposes. Second, the distribution pattern of the electric field is correlated with the electrical current distribution, whereas the distribution pattern of the magnetic field has a better correlation with the water saturation than the electric field. Third, the SRV calculated from pressure maps (or their corresponding SRV from microseismic cloud) is different from the SRV calculated from the electric and magnetic anomalies, the second one being a direct indicator of conductive fluid saturation, effective connectivity, and proppant location. Thus, the EM monitoring of hydraulic fracturing might be useful to determine the fracture geometry, the well production calculations, or the reservoir development optimization (for instance, when planning in-fill wells). With these results in mind, the next step is to study the sensitivity of the fields to the different geological scenarios, symmetries and receiver–transmitter configurations and also to provide some tools for their evaluation.

There are some CSEM modeling applied to unconventional scenarios like the presented by Kumar and Hoversten (2012) who analyzed the E_x response from a 1D isotropic shale, T_x source and monitoring from 0.01 to 1 s. Davydycheva et al (2017) modeled a waterflooding scenario in 2D VTI anisotropic layers, T_x source, reporting only the E_z response; also, she presented a flooding simulation in an unconventional shale scenario through a 3D VTI modeling (T_x source and borehole receivers and showing the E_z dB_y/dt and dB_x/dt responses). In both cases, the weak anisotropy were estimated form well logs and the monitoring window time was less than 1 s.

Although these T_x CSEM applications studied the EM response in unconventional shales, a vertical fractures scenario (i.e., HTI anisotropy) and the EM response to combination of symmetries (i.e., VTI and HTI) are not provided; also, in the current study a strong anisotropy is considered when a resistive shale is hydraulically fractured by a conductive fracturing fluid. In addition, it is presented the time-evolution of a 2D map, which is more meaningful than a set of isolated receivers. Also, it was found that after 1 s the EM response could be monitored having valuable information.

In a simple model the geometry of the hydraulic fracture can be either a horizontal fracture, which corresponds to a vertical well, or can be a vertical fracture, which corresponds to a horizontal well. Other symmetries like tilted and T-shape are inspected. Note that although a tilted fracture shall be of interest, there are some special cases more suitable for unconventional shales like T-shape geometries, originated by the interaction of the rock hydraulically fractured with natural fractures in the formation (Aguilera 2018; Maxwell 2014). Although it is possible to model both cases, a T-shape geometry and Dog-leg geometry are more precise in the current approach since the elements are rectangular elements of the partition.

In this approach, only interest to study the EM response to an anisotropic formation that is hydraulically fractured, independently from other effects and noise that in practice could be removed, like steel-casing effects (Orujov et al. 2020). However, to evaluate its application it is important to estimate how strong could be the casing effect that, in practice can mask the signal and/or enhance the signal (Hickey 2019). Heagy and Oldenbourg (2018) provided a rigorous analysis of the EM casing effect of one vertical well (200 m length and casing electrical resistivity of 10⁶ to 10⁷ S/m) in background sediments (30 Ω m). They concluded the following: first, the radial electric field decay in time for different distances to the well (from 5 to 300 m) was compared with Commer et al. (2015) and Haber et al. (2016), showing that after 6 × 10^–2 s the EM field response in time is the same for all offsets (below 10^–7 V/m) and, from time 9 × 10^–1 s, the signal is lower than 10^–8 V/m. Second, for a short well approximation where a short well is defined by α x L_c ≪ 1, (L_c is the casing length; α² = 1/(S.T); S the transversal conductance and T the transversal resistance) the electrical current decrease linearly with distance and the behavior of the currents is independent of conductivity. In a short well approximation, when the relation depth/casing length is around 0.9 (that corresponds to the numerical examples in this study) predicts, according to Figure 6 in Heagy and Oldenbourg (2018) an induced current of 0.1 A. When the relation depth/casing is close to 1, the induced current is close to zero Ampere. Third, they examine the behaviour of electric currents in an experiment where the 1 km casing length is used as an “extended electrode”, step-off source, showing that after 5 milliseconds the induced current is negligible. Fourth, the authors conclude that for a conductive and permeable vertical casing, excited by a circular current source, there is a complicated magnetic field that occurs in the top few centimeters of the pipe.

Orujov et al. (2020) studied the effect of well casings in surface-to surface time-lapse EM of a single steel-cased well and multiple cased wells in time lapse experiments, showing that it is possible to subtract the baseline from monitor data, removing the effect of infrastructure allowing the detection of subtle time lapse fluid changes in a reservoir. Also, they concluded that although the receivers located near the casing (< 100 m) the electric fields induced by the casing are comparable with the electric fields induced by the source (with amplitudes of 10^–10 V/m to 10^–11 V/m), the casing effect is significantly smaller than a single casing effect.

In addition, regarding the level of ambient noise that CSEM must overcome to be detectable there are some preliminary studies to consider (Strack 2020). Nieuwenhuis et al. (2016) modeled different fracturing geometries at 2300 m depth and collected signals with Depth to Surface (DSR) method, reporting a total Electric field of 4 × 10⁻¹⁰ V/m to 9 × 10⁻¹⁰ V/m. Hickey (2019) reported a noise dependent on casing length, depth, source receiver geometry, and host conductivity of the E_x field amplitude of around 2 × 10^–8 V/m at a location near the transmitter, configuration SS, target at approximately 3000 m. With no casing, the E_x reported, SS configuration is around 2.2 × 10^–10 V/m.

In consequence, the theoretical and practical noise that could be induced by the steel-casing, and other noise allows to perform a numerical study focusing only in the EM response to the anisotropic formation hydraulically fractured.

3 The electromagnetic continuous model and the variational formulation

Consider the fields E measured in V/m and H measured in A/m (1.25 × 10^–6 T), which denote the electric and magnetic fields, respectively, and the external current J measured in A/m². Maxwell's equations in the diffusive range (i.e., εω² ≪ σω), are

$$\sigma \vec E - \nabla x\vec H = \vec J,$$

(1)

$$\nabla \times \vec E + \mu \frac{\partial \vec H}{{\partial t}}\; = 0.$$

(2)

The magnetic permeability $\mu$ is measured in H/m and the tensor $\underline{\underline \sigma }$, measured in S/m, is the anisotropic electrical conductivity 2D tensor

$$\underline{\underline \sigma } = \left[ {\begin{array}{*{20}{c}} {{\sigma_{xx}}}&{{\sigma_{xz}}} \\ {{\sigma_{zx}}}&{{\sigma_{zz}}} \end{array}} \right]$$

(3)

Consider the polarization mode that involves the field components (E_x, 0, E_z) and (0, H_y, 0). Thus, in this case Eq. (1) becomes:

$$\left( {{\sigma_{xx}}{E_x} + {\sigma_{xz}}{E_z},{\sigma_{zx}}{E_x} + {\sigma_{zz}}{E_z}} \right) - \left( { - \frac{{\partial {H_y}}}{\partial z},\frac{{\partial {H_y}}}{\partial x}} \right) = \left( {{J_x},{J_z}} \right),$$

(4)

which expressed in principal axis for each component becomes

$${\sigma_{xx}}{E_x} + \frac{{\partial {H_y}}}{\partial z} = {J_x},$$

(5)

$${\sigma_{zz}}{E_z} - \frac{{\partial {H_y}}}{\partial x} = {J_z}.$$

(6)

The symmetry of the system is defined by tensor $\underline{\underline \sigma }$ and, for simplicity, we shall write ${\sigma_{xx}}$ = ${\sigma_x}$ and ${\sigma_{zz}}$ = ${\sigma_z}$. In a geologically plausible 2D model, a vertical isotropic transverse (VTI) symmetry comprises a system such that ${\sigma_z}$ < ${\sigma_x}$, which might be identified with a layer-cake model. A 2D horizontal isotropic transverse (HTI) symmetry comprises a system such that ${\sigma_z}$ > ${\sigma_x}$ which might be identified with a vertical fractures model.

In consequence, in this case Maxwell Eqs. (5), (6) and (2) become respectively

$${\sigma_x}{E_x} + \frac{{\partial {H_y}}}{\partial z} = {J_x}$$

(7)

$${\sigma_z}{E_z} - \frac{{\partial {H_y}}}{\partial x} = {J_z}$$

(8)

$$\frac{{\partial {E_x}}}{\partial z} - \frac{{\partial {E_z}}}{\partial x} + \mu \frac{{\partial {H_y}}}{\partial t} = 0.$$

(9)

The following vanishing conductivity boundary condition was imposed

$$E \cdot \tau = 0$$

(10)

In a 2D tilted transverse isotropy (TTI), the conductivity tensor is diagonal in a system aligned with the lamination or beds and is obtained using the rotation matrix R from the principal coordinates to the coordinates aligned with the horizontal and vertical directions

$${\underline{\underline \sigma }^{TTI}} = {R^T}.\left[ {\begin{array}{*{20}{c}} {{\sigma_{xx}}}&{{\sigma_{xz}}} \\ {{\sigma_{zx}}}&{{\sigma_{zz}}} \end{array}} \right].R,$$

(11)

$$R = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - sen\theta } \\ {sen\theta }&{\cos \theta } \end{array}} \right]$$

(12)

where R is the rotation matrix and θ is the angle between the bed or lamination strike and the horizontal axis.

The model is assumed such that variations in the magnetic permeability of rocks are negligible compared with variations in the bulk rock conductivities (Simpson and Bahr 2005), in which the physical quantities $\mu$ and ${\sigma_{ij}}$ are bounded from below and from above by positive constants, i.e.,

$$0 < {\sigma_*} < \sigma < {\sigma^*} < \infty ;0 < {\mu_*} < \mu < {\mu^*} < \infty .$$

(13)

In particular in this model the magnetic permeability is considered isotropic and homogeneous. In addition, this 2D approach could have a source of imprecision in presence of 3D geometries in subsurface, such as a fold thrust belts geology (Meju 2018).

In order to define a mixed variational formulation for 7, 8 and 9, let us introduce some notation. For $\Omega \subset {R^d}$ with boundary $\partial \Omega$, let $\left( {.,.} \right)$ and $\left\langle {.,.} \right\rangle$ denote the complex L²($\Omega$) and L²($\partial \Omega$) inner products for scalar, vector, or matrix valued functions. For all nonnegative integers $s \in R$, ${\left\| . \right\|_{s,\Omega }}$ will denote the usual norm in the Sobolev space ${H^s}\left( \Omega \right)$ with its associated inner products on $\Omega$ and $\partial \Omega$. In this space and following Santos et al. (2012), for a scalar $\varphi$ and a vector $\overrightarrow \psi = \left( {{\psi_x},{\psi_z}} \right)$ this approach uses the notation

$$curl\left( \varphi \right) = - \left( {\frac{\partial \varphi }{{\partial z}} - \frac{\partial \varphi }{{\partial x}}} \right)$$

(14)

$$curl\left( {\overrightarrow \psi } \right) = - \left( {\frac{\partial \overrightarrow \psi }{{\partial z}} - \frac{\partial \overrightarrow \psi }{{\partial x}}} \right)$$

(15)

to perform the continuous time variational mixed finite element formulation.

4 The continuous time variational mixed finite element formulation.

Let ${\tau^h}$ be a quasi regular partition of $\Omega$ into non-overlapping rectangles ${\Omega_j}$ of diameter bounded by h. To approximate the EM fields $\left( {\vec E\left( t \right),{H_y}\left( t \right)} \right)$ the mixed finite element (FE) Nédélec space ${V^h}x{W^h}$ defined by Nédélec (1986) was used:

$${V^h} = \left\{ {\overrightarrow \psi \in H\left( {curl,\Omega } \right):\psi {|_{\Omega_j}} \in {V^h} \equiv {P_{0,1}}\left( {\Omega_j} \right)x{P_{1,0}}\left( {\Omega_j} \right)} \right\},$$

(16)

$${W^h} = \left\{ {\varphi \in \left( {{L^2}\left( \Omega \right)} \right):\varphi {|_{\Omega_j}} \in {W^h} \equiv {P_0}\left( {\Omega_j} \right)} \right\}.$$

(17)

here ${P_{s,t}}$ indicates the polynomials of degree not greater than s in x and not greater than t in z. Also, ${P_0}({\Omega_j})$ denotes the piecewise constant functions on ${\Omega_j}$.

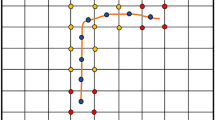
The local degrees of freedom associated with the space ${V^h}x{W^h}$ on any rectangular element ${\Omega_j}$ of the partition ${\tau^h}$ are the values of ${\vec E^h}$ at the midpoints of the sides of ${\Omega_j}$ and the values of $H_y^h$ at the center of ${\Omega_j}$ (Fig. 1). The mixed finite element continuous time formulation of Maxwell Eqs. (1) and (2) is: find $\left( {{{\vec E}^h}\left( t \right),H_y^h(t)} \right) \in {V^h}x{W^h}$ such that

$$\left( {\underline{\underline \sigma } {{\vec E}^h}\left( t \right),\overrightarrow \psi } \right) - \left( {{{\overrightarrow H }^h}\left( t \right),curl\left( {\overrightarrow \psi } \right)} \right) = \left( {\overrightarrow J ,\overrightarrow \psi } \right), \quad \overrightarrow \psi \in {V^h},$$

(18)

$$\left( {curl{{\vec E}^h}\left( t \right),\varphi } \right) + \left( {\mu \frac{{\partial {{\overrightarrow H }^h}\left( t \right)}}{\partial t},\varphi } \right) = 0, \quad \varphi \in {W^h}.$$

(19)

Fig. 1

Distribution of the electric and magnetic fields under the Nédélec scheme

This choice of mixed FE spaces is of particular interest since Nedelec (1980) has demonstrated that for a finite element space V^h to be a subspace of H(curl, Ω) it suffices that the functions in V^h have continuous tangential component across the edge in the mesh and the element is a H (curl; Ω) conforming element. So, applied to the electromagnetic problem, the FE spaces allows the electric conductivity be discontinuous, as opposed to methods based on standard continuous piecewise-linear elements.

Monk (1992) indicated that another interesting property is that, since the magnetic field is piecewise-constant in $\Omega$ and $\mu$ is constant, the magnetic field equation is satisfied exactly and also provides the numerical error of the mixed FE method. The mixed FE procedure used here is most accurate and has greater stability than other numerical methods, in particular in cases of greater grid anisotropy; in addition, note that other methods, like that of Lee and Mandsen, may be preferable to the Nédélec method when perfectly conducting boundary conditions are used (Lee and Madsen 1990; Nédélec 1986; Monk 1992).

4.1 Leapfrog time stepping

The time dependent Maxwell equations have several difficulties related to the imposition of boundary conditions. Yee (1966) introduced the idea of solving Maxwell equations using a finite difference leapfrog time stepping scheme and imposing the appropriate boundary conditions for a perfect conductor. He showed that with an appropriate choice of the spatial points at which the various field components are to be evaluated, the finite difference equations can be solved with the solution satisfying the boundary conditions. The present approach takes this idea by using a leapfrog time stepping where the electric fields are calculated at whole time steps while the magnetic fields are calculated at half time steps:

$$\overrightarrow E \cong \frac{{{{\vec E}^{h,n + 1}} + {{\vec E}^{h,n}}}}{2},$$

(20)

$${H_y} \cong H_y^{^{h,n + \frac{1}{2}}},$$

(21)

$$\frac{{\partial {H_y}}}{\partial t} \cong \frac{{H_y^{h,n + \frac{3}{2}} - H_y^{h,n + \frac{1}{2}}}}{\Delta t}.$$

(22)

In consequence, Maxwell equations are discretized in space and time and the problem is now reduced to find $\left( {{{\vec E}^{h,n + 1}},H_y^{h,n + \frac{3}{2}}} \right) \in {V^h}x{W^h}$ such that

$$\left( {\frac{{{{\underline{\underline \sigma } }^{h,n}}}}{2}{{\vec E}^{h,n + 1}},\overrightarrow \psi } \right) = - \left( {\frac{{{{\underline{\underline \sigma } }^{h,n}}}}{2}{{\vec E}^{h,n}},\overrightarrow \psi } \right) - \left( {H_y^{h,n + \frac{1}{2}},curl\left( {\overrightarrow \psi } \right)} \right) + \left( {{{\overrightarrow J }^{h,n}},\overrightarrow \psi } \right),\quad \overrightarrow \psi \in {V^h},$$

(23)

$$\left( {\frac{\mu }{\Delta t}H_y^{h,n + \frac{3}{2}},\varphi } \right) = \left( {\frac{\mu }{\Delta t}H_y^{h,n + \frac{1}{2}},\varphi } \right) - \left( {curl\left( {\frac{{{{\vec E}^{h,n + 1}} + {{\vec E}^{h,n}}}}{2}} \right),\varphi } \right),\quad \varphi \in {W^h}.$$

(24)

and the electrical current at each time step is updated through Ohm's law:

$${\overrightarrow J^{h,n}} = {\underline{\underline \sigma }^{^{h,n}}}{\vec E^{h,n}}.$$

(25)

The fully discrete sequence is first solved for the electric field using pre-conditioned conjugate gradients iteration (PCGI) (Hestenes and Stiefel 1952), and then for the magnetic field: Given ${\vec E^0}$ and $H_y^\frac{1}{2}$, calculate ${\vec E^{n + 1}}$ from (23). Then, use ${\vec E^{n + 1}}$ and (24) to determine $H_y^{n + \frac{3}{2}}$. Finally, update the electrical current using (25), go to (23) and restart.

In this Leapfrog-FE method, the matrix associated to the ratio μ/∆t is diagonal and easily inverted; also, although (23) is solved by conjugate gradients, on a regular grid it is not necessary. In addition, the number of conjugate gradient iterations per step for the preconditioned matrix is usually less than other methods which are analyzed in Monk (1992).

Regarding the leapfrog time stepping used to solve Maxwell equations, there are some interesting approaches like the presented by Mahalov and Moustaoui (2016) and Räbinä (2014). In the first case, it was provided a staggered leapfrog-type iteration and stability analysis whereas in the second case it was presented an algorithm based in a leapfrog time stepping scheme with unstaggered temporal grids; both cases also performs a stability analysis. However, they solve the electromagnetic wave problem.

For the diffusive problem (i.e., when the displacement currents are neglected), the bounds in (13) allowed us (Curcio and Macias 2019) to perform a stability analysis of the leapfrog mixed FE procedure that is extended to the anisotropic case which condition $\Delta t$ that satisfies the relation

$$\frac{\Delta t}{{\mu_*}}\frac{{\sigma^*}}{{\sigma_*}}{C^2}{h^{ - 2}} \leqslant \frac{{\sigma_*}}{4}$$

(26)

drives to the stability result

$$\frac{{\sigma_*}}{2}\sum\limits_{n = 0}^N {\left\| {\frac{{{{\vec E}^{n + 1}} + {{\vec E}^n}}}{2}} \right\|_0^2} \Delta t + \frac{1}{2}\left( {\mu H_y^{N + \frac{3}{2}},H_y^{N + \frac{3}{2}}} \right) \leqslant C\sum\limits_{n = 0}^N {\left\| {{{\overrightarrow J }^{n + \frac{1}{2}}}} \right\|}_0^2\Delta t + \frac{1}{2}\left( {\mu H_y^\frac{1}{2},H_y^\frac{1}{2}} \right),$$

(27)

where C is a positive constant.

5 Numerical examples

The EM anisotropic response was modeled for a 2D section whose dimensions are 200 m in x (lateral direction) and 200 m in z (depth) for different configurations of transmitter–receivers and geometries. The elemental cell has a 5 m x length and a 5 m z depth.

The configuration of the acquisition is the receiver to transmitter layout: surface to borehole (SB) means transmitter in surface and receivers in borehole whereas surface to surface (SS) means transmitter in surface and receivers in surface or very near the surface.

The step-off source in x direction, called T_x, is located at coordinates x = 0 m and z = 10 m and has an electrical current of 25 A/m². The receivers R1 to R6 are sensitive to the electric field in direction x, to the electric field in direction z and to the magnetic field in direction y, so that each one of those receivers has three fields associated with it. Figure 2 shows the layout of the numerical examples, where the circles are the receivers located in the background formation (SB, R1 in red at x = 190 m and z = 120 m), in the top of the formation (SB, R2 in yellow at x = 190 m and z = 100 m) and inside the formation (SB, R3 in violet at x = 190 m and z = 80 m) while the rectangles are near surface receivers buried at a depth of 10 m, which are R4 (SS, red), R5 (SS, yellow) and R6 (SS, violet), located at z = 190 m and x = 140 m, x = 160 m, x = 180 m, respectively. Note that the configuration near the surface improves the signal because it avoids the effect due to the currents in the limit sediments-air. The meaningful information that this simulation can provide for a given configuration and plausible scenarios will be analyzed; in particular the following cases where $\rho$ is the isotropic electrical resistivity, ${\rho_x}$ is the horizontal electrical resistivity and ${\rho_z}$ is the vertical electrical resistivity (Fig. 2):

• Case 1: Anisotropic VTI resistive layer embedded in an isotropic background, transmitter in surface, borehole receivers (SB). The background resistivity has 20 Ω m; the anomaly is a 50 m height VTI layer located between z = 50 m and z = 100 m, which has a horizontal resistivity of ${\rho_x}$ = 100 Ω m and a vertical resistivity of ${\rho_z}$ = 200 Ω m. This case might be identified with a resistive shale reservoir embedded in sediments.

• Case 2: Anisotropic VTI resistive layer embedded in an isotropic background, transmitter in surface, near surface receivers (SS). The description is the same as in 1, but the configuration is SS.

• Case 3: Anisotropic HTI resistive layer embedded in an isotropic background, transmitter in surface, borehole receivers (SB). The background resistivity is 20 Ω m; the anomaly is a 50 m height HTI layer located between z = 50 m and z = 100 m, which has a horizontal resistivity of ${\rho_x}$ = 200 Ω m and a vertical resistivity of ${\rho_z}$ = 100 Ω m. This case can be identified with a resistive fractured reservoir embedded in sediments and the objective now is to analyze the EM response when the ${\rho_x}$ and ${\rho_z}$ values are inverted with respect to those of case 1.

• Case 4: Anisotropic HTI resistive layer embedded in an isotropic background, transmitter in surface, near surface receivers (SS). The description is the same as in 3, but the configuration is SS.

• Case 5: Vertical hydraulic fractures (horizontal well). The EM response to 4 vertical fractures was studied, each one of them having ${\rho_x}$ = 3 Ω m and ${\rho_z}$ = 0.5 Ω m, and embedded in a resistive shale with ${\rho_x}$ = 100 Ω m and ${\rho_z}$ = 200 Ω m. The length and size of the shale layer are 160 m in the x direction and 50 m in the z direction, located between z = 50 m and z = 100 m. The geometry of each vertical fracture is 30 m in the x direction and 50 m in the z direction.

• Case 6: T-shape fractures. The EM response to a T-shape fracture embedded in a background of 50 Ω m was simulated. The geobody comprises a horizontal block of 60 m length (from x = 40 m to x = 100 m) and 30 m height (from z = 70 m to z = 100 m) with ${\rho_x}$ = 1 Ω m and ${\rho_z}$ = 4 Ω m; and a vertical block of 20 m length (from x = 100 to x = 120 m) and 70 m height (from z = 50 m to z = 120 m) with ${\rho_x}$ = 4 Ω m and ${\rho_z}$ = 1 Ω m.

• Case 7: Tilted fractures. The EM response to a tilted fracture embedded in a background of 50 Ω m was simulated. The geobody is a horizontal block of 60 me length and 15 m height, rotated 45 degrees, so, this is a 2D TTI model with rotation angle of 45°, with horizontal and vertical resistivities of ${\rho_x}$ = 2 Ω m and ${\rho_z}$ = 20 Ω m respectively.

Fig. 2

Scheme of the different scenarios analyzed. a 2D VTI layer of ${\rho_x}$ = 100 Ω m and ${\rho_z}$ = 200 Ω embedded in isotropic sediments of $\rho$ = 20 Ω m, b 2D HTI layer of ${\rho_x}$ = 200 Ω m and ${\rho_z}$ = 100 Ω embedded in isotropic sediments of $\rho$ = 20 Ω m, c Vertical fractures of ${\rho_x}$ = 3 Ω m and ${\rho_z}$ = 0.5 Ω m embedded in a VTI shale of ${\rho_x}$ = 100 Ω m and ${\rho_z}$ = 200 Ω m and background sediments of $\rho$ = 20 Ω m, d T-shape fracture, horizontal block with ${\rho_x}$ = 1 Ω m and ${\rho_z}$ = 4 Ω m and vertical block with ${\rho_x}$ = 4 Ω m and ${\rho_z}$ = 1 Ω m, e Tilted fracture, ${\rho_x}$ = 2 Ω m and ${\rho_z}$ = 20 Ω m and rotation angle of 45°

The different scenarios might be plausible in any unconventional reservoir hydraulically fractured or not, in particular shallow reservoirs such as Agrio formation (Barrionuevo 2002) and those that due to the hydraulic fracturing operation present considerable anisotropy resultant from the combination of a anisotropic resistive shale and fractures filled with conductive fluid, like the fluid of 0.3 Ω m reported by Rees et al. (2016).

Regarding the configuration, SS or SB, there are two questions to answer: first, which configuration provides more information about the type of symmetry of the target and about the field sensitivity? and second, which configuration encourages collecting higher response signals? To answer the second question it is necessary to determine the relative percent difference of the fields, which is the ratio of the difference between the total field and the background field to the total field × 100, i.e.,

$$\% \frac{{\Delta {E_x}}}{{E{}_x}} = \frac{{E_x^{total} - E_x^{background}}}{{E_x^{total}}} \times 100,$$

(28)

$$\% \frac{{\Delta {E_z}}}{{E{}_z}} = \frac{{E_z^{total} - E_z^{background}}}{{E_z^{total}}} \times 100,$$

(29)

$$\% \frac{{\Delta {H_y}}}{{H_y}} = \frac{{H_y^{total} - H_y^{background}}}{{H_y^{total}}} \times 100,$$

(30)

whereas for the first question in this example the total field response will also be analyzed. In addition, once the most suitable configuration is determined it is important to analyze which fields are the most sensitive to the location of the receivers, to the geometry and to the symmetry.

5.1 Sensitivity of the fields to the configuration.

Let start with question 1. Table 1 shows the ratios $\frac{{E_x^{VTI}}}{{E_x^{HTI}}}$, $\frac{{E_z^{VTI}}}{{E_z^{HTI}}}$, $\frac{{H_y^{VTI}}}{{H_y^{HTI}}}$ and at time t = 10 s for each sensor in SB configuration (R1, R2, and R3 sensors) and SS configuration (R4, R5 and R6 sensors), showing that for this numerical example the SB configuration discriminates better the type of symmetry than the SS configuration. The same conclusion is obtained for times t = 0.025, t = 0.50, t = 0.125, t = 0.250, t = 0.5, t = 1.25, t = 2, 5, t = 15 and t = 20 s.

Table 1 Ratio of the fields E_x, E_z and H_y in VTI symmetry to HTI symmetry at time t = 10 s

Regarding question 2, let us see Figs. 3, 4, 5, 6 and 7 (case 5 to case 7), that present the time evolution of the relative percent difference of each field, $\% \frac{{\Delta {E_x}}}{{E{}_x}}$, $\% \frac{{\Delta {E_z}}}{{E{}_z}}$ and $\% \frac{{\Delta {H_y}}}{{H_y}}$, at times t = 0.025, t = 0.50, t = 0.125, t = 0.250, t = 0.5, t = 1.25, t = 2.5, t = 5, t = 10, t = 15 and t = 20 s after turning off the source for case 5; at times t = 0.025, t = 0.50 and t = 0.125 s after turning off the source for case 6; and at time t = 0.5 s for case 7. The violet color indicates the differences equal or below 2% showing that, in all cases, the SB configuration encourages collecting higher response signals than the SS configuration. This observation is in concordance with Streich (2015) and Davydycheva et al. (2017).

Fig. 3

Case 1 and case 3 field responses, surface to borehole configuration: a $E_z^{VTI}$ field, b $E_x^{VTI}$ field, c $H_y^{VTI}$ field, d $E_z^{HTI}$ field, e $E_x^{HTI}$ field, f $H_y^{HTI}$ field

Fig. 4

Case 2 and case 4 field responses, surface to surface configuration: a $E_z^{VTI}$ field, b $E_x^{VTI}$ field, c $H_y^{VTI}$ field, d $E_z^{HTI}$ field, e $E_x^{HTI}$ field, f $H_y^{HTI}$ field

Fig. 5

Horizontal electric current, J_x, and vertical electric current J_z, for VTI and HTI, surface to borehole configuration: a $J_z^{VTI}$, b $J_x^{VTI}$, c $J_z^{HTI}$, d $J_x^{HTI}$

Fig. 6

Case 5. Maps of the relative percent difference of E_x, $\% \frac{{\Delta {E_x}}}{{E_x}}$, at times 0.025, 0.50, 0.125, 0.250, 0.5, 1.25, 2, 5, 10, 15 and 20 s after turn off the source. Circles represent R1, R2 and R3 borehole receivers and squares represent R4, R5 and R6 receivers. Source in x

Fig. 7

Case 5. Maps of the relative percent difference of E_z, $\% \frac{{\Delta {E_z}}}{{E_z}}$, at times 0.025, 0.50, 0.125, 0.250, 0.5, 1.25, 2, 5, 10, 15 and 20 s after turn off the source. Circles represent R1, R2 and R3 borehole receivers and squares represent R4, R5 and R6 receivers. Source in x

5.2 Sensitivity of fields to the location of the receivers.

Figure 3 corresponds to case 1 versus case 3 and Table 2 presents the fields and electrical current values for each receiver at time t = 10 s. In Fig. 3a, the E_z field shows low amplitudes for the receivers R1 and R2 with values − 1.83 × 10^–7 V/m and − 3.14 × 10^–7 V/m, whereas the receiver R3, located inside the formation, shows an increase of the amplitude to − 3.22 × 10^–6 V/m, that correlates with the highest value of resistivity, that is in ${\rho_z}$. In Fig. 3b, the E_x amplitude in R3 is lower than R2 and R1 with values − 4.50 × 10^–7 V/m, − 6.92 × 10^–6 V/m and − 3.02 × 10^–6 V/m, respectively. In Fig. 3d the E_z values are − 1.39 × 10^–7 V/m, − 2.63 × 10^–7 V/m and − 1.36 × 10^–6 V/m for R1, R2 and R3, respectively, showing that in R3 the E_z field has the highest amplitude in the HTI layer. It may be seen that both in case 1 and case 3, H_y values in R2 and R3, which present the maximum amplitude, are close to each other (Fig. 3c, f).

Table 2 Values of the E_x, E_z and H_y fields and J_x, J_z currents for VTI and HTI symmetries at time t = 10 s

Table 3 shows the ratio $\frac{{E_x}}{{E{}_z}}$ for case 1 and case 3 at time t = 10 s. It may be remarked that, for both VTI and HTI cases, in R1 and R2 the total E_x field is higher than the total E_z field, but in R3, located in the anisotropic resistor, this ratio changes. It may be seen that E_x is one order of magnitude higher than the E_z amplitude; in particular, in R2, in the boundary of the geobody, the difference is the highest, so that the receiver location is very sensitive in a SB configuration.

Table 3 Ratio of the total fields E_x and E_z in VTI symmetry and HTI symmetries at time t = 10 s

Figure 4, which corresponds to case 2 and case 4, shows, for all receivers, distance dependence on the transmitter, where the onset of the arrivals for each field occurs first for the red receiver (R4), then for the yellow one (R5) and then for the violet one (R6). Note that, as expected, the SS configuration for cases 2 and 4 is not sensitive to the horizontal boundary of the geobody. Finally, Table 3 also shows that the SS configuration has practically the same ratio for all receivers (R4, R5 and R6 sensors), which is due to the fact that the anisotropic layer extends over the entire domain.

5.3 Sensitivity of the fields to the symmetry

The results in Table 2 show that, in the SB configuration, all the fields have higher values in the VTI case than in the HTI case, resulting from two effects: current flow and source signature, being the most important the direction in which the diffusive current flows and, to a lesser extent, the signature of the source. The explanation is as follows: in the VTI case, associated with horizontal lamination or stratification, the current within the layer tends to flow horizontally (i.e., in x direction), so that the horizontal electric field E_x will increase the signal, while, in the HTI case, associated with vertical fractures, the electric current tends to flow vertically (i.e., in z direction), so that the vertical electric field E_z will increase the signal in combination with the signature of the source. This is seen in the Table 2 and more clear in Table 3 which shows that although the E_x field is slightly higher than E_z, the E_x/E_z ratios shows that the E_z field effect is much greater in the HTI case than in the VTI case. Figure 5 presents the diffusive current J_x and J_z values for the receivers R1, R2 and R3 showing that J_x in a VTI medium can be two order of magnitude higher than in a HTI medium whereas J_z in HTI and VTI medium have the same order of magnitude.

Let analyze case 5 (Figs. 6, 7, 8). Considering that part of the energy is induced inside and below the hydraulic fracturing geobody and part is induced back to the surface, one can see that back to the surface the $\% \frac{{\Delta {E_x}}}{{E{}_x}}$ is higher than 5% after 5 s; the $\% \frac{{\Delta {E_z}}}{{E{}_z}}$ is higher than 5% later, after 10 s; and $\% \frac{{\Delta {H_y}}}{{H_y}}$ is higher than 5% after 15 s. Also note that, since the whole geobody, composed by 4 vertical fractures embedded in shale reservoir, has a 75 Ω m transversal resistivity and a 3 Ω meters longitudinal resistivity, the whole geobody has a VTI behavior and, in consequence, due to layering the $\% \frac{{\Delta {E_z}}}{{E{}_z}}$ is more sensitive than the other fields.

Fig. 8

Case 5. Maps of the relative percent difference of H_y, $\% \frac{{\Delta {H_y}}}{{H_y}}$, at times 0.025, 0.50, 0.125, 0.250, 0.5,1.25, 2, 5, 10, 15 and 20 s after turn off the source. Circles represent R1, R2 and R3 borehole receivers and squares represent R4, R5 and R6 receivers. Source in x

Comparison with literature shows good correlation with previous modeling. Kumar and Hoversten (2012) modeled the 1D response in an isotropic shale reservoir located at a 3 km depth, finding that the relative difference in E_x field is up to 15% for SS configuration. Davydycheva et al. (2017), who studied a 2 km depth target with VTI weak anisotropy, reported in a near-surface (30 m depth) borehole configuration and sensors located in x, at a 0 to 200 m distance to the waterfront, a 15% maximum change in E_z for near surface receivers and a 1% to 2% maximum change for surface receivers. Streich (2015), who analyzed the response of an isotropic thin resistor embedded in sediments and with a dipole source in x, reported that the E_x measured in surface is one order of magnitude higher than the E_z measured in a shallow well at a 105 m depth.

Although the maps present the relative percent difference of each field, it is possible to have some understanding of them. First, Fig. 7 shows that the E_z field is more sensitive to the horizontal boundary of the geobody, z = 50 m, whereas Fig. 6 shows that the E_x field is more sensitive to the vertical limit of the geobody, x = 160 m. This effect can be explained by the fact that, due to conservation laws, the electrical current normal to the boundary is preserved, so that the electric field orthogonal to each limit shifts as there are different conductivity values.

Analysis of the data in Table 1 allows us to make a comparison of the response of each field to each type of symmetry. Focus will be on the SB configuration (R1, R2, and R3 sensors), where it is seen that the most sensitive field discriminating the type of symmetry is H_y; in addition, Fig. 3c, e show that its amplitude is higher in the VTI layer, having values 4.20 × 10^–7 T, 1.24 × 10^–6 T and 1.40 × 10^–6 T for R1, R2 and R3, respectively, whereas for the HTI layer the R1, R2 and R3 values are 1.34 × 10^–7 T, 4.05 × 10^–7 T and 4.33 × 10^–7 T (Table 2). The E_x field presents higher sensibility to the type of symmetry in R1 and, to a lesser extent, in R2; both of them measure the energy diffused back to the surface, whereas R3 is less sensitive. This means that the effect of the HTI medium in E_x, closer to the anisotropic resistor, is more important. In contrast, the E_z in VTI is more sensitive to the energy induced inside and, recalling Fig. 7, below the body.

Figure 9 presents the relative percentage differences $\% \frac{{\Delta {E_x}}}{{E{}_x}}$, $\% \frac{{\Delta {E_z}}}{{E{}_z}}$, $\% \frac{{\Delta {H_y}}}{{H_y}}$ and total electric current at times t = 0.50, t = 0.125 and t = 0.250 s for Case 6, showing significant differences related to case 5. This differences can be explained as follows: first, the geometry of the geobody; second, the way to combine symmetries, since it is a conductive VTI block followed by a conductive HTI block whereas Case 5 comprises 4 conductive HTI blocks immersed in a resistive VTI medium and third, the differences in ${\rho_x}$ and ${\rho_z}$ with respect to ρ because, in Case 5, the whole geobody has ${\rho_z}$ >  ρ and ${\rho_x}$ <  ρ whereas in Case 6 the whole geobody has ${\rho_z}$ <  ρ and ${\rho_x}$ <  ρ. The three facts in might explain that the E_x, E_z and H_y presents higher relative percentage differences than Case 5 at earlier times: before 250 ms, the values of $\% \frac{{\Delta {E_x}}}{{E{}_x}}$ are higher below the geobody whereas the values of and $\% \frac{{\Delta {H_y}}}{{H_y}}$ are higher inside the geobody and in the middle area of the model. However, at the times presented the signal is lower than the measurable threshold. Regarding the diffusive current, the vector map in Fig. 9 shows that the total electric current, which have both J_x and J_z components and, at t = 250 milliseconds tends to follow the symmetry in each block.

Fig. 9

Case 6. Maps of the relative percent difference of E_x ($\% \frac{{\Delta {E_x}}}{{E_x}}$, first row), E_z ($\% \frac{{\Delta {E_z}}}{{E_z}}$, second row) and H_y ($\% \frac{{\Delta {H_y}}}{{H_y}}$, third row), at times 0.50, 0.125 and 0.250, seconds after turn off the source, for a T-shape, fracture, in dash line. Circles represent R1, R2 and R3 borehole receivers and squares represent R4, R5 and R6 receivers. Source in x. The fourth row shows a vector map of the total electrical current, in A/m²

Finally, the simulation also allows modeling a tilted fracture (Fig. 10). In this case the values $\% \frac{{\Delta {E_x}}}{{E{}_x}}$, $\% \frac{{\Delta {E_z}}}{{E{}_z}}$ and $\% \frac{{\Delta {H_y}}}{{H_y}}$, in horizontal x and vertical z directions are lower than 30% in the three cases. It is found that the E_x field presents values higher than 2% below the tilted fracture and H_y the highest values. Again, the best place to record the signal is inside and below the geobody.

Fig. 10

Case 7. Maps of the relative percent difference of E_x, $\% \frac{{\Delta {E_x}}}{{E_x}}$, H_y, $\% \frac{{\Delta {H_y}}}{{H_y}}$, at times 0.50, 0.125, 0.250, seconds after turn off the source. Circles represent R1, R2 and R3 borehole receivers and squares represent R4, R5 and R6 receivers. Source in x

6 Conclusions

The electromagnetic monitoring applied to the study of unconventional reservoirs before, during and after the hydraulic fracturing procedure can provide meaningful information related to the preliminary geological scenario, fracking geometry, SRV and proppant location, adding value to the conventional technology. In an unconventional reservoir it is essential to consider the electrical anisotropy, so that, in this approach, the approximate solution of the Maxwell equations includes electrical anisotropy obtained using a mixed FE method combined with a leapfrog time-stepping procedure. A stability analysis of the numerical method is extended to the anisotropic case.

For a given geological scenario, it is important to know for what configuration the anomaly is better detected, what fields are more sensitive to the geometry and symmetry, and which can be a suitable receivers location. In this study, strong anisotropy, combination of anisotropies and geometries, and larger monitoring times than conventional ones were considered.

In this numerical example, for all cases the signals have a long period, larger than 20 s. The SS configuration is not useful to discriminate the type of anisotropy and percentage of relative differences for all fields (in concordance with the literature), whereas, conversely, the SB configuration can discriminate them.

In a VTI and HTI scenario (Cases 1 to 4), the total amplitudes of the fields are shown, there are some interesting conclusions related to the sensitivity of fields to the location of receivers. First, both in case 1 (VTI layer) and 3 (HTI layer), the E_z and H_y total fields have higher amplitudes in R3, inside the formation, whereas the E_x total field has the lowest amplitude in R3. This might be related to the resistivity values in the anisotropic layer.

In a SB configuration the ratios $\frac{{E_x^{VTI}}}{{E_z^{VTI}}}$ and $\frac{{E_x^{VTI}}}{{E_z^{HTI}}}$ show that the fields are very sensitive to the receiver location; E_x is one order of magnitude higher than E_z in R1 and R2; they are also the maximum ratios for both case 1 and case 3. The most sensitive field to discriminate the type of symmetry for all receivers is H_y, its amplitude being highest in the VTI layer. The E_x field presents a higher sensibility to symmetry mainly in R1 and to a lesser extent in R2 and then in R3. That means that the effect of the HTI layer is more important closer to the anisotropic resistor. In contrast, the E_z field in VTI is more sensitive to the energy induced inside and below the body.

The simulation also allows modeling other type of symmetries like TTI and combination of symmetries like vertical fractures in a horizontal shape, T-shape fractures or Dog-leg fractures.

In a vertical fractures embedded in an unconventional shale (case 5), there is a combination of anisotropies that results in a whole geobody with VTI anisotropy, so that its behavior is VTI and, in consequence, $\% \frac{{\Delta {E_z}}}{{E_z}}$ values are higher than those for the other fields. It may be seen that E_z is more sensitive to horizontal boundary of the geobody, whereas E_x is more sensitive to vertical boundary; this is explained by the fact that, due to conservation laws, the electrical current normal to the boundary shifts depending on the different conductivity values. Also, in this case the energy induced back to the surface presents percent differences higher than 5% after 5 s in $\% \frac{{\Delta {E_x}}}{{E_x}}$ and after 10 s for $\% \frac{{\Delta {E_z}}}{{E_z}}$ and $\% \frac{{\Delta {H_y}}}{{H_y}}$.

Case 6 and Case 7 shows some differences related to Case 5. The reasons are due to the geometry of the geobody; second, the way to combine symmetries, since it is a conductive VTI block followed by a conductive HTI block whereas Case 5 comprises 4 conductive HTI blocks immersed in a resistive VTI medium and third, the differences in ${\rho_x}$ and ${\rho_z}$ with respect to ρ because, in Case 5, the whole geobody has ${\rho_z}$ > ρ and ${\rho_x}$ < ρ whereas in Case 6 the whole geobody has ${\rho_z}$ < ρ and ${\rho_x}$ < ρ. The three facts in might explain that the E_x, E_z and H_y presents higher relative percentage differences than Case 5 at earlier times: before 250 ms, the values of $\% \frac{{\Delta {E_x}}}{{E{}_x}}$ are higher below the geobody whereas the values of and $\% \frac{{\Delta {H_y}}}{{H_y}}$ are higher inside the geobody and in the middle area of the model.

Some insight related to the electrical current diffusion in VTI and HTI scenarios is presented, based on the modeling results. In the VTI case, associated with horizontal lamination or stratification, the current within the layer tends to flow horizontally (i.e., in x direction), so that the horizontal electric field E_x will increase the signal, while, in the HTI case, associated with vertical fractures, the electric current tends to flow vertically (i.e., in z direction), so that the vertical electric field E_z will increase the signal in combination with the signature of the T_x source. For most complicated cases like T-shape it is seen that from 250 ms the currents tend to follow the symmetry in each one of the block that comprises the T-shape.