Motor Protein Transport Along Inhomogeneous Microtubules

Abstract

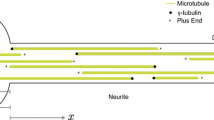
Many cellular processes rely on the cell’s ability to transport material to and from the nucleus. Networks consisting of many microtubules and actin filaments are key to this transport. Recently, the inhibition of intracellular transport has been implicated in neurodegenerative diseases such as Alzheimer’s disease and Amyotrophic Lateral Sclerosis. Furthermore, microtubules may contain so-called defective regions where motor protein velocity is reduced due to accumulation of other motors and microtubule-associated proteins. In this work, we propose a new mathematical model describing the motion of motor proteins on microtubules which incorporate a defective region. We take a mean-field approach derived from a first principle lattice model to study motor protein dynamics and density profiles. In particular, given a set of model parameters we obtain a closed-form expression for the equilibrium density profile along a given microtubule. We then verify the analytic results using mathematical analysis on the discrete model and Monte Carlo simulations. This work will contribute to the fundamental understanding of inhomogeneous microtubules providing insight into microscopic interactions that may result in the onset of neurodegenerative diseases. Our results for inhomogeneous microtubules are consistent with prior work studying the homogeneous case.

Appendices

A Homogeneous Microtubules: Proof of Theorem 1 and Corollary 1

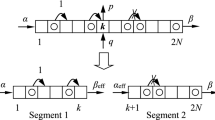
Equation (17) may be rewritten in the form of a system of two first order ODEs for density $\rho _\varepsilon$ and flux $\mathcal {F}_\varepsilon$ (see also (14)):

$$\begin{aligned} \left\{ \begin{array}{rl} \dfrac{\varepsilon }{2}\rho _\varepsilon ' &{}= -\omega _0^{-1}\mathcal {F}_\varepsilon +\rho _\varepsilon (1-\rho _\varepsilon ), \\ \mathcal {F}_\varepsilon '&{}=\varOmega _\mathrm{A}-(\varOmega _\mathrm{A}+\varOmega _\mathrm{D}) \rho _\varepsilon . \end{array}\right. \end{aligned}$$

(47)

Fig. 7

Left: phase portrait for (47) with $\varepsilon =0.01$, $\varOmega _\mathrm{A}=0.7$ and $\varOmega _\mathrm{D}=0.3$; Right: sketch of the phase portrait for (47) with $\varepsilon \ll 1$, the black circle represents the stationary point

Next, we discuss the phase portrait for this system with $\varepsilon \ll 1$, depicted in Fig. 7. Away from curve $\gamma$ defined by

$$\begin{aligned} \gamma :=\left\{ (\rho ,\mathcal {F})\left| \mathcal {F}=\omega _0\rho (1-\rho ) \text { and }\begin{array}{l}0\le \rho \le 1,\\ 0\le \mathcal {F} \le \omega _0/4\end{array}\right. \right\} , \end{aligned}$$

(48)

the trajectories of (47), parametrized by $0\le x\le \ell$, have almost horizontal slope in $(\rho ,\mathcal {F})$ plane. This is because the slope of $\rho _\varepsilon$ is of the order $\varepsilon ^{-1}$, that is $\rho _\varepsilon '(x)\sim \varepsilon ^{-1}$, whenever the point $(\rho _\varepsilon (x),\mathcal {F}_\varepsilon (x))$ is away from $\gamma$ (it follows from the first equation in (47)). It would be natural to expect that as $\varepsilon$ vanishes, trajectory $\left\{ (\rho _\varepsilon (x),\mathcal {F}_\varepsilon (x)),0\le x \le \ell \right\}$ approaches the arch $\gamma$ and this trajectory is contained in a given thin neighborhood of $\gamma$ for sufficiently small $\varepsilon$. In this subsection, it will be shown that the behavior of the solution is more complicated than simply evolving near $\gamma$.

To describe how the solution $\rho _\varepsilon (x)$ behaves for $\varepsilon \ll 1$, we introduce the following notation for parts of curve $\gamma$. Namely,

$$\begin{aligned} \gamma _{l}:= & {} \gamma \cap \left\{ 0\le \rho < 0.5 \right\} ,\\ \gamma _{r,+}:= & {} \gamma \cap \left\{ 0.5\le \rho \le \rho _\text {eq} \right\} ,\\ \gamma _{r,-}:= & {} \gamma \cap \left\{ \rho _\text {eq}\le \rho \le 1 \right\} . \end{aligned}$$

Here $\rho _\text {eq}:=\varOmega _\mathrm{A}/(\varOmega _\mathrm{A}+\varOmega _\mathrm{D})$. Let us also introduce the following horizontal segment

$$\begin{aligned} \varGamma :=\left\{ (\rho ,\mathcal {F}):\mathcal {F}=\omega _0/4,~ 0\le \rho \le 0.5 \right\} , \end{aligned}$$

and the solution g(x; s, a) to (19), i.e., the initial value problem of the first order obtained by the formal limit as $\varepsilon \rightarrow 0$ in (17):

$$\begin{aligned} \omega _0(1-2g)\partial _x g=\varOmega _\mathrm{A}-(\varOmega _\mathrm{A}+\varOmega _\mathrm{D})g,~~~g(s;s,a)=a. \end{aligned}$$

(49)

First, note that $\gamma _l$, which is the left part of the curve $\gamma$, is unstable, that is all trajectories, excluding $\gamma _l$, are directed away from $\gamma _l$ in the vicinity of $\gamma _l$. The right part of the curve $\gamma$, consisting of curve segments $\gamma _{r,+}$ and $\gamma _{r,-}$, is stable, attracting all trajectories in its vicinity, except those that follow $\varGamma$. We note that this exception, when $\gamma _{r,+}$ loses its stability, occurs at the interface point $(\rho =1/2,\mathcal {F}=\omega _0/4)$ where $\gamma _{r,+}$ meets $\gamma _l$. All trajectories reaching this point near (not necessarily intersecting) the curves $\gamma _{r,+}$ and $\gamma _l$ continue along $\varGamma$.

Given specific values of $\alpha ,\beta \in (0,1)$ in boundary conditions (18), the statement of Theorem 1 as well as representation formula (23) can be simply verified by careful inspection of the phase portrait depicted in Fig. 7. Specifically, for all $0<\alpha ,\beta <1$, one can draw a path $\left\{ (\rho (x),\mathcal {F}(x)):0\le x\le \ell \right\}$ along arrows in Fig. 7 (right), which starts at vertical line $\rho =\alpha$ and ends at vertical line $\rho =1-\beta$, and such a path will be unique for given $\alpha$ and $\beta$ (see also left column of Fig. 8 for specific examples). Instead of checking each couple $(\alpha ,\beta )$, one would split ranges of $(\alpha ,\beta )$ into sub-domains within which the outer solution has constant or smoothly varying shape, as it is done in proof below.

Proof of Theorem 1

Consider the following functions:

$$\begin{aligned} \rho _\alpha (x)=g(x;0,\alpha ) \text { and } \rho _\beta (x)=g(x;\ell ,\max \left\{ 0.5,1-\beta \right\} ). \end{aligned}$$

These functions can be thought of as one-sided solutions (i.e., satisfying one of the boundary conditions, either $\rho (0)=\alpha$ or $\rho (\ell )=\max \left\{ 0.5,1-\beta \right\}$) of Equation (17) for $\varepsilon =0$. The reason we choose $\rho (\ell )=\max \left\{ 0.5,1-\beta \right\}$ instead of $\rho _\beta (\ell )=1-\beta$ is because there is no solution continuous at $x=\ell$ with $\rho (\ell )<0.5$ as visible in Fig. 7 (curve $\gamma$ is unstable in region $\left\{ 0\le \rho < 0.5 \right\}$).

Introduce also the corresponding fluxes:

$$\begin{aligned} \mathcal {F}_\alpha (x)=\omega _0\rho _\alpha (x) (1-\rho _{\alpha }(x))\text { and }\mathcal {F}_{\beta }(x)=\omega _0\rho _\beta (x) (1-\rho _{\beta }(x)). \end{aligned}$$

From the definition of function g it follows that $\mathcal {F}_\alpha (x)$ and $\mathcal {F}_\beta (x)$ are both monotonic functions, and function $\mathcal {F}_\beta (x)$ is defined for all $0\le x < \ell$. Moreover, $\mathcal {F}_\beta (x)$ can be extended onto $(-\infty ,\ell ]$ and

$$\begin{aligned} \lim \limits _{x\rightarrow -\infty }\mathcal {F}_{\beta }(x)=\mathcal {F}_\text {eq}, \text { where }\mathcal {F}_\text {eq}:=\omega _0\dfrac{\varOmega _\mathrm{A}\varOmega _\mathrm{D}}{(\varOmega _\mathrm{A}+\varOmega _\mathrm{D})^2}. \end{aligned}$$

Consider case $\alpha \ge 0.5$. From Fig. 7, it follows that a trajectory emanating for initial point $(\alpha ,\mathcal {F})$ for any $0<\mathcal {F}<\omega _0/4$ immediately reaches $\gamma _r$ and stays on $\gamma _r\cup \varGamma$ for $0<x\le \ell$. Thus, at $x=0$ trajectory $\left\{ (\rho _0(x),\mathcal {F}_0(x)): 0\le x \le \ell \right\}$, describing the outer solution, jumps from $(\alpha ,\mathcal {F}_0(0))$ at $t=0$ to $\gamma _r$:

$$\begin{aligned} \rho _0(x)= \left\{ \begin{array}{ll} \alpha , &{} x=0,\\ \rho _\beta (x),&{} 0< x \le \ell . \end{array} \right. \end{aligned}$$

(50)

In the case where $\alpha < 0.5$, denote by $0\le x_J\le \ell$ location at which fluxes $\mathcal {F}_\alpha (x)$ and $\mathcal {F}_\beta (x)$ intersect, that is,

$$\begin{aligned} \mathcal {F}_\alpha (x_J)=\mathcal {F}_\beta (x_J). \end{aligned}$$

(51)

Equality (51) implies that either $\rho _\alpha (x_J)=1-\rho _\beta (x_J)$ or $\rho _\alpha (x_J)=\rho _\beta (x_J)$. If $\rho _\alpha (x_J)=\rho _\beta (x_J)$, then since $\rho _\alpha$ and $\rho _\beta$ are solutions of the same first order ordinary differential equation, these two functions coincide $\rho _\alpha (x)\equiv \rho _\beta (x)$.

We show now that either

$$\begin{aligned} \text {there exists at most one }x_J \le 1\hbox { or }\rho _\alpha (x)\equiv \rho _{\beta }(x). \end{aligned}$$

(52)

Indeed, since $\alpha <0.5$, trajectory $(\rho _\alpha (x),\mathcal {F}_\alpha (x))$ evolves on $\gamma _{l}$ for all $0\le x \le \ell$ where solution $\rho _\alpha (x)$ exists, and $\mathcal {F}_{\alpha }(x)$ monotonically increases. Trajectory $(\rho _\beta (x),\mathcal {F}_\beta (x))$ evolves also for all $0\le x \le \ell$ within either $\gamma _{r,+}$ or $\gamma _{r,-}$. If $(\rho _\beta (x),\mathcal {F}_\beta (x))$ evolves within $\gamma _{r,-}$, then $\mathcal {F}_\beta (x)$ is monotonically decreasing in x whereas $\mathcal {F}_\alpha (x)$ is monotonically increasing x, and thus equation $\mathcal {F}_\alpha (x)=\mathcal {F}_\beta (x)$ can have at most one root in this case. If $(\rho _\beta (x),\mathcal {F}_\beta (x))$ evolves within $\gamma _{r,+}$, then both $\mathcal {F}_\alpha (x)$ and $\mathcal {F}_\beta (x)$ increase with x. Assume that there are at least two distinct numbers $x_J^{(1)}$, $x_J^{(2)}$ such that $x_J^{(1)}<x_J^{(2)}$ and $\mathcal {F}_\alpha (x_J^{(i)})=\mathcal {F}_{\beta }(x_J^{(i)})$, $i=1,2$. Assume also that $x_J^{(1)}$ and $x_J^{(2)}$ are neighbor roots of equation $\mathcal {F}_\alpha (x)= \mathcal {F}_{\beta }(x)$, i.e., for all $x\in (x_J^{(1)},x_J^{(2)})$ we have $\mathcal {F}_\alpha (x)\ne \mathcal {F}_{\beta }(x)$. Then due to

$$\begin{aligned} \partial _x \mathcal {F}=\varOmega _\mathrm{A}-(\varOmega _\mathrm{A}+\varOmega _\mathrm{D})g, \text { where }\mathcal {F}(x)=\omega _0 g(x)(1-g(x)) \end{aligned}$$

and $\rho _\alpha (x_J^{(i)})<0.5$ $\rho _\alpha (x_J^{(i)})>0.5$, $i=1,2$, we have that $\partial _x \mathcal {F}_\alpha (x_J^{(i)})>\partial _x \mathcal {F}_\beta (x_J^{(i)})$, $i=1,2$. Noting that a smooth function can’t have the same sign of its derivative at two successive roots we arrive to contradiction. Therefore, such $x_J$ is at most one and (52) is shown.

Fig. 8

Left: the thick line represents the trajectories from Examples 1–4; it starts at $\rho =\alpha$ and ends at $\rho =1-\beta$, the black circle at (0.8,0.16) represents the stationary solution. Right: The thick line represents the outer solution $\rho _0(x)$ for Examples 1-4. In Examples 2 and 3, branches $g(x;0,\alpha )$ and $g(x;1,\max \{0.5,1-\beta \})$ extend slightly beyond the intervals where they are a part of the outer solution $\rho _0(x)$ (thin curves)

Fig. 9

The thick line represents the trajectories from Example 5; it starts at $\rho =\alpha$ and ends at $\rho =1-\beta$, the black circle at (0.8,0.16) represents the stationary solution. Right: the thick line represents the outer solution $\rho _0(x)$ for Example 5

If $\mathcal {F}_\alpha (x)\ne \mathcal {F}_\beta (x)$ for all $0\le x \le 1$, then define $x_J$ as follows:

$$\begin{aligned} x_J=\left\{ \begin{array}{ll} 0, &{} \mathcal {F}_\beta (x)<\mathcal {F}_\alpha (x)\text { for all }0<x<\ell , \\ 1, &{} \mathcal {F}_\alpha (x)<\mathcal {F}_\beta (x)\text { for all }0<x<\ell . \end{array} \right. \end{aligned}$$

We note that point $x=x_J$ is where the outer solution jumps from $\rho _\alpha (x)$ to $\rho _\beta (x)$, thus

$$\begin{aligned} \rho _0(x)=\left\{ \begin{array}{ll} \rho _\alpha (x),&{}0\le x<x_J,\\ \rho _\beta (x),&{}x_J<x<\ell . \end{array} \right. \end{aligned}$$

(53)

and $\rho _0(\ell )=1-\beta$.

Formulas (50), (53), and (18) complete the proof of Theorem 1. $\square$

B Examples of Solutions Given by (23)

To illustrate the result of Theorem 1 we continue with the following examples. We take $\omega _0=1$, $\ell =1$, $\varOmega _\mathrm{A}=0.8$ and $\varOmega _\mathrm{D}=0.2$, and we vary the boundary rates $\alpha$ and $\beta$. The outer solution for each example, as both a trajectory in $(\rho , \mathcal {F})$ plane and the plot of $\rho _0(x)$, is depicted in Fig. 8.

Example 1

$\alpha =0.4$ and $\beta =0.39$.

$$\begin{aligned} \rho _0(x)=\left\{ \begin{array}{ll}0.4,&{}x=0\\ g(x;1,0.61),&{}0<x\le 1.\end{array}\right. \end{aligned}$$

Example 2

$\alpha =0.1$ and $\beta =0.4$.

$$\begin{aligned} \rho _0(x)=\left\{ \begin{array}{ll} g(x;0,0.1),&{} 0\le x \le x_J,\,x_J\approx 0.133\\ g(x;1,0.6),&{} x_J< x \le 1. \end{array}\right. \end{aligned}$$

Example 3

$\alpha =0.1$ and $\beta =0.85$.

$$\begin{aligned} \rho _{0}(x)=\left\{ \begin{array}{ll} g(x;0,0.1),&{} 0\le x \le x_J,\, x_J\approx 0.135,\\ g(x;1,1/2),&{} x_J<x<1,\\ 0.15,&{} x=1.\end{array}\right. \end{aligned}$$

Example 4

$\alpha =0.9$ and $\beta =0.8$.

$$\begin{aligned} \rho _{0}(x)=\left\{ \begin{array}{ll} 0.9,&{} x=0,\\ g(x;1,1/2),&{} 0<x<1,\\ 0.2,&{} x=1. \end{array} \right. \end{aligned}$$

The case $x_J>1$ corresponds to the case of fast motor proteins or, more precisely, unidirectional motion dominates attachment/detachment, and thus resulting density is low in MT, $\rho _0(x)<0.5$ for $x\in (0,1)$. Consider the following example:

Example 5

$\alpha =0.05$, $\beta =0.85$, $\varOmega _\mathrm{A}=0.16$ and $\varOmega _\mathrm{D}=0.04$.

$$\begin{aligned} \rho _0(x)=\left\{ \begin{array}{ll} g(x,0,\alpha ), &{} 0\le x<1,\\ 1-\beta , &{} x=1. \end{array} \right. \end{aligned}$$

The solution is depicted in Fig. 9.