Neutral Vortex Necklace in a Trapped Planar Superfluid

Abstract

We study quantum vortex states consisting of a ring of vortices with alternating sign, in a homogeneous superfluid confined to a circular domain. We find an exact stationary solution of the point vortex model for the neutral vortex necklace. We investigate the stability of the necklace state within both the point-vortex model and the Gross–Pitaevskii equation describing a trapped atomic Bose–Einstein condensate at low temperature. The point-vortex stationary states are found to also be stationary states of the Gross–Pitaevskii equation provided the finite thickness of the outer fluid boundary is accounted for. Under significant perturbation, the Gross–Pitaevskii evolution and point-vortex model exhibit instability as expected for metastable states. The perturbed vortex necklace exhibits sensitivity to the perturbation, suggesting a route to seeding vortex chaos or quantum turbulence.

Appendices

A Vortex Sums

1.1 Inter-Vortex Terms

The sum $S_1$ gives the contributions to the motion of $z_1$ from each of $N-1$ vortices

$$\begin{aligned} S_1 = \sum _{n = 2}^{N} \frac{e^{i\pi n}}{1 - e^{i 2\pi (n-1)/N}}. \end{aligned}$$

(29)

If the system being solved consists of a single dipole, then the total number of vortices is $N = 2$ and the summation $S_1$ is reduced to the single term

$$\begin{aligned} S_1 = \left( \frac{e^{i\pi 2}}{1 - e^{i 2\pi (2-1)/N}}\right) = \frac{1}{2}. \end{aligned}$$

(30)

As we now show, this result holds for any even number of vortices. If the number of dipoles is greater than one, then we can shift the index of the summation and use the fact that the sum is always over an odd number of terms to find

$$\begin{aligned} S_1= & {} - \sum _{k = 1}^{N-1} \frac{e^{i\pi k}}{1 - e^{i 2\pi k/N}}\nonumber \\= & {} - \Bigg [ \sum _{k = 1}^{N/2-1} \frac{e^{i\pi k}}{1 - e^{i 2\pi k/N}} + \frac{e^{i\pi N/2}}{1 - e^{i 2\pi (N/2)/N}} + \sum _{k = N/2 + 1}^{N-1} \frac{e^{i\pi k}}{1 - e^{i 2\pi k/N}} \Bigg ],\quad \end{aligned}$$

(31)

or

$$\begin{aligned} S_1 = -\frac{e^{i\pi N/2}}{2} - \left[ \sum _{k = 1}^{N/2-1} \frac{e^{i\pi k}}{1 - e^{i 2\pi k/N}} + \sum _{k = N/2 + 1}^{N-1} \frac{e^{i\pi k}}{1 - e^{i 2\pi k/N}} \right] . \end{aligned}$$

(32)

The second sum can be cast in terms of the same index as the first. We first shift the index on the second sum

$$\begin{aligned} S_1 = -\frac{e^{i\pi N/2}}{2} - \left[ \sum _{k = 1}^{N/2-1} \frac{e^{i\pi k}}{1 - e^{i 2\pi k/N}} + \sum _{k = 1}^{N/2-1} \frac{e^{i\pi (k+N/2)}}{1 - e^{i 2\pi (k+N/2)/N}} \right] , \end{aligned}$$

(33)

and then invert the order of summation by letting $l = N/2-k$ and substituting it into the second sum, and finally relabel $l\rightarrow k$ to give

$$\begin{aligned} S_1 = -\frac{e^{i\pi N/2}}{2} - \sum _{k = 1}^{N/2-1} \left[ \frac{e^{i\pi k}}{1 - e^{i 2\pi k/N}} + \frac{e^{i\pi (N-k)}}{1 - e^{i 2\pi (N-k)/N}} \right] . \end{aligned}$$

(34)

Using the fact that $e^{i\pi k}=e^{i\pi (N-k)}$ since N is even, we have

$$\begin{aligned} S_1= & {} -\frac{e^{i\pi N/2}}{2} - \sum _{k = 1}^{N/2-1} e^{i\pi k} \left[ \frac{1}{1 - e^{i 2\pi k/N}} + \frac{1}{1 - e^{-i 2\pi k/N}} \right] \\= & {} -\frac{e^{i\pi N/2}}{2} - \sum _{k = 1}^{N/2-1} e^{i\pi k} \\= & {} \frac{(-1)^{N/2-1}}{2} - \sum _{k = 1}^{N/2-1} e^{i\pi k}. \end{aligned}$$

If $N/2-1$ is even, the first term is 1/2 and the second is 0; if $N/2-1$ is odd the first term is $-1/2$ and the second is 1. Hence, $S_1= 1/2$.

1.2 Vortex Image Terms

The second summation is the contribution from all of the vortex-images to the motion of the vortex $z_1$. It is given by

$$\begin{aligned} S_2 = - \left( \frac{d_N}{R}\right) ^2\sum _{n=1}^{N} \frac{\kappa _n e^{-i 2\pi (n-1)/N}}{1- (d_N/R)^2 e^{-i 2\pi (n-1)/N} }. \end{aligned}$$

(35)

To simplify, we let $a = (d_N/R)^2$

$$\begin{aligned} S_2= -a\sum _{n=1}^N\frac{e^{i\pi n} e^{-i(n-1)2\pi /N}}{1-a e^{-i(n-1)2\pi /N}} = a\sum _{k=0}^{N-1}\frac{e^{ik(N/2-1)2\pi /N}}{1-a e^{-ik2\pi /N}}. \end{aligned}$$

(36)

The geometric series Fourier transform pairs, valid for $a\ne 1$ are

$$\begin{aligned}&\sum _{j=0}^{N-1}e^{-ijk2\pi /N}\;a^j=\frac{1-a^N}{1-ae^{-ik2\pi /N}}, \end{aligned}$$

(37)

$$\begin{aligned}&\frac{1}{N}\sum _{k=0}^{N-1}e^{ijk2\pi /N}\frac{1-a^N}{1-ae^{-ik2\pi /N}}=a^j, \end{aligned}$$

(38)

where j can be chosen either positive or negative (the latter requiring $a\rightarrow a^{-1}$). Since we have initially made the choice $(-1)^k=e^{ik\pi }$, the transform (38) with positive choice $j\equiv N/2-1$ gives

$$\begin{aligned} a\sum _{k=0}^{N-1}\frac{e^{ik(N/2-1)2\pi /N}}{1-ae^{-ik2\pi /N}}=aN\frac{a^{(N/2-1)}}{1-a^N}, \end{aligned}$$

(39)

with the result

$$\begin{aligned} S_2=\frac{N(d_N/R)^N}{1-(d_N/R)^{2N}}. \end{aligned}$$

(40)

If we combine (11) and (40), Eq. (10) becomes

$$\begin{aligned} \frac{1}{2}+\frac{N(d_N/R)^N}{1-(d_N/R)^{2N}}=0, \end{aligned}$$

(41)

or, in terms of $x=(d_N/R)^N$, the equation $x^2-2Nx-1=0$, with positive root $x=N+\sqrt{N^2+1}$ giving

$$\begin{aligned} d_N/R=(N+\sqrt{N^2+1})^{1/N} >1, \end{aligned}$$

(42)

that describes the location of the images. The vortex locations are given by the second allowed choice for the phases: $(-1)^k=e^{ik\pi }$, and $j=-N/2-1$, instead giving the sum (12) and the location of the vortices (14).

B GPE Stationary States from Point-Vortex

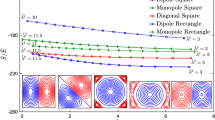
In Fig. 7 the $N = 4,6,8,10$ stationary PVM necklace state positions of the first vortex in each necklace are marked in yellow. To the left of each PVM stationary position marked in yellow, are the perturbed GPE trajectories of the first vortex in each necklace simulated over duration $t = 2000 \xi /c$. To the left of the $N=4$, PVM stationary position is three perturbed GPE trajectories. The trajectories that had their initial positions perturbed from the PVM stationary position by $-0.4$ and $-0.6$ are shown in orange and sky-blue, respectively. These trajectories orbit a common center. The trajectory with initial position perturbed by $-0.5$ stays within a range of $0.1\xi$ from the duration of the simulation.

Fig. 7

Trajectories from GPE simulations of perturbed necklace states. Only the trajectories of the first vortex in each state are shown. $d_4,d_6,d_8$ and $d_{10}$ mark the positions of the PVM stationary necklace state. To the left of each PVM stationary state marker are the trajectories of the first vortex in each state for different perturbed initial conditions (Color figure online)

The GPE trajectories of the perturbed $N=6$ necklace state are to the left of the $d_6$ yellow marker. The trajectory of the first vortex in the necklace perturbed inward by $-0.6\xi$ from the PVM prediction is shown in sky-blue, and stays within a range of $0.1\xi$ over duration $t = 2000 \xi /c$. Similarly, the perturbation of $-0.6\xi$ from the PVM leads to a tight oscillation around the true stationary point for both the $N=8$ and $N=10$ necklace respectively. For necklace states with $N>10$, the GPE trajectories become unstable on increasing shorter time scales.