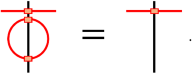1 Introduction

Classifying phases of matter is one of the most important problems in condensed matter physics. Landau’s theory of symmetry breaking [1] has been extremely successful in characterizing phases in terms of local order parameters, but it has been known since the work of Wegner [2] that topological theories do not necessarily exhibit such a local order parameter and hence that different topological phases cannot be distinguished locally. One of the main reasons to call such phases topological is the fact that the ground state degeneracy depends on the topology of the surface on which the system is defined [3]. Since the realization that quantum Hall systems exhibit topological quantum order [4], significant effort has been put into classifying all topological phases [5,6,7,8,9,10]. A very large class of models exhibiting topological order was constructed by Levin and Wen [11], which is conjectured to provide a complete characterization of non-chiral topological theories in two dimensions.

A recent development at the interface of quantum information and condensed matter theory is the growing use of projected entangled-pair states (PEPS) and more general tensor network states [12,13,14]. To construct a PEPS, one associates a tensor, representing a map from some virtual vector space to the local physical Hilbert space, to each site of a lattice and performs tensor contractions on the virtual space according to the graph of the lattice. The resulting quantum state can then be used as an ansatz for the ground state of a local Hamiltonian on that lattice [15,16,17]. There are two immediate and very important properties of PEPS. Firstly, for every PEPS there exists a local, positive-semi-definite, frustration-free operator called the parent Hamiltonian whose kernel contains the PEPS. Secondly, the entanglement entropy of a region R is upper bounded by \(|\partial R| \log D\) rather than the volume, where D is the virtual dimension and \(|\partial R|\) is the number of virtual bonds crossing the boundary of the region. Hence, PEPS are the ground states of local Hamiltonians and obey an area law (provided the bond dimension is upper bounded by a fixed constant D as the system size increases).

In this work, we propose a framework for the complete characterization of quantum order in gapped ground states using PEPS, based on the virtual symmetries of the local tensors. The PEPS network encodes the physical state in a region as a linear map from the virtual boundary space to the physical space. The symmetry dictates that this map can have no support outside the invariant subspace of the virtual symmetry action. Our framework thus starts from the consistent characterization of this invariant subspace across arbitrary lattice bipartitions in terms of local tensors that form a projection matrix product operator (MPO). This contains and generalizes the concept of \({\mathsf {G}}\) injectivity [18], where the symmetry corresponds to the tensor product action of some symmetry group \({\mathsf {G}}\), and its extension to twisted group actions [19]. The generalized notion of MPO injectivity developed in this work provides a natural extension that applies even when no group symmetry is involved, which is required for the description of more general topological orders including the string-net models.

We first define MPO injectivity, proceed by formulating a set of algebraic conditions that have to be satisfied by valid MPOs, and then show how the ground state degeneracy and topological order is determined by those MPOs. We go on to illustrate that all ground states of the string-net models satisfy the proposed algebraic conditions and that the key pulling-through condition for these models is implied by the pentagon equation for the F-symbols. We conclude by providing an outlook toward possible extensions of the framework to fermionic models and higher-dimensional theories and a discussion of the potential relevance of our formalism to the development of more efficient PEPS contraction schemes.

2 Algebraic Rules for MPO Injectivity and Consequences

Consider a PEPS on a lattice with coordination number c, such that the PEPS tensors \(A\) can be understood as a linear map from the c D-dimensional virtual spaces to the d-dimensional physical space, \(A: {\mathbb {C}}^D \otimes {\mathbb {C}}^D \otimes \ldots \otimes {\mathbb {C}}^D \rightarrow {\mathbb {C}}^d\). (Note that throughout the text, we use either a hexagonal lattice, i.e., the coordination number \(c=3\), or a square lattice, i.e., the coordination number \(c=4\).) By contracting the tensors within an arbitrary region V, the PEPS network defines a map \(A_V\) from the virtual boundary space \(({\mathbb {C}}^D)^{\otimes |\partial V|}\) to the physical bulk \(({\mathbb {C}}^{d})^{\otimes |V|}\).

Definition 2.1

(MPO-injectivity). Let \(A_V: ({\mathbb {C}}^D)^{\otimes |\partial V|} \rightarrow ({\mathbb {C}}^{d})^{\otimes |V|}\) be the PEPS map from the boundary to the bulk of a given compact, topologically trivial region V. \(A_V\) is called MPO-injective if it is injective on a subspace \(S_V \subset ({\mathbb {C}}^{D})^{\otimes |\partial V|}\) for which the corresponding projector is given by the MPO obtained from contracting the tensors M associated with the links along the boundary.Footnote 1

Throughout the remainder of this paper, we make use of standard tensor diagram notation, depicting each tensor as a shape with a leg emerging for each vector space it acts upon, and where a leg joining two tensors implies contraction of the associated indices.

Definition 2.1 is equivalent to the existence of a pseudo-inverse \(A^{+}_V\), such that given \(A_V\), \(A^{+}_V A_V = P_{S_V}\), and \(P_{S_V}: ({\mathbb {C}}^{D})^{\otimes |\partial V|} \rightarrow ({\mathbb {C}}^{D})^{\otimes |\partial V|}\) is a projector that can be expressed as a MPO with local MPO tensor M. At the level of a single site, MPO injectivity requires that the PEPS tensor \(A\) has a pseudo-inverse \(A^{+}\) such that, pictorially,

(1)

For the sake of introducing the tensor contraction rule, we note that above diagrammatic equation reads as

$$\begin{aligned} \sum _a (A^{+})^{a}_{i' j' k'}A^{a}_{ijk} = \sum _{a,b,c} M^{i i'}_{ab} M^{j j'}_{bc} M^{k k'}_{ca} \end{aligned}$$

where sums are performed over the contracted indices. From now on, we use the standard tensor network notation, where contracted indices are implied to be summed over. We remark that the arrows in the tensor networks seen in Eq. (1) matches Definition 2.1 where the PEPS \(A\) is a linear map from the virtual degrees of freedom on \(\partial V\) (input= ingoing arrow) to the physical degrees of freedom in V (output= outgoing arrow). The arrows on the legs of the MPO M are such that they match to the left hand side of Eq. (1). The only ingredient we need to construct a tensor network state with consistent arrow directions out of the local tensor A, is an arrow-reversing tensor \(\delta := \sum ^{D}_{i=1} |i\rangle \langle i|\). This tensor has to be attached on every virtual tensor leg whenever it is contracted with another virtual leg that has an unmatching arrow direction. Apart from this conventional detail, there is no crucial ingredient. Hence, we assume the above convention is adjusted and we omit the arrows for the rest of the paper.Footnote 2

We now formulate a set of local algebraic rules which imply that the PEPS built from local tensor A is MPO-injective with respect to the MPO built from M, Eq. (1).

Definition 2.2

(Algebraic conditions). Let A be a MPO-injective tensor, i.e., there exists a pseudo-inverse \(A^{+}\) and MPO M as in Definition 2.1. Then, we define the following algebraic conditions.

  1. 1.

    Pulling-through condition: The MPO can pass through the PEPS tensor \(A\) at the virtual level

    (2)

    and thus acts as a generalized symmetry.Footnote 3

  2. 2.

    Trivial-loop condition:Footnote 4 The MPO is such that a trivial loop is equal to no loop, i.e.,

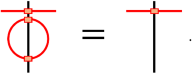    (3)
  3. 3.

    X-inverse: There exists a tensor X such that

    (4)

    henceforth referred to as the X-inverse, such that

    (5)

Together with the pulling-through condition [Eq. (2)], Eq. (5) implies that the injectivity of the PEPS tensors is stable when multiple tensors are concatenated, i.e., on any contiguous region V there exists a pseudo-inverse \(A_V^\dagger \) which can be applied on the physical degrees of freedom in V to give access to the virtual degrees at the boundary within the subspace defined by the MPO projector (see Lemma 2.3). The PEPS thus satisfies the definition of MPO injectivity. These conditions further imply the existence of a local, frustration-free parent Hamiltonian for which the ground state subspace in a contiguous region V corresponds exactly to the range of \(A_V\), i.e., the concatenated PEPS tensors with an arbitrary state on the virtual boundary (see Lemma 2.6). This is known as the intersection property and will be proven below, together with the stability under concatenation.

We conjecture that in two spatial dimensions all gapped ground states admitting a PEPS description can be constructed from MPO injective [Eq. (1)] tensors, with the MPO arising as a solution of Eqs. (2) and (3) for which there exists a tensor X satisfying Eq. (5). Note that this includes the particular cases of injective PEPS, where the MPO is just a product operator (\(m=1\)) of identities \({\mathbb {I}}_D\), and \({\mathsf {G}}\)-injective PEPS [18], where the projector MPO \(P_{S_V}\) is \(\sum _{g\in {\mathsf {G}}} U_g^{\otimes |\partial V|}\)Footnote 5 and M thus takes a diagonal form with \(m=|G|\) diagonal elements. In the generic case, the MPO tensors M will have a canonical block-diagonal form, in which each different block will yield an injective MPO that individually satisfies Eq. (2) and these MPOs together define the virtual symmetries of the local PEPS tensors. They act as virtual strings that can move freely through the lattice and are thus locally unobservable, except at open endpoints. The appearance of string operators in the characterization of two-dimensional topological models comes as no surprise [20, 21]. Indeed, the notion of MPO injectivity places the physical degrees of freedom in one-to-one correspondence with the virtual degrees of freedom in a certain subspace, allowing us to import the physical string operators to the virtual level. Furthermore, the PEPS description is advantageous for models away from a renormalization fixed point, as we can essentially treat the virtual string operators as if we were at a fixed point, avoiding the need to explicitly broaden them over some correlation length.

Now we give detailed proofs of the consequences of the algebraic rules of MPO injectivity.

2.1 Stability Under Concatenation

We now show that the conditions we have placed on the MPO tensors [Eq. (2), Eq. (3) and Eq. (4)] ensure that the projector \(P_{S_V}\) onto the virtual subspace \(S_V\), on which the PEPS map acts injectively, is represented by the MPO obtained from contracting the tensors M along the boundary of the region for any simply connected region of the lattice with non-trivial boundary.

Lemma 2.3

(Stability under concatenation). Let \(A_{V_1}\), \(A_{V_2}\) be the PEPS tensors for the regions \(V_1\) and \(V_2\), \(A^{+}_{V_1}\) and \(A^{+}_{V_2}\) be their pseudo-inverses. Let \(A\) be the local PEPS tensor and M be the MPO tensor as given in Definitions 2.1 and 2.2. Assume \(V_1\) and \(V_2\) are neighboring regions with no overlap. Then, there exists a pseudo-inverse for the PEPS tensor \(A_{V_1 \cup V_2}\) such that the projector \(P_{S_{V_1 \cup V_2}}\) is an MPO on the boundary of \(V_1 \cup V_2\) with the local MPO tensor M.

Proof

Without loss of generality, we assume a hexagonal lattice (with trivalent vertices), and the regions \(V_1\) and \(V_2\) both consist of single site and neighbors of each other. Our proof is constructive, i.e., we give a construction of the pseudo-inverse \(A^+_{V_1 \cup V_2}\) of the concatenated PEPS \(A_{V_1 \cup V_2}\).

The pseudo-inverse of the PEPS map on a larger region can be constructed by first applying a pseudo-inverse to each site given in Eq. (52), and then using the pulling-through condition [Eq. (2)] which leads to:

(6)

and then applying the X-inverse [Eq. (5)] to obtain

(7)

The same two moves can be used to inductively grow a region from N to \(N{+}1\) sites. The only complication arises when the injective region encloses an elementary plaquette, this involves growing the region onto a new site with two virtual bonds in common, which is possible using a slight variation of the above process. \(\square \)

2.2 Renormalization Group Move

Now, we find out a sequence of moves, that we call the renormalization-group moves that yield linear maps between MPO-injective PEPS on lattices of different sizes [Lemma 2.4] and allow one to define an X-inverse acting on any number of legs of an arbitrarily large MPO loop, and to show that the pulling-through condition holds for arbitrarily large MPO loops [Corollary 2.5]. Both the coarse-grained pseudo-inverse and coarse-grained pulling-through condition will be utilized in the following sections.

Lemma 2.4

(Renormalization group move). Let \(P_{S_V}\) be the MPO loop acting on \(|\partial V|\)-many sites on \(\partial V\), which is constructed from M such that conditions in Definitions 2.1 and 2.2 are satisfied. Then, there exists a local linear map that decreases (increases) the size of the MPO.

Proof

The pulling-through [Eq. (2)], the trivial loop condition [Eq. (3)], and the X-inverse [Eq. (4)], given in Definition 2.2, yield natural maps (acting only upon the black indices) for the addition or removal of degrees of freedom to or from a MPO. One can construct a linear map which removes a single degree of freedom from an MPO as follows:

(8)

where at step 1 we act with two MPO loops, at step 2 we contract two open indices, at step 3 we act with an X-inverse, and at step 4 we contract two open indices and apply the trivial-loop condition. Adding a single degree of freedom can be done similarly

(9)

where at step 1 we act with a single MPO loop and at step 2 we apply an X-inverse. Above, each move is a linear map, hence the claim follows. \(\square \)

Corollary 2.5

(Coarse-grained X-inverse and pulling-through). Let A be MPO-injective, M be the MPO tensor and X be the X-inverse, satisfying the conditions in Definitions 2.1 and 2.2. Then there exists a coarse-grained X-inverse that generalizes Eq. (5) to arbitrarily large MPOs where X can trace out many legs. Furthermore, pulling-through can be performed through larger MPO loops.

Proof

The coarse-grained X-inverse is obtained by applying pulling-through and RG moves [given in Eq. (8), Lemma 2.4] to first reduce the size of the MPO, which is then followed by the application of the X-inverse. Finally we apply the RG moves in the reverse way [given in Eq. (9), Lemma 2.4] to get back to the original lattice. The coarse-grained pulling-through can be shown to hold in the same way, i.e., first using RG moves [Eq. (8)] so that we can apply a single site pulling through, and then undo these moves with the reverse RG moves [Eq. (9)] to get back to the original MPO loop through which the coarse-grained pulling through has just been realized. \(\square \)

2.3 Intersection

In this section, we show that the MPO-injective PEPS parent Hamiltonian defined on any simply connected region of the lattice with non-trivial boundary is frustration-free and, furthermore, that all states within the ground subspace are given by a unique tensor network representation built from the original PEPS tensors \(A\) in the bulk with arbitrary tensors closing the network at the virtual boundary.

Lemma 2.6

(Intersection property). Let \(H_{V_1}= \sum _{i \in V_1} h_i\), \(H_{V_2}= \sum _{i \in V_2} h_i\), where \(h_i\) are local Hamiltonian terms, be parent Hamiltonians, respectively, on simply connected regions \(V_1\), \(V_2\), of a MPO-injective tensor \(A\) such that \(A\) and M satisfy the conditions in Definitions 2.1 and 2.2. Assume the regions \(V_1\) and \(V_2\) has non-trivial overlap, i.e., \(V_1 \cap V_2 \ne \emptyset \). Then, the parent Hamiltonian for the region \(V_1 \cup V_2\), given by \(H_{V_1 \cup V_2}= \sum _{i \in V_1 \cup V_2} h_i\), is frustration-free, i.e., there exist ground states \(|\psi \rangle \), such that \(h_i |\psi \rangle = 0\).

Furthermore, the ground states of this parent Hamiltonian are given by tensor network states constructed by the MPO-injective tensor \(A\) in the bulk contracted with an arbitrary boundary tensor.

Proof

Without loss of generality, we assume PEPS on square lattice, and define the parent Hamiltonian as a sum of \(2\times 2\) plaquette terms that each project locally onto the subspace spanned by the PEPS on that plaquette with arbitrary virtual boundary tensors. Both claims in the lemma are proven by constructively finding the subspace of ground states of the parent Hamiltonian on the larger region. In order to achieve this, we consider the mutual ground state subspace of two neighboring plaquette terms, any state within this subspace must be of the following form

(10)

for some bulk-extended boundary tensors A and B, note that we are free to choose B to be invariant under a loop of MPO on the virtual boundary. By applying the pseudo-inverse to all sites, we find

(11)

which, after pulling through and applying an X-inverse [Eq. (5)], leads to

(12)

The application of another X-inverse yields

(13)

and after applying a coarse-grained X-inverseFootnote 6 over two legs we find

(14)

We define a new boundary tensor

(15)

and find that \(B'\) must take the following particular form

(16)

where we have used the invariance of B under a loop of MPO on the virtual boundary of the right plaquette. Hence, all states within the mutual ground space of neighboring plaquette terms are of the form

(17)

for some boundary tensor C.

It is possible to iterate this argument to show that the ground space of the parent Hamiltonian on any simply connected region with a non-trivial boundary is spanned by the PEPS on that region with an arbitrary virtual boundary tensor. More precisely, one starts from Eq. (10), with more bulk MPO-injective tensors, e.g., a \(2 \times 3\) bulk region. Then, one follows the same steps from Eqs. 10 to 16, which results in extending the ground state tensor network to a larger lattice, e.g., a \(2 \times 4\) lattice. Note that extending the lattice in this way can be performed in either direction of the lattice, i.e., one can extend from \(n \times m\) to \((n+1) \times m\) or \(n \times (m+1)\) lattices. \(\square \)

2.4 Closure on Torus

In the previous section, we have shown that the ground state subspace on any simply connected region of the lattice with non-trivial boundary is spanned by a tensor network built from the PEPS tensor \(A\) in the bulk and closed by an arbitrary tensor on the virtual boundary. If we proceed to close the region on a compact manifold, the additional plaquette terms of the parent Hamiltonian now crossing the boundary will further restrict the possible form of the boundary tensor in a way that depends on the topology of the manifold. Below, we show the structure of the resulting tensor network state that is obtained by closing it on torus.

Theorem 2.7

(Closure on torus). Let \(H=\sum _i h_i\) be a parent Hamiltonian of a MPO-injective tensor \(A\) such that \(A\) and M satisfy the conditions in Definitions 2.1 and 2.2. Let the (square) lattice, on which the parent Hamiltonian acts, be topologically a torus. Then, the ground space of the parent Hamiltonian is spanned by the tensor network states constructed with the local tensor \(A\) together with a Q-tensor that connects to the tensor network as follows:

(18)

and the Q-tensor satisfies a pulling-through equation

(19)

such that \(Q \sim Q'\) in the sense of the following equivalence relation:

(20)

The PEPS created by Q and \(Q'\) are the same quantum state, as long as \(Q \sim Q'\).

Proof

Without loss of generality, we consider the specific case of closure on a \(2\times 2\) torus below, and note that a direct generalization of the argument to any size of torus leads to the same conclusion. By examining several different possible closures we refine the description of the boundary tensors that lead to a linearly independent set of ground states. We begin by looking at states in the intersection of two subspaces obtained from the following two different closures

(21)

which must be of this form, for some A and B. We utilize the pulling-through condition twice and apply two X-inverses [Eq. (5)] to achieve

(22)

Next we apply a coarse-grained X-inverse [Eq. (5) and Corollary 2.5] over two legs and find

(23)

We note the following equality, attained after using coarse-grained pulling through [Eq. (2) and Corollary 2.5] twice,

(24)

and define the tensor \(B'\),

(25)

for which we have the following equality

(26)

It is possible to repeat the preceding arguments to find states in the intersection of the \(90^{\circ }\) rotated versions of the above boundary configurations. For states in the triple intersection, we must have both Eq. (26) and the following

(27)

and hence

(28)

for some A, \(B'\) and C. Viewing the tensors in Eq. (28) as linear maps from the vertical to horizontal indices (where the vertical and horizontal indices are labeled by capitol letters V and H next to them, respectively) we have

$$\begin{aligned} C_H C_V=B_H B_V \end{aligned}$$
(29)

where \(C_V\) and \(B_H\) are MPOs of length two. Writing \(B_H^+\) for the pseudo-inverse of \(B_H\) we have that

$$\begin{aligned} C_H C_V=B_H \left( B_H^+ C_H \right) C_V \end{aligned}$$
(30)

and, defining \(Q:= B_H^+ C_H\), the equality in Eq. (28) thus ensures the boundary tensor is of the following form

(31)

Repeating the above argument for the four different possible closures we have a set of equalities

(32)

for some possibly different boundary tensors \(Q_i\).

The ground state tensors Q are only defined up to transformations that do not affect the physical state. We first note that the equality of physical states for two different tensors Q and \(Q'\) on the same plaquette,

(33)

is equivalent to equality of the physical states arising from the same tensors only involving the virtual bonds they directly act upon,

(34)

by utilizing the pseudo-inverse on the topologically trivial region not acted upon by the MPO. We are assuming periodic boundary conditions in the above two equalities and for all lattices throughout the remainder of this section.

By further utilizing the RG moves, we find that this is logically equivalent to equality of the states formed by Q and \(Q'\) on the smallest possible torus. Hence, we use this condition [Eq. (35)] to define an equivalence relation on four index tensors, whose equivalence classes capture all tensors that lead to the same physical state,

(35)

note that there are periodic boundary conditions for the left equality and open boundary conditions for the right equivalence relation.

By the arguments above, we know that it is possible to close the PEPS tensor network, with a possibly site dependent Q tensor, on any plaquette of the lattice to achieve the same physical state. We now compare the closures at different points, first considering Q tensors at two different locations along the same row of the dual lattice that give rise to the same physical state

(36)

where we have pulled through the MPO such that the boundary regions match. Now by employing the pseudo-inverse on the bulk tensors, followed by RG moves, we arrive at the equation

(37)

which must be satisfied by Q and \(Q'\) if they give rise to the same physical state.

Now consider a third \(Q''\) at a different plaquette along the same row, we proceed to compare each of the original tensors \(Q,\ Q'\) to the new one \(Q''\) via two different maps (constructed from RG moves) to arrive at two similar conditions

(38)

and

(39)

which, together, imply equality of the two physical states that arise from Q and \(Q'\) on the same plaquette of the PEPS, i.e., \(Q\sim Q'\). Note a similar argument applies to boundary conditions shifted in the vertical direction, which then implies (in combination with the horizontal) that any two tensors closing the PEPS tensor network (possibly on different plaquettes) to give the same physical state must be equivalent.

\(\square \)

Hence, Theorem 2.7 implies that on the level of equivalence classes we are searching for tensor solutions of the elementary pulling-through equation [Eq. (40)] in both the horizontal and vertical direction and it suffices to consider a particular representative Q for each class. This ensures that the resulting tensor networks, with the same PEPS tensor on every site and a Q tensor on the virtual level, will be translation invariant. To determine the degeneracy on the torus, we must then look at the dimension of the subspace spanned by physical ground states coming from all the different Q tensor solutions. Since the RG maps yield linear transformations between MPO-injective PEPS on lattices of different sizes, which are invertible on the subspaces spanned by states of the form given in Eqs. (35) and (33), we can be sure that the exact degeneracy does not change for any finite system size. However, it is possible that as the system grows in size any number of states within the ground state subspace may converge to a single ground state or to zero in the thermodynamic limit. Hence, one must examine the stability of the subspace as the system grows. We summarize these properties of the ground state subspace as in the following corollary that follows immediately from Theorem 2.7.

Corollary 2.8

(Ground state subspace on torus). Let \(H=\sum _i h_i\) be a parent Hamiltonian of a MPO-injective tensor \(A\) on a (square) lattice on torus. Further assume that \(A\) and M satisfy the conditions in Definitions 2.1 and 2.2, Then, the ground space is spanned by a finite number of states, obtained from the tensors, Q, that satisfy

(40)

and the equivalent equation for the vertical direction, with the dots indicating periodic boundary conditions. The ground state degeneracy on the torus is then given by the number of linearly independent physical states arising from the solution of Eq. (40) that remain distinct and normalizable in the thermodynamic limit.

Finally, we note that these closure arguments imply that any transformation preserving the ground state subspace can implicitly be rewritten as a transformation directly upon the Q tensors, although there is no explicit formula in general.

As this formalism was set up in order to characterize all gapped quantum phases, it naturally also includes states with discrete symmetry breaking (i.e., GHZ states a.k.a. cat states). In that case, the different ground states can have local order parameters and the degeneracy will be independent of the topology. Throughout the remainder of this letter, we focus on the more interesting case of topological phases. To determine whether any of the degeneracy is truly topological in nature, one must compare the ground state degeneracy of the tensor network on the topological manifold of interest to that arising on a topologically trivial manifold (such as the sphere). This provides a deterministic recipe for checking, for any given model, the topological dependency of the ground state subspace.

3 Example: String-Net Models

In this section, we first give a review of string-net models and derive the PEPS for one of the ground states of them. Then, we show that the set of models described by MPO-injective PEPS contains all string-net models [11]—the largest set of many-body bosonic lattice models exhibiting non-chiral topological order available in the literature.

As first described in [22, 23], the ground states of the string-net models have exact PEPS representations. Inside of every hexagon there is one virtual degree of freedom, these are connected to one another and to the degrees of freedom on the edges by tensors that sit on every vertex. The ground state is represented by the following tensor network

(41)

where the tensor sitting on the vertices is

(42)

\(d_s=v^2_s\) is the quantum dimension for sector s and \(D=\sqrt{\sum _s d^2_s}\) is the total quantum dimension. In the tensor network description, we make the convention that every closed loop comes with the multiplicative factor \(a_s= d_s/D\) and the middle legs that connect each pair of tensors are copied to physical degrees of freedom on the adjacent vertices. In the above expressions G is a six index tensor, known as the symmetric F-symbol. For the sake of completeness, we define these symbols and describe their symmetry properties which have been used in proving that the string nets satisfy our axioms. The F-symbol is defined to be a scalar map (when the branching is multiplicity-free, i.e., \(N_{ijk}\) is either 0 or 1) from one fusion path to another

(43)

Then, we define the G-symbol by the first line of the following expression

(44)

The second line of the above equation follows from the definition of the F-symbol and the fact that

(45)

regardless of arrow directions of m and n. Graphically, the G-symbol corresponds to the following scalar map

(46)

By Eq. (44), we find \(G^{ijk}_{\lambda \mu \nu }:= F^{\nu ^* j \lambda }_{k \mu i^*}/ (v_\lambda v_i)\). F and G-symbols have nice symmetry properties, referred to as tetrahedral symmetry, shown in the following equations

$$\begin{aligned} F^{ijm}_{kln}= F^{lkm^*}_{jin}= F^{jim}_{lkn^*}= F^{imj}_{k^*nl} \dfrac{v_m v_n}{v_j v_l}. \end{aligned}$$
(47)

Using the above symmetry relations, one finds that

$$\begin{aligned} G^{ijk}_{\lambda \mu \nu } = \frac{1}{v_k v_{\nu }} F^{i^*j^*k^*}_{\lambda ^* \mu \nu ^*} \end{aligned}$$
(48)

and clearly the G-symbols possess symmetry properties following from those in Eq. (47).

The pentagon equation for these G-symbols follows from the pentagon equation for the F-symbols and is given by

$$\begin{aligned} G^{i j k}_{\lambda \mu \nu }G^{i^* j^* k^*}_{\alpha ^* \beta ^* \gamma ^* } = \sum _n d_n G^{k \alpha ^* \beta }_{n \mu ^* \lambda ^*} G^{j \gamma ^* \alpha }_{n\lambda ^* \nu ^*} G^{i \beta ^* \gamma }_{n \nu ^* \mu ^*}\ . \end{aligned}$$
(49)

We now start from the definition of the string-net PEPS tensor

(50)

where the i, j, k legs are copied to the physical level and define the corresponding MPO tensor

(51)

Note that we explicitly depict all tensors as 2D shapes for the string-net PEPS. The G-symbol is a symmetrized version of the F-symbol, defined in Eq. (48), which is invariant under simultaneous cyclic permutation of the upper and lower indices. These diagrams use the convention that a pair of tensor legs i, \(i'\) that are connected through the body of a tensor corresponds to a Kronecker delta on the associated indices, i.e., \(T_{\{j\},i,i'}={\tilde{T}}_{\{j\},i} \delta _{i,i'}\); we therefore use a single label in the pictures. In particular, the MPO tensor has a block diagonal structure because it acts diagonally on f, which therefore acts as a label for the different virtual strings that can be constructed. As a final convention, we always associate a multiplicative factor \(d_{\lambda }\) (the quantum dimension) to each term in a sum over any index \(\lambda \) (appearing as a closed loop in the diagrams below).Footnote 7

The pseudo-inverse of the PEPS tensor [Eq. (50)] is

(52)

and it can readily be verified that Eq. (1), here given by

(53)

is directly equivalent to the pentagon equation [Eq. (49)] (note the sum over n and the associated quantum dimension \(d_n\)), as shown by

(54)

The number labeling each move in the above diagram indicates which of the tensors in Eq. (53) the move corresponds to. The G-symbol next to each move in Eq. (54) comes from the definition in Eq. (46) and is equal to the corresponding tensor in Eq. (53), as follows from employing several identities of the G-symbol [Eq. (47)].

The pulling-through condition for the string-net PEPS and MPO tensors is represented as

(55)

and is again equivalent to the pentagon equation [Eq. 49]

(56)

The loop condition [Eq. (3)] for string-net PEPS follows from the unitarity of the F-symbols as a basis transformation. The X-inverse for string nets is also given by the G-symbol as follows:

(57)

for which Eq. (5) holds. This follows from Eq. (53) (i.e., the pentagon equation) and the unitarity of the F-symbols.

It is instructive to see that the necessary conditions for MPO injectivity in the string-net PEPS are equivalent to the pentagon equation (49), which appears as a compatibility condition for the F-symbols [11] and is thus guaranteed to be true for any string-net model.

One can readily verify that a closed string-net MPO constructed from the tensors in Eq. (51), with a weighting of the normalized quantum dimension \(d_i/D^2\) associated with the internal index forming a closed loop, is a projector for any length. Since the MPO is a projector, its rank is easily obtained by calculating the trace. By examining the behavior of this rank for increasing length, the topological entanglement entropy is seen to be \(\log (D^2)\), originating from the normalization factor \(D^{-2}\).

4 Identifying the Topological Order

Let us now discuss how to identify the topological order in MPO injective PEPS. Since MPO injectivity is stable under concatenation, for any contiguous region the virtual indices at the boundary are supported on the invariant subspace of the MPO. This is, on the one hand, reflected in the low-energy excitations at the edge, which are in one-to-one correspondence with admissible boundary conditions. The edge dynamics are thus restricted to the invariant subspace of the MPO [24], which provides topological protection to the edge and allows one to infer the structure of the MPO from the edge physics. At the same time, it is reflected in the entanglement spectrum and the corresponding entanglement Hamiltonian [25]. The entanglement spectrum is also restricted to the invariant subspace, and therefore, the entanglement Hamiltonian contains a universal term with infinite strength which restricts the system to be in the invariant subspace [26]. A consequence of this restriction (together with the MPO injectivity) is that the number of nonzero eigenvalues is equal to the dimension of the invariant subspace of the MPO, which gives rise to a topological correction to the zero Rényi entropy. In the case of RG fixed points, the correction should not depend on the Rényi index (as has been shown for string-net models [27]), which implies a corresponding topological correction to the entanglement entropy [28, 29]. Note that a nonzero correction in the zero Rényi entropy requires an MPO projector with several blocks in its canonical form, as a single blocked MPO defines a subspace \(S_V\) whose dimension scales exactly as \(\log (\text {dim} S_V)=c|\partial V|+ {\mathcal {O}}(1/|\partial V|)\) without constant term.

The topological correction does not fully characterize the topological phase. To this end, one must obtain the modular S and T matrices, which contain the mutual and self-braiding statistics of the topological excitations [30]. The fusion rules of the topological excitations can also be obtained from the S matrix via the Verlinde formula. An advantage of the MPO formalism is that it allows for an unambiguous definition of modular transformations on the ground states of a lattice system on a torus, obtained by solving Eq. (40). The \(90^{\circ }\) rotation can be performed directly on the ground state tensors \(Q_i\) defined in Eq. (40). The Dehn twist, on the other hand, corresponds to increasing the winding number of the MPO along the twisting direction by one. If one uses \(A^{+}A\) for the PEPS tensors, then the overlap matrix of the original ground states with the rotated (twisted) ground states will only contain universal information and therefore correspond to the S (T) matrix [31,32,33].

The solutions of Eq. (40) will in general not correspond to the minimally entangled states (MES), i.e., the states that have the physical interpretation of being threaded with a definite anyon flux through one of the holes of the torus [31]. One has to find a unitary basis transformation of the ground state subspace (a basis transformation of the tensors Q) that makes T diagonal and S symmetric [34] in order to read off the topological properties of the excitations. Note that, by wrapping the projection MPO around the torus in one direction, we can construct a state with a topological flux corresponding to some Abelian anyon threaded through the hole in the orthogonal direction, since these states have maximal topological entropy \(2\gamma \) (while for general topological fluxes, the correction is \(2\gamma - \log (d_i^2)\) with \(d_i\) the quantum dimension). In the case that all anyons are non-Abelian, this MES clearly corresponds to the one with a trivial flux. But since this construction works for any anyon theory, it is very likely that it will always lead to the MES with a trivial flux.

Now, we show that the modular transformations can be performed directly on the virtual level of string-net PEPS on a torus. One can check that the tensors \(Q_{stu} = v_s v_tv_u G^{b^{*}du}_{t^{*}sa}G^{d^{*}bu^{*}}_{ts^{*}c}\), shown in Eq. (58), satisfy all the requirements on the ground state tensor of the string-net PEPS.

(58)

In Eq. (58) the tensors are defined to be

(59)

the vertical indices t must match since the PEPS is defined on a torus, and similarly for the horizontal indices s.

In general, \(\left\{ Q_{stu}\right\} \) will form an overcomplete set in the sense that not all \(Q_{stu}\) will lead to linearly independent ground states. By utilizing the pentagon equation one can show that the \(90^{\circ }\) rotated ground state tensor can be expressed as a linear combination of the original ground state tensors in the following way

$$\begin{aligned} S(Q_{stu}) = \sum _n F^{stu}_{s^*t^*n} Q_{tsn}. \end{aligned}$$
(60)

This agrees with the results of [34].

By further utilizing the specific form of the \(Q_{stu}\) tensors for the string-net PEPS [Eq. (58)] (and the pulling-through condition [Eq. (55)]) one can express the ground state tensors of the ground states with a Dehn twist as a linear combination of the original ground state tensors via the explicit relation which we give here for completeness

$$\begin{aligned} Q^{\text {twisted}}_{stu} = \sum _n F^{stu}_{s^*t^*n}\ Q_{snt^*} \, , \end{aligned}$$
(61)

where t is the label wrapping around the torus in the direction of the twist in and s is in the direction orthogonal to the twist, again agreeing with [34].

After determining the appropriate linear combinations of \(Q_{stu}\) that lead to different ground states for a particular string-net model Eq. (60) and Eq. (61) can be used to obtain the elements of the S and T matrices, respectively. As emphasized in the first part of this section, the modular S and T matrices are key ingredients of a full physical characterization of topological order, which can be obtained in the formalism of PEPS.

5 Conclusions and Outlook

In this work, we have presented a general framework for the characterization of topological phases in two dimensions using the PEPS formalism. The key ingredient is a generalized notion of injectivity, in which the central object is a MPO fulfilling a fundamental pulling-through condition. This encompasses the cases of normal injectivity, \({\mathsf {G}}\)-injectivity [18] and twisted injectivity [19], which can be verified directly by constructing the relevant MPOs. As a very general example, we have illustrated that all string-net models satisfy our axioms by explicitly constructing the appropriate MPOs and elucidating the correspondence between the pentagon equation and our pulling-through condition.

The characterization of topological order in terms of MPOs opens up the possibility of classifying topological phases via their MPOs, similar to results on 2D symmetry-protected topological (SPT) phases [35]. In fact, for string-net models with Abelian group elements as local degrees of freedom on edges and with group multiplication as the trivalent vertex constraints, the pentagon equation reduces to a 3-cocycle condition. This close connection between the boundary symmetry MPOs of SPT states and the virtual gauge symmetry MPOs of intrinsic topological states is explicitly described by a gauging duality in the PEPS picture [36, 37].

The framework set forth in this paper can be easily generalized to fermionic PEPS [38], as well as to higher-dimensional systems by replacing MPOs with their higher dimensional generalization, projected entangled pair operators (PEPOs); it thus provides a systematic way to understand both topological phases of interacting fermions and exotic topological order in three dimensions such as the Haah code [39].

A natural question is whether our framework contains topological phases outside the string-net picture. Since the excitations of the doubled phases described by string nets all have a Lagrangian subgroup, we know that their edge modes can be gapped out [40]. Thus, to obtain phases outside string nets we need to look at models with protected gapless edge modes (or models which do not correspond to a TQFT). Given the close connection between edge physics and the MPO, this amounts to understanding which MPOs give rise to protected gapless edge modes; indeed, in the recently discovered chiral fPEPS [41], fermionic MPOs satisfying a pulling-through condition have been identified [42].

Finally, an equation closely related to the pulling-through condition [Eq. (2)] could yield an algorithm to bring 2D PEPS into a normal form that facilitates the calculation of physical observables. Intuitively, this is because once the algorithm has converged, we find an MPO that approximates the transfer matrix of the model. Hence, contracting the whole PEPS with a physical observable reduces to contracting the PEPS in a local region around the observable and using a MPO to approximate the boundary. We leave these directions to future work.