Abstract
In this work, we construct the genuine Durrmeyer–Stancu type operators depending on parameter α in \([0,1]\) as well as \(\rho >0\) and study some useful basic properties of the operators. We also obtain Grüss–Voronovskaja and quantitative Voronovskaja types approximation theorems for the aforesaid operators. Further, we present numerical and geometrical approaches to illustrate the significance of our new operators.
Similar content being viewed by others
1 Introduction
Let \(L_{B}[0,1]\) denote the space of bounded Lebesgue integrable functions on \([0,1]\) and \(\mathbb{N}\) the set of natural numbers. We use the symbol \(\Pi _{m}\) \((m\in \mathbb{N})\) to denote the space of polynomials of degree at most m. By taking Bernstein polynomials into account, Chen [14] and Goodman and Sharma [21] independently introduced the operators \(U_{m}\) (we can also call them genuine Bernstein–Durrmeyer operators) acting from \(L_{B}[0,1]\) into \(\Pi _{m}\), defined by
for all \(f\in L_{B}[0,1]\), where \(p_{m,i}(y)\) \((m,i\in \mathbb{N})\) is considered by
The above operators are limits of the Bernstein–Durrmeyer operators with Jacobi weights, \(M_{m}^{c,d}\) for \(c,d>-1\), which was studied by Păltănea [40], that is,
where \(C[0,1]\) denotes the space of functions which are continuous on \([0,1]\) and
Păltănea [41] presented a generalization of the operators \(U_{m}\) with the help of \(\rho >0\), namely genuine ρ-Bernstein–Durrmeyer operators, and denoted them by \(U_{m}^{\rho }\). For any \(f\in C[0,1]\), in the same paper, he showed that the classical Bernstein operators are the limits of the operators \(U_{m}^{\rho }\) and also obtained a Voronovskaja-type result. Gonska and Păltănea [17] proved that the operators \(U_{m}^{\rho }\) preserve convexity of all orders and also obtained the degree of simultaneous approximation.
It is well known that Bernstein polynomials are one of the most widely-investigated polynomials in the theory of approximation, and so, to obtain another generalization of classical Bernstein operators, Cai et al. [13] considered the Bézier bases with shape parameter λ in \([-1,1]\) and introduced λ-Bernstein operators. Later, Kantorovich, Schurer, and Stancu variants of λ-Bernstein operators were discussed by Cai [11], Özger [36–38], and Srivastava et al. [43]. By taking λ-Bernstein polynomials into account, in a very recent past, Acu et al. [4] defined a new family of modified \(U_{m}^{\rho }\) operators and denoted the new operators by \(U_{m,\lambda }^{\rho }\).
Chen et al. [15] recently presented a generalization of classical Bernstein operators with the help of any fixed α in \(\mathbb{R}\), which they called α-Bernstein operators (linear and positive for \(\alpha \in [0,1]\)), and discussed the rate of convergence, Voronovskaja-type formula, and shape preserving properties of these positive linear operators. Mohiuddine et al. [26] constructed the Kantorovich variant of α-Bernstein operators. The bivariate version of α-Bernstein–Durrmeyer operators was constructed and studied by Kajla and Miclăuş [23] (also see [25] for recent work), in which they also discussed GBS operator (or generalized boolean sum operators) of α-Bernstein–Durrmeyer, while the two interesting forms of α-Baskakov–Durrmeyer were introduced by Kajla et al. [24] and Mohiuddine et al. [31]. For the classical Bernstein–Durrmeyer operators, we refer the interested reader to [16]. We also refer to [2, 3, 7, 8, 10, 12, 18, 19, 22, 27–30, 32–35, 39, 42, 45, 46] for some recent work on various Bernstein, Durrmeyer, and genuine type operators as well as statistical approximation.
We will now recall the α-Bernstein operators due to Chen et al. [15] as follows: For \(g\in C[0,1]\), \(\alpha \in [0,1]\) is fixed, and \(m\in \mathbb{N}\), the α-Bernstein operators are defined by
where
and
Note that \(p_{m,i}^{ ( \alpha )}\) in relation (1.1) is called α-Bernstein polynomials of order m and the binomial coefficients
For \(\alpha =1\), (1.1) is reduced to the classical Bernstein operators [9].
2 Generalized \(U_{m}^{\rho }\) operators and approximation properties
For \(m\in \mathbb{N}\) and \(\rho >0\), the functional (see [41])
is defined by
where \(\mu _{m,i}^{\rho }(t)\) in (2.1) is given by the formula
and Euler’s beta function in the last equality is defined by
Assume that θ and β are two real parameters satisfying \(0\leq \theta \leq \beta \). In view of α-Bernstein operators, for \(m\in \mathbb{N}\), \(\alpha \in \mathbb{R}\) is fixed, and given a function \(g\in C[0,1]\), we define the operators \(U_{m,\alpha }^{\beta ,\theta ,\rho }\) (or genuine \((\alpha ,\rho )\)-Durrmeyer–Stancu operators) by
where
for \(i=1,2,\dots ,m-1\), \(F_{m,0}^{\beta ,\theta ,\rho } (g )=g ( \frac{\theta }{m+\beta } )\) and \(F_{m,1}^{\beta ,\theta ,\rho } (g )=g ( \frac{m+\theta }{m+\beta } )\). Consequently, we can re-write our operators \(U_{m,\alpha }^{\beta ,\theta ,\rho }\) as follows:
For the choice of \(\theta =0\) and \(\beta =0\), the operators defined by (2.3) reduce to the operators \(U_{m,\alpha }^{\rho }(g;y)\) which were studied in [6]. In addition, if \(\rho =1\), then we get the genuine α-Bernstein–Durrmeyer operators \(U_{m,\alpha }\) defined in [1]. If we take \(\rho =1\), \(\alpha =1\), \(\theta =0\), and \(\beta =0\), then we obtain genuine Bernstein–Durrmeyer operators. Throughout the paper, we assume that \(\alpha \in [0,1]\) for which our new operators \(U_{m,\alpha }^{\beta ,\theta ,\rho }\) are linear and positive. For interested readers who want to see the details of Stancu operators, we refer to [44].
The moments of our newly constructed operators \(U_{m,\alpha }^{\beta ,\theta ,\rho }\) are given in the following lemma.
Lemma 1
Let \(e_{i} ( y )=y^{i}\), \((i=0,1,2,3,4)\). Then the operators \(U_{m,\alpha }^{\beta ,\theta ,\rho }\) satisfy
Proof
We give a short proof for the first three parts, one can prove the rest using the same idea.
Using the properties of Euler beta function, we have
□
Corollary 1
The central moments of (2.3) are as follows:
Theorem 1
If g is continuous on \([0,1]\) for any \(\alpha \in [0, 1]\), then \(U_{m,\alpha }^{\beta ,\theta ,\rho } (g)\) converge uniformly to g on \([0,1]\), that is,
Proof
We obtain by Lemma 1 that
and similarly \(\lim_{m \to \infty } \Vert U_{m,\alpha }^{\beta ,\theta ,\rho } (e_{2})-e_{2} \Vert =0\). Consequently, the Korovkin theorem gives
□
Lemma 2
Let \(g\in C [ 0,1 ]\), and let \(\Vert \cdot \Vert \) be a uniform norm on \([0,1]\). Then
Proof
With a view of last lemma, we have \(\vert U_{m,\alpha }^{\beta ,\theta ,\rho } ( g;y ) \vert \leq U_{m,\alpha }^{\beta ,\theta ,\rho } ( e_{0};y ) \Vert g \Vert = \Vert g \Vert \). □
Recall that the usual modulus of continuity for g is defined by
Theorem 2
Assume that \(g\in C [ 0,1 ]\) and \(\alpha \in [ 0,1 ] \). Then
where \(\tau _{m,\alpha }^{\beta ,\theta ,\rho } = U_{m,\alpha }^{\beta , \theta ,\rho } ((e_{1}-y)^{2}; y)\).
Proof
From the monotonicity of the operators \(U_{m,\alpha }^{\beta ,\theta ,\rho } \) and taking Lemma 1 into our account, we write
Since
we fairly obtain
Here, the assertion of Theorem 2 is acquired by taking into account \(\varepsilon = [4]\sqrt{ U_{m,\alpha }^{\beta ,\theta ,\rho } ( ( e_{1}-y ) ^{2};y )}\). □
Theorem 3
Let \(g \in C^{1}[0 ,1]\). For any \(y\in [0 ,1]\), the following inequality holds:
where \(\nu _{m }^{\beta ,\theta } = U_{m,\alpha }^{\beta ,\theta ,\rho } (e_{1}-y;y)\) and \(\tau _{m,\alpha }^{\beta ,\theta ,\rho } = U_{m,\alpha }^{\beta , \theta ,\rho } ((e_{1}-y)^{2};y)\).
Proof
One writes
for any \(t \in [0 ,1]\) and \(y\in [0 ,1]\). Operating \(U_{m,\alpha }^{\beta ,\theta ,\rho }(g;y)\) on both sides of the above relation, we obtain
We know that
for any \(\varepsilon >0\) and each \(u \in [0 ,1]\). By taking (2.5) into our consideration, we obtain
Thus,
Consequently, (2.4) follows by choosing \(\varepsilon =U_{m,\alpha }^{\beta ,\theta ,\rho }((t-y)^{2};y)=\sqrt{ \tau _{m,\alpha }^{\beta ,\theta ,\rho } }\), which proves our result. □
3 Voronovskaja-type theorems
We obtain some Voronovskaja-type theorems including a Grüss–Voronovskaja-type theorem and a quantitative Voronovskaja-type theorem for \(U_{m,\alpha }^{\beta ,\theta ,\rho } \). We first obtain a quantitative Voronovskaja-type theorem for our operators \(U_{m,\alpha }^{\beta ,\theta ,\rho } \) using the Ditzian–Totik modulus of smoothness. To do this, we need the following definitions.
We first recall the Ditzian–Totik modulus of smoothness defined as follows:
where \(g \in C[0 ,1]\) and \(\phi (y)=\sqrt{y(1-y)}\). The corresponding Peetre’s K-functional is defined by
where
and \(AC_{loc}[0 ,1]\) in the last equality denotes the class of all absolutely continuous functions defined on the closed interval \([a, b] \subset [0 ,1]\). Then ∃ a constant \(M>0\) such that
Theorem 4
Suppose that \(g,g',g'' \in C[0,1]\) and \(y\in [0 ,1]\). Suppose also that ρ is a positive number. Then we have
for sufficiently large m, where
Proof
The following equality
is satisfied for \(g\in C[0, 1]\). This equality implies
If we apply the operators \(U_{m,\alpha }^{\beta ,\theta ,\rho } \) to each side of (3.1), we get
Let us estimate the right-hand side of (3.2) as follows:
for \(g \in W_{\phi }[0,1]\). Then there is a constant \(M>0\) such that
hold for sufficiently large m. Using the Cauchy–Schwarz inequality, one obtains
by (3.2)–(3.3). Considering \(\inf_{g \in W_{\phi }[0,1]}\) on the right-hand side of the last inequality, we deduce the desired result. □
The following corollary can be obtained from Theorem 4.
Corollary 2
Let \(g,g', g'' \in C[0,1]\), then
The Grüss-type inequalities were defined and studied by Acu et al. [5], and Gonska and Tachev [20] for a class of sequences of positive linear operators. To obtain a Grüss–Voronovskaja-type theorem for our operators \(U_{m,\alpha }^{\beta ,\theta ,\rho } \), we write
Theorem 5
Assume that \(\rho >0 \) and \(g,h\in C^{2}[0, 1]\). Then we have
for each \(y\in [0, 1]\).
Proof
We write
Since the operators \(U_{m,\alpha }^{\beta ,\theta ,\rho }\) converge uniformly to the function \(g(y)\), we have
by Theorem 1. We immediately prove the theorem if we pass to the limit because limits of \(m U_{m,\alpha }^{\beta ,\theta ,\rho } (e_{1}-y;y) \) and \(m U_{m,\alpha }^{\beta ,\theta ,\rho } ((e_{1}-y)^{2};y) \) are finite by Corollary 1. □
Theorem 6
For every g in \(C_{B}[0,1]\) (the set of all real-valued bounded and continuous functions defined on \([0,1]\)) such that \(g', g'' \in C_{B}[0,1]\). Then, for each \(y\in [0 ,1]\) and \(\rho >0 \), we have
uniformly on \([0 ,1]\).
Proof
Let \(y\in [0 ,1]\) and \(\rho >0 \). For any g in \(C_{B}[0, 1]\), it follows from Taylor’s theorem that
Here, \(r_{y}(t)\) stands for the Peano form of the remainder. Note that \(r_{y}\in C[0, 1]\) and \(r_{y}(t)\to 0\) as \(t\to y\). By applying \(U_{m,\alpha }^{\beta ,\theta ,\rho } (g;y)\) to identity (3.4), we get
Using the Cauchy–Schwarz inequality, we have
Since
from Lemma 1 and \(\lim_{m \to \infty } U_{m,\alpha }^{\beta ,\theta ,\rho } (r^{2}_{y}(t);y)=0\), it means
Thus we immediately obtain the desired result by applying limit to (3.5) and by considering Corollary 1. □
4 Numerical analysis
With the help of MATHEMATICA, we numerically examine our theoretical results with a view of convergence and error of approximation of our newly constructed operators (2.3). We first choose the parameters β, θ, ρ, α as \(\beta =0.2\), \(\theta =0.1\), \(\rho =1.5\), \(\alpha =0.9\) and the function
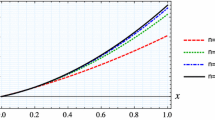
In Fig. 1, we examine the convergence of (2.3) for different m values, and in Fig. 2, we compare the convergence of our operators with \(U_{m,\alpha }^{\rho }\).
We also study the approximation properties of (2.3) by considering the following function:
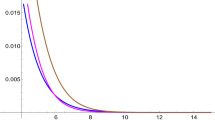
We take \(m=20\), \(\alpha =0.9 \), \(\beta =1\), \(\theta =1\) \(\rho =2\) to obtain Fig. 3 to see the approximation of our operators. In Fig. 4, we give the approximations of our operators for \(\alpha =0.9 \), \(\beta =\theta =1\), \(\rho =2\) and for different values of m. We give a table to compare the approximations.
It is clear from the Tables 1–2 and Figures 1–4 that our new operators are the generalization of the operators presented in the literature. They have fewer errors of approximation if we change the parameters α, β, θ, and ρ. Finally they have better approximations if we increase the values of m.
Availability of data and materials
Not applicable.
References
Acar, T., Acu, A.M., Manav, N.: Approximation of functions by genuine Bernstein-Durrmeyer type operators. J. Math. Inequal. 12(4), 975–987 (2018)
Acar, T., Aral, A., Mohiuddine, S.A.: Approximation by bivariate \((p,q)\)-Bernstein-Kantorovich operators. Iran. J. Sci. Technol. Trans. A, Sci. 42, 655–662 (2018)
Acar, T., Mohiuddine, S.A., Mursaleen, M.: Approximation by \((p,q)\)-Baskakov-Durrmeyer-Stancu operators. Complex Anal. Oper. Theory 12, 1453–1468 (2018)
Acu, A.M., Acar, T., Radu, V.A.: Approximation by modified \(U_{n}^{\rho }\) operators. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 113, 2715–2729 (2019)
Acu, A.M., Gonska, H.H., Rasa, I.: Grüss-type and Ostrowski-type inequalities in approximation theory. Ukr. Math. J. 63(6), 843–864 (2011)
Acu, A.M., Radu, V.A.: Approximation by certain operators linking the α-Bernstein and the genuine α-Bernstein-Durrmeyer operators. In: N. Deo, V. Gupta, A.M. Acu, P.N. Agrawal (eds.) Mathematical Analysis I: Approximation Theory, ICRAPAM 2018. Springer Proceedings in Mathematics & Statistics, vol. 306. Springer, Singapore (2020)
Aral, A., Erbay, H.: Parametric generalization of Baskakov operators. Math. Commun. 24, 119–131 (2019)
Belen, C., Mohiuddine, S.A.: Generalized weighted statistical convergence and application. Appl. Math. Comput. 219, 9821–9826 (2013)
Bernstein, S.N.: Démonstration du théorème de Weierstrass fondée sur le calcul des probabilités. Commun. Kharkov Math. Soc. 13, 1–2 (1912/1913)
Braha, N.L., Srivastava, H.M., Mohiuddine, S.A.: A Korovkin’s type approximation theorem for periodic functions via the statistical summability of the generalized de la Vallée Poussin mean. Appl. Math. Comput. 228, 162–169 (2014)
Cai, Q.-B.: The Bézier variant of Kantorovich type λ-Bernstein operators. J. Inequal. Appl. 2018, Article 90 (2018)
Cai, Q.-B., Cheng, W.-T., Çekim, B.: Bivariatea α, q-Bernstein-Kantorovich operators and GBS operators of bivariate α, q-Bernstein-Kantorovich type. Mathematics 7(12), Article ID 1161 (2019)
Cai, Q.-B., Lian, B.Y., Zhou, G.: Approximation properties of λ-Bernstein operators. J. Inequal. Appl. 2018, Article 61 (2018)
Chen, W.: On the modified Bernstein-Durrmeyer operator, Report of the Fifth Chinese Conference on Approximation Theory, Zhen Zhou, China (1987)
Chen, X., Tan, J., Liu, Z., Xie, J.: Approximation of functions by a new family of generalized Bernstein operators. J. Math. Anal. Appl. 450, 244–261 (2017)
Durrmeyer, J.L.: Une formule dinversion de la transformée de Laplace: applications á la théorie des moments, Thése de 3e cycle Paris (1967)
Gonska, H.H., Păltănea, R.: Simultaneous approximation by a class of Bernstein-Durrmeyer operators preserving linear functions. Czechoslov. Math. J. 60(135), 783–799 (2010)
Gonska, H.H., Păltănea, R.: Quantitative convergence theorems for a class of Bernstein-Durrmeyer operators preserving linear functions. Ukr. Math. J. 62, 913–922 (2010)
Gonska, H.H., Raşa, I., Stănilă, E.D.: The eigenstructure of operators linking the Bernstein and the genuine Bernstein-Durrmeyer operators. Mediterr. J. Math. 11(2), 561–576 (2014)
Gonska, H.H., Tachev, G.: Grüss-type inequalities for positive linear operators with second order moduli. Mat. Vesn. 63(4), 247–252 (2011)
Goodman, T.N.T., Sharma, A.: A modified Bernstein-Schoenberg operator. In: Sendov, B., et al. (eds.) Proc. Conf. Constructive Theory of Functions, Varna, 1987, pp. 166–173. Publ. House Bulg. Acad. Sci, Sofia (1988)
Kadak, U., Mohiuddine, S.A.: Generalized statistically almost convergence based on the difference operator which includes the \((p,q)\)-gamma function and related approximation theorems. Results Math. 73, 9 (2018)
Kajla, A., Miclăuş, D.: Blending type approximation by GBS operators of generalized Bernstein-Durrmeyer type. Results Math. 73, 1 (2018)
Kajla, A., Mohiuddine, S.A., Alotaibi, A., Goyal, M., Singh, K.K.: Approximation by ϑ-Baskakov-Durrmeyer-type hybrid operators. Iran. J. Sci. Technol. Trans. A, Sci. 44, 1111–1118 (2020)
Mohiuddine, S.A.: Approximation by bivariate generalized Bernstein-Schurer operators and associated GBS operators. Adv. Differ. Equ. 2020, 676 (2020)
Mohiuddine, S.A., Acar, T., Alotaibi, A.: Construction of a new family of Bernstein-Kantorovich operators. Math. Methods Appl. Sci. 40, 7749–7759 (2017)
Mohiuddine, S.A., Ahmad, N., Özger, F., Alotaibi, A., Hazarika, B.: Approximation by the parametric generalization of Baskakov-Kantorovich operators linking with Stancu operators. Iran. J. Sci. Technol. Trans. A, Sci. (2020). https://doi.org/10.1007/s40995-020-01024-w
Mohiuddine, S.A., Alamri, B.A.S.: Generalization of equi-statistical convergence via weighted lacunary sequence with associated Korovkin and Voronovskaya type approximation theorems. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 113(3), 1955–1973 (2019)
Mohiuddine, S.A., Asiri, A., Hazarika, B.: Weighted statistical convergence through difference operator of sequences of fuzzy numbers with application to fuzzy approximation theorems. Int. J. Gen. Syst. 48(5), 492–506 (2019)
Mohiuddine, S.A., Hazarika, B., Alghamdi, M.A.: Ideal relatively uniform convergence with Korovkin and Voronovskaya types approximation theorems. Filomat 33(14), 4549–4560 (2019)
Mohiuddine, S.A., Kajla, A., Mursaleen, M., Alghamdi, M.A.: Blending type approximation by τ-Baskakov-Durrmeyer type hybrid operators. Adv. Differ. Equ. 2020, 467 (2020)
Mohiuddine, S.A., Özger, F.: Approximation of functions by Stancu variant of Bernstein-Kantorovich operators based on shape parameter α. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 114, 70 (2020)
Mursaleen, M., Ansari, K.J., Khan, A.: Approximation by a Kantorovich type q-Bernstein-Stancu operators. Complex Anal. Oper. Theory 11(1), 85–107 (2017)
Mursaleen, M., Rahman, S., Ansari, K.J.: Approximation by Jakimoski-Leviatan-Stancu-Durrmeyer type operators. Filomat 33(6), 1517–1530 (2019)
Nasiruzzaman, M., Rao, N., Wazir, S., Kumar, R.: Approximation on parametric extension of Baskakov-Durrmeyer operators on weighted spaces. J. Inequal. Appl. 2019, Article ID 103 (2019)
Özger, F.: Weighted statistical approximation properties of univariate and bivariate λ-Kantorovich operators. Filomat 33(11), 1–15 (2019)
Özger, F.: On new Bézier bases with Schurer polynomials and corresponding results in approximation theory. Commun. Fac. Sci. Univ. Ank. Sér. A1 Math. Stat. 69(1), 376–393 (2020)
Özger, F., Demirci, K., Yıldız, S.: Approximation by Kantorovich variant of λ-Schurer operators and related numerical results. In: Topics in Contemporary Mathematical Analysis and Applications, pp. 77–94. CRC Press, Boca Raton (2020). ISBN 9780367532666
Özger, F., Srivastava, H.M., Mohiuddine, S.A.: Approximation of functions by a new class of generalized Bernstein-Schurer operators. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 114, 173 (2020)
Păltănea, R.: Sur un operateur polynômial défini sur l’ensemble des fonctions intégrables. Babeş Bolyai Univ., Fac. Math., Res. Semin. 2, 101–106 (1983)
Păltănea, R.: A class of Durrmeyer type operators preserving linear functions. Ann. Tiberiu Popoviciu Sem. Funct. Equat. Approxim. Convex., Cluj-Napoca 5, 109–117 (2007)
Rao, N., Nasiruzamman, M.: A generalized Dunkl type modifications of Phillips operators. J. Inequal. Appl. 2018, 323 (2018)
Srivastava, H.M., Özger, F., Mohiuddine, S.A.: Construction of Stancu-type Bernstein operators based on Bézier bases with shape parameter λ. Symmetry 11(3), Article ID 316 (2019)
Stancu, D.D.: Approximation of functions by a new class of linear polynomial operators. Rev. Roum. Math. Pures Appl. 13(8), 1173–1194 (1968)
Wafi, A., Rao, N.: Szász-gamma operators based on Dunkl analogue. Iran. J. Sci. Technol. Trans. A, Sci. 43, 213–223 (2019)
Wafi, A., Rao, N., Deepmala: Approximation properties of \((p,q)\)-variant of Stancu-Schurer operators. Bol. Soc. Parana. Mat. 37(4), 137–151 (2019)
Acknowledgements
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant no. (RG-84-130-38). The authors, therefore, acknowledge with thanks DSR for technical and financial support.
Funding
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant no. (RG-84-130-38).
Author information
Authors and Affiliations
Contributions
The authors contributed equally and significantly in writing this paper. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alotaibi, A., Özger, F., Mohiuddine, S.A. et al. Approximation of functions by a class of Durrmeyer–Stancu type operators which includes Euler’s beta function. Adv Differ Equ 2021, 13 (2021). https://doi.org/10.1186/s13662-020-03164-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03164-0