Abstract
The coherent propagation and amplification of high-power laser beams in a multicore fiber (MCF) of 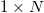 and
and 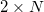 lattices of weakly coupled cores is studied. Exact stable analytical nonlinear solutions are found in the form of the out-of-phase distribution that describe the coherent propagation of wave beams in such MCFs. The use of these distributions makes it possible to operate with laser radiation with a power of up to 2N times of the critical self-focusing power in homogeneous media. The analytical results are confirmed by the direct numerical simulation of the wave equation. The limitations on active fiber parameters for stable amplification of the found out-of-phase solution are determined.
lattices of weakly coupled cores is studied. Exact stable analytical nonlinear solutions are found in the form of the out-of-phase distribution that describe the coherent propagation of wave beams in such MCFs. The use of these distributions makes it possible to operate with laser radiation with a power of up to 2N times of the critical self-focusing power in homogeneous media. The analytical results are confirmed by the direct numerical simulation of the wave equation. The limitations on active fiber parameters for stable amplification of the found out-of-phase solution are determined.
Export citation and abstract BibTeX RIS
Introduction
Transverse filamentation instability in media with cubic nonlinearity is the most important mechanism restricting the propagation of high-power laser pulses [1]. In fact, this is a fundamental limitation for the generation of high-power laser pulses. Currently, several mechanisms are proposed to bypass this dangerous self-focusing instability. First, the transverse filamentation instability in media with an inertial nonlinear response [2] has no specific transverse scale with the maximum growth rate. Second, the instability is suppressed for partially coherent radiation, if the correlation radius is less than the scale of the maximal growth rate [3–5]. Third, the filamentation instability can be suppressed in the case of few-cycle laser pulses, for which the synchronization between pulses and growing field perturbations can be disturbed [6,7]. This takes place for intense laser pulses of ultrashort durations, when the nonlinear dependence of the group velocity on the light intensity comes into play.
To eliminate filamentation instability, multicore fibers (MCF) can be used to achieve coherent propagation of laser pulses at a power level significantly exceeding the critical self-focusing power in homogeneous media [8–12]. However, there is a specific critical self-focusing power for in-phase wave field distributions in such MCF [13–19]. Nevertheless, a number of interesting results were obtained for such systems: generation of a supercontinuum [20–22], shortening of the laser pulse duration [15,16,21–25], demonstration of the nonlinear switching [26], and formation of light bullets [16,21–24,27–31]. Recently, strongly varying stable nonlinear solutions have been found in MCF from cores located in a ring, allowing to operate with a total power being noticeably larger than the power that can be transmitted in a single core [32]. Moreover, these out-of-phase nonlinear solutions still survive even in a strongly deformed MCF [25].
However, the technological problems in the manufacturing of such MCFs are quite large. At the same time, significant success was achieved in the creation of MCF with quasi-one-dimensional coupled cores [16]. These MCFs consist of a small number of lines with tens or hundreds of cores along. Therefore, the generalization of the methods of coherent radiation transport to such quasi-one-dimensional MCFs seems to be interesting and important.
In this paper, we generalize the out-of-phase distribution of the wave field [32] to the case of MCF that consist of one-dimensional and two-dimensional lattices of cores. Let the fundamental guided modes of optical waveguides oriented parallel to the z-axis be weakly coupled to each other. Then, the propagation of laser radiation in the MCF can be approximately described as a superposition of modes localized in each core. Considering one-dimensional arrays of cores and assuming all cores to be the same, we obtain the system of equations for the field amplitudes in the cores [33,34]

The envelope amplitude un
in the n-th core changes during propagation along the z-axis under the influence of the following factors: the Kerr nonlinearity of a single core, amplification in an active media, and interaction with the nearest neighboring cores. Here, the index n varies from 1 to N, the evolutionary coordinate z is normalized to the coupling coefficient χ between neighboring cores, the envelope complex amplitude of the wave packet is measured in 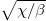 , β is the nonlinearity coefficient, and
, β is the nonlinearity coefficient, and  is the normalized gain ratio. Equation (1) preserves the total power
is the normalized gain ratio. Equation (1) preserves the total power 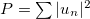 in the absence of amplification
in the absence of amplification 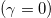 . The applicability of eqs. (1) is limited by the approximation of the single-mode wave field propagation in each core. It is violated, when the radiation power in any core becomes close to the critical self-focusing power in homogeneous media
. The applicability of eqs. (1) is limited by the approximation of the single-mode wave field propagation in each core. It is violated, when the radiation power in any core becomes close to the critical self-focusing power in homogeneous media 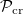 .
.
Long-wave approximation
Let us consider the case of no gain 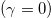 in this section. The dispersion relation for equation (1) is
in this section. The dispersion relation for equation (1) is 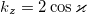 for
for 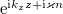 processes. Since we are interested in stationary distributions, we will search for them near the points of zero group velocity:
processes. Since we are interested in stationary distributions, we will search for them near the points of zero group velocity: 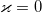 and
and 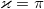 . They correspond to in-phase
. They correspond to in-phase 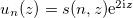 and out-of-phase
and out-of-phase 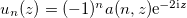 field distributions. Here s > 0 and a > 0 are the envelopes of the desired solutions,
field distributions. Here s > 0 and a > 0 are the envelopes of the desired solutions, 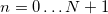 is the coordinate along the lattice. We specially added two "virtual" points
is the coordinate along the lattice. We specially added two "virtual" points 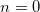 and
and 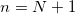 at the boundaries, so that the field at these points is zero:
at the boundaries, so that the field at these points is zero:

Let us analyze a one-dimensional lattice consisting of a large but finite number of cores 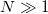 . Assuming that the envelopes of the field are a smooth function
. Assuming that the envelopes of the field are a smooth function

we arrive at the nonlinear Schrödinger equations for in-phase and out-of-phase envelopes


Here and below, we analyze in-phase and out-of-phase solutions in parallel due to their similarity. A distinctive feature of eq. (5) for the out-of-phase envelope is the presence of the negative sign of the second derivative. As a result, the focusing nonlinearity of the medium behaves as the defocusing one for the out-of-phase distribution of the wave field. This suggests the existence of a stable out-of-phase distribution of the wave field, which is not subject to filamentation instability.
We will seek a solution in the form 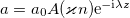 and
and 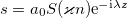 , where a0 is the wave beam amplitude and λ is the longitudinal wave number. Substituting this expression into eqs. (4), (5) we obtain the equation for the envelopes A, S
, where a0 is the wave beam amplitude and λ is the longitudinal wave number. Substituting this expression into eqs. (4), (5) we obtain the equation for the envelopes A, S


These equations have a solution in the form 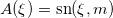 ,
, 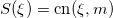 with parameters obtained from the boundary conditions (2):
with parameters obtained from the boundary conditions (2):

Here, 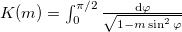 is the complete elliptic integral of the first kind, the parameter m varies in the range
is the complete elliptic integral of the first kind, the parameter m varies in the range ![$[0,1]$](https://content.cld.iop.org/journals/0295-5075/132/5/54001/revision2/epl20383ieqn24.gif) and is found from the transcendental equation
and is found from the transcendental equation

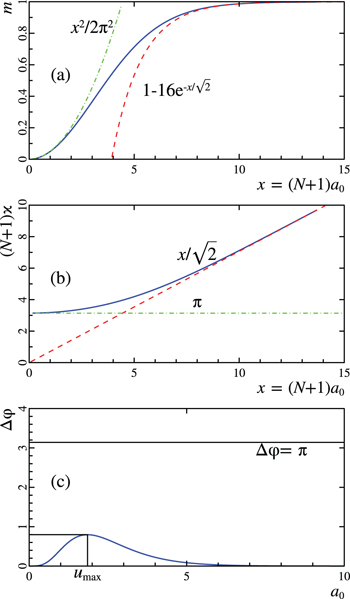
The graphical solution for the parameter m is shown in fig. 1(a), which has the form of a step with an inflection point 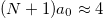 . The asymptotics of this solution at small and large amplitudes have the form
. The asymptotics of this solution at small and large amplitudes have the form

It is seen that the asymptotics for the solution of the parameter m are in good agreement with the graphic solution. Accordingly, for the transverse wave number ϰ , we obtain approximations

Fig. 1: (a), (b): dependences of m and ϰ on the dimensionless parameter 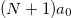 , and their approximations (10), (11). (c) Maximum of phase difference according to eq. (15).
, and their approximations (10), (11). (c) Maximum of phase difference according to eq. (15).
Download figure:
Standard imageAsymptotics of the parameters 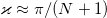 ,
, 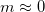 for small amplitudes give the same solutions similar to the field in a plane waveguide [35]
for small amplitudes give the same solutions similar to the field in a plane waveguide [35]

Asymptotics of the parameters  ,
, 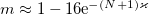 for large amplitudes give fundamentally different solutions
for large amplitudes give fundamentally different solutions


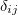 is the Kronecker symbol.
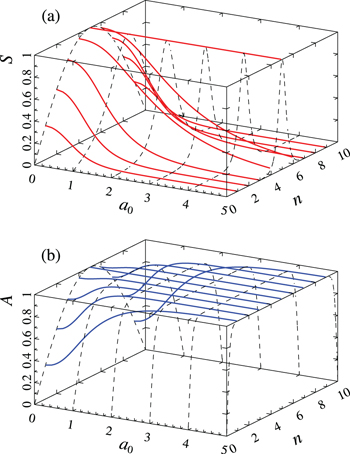
is the Kronecker symbol.The in-phase distribution of wave beams tends to localize in one core with an increase in amplitude (13). Amplitude distributions are shown in fig. 2(a). This is a discrete analogue of the NSE soliton [33]. We note that the applicability conditions (3) of the shortened solution for s are violated at large amplitudes. Nevertheless, the tendency toward localization and self-isolation of the field in individual core is maintained [6,33].
Fig. 2: Amplitude profiles (14) of the in-phase (a) and out-of-phase (b) solutions depending on the amplitude of a0 for N = 9.
Download figure:
Standard imageOn the contrary, the out-of-phase distribution of wave beams evenly fills all the optical cores with an increase in amplitude (13a). This effect can be used to transport strongly powerful laser beams, whose power can significantly exceed the critical self-focusing power in single core. Amplitude distributions are shown in fig. 2(b). Thus, the most useful stationary solution for the complex envelopes of the wave field has the form

Stability analysis
Solution (14) was obtained within the framework of the approximate equation (4). The discreteness presented in eq. (1) can violate the stability of this approximate solution and lead to stochastic dynamics, if the difference in the nonlinear phase change  between adjacent cores at the coupling length between them (equal to 1 for eq. (1)) will exceed π [17,36]. In our case, the phase change difference is equal to the difference in intensities
between adjacent cores at the coupling length between them (equal to 1 for eq. (1)) will exceed π [17,36]. In our case, the phase change difference is equal to the difference in intensities  near the boundary, where the gradients are maximal. The value of
near the boundary, where the gradients are maximal. The value of 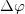 can become somehow noticeable only for the field amplitudes
can become somehow noticeable only for the field amplitudes 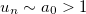 . So, it suffices to estimate the phase change difference in the region
. So, it suffices to estimate the phase change difference in the region 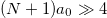 . Then the series expansion of the solution (14) at the boundary yields
. Then the series expansion of the solution (14) at the boundary yields

Here, we used approximations 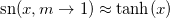 and
and 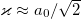 for
for 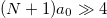 (see fig. 1). The maximum phase change difference
(see fig. 1). The maximum phase change difference  is achieved at the field amplitude
is achieved at the field amplitude 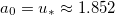 . So, reaching the threshold of stochastic dynamics on solution (14) is impossible (fig. 1(c)). The reason is as follows. Despite the large values of ϰ for
. So, reaching the threshold of stochastic dynamics on solution (14) is impossible (fig. 1(c)). The reason is as follows. Despite the large values of ϰ for  , the entire difference in the wave field distribution a(n) from 0 to a0 falls into the "virtual" region
, the entire difference in the wave field distribution a(n) from 0 to a0 falls into the "virtual" region  , and there are no sharp gradients of the wave field in the physically correct region
, and there are no sharp gradients of the wave field in the physically correct region 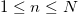 .
.
The knowledge of out-of-phase solution (14) allows us to predict the nonlinear dynamics of the wave field in the active MCF when the power and, correspondingly, the maximum amplitude 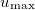 increase on the scale of the gain length being much longer than the coupling one
increase on the scale of the gain length being much longer than the coupling one 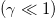 . As the wave beam power increases exponentially, we should expect adiabatically smooth equalization of the amplitudes in all cores for
. As the wave beam power increases exponentially, we should expect adiabatically smooth equalization of the amplitudes in all cores for 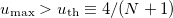 . Adiabaticity will not be violated if the gain ratio is less than the difference in the propagation constants between the out-of-phase mode and other MCF modes. The propagation constants in the MCF are
. Adiabaticity will not be violated if the gain ratio is less than the difference in the propagation constants between the out-of-phase mode and other MCF modes. The propagation constants in the MCF are 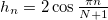 . The smallest of them,
. The smallest of them, 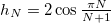 , corresponds to the found out-of-phase distribution, eq. (14). Then, the condition of the amplification adiabaticity takes the form
, corresponds to the found out-of-phase distribution, eq. (14). Then, the condition of the amplification adiabaticity takes the form

It can be seen from the expression that the limiting gain, at which there is no excitation of other modes, decreases quite rapidly as the number of the cores increases.
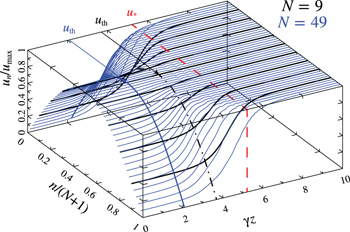
Figure 3 shows the evolution of the spatial distribution of the wave beam in the active MCF with the gain ratio 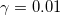 . The calculations were performed for MCF with 9 cores (black curves) and 49 cores (blue curves) in the framework of eq. (1). The field amplitude is normalized to the maximum value
. The calculations were performed for MCF with 9 cores (black curves) and 49 cores (blue curves) in the framework of eq. (1). The field amplitude is normalized to the maximum value 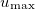 . It is seen that the beam distribution is close to
. It is seen that the beam distribution is close to 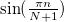 up to the amplitudes
up to the amplitudes 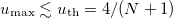 . The adiabatic equalization of the amplitude distribution is observed with a further increase in the field amplitude during amplification. When the field amplitude is
. The adiabatic equalization of the amplitude distribution is observed with a further increase in the field amplitude during amplification. When the field amplitude is 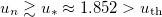 , the beam distribution over all cores becomes completely uniform. Thus, the results of numerical simulations confirm the stability of the found solution (14) and the adiabatic equalization of the beam distribution from the inhomogeneous to uniform ones with an increase in the total power.
, the beam distribution over all cores becomes completely uniform. Thus, the results of numerical simulations confirm the stability of the found solution (14) and the adiabatic equalization of the beam distribution from the inhomogeneous to uniform ones with an increase in the total power.
Fig. 3: Structure of the numerically found solution depending on the evolutionary coordinate for a different number of cores: 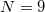 (black curves) and
(black curves) and 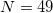 (blue curves). The gain ratio is
(blue curves). The gain ratio is 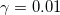 . The initial distribution corresponds to solution (14). The transverse curves denote the thresholds
. The initial distribution corresponds to solution (14). The transverse curves denote the thresholds  and
and 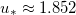 .
.
Download figure:
Standard imageCase of  lattice
lattice
Out-of-phase solution (14) can be generalized to the case of the lattice 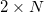 . In this case, the system of equations for the field amplitudes takes the form
. In this case, the system of equations for the field amplitudes takes the form


Neglecting the diagonal coupling 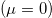 and making the change of variables
and making the change of variables 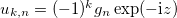 , we arrive at the equation
, we arrive at the equation

which matches eq. (1) with  exactly. Thus, found solution (14) for a one-dimensional lattice can be easily generalized for the
exactly. Thus, found solution (14) for a one-dimensional lattice can be easily generalized for the  lattice.
lattice.
The presence of a weak diagonal coupling  allows the development of filamentation instability. Let us determine the conditions for the development of this instability. It has been shown above that the amplitude distribution in the cores is uniform (eq. (14)) in the case of
allows the development of filamentation instability. Let us determine the conditions for the development of this instability. It has been shown above that the amplitude distribution in the cores is uniform (eq. (14)) in the case of 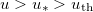 . Then, the unperturbed solution with the amplitude a0 can be written in the form
. Then, the unperturbed solution with the amplitude a0 can be written in the form 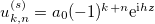 , where
, where 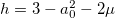 . Linearization of eqs. (17) for a wave field of the form
. Linearization of eqs. (17) for a wave field of the form ![$u_{1,n}=a_0[(-1)^n+\delta a\mathrm{e}^{\mathrm{i} \lambda z + \mathrm{i} \varkappa n}]\mathrm{e}^{\mathrm{i} h z}$](https://content.cld.iop.org/journals/0295-5075/132/5/54001/revision2/epl20383ieqn70.gif) ,
, ![$u_{2,n}=a_0[(-1)^{n+1}+\delta b\mathrm{e}^{\mathrm{i} \lambda z + \mathrm{i} \varkappa n}]\mathrm{e}^{\mathrm{i} h z}$](https://content.cld.iop.org/journals/0295-5075/132/5/54001/revision2/epl20383ieqn71.gif) with small perturbations
with small perturbations 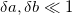 gives the dispersion relations
gives the dispersion relations
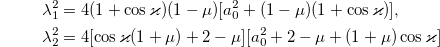
from the condition for the existence of nonzero perturbations. Analysis of the dispersion relations shows the presence of filamentation instability 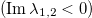 for the diagonal coefficient
for the diagonal coefficient 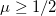 . This corresponds to a rather large coupling coefficient, which violates the approximation of weakly coupled cores that we use. Therefore, the found out-of-phase distribution of the wave field in the two-dimensional lattice
. This corresponds to a rather large coupling coefficient, which violates the approximation of weakly coupled cores that we use. Therefore, the found out-of-phase distribution of the wave field in the two-dimensional lattice  is not subject to filamentation instability.
is not subject to filamentation instability.
Numerical simulations
To confirm the existence of the found out-of-phase mode in the case of a two-dimensional lattice and adiabatic equalization of amplitude distribution with the increasing power, detailed numerical studies were carried out within the framework of a more general model described by the nonlinear unidirectional wave equation [32]

with the potential ![$U = \sum_n \exp[-\frac{((x-x_n)^2+(y-y_n)^2)^2}{r_n^4}]$](https://content.cld.iop.org/journals/0295-5075/132/5/54001/revision2/epl20383ieqn76.gif) . Here, xn
, yn
, rn
are the position and radius of the cores, n0 is the refractive index of the cladding,
. Here, xn
, yn
, rn
are the position and radius of the cores, n0 is the refractive index of the cladding, 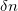 is the difference between the refractive indices of the cores and the medium, and n2 is the nonlinear refractive index. The operator
is the difference between the refractive indices of the cores and the medium, and n2 is the nonlinear refractive index. The operator 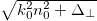 can be easily calculated in Fourier space and allows one to properly describe wave fields with transverse scales of order of the wavelength by taking into account spherical aberrations.
can be easily calculated in Fourier space and allows one to properly describe wave fields with transverse scales of order of the wavelength by taking into account spherical aberrations.
The calculations were performed for the wavelength 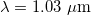 for a silica fiber (refractive index
for a silica fiber (refractive index  and the critical self-focusing power 4 MW). The difference in the refractive indices between the cores and the cladding was
and the critical self-focusing power 4 MW). The difference in the refractive indices between the cores and the cladding was 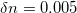 . The diameters of the cores with a super-Gaussian profile were
. The diameters of the cores with a super-Gaussian profile were 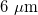 , and the distance between them was
, and the distance between them was 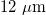 . The fields in each core were specified in the form of a Gaussian function closest to the field of the fundamental mode of an individual core.
. The fields in each core were specified in the form of a Gaussian function closest to the field of the fundamental mode of an individual core.
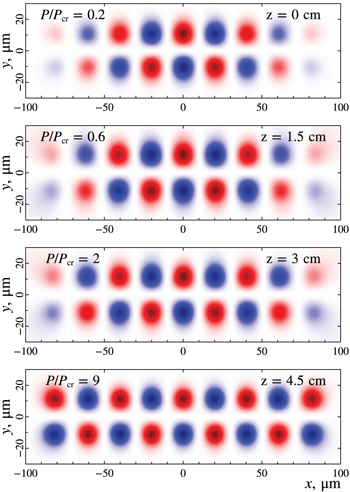
Figure 4 shows the results of numerical simulations in the active MCF for a two-dimensional lattice 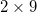 with a gain ratio of
with a gain ratio of 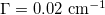 . The initial wave field have a low power
. The initial wave field have a low power 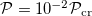 with amplitudes in each of the cores determined by the found solution
with amplitudes in each of the cores determined by the found solution 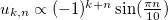 . The initial noise level was about 3%. It is seen that the field amplitudes in all the cores become uniform with the growth of the total power, which confirms the stability of the found solution with respect to the filamentation instability. Numerical results show the possibility of transporting up to
. The initial noise level was about 3%. It is seen that the field amplitudes in all the cores become uniform with the growth of the total power, which confirms the stability of the found solution with respect to the filamentation instability. Numerical results show the possibility of transporting up to 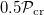 in each core, even if the wave field narrowing in the cores becomes noticeable (fig. 4). For an MCF of
in each core, even if the wave field narrowing in the cores becomes noticeable (fig. 4). For an MCF of 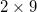 cores, this is about 35 MW of total power. Thus, the results of numerical simulation confirm the stability of the solutions found for the two-dimensional matrix and adiabatic equalization of amplitudes in the found out-of-phase mode with the increasing total power in the active MCF. Along with this, simulation was carried out for a larger number of optical cores. For example, according to (16), one should use
cores, this is about 35 MW of total power. Thus, the results of numerical simulation confirm the stability of the solutions found for the two-dimensional matrix and adiabatic equalization of amplitudes in the found out-of-phase mode with the increasing total power in the active MCF. Along with this, simulation was carried out for a larger number of optical cores. For example, according to (16), one should use 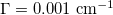 for an MCF of
for an MCF of 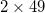 cores, which give a quasi-uniform distribution of wave field intensities on the length of less than 1 m. In this case, the total power will be about 200 MW.
cores, which give a quasi-uniform distribution of wave field intensities on the length of less than 1 m. In this case, the total power will be about 200 MW.
Fig. 4: Distributions of 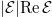 in a wave beam at different power values
in a wave beam at different power values 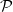 in the two-dimensional
in the two-dimensional 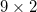 lattice with the gain ratio
lattice with the gain ratio  .
.
Download figure:
Standard imageConclusion
The propagation of laser beams in a multi-core fiber consisting of 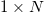 and
and 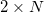 lattices of weakly coupled cores is considered. Exact stable nonlinear solutions are found for the out-of-phase mode, which describe the coherent propagation of wave beams in such fibers. Equalization of the wave field amplitudes in all cores with an increase in the total radiation power is shown. This makes it possible to operate with laser radiation with a power 2N times greater than the critical self-focusing power in homogeneous media. The stability of the solutions found is studied both with respect to filamentation instability and with respect to weak amplification in the active medium. The analytical results are confirmed by direct numerical simulations within the framework of the wave equation.
lattices of weakly coupled cores is considered. Exact stable nonlinear solutions are found for the out-of-phase mode, which describe the coherent propagation of wave beams in such fibers. Equalization of the wave field amplitudes in all cores with an increase in the total radiation power is shown. This makes it possible to operate with laser radiation with a power 2N times greater than the critical self-focusing power in homogeneous media. The stability of the solutions found is studied both with respect to filamentation instability and with respect to weak amplification in the active medium. The analytical results are confirmed by direct numerical simulations within the framework of the wave equation.
Acknowledgments
This work was supported by the Center of Excellence "Center of Photonics" funded by the Ministry of Science and Higher Education of the Russian Federation, contract No. 075-15-2020-906.