Introduction

The sampling plans are important instruments to judge the quality of manufactured products and components in many fields, including the packing industry, food industry, electrical engineering, aeronautical engineering, and automobile engineering. For instance, before final delivery of items to the customers, it is essential to confirm whether the product meets the specification laid down by the company. The decision of selecting reliable and higher quality products can be made through a statistical sampling approach. In the method of sampling, if the aim is to decide whether to accept or reject many manufactured products, this type of assessment system is usually called acceptance sampling; for more details, see Montgomery [36]. Thus, an acceptance-sampling plan is an investigative method in statistical quality control to make a judgment on submitted manufactured product lots, either to accept or reject. If the quality of the product is the lifetime of the product, then a sample of such products considered exemplify of the observed lifetimes of the goods are put further for testing. When a decision to accept or reject the lot, subject to the risks associated with the two types of errors (rejecting a good lot/accepting a bad lot), is possible, then such a procedure is known as acceptance-sampling plans based on life test. It needs specifications of a certain probability model prevailing the life of the products. Acceptance sampling was initiated by Dodge and Romig [22], and this method played a significant role in the manufacturing industry as well as quality management in business development. Bray and Lyon [19] have given the application of acceptance-sampling plans in the food industry. Broadly, acceptance-sampling plans are classified as variables sampling plans and attribute sampling plans. Variables sampling plans are useful when quality characteristics are measurable. When quality characteristics are not measurable, they can be classified as conforming or nonconforming.

A chief advantage in an acceptance-sampling plan is to optimize both the time and cost necessary for the conclusion about the acceptance or rejection of the submitted lot of products in quality control or reliability tests. The acceptance-sampling plans could also give the preferred safeguard to both producers and consumers. Thus, in decision-making using acceptance-sampling schemes, both producer’s and consumer’s risks are required. An acceptance-sampling plan, which gives protection to both producer’s and consumer’s risks, is known as a well-designed plan. In life testing experiments, the sample size directly influences the cost of experimentation. Hence, a sampling plan is said to be more economical if it gives the smaller sample size, and to meet these situations, researchers are using more frequently single sampling plans. Whereas, if it is not possible to get the decision-based on the first sample, a double sampling plan can be employed. A generalized sampling plan is known as a double sampling plan and it performs better than a single sampling plan with respect to the sample size. Hence, there is a need to developing an edition of a double sampling plan for life test using groups, which will be called a two-stage group sampling in this paper. As compared to the single sampling plan, the two-stage sampling plan is more complex to handle. Some of the references on single and double acceptance-sampling plans under various life distributions based on truncated life tests can be seen; for example, Epstein [23], Goode and Kao [24], Gupta and Groll [26], Tsai and Wu [51], Balakrishnan et al. [15], Kantam et al. [33], Baklizi [13], Baklizi and El Masri [14], Aslam [2], Aslam and Jun [8], Aslam et al. [9, 11].

The main goal of acceptance-sampling plans in quality control is to minimize the sample size to save cost, time, and efforts. To achieve this, sometimes, an experimenter can test multiple items in practice, because testing time and cost can be saved by testing those items simultaneously. The items in a tester can be regarded as a group and the number of items in a group is called the group size. An acceptance-sampling plan based on such groups of items is called a group acceptance-sampling plan (GASP). If the GASP is used in conjunction with truncated life tests, it is called a GASP based on truncated life test, assuming that the lifetime of the product follows a certain probability distribution. For such a type of test, the determination of the sample size is equivalent to determine the number of groups. Pascual and Meeker [37] and Jun et al. [31] initiated these group-sampling plans. Subsequently, many authors concentrated on grouped sampling plan for the truncated life test; see example, Aslam et al. [10], Aslam and Jun [7], Rao [43, 44], Aslam et al. [11]. Rao and Rameshnaidu [45], Aslam et al. [12] proposed a new type of grouped sampling plan for truncated life tests, which are based on single and double group-sampling plans under the total number of failures from all groups under testing.

The group-sampling plans developed by the aforementioned researchers under classical statistics can only be applied when there is no uncertainty in the sample or parameters. If the observations or parameters are uncertain or indeterminate, the more popular approach is based on the fuzzy method. Hence, the sampling plans designed using fuzzy logic can be applied to make a decision on a lot of the product. More details about the fuzzy approach in different areas (such as engineering, project management, pattern recognition, transmission systems, multiobjective optimization, etc.) can be seen in Beg and Tabasam [16], Biswas et al. [18], Huang and Wei [27], Majumdar and Samanta [35], Peng and Dai [39], Peng and Liu [40], Peng and Yang [41], Peng [38], and Zhang and Xu [57]. In recent years, more attention has been given to developing a sampling plan using the fuzzy approach [1, 20, 21, 29,28,30, 32, 34, 46, 50, 52,53,54, 56].

The neutrosophic logic was introduced by Smarandache [47]. The neutrosophic logic is the extension of the fuzzy logic, and is a combination of measure of truth, a measure of falsehood, and measure of indeterminacy. The fuzzy logic is unable to give information about the measure of indeterminacy. Gulistan and Salma [25] discussed the application of neutrosophic logic using complex fuzzy sets. More information about neutrosophic logic can be seen in Yang [55], Peng and Dai [42], Zhang et al. [58], and Zhang et al. [59].

In recent years, neutrosophic logic is used as the generalization of fuzzy logic. Based on the neutrosophic logic, Smarandache [48, 49] introduced the neutrosophic statistics (NS) as an extension of classical statistics. The classical statistics cannot be applied when the data are obtained from the complex process and have indeterminate or uncertain values. In such a case, to analyze the data, neutrosophic statistics can be applied. The neutrosophic statistics provide information about the measure of indeterminacy which classical statistics does not provide. Therefore, neutrosophic statistics can be considered as the generalization of classical statistics. The neutrosophic statistics approach in sampling schemes was extensively used by different researchers including Aslam and Arif [5], Aslam and Raza [6], and Aslam [4]. Mostly, in earlier literature, Aslam et al. [12] studied a traditional improved group-sampling plans for Weibull distribution, while there is no research on improved group-sampling plans for Weibull distribution under the neutrosophic statistics. Aslam and Arif [5] worked on the sampling plan using the idea of sudden death testing. Aslam [4] proposed the attribute sampling plan using neutrosophic statistics. Aslam et al. [3] proposed the group-sampling plan under neutrosophic statistics.

In Aslam et al. [3] plan, the number of failures from each group is recorded and a lot of the product is rejected if in any group the number of failures is larger than the allowed number of failures. Note here that the plan proposed by Aslam et al. [3] can be improved by making the decision about the lot based on the total number of failures from all groups. In the literature, the group-sampling plan under neutrosophic statistics based on the total number of failures is not available. To address this gap, this paper proposes a single and a double group-sampling plan using the neutrosophic statistics. In the proposed sampling plans, the decision about the acceptance or rejection of the lot is made on the basis of the total number of failures from all groups. We assume that the lifetime of the manufactured goods follows the neutrosophic Weibull distribution. The proposed plan will be more efficient and effective than the crisp method of competitive sampling plans in terms of the average sample number. The rest of the paper is organized as follows: “Design of single group-sampling plan for Weibull distribution under neutrosophic statistics” deals with a single group-sampling plan for Weibull distribution based on neutrosophic statistics and compares it with the classical single group-sampling plan. In “Comparison with classical single group-sampling plan”, a design of a two-stage group-sampling plan for Weibull distribution under neutrosophic statistics is developed and compared with the classical two-stage group-sampling plan. Finally, in “Design of two-stage group-sampling plan for Weibull distribution under neutrosophic statistics”, some closing remarks are given.

Design of single group-sampling plan for Weibull distribution under neutrosophic statistics

Assume that the lifetime of the neutrosophic random variable \({T}_{\mathrm{N}}\epsilon \left[{T}_{\mathrm{L}},{T}_{\mathrm{U}}\right]\) where \(T_{L}\) denotes the determinate part and \(T_{U}\) denotes the indeterminate part follows the neutrosophic Weibull distribution. The neutrosophic random variable (nrv) in neutrosophic form can be written as follows: \({T}_{\mathrm{N}}={T}_{\mathrm{L}}+{T}_{\mathrm{U}}{I}_{\mathrm{N}};{I}_{\mathrm{N}}\epsilon \left[{I}_{\mathrm{L}},{I}_{\mathrm{U}}\right]\), where \({T}_{\mathrm{L}}\) and \({T}_{\mathrm{U}}{I}_{\mathrm{N}}\) are determinate and indeterminate parts of nrv, respectively. Note here that \({I}_{\mathrm{N}}\epsilon \left[{I}_{\mathrm{L}},{I}_{\mathrm{U}}\right]\) represents the indeterminate interval. The nrv reduces to the random variable under classical statistic if no indeterminate observation is in the data. The neutrosophic Weibull distribution was developed by Aslam and Arif [5] and neutrosophic cumulative distribution function (ncdf) is given below:

$${F}_{\mathrm{N}}\left({t}_{\mathrm{N}};{b}_{\mathrm{N}},{\sigma }_{\mathrm{N}}\right)=1-\mathrm{exp}\left(-{\left({t}_{\mathrm{N}}/{\sigma }_{\mathrm{N}}\right)}^{{b}_{\mathrm{N}}}\right);{t}_{\mathrm{N}}\ge 0,{b}_{\mathrm{N}}\epsilon \left[{b}_{\mathrm{L}},{b}_{\mathrm{U}}\right],{\sigma }_{\mathrm{N}}\epsilon \left[{\sigma }_{\mathrm{L}},{\sigma }_{\mathrm{U}}\right],$$
(1)

where \({b}_{\mathrm{N}}\epsilon \left[{b}_{\mathrm{L}},{b}_{\mathrm{U}}\right]\) is the neutrosophic shape parameter and \({\sigma }_{\mathrm{N}}\epsilon \left[{\sigma }_{\mathrm{L}},{\sigma }_{\mathrm{U}}\right]\) is the neutrosophic scale parameter. The mean lifetime \(\sigma_{{\text{N}}}\) of a neutrosophic Weibull distribution is \(\mu_{{\text{N}}} = \left( {{{\sigma_{{\text{N}}} } \mathord{\left/ {\vphantom {{\sigma_{{\text{N}}} } {b_{{\text{N}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} }}} \right)\Gamma \left( {{1 \mathord{\left/ {\vphantom {1 {b_{{\text{N}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} }}} \right)\). The neutrosophic form of ncdf and mean under indeterminacy can be written as, respectively, follows:

$${F}_{\mathrm{N}}\left({t}_{\mathrm{N}};{b}_{\mathrm{N}},{\sigma }_{\mathrm{N}}\right)=F\left(t;b,\sigma \right)+{b}_{\mathrm{N}}{I}_{\mathrm{NF}};s {I}_{\mathrm{N}}\epsilon \left[{I}_{\mathrm{LF}},{I}_{\mathrm{UF}}\right].$$
(2)
$${\mu }_{\mathrm{N}}=\mu +{c}_{\mathrm{N}}{I}_{\mathrm{N}\mu };{ I}_{\mathrm{N}\mu }\epsilon \left[{I}_{\mathrm{L}\mu },{I}_{\mathrm{U}\mu }\right].$$
(3)

Note here that \(F\left(t;b,\sigma \right)\) and \(\mu \) denote the cumulative distribution function (cdf) and mean under classical statistics, respectively. Also, \({b}_{\mathrm{N}}{I}_{\mathrm{NF}}; {I}_{\mathrm{N}}\epsilon \left[{I}_{\mathrm{LF}},{I}_{\mathrm{UF}}\right]\) and \({a}_{\mathrm{N}}{I}_{\mathrm{N}\mu }\); \( {I}_{\mathrm{N}}\epsilon \left[{I}_{\mathrm{L}\mu },{I}_{\mathrm{U}\mu }\right]\) denote the corresponding indeterminate parts.

The unknown neutrosophic scale parameter can be expressed in terms of the mean lifetime of a neutrosophic Weibull distribution as \(\sigma_{{\text{N}}} = \mu_{{\text{N}}} \left( {{{b_{{\text{N}}} } \mathord{\left/ {\vphantom {{b_{{\text{N}}} } {\Gamma ({1 \mathord{\left/ {\vphantom {1 {b_{{\text{N}}} )}}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} )}}}}} \right. \kern-\nulldelimiterspace} {\Gamma ({1 \mathord{\left/ {\vphantom {1 {b_{{\text{N}}} )}}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} )}}}}} \right)\). Let \(t_{{0{\text{N}}}}\) is denoted as specified experiment neutrosophic termination time, and \(\mu_{{0{\text{N}}}}\) is denoted as a neutrosophic target mean life. Thus, it is convenient to express specified experiment neutrosophic termination time as a multiple of the neutrosophic target mean life. That is, we consider \(t_{{0{\text{N}}}} = a\mu_{{0{\text{N}}}}\), where \(a\) is an experiment neutrosophic termination ratio. Hence, the failure probability of an item before the experiment time \(t_{{0{\text{N}}}}\) is obtained by putting \(t_{{0{\text{N}}}} = a\mu_{{0{\text{N}}}}\) and \(\mu_{{\text{N}}} = \left( {{{\sigma_{{\text{N}}} } \mathord{\left/ {\vphantom {{\sigma_{{\text{N}}} } {b_{{\text{N}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} }}} \right)\Gamma \left( {{1 \mathord{\left/ {\vphantom {1 {b_{{\text{N}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} }}} \right)\) into Eq. (1) can be expressed as follows:

$$ p_{{\text{N}}} = 1 - \exp \left( { - a_{{}}^{{b_{{\text{N}}} }} \left( {{{\mu_{{0{\text{N}}}} } \mathord{\left/ {\vphantom {{\mu_{{0{\text{N}}}} } {\mu_{{\text{N}}} }}} \right. \kern-\nulldelimiterspace} {\mu_{{\text{N}}} }}} \right)^{{b_{{\text{N}}} }} \left( {{{\Gamma ({1 \mathord{\left/ {\vphantom {1 {b_{{\text{N}}} )}}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} )}}} \mathord{\left/ {\vphantom {{\Gamma ({1 \mathord{\left/ {\vphantom {1 {b_{{\text{N}}} )}}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} )}}} {b_{{\text{N}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{N}}} }}} \right)^{{b_{{\text{N}}} }} } \right). $$
(4)

The probability of failure of an item in neutrosophic form can be written as:

$${p}_{\mathrm{N}}=p+{d}_{\mathrm{N}}{I}_{\mathrm{Np}};{I}_{\mathrm{Np}}\epsilon \left[{I}_{\mathrm{Lp}},{I}_{\mathrm{Up}}\right].$$
(5)

Note here that \(p\) denotes the probability of failure of an item under classical statistics and \({d}_{\mathrm{N}}{I}_{\mathrm{Np}}; {I}_{\mathrm{Np}}\epsilon \left[{I}_{\mathrm{Lp}},{I}_{\mathrm{Up}}\right]\) represents its indeterminate part.

The systematic procedure for a single group-sampling plan for Weibull distribution using neutrosophic statistics is as follows:

  1. Step 1.

    Select a neutrosophic random sample of size \(n_{{\text{N}}}\) from a lot.

  2. Step 2.

    Allot \(r_{{\text{N}}}\) items to each of \(g_{{\text{N}}}\) groups or testers, such that \(n_{{\text{N}}} = r_{{\text{N}}} g_{{\text{N}}}\).

  3. Step 3.

    Conduct the test for \(r_{{\text{N}}}\) items before the termination time \(t_{{0{\text{N}}}}\).

  4. Step 4.

    The lot will be accepted if the total number of failures from \(g_{{\text{N}}}\) groups is smaller than or equal to \(c_{{\text{N}}}\) before termination time \(t_{{0{\text{N}}}}\), otherwise reject the lot.

The proposed neutrosophic single group-sampling plan becomes a classical single group-sampling plan if \(r_{{\text{N}}} = r\), \(g_{{\text{N}}} = g\), and \(c_{{\text{N}}} = c\). In this plan, we are interested to find the design parameters like number of neutrosophic groups \(g_{{\text{N}}}\) and the neutrosophic acceptance number \(c_{{\text{N}}}\), in addition, to satisfying both producer’s risk (\(\alpha\)) and consumer’s risk (\(\beta\)) for specified values of the group sizes and true quality levels. Based on Step 4, the lot acceptance probability for the proposed plan is given by:

$$L\left({p}_{\mathrm{N}}\right)=\sum_{i=0}^{{c}_{\mathrm{N}}}\left(\begin{array}{c}{r}_{\mathrm{N}}{g}_{\mathrm{N}}\\ i\end{array}\right){p}_{\mathrm{N}}^{i}{\left(1-{p}_{\mathrm{N}}\right)}^{{r}_{\mathrm{N}}{g}_{\mathrm{N}}-i},$$
(6)

where \(p_{{\text{N}}}\) is given in Eq. (4).

The lot acceptance probability in the form of the indeterminate interval can be given as:

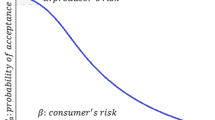
$$L\left({p}_{\mathrm{N}}\right)=L\left(\mathrm{p}\right)+{e}_{\mathrm{N}}{I}_{\mathrm{NL}}; {I}_{\mathrm{NL}}\epsilon \left[{I}_{\mathrm{LL}},{I}_{\mathrm{UL}}\right],$$
(7)

where \(L\left(\mathrm{p}\right)\) denote the lot acceptance probability under classical statistics and \({e}_{\mathrm{N}}{I}_{\mathrm{NL}}; {I}_{\mathrm{NL}}\epsilon \left[{I}_{\mathrm{LL}},{I}_{\mathrm{UL}}\right]\) shows the indeterminate part. Equation (7) reduces to lot acceptance probability under classical statistics when \({I}_{\mathrm{L}}=0\). The plan parameters are obtained using a two-point approach where producers aim that the probability of acceptance should be greater than 1 − \(\alpha\) at the acceptable quality limit (AQL), say \({p}_{1\mathrm{N}}\) and consumer’s wish that the probability of acceptance should be smaller than \(\beta\) at the limiting quality level (LQL), say \({p}_{2\mathrm{N}}\). Therefore, we obtain the design neutrosophic parameters by solving the following two inequalities:

$$L\left({p}_{1\mathrm{N}}\right)=\sum_{i=0}^{{c}_{\mathrm{N}}}\left(\begin{array}{c}{r}_{\mathrm{N}}{g}_{\mathrm{N}}\\ i\end{array}\right){p}_{\mathrm{N}}^{i}{\left(1-{p}_{\mathrm{N}}\right)}^{{r}_{\mathrm{N}}{g}_{\mathrm{N}}-i}\ge 1-\alpha $$
(8)
$$L\left({p}_{2\mathrm{N}}\right)=\sum_{i=0}^{{c}_{\mathrm{N}}}\left(\begin{array}{c}{r}_{\mathrm{N}}{g}_{\mathrm{N}}\\ i\end{array}\right){p}_{\mathrm{N}}^{i}{\left(1-{p}_{\mathrm{N}}\right)}^{{r}_{\mathrm{N}}{g}_{\mathrm{N}}-i}\le \beta .$$
(9)

If \(k_{1}\) is the AQL as mean ratio at the producer's risk and \(k_{2}\) is the LQL at the consumer’s risk, then design neutrosophic parameters can be found by satisfying the following inequalities:

$$L\left({p}_{1\mathrm{N}}|{\mu }_{\mathrm{N}}/{\mu }_{0\mathrm{N}}={k}_{1}\right)\ge 1-\alpha. $$
(10)
$$L\left({p}_{2\mathrm{N}}|{\mu }_{\mathrm{N}}/{\mu }_{0\mathrm{N}}={k}_{2}\right)\le \beta .$$
(11)

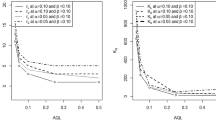
The above-mentioned inequalities are used to find the plan parameters of the proposed plan using the grid search method. Grid search is a process that searches exhaustively through a manually specified subset of the hyperparameter space of the targeted algorithm for more details refer to Bergstra and Bengio [17]. In grid search, several combinations are found that meet the given conditions, we choose those values of parameters where n or average sample number (ASN) is minimum. During the simulation, it is noted that several combinations of the parameters exist which satisfied the given conditions. The plan parameters where \({g}_{\mathrm{N}}\epsilon \left[{g}_{\mathrm{L}},{g}_{\mathrm{U}}\right]\) is minimum. Here, we regard as \(k_{2}\) = 1. Tables 1, 2 were built for neutrosophic Weibull distribution with neutrosophic shape parameter \({b}_{\mathrm{N}}\epsilon \left[\mathrm{1.9,2.1}\right]\) at \(\beta\) \(\epsilon \left[0.25, 0.10, 0.05, 0.01\right]\), mean ratios \(k_{1}\) \(\epsilon \left[\mathrm{2,4},\mathrm{6,8},10\right]\), two group sizes \({r}_{\mathrm{N}}\epsilon \left[\mathrm{4,6}\right]\) and \({r}_{\mathrm{N}}\epsilon \left[\mathrm{10,12}\right]\), and two termination times a = 0.5, 1.0. From tables, we noticed the following tendency:

  1. i.

    When the consumer’s risk value decreases, the number of groups (\(g_{{\text{N}}}\)) is increased.

  2. ii.

    When the mean ratio value increases, the number of groups (\(g_{{\text{N}}}\)) is decreased.

  3. iii.

    The number of groups (\(g_{{\text{N}}}\)) decreases with the increase of \(r_{{\text{N}}}\). That is, e.g., when other parametric values are fixed at \(\beta\) = 0.25, \({\mu }_{\mathrm{N}}/{\mu }_{0\mathrm{N}}=4\), \(b_{{\text{N}}}\) \(\epsilon \) [1.9, 2.1] from Tables 1 for \(r_{{\text{N}}}\) \(\epsilon \) [4, 6] with group size \(g_{{\text{N}}}\) \(\epsilon \) [5, 7], whereas from Tables 2 for \(r_{{\text{N}}}\) \(\epsilon \) [10, 12] with group size \(g_{{\text{N}}}\) = [2, 4].

Table 1 Proposed single group sampling plan for Weibull distribution under neutrosophic statistics \(r_{\rm N}\) \(\epsilon \) [4, 6], \(b_{\rm N}\) \(\epsilon \) [1.9, 2.1], and various \({I}_{\rm N}\epsilon \left[{I}_{\rm L},{I}_{\rm U}\right]\)
Full size table
Table 2 Proposed single group-sampling plan for Weibull distribution under neutrosophic statistics \(r_{\rm N}\) \(\epsilon \) [10, 12], \(b_{\rm N}\) \(\epsilon \) [1.9, 2.1], and various \({I}_{N}\epsilon \left[{I}_{\rm L},{I}_{\rm U}\right]\)
Full size table

Comparison with classical single group-sampling plan

In this subsection, a comparison is made between the crisp method classical single group-sampling plan proposed by Aslam et al. [12] and a single group-sampling plan under neutrosophic statistics. The proposed sampling plan is more economical than the crisp method sampling plan due to less number of groups. The comparison between the proposed sampling plan and the crisp method grouped sampling plans is given in Table 3. From Table 3, it is clear that the proposed group-sampling plan significantly decreases the number of groups required as compared with the crisp method group-sampling plan. In particular, when the mean ratio is small, the proposed plan shows better performance than the crisp method plan, whereas if the mean ratio is large, the proposed plan is reduced to the crisp method plan. For example, if we consider at \(\beta\) = 0.25, \(\alpha\) = 0.05, b = 2, r = 4, a = 1.0, and r1 = 4, the crisp method plan proposed by Aslam et al. [12] needs g = 2 and c = 2, whereas in the proposed plan under neutrosophic statistics needs a number of groups and acceptance numbers in indeterminate form as: \({g}_{\mathrm{N}}=1+3{I}_{\mathrm{N}}\), \({I}_{\mathrm{N}} \varepsilon \left[\mathrm{0,0.6}\right]\), and \({c}_{\mathrm{N}}=1+5{I}_{\mathrm{N}}\); \({I}_{\mathrm{N}}\varepsilon \left[\mathrm{0,0.8}\right]\). Here, we note that the chance of indeterminacy in the selection of group size and acceptance numbers is 60% and 80%, respectively. We note that the values of \(g\) and \(c\) from the crisp method sampling plan lie in the group size indeterminacy interval [1, 3] and acceptance number indeterminacy interval [1, 5]. From this comparison, it can be seen that the new algorithm calculates more compactly a set of parameters, containing the values of the classical one. In addition, the proposed sampling plan provides the smaller values of \({g}_{\rm N}\) as compared to the crisp method plan.

Table 3 Comparison of group-sampling plan under classical statistics and under neutrosophic statistics when \(r_{\rm N}\) \(\epsilon \) [4, 6] and \(b_{\rm N}\) \(\epsilon \) [1.9, 2.1] with classical for r = 4, b = 1.9
Full size table

Design of two-stage group-sampling plan for Weibull distribution under neutrosophic statistics

We present the design of a two-stage group-sampling plan for Weibull distribution under neutrosophic statistics in this section. Aslam et al. [12] studied similar plans for classical statistics and we used the same algorithm under neutrosophic statistics.

The systematic procedure to obtain design parameters in this plan is given below:

First stage:

  1. Step 1.

    Select at random the first sample of size \(n_{{1{\text{N}}}}\) from a lot.

  2. Step 2.

    Assign \(r\) items to each of \(g_{{{\text{1N}}}}\) groups (or testers), such that \(n_{{1{\text{N}}}} = rg_{{1{\text{N}}}}\).

  3. Step 3.

    Conduct the test for \(r\) items before the termination time \(t_{{0{\text{N}}}}\).

  4. Step 4.

    The lot will be accepted if the total number of failures from \(g_{{1{\text{N}}}}\) groups is smaller than or equal to \(c_{{1{\text{aN}}}}\).

  5. Step 5.

    Terminate the test and reject the lot when the total number of failures is greater than or equal to \(c_{{1{\text{rN}}}} \,\left( { > c_{{1{\text{aN}}}} } \right)\) before termination time \(t_{{{\text{0N}}}}\). Otherwise, go to the second stage.

Second stage:

  1. Step 1.

    Choose the second random sample of size \(n_{{2{\text{N}}}}\) from a lot.

  2. Step 2.

    Assign \(r\) items to each of \(g_{{2{\text{N}}}}\) groups, such that \(n_{{2{\text{N}}}} = rg_{{2{\text{N}}}}\).

  3. Step 3.

    Conduct the test for \(r\) items before the termination time \(t_{0N}\).

  4. Step 4.

    The lot will be accepted if the total number of failures from \(g_{{1{\text{N}}}}\) and \(g_{{2{\text{N}}}}\) groups is smaller than or equal to \(c_{{2{\text{aN}}}} \left( { \ge c_{{1{\text{aN}}}} } \right)\) before termination time \(t_{{0{\text{N}}}}\); otherwise, reject the lot.

The projected two-stage group-sampling plan for Weibull distribution under neutrosophic statistics is differentiated by five design parameters, namely \(g_{{{\text{1N}}}}\), \(g_{{2{\text{N}}}}\), \(c_{{1{\text{aN}}}}\), \(c_{{{\text{1rN}}}}\), and \(c_{{2{\text{aN}}}}\). The proposed plan can be reduced to a single group-sampling plan based on neutrosophic statistics outlined in “Design of single group-sampling plan for Weibull distribution under neutrosophic statistics” when \(c_{{1{\text{rN}}}}\) = \(c_{{1{\text{aN}}}}\) + 1. As a result, the total number of failures from \(g_{{{\text{1N}}}}\) groups (denoted by \(X_{{1{\text{N}}}}\)) follows a binomial distribution with parameters \(n_{{1{\text{N}}}}\) and \(p_{{\text{N}}}\). Hence, the probabilities of acceptance and rejection of the lot at the first stage under the proposed two-stage group-sampling plan are given below:

$${P}_{\mathrm{aN}}^{(1)}=\sum_{i=0}^{{c}_{1\mathrm{aN}}}\left(\begin{array}{c}r{g}_{1\mathrm{N}}\\ i\end{array}\right){p}_{\mathrm{N}}^{i}{\left(1-{p}_{\mathrm{N}}\right)}^{r{g}_{1\mathrm{N}}-i}. $$
(12)
$${P}_{\mathrm{rN}}^{(1)}=\sum_{i={c}_{1\mathrm{rN}}}^{{n}_{1\mathrm{N}}}\left(\begin{array}{c}r{g}_{1\mathrm{N}}\\ i\end{array}\right){p}_{\mathrm{N}}^{i}{\left(1-{p}_{\mathrm{N}}\right)}^{r{g}_{1\mathrm{N}}-i}.$$
(13)

Also, the probability of acceptance of lot from the second stage if the decision has not been completed at the first stage and the total number of failures from \(g_{{1{\text{N}}}}\), \(g_{{2{\text{N}}}}\) groups (denoted by \(X_{{{\text{2N}}}}\)) is smaller than or equal to \(c_{{{\text{2a}}}}\). Therefore:

$${P}_{\mathrm{aN}}^{(2)}=P\left({c}_{1\mathrm{aN}}+1\le {X}_{1\mathrm{N}}\le {c}_{1\mathrm{rN}}-1,{X}_{1\mathrm{N}}+{X}_{2\mathrm{N}}<{c}_{2\mathrm{aN}}\right)=\sum_{x={c}_{1\mathrm{aN}}+1}^{{c}_{1\mathrm{rN}}-1}\left(\begin{array}{c}r{g}_{1\mathrm{N}}\\ i\end{array}\right){p}_{\mathrm{N}}^{i}{\left(1-{p}_{\mathrm{N}}\right)}^{r{g}_{1\mathrm{N}}-i}\left[\sum_{i=0}^{{c}_{2\mathrm{aN}-x}}\left(\begin{array}{c}r{g}_{2\mathrm{N}}\\ i\end{array}\right){p}_{\mathrm{N}}^{i}{\left(1-{p}_{\mathrm{N}}\right)}^{r{g}_{2\mathrm{N}}-i}\right].$$
(14)

Hence, the probability of lot acceptance for the proposed two-stage group-sampling plan based on neutrosophic statistics is given below:

$$ L\left( {p_{{\text{N}}} } \right) = P_{{{\text{aN}}}}^{(1)} + P_{{{\text{aN}}}}^{(2)} . $$

The lot acceptance probability in the form of the indeterminate interval can be given as:

$$L\left({p}_{\mathrm{N}}\right)=L\left(p\right)+{f}_{\mathrm{N}}{I}_{\mathrm{N}}; {I}_{\mathrm{N}}\epsilon \left[{I}_{\mathrm{L}},{I}_{\mathrm{U}}\right],$$
(15)

where \(L\left(p\right)\) denotes the lot acceptance probability for Aslam et al.’s [11] plan and \({f}_{\mathrm{N}}{I}_{\mathrm{N}}\), \({I}_{\mathrm{N}}\epsilon \left[{I}_{\mathrm{L}},{I}_{\mathrm{U}}\right]\) denotes the indeterminate part. The optimum plan parameters are obtained by minimizing the average sample number (ASN), Aslam et al. [11]. Hence, the optimum plan parameters are a solution to the following neutrosophic non-linear optimization problem:

$$ {\text{Minimize}}\,\,{\text{ASN}}\left( {p_{{2{\text{N}}}} } \right) = r_{{\text{N}}} g_{{1{\text{N}}}} + r_{{\text{N}}} g_{{2{\text{N}}}} \left( {1 - P_{{{\text{aN}}}}^{(1)} - P_{{{\text{rN}}}}^{(1)} } \right). $$
(16)

Subject to

$$L\left({p}_{1\mathrm{N}}\right)={P}_{\mathrm{aN}}^{\left(1\right)}\left({p}_{1\mathrm{N}}\right)+{P}_{\mathrm{aN}}^{\left(2\right)}\left({p}_{2\mathrm{N}}\right)\ge 1-\alpha .$$
(17)
$$L\left({p}_{2\mathrm{N}}\right)={P}_{\mathrm{aN}}^{\left(1\right)}\left({p}_{1\mathrm{N}}\right)+{P}_{\mathrm{aN}}^{\left(2\right)}\left({p}_{2\mathrm{N}}\right)\le \beta .$$
(18)

The above-mentioned inequalities are used to find the plan parameters of the proposed plan using a grid search method. During the simulation, it is noted that several combinations of the parameters exist, which satisfies the given conditions. The plan parameters which have minimum ASN is selected and reported. The design parameters are displayed in Tables 4, 5 for neutrosophic Weibull distribution with neutrosophic shape parameter \({b}_{\mathrm{N}}\epsilon \left[\mathrm{1.9,2.1}\right]\) at \(\beta\) = [0.25, 0.10, 0.05, 0.01], mean ratios \(k_{1}\) = [2, 4, 6, 8, 10], two group sizes \(r = 10,20\), and two termination times, a = 0.5 and 1.0. Smarandache [49] suggested that de-neutrosophication can be done using the average of each interval or minimum/maximum value of intervals can be considered. From tables, we noticed the following tendency by considering the minimum values of intervals:

  1. i.

    The ASN value decreases as \(k_{1}\) increases from 2 to 6 for the fixed value of \(\beta \).

  2. ii.

    The ASN value decreases as \(a\) increases from 0.5 to 1.0 for the fixed value of \({b}_{\mathrm{N}}\).

  3. iii.

    The values of ASN increases as the values of \(r\) increase from 10 to 20 when other parameters are fixed.

Table 4 Proposed two-stage group-sampling plan for Weibull distribution under neutrosophic
Full size table
Table 5 Proposed two-stage group-sampling plan for Weibull distribution under neutrosophic statistics \(r\) = 20, \(b_{N}\) = [1.9, 2.1], and various \({I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]\)
Full size table

Comparison with classical two-stage group-sampling plan

In this subsection, a comparison is made between a single group-sampling plan under neutrosophic statistics, the crisp method, classical two-group-sampling plan proposed by Aslam et al. [12], and proposed two group-sampling plans under neutrosophic Statistics. The proposed sampling plan is said to be more effective than the crisp method sampling plan if it gives less ASN and, hence, the plan is more economical. For comparison, we considered common parameters \(\beta\) = 0.25, \(\alpha\) = 0.05, b = 2, a = 0.5, and r1 = 4 for three plans. From Tables 2 and 4, we noticed that the neutrosophic interval is smaller in the two-group-sampling plan under neutrosophic statistics than in a single group-sampling plan under neutrosophic statistics. For example from Table 4 when the neutrosophic shape parameter \(b_{{\text{N}}}\) \(\epsilon \) [1.9, 2.1], the neutrosophic ASN in a two-stage group-sampling plan under neutrosophic statistics gives [23.064, 40.474], whereas from Table 2 in single group, sampling plan under neutrosophic statistics gives [2 \(\times \) 10 = 20, 4 \(\times \) 12 = 48]. Furthermore, the two-stage group-sampling plan under neutrosophic statistics shows better performance than the crisp method classical two-stage group-sampling plan proposed by Aslam et al. [12]. For example, in Table 4, when \({\mu }_{\mathrm{N}}/{\mu }_{0\mathrm{N}}=2\), \(\beta =\) 0.25, neutrosophic ASN in a two-stage group-sampling plan under neutrosophic statistics gives [23.064, 40.474], whereas in the double group-sampling plan proposed by Aslam et al. [12] needs an ASN value of 39.8. When \({\mu }_{\mathrm{N}}/{\mu }_{0\mathrm{N}}=2\), \(\beta =\) 0.05, neutrosophic ASN in a two-stage group-sampling plan under neutrosophic statistics gives [51.584, 71.37], whereas in the double group-sampling plan proposed by Aslam et al. [12] needs ASN value of 52.4. When \({\mu }_{\mathrm{N}}/{\mu }_{0\mathrm{N}}=2\), \(\beta =\) 0.01, neutrosophic ASN in a two-stage group-sampling plan under neutrosophic statistics gives [61.893, 88.402], whereas in the double group-sampling plan proposed by Aslam et al. [12] needs ASN value 62.9. From this study, it is clear that the proposed plan has smaller values of ASN as compared to the crisp method plan proposed by Aslam et al. [12]. Hence, the proposed neutrosophic approach is more cost-effective and saving of experiment time.

Conclusions

In this article, two types of group acceptance-sampling plans using neutrosophic statistics are considered for Weibull distribution. The neutrosophic plan parameters are developed for both single and two-stage group-sampling plans using neutrosophic statistics. Various tables are provided for industrial applications. A comparative study is also carried out, and it shows that the proposed two-stage group-sampling plan under neutrosophic statistics performs better than the crisp method classical double group-sampling plan and the proposed single group-sampling plan under neutrosophic statistics based on the ASN values. From the comparison, it is found that the proposed sampling plans have smaller values of group size as compared to the crisp method sampling plans. In addition, the comparisons show that the proposed sampling plans are effective, flexible, and adequate to be applied when indeterminacy is presented. The proposed plan can be applied in the industry when there is uncertainty in observations or parameters or both. The proposed group-sampling plan using repetitive sampling and multiple dependent state sampling can be considered as future research.