1 Introduction

As already predicted in the late 1970s [1], space debris becomes a major issue for use of space [2, 3]. In particular, the amount of space debris in low earth orbit (LEO) is increasing rapidly [3]. To detect and map space debris, high-performance radar sensors can be used [3, 4]. Due to the enormous progress in the field of high-power microwave technology, corresponding radar sensors can also be operated in high-frequency bands such as the W-band [5]. Due to the high bandwidth available there, very high resolutions can be achieved [5, 6]. In the near future, even W-band transmission powers in the range of 100 kW may be achieved [7]. To realize a W-band radar sensor with such a high transmission power, a suitable high-power amplifier and an appropriate transmission line are required. The transmission line connects the output of the high-power amplifier with the antenna feed. Due to the high power, overmoded transmission lines are required. A suitable transmission mode is the HE11 hybrid mode in a corrugated waveguide. Low ohmic loss and small mode conversion can be achieved [8, 9].

In principle, for a highly overmoded HE11 transmission line, a rotary joint can be realized by a simple transmission line gap. Due to the low HE11-field components at the waveguide walls, no major influences are expected. The HE11 mode power loss through a transmission line gap can be estimated by [10]:

$$ \Delta {P}_{\mathrm{HE}11}=0.39\cdotp {\left(\frac{L\lambda}{2{a}^2}\right)}^{3/2} $$
(1)

with L as the gap length, λ as the free space wavelength, and D = 2a as the waveguide diameter. The HE11 power loss can be already neglected for Lλ/2a2 ≤ 1/100. A commonly utilized standard waveguide diameter for high-power transmission lines is D = 63.5 mm. With a wavelength of λ = 3 mm follows: L ≤ 6.7 mm. For a technical realization, this is noncritical. However, by rotation of such a rotary joint, the polarization plane of a linearly polarized mode, like HE11, is twisted. To avoid such issues, the circularly polarized HE11 mode can be used for transmission. Owing to the circular symmetry, no twist of the polarization plane occurs.

To change the polarization of the HE11 mode, suitable broadband polarizers are required: A first polarizer converts the incident linearly polarized HE11 mode to a circularly polarized wave, and a second polarizer restores the linearly polarized HE11 mode after the transmission line gap. This method provides a simple broadband rotary joint concept for high-power radar applications. Following the reachable cross polarization for such a rotary joint concept shall be investigated.

The paper is organized as follows: Section 2 starts with a suitable polarizer design and discusses possible polarization errors. In Section 3, simple formulas to calculate the cross polarization of the proposed rotary joint concept are derived. Section 4 addresses the issue of mode conversion due to diffraction. Section 5, the conclusions, closes with a summary of the considered aspects and the proposed rotary joint concept.

2 Polarizer

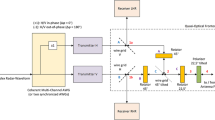
A linearly polarized wave can be polarized circularly by introducing a 90° phase shift of orthogonal field components [11]. For high-power microwave applications, reflection grids [12] are widely used: Electrical field components parallel to the grid are reflected at the surface of the grid; electrical field components perpendicular to the grid penetrate into the grid and are reflected at the bottom. The resulting time delay can be used for polarization tailoring. Figure 1 shows a rectangular reflection grid with the grid height h, the grid period p, and the grid width a.

Fig. 1
figure 1

Rectangular reflection grid with the grid height h, the grid width a, and the grid period p (photo from [13])

Full size image

In the ideal case, an exact phase shift by 90° and an amplitude balance of orthogonal field components by 0 dB can be achieved, within the considered frequency range. At a real polarizer, a phase error Δφ and an amplitude error ΔA occur. In general, a frequency-dependent elliptical polarization results:

$$ {\displaystyle \begin{array}{c}{E}_{\mathrm{x}}=\Delta A\cdotp \cos \kern0.2em \left(\omega t+\Delta \varphi \right)\\ {}{E}_{\mathrm{y}}=\sin \kern0.2em \left(\omega t\right)\end{array}} $$
(2)

In the ideal case (purely circular polarization) applies: Δφ = 0 and ΔA = 1. The design of a suitable polarization grid for high-power W-band radar applications is discussed in detail in [13]: Good broadband frequency behavior can be achieved for a grid width a = 0.25 mm, a grid period p = 1 mm, and a grid height h = 0.48 mm. To avoid critical field strengths and electrical arc breakdown, curvature radii at the upper end of the grid are used (R = 0.1 mm [13]). Figure 2 shows the corresponding phase error Δφ (in blue, solid) and amplitude error ΔA (in brown, solid) for the grid parameters introduced above, within the frequency range from 90 GHz to 100 GHz [13]. Note that the amplitude error ΔA is scaled in decibels. Figure 2 shows that the phase error can be limited to Δφ ≤ ± 5.8°. The small variation of the amplitude error ΔA is a result of numerical uncertainties [13] and can be neglected. For comparison, also results of a less suitable parameter combination are shown (a = 1.06 mm, p = 1.75 mm, and h = 0.42 mm, dashed curves [13]). The polarization errors are much larger in this case.

Fig. 2
figure 2

Phase error Δφ and amplitude error ΔA of a rectangular phase grid with suitable (solid curves) and less suitable (dashed curves) parameter combination [13]. The grid width a, the grid period p, and the grid height h are defined in Fig. 1

Full size image

3 Cross Polarization

In the following, the cross polarization of the proposed rotary joint concept is derived. For simplification, a plane wave approximation is used. For a waveguide diameter D ≥ 12λ, the results of a plane wave approximation can be transferred to a HE11 wave [12]. Two identical polarizers are used. Figure 3 shows a corresponding CAD (computer-aided design) model, which will be used for future full wave simulations.

Fig. 3
figure 3

CAD model of the rotary joint, with polarizer grids discussed in the text and corrugated waveguides with an effective corrugation depth of λ/4

Full size image

3.1 Principle Approach

As input, an ideal 45° linearly polarized plane wave with unit amplitude is assumed. The propagation direction shall be in positive z-direction (Ez = 0). Therefore, the other two field components are given by:

$$ {\displaystyle \begin{array}{c}{E}_{\mathrm{x}}=\sin \left(\omega t\right)\\ {}{E}_{\mathrm{y}}=\sin \left(\omega t\right)\end{array}} $$
(3)

At the first polarizer, the Ex component is delayed by φx = π/2 + Δφ. The present phase error is considered by Δφ. As already mentioned, the amplitude error ΔA can be neglected. With sin(x + π/2) = cos(x) follows:

$$ {\displaystyle \begin{array}{c}{E}_{\mathrm{x}}=\cos \left(\omega t+\Delta \varphi \right)\\ {}{E}_{\mathrm{y}}=\sin \left(\omega t\right)\end{array}} $$
(4)

A rotation by ϕ of the rotary joint can be described by the rotation matrix:

$$ \left(\begin{array}{c}{E}_{\mathrm{x}}^{\prime}\\ {}{E}_{\mathrm{y}}^{\prime}\end{array}\right)=\left(\begin{array}{cc}\cos \kern0.2em \left(\phi \right)& \sin \kern0.2em \left(\phi \right)\\ {}-\sin \kern0.2em \left(\phi \right)& \cos \kern0.2em \left(\phi \right)\end{array}\right)\cdotp \left(\begin{array}{c}{E}_{\mathrm{x}}\\ {}{E}_{\mathrm{y}}\end{array}\right) $$
(5)

With Eq. (4) follows:

$$ \left(\begin{array}{c}{E}_{\mathrm{x}}^{\prime}\\ {}{E}_{\mathrm{y}}^{\prime}\end{array}\right)=\left(\begin{array}{cc}\cos \kern0.2em \left(\omega t+\varDelta \varphi \right)& \sin \kern0.2em \left(\omega t\right)\\ {}\sin \kern0.2em \left(\omega t\right)& -\cos \kern0.2em \left(\omega t+\Delta \varphi \right)\end{array}\right)\cdotp \left(\begin{array}{c}\cos \kern0.2em \left(\phi \right)\\ {}\sin \kern0.2em \left(\phi \right)\end{array}\right) $$
(6)

At the second polarizer the \( {E}_{\mathrm{y}}^{\prime } \) component is delayed by φy = π/2 + Δφ. With sin(x + π/2) = cos(x) and cos(x + π/2) =  − sin(x) follows:

$$ \left(\begin{array}{c}{E}_{\mathrm{x}}^{\prime}\\ {}{E}_{\mathrm{y}}^{\prime}\end{array}\right)\kern0.5em =\left(\begin{array}{cc}\cos \kern0.2em \left(\omega t+\varDelta \varphi \right)& \sin \kern0.2em \left(\omega t\right)\\ {}\cos \kern0.2em \left(\omega t+\varDelta \varphi \right)& \sin \kern0.2em \left(\omega t+2\Delta \varphi \right)\end{array}\right)\cdotp \left(\begin{array}{c}\cos \kern0.2em \left(\phi \right)\\ {}\sin \kern0.2em \left(\phi \right)\end{array}\right) $$
(7)

The cross polarization is defined as the ratio of the time averaged signal power in the desired polarization plane and the time averaged signal power in the orthogonal polarization plane. Equation (7) describes a 45° linearly polarized wave. To separate the orthogonal polarization planes, an appropriate rotation matrix is used. This rotates the coordinate system by 45°:

$$ \left(\begin{array}{c}{E}_{\mathrm{x}}^{\prime \prime}\\ {}{E}_{\mathrm{y}}^{\prime \prime}\end{array}\right)=\left(\begin{array}{cc}\cos \kern0.2em \left(\pi /4\right)& \sin \kern0.2em \left(\pi /4\right)\\ {}-\sin \kern0.2em \left(\pi /4\right)& \cos \kern0.2em \left(\pi /4\right)\end{array}\right)\cdotp \left(\begin{array}{c}{E}_{\mathrm{x}}^{\prime}\\ {}{E}_{\mathrm{y}}^{\prime}\end{array}\right) $$
(8)

The cross polarization follows as:

$$ {X}_{\mathrm{pol}}=\frac{\left\langle {E}_{\mathrm{y}}^{\prime \prime },{E}_{\mathrm{y}}^{\prime \prime}\right\rangle }{\left\langle {E}_{\mathrm{x}}^{\prime \prime },{E}_{\mathrm{x}}^{\prime \prime}\right\rangle } $$
(9)

The inner product ⟨x, y⟩ is defined as [14]:

$$ \left\langle x,y\right\rangle =\underset{T\to \infty }{\lim}\frac{1}{T}\underset{-T/2}{\overset{+T/2}{\int }}x\cdot {y}^{\ast}\kern0.2em \mathrm{d}t $$
(10)

Using a small-angle approximation, the introduced equations lead to the cross polarization:

$$ {X}_{\mathrm{pol}}\approx \frac{\Delta {\varphi}^2}{1+\Delta {\varphi}^2}\cdotp {\sin}^2\left(\phi \right) $$
(11)

3.2 Results

Figure 4 shows the numerically calculated cross polarization, using Eqs. (7), (8), and (9) without small-angle approximation. The polarization errors introduced in Section 2 are used (see Fig. 2, solid lines). The amplitude error ΔA is neglected. Figure 4 shows that just for ϕ = 180° the cross polarization is frequency independent. This is related to constructive/destructive superposition of the single polarization errors of the first and the second polarizer. However, the cross polarization is always below − 20 dB. This corresponds to a suitable value for radar applications [15]. Furthermore, the worst-case value of Xpol ≈ − 20 dB just occurs at the frequency band edges at 90 GHz and 100 GHz. Within the frequency range, the cross polarization is even better. Comparison of the results shown in Fig. 4 and the approximation derived in Eq. (12) shows good agreement.

Fig. 4
figure 4

Cross polarization in decibels as function of the frequency f and the rotation angle ϕ of the rotary joint, with suitably designed polarizers

Full size image

The rotary joint concept will be experimentally proven later, when the whole transmission line will be manufactured.

4 Mode Conversion

In the utilized polarizer arrangement, mode conversion due to diffraction occurs [10, 16]. The amount of mode conversion loss of the HE11 mode can be estimated with Eq. (1) and L = D [10]. For radar applications, also the exact mode content is important. Spurious modes could impair the cross polarization and the sidelobe level of the radar antenna. For a high-performance radar sensor, these effects have to be taken into account.

To calculate the mode conversion at a miter bend, the gap theory is commonly employed [10, 16, 17]. The miter bend is represented as a gap with the gap length L = D. To determine the electric/magnetic field components at the output plane, the radiated field components from the input plane are calculated, at the location of the output plane. The field components at the position \( \overrightarrow{r} \), radiated from an arbitrary aperture A, can be calculated for k \cdot R ≫ 1 by [18]:

$$ {\displaystyle \begin{array}{l}\overrightarrow{E}= jk\kern0.2em {\int}_A\left[\left(\overrightarrow{e_R}\times \overrightarrow{M}\right)+Z\cdotp \overrightarrow{e_R}\times \left(\overrightarrow{e_R}\times \overrightarrow{J}\right)\right]\cdotp G\kern0.2em \mathrm{d}\overrightarrow{A}\\ {}\overrightarrow{H}=-j\frac{k}{Z}\kern0.2em {\int}_A\left[Z\cdotp \left(\overrightarrow{e_R}\times \overrightarrow{J}\right)-\overrightarrow{e_R}\times \left(\overrightarrow{e_R}\times \overrightarrow{M}\right)\right]\cdotp G\kern0.2em \mathrm{d}\overrightarrow{A}\end{array}} $$
(12)

with:

$$ {\displaystyle \begin{array}{c}G=\frac{e^{- jk\mid \overrightarrow{r_0}-\overrightarrow{r}\mid }}{\mid \overrightarrow{r_0}-\overrightarrow{r}\mid}\\ {}\overrightarrow{e_R}=\frac{\overrightarrow{R}}{R}=\frac{\overrightarrow{r_0}-\overrightarrow{r}}{\mid \overrightarrow{r_0}-\overrightarrow{r}\mid}\end{array}} $$
(13)

k = 2π/λ, Z = 120π Ω and the equivalent electric/magnetic current densities [11, 18]:

$$ {\displaystyle \begin{array}{l}\overrightarrow{J}=\overrightarrow{n}\times \overrightarrow{H_0}\\ {}\overrightarrow{M}=-\overrightarrow{n}\times \overrightarrow{E_0}\end{array}} $$
(14)

The vector \( \overrightarrow{r_0} \) represents a point at the radiating aperture A, \( \overrightarrow{E_0} \)/\( \overrightarrow{H_0} \) the electric/magnetic field components at the aperture, and \( \overrightarrow{n} \) the normal vector orthogonal to the aperture.

The assumption k \cdot R ≫ 1 implied that the distance \( R=\mid \overrightarrow{r_0}-\overrightarrow{r}\mid \) is larger than ≈ 2λ [18]. This does not imply that Eq. (12) is limited to the far field condition R > 2D2/λ [11] with D as the largest aperture dimension.

In [10, 17], analytical approaches are used to calculate the HE11-mode power loss with good results. However, simplifications are used which impair the accuracy at high-order modes [10]. For radar applications, the HE11-mode power loss and the exact mode content are important. Therefore, Eq. (12) is solved numerically. With the MATLAB Parallel Computing Toolbox, the required computing time can be still limited to a few minutes.

To determine the mode content at the output plane, the electric field components are interpreted as the superposition of the normal modes within the corrugated waveguide [19]:

$$ \overrightarrow{E}={\sum}_n\left({\vartheta}_n^{+}+{\vartheta}_n^{-}\right)\cdotp \overrightarrow{e_n} $$
(15)

with \( {\vartheta}_n^{+/-} \) as the complex mode amplitude in the forward/backward direction and \( \overrightarrow{e_n} \) as the electric field components of the nth normal mode.

Equation (15) is multiplied by the conjugated transverse electric field components \( {\overrightarrow{e}}_{\perp m} \) of the mth normal mode and then integrated in respect of the waveguide cross section:

$$ {\int}_A\left(\overrightarrow{E_{\perp }}\cdotp {\overrightarrow{e}}_{\perp m}^{\ast}\right)\kern0.2em \mathrm{d}\overrightarrow{A}={\sum}_n\left({\vartheta}_n^{+}+{\vartheta}_n^{-}\right){\int}_A\left({\overrightarrow{e}}_{\perp n}\cdotp {\overrightarrow{e}}_{\perp m}^{\ast}\right)\kern0.2em \mathrm{d}\overrightarrow{A} $$
(16)

In consideration of the power orthogonality condition \( {\int}_A\left({\overrightarrow{e}}_{\perp n}\cdotp {\overrightarrow{e}}_{\perp m}^{\ast}\right)\kern0.2em \mathrm{d}\overrightarrow{A}=0 \) for n ≠ m [19, 20], each summand with n ≠ m is vanished. Therefore follows:

$$ {\vartheta}_m^{+}+{\vartheta}_m^{-}=\frac{\int_A\left({\overrightarrow{E}}_{\perp}\cdotp {\overrightarrow{e}}_{\perp m}^{\ast}\right)\kern0.2em \mathrm{d}\overrightarrow{A}}{\int_A\left({\overrightarrow{e}}_{\perp m}\cdotp {\overrightarrow{e}}_{\perp m}^{\ast}\right)\kern0.2em \mathrm{d}\overrightarrow{A}} $$
(17)

With \( {\vartheta}_m^{-}=0 \), just the transversal components of the electric field are required. This can be used to reduce the required computational effort to calculate the field components at the output plane. Due to the circular symmetry, just HE1n modes have to be considered for the mode decomposition [10, 17].

As discussed in [10, 16], the gap theory neglected mode conversion to high-order modes close to cut-off. However, due to their high ohmic wall losses, these modes are less critical for radar applications, since those will be damped and not radiated from the radar antenna.

Figures 5 and 6 show simulation results for the mode conversion to parasitic low-order modes in dependence of ka = 2π \cdot a/λ. In Fig. 5, the corresponding mode power is plotted and in Fig. 6 the phase relation, relative to the HE11 mode. As predicted from theory [10, 16], mode conversion decreases with increasing ka. Both figures show that an appropriate choice of the waveguide diameter is essential. At f = 95 GHz, a suitable waveguide diameter is D = 63.5 mm (ka ≈ 63). Mode conversion due to diffraction is less critical here.

Fig. 5
figure 5

Power of the parasitic low-order modes

Full size image
Fig. 6
figure 6

Phase relation of the parasitic low-order modes, relative to the HE11 mode

Full size image

In principle, the diffraction losses can be further reduced by choosing a larger diameter. However, above a certain value, mode conversion losses due to alignment tolerances (flange offsets and tilts) of the waveguide segments become dominant. Corresponding calculations are out of scope of the present paper and will be addressed in an upcoming manuscript.

5 Conclusions

The present paper addresses a broadband rotary joint concept for high-power W-band radar applications, within the frequency range from 90 GHz to 100 GHz. A combination of two broadband polarizers and a simple transmission line gap is proposed as rotary joint. Broadband frequency behavior and negligible power loss can be achieved. At the frequency band edges 90 GHz and 100 GHz, a worst-case cross polarization of Xpol ≈ − 20 dB occurs. This corresponds to a suitable value for radar applications. Within the whole considered frequency band, the cross polarization is even lower.

For a high-performance radar sensor, spurious modes may be critical, which may impair the cross polarization and the sidelobe level of the radar antenna. At the center frequency of 95 GHz, an appropriate waveguide diameter is D = 63.5 mm, for which mode conversion due to diffraction is less critical.