A New Symmetry of the Colored Alexander Polynomial

Abstract

We present a new conjectural symmetry of the colored Alexander polynomial, that is the specialization of the quantum $\mathfrak {sl}_N$ invariant widely known as the colored HOMFLY-PT polynomial. We provide arguments in support of the existence of the symmetry by studying the loop expansion and the character expansion of the colored HOMFLY-PT polynomial. We study the constraints this symmetry imposes on the group theoretic structure of the loop expansion and provide solutions to those constraints. The symmetry is a powerful tool for research on polynomial knot invariants and in the end we suggest several possible applications of the symmetry.

The Quantum Dimensions

Here we show that the quantum dimensions can only change the sign under the action of the tug-the-hook symmetry.

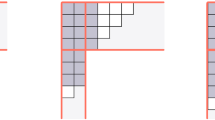
Let us consider a Young diagram R as the union of 5 parts.

• 1. The white part of the size $h \times h$, where h is the number of hooks

• 2. The green part of the size $g \times h$

• 3. The yellow part of the size $y \times h$

• 4. The red part that consists of $h-1$ rows of length $r_1, r_2, \dots , r_{h - 1}$

• 5. The pink part that consists of $h - 1$ columns of length $p_1, p_2, \dots , p_{h - 1}$

The formula for the quantum dimension of irreducible representation R

$$\begin{aligned} s_R^{*} = \prod _{(i,j) \in R} \frac{[N - i + j]}{[h_{ij}]} = \prod _{\text {color parts}} \ \prod _{(i,j) \in \text {part}} \frac{[N - i + j]}{[h_{ij}]} \end{aligned}$$

(94)

We consider the case $N = 0$. Let us note that:

• 1. The white part of the product in (94) remains the same under the action of the symmetry.

• 2. The hook part (denominators) corresponding to the red and pink parts remains the same under the action of the symmetry.

Consider the green and yellow parts entirely and the numerators in the red and pink parts. To do this consider the ith row in the red part and the corresponding row in the green part. The contribution reads:

$$\begin{aligned} \left( \frac{[r_i + g + h - i]!}{[h - i]!} \right) _{\text {red and green num.}} \left( \frac{[r_i + h - i]!}{[r_i + g + h - i]!} \right) _{\text {green denom.}} = \frac{[r_i + h - i]!}{[h - i]!}. \end{aligned}$$

(95)

We see that the contribution does not depend on the green and yellow parts, namely g, b does not appear in the contribution. It means that this part is invariant under the tug-the-hook symmetry.

Next, consider the ith column in the pink part and the corresponding column in the yellow part. The contribution reads:

$$\begin{aligned}&\left( (-1)^{p_i + y} \ \frac{[p_i + y + h - i]!}{[h - i]!} \right) _{\text {pink and yellow num.}} \left( \frac{[p_i + h - i]!}{[p_i + y + h - i]!} \right) _{\text {yellow denom.}}\nonumber \\&\quad = (-1)^{p_i + y} \ \frac{[p_i + h - i]!}{[h - i]!}. \end{aligned}$$

(96)

The contribution has y dependent part $(-1)^y$. the factor $(-1)^y$ comes from each yellow column and we get the resulting factor $(-1)^{y h}$. Under the action of the tug-the-hook symmetry only y, g parameters can change, namely $y \rightarrow y - \epsilon$ and $g \rightarrow g + \epsilon$. Considering the ratio we get

$$\begin{aligned} \frac{s^{*}_{\mathbf {T}_{\epsilon }(R)}}{s^{*}_{R}} \Bigg |_{N = 0} = (-1)^{\epsilon \cdot h(R)} \end{aligned}$$

because all contributions except the factors $(-1)^{y}$ remain the same and cancel.