Abstract
The economic role of elderly people is underestimated in the context of the debate on pension reforms. This is because, as healthy life expectancy increases, the elderly become more active not only in the labor market but also in household production. Using a three-period overlapping-generations model in which grandparents allocate time between labor and informal childcare (“grandparenting”), we analyze the interaction among grandparenting, fertility, elderly labor, and public pensions. We obtain two analytical results. First, increasing the pension contribution rate increases grandparenting. Second, elderly labor force participation rates are negatively (positively) related to the fertility rates among countries with small (large) public pensions. The nonlinear relationship between elderly labor and fertility is empirically supported.



Similar content being viewed by others
Notes
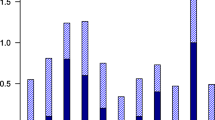
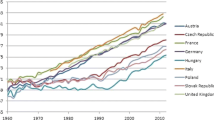
A simple ordinary least squares estimate shows
$$\begin{aligned} {\mathrm{ELPR}}=\underset{(3.04)}{1.86}-\underset{(-2.82)}{2.10}{\mathrm{TFR}}+\underset{(3.05)}{ 0.68}{\mathrm{TFR}}*{\mathrm{TFR}}-\underset{(-3.02)}{0.13}{\mathrm{TFR}}*{\mathrm{PRR}}, \end{aligned}$$where the figures in parentheses are t-values.
The goods market-clearing condition,
$$\begin{aligned} Y_{t}=N_{t}c_{1t}+N_{t}w_{t}e_{t}+N_{t-1}c_{2t}+K_{t+1} \end{aligned}$$can be derived by Walras’ law.
References
Aassve, A., Meroni, E., & Pronzato, C. (2012). Grandparenting and childbearing in the extended family. European Journal of Population, 28, 499–518.
Aisa, R., Pueyo, F., & Sanso, M. (2012). Life expectancy and labor supply of the elderly. Journal of Population Economics, 25, 545–568.
Arrow, K. J. (1962). The economic implications of learning by doing. Review of Economic Studies, 29, 155–173.
Benhabib, J., Rogerson, R., & Wright, R. (1991). Homework in macroeconomics: Household production and aggregate fluctuations. Journal of Political Economy, 99, 1166–1187.
Chen, H.-J. (2018). Fertility, retirement age, and pay-as-you-go pensions. Journal of Public Economic Theory, 20, 944–961.
Chen, H.-J., & Miyazaki, K. (2018). Fertility and labor supply of the old with pay-as-you-go pension and child allowances. BE Journal of Macroeconomics, 18, 1–19.
Greenwood, J., & Hercowitz, Z. (1991). The allocation of capital and time over the business cycle. Journal of Political Economy, 99, 1188–1214.
Grossman, G. M., & Yanagawa, N. (1993). Asset bubbles and endogenous growth. Journal of Monetary Economics, 31, 3–19.
Hank, K., & Buber, I. (2009). Grandparents caring for their grandchildren: Findings from the 2004 Survey of Health, Ageing, and Retirement in Europe. Journal of Family Issues, 30, 53–73.
Hirazawa, M., & Yakita, A. (2017). Labor supply of elderly people, fertility, and economic development. Journal of Macroeconomics, 51, 75–96.
Hochman, O., & Lewin-Epstein, N. (2013). Determinants of early retirement preferences in Europe: The role of grandparenthood. International Journal of Comparative Sociology, 54, 29–47.
ILO (International Labour Organization). (2019). ILOSTAT. https://ilostat.ilo.org/. Accessed 14 April 2019
Kaptijn, R., Thomese, F., van Tilburg, T. G., & Liefbroer, A. C. (2010). How grandparents matter: Support for the cooperative breeding hypothesis in a contemporary Dutch population. Human Nature, 21, 393–405.
Kridahl, L. (2017). Retirement timing and grandparenthood in Sweden: Evidence from population-based register data. Demographic Research, 37, 957–994.
Lakomý, M., & Kreidl, M. (2015). Full-time versus part-time employment: Does it influence frequency of grandparental childcare? European Journal of Ageing, 12, 321–331.
Miyazawa, K. (2016). Grandparental child care, child allowances, and fertility. Journal of the Economics of Ageing, 7, 53–60.
Myrskylä, M., Goldstein, J. R., & Cheng, Y. A. (2013). New cohort fertility forecasts for the developed world: Rises, falls, and reversals. Population and Development Review, 39, 31–56.
OECD (Organization for Economic Co-operation and Development). (2017). Pensions at a Glance 2017: OECD and G20 Indicators. Paris: OECD Publishing.
OECD. (2019). OECD Data. https://data.oecd.org/. Accessed 14 April 2019
Pestieau, P., & Ponthiere, G. (2017). Optimal fertility under age-dependent labour productivity. Journal of Population Economics, 30, 621–646.
Pink, S. (2018). Anticipated (grand-) parental childcare support and the decision to become a parent. European Journal of Population, 34, 691–720.
Rogerson, R., & Wallenius, J. (2016). Retirement, home production and labor supply elasticities. Journal of Monetary Economics, 78, 23–34.
Romer, P. M. (1986). Increasing returns and long-run growth. Journal of Political Economy, 94, 1002–1037.
Thomese, F., & Liefbroer, A. C. (2013). Child care and child birth: The role of grandparents in the Netherlands. Journal of Marriage and Family, 75, 403–421.
Van Bavel, J., & De Winter, T. (2013). Becoming a grandparent and early retirement in Europe. European Sociological Review, 29, 1295–1308.
Waynforth, D. (2012). Grandparental investment and reproductive decisions in the longitudinal 1970 British cohort study. Proceedings of the Royal Society B, 279, 1155–1160.
World Bank. (2019). World Bank Open Data. https://data.worldbank.org/. Accessed 14 April 2019
Železná, L. (2018). Care-giving to grandchildren and elderly parents: Role conflict or family solidarity? Ageing and Society, 38, 974–994.
Zhang, J., Zhang, J., & Lee, R. (2001). Mortality decline and long-run economic growth. Journal of Public Economics, 80, 485–507.
Acknowledgements
I would like to thank a referee for constructive comments. I also thank Akira Yakita, Makoto Hirazawa, Keshab Bhattarai, Shinji Miyake, Moriki Hosoe, Tohru Naito, participants at PET19, Strasbourg, and seminar participants at Nanzan University and Fukuoka University for useful comments. This research is financially supported by the Japan Society for the Promotion of Science (JSPS KAKENHI Grant Nos. JP16H03625, JP16H03635, JP17K03784, and JP18H00865). Any remaining errors are my own.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Proof of Lemma 1
Substituting \(w_{t+1}/w_{t}=\gamma _{t}\), and \(R_{t+1}=\alpha A\) into (7), we obtain (14).
Combining the market-clearing conditions (12) and (13), the capital–labor ratio in period \(t+1\) is given by
Substituting the saving function (8) into this, and using \(w_{t}=(1-\alpha )Ak_{t}\), we obtain (15).
Let us denote the relative wage rate of old adults to young adults in period \(t+1\) by \(p_{t+1}\),
Meanwhile, Eqs. (11) and (12) in period \(t+1\) give the pension benefit in period \(t+1\),
Using this, we obtain
which yields (18). Solving (17) and (18), we obtain (16). \(\square\)
Appendix 2
Proof of Lemma 3
Without loss of generality, we omit the time script. Let us denote the left-hand side by f(n),
Obviously, \(f(n)<n\). Furthermore, we know that
which implies that the curve \(z=f(n)\) has an asymptotic line,
Therefore, the range of f(n) is given by
Next, differentiating (31) with respect to n, we obtain
Obviously, \(f^{\prime \prime }>0\). Furthermore, we know that
which implies
In Fig. 4, the solid curve is \(z=f(n)\) and the solid horizontal line is \(z=(1-\tau )\rho \phi (g)\). The dashed lines represent a 45-degree line and the asymptotic line (32). At the intersection of the solid curve and the solid line, the unique solution, \(n^{*}=n(g)\), is obtained. When \(g\) increases, the horizontal line shifts upward, which increases \(n^{*}\).
In Fig. 4, the range of \(n^{*}\) is given by
Next, we derive the range of \(\varepsilon _{n}=gn^{\prime }(g)/n(g)\). By total-differentiating both sides of (19), we obtain
which yields
Using (33), the range of \(n^{\prime }(g)\) is given by
Using the elasticity of grandparenting \(\varepsilon =g\phi ^{\prime }(g)/\phi (g)\), and the elasticity of fertility \(\varepsilon _{n}=gn^{\prime }(g)/n(g)\), (35) can be rewritten as
Finally, using (34), we obtain
which is (22) in Lemma 3. \(\square\)
Appendix 3
Proof of Proposition 5
Differentiating (25) with respect to \(g_{t}\), we obtain
The steady state is locally stable if
Using the elasticity of fertility in the steady state, \(\varepsilon _{n}^{*}=g^{*}n^{\prime }(g^{*})/n(g^{*})\), (37) can be rewritten as
Here, the range of \(\varepsilon _{n}^{*}\) is given by (22) in Lemma 3. For any pair (n, g) that satisfies (22), the condition (38) is satisfied if
where \(\varepsilon ^{*}=g^{*}\phi ^{\prime }(g^{*})/\phi (g^{*})\) is the elasticity of grandparenting in the steady state.
Note that (25) yields
Substituting (40) into (39), we obtain
One of the sufficient conditions to make this inequality hold is
which is (26) in Proposition 5. \(\square\)
Appendix 4
Proof of Proposition 7
By total-differentiating (27) and (28), we obtain
The determinant of the \(2\times 2\) matrix is \(\Delta =-\phi ^{\prime }\Gamma _{n}^{2}+\Gamma _{n}^{1}>0\). Using the inverse matrix, we obtain
That is,
In the following, we examine the sign of \(\mathrm{d}n^{*}/\mathrm{d}\tau\).
First, differentiating (27) with respect to \(\tau\) yields
Next, differentiating (28) with respect to \(\tau\) yields
Meanwhile, (28) gives
Using this, \(\Gamma _{\tau }^{2}\) is rewritten as
Substituting \(\Gamma _{\tau }^{1}\) and \(\Gamma _{\tau }^{2}\) into (42), we obtain
where \(\varepsilon ^{*}=g^{*}\phi ^{\prime }(g^{*})/\phi (g^{*})\ge 0\) represents the elasticity of grandparenting.
Evaluating this at \(\tau =0\) yields
Therefore, the following statements are true.
-
1.
If \(\eta -\beta (1-\alpha )\varepsilon ^{*}\le 0\),
$$\begin{aligned} \frac{\mathrm{d}n^{*}}{\mathrm{d}\tau }|_{\tau =0}>0. \end{aligned}$$ -
2.
If \(\eta -\beta (1-\alpha )\varepsilon ^{*}>0\),
$$\begin{aligned} g^{*}<\frac{\eta (1-\alpha )\varepsilon ^{*}}{\theta [\eta -\beta (1-\alpha )\varepsilon ^{*}]}\Rightarrow \frac{\mathrm{d}n^{*}}{\mathrm{d}\tau } |_{\tau =0}>0 \\ g^{*} >\frac{\eta (1-\alpha )\varepsilon ^{*}}{\theta [\eta -\beta (1-\alpha )\varepsilon ^{*}]}\Rightarrow \frac{\mathrm{d}n^{*}}{\mathrm{d}\tau } |_{\tau =0}<0 \end{aligned}$$which completes the proof of Proposition 7. \(\square\)
Appendix 5
[Parameters and simulation results]
-
1.
Time allocation
We use time data in Rogerson and Wallenius (2016), which indicate the time use by age compiled from the American Time Use Survey (ATUS) from 2003 to 2011. Market work at age 60 is 26.17 hours per week, which decreases to 11.20 at age 65. By normalizing the former market work to unity, the elderly labor in our model is given by \(l_{0}=0.43\), where a subscript 0 indicates variables when the contribution rate of public pensions is zero. The remaining time is allocated between leisure (0.31) and home production, etc. (0.26). Therefore, we set time endowment in old age by \({\bar{l}}=0.69\), and time input in home production by \(l_{0}^{H}=0.26\), respectively.
We normalize the fertility rate to unity when the contribution rate is zero (\(n_{0}=1\)). Since \(l_{0}^{H}=n_{0}g_{0}\), grandparenting per child is given by \(g_{0}=0.26\).
-
2.
Preference parameters
We assume that one period in the model economy is 30 years. Assuming that annual rate of time preference is 1%, the private discount factor is given by \(\delta =1.01^{-30}=0.742\).
In our model setting, \(\delta =\beta /(1-\rho -\beta -\eta )\). Therefore, we obtain
In a benchmark case, we assume that the productivity of old workers is the same as young workers (\(\theta =1\)). Then, Eq. (24) with \(\tau =0\) yields
(43) and (44) solve for \(\beta\) and \(\eta\) as follows:
We assume the capital share is \(\alpha =0.33\), and the preference for the number of children is \(\rho =0.1\). Using \(\delta =0.742\), \({\bar{l}}=0.69\), \(l_{0}=0.43\), \(n_{0}=1\), we obtain \(\beta =0.349\), and \(\eta =0.08\).
-
3.
\(\phi (g)\)
Since analytical results in our model are represented in terms of elasticity of grandparenting, we use a power function, \(\phi (g)=\phi g^{\varepsilon }\) , where \(0<\varepsilon <1\) and \(\phi >0\). The stability condition in Proposition 5 is given by \(\varepsilon \le 1-\eta -\beta (1-\alpha )=0.686\) , and the condition for Proposition 7 (i) is \(\varepsilon \ge \eta /[\beta (1-\alpha )]=0.342\). We use \(\varepsilon =0.4\) in a benchmark case of efficient grandparenting. Alternatively, we use \(\varepsilon =0.2\) when grandparenting is inefficient.
Equation (27) with \(\tau =0\) and \(\theta =1\) yields
Using parameter values derived above, we obtain \(\phi =13.501\) when \(\varepsilon =0.4\), and \(\phi =10.313\) when \(\varepsilon =0.2\).
-
4.
Growth rate
Assuming that annual growth rate of per capita income is 2% without public pensions, \(\gamma _{0}=1.02^{30}=1.8114\). From (23) with \(\theta =1\),
which yields \(A=14.053\). The interest factor is \(R=\alpha A=4.6375\), which implies that annual interest rate is 5.25%.
-
5.
Simulation results
We calculated the steady-state values of fertility, grandparenting, elderly labor, and annual growth rate. For the interior solution, we use (19), (25), and (23) in the main body. For the corner solution, we use (45)–(47) in Appendix 6. Table 1 shows a benchmark case in which grandparenting is assumed to be efficient (\(\varepsilon =0.4\)). Tables 2 and 3 show a case of inefficient grandparenting (\(\varepsilon =0.2\)), and low productivity of elderly labor (\(\theta =0.8\)), respectively.
Appendix 6
[Corner solution]
As the contribution rate increases, the elderly labor could decrease to reach zero. The time constraint at the corner solution is given by
The household maximization problem is modified as
subject to
Solving the problem yields the fertility rate and the saving function:
where \(I_{t}\equiv (1-\tau )w_{t}+P_{t+1}{\bar{l}}/R_{t+1}\) represents lifetime income.
The government budget constraint and the labor market-clearing condition are modified as follows:
Substituting the saving function into the capital market-clearing condition, \(k_{t+1}=s_{t}/n_{t}\), and using the government budget constraint, \(P_{t+1} {\bar{l}}=\tau w_{t+1}n_{t}\), the growth rate of the capital–labor ratio is given by
Substituting (46) into the present value of pension benefits, \(P_{t+1}{\bar{l}} /R_{t+1}=(1-\alpha )\tau n_{t}k_{t+1}/\alpha\), we obtain
which yields the fertility equation,
Given \(g_{0}\), Eqs. (45) and (47) determine the dynamics of \((n_{t},g_{t})\).
Rights and permissions
About this article
Cite this article
Miyazawa, K. Elderly empowerment, fertility, and public pensions. Int Tax Public Finance 28, 941–964 (2021). https://doi.org/10.1007/s10797-020-09644-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10797-020-09644-z