Abstract
We study the relationship between session types and behavioural contracts, representing Communicating Finite State Machines (CFSMs), under the assumption that processes communicate asynchronously. Session types represent a syntax-based approach for the description of communication protocols, while behavioural contracts, formally expressing CFSMs, follow an operational approach. We show the existence of a fully abstract interpretation of session types into a fragment of contracts that maps session subtyping into binary compliance-preserving CFSMs/behavioural contract refinement. In this way, on the one hand, we enrich the theory of session types with an operational characterization and, on the other hand, we use recent undecidability results for asynchronous session subtyping to obtain an original undecidability result for asynchronous CFSMs/behavioural contract refinement.
Similar content being viewed by others
1 Introduction
Session types are used to specify the structure of communication between the endpoints of a distributed system or the processes of a concurrent program. In recent years, session types have been integrated into several mainstream programming languages (see, e.g. [2, 28, 31, 36,37,38,39]) where they specify the pattern of interactions that each endpoint must follow, i.e. a communication protocol. In this way, once the expected communication protocol at an endpoint has been expressed in terms of a session type, the behavioural correctness of a program at that endpoint can be checked by exploiting syntax-based type checking techniques. The overall correctness of the system is guaranteed when the session types of the interacting endpoints satisfy some deadlock/termination related (see, e.g. [16, 23]) compatibility notion. For instance, in case of binary communication, i.e. interaction between two endpoints, session duality rules out communication errors like, e.g. deadlocks: intuitively, session duality means that each send (resp. receive) action in the session type of one endpoint, is matched by a corresponding receive (resp. send) action of the session type at the opposite endpoint. Namely, we have that two endpoints following respectively session types T and \({\overline{T}}\) ( \({\overline{T}}\) is the dual of T) will communicate correctly.
Duality is a rather restrictive notion of compatibility since it forces endpoints to follow specular protocols. In many cases, endpoints correctly interact even if their corresponding session types are not dual. A typical example is when an endpoint is in receiving state and has the ability to accept more messages than those that could be emitted by the opposite endpoint. These cases are dealt with by considering session subtyping: an endpoint with session type \(T_1\) can always be safely replaced by another endpoint with session type \(T_2\), whenever \(T_2\) is a subtype of \(T_1\) (here denoted by \(T_2 \le T_1\)). In this way, besides being safe to combine an endpoint with type \(T_1\) with a specular one with type \({\overline{T_1}}\), it is also safe to combine any such \(T_2\) with \({\overline{T_1}}\). The typical notion of subtyping for session types is the one by Gay and Hole [26] defined by considering synchronous communication: synchronous session subtyping only allows for a subtype to have fewer internal choices (sends), and more external choices (receives), than its supertype.Footnote 1Asynchronous session subtyping has been more recently investigated [8, 10, 22, 34, 35]: it is more permissive because it widens the synchronous subtyping relation by allowing the subtype to anticipate send actions, under the assumption that the subsequent communication protocol is not influenced by the anticipation. Anticipation is admitted because, in the presence of message queues, the effect of anticipating a send is simply that of enqueueing earlier, in the communication channel, the corresponding message. As an example, a session type \( \oplus \{l: \& \{ l': {\mathbf {end}}\}\}\) with a send action on l followed by a receive action on \(l'\), is an asynchronous subtype of & \(\{ l': \oplus \{l: {\mathbf {end}}\}\}\) that performs the same actions, but in reverse order. This admits the safe combination of two endpoints with session types \( \oplus \{l: \& \{ l': {\mathbf {end}}\}\}\) and \( \oplus \{l': \& \{ l: {\mathbf {end}}\}\}\), respectively, because each program has a type which is an asynchronous subtype of the dual type of the partner. Intuitively, the combination is safe in that the initially sent messages are first enqueued in the communication channels, and then consumed.
Behavioural contracts [11,12,13, 20, 29] (contracts, for short) represent an alternative way for describing the communication behaviour of processes. While session types are defined to be checked against concurrent programs written in some specific programming language, contracts can be considered a language independent approach strongly inspired by automata-based communication models. Contracts follow the tradition of Communicating Finite State Machines (CFSMs) [6, 21], which describe the possible send/receive actions in terms of a labelled-transition system: each transition corresponds with a possible communication action and alternative transitions represent choices that can involve both sends and receives (so-called mixed-choices, which are usually disregarded in session types). A system is then modelled as the parallel composition of the contracts of its constituting processes. Also in the context of contracts, safe process replacement has been investigated by introducing the notion of contract refinement: if a contract \(C_1\) is part of a correct system, then correctness is preserved when \(C_1\) is replaced by one of its subcontracts \(C_2\) (written \(C_2 \preceq C_1\) in this paper). Obviously, different notions of contract refinement can be defined, based on possible alternative notions of system correctness. For instance, for binary client/service interaction where correctness is interpreted as the successful completion of the client protocol, the server pre-order (see e.g. [4, 5]) has been defined as a refinement of server contracts that preserves client satisfaction. On the other hand, if we move to multi-party systems, and we consider a notion of correctness, called compliance, that requires the successful completion of all the partners, an alternative compliance preserving subcontract relation [12] is obtained.
Given that both session types and behavioural contracts have been developed for formal reasoning on communication-centered systems, and given that session subtyping and contract refinement have been respectively defined to characterize the notion of safe replacement, it is common understanding that there exists a strong correspondence between session subtyping and contract refinement. Such a correspondence has been formally investigated for synchronous communication by Barbanera and de’Liguoro [4] and by Bernardi and Hennessy [5]: there exists a natural interpretation of session types into a fragment of contracts where mixed-choice is disallowed, called session contracts, such that synchronous subtyping is mapped into a notion of refinement that preserves client satisfaction (but can be applied to both clients and servers; and not only to servers as the server pre-order mentioned above).
The correspondence between session subtyping and contract refinement under asynchronous communication is still an open problem. In this paper, we solve such a problem by identifying the fragment of asynchronously communicating contracts for which refinement corresponds to asynchronous session subtyping: besides disallowing mixed-choices as for the synchronous case, we consider a specific form of communication (i.e. FIFO channels for each pair of processes as in the communication model of CFSMs) and restrict to binary systems (i.e. systems composed of two contracts only).
In all, this paper contribution encompasses: (i) a new theory of asynchronous behavioural contracts that coincide with CFSMs and includes the notions of contract compliance (correct, i.e. deadlock free, system of CFSMs) and contract refinement (preservation of compliance under any test); (ii) a precise discussion about the notion of refinement, showing under which conditions it coincides with asynchronous session subtyping, which is known to be undecidable [9]; and (iii) a gentle introduction to session types and asynchronous subtyping, which, thanks to our mapping to behavioural contracts and refinement, can be explained from an operational (transition system based) point of view.
More precisely, concerning (ii), we show asynchronous subtyping over session types to be encodable into refinement over binary and non mixed-choice asynchronous behavioural contracts (CFSMs). This means that for contracts of this kind, refined contracts can anticipate outputs w.r.t. the original contract as it happens in the context of session subtyping. Moreover, we show that it is crucial, for such a correspondence to hold, that, when establishing refinement between two binary and non mixed-choice asynchronous behavioural contracts, only tests that are actually binary (a single interacting contract) and non mixed-choice are considered: if we also consider tests that are either multiparty (multiple interacting contracts) or mixed-choice, in general, a binary and non mixed-choice contract \(C'\) that anticipates output w.r.t. a binary and non mixed-choice contract C is not a subcontract of it. This observation has deep implications on decidability properties in the context of general asynchronous behavioural contracts (CFSMs), while compliance, i.e. (non) reachability of deadlocking global CFSM states over asynchronous behavioural contracts (CFSMs) is known to be undecidable [6], an obvious argument showing undecidability cannot be found for the refinement relation; such a relation can be put in direct correspondence with asynchronous session subtyping only for the restricted binary and non mixed-choice setting (including also tests). Therefore, since in general an asynchronous behavioural contract (CFSMs) \(C'\) that anticipates output w.r.t. a contract C is not a subcontract of it, decidability of refinement over general asynchronous behavioural contracts (CFSMs) remains, quite unexpectedly, an open problem.
Structure of the paper. In Sect. 2, we define our model of asynchronous behavioural contracts inspired by CFSMs [6, 21]; we define syntax, semantics, correct contract composition, and the notion of contract refinement. In Sect. 3, we recall session types, focusing on the notion of asynchronous session subtyping [9, 35]. In Sect. 4, we present a fragment of behavioural contracts, and we prove that there exists a natural encoding of session types into this fragment of contracts which maps asynchronous session subtyping into contract refinement. In Sect. 5, we discuss related work, while Sect. 6 reports some concluding remarks.
This paper is an extended version of the conference paper [18]. We improved presentation by introducing main concepts in a more gentle manner (e.g. by starting from the simpler synchronous versions of session types and contracts before moving to the more complex asynchronous versions) and by enriching it with additional examples and more details about related and future work. Moreover, we here present technical results and their proofs in full details.
2 Behavioural contracts
In this section, we present behavioural contracts (simply contracts for short), in the form of a process algebra (see, e.g. [1, 3, 7, 32, 33]) based formalization of Communicating Finite State Machines (CFSMs) [6, 21]. CFSMs are used to represent FIFO systems, composed by automata performing send and receive actions having the effect of introducing/retrieving messages to/from FIFO channel. One channel is considered for each pair of sender/receiver automata.
As an example, we can consider a client/service interaction (inspired by the UDP communication protocol) depicted in Fig. 1. Communication protocols are denoted by means of automata with transitions representing communication actions; overlined labels denote send actions, while non-overlined labels denote receive actions. The server is available to serve both \({\mathsf {Write}}\) (\({ w }\) for short) and \({\mathsf {WriteTo}}\) (\({ wto }\)) requests. In the first case, the server replies with \({\mathsf {OK}}\) (\({ ok }\)) or \({\mathsf {DataTooLarge}}\) (\({ dtl }\)), depending on the success of the request or its failure due to an exceeding size of the message. On the other hand, in case of \({\mathsf {WriteTo}}\), the server has a third possible reply, \({\mathsf {InvalidEndPoint}}\) (\({ iep }\)), in case of wrongly specified destination. We consider two possible clients: a client following a specular protocol, and an alternative client that (given the connectionless nature of UDP) does not synchronize the reception of the server replies with the corresponding requests. More precisely, such a client follows an optimistic speculative behaviour; if it has to send a sequence of \({\mathsf {Write}}\) requests, and no error message is received from the server after sending the first one (i.e. it receives \({\mathsf {OK}}\)), then it sends two requests in sequence (another \({\mathsf {Write}}\) followed by a \({\mathsf {Write}}\) or a \({\mathsf {WriteTo}}\)) without blocking waiting for the server reply in between.
2.1 Behavioural contracts as terms
We now present behavioural contracts, that can be seen as a syntax for individual machines of CFSMs [6, 21]. Differently from the examples of communicating automata reported in Fig. 1, the send (resp. receive) actions will be decorated with a location identifying the expected receiver (resp. sender) contract. This was not considered in the example because, in case of two interacting partners, the sender and receiver of the communication actions can be left implicit.
Definition 1
(Behavioural Contracts) We consider three denumerable sets: the set \({{{\mathcal {N}}}}\) of message names ranged over by a, b, \(\cdots \), the location names \({ Loc }\), ranged over by l, \(l'\), \(\cdots \), and the contract variables \({ Var }\) ranged over by X, Y, \(\cdots \). The syntax of contracts is defined by the following grammar:
where the finite set of indices \(I \subset {\mathbb {N}}\) is assumed to be non-empty, and \(rec X.\_\) is a binder for the process variable X denoting recursive definition of processes: in recX.C an occurrence of X that is free (i.e. it is not bound) inside C represents a jump going back to the beginning of C. We assume that in a contract C all process variables are bound and all recursive definitions are guarded, i.e. in recX.C all free occurrences of X are guarded by (i.e. included in the scope of) a prefix operator \(\sum _{i \in I} \alpha _i.C_i\). Following CFSMs, we assume contracts to be deterministic, i.e. in \(\sum _{i \in I} \alpha _i.C_i\), we have \(\alpha _i = \alpha _j\) iff \(i=j\).
We use \(\alpha \) to range over the actions: \({\overline{a}}_l\) is a send action, with message a, towards the location l; \(a_l\) is the receive of a sent from the location l. The contract \(\sum _{i \in I} \alpha _i.C_i\) (also denoted with \(\alpha _1.C_1+\alpha _2.C_2+\dots +\alpha _n.C_n\) when \(I=\{1,2,\dots ,n\}\)) performs any of the actions \(\alpha _i\) and activates the continuation \(C_i\). In case there is only one action, we use the simplified notation \(\alpha .C\), where \(\alpha \) is such a unique action, and C is its continuation. The contract \({{\mathbf {1}}}\) denotes a final successful state. In the following, we will omit trailing “ \(.{{\mathbf {1}}}\)” when writing contracts.
The operational semantics of contracts C is defined in terms of a transition system labelled over \(\{a_l,{\overline{a}}_l \ |\ a \in {{{\mathcal {N}}}}, l \in Loc\}\), ranged over by \(\alpha \), \(\alpha '\), ..., obtained by the rules in Table 1. We use \(C \{ \_ / \_ \}\) to denote syntactic replacement. The first rule states that contract \(\sum _{i \in I}\alpha _i.C_i\) can perform any of the actions \(\alpha _i\) and then activate the corresponding continuation \(C_i\). The second rule is the standard one for recursion unfolding (replacing any occurrence of X with the operator recX.C binding it, so to represent the backward jump described above).
The semantics of a contract C yields a finite-state labelled transition system,Footnote 2 whose states are the contracts reachable from C. It is interesting to observe that such a transition system can be interpreted as a communicating automaton of a CFSM, with transitions \({\overline{a}}_l\) (resp. \(a_l\)) denoting send (resp. receive) actions. The final contract \({{\mathbf {1}}}\) coincides with states of communicating automata that have no outgoing transitions.
Moreover, we have that each communicating automaton can be expressed as a contract; this is possible by adopting standard techniques [32] to translate finite labelled transition systems into recursively defined process algebraic terms. Hence, we can conclude that our contracts coincide with the communicating automata as defined for CFSMs.
Example 1
As an example of contracts used to denote communicating automata, the alternative client and the server in Fig. 1 respectively correspond to the following contracts:Footnote 3
Notice that we have not explicitly indicated the locations associated to the send and receive actions; in fact, interaction is binary and the sender and receiver of each communication is obviously the partner location, and we leave it implicit.
2.2 Synchronous contract composition
We now move to the formalization of contract systems. A contract system is the parallel composition of contracts, each one located at a given location. More precisely, we use \([C]_l\) to denote a contract C located at location l.
Definition 2
(Contract Synchronous Systems) The syntax of contract (synchronous) systems is defined by the following grammar:
We assume that every contract synchronous system P is such that (i) all locations are different (i.e. every subterm \([C]_l\) occurs in P with a different location l), (ii) all actions refer to locations present in the system (i.e. for every \(a_l\) or \({\overline{a}}_l\) occurring in P, there exists a subterm \([C]_l\) of P), and (iii) receive and send actions executed by a contract consider a location different from the location of that contract (i.e. every action \(a_l\) or \({\overline{a}}_l\) does not occur inside a subterm \([C]_l\) of P).
Example 2
The contract synchronous system
is the parallel composition of three contracts located at \(l_1\), \(l_2\) and \(l_3\), which communicate with one another by specifying the destination location (in outputs) and the sending location (in inputs).
The operational semantics of contract synchronous systems is defined in terms of a transition system labelled over \(\{a_{l,l'},{\overline{a}}_{l,l'}, \tau \ |\ l,l' \in Loc, a \in {{\mathcal {N}}} \}\), ranged over by \(\lambda \), \(\lambda '\), ..., obtained by the rules in Tables 2 and 3 (plus the symmetric version for the two rules for parallel composition). The first rule of Table 2 indicates that a send action \({\overline{a}}_{l'}\) executed by a contract located at location l, becomes an action \({\overline{a}}_{l,l'}\) (the two locations l and \(l'\) denote the sender and receiver locations, respectively); the second rule, symmetrically, states that a receive action \(a_l\) executed by a contract located at location \(l'\), becomes an action \(a_{l,l'}\). The first rule of Table 3 is the synchronization rule between the two complementary labels \({\overline{a}}_{l,l'}\) and \(a_{l,l'}\); the second rule is the usual one that extends, to the entire system, transitions performed by a part of it. Notice that \(a_{l,l'}\) and \({\overline{a}}_{l,l'}\) labelled transitions are just needed to compute synchronizations, i.e. \(\tau \) transitions, which represent actual system evolutions.
Example 3
The contract synchronous system of Example 2 evolves as follows:
performs a \(\tau \) transition, due to the synchronization of \({\overline{a}}_{l_2,l_1}\) with \(a_{l_2,l_1}\), leading to
which, in turn, performs a \(\tau \) transition, due to the synchronization of \({\overline{a}}_{l_1,l_3}\) with \(a_{l_1,l_3}\), leading to
We now define system successful completion: the predicate \(P\surd \) checks whether all contracts in a system P have reached a succesfully terminated contract \({{\mathbf {1}}}\).
Definition 3
(Successful Completion) The notion of successful completion for a system is formalized by a predicate \(P\surd \) defined as follows:
Example 4
The system of Example 2 reaches successful completion with the execution trace shown in Example 3, i.e. we have
Definition 4
The notion of deadlock for a system is formalized as follows. P is in deadlock if \(P \surd \) does not hold and there is no \(P'\) such that \(P {\mathop {\longrightarrow }\limits ^{\tau }} P'\).
Example 5
The contract synchronous system
is obtained from that of Example 2 by introducing an extra output and input action on b. It is immediate to observe that such a system is in deadlock; in that, \(l_1\) is unable to perform the output \({\overline{b}}_{l_2}\) (which has been introduced at the beginning of its behaviour) because even if \(l_2\) can perform a corresponding receive on \(b_{l_1}\); it does so only after performing output \({\overline{a}}_{l_1}\); in turn, \(l_2\) cannot perform output \({\overline{a}}_{l_1}\) because even if \(l_1\) can perform a corresponding receive on \(a_{l_2}\), it does so only after performing output \({\overline{b}}_{l_2}\).
2.3 Asynchronous FIFO contract composition
We now move to the formalization of FIFO contract asynchronous systems; parallel composition of contracts, each one located at a given location, which communicate by means of FIFO channels. More precisely, we use \([C,{{\mathcal {Q}}}]_l\) to denote a contract C located at location l with an input queue \({{\mathcal {Q}}}\). The queue contains messages denoted with \(a_{l'}\), where \(l'\) is the location of the sender of such message a. This queue should be considered as the union of many input channels, one for each sender; in fact, the FIFO order of reception is guaranteed only among messages coming from the same sender, while two messages coming from different senders can be consumed in any order, independently from the order of introduction in the queue \({{\mathcal {Q}}}\). This coincides with the communication model considered in CFSMs [6, 21].
Definition 5
(FIFO Contract Asynchronous Systems) The syntax of FIFO contract asynchronous systems is defined by the following grammar:
We assume that every FIFO contract asynchronous system P is such that: items \((i)-(iii)\) of Definition 2, with \([C,{{\mathcal {Q}}}]_l\) replacing \([C]_l\), are satisfied, and it also holds (iv) messages in a queue come from a location different from the location of the queue (i.e. there is no message \(a_l\) inside the queue \({{\mathcal {Q}}}\) of a subterm \([C,{{\mathcal {Q}}}]_l\) of P).
Terms \({{\mathcal {Q}}}\) denote message queues; they are sequences of messages \(a^1_{l_1} {::} a^2_{l_2} {::} \dots {::} a^n_{l_n} {::} \epsilon \),Footnote 4 where “\(\epsilon \)” denotes the empty message queue. Trailing \(\epsilon \) are usually left implicit. (Hence, the above queue is denoted with \(a^1_{l_1} {::} a^2_{l_2} {::} \dots {::} a^n_{l_n}\).) We overload : : to denote also queue concatenation, i.e. given \({{\mathcal {Q}}}= a^1_{l_1} {::} a^2_{l_2} {::} \dots {::} a^n_{l_n}\) and \({{\mathcal {Q}}'}= b^1_{l'_1} {::} b^2_{l'_2} {::} \dots {::} b^m_{l'_m}\), then \({{\mathcal {Q}}}{::}{{\mathcal {Q}}'} = a^1_{l_1} {::} a^2_{l_2} {::} \dots {::} a^n_{l_n} {::} b^1_{l'_1} {::} b^2_{l'_2} {::} \dots {::} b^m_{l'_m}\). In the following, we will use the notation  to state that if \(a_{l'}\) is in \({{\mathcal {Q}}}\), then \(l \ne l'\). Moreover, we will use the shorthand \([C]_l\), standing for \([C,\epsilon ]_l\), to represent contract C located at l in the initial system state; queues are assumed to be initially empty.
to state that if \(a_{l'}\) is in \({{\mathcal {Q}}}\), then \(l \ne l'\). Moreover, we will use the shorthand \([C]_l\), standing for \([C,\epsilon ]_l\), to represent contract C located at l in the initial system state; queues are assumed to be initially empty.
Example 6
The FIFO contract asynchronous system
is formed by three contracts located at \(l_1\), \(l_2\) and \(l_3\); their input queues are assumed to be initially empty, due to the above defined shorthand notation. When, in the following, we will consider its evolution, and we will represent its execution states by means of FIFO contract asynchronous systems with explicit representation of (possibly non-empty) queues. Notice that also due to the adopted shorthand notation, the system is written in exactly the same way as for the deadlocked synchronous system of Example 5. However, under asynchronous communication, as we will see, such a system is not deadlocked, in that locations \(l_1\) and \(l_2\) can perform their initial outputs even without an immediately available corresponding receive action.
The operational semantics of FIFO contract asynchronous systems is defined in terms of a labelled transition system obtained by the rules in Tables 4 and 3 (plus the symmetric version for the two rules for parallel composition). The set of labels is \(\{a_{l,l'},{\overline{a}}_{l,l'}, \tau \ |\ l,l'\) \(\in Loc, a \in {{\mathcal {N}}} \}\), ranged over by \(\lambda \), \(\lambda '\), ..., as for the synchronous case. The first rule of Table 4, similar to that for the synchronous case, indicates that a send action \({\overline{a}}_{l'}\) executed by a contract located at location l, becomes an action \({\overline{a}}_{l,l'}\) (the two locations l and \(l'\) denote the sender and receiver locations, respectively). The second rule states that at the receiver location \(l'\), it is always possible to execute a complementary action \(a_{l,l'}\) (that can synchronize with \({\overline{a}}_{l,l'}\)) whose effect is to enqueue message \(a_l\) in the local queue. Notice that this complementary action is not executed by the contract at the receiver location \(l'\), but by the location itself, with the effect of enqueueing the new message in the local queue at the receiver location \(l'\). So, there is no synchronization between the sender and the receiver contracts, but between the sender and the queue at the receiver location. The third rule is for message consumption; a contract can remove a message \(a_l\) from its queue, only if \(a_l\) is not preceded by messages sent from the same location l. This guarantees that messages coming from the same location are consumed in FIFO order. The rules for parallel composition of Table 3 are the same as those considered in the synchronous case.
Example 7
An execution trace of the FIFO contract asynchronous system of Example 6 is the following one:
may perform a \(\tau \) transition obtained as synchronization of \({\overline{a}}_{l_2,l_1}\) with \(a_{l_2,l_1}\) (enqueuing \(a_{l_2}\) in the local queue of process \(l_1\)), leading to
which, in turn, performs a \(\tau \) transition obtained as synchronization of \({\overline{b}}_{l_1,l_2}\) with \(b_{l_1,l_2}\) (enqueuing \(b_{l_1}\) in the local queue of process \(l_2\)), leading to
Now, due to process \(l_1\) reading from its local queue, the system may perform a subsequent \(\tau \) transition to
Then, similarly, due to process \(l_2\) reading from its local queue, another \(\tau \) transition is performed leading to
Finally, the system performs a \(\tau \) transition (enqueuing \(a_{l_1}\) in the local queue of process \(l_3\)) to
and then a \(\tau \) transition (process \(l_3\) reading from its local queue) to
The notion of system successful completion, defining when a system P is such that \(P\surd \), is as in Definition 3 (remember that we assume \([C]_l\) to stand for \([C,\epsilon ]_l\); thus, the predicate also checks whether input queues of contracts in P are all empty). So the system of Example 6 reaches successful completion with the execution trace shown in Example 7 that ends with \([{{\mathbf {1}}},\epsilon ]_{l_1} {||}[{{\mathbf {1}}},\epsilon ]_{l_2} {||}[{{\mathbf {1}}},\epsilon ]_{l_3} \surd \).
Finally, also the notion of system deadlock is as in Definition 4. Thus, for example, differently from the synchronous case, the system of Example 6 is not in deadlock; in that, as shown in Example 7, it can perform a \(\tau \) transition.
2.4 Contract compliance and refinement
In the following, we will present definitions that hold for both the synchronous and asynchronous case in an uniform way. We call computation step a \(\tau \)-labelled transition \(P {\mathop {\longrightarrow }\limits ^{\tau }} P'\); a computation, on the other hand, is a (possibly empty) sequence of \(\tau \)-labelled transitions \(P {\mathop {\longrightarrow }\limits ^{\tau }}^* P'\), in this case starting from the system P and leading to \(P'\). To simplify the notation, we omit the \(\tau \) labels, i.e. we use \(P {\mathop {\longrightarrow }\limits ^{}} P'\) for computation steps, and \(P {\mathop {\longrightarrow }\limits ^{}}^* P'\) for computations.
We now move to the definition of correct composition of contracts. A contract system is correct if, during any of its computations, it is not possible to reach a deadlock, i.e. a system that is in deadlock according to Definition 4. This means that all its reachable states (via any computation) are such that the system has successfully completed or it is able to perform computation steps (i.e. \(\tau \) transitions) and after each step it moves to a system which is, in turn, correct. In other terms, a system is correct if all of its maximal sequences of \(\tau \) labelled transitions either lead to a successfully completed system or are infinite (do not terminate). The notion of contract compliance that we obtain is along the lines of that defined, e.g. by Barbanera and de’Liguoro in [4] or Bernardi and Hennessy in [5] (even if they consider a client/server setting instead of a multiparty one as in our definition).
We are now ready to define our notion of correct contract composition.
Definition 6
(Correct Contract Composition – Compliance) A system P is a correct contract composition according to compliance, denoted  , if for every \(P'\) such that \(P {\mathop {\longrightarrow }\limits ^{}}^* P'\), then either \(P'\) is a successfully completed system, i.e. \(P'\surd \), or there exists an additional computation step \(P' {\mathop {\longrightarrow }\limits ^{}} P''\).
, if for every \(P'\) such that \(P {\mathop {\longrightarrow }\limits ^{}}^* P'\), then either \(P'\) is a successfully completed system, i.e. \(P'\surd \), or there exists an additional computation step \(P' {\mathop {\longrightarrow }\limits ^{}} P''\).
Example 8
The synchronous system of Example 2 is a correct contract composition because it can evolve just as shown in Example 3, so any of its computations can reach successful completion. The synchronous system of Example 5 is, instead, not correct because it is immediately deadlocked. The same system considered as a FIFO asynchronous system (Example 6) is, instead, correct, because from all its computations it is possible to reach successful completion, see, e.g. Example 7.
Consider now the contract \(C = rec X.{\overline{a}}_{l}.X\). We have that the FIFO asynchronous system \([C]_{l'} {||}P\), with P including location l, is trivially a correct contract composition for every P. In fact, every computation cannot terminate in that C is always allowed to perform an output operation \({\overline{a}}_{l}\).
As a more significant example of correct FIFO asynchronous system, we can consider \([{ AltClient }]_c {||}[{ Server }]_s\), with \({ AltClient }\) being the contract (for the alternative client in Fig. 1) defined in Example 1 where we assume all actions to be decorated with s; and \({ Server }\) being the contract for the server, where we assume all actions to be decorated with c. In this system, successful completion cannot be reached, but the system never reaches a deadlock, i.e. every system reachable via a computation always has an additional computation step. Notice that \([{ AltClient }]_c {||}[{ Server }]_s\) considered as a synchronous system is, instead, not correct because, e.g. after synchronization on \({ w }\), \({ ok }\) and \({ w }\), the system reaches a deadlock (both the client c and the server s want to do just outputs).
Notice that the above client/server FIFO asynchronous system is a correct contract composition even if the considered client \({ AltClient }\) does not behave specularly w.r.t. the server \({ Server }\). When we replace a contract with another one by preserving system correctness, we say that we refine the initial contract. As an example, consider the correct system \({[b_{l'}.{{{\overline{a}}}}_{l'}]_l}\ {||}\ {[{{{\overline{b}}}}_l.a_l]_{l'}}\) composed of two specular contracts. We can replace the contract \(b_{l'}.{{{\overline{a}}}}_{l'}\) with \({{{\overline{a}}}}_{l'}.b_{l'}\) by preserving system correctness (i.e. \({[{{{\overline{a}}}}_{l'}.b_{l'}]_l}\ {||}\ {[{{{\overline{b}}}}_l.a_l]_{l'}}\) is still correct). The latter differs from the former in that it anticipates the send action \({{{\overline{a}}}}_{l'}\) w.r.t. the receive action \(b_{l'}\). This transformation is usually called output anticipation (see e.g. [35]). Intuitively, output anticipation is possible because, under asynchronous communication, its effect is simply that of anticipating the introduction of a message in the partner queue. In the context of asynchronous session types, for instance, output anticipation is admitted by the notion of session subtyping [22, 35] that, as we will discuss in the following sections, is the counterpart of contract refinement in the context of session types.
We now formally define contract refinement and we observe that, differently from session types, in the FIFO asynchronous setting, output anticipation is not admitted as a general contract refinement mechanism.
Definition 7
(Contract Refinement) A contract \(C'\) is a refinement of a contract C, denoted \(C' \preceq C\), if and only if, for all contract systems \(([C]_l {||}P)\) we have that, if  then
then  .
.
In the following, whenever \(C' \preceq C\), we will also say that \(C'\) is a subcontract of C (or equivalently that C is a supercontract of \(C'\)).
The above definition contains a universal quantification on all possible contract systems P and locations l; hence, it cannot be directly used to algorithmically check contract refinement. To the best of our knowledge, in the asynchronous case, there exists no general algorithmic characterization (or proof of undecidability) for such a relation. Nevertheless, we can use the definition on some examples.
As an initial trivial example of refinement consider the contract \(C = rec X.{\overline{a}}_{l}.X\) discussed in the Example 8. We have commented that  for every P including location l. But this holds also if we replace C with any contract \(C'\) willing to perform infinitely many outputs towards location l; hence, we have that \(C' \preceq C\) (and also \(C \preceq C'\)) for all such contracts \(C'\).
for every P including location l. But this holds also if we replace C with any contract \(C'\) willing to perform infinitely many outputs towards location l; hence, we have that \(C' \preceq C\) (and also \(C \preceq C'\)) for all such contracts \(C'\).
Another more interesting example considers the two contracts \(C=b_{l'}.{{{\overline{a}}}}_{l'}\) and \(C'={{{\overline{a}}}}_{l'}.b_{l'}\) discussed above. We have seen that in the FIFO asynchronous setting, \(C'\) is a safe replacement of C in the specific context \([\,]_l {||}[{{{\overline{b}}}}_{l}.a_l ]_{l'}\). But we have that \(C' \not \preceq C\) because there exists a discriminating context \([\,]_l {||}[{{{\overline{b}}}}_{l}.a_l + a_{l}]_{l'}\). In fact, when combined with \(C'\), the contract in \(l'\) can take the alternative branch \(a_{l}\), leading to an incorrect system where the contract at l blocks waiting for a never incoming message \(b_{l'}\).
The above example shows that output anticipation, admitted in the context of asynchronous session types, is not a correct refinement mechanism for contracts. The remainder of the paper is dedicated to the definition of a fragment of contracts in which it is correct to admit output anticipation. We will, however, need to first recall session types and asynchronous subtyping.
3 Session types
In this section, we recall session types; in particular, we discuss binary session types for asynchronous communication. In fact, for this specific class of session types, subtyping admits output anticipation. We do this by presenting the basic definitions of session type syntax and synchronous and asynchronous session subtyping.
We start with the formal syntax of binary session types, adopting a simplified notation (used, e.g. in [9, 10]) without dedicated constructs for sending an output/receiving an input. We instead represent outputs and inputs directly inside choices. More precisely, we consider output selection \(\oplus \{{l}_{i}:{T}_{i}\}_{i\in I}\), expressing an internal choice among outputs, and input branching \( { \& }\{{l}_{i}:{T}_{i}\}_{i\in I}\), expressing an external choice among inputs. Each possible choice is labelled by a label \(l_i\), taken from a global set of labels L, followed by a session continuation \(T_i\). Labels in a branching/selection are assumed to be pairwise distinct.
Definition 8
(Session Types) Given a set of labels L, ranged over by l, the syntax of binary session types is given by the following grammar:
where the finite set of indices \(I \subset {\mathbb {N}}\) is assumed to be non-empty, and \(\mu {\mathbf {t}}.\_\) is a binder for the variable \({\mathbf {t}}\) denoting recursive definition of types. We assume that in a type T all variables \({\mathbf {t}}\) are bound and all recursive definitions are guarded, i.e. in \(\mu {\mathbf {t}}.T\) all free occurrences of \({\mathbf {t}}\) are guarded by (i.e. included in the scope of) an output or an input type. In the sequel, we leave implicit the index set \(i \in I\) in input branchings and output selections when it is already clear from the denotation of the types. Note also that we abstract from the type of data that is transmitted via outputs/inputs, since this is orthogonal to our results in this paper.
For session types, two types are dual when they behave symmetrically; output selections in one type are matched by corresponding input branchings in the other type. There are alternative definitions of duality in the literature (for a discussion about duality in session types see the recent paper [27]); for the sake of the present paper, the simplest form of duality, called naive duality, is sufficient.
Definition 9
(Duality) Given a session type T, its dual \({\overline{T}}\) is inductively defined as:
3.1 Synchronous session subtyping
We now move to the session subtyping relation. The subtyping relation was initially defined by Gay and Hole [26] for synchronous communication; we adopt a similar co-inductive definition but, to be more consistent with the behavioural contract theory of Sect. 2, we follow a slightly different approach that is process-oriented instead of channel-oriented, following the terminology in [25].Footnote 5 Moreover, following [35], we consider a generalized version of unfolding that allows us to unfold recursions \(\mu {\mathbf {t}}.T\) as many times as needed. This is formalized by the following function:
Definition 10
( n -unfolding)
We are now in a position to present synchronous subtyping.
Definition 11
(Synchronous Subtyping, \({\le }_{sy}\)) \({\mathcal {R}}\) is a synchronous subtyping relation whenever \((T,S)\in {\mathcal {R}}\) implies that:
-
1.
if \(T={\mathbf {end}}\) then \(\exists n\ge 0\) such that \({\mathsf {unfold}}^{n}(S) = {\mathbf {end}}\);
-
2.
if \(T=\oplus \{{l}_{i}:{T}_{i}\}_{i\in I}\) then \(\exists n\ge 0\) such that \({\mathsf {unfold}}^{n}(S) = \oplus \{{l}_{j}:{S}_{j}\}_{j\in J}\), \(I\subseteq J\) and \(\forall i\in I .(T_i,S_i)\in {\mathcal {R}}\);
-
3.
if \( T={ \& }\{{l}_{i}:{T}_{i}\}_{i\in I}\) then \(\exists n\ge 0\) such that \( {\mathsf {unfold}}^{n}(S) = { \& }\{{l}_{j}:{S}_{j}\}_{j\in J}\), \(J\subseteq I\) and \(\forall j\in J .(T_j,S_j)\in {\mathcal {R}}\);
-
4.
if \(T= \mu {\mathbf {t}}.{T'} \) then \((T'\{T/{\mathbf {t}}\}, S)\in {\mathcal {R}}\).
T is a synchronous subtype of S, written \(T {\le }_{sy} S\), if there is a synchronous subtyping relation \({\mathcal {R}}\) such that \((T,S) \in {\mathcal {R}}\).
Example 9
As an example of session types in subtyping relation, consider
that describes a cyclic protocol that initially accepts two possible messages \({ coffee }\) or \({ tea }\), and then respectively replies with \({ american }\) or \({ green }\), and
that initially accepts only the \({ coffee }\) messages and then replies with either \({ american }\) or \({ espresso }\). We have that \(T {\le }_{sy} S\) because of the following subtyping relation:
Notice that T, and its derived types, have input branchings with more labels than those of the corresponding input branchings in S, or in its derived types (input contravariance). On the other hand, they have output selections with less labels (output covariance).
Two types T and S are related by \({\le }_{sy}\), whenever S is able to simulate T with output and input types enjoying covariance and contravariance properties, respectively. Notice the asymmetric use of unfolding between the left- and right-hand terms T and S; in T, recursion is always unfolded once, while in S many unfoldings can be needed in order to expose the starting operator of T.
Synchronous subtyping \({\le }_{sy}\) is dual closed, i.e. when we move to the dual of two session types that are in subtyping relation, their ordering is also complemented, that is, their subtyping relation is inverted.
Definition 12
(Dual Closeness) We say that a relation \({\mathcal {R}}\) on session types is dual closed if \((S,T) \in {\mathcal {R}}\) implies \(({\overline{T}},{\overline{S}}) \in {\mathcal {R}}\).
Dual closure of \({\le }_{sy}\) directly follows from basic properties of session subtyping, like the inversion properties formalized by Lemma 2 in [26].
3.1.1 Aynchronous session subtyping
We now consider the standard notion of asynchronous subtyping [22, 34].
We start by introducing the auxiliary notion of input contexts, which we use to denote sequences of initial input branchings in a session type. This is needed because, as we will discuss in the following, in the definition of asynchronous session subtyping, it is important to identify those output selections that are guarded by input branchings.
Definition 13
(Input Context) An input context \({\mathcal {A}}\) is a session type with multiple holes defined by the syntax:
The holes \([\,]^n\), with \(n \in {\mathbb {N}}^+\), of an input context \({\mathcal {A}}\) are assumed to be consistently enumerated, i.e. there exists \(m \ge 1\) such that \({\mathcal {A}}\) includes one and only one \([\,]^n\) for each \(n \le m\). Given types \(T_1\),..., \(T_m\), we use \(\mathcal {A}[{T_k}]^{k\in \{1,\ldots , m\}}\) to denote the type obtained by filling each hole k in \({\mathcal {A}}\) with the corresponding term \(T_k\).
As an example of how input contexts are used, consider the session type&\(\big \{l_{1}:\oplus \{l:{\mathbf {end}}\}, l_{2}:\oplus \{l:{\mathbf {end}}\} \big \}\). It can be decomposed as the input context&\(\big \{l_{1}:[\,]^1,l_{2}:[\,]^2\big \}\) with two holes that can be both filled with \(\oplus \{l:{\mathbf {end}}\}\).
We are now ready to define the asynchronous subtyping \({\le }\) relation. In particular, we consider the definition in [9], which constitutes a simplified formulation of the definition in [34] (and, in our setting, also of the definition in [22], as we discuss below).
Definition 14
(Asynchronous Subtyping, \({\le }\)) \(\,{\mathcal {R}}\;\) is an asynchronous subtyping relation whenever \((T,S)\in {\mathcal {R}}\) implies 1., 3., and 4. of Definition 11 plus the following modified version of 2.:
-
2.
if \(T=\oplus \{{l}_{i}:{T}_{i}\}_{i\in I}\) then \(\exists n\ge 0,{\mathcal {A}}\) such that
-
\({\mathsf {unfold}}^{n}(S) = \mathcal {A}[{\oplus \{{l}_{j}:{S_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\),
-
\(\forall k\in \{1,\ldots , m\}. \, I\subseteq J_k\) and
-
\(\forall i\in I, (T_i,\mathcal {A}[{{S_{ki}}}]^{k\in \{1,\ldots , m\}})\in {\mathcal {R}}\);
-
T is an asynchronous subtype of S, written \(T \, {\le }\, S\), if there is an asynchronous subtyping relation \({\mathcal {R}}\) such that \((T,S) \, \in \, {\mathcal {R}}\).
Intuitively, the above co-inductive definition says that it is possible to play a simulation game between a subtype T and its supertype S as follows: if T is the \({\mathbf {end}}\) type, then also S is ended; if T starts with an output selection, then S can reply by outputting at least all the labels in the selection (output covariance), and the simulation game continues; if T starts with an input branching, then S can reply by inputting at most some of the labels in the branching (input contravariance), and the simulation game continues. The unique nontrivial case is the case of output selection; in fact, in this case the supertype could reply with output selections that are guarded by input branchings.
As an example of application of this rule for output selection, consider the session type \( T=\oplus \big \{l: \& \{l_{1}:{\mathbf {end}}, l_{2}:{\mathbf {end}}\} \big \}\). We have that T is a subtype of \( S= \& \big \{l_{1}:\oplus \{l:{\mathbf {end}}\}, l_{2}:\oplus \{l:{\mathbf {end}}\} \big \}\), previously introduced. In fact, we have that the following relation
is an asynchronous subtyping relation. Rule \({ 2. }\) of the definition is applied on the first pair (T, S). The first item of the rule is used to decompose S (as discussed above) as the input context&\(\big \{l_{1}:[\,]^1,l_{2}:[\,]^2\big \}\) with two holes both filled with \(\oplus \{l:{\mathbf {end}}\}\). The second item trivially holds because the output selection at the beginning of T has only one label l, as also the output selections filling the holes in the decomposition of S. Finally, the third item holds because of the pair (&\( \{l_{1}:{\mathbf {end}}, l_{2}:{\mathbf {end}}\}, \& \{l_{1}:{\mathbf {end}}, l_{2}:{\mathbf {end}}\}\)) present in the relation. The first element of the pair is obtained by consuming the output selection at the beginning of T, while the second element by consuming the initial output selection of the terms filling the holes of the considered input context.
The rationale behind asynchronous session subtyping is that under asynchronous communication it is unobservable whether an output is anticipated before an input or not. In fact, anticipating an output simply introduces in advance the corresponding message in the communication queue. For this reason, rule \({ 2. }\) of the asynchronous subtyping definition admits the supertype to have inputs in front of the outputs used in the simulation game.
As a further example, consider the types \( T=\mu {\mathbf {t}}.{ \& }\{{l}:{\oplus \{{l}:{{\mathbf {t}}}\}}\}\) and \( S=\mu {\mathbf {t}}.{ \& }\{{l}:{{ \& }\{{l}:{\oplus \{{l}:{{\mathbf {t}}}\}}\}}\}\). We have \(T \, {\le }\, S\) by considering an infinite subtyping relation including pairs \((T, S')\), with \(S'\) being \( { \& }\{{l}:{S}\}\), \( { \& }\{{l}:{{ \& }\{{l}:{S}\}}\}\), \( { \& }\{{l}:{{ \& }\{{l}:{{ \& }\{{l}:{S}\}}\}}\}\), ...; that is, the effect of each output anticipation is that a new input \( { \& }\{{l}:{\_}\}\) is accumulated in the initial part of the r.h.s. It is worth to observe that every accumulated input \( { \& }\{{l}:{\_}\}\) is eventually consumed in the simulation game, but the accumulated inputs grows unboundedly.
Example 10
As a less trivial example, we can express as session types the two client protocols depicted in Fig. 1:
We have that \({ AltClient } \le { Client }\) because the subtyping simulation game can go on forever: when one of the derived types of \({ AltClient }\) selects the output \({ w }\) while the corresponding derived types of \({ Client }\) starts with an input branching, this input branching is accumulated in front of such derived type of \({ Client }\).
We now discuss specific limit cases of application of Definition 14 of asynchronous subtyping:
-
Concerning rule \({ 2. }\), as discussed above, it assumes the possibility to decompose the candidate supertype into an initial input context, with holes filled by types starting with output selections. We notice that there exist session types that cannot be decomposed in such a way. Consider, for instance, the session type \( S=\mu {\mathbf {t}}. \& \{l_1: {\mathbf {t}}, l_2:\oplus \{l: {\mathbf {t}}\}\}\). S cannot be decomposed as an input context with holes filled by output branchings because, for every n, \({\mathsf {unfold}}^{n}(S)\) will contain a sequence of input branchings (labelled with \(l_1\)) that terminate in a term starting with the recursive definition \(\mu {\mathbf {t}}. \_\). Our opinion is that the definition of asynchronous subtyping does not manage properly these limit cases. For instance, the above session type S could be reasonably considered a supertype of \( \mu {\mathbf {t}}.\oplus \{l: \& \{l_1: {\mathbf {t}}, l_2:{\mathbf {t}}\}\), that simply anticipates the output selection with label l. Such a type has runs with more output selections, because S has a loop that does not include the output selection; but this is not problematic because such outputs could be simply stored in the message queue. Nevertheless, we have that such a session type is not a subtype of S due to the above observation about the inapplicability of rule \({ 2. }\)
-
On the other hand, there are cases in which rule \({ 2. }\) is applicable but the input that it accumulates in the r.h.s. is never consumed. Consider, e.g. the infinite simulation game between \(T=\mu {\mathbf {t}}.\oplus \{{l}:{{\mathbf {t}}}\}\) and \( S=\mu {\mathbf {t}}.{ \& }\{{l'}:{\oplus \{{l}:{{\mathbf {t}}}\}}\}\): only output selections are present in the subtype T, and an instance of the input branching in the supertype S is accumulated in each step of the simulation game. These limit cases are allowed in [34], on which our Definition 14 is based, but are, instead, disregarded in [22] by means of a specific “orphan message free” constraint that is added to the definition of asynchronous subtyping: considering T to be subtype (i.e. a replacement) of S conceptually means allowing for messages \(l'\) that are sent to T to remain “orphan” (never actually read by T). Moreover, the fact that, as in [34], we have \(T \, {\le }\, S\) implies that \({\le }\) is not dual closed on (arbitrary) binary session types. This because, if we consider the dual of T, i.e. \( {\overline{T}}=\mu {\mathbf {t}}.{ \& }\{{l}:{{\mathbf {t}}}\}\), and the dual of S, i.e. \( {\overline{S}}=\mu {\mathbf {t}}.\oplus \{{l'}:{{ \& }\{{l}:{{\mathbf {t}}}\}}\}\), we have that
 (\({\overline{T}}\) cannot match the \(l'\) output).
(\({\overline{T}}\) cannot match the \(l'\) output).
In order to avoid such limit cases (which lead to either complicating the definition of asynchronous subtyping as in [22] or to lose the dual closeness property as in [34]), in the following, we will restrict to session types that do not include output divergent or input divergent recursions. An output (input, resp.) divergent recursion is a recursion where it is possibile to advance forever by just executing outputs (inputs, resp.). The intuition is that any significant session type should represent a conversation and not have the possibility to end up in a permanent mono-directional communication.
Formally, given a session type S and any subterm \(\mu {\mathbf {t}}. T\) of S, we assume that all free occurrences of \({\mathbf {t}}\) are guarded in T by both a send and a receive action, i.e. \({\mathbf {t}}\) is included both in the scope of an output selection \(\oplus \{\_\}\) and of an input branching&\(\{\_\}\). A formal operational characterization of this constraint will be given in Sect. 4 by mapping session types into behavioural contracts. Essentially, the constraint yields an input/output alternation property: any infinite execution contains infinitely many inputs as well as infinitely many outputs.
Notice that the restriction that we consider is consistent with session type duality, in that, if a session type T satisfies the constraint above, then also its dual \({\overline{T}}\) satisfies it. Under such a restriction for session types it is immediate to show that also asynchronous subtyping of [22] reduces to the Definition 14 considered here (see, e.g. the reformulation presented in [8] where the orphan message-free constraint of [22] is expressed as absence of output divergent behaviour). Intuitively, this is due to the fact that it is no longer possible to express output divergent recursive types originating orphan messages. An important consequence is that since asynchronous subtyping of [22] is dual closed (see [10]), also the subtyping relation \({\le }\) of Definition 14 enjoys such a property.
Proposition 1
The asynchronous subtyping relation \({\le }\) is dual closed.
We conclude this section by observing that asynchronous session subtyping was considered decidable (see [35]), but recently Bravetti, Carbone and Zavattaro proved that it is undecidable [9].Footnote 6 After undecidability was proven, efforts have been spent in detecting decidable fragments or sound algorithmic characterizations, see Sect. 6.
4 Mapping session types into behavioural contracts
In Sect. 2 we have defined a notion of refinement for contracts and we have seen that, even when communication is asynchronous, output anticipation is not admitted as a general refinement mechanism. Then, in Sect. 3, we have recalled session types where, on the contrary, output anticipation is admitted by asynchronous session subtyping. In this section we show that in the asynchronous setting, it is possible to define a fragment of contracts for which refinement turns out to coincide with asynchronous session subtyping. More precisely, we will identify a fragment of contracts that are sufficient to naturally encode session types. Moreover, we will prove that such a natural encoding maps asynchronous session subtyping into refinement, in the sense that two types are in subtyping relation if and only if the corresponding contracts are in refinement relation.
The first restriction that we discuss is about mixed-choice, i.e. the possibility to perform from the same state both send and receive actions. Consider, for instance, the system:
Such a system is a correct contract composition in that there is only one possible deterministic computation terminating in a successful configuration. On the contrary, if we replace the first contract with the contract obtained simply by anticipating the output \({\overline{b}}_{l_2}\), we obtain the system
which is not correct because there is a computation that activates the alternative branching of the second contract. In this alternative branching, the message z is produced that cannot be consumed. For this reason, we start by removing mixed-choices from contracts. This is justified also by the fact that mixed-choices are not present in session types, where we have either output selections or input branchings.
But removing mixed-choice from contracts is not sufficient to admit output anticipation. For instance, consider the system
which is correct; but if we replace the contract at location \(l_1\) with \({\overline{c}}_{l_2}.b_{l_2}\), that simply anticipates an output, we obtain
which is no longer correct in that the alternative branch \(c_{l_1}\) can be taken by the contract in \(l_2\), thus reaching a system in which the contract at \(l_1\) will wait indefinitely for \(b_{l_2}\).
For this reason, we need an additional restriction on choices: besides requiring any choice to involve either send actions only or receive actions only, we also impose all such actions to address the same location l. This is obtained by restricting to systems with only two locations. This restriction is in line with our objective, i.e. obtain a refinement which is fully abstract w.r.t. asynchronous subtyping defined in Sect. 3.1.1, where we considered binary session types (i.e. types for sessions between two endpoints). Given that there are only two locations, each contract can send to or receive from only the partner’s location; hence, all sends or receives in a choice address the same location. In general, we will omit the locations associated to send and receive actions: in fact, as already discussed also in Example 1, these can be left implicit because, when there are only two locations, all actions in one location consider the other location. A final restriction follows from the decision (see Sect. 3.1.1) to focus our analysis on session types that do not include output divergent or input divergent recursions, i.e. session types that do not end up in a permanent (infinite) mono-directional communication.
We are now ready to formally define the restricted syntax of contracts considered in this section; it is similar to session behaviours, as defined in [4], and session contracts, as defined in [5], for synchronous communication, plus the above-mentioned restriction that excludes output divergent and input divergent recursions. The only significant difference is that here we do not make use of a special internal choice operator \(\bigoplus _{i \in I} \overline{a^i}.C_i\) to represent a choice among a set of send actions \(\overline{a^i}\), with \(i \in I\). As a matter of fact, internally choosing send actions in behavioural contracts is natural in the case of synchronous communication, so to represent that the decision on which action to communicate is taken from the sender side: the behaviour of \(\bigoplus _{i \in I} \overline{a^i}.C_i\) in [4, 5] can be represented as \(\sum _{i \in I} \tau .\overline{a^i}.C_i\) by introducing internal \(\tau \) actions in the syntax of Definition 1 (see, e.g. [15, 19] and the more general characterization of output persistent contracts therein). In the context of synchronous communication, this is also needed to obtain covariance of output choices and contravariance of input choices in contract refinement. In the context of asynchronous communication, instead, the decision on which action to communicate is already implicitly taken by the sender and the introduction of an internal choice operator/\(\tau \) actions in contracts is not needed.
Definition 15
(Session contracts) Session contracts are behavioural contracts obtained by considering the following restricted syntax:
where besides the assumptions in Definition 1, we also consider the same restriction defined, in the context of session types, in Sect. 3.1.1; in recursive definitions recX.C, all free occurrences of X are guarded by both a send and a receive action, i.e. X is included both in the scope of a prefix \(\sum _{i \in I} \overline{a^i}.C_i\) and of a prefix \(\sum _{j \in J} a^j.C_J\). Notice that we omit the locations l associated to the send and receive actions (which are present in the contract syntax as defined in Definition 1). This simplification is justified because we will consider systems with only two locations, and we implicitly assume all actions of the contract in one location to be directed to the other location.
Operationally, the syntactical restriction considered above means that C cannot perform a trace of transitions that ends up in an output divergent or in an input divergent execution. An output (input, resp.) divergent execution is an infinite sequence of output (input, resp.) transitions. Thus, C enjoys an input/output alternation property; any infinite execution contains infinitely many inputs as well as infinitely many outputs. Formally, assuming \(\alpha \) meta-variables to range over \(\{a,{\overline{a}} \ |\ a \in {{\mathcal {N}}}\}\), i.e. input and output actions without a location, session contracts C satisfy the following property.
If there exist infinite contracts \(C_i\) and labels \(\alpha _i\), with \(i \in {\mathbb {N}}\), such that C can perform an infinite trace \(C {\mathop {\longrightarrow }\limits ^{\alpha _1}} C_1 {\mathop {\longrightarrow }\limits ^{\alpha _2}} C_2 {\mathop {\longrightarrow }\limits ^{\alpha _3}} \dots \) (i.e. formally, \(\forall i \in {\mathbb {N}} .C_{i-1} {\mathop {\longrightarrow }\limits ^{\alpha _i}} C_i\) with \(C_0=C\)), then for all \(i \in {\mathbb {N}}\) there exist \(j,k \in {\mathbb {N}}\), with both \(j > i\) and \(k > i\), such that: \(\alpha _j = a\), for some a (i.e. \(\alpha _j\) is an input label), and \(\alpha _k = {\overline{a}}\), for some a (i.e. \(\alpha _k\) is an output label).Footnote 7
As mentioned above, we restrict our investigation to FIFO contract systems with only two locations and by considering only session contracts. We will omit the location names also in the denotation of such binary contract systems. Namely, we will use \([C,\mathcal {Q}] {||}[C',\mathcal {Q}']\) to denote binary contract systems, thus omitting the names of the two locations as any pair of distinct locations l and \(l'\) could be considered. In the restricted setting of binary session contracts, we can redefine the notion of refinement as follows.
Definition 16
(Binary Session Contract Refinement) A session contract \(C'\) is a binary session contract refinement of a session contract C, denoted with \(C' \preceq _s C\), if and only if, for all session contract D, if  then
then  .
.
We now move to the proof of correspondence between session types and session contracts. The first step is the definition of a syntactic translation from session types to session contracts.
Definition 17
Let T be a session type. We inductively define a function \([[T]]\) from session types to session contracts as follows:
Notice that \([[\_]]\) defines a direct mapping from constructs of the syntax of session types to corresponding constructs of the syntax of session contracts.
The remainder of this section reports the proof that given two session types T and S, we have that \(T \le S\) if and only if \([[T]] \preceq _s [[S]]\). This result has two main consequences. On the one hand, as a positive consequence, we can use the characterization of session subtyping in Definition 14 to prove also session contract refinement. For instance, if we consider the two session types \({ AltClient }\) and \({ Client }\) of Example 10, we can conclude that
because these two contracts are respectively the encoding of the session type \({ AltClient }\), and of its supertype \({ Client }\), according to \([[\,]]\) (notice that these two contracts coincide with the two clients represented in Fig. 1). On the other hand, as a negative consequence, we have that session contract refinement \(\preceq _s\) is in general undecidable, because asynchronous subtyping \(\le \) is undecidable as recalled in Sect. 3.
4.1 Proving the coincidence of session subtyping with contract refinement
We start with the presentation of a roadmap of the technical results proved in this section. There are two main results: soundness (Theorem 1), stating that if two types are in subtyping relation then their corresponding contracts are in refinement relation, and completeness (Theorem 2), stating that also the vice versa holds.
The proof of soundness relies on the possibility to anticipate outputs without breaking system correctness, i.e. given a correct binary session contract system with a contract having an output on a specific label that is eventually executable after every possible sequence of inputs, the system remains correct even if we replace this contract with another one that performs immediately this output, and for the rest behaves as the previous contract. This property is formalized in terms of two Propositions, Proposition 2 dealing with the anticipation of output selections with only one branch, and Proposition 3 that considers also output selections with more than one branch. The proof of such Propositions exploits a couple of preliminary lemmata (Lemma 1 and 2).
The proof of completeness actually considers the contrapositive statement; if two types are not in subtyping relation then their corresponding session contracts are not in refinement relation. In particular, given T and S, such that \( S\) then there exists a session contract D such that  while
while  (i.e.
(i.e.  does not hold), hence \([[T]]\) is not a refinement of \([[S]]\). As a discriminating context, we take \(D=[[{\overline{S}}]]\). We prove that
does not hold), hence \([[T]]\) is not a refinement of \([[S]]\). As a discriminating context, we take \(D=[[{\overline{S}}]]\). We prove that  in Proposition 4. On the other hand, in order to prove that
in Proposition 4. On the other hand, in order to prove that  , we show the existence of a computation starting from \(([[[T]]] {||}[[[{\overline{S}}]]])\) and leading to a deadlock, i.e. a configuration which is not successful and from which there are exiting transitions. Such a computation (at least an initial part of it) is discussed and formalized in Proposition 5.
, we show the existence of a computation starting from \(([[[T]]] {||}[[[{\overline{S}}]]])\) and leading to a deadlock, i.e. a configuration which is not successful and from which there are exiting transitions. Such a computation (at least an initial part of it) is discussed and formalized in Proposition 5.
We now start from the auxiliary lemmata used in the formalization of our first result about the possibility to anticipate outputs without breaking system correctness.
Lemma 1
Consider the two session contract systems
\(P_1=[[[\mathcal {A}[{S_k}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}'{::}l]\) and
\(P_2=[[[\mathcal {A}[{\oplus \{l:S_k\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\).
If  then one of the following holds:
then one of the following holds:
-
\({\mathcal {A}}\) is a single hole and \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_1\);
-
\({\mathcal {A}}\) is not a single hole and \(P_1\) has at least one outgoing transition. For every possible transition \(P_1 {\mathop {\longrightarrow }\limits ^{}} P_1'\), we have that one of the following holds:
-
1.
\(P_1\) does not consume the label l and there exist \({\mathcal {A}}'\), \(D'\), \({{\mathcal {Q}}}''\) and \({{\mathcal {Q}}}'''\) s.t. \(P_1' = [[[\mathcal {A'}[{S_k}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}\) \( [D',{{\mathcal {Q}}}'''{::}l]\) and
\(P_2 {\mathop {\longrightarrow }\limits ^{}} [[[\mathcal {A'}[{\oplus \{l:S_k\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}''']\);
-
2.
\(P_1\) consumes the label l, hence \(P_1' \!\!= \!\![[[\mathcal {A}[{S_k}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}] {||}[D',{{\mathcal {Q}}}']\), and \(\exists j \in \{1,\ldots , m\}\) s.t. \(P_2 {\mathop {\longrightarrow }\limits ^{}}^* [[[S_j]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}']\) and \({{\mathcal {Q}}}=a_1 {::} \dots {::} a_w {::} {{\mathcal {Q}}}''\), where \(a_1,\dots ,a_w\) are the labels in the path to \([\,]^j\) in \({\mathcal {A}}\).
-
1.
Proof
A simple case analysis on the possible transitions of the two considered systems \(P_1\) and \(P_2\). In the case 2. of the second item, we also have to observe that if the label l is consumed in one step by \(P_1\), then \({{\mathcal {Q}}}'=\epsilon \) and \(D'\) starts with an input branching. Given that  , the l.h.s. should be able to eventually produce a label that can be consumed by the initial input branching of the r.h.s. Hence, \({\mathcal {A}}\) should have a sequence of input branchings that consumes initial labels in \({{\mathcal {Q}}}\) and then reaches a hole. We simply assume \(a_1,\dots ,a_w\) to be such labels and \([\,]^j\) to be such hole. \(\square \)
, the l.h.s. should be able to eventually produce a label that can be consumed by the initial input branching of the r.h.s. Hence, \({\mathcal {A}}\) should have a sequence of input branchings that consumes initial labels in \({{\mathcal {Q}}}\) and then reaches a hole. We simply assume \(a_1,\dots ,a_w\) to be such labels and \([\,]^j\) to be such hole. \(\square \)
Lemma 2
Consider the two session contract systems
\(P_1=[[[\mathcal {A}[{S_k}]^{k\in \{1,\ldots , m\}}]],a_1 {::} \dots {::} a_w {::} {{\mathcal {Q}}}]{||}[D',{{\mathcal {Q}}}']\) and
\(P_2=[[[S_j]],{{\mathcal {Q}}}]{||}[D',{{\mathcal {Q}}}']\)
with \(j \in \{1,\ldots , m\}\) and \(a_1,\dots ,a_w\) that are the labels in the path to \([\,]^j\) in \({\mathcal {A}}\).
If  then also
then also  .
.
Proof
By contradiction, assume there exists a computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P_1'\) with \(P_1'\) blocked (\(P_1'\) without exiting transitions and not successful). We have that such computation consumes the messages \(a_1,\dots ,a_w\) in the queue. Hence, we can reorder the computation by anticipating, at the beginning, the corresponding input consumption. At the end of this initial part of the computation, the system is identical to \(P_2\), hence also \(P_2 {\mathop {\longrightarrow }\limits ^{}}^* P_1'\), but this contradicts  . \(\square \)
. \(\square \)
We now formalize the possibility to anticipate outputs without breaking system correctness; we start with a first Proposition that considers outputs without alternative branchings.
Proposition 2
Consider the two following session contract systems
\(P_1=[[[\mathcal {A}[{S_k}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}'{::}l]\) and
\(P_2=[[[\mathcal {A}[{\oplus \{l:S_k\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\).
If  then also
then also  .
.
Proof
By contradiction, assume that  , while
, while  . The latter ensures the existence of a computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P\) with P blocked (P without exiting transitions and not successful). We now observe that we can apply Lemma 1 on \(P_1\) and \(P_2\). The first item cannot hold, otherwise \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_1 {\mathop {\longrightarrow }\limits ^{}}^* P\) with P blocked, that implies that
. The latter ensures the existence of a computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P\) with P blocked (P without exiting transitions and not successful). We now observe that we can apply Lemma 1 on \(P_1\) and \(P_2\). The first item cannot hold, otherwise \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_1 {\mathop {\longrightarrow }\limits ^{}}^* P\) with P blocked, that implies that  , thus contradicting the thesis. Hence, the second item must hold, implying that the computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P\) is not of length 0, i.e. there exists \(P_1'\) s.t. \(P_1 {\mathop {\longrightarrow }\limits ^{}} P_1' {\mathop {\longrightarrow }\limits ^{}}^* P\). By considering also Lemma 2 we have that only 1. in the second item of Lemma 1 can hold, i.e. there exist \({\mathcal {A}}'\), \(D'\), \({{\mathcal {Q}}}''\) and \({{\mathcal {Q}}}'''\) such that \(P_1' = [[[\mathcal {A'}[{S_k}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}'''{::}l]\) and \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_2'= [[[\mathcal {A'}[{\oplus \{l:S_k\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}''']\). But we can apply our reasoning again on \(P_1'\) and \(P_2'\), because
, thus contradicting the thesis. Hence, the second item must hold, implying that the computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P\) is not of length 0, i.e. there exists \(P_1'\) s.t. \(P_1 {\mathop {\longrightarrow }\limits ^{}} P_1' {\mathop {\longrightarrow }\limits ^{}}^* P\). By considering also Lemma 2 we have that only 1. in the second item of Lemma 1 can hold, i.e. there exist \({\mathcal {A}}'\), \(D'\), \({{\mathcal {Q}}}''\) and \({{\mathcal {Q}}}'''\) such that \(P_1' = [[[\mathcal {A'}[{S_k}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}'''{::}l]\) and \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_2'= [[[\mathcal {A'}[{\oplus \{l:S_k\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}''']\). But we can apply our reasoning again on \(P_1'\) and \(P_2'\), because  in that it is a derivative of \(P_2\) and
in that it is a derivative of \(P_2\) and  , while
, while  , because we can consider the shorter computation \(P_1' {\mathop {\longrightarrow }\limits ^{}}^* P\) to the blocked system P. Each time the arguments are applied, the computation is shortened, and at the end we would have that the first of the two considered systems (\(P_1\) in the proposition statement) should be already blocked, but this contradicts Lemma 1. \(\square \)
, because we can consider the shorter computation \(P_1' {\mathop {\longrightarrow }\limits ^{}}^* P\) to the blocked system P. Each time the arguments are applied, the computation is shortened, and at the end we would have that the first of the two considered systems (\(P_1\) in the proposition statement) should be already blocked, but this contradicts Lemma 1. \(\square \)
The above proposition formalizes a condition under which anticipating an output does not break system correctness. The direct application of the above proposition is limited to outputs with only one branch. The following proposition generalizes its applicability to outputs with more branchings, provided that all the involved outputs have at least one branching with the same label.
Proposition 3
Consider the following session contract system
\(P_1=[[[\mathcal {A}[{\oplus \{l_j:S_{kj}\}_{j \in J_k}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\).
If  and \(i \in \bigcap _{k \in \{1,\ldots , m\}} J_k\), then also
and \(i \in \bigcap _{k \in \{1,\ldots , m\}} J_k\), then also  with
with
\(P_2=[[[\mathcal {A}[{\oplus \{l_i:S_{ki}\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\).
Proof
By contradiction assume that  . Then, there exists a computation \(P_2 {\mathop {\longrightarrow }\limits ^{}}^* P_2'\) s.t. \(P_2'\surd \) does not hold and there exists no additional computation step \(P_2' {\mathop {\longrightarrow }\limits ^{}} P_2''\). Notice that \(P_1\) and \(P_2\) are identical excluding the output selections filling the holes in \({\mathcal {A}}\) that in \(P_1\) could include more branches. Hence, \(P_1\) can mimic the same computation steps of \(P_2\).
. Then, there exists a computation \(P_2 {\mathop {\longrightarrow }\limits ^{}}^* P_2'\) s.t. \(P_2'\surd \) does not hold and there exists no additional computation step \(P_2' {\mathop {\longrightarrow }\limits ^{}} P_2''\). Notice that \(P_1\) and \(P_2\) are identical excluding the output selections filling the holes in \({\mathcal {A}}\) that in \(P_1\) could include more branches. Hence, \(P_1\) can mimic the same computation steps of \(P_2\).
Going back to the above computation \(P_2 {\mathop {\longrightarrow }\limits ^{}}^* P_2'\), we notice that there are two possibilities; either the sequence of computation steps entirely consumes the input context \({\mathcal {A}}\), or not. In the first case, we have that \(P_1\) can perform an equivalent computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P_1'\) s.t. \(P_1'\surd \) does not hold and there exists no additional computation step. But this contradicts the assumption  . In the second case, we have \(P_2'=[[[\mathcal {A'}[{\oplus \{l_i:S_{ki}\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}''']\). As observed above, there exists also the computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P_1'\) with \(P_1'\!\!=\!\![[[\mathcal {A'}[{\oplus \{l_j:S_{kj}\}_{j \in J_k}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}\) \([D',{{\mathcal {Q}}}'']\). But also this cannot hold because also \(P_1'\) is blocked (\(P_1'\surd \) does not hold and there exists no additional computation step \(P_1' {\mathop {\longrightarrow }\limits ^{}} P_1''\)), and this contradicts the assumption
. In the second case, we have \(P_2'=[[[\mathcal {A'}[{\oplus \{l_i:S_{ki}\}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}[D',{{\mathcal {Q}}}''']\). As observed above, there exists also the computation \(P_1 {\mathop {\longrightarrow }\limits ^{}}^* P_1'\) with \(P_1'\!\!=\!\![[[\mathcal {A'}[{\oplus \{l_j:S_{kj}\}_{j \in J_k}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}'']{||}\) \([D',{{\mathcal {Q}}}'']\). But also this cannot hold because also \(P_1'\) is blocked (\(P_1'\surd \) does not hold and there exists no additional computation step \(P_1' {\mathop {\longrightarrow }\limits ^{}} P_1''\)), and this contradicts the assumption  . \(\square \)
. \(\square \)
We are now ready to prove our soundness result, i.e. if two types are in subtyping relation, then the corresponding contracts are in refinement relation.
Theorem 1
(Soundness) Given two session types T and S, if \(T{\le }S\) then \([[T]] \preceq _s [[S]]\).
Proof
We start by defining the following relation \({\mathcal {S}}\) on systems:
We now prove that \({\mathcal {S}}\) has the following property: given \((P_1,P_2) \in {\mathcal {S}}\) we have that if  then
then  . This is proved by showing that if \((P_1,P_2) \in {\mathcal {S}}\) and
. This is proved by showing that if \((P_1,P_2) \in {\mathcal {S}}\) and  then one of the following holds:
then one of the following holds:
-
1.
\(P_2{\surd }\);
-
2.
for every \(P_2'\) s.t. \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_2'\) and there exists
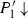 such that \((P_1',P_2') \in {\mathcal {S}}\).
such that \((P_1',P_2') \in {\mathcal {S}}\).
We first show that if  then \(P_2\) cannot be blocked, i.e. either \(P_2\surd \) or there exists \(P_2'\) such that \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_2'\). If
then \(P_2\) cannot be blocked, i.e. either \(P_2\surd \) or there exists \(P_2'\) such that \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_2'\). If  we have that either \(P_1\surd \) or \(P_1{\mathop {\longrightarrow }\limits ^{}} P_1'\) for some \(P_1'\).
we have that either \(P_1\surd \) or \(P_1{\mathop {\longrightarrow }\limits ^{}} P_1'\) for some \(P_1'\).
If \(P_1\surd \) then \(P_1=[[[S]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\) with \([D,{{\mathcal {Q}}}']{\surd }\), \({{\mathcal {Q}}} = \epsilon \), and \([[S]] = {{\mathbf {1}}}\) (possibly guarded by some recursive definitions). This implies, by definition of \([[\ ]]\), that \(S={\mathbf {end}}\) (possibly guarded by some recursive definitions). Hence \(P_2=[[[T]],\epsilon ]{||}[D,{{\mathcal {Q}}}']\) with T, by definition of session subtyping, either equal to \({\mathbf {end}}\) or \({\mathbf {end}}\) guarded by some recursive definitions. This implies \([[T]]\) equal to \({{\mathbf {1}}}\) or \({{\mathbf {1}}}\) guarded by some recursive definitions, hence also \(P_2{\surd }\) holds.
If \(P_1{\mathop {\longrightarrow }\limits ^{}} P_1'\), i.e. \(P_1= [C,{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\), with \(C=[[S]]\), has a reduction, then also \(P_2= [C',{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\), with \(C'=[[T]]\), has the possibility to perform a reduction. This is proved by observing that there are four types of reductions that \(P_1\) can perform: (i) a transition performed by \([D,{{\mathcal {Q}}}']\) in isolation, (ii) the insertion in the queue \({{\mathcal {Q}}}\) of a message sent from D, (iii) the insertion in the queue \({{\mathcal {Q}}}'\) of a message sent from C, (iv) a transition performed by \([C,{{\mathcal {Q}}}]\) in isolation. In all cases, but the last one, it is trivial to see that also \(P_2= [C',{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\) can perform the same type of transition. The unique non trivial case, i.e. the last one, is that of the consumption of a message from the local queue \({{\mathcal {Q}}}\); let \(l_k\) be such message (hence \({{\mathcal {Q}}}=l_k{::}{{\mathcal {Q}}}''\)). In this case we have that \(C=[[S]]\) with S that coincides (possibly after some unfolding) with \( { \& }\{{l}_{i}:{S}_{i}\}_{i\in I}\), with \(k \in I\). Being \(T {\le }S\), T does not coincide (neither applying unfolding) with \({\mathbf {end}}\). Possibly by applying some unfolding, it will either start with an output selection or an input branching. In the former case, \([[T]]\) has the possibility to execute in the system \(P_2\) one of its initial output actions. In the latter, due to input contravariance, the subtype T will be (possibly after some unfoldings) of kind \( { \& }\{{l}_{j}:{S}_{j}\}_{j\in J}\), with \(k \in J\). This guarantees that also \([[T]]\) can perform in \(P_2\) the same local message consumption of \(l_k\).
So far, we have proved that if \(P_2\surd \) does not hold then \(P_2\) has at least one outgoing transition. We now show that for each transition \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_2'\) then item 2. holds. We proceed by analysing the possible transitions \(P_2 {\mathop {\longrightarrow }\limits ^{}} P_2'\); there are four possible cases:
-
1.
a local reduction of \([D,{{\mathcal {Q}}}']\);
-
2.
the insertion in the queue \({{\mathcal {Q}}}\) of a new message emitted by D;
-
3.
the insertion in the queue \({{\mathcal {Q}}}'\) of a new message emitted by C;
-
4.
a local reduction of \([C,{{\mathcal {Q}}}]\).
In the first two cases it is trivial to see that also \(P_1 {\mathop {\longrightarrow }\limits ^{}} P_1'\), by performing the same type of transition, with \((P_1',P_2') \in {\mathcal {S}}\) and, obviously,  because \(P_1'\) is itself reachable from \(P_1\).
because \(P_1'\) is itself reachable from \(P_1\).
In case 3. we have that \([[T]]\) coincides (possibly after some unfoldings) with \(\sum _{i \in I} \overline{l_i}. [[T_i]]\). This implies that T coincides (possibly after some unfoldings) with \(\oplus \{{l}_{i}:{T}_{i}\}_{i\in I}\), and \(P_2'=[[[T_i]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}'{::}l_i]\). As S is a supertype of T, the corresponding output selection could be guarded by input branchings. Any way we have that S coincides (possibly after some unfoldings) with \(\mathcal {A}[{\oplus \{{l}_{j}:{S_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\), such that \(\forall k \in \{1,\ldots , m\}.i \in J_k\) and \(T_i {\le }\mathcal {A}[{{S_{ki}}}]^{k\in \{1,\ldots , m\}}\). The latter ensures that \(([[[\mathcal {A}[{{S_{ki}}}]^{k\in \{1,\ldots , m\}}]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}'{::}l_i],\) \([[[T_i]],{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}'{::}l_i]) \in {\mathcal {S}}\). Moreover, given that  , we also have that \(\big (\,[[[\mathcal {A}[{\oplus \{{l}_{j}:{S_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}]], {{\mathcal {Q}}}]{||}[D,\) \({{\mathcal {Q}}}']\,\big )\) holds. From Proposition 3, we have that \(\big (\,[[[\mathcal {A}[{\oplus \{l_i:}]^{]}]\) \({{S_{ki}\}} {k\in \{1,\ldots , m\}}},{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\,\big )\downarrow \) holds and from Proposition 2 we finally conclude that also \(\big (\,[\mathcal {A}[{{S_{ki}}}]^{k\in \{1,\ldots , m\}},{{\mathcal {Q}}}]{||}\) \( [D,{{\mathcal {Q}}}'{::}l_i]\,\big )\downarrow \) holds.
, we also have that \(\big (\,[[[\mathcal {A}[{\oplus \{{l}_{j}:{S_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}]], {{\mathcal {Q}}}]{||}[D,\) \({{\mathcal {Q}}}']\,\big )\) holds. From Proposition 3, we have that \(\big (\,[[[\mathcal {A}[{\oplus \{l_i:}]^{]}]\) \({{S_{ki}\}} {k\in \{1,\ldots , m\}}},{{\mathcal {Q}}}]{||}[D,{{\mathcal {Q}}}']\,\big )\downarrow \) holds and from Proposition 2 we finally conclude that also \(\big (\,[\mathcal {A}[{{S_{ki}}}]^{k\in \{1,\ldots , m\}},{{\mathcal {Q}}}]{||}\) \( [D,{{\mathcal {Q}}}'{::}l_i]\,\big )\downarrow \) holds.
In case 4. we have that \([[T]]\) coincides (possibly after some unfoldings) with \(\sum _{i \in I} l_i. [[T_i]]\), with \(C=[[T_i]]\). As S is a supertype of T, it also starts with an input action, and because \(P_1\downarrow \) holds, such an initial input will include also the label \(l_i\) (because we have that \({{\mathcal {Q}}}=l_i{::}{{\mathcal {Q}}}''\)). Moreover, after such label, the type S continues with a type \(S_i\) such that \(T_i {\le }S_i\). This implies that \(P_1 {\mathop {\longrightarrow }\limits ^{}} [[[S_i]],{{\mathcal {Q}}}'']{||}[[[D]],{{\mathcal {Q}}}']\). Moreover, \(([[[S_i]],{{\mathcal {Q}}}'']{||}[[[D]],{{\mathcal {Q}}}'], [[[T_i]],{{\mathcal {Q}}}'']{||}[[[D]],{{\mathcal {Q}}}']) \in {\mathcal {S}}\). Being \([[[S_i]],{{\mathcal {Q}}}]{||}[[[D]],{{\mathcal {Q}}}']\) reachable from \(P_1\), we have that \([[[S_i]],{{\mathcal {Q}}}]{||}[[[D]],{{\mathcal {Q}}}']\downarrow \) holds.
We now conclude the proof by considering two types T and S, such that \(T {\le }S\). We have that, for every contract D, \(\big (\ [[[S]]] {||}[D]\ ,\ [[[T]]]{||}[D]\ \big ) \in {\mathcal {S}}\). Assume that \([[[S]]]{||}[D]\downarrow \) holds. Consider now a computation \([[[T]]]{||}[D] {\mathop {\longrightarrow }\limits ^{}}^* P'\) of length n (i.e. composed of n transitions). By applying n times the property 2 proved for the relation \({\mathcal {S}}\), we can conclude that \(P'\) is such that \(P'\surd \) (property 1 of \({\mathcal {S}}\)) or \(P' {\mathop {\longrightarrow }\limits ^{}} P''\) (property 2 of \({\mathcal {S}}\)). This guarantees that also \([[[T]]]{||}[D]\downarrow \) holds, hence we can conclude that \([[T]] \preceq _s [[S]]\). \(\square \)
We now move to the proof of completeness. The first preliminary result states that the composition of a session contract \([[T]]\) with its specular contract \([[{\overline{T}}]]\) generates a correct contract system.
Proposition 4
Given a session type T, we have that \([ [[T]] ] {||}\) \( [ [[{\overline{T}}]]]\downarrow \).
Proof
We first prove that given a computation \([ [[T]] ] {||}[ [[{\overline{T}}]]] \) \({\mathop {\longrightarrow }\limits ^{}}^* [ C, {{\mathcal {Q}}}] {||}[C', {{\mathcal {Q}}}']\) we have that:
-
either the two queues are empty (i.e. \({{\mathcal {Q}}}={{\mathcal {Q}}}'=\epsilon \)) and \(C=[[S]]\), \(C'=[[{\overline{S}}]]\), for some S;
-
or only one queue between \({{\mathcal {Q}}}\) and \({{\mathcal {Q}}}'\) is non empty and
-
if \({{\mathcal {Q}}}\) is not empty then C has \(|{{\mathcal {Q}}}|\) initial inputs that it can use to consume all messages in \({{\mathcal {Q}}}\), and then it becomes \(C''\) such that \(C''=[[S]]\) and \(C'=[[{\overline{S}}]]\), for some S, or
-
if \({{\mathcal {Q}}}'\) is not empty then \(C'\) has \(|{{\mathcal {Q}}}'|\) initial inputs that it can use to consume all messages in \({{\mathcal {Q}}}'\), and then it becomes \(C''\) such that \(C''=[[S]]\) and \(C=[[{\overline{S}}]]\), for some S.
-
The proof is by induction on the length of the computation \([ [[T]] ] {||}[ [[{\overline{T}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [ C, {{\mathcal {Q}}}] {||}[C', {{\mathcal {Q}}}']\).
If the length of the computation is 0, then the two queues are empty and \(C=[[T]]\), \(C'=[[{\overline{T}}]]\).
By inductive hypothesis, let the above condition holds for \([ [[T]] ] {||}[ [[{\overline{T}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [ C, {{\mathcal {Q}}}] {||}[C', {{\mathcal {Q}}}']\). Consider now \([ C, {{\mathcal {Q}}}] {||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}} [ C_1, {{\mathcal {Q}}}_1] {||}[C_1', {{\mathcal {Q}}}_1']\). There are two possible cases for this last transition: it is (i) either the consumption of one label in a queue, (ii) or the production of a new message.
In case (i), such input is the initial one of the sequence of inputs able to empty the queue, that exists by inductive hypothesis. At the end of the execution of this sequence of inputs, the above condition is guaranteed to hold (still by inductive hypothesis).
In case (ii), it is not restrictive to assume that the output is performed by C (in fact, a symmetric reasoning can be applied to the case in which \(C'\) performs the output). Let l be the emitted message. As C starts with an output, by inductive hypothesis its queue \({{\mathcal {Q}}}\) is empty and there exists a session type S, such that \(C=[[S]]\), that begins with an output selection with a branch labelled with l. Let \(S'\) the continuation after such label; we have that \(C_1=[[S']]\). Still by inductive hypothesis, we also have that \(C'\) can consume all the messages in its queue \({{\mathcal {Q}}}'\) and then becomes \([[{\overline{S}}]]\). Given that S starts with an output selection with the label l, we have that \({\overline{S}}\) starts with an input branching with a branch labelled with l, and \({\overline{S'}}\) is the continuation after such label. The above guarantees that \(C_1'=C'\) is able to consume all the messages in its queue \({{\mathcal {Q}}}_1'={{\mathcal {Q}}}'{::}l\) and then becomes \([[{\overline{S'}}]]\).
We now observe that the above condition guarantees that \([ [[T]] ] {||}[ [[{\overline{T}}]]]\downarrow \) actually holds. Consider a computation \([ [[T]] ] {||}[ [[{\overline{T}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [ C, {{\mathcal {Q}}}] {||}[C', {{\mathcal {Q}}}']\). If the queues are empty (i.e. \({{\mathcal {Q}}}={{\mathcal {Q}}}'=\epsilon \)), we have that the two contracts C and \(C'\) either (i) starts one with an input and one with an output or (ii) they are both ended (i.e. equal to \({{\mathbf {1}}}\), possibly guarded by some recursive definitions). In the case (i) we have that at least one computation is possible (the output action), while in the case (ii) we have that \([ C, {{\mathcal {Q}}}] {||}[C', {{\mathcal {Q}}}']\surd \). On the other hand, if one of the queues is not empty, the corresponding contract can perform at least one input transition. \(\square \)
Another preliminary result used in the completeness proof is about a relationship between the so-called subtyping simulation game discussed after Definition 14 and a computation of the corresponding contract system. To formalize such a relationship, we need some additional notation; \({\mathsf {topunfold}}(T)\) used to unfold initial recursive definitions and \(\, {\mathsf {ant}}(C,{\mathcal {Q}}) \,\) that removes from the contract C input actions that C itself can use to consume the messages in the queue \({{\mathcal {Q}}}\).
Given a session type T we define:
Given a session contract C and a queue \({{\mathcal {Q}}}\) we define \(\, {\mathsf {ant}}(C,{\mathcal {Q}}) \,\) as follows:
Notice that \(\, {\mathsf {ant}}(C,{\mathcal {Q}}) \,\) could be undefined, in particular when \(\{ n|{\mathsf {unfold}}^{n}(S) = \mathcal {A}[{\oplus \{{l}_{j}:{T_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\}\) in the second item is empty.
Proposition 5
Given two session types T and S such that  , we have that there exist two session types \(T'\) and \(S'\) for which there exists a computation \([[[T]]]{||}[[[{\overline{S}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) with \(C = [[T']]\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\), and
, we have that there exist two session types \(T'\) and \(S'\) for which there exists a computation \([[[T]]]{||}[[[{\overline{S}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) with \(C = [[T']]\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\), and
-
1.
if \({\mathsf {topunfold}}(T')={\mathbf {end}}\) then
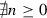 such that \({\mathsf {unfold}}^{n}(S') = {\mathbf {end}}\);
such that \({\mathsf {unfold}}^{n}(S') = {\mathbf {end}}\); -
2.
if \({\mathsf {topunfold}}(T')=\oplus \{{l}_{i}:{T'}_{i}\}_{i\in I}\) then
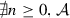 such that
such that-
\({\mathsf {unfold}}^{n}(S') = \mathcal {A}[{\oplus \{{l}_{j}:{S'_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\) and
-
\(\forall k\in \{1,\ldots , m\}. \, I\subseteq J_k\).
-
-
3.
if \( {\mathsf {topunfold}}(T')={ \& }\{{l}_{i}:{{T'}}_{i}\}_{i\in I}\) then \(\not \exists n\ge 0\) s.t. \( {\mathsf {unfold}}^{n}(S') = { \& }\{{l}_{j}:{S'}_{j}\}_{j\in J}\) with \(J\subseteq I\).
Proof
We first prove the following statement.
Consider the session contract system \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) and the session types T, S, \(T_1\), and \(S_1\) such that \(C=[[T_1]]\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S_1}}]]\), \({\mathsf {topunfold}}(T)={\mathsf {topunfold}}(T_1)\) and \(\exists n. {\mathsf {unfold}}^{n}(S_1)=S\). Let \(T'\) and \(S'\) be two session types obtained from T and S by applying one step of the subtyping simulation game discussed after Definition 14. We have that there exist \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* [C_1, \epsilon ]{||}[C_1', {{\mathcal {Q}}}_1']\), \(T_1'\), and \(S_1'\) such that \(C_1=[[T_1']]\), \(\, {\mathsf {ant}}(C_1',{{\mathcal {Q}}}_1') \,= [[{\overline{S_1'}}]]\), \({\mathsf {topunfold}}(T')={\mathsf {topunfold}}(T_1')\), and \(\exists n. {\mathsf {unfold}}^{n}(S_1')=S'\).
The proof of the above statement is by case analysis considering the three possible steps in the subtyping simulation game: (i) output selection, (ii) input branching, and (iii) unfolding.
In the case (i) it is sufficient to consider the computation \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}} [C_i, \epsilon ]{||}[C', {{\mathcal {Q}}}'{::}l_i]\) where \(l_i\) is the label of the selected branching in the subtyping simulation game, and \(C_i\) is the session contract obtained from C after execution of the output \(l_i\). We immediately observe that \(C_i=[[T']]\) because in this case \(T'\) is the session type in the continuation of the branching with label \(l_i\). Definition 14 guarantees that there exist \( n\ge 0\) and \({\mathcal {A}}\) such that \({\mathsf {unfold}}^{n}(S) = \mathcal {A}[{\oplus \{{l}_{j}:{S_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\) and \(\forall k\in \{1,\ldots , m\}. \, i\in J_k\). From the latter we have that also \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}'{::}l_i) \,\) is defined because \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,=[[{\overline{S_1}}]]\). Let \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}'{::}l_i) \,=[[{\overline{S''}}]]\): we have that \(S''\) is like \(S'\), but possibly less unfolded; in fact, \([[{\overline{S''}}]]\) is obtained by the partial function \(\, {\mathsf {ant}}(\_,\_) \,\) that unfolds as less as possible.
In the case (ii) it is sufficient to consider the computation \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C'', {{\mathcal {Q}}}''] {\mathop {\longrightarrow }\limits ^{}} [C, l_i]{||}[C_i', {{\mathcal {Q}}}''] {\mathop {\longrightarrow }\limits ^{}} [C_i, \epsilon ]{||}[C_i', {{\mathcal {Q}}}'']\) in which \(C'\) performs input actions until it reaches the possibility to perform an output action, then it performs the output \(l_i\), where \(l_i\) is the label of the selected branching in the subtyping simulation game, \(C_i'\) is the session contract obtained from \(C'\) after execution of the output \(l_i\), and finally C performs the consumption of \(l_i\) and becomes \(C_i\). Such a computation exists in that \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,=[[{\overline{S_1}}]]\), \(\exists n. {\mathsf {unfold}}^{n}(S_1)=S\) (by hypothesis) and \(\exists {n'}. {\mathsf {unfold}}^{n'}(S)\) starts with an input branching that includes a branch with label \(l_i\) and continuation \(S'\) (this follows from the second item in Definition 14 that defines the subtyping simulation game steps for input branchings). In other terms, we have that if \(C'\) starts with inputs, such initial inputs cannot be more than the length of \({{\mathcal {Q}}}'\); when an output choice is reached, such choice will include also the possibility to emit \(l_i\). Let \({{\mathcal {Q}}}''\) be the queue after the execution of the initial inputs; we have that \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}'') \,=[[{\overline{S_1}}]]\). Considering that the operational semantics of contracts unfolds only initial recursive definitions, the session contract \(C_i'\), reached after the execution of the output \(l_i\), will be such that \(C_i'=[[{\overline{S''}}]]\) for some session type \(S''\) which is like \(S'\), but possibly less unfolded. We conclude this case by observing that \(C_i=[[T']]\) because in this case \(T'\) is the session type that occurs in T after the label \(l_i\).
In the case (iii) we have that \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) already satisfies the required constraints. In fact, \(S=S'\) and \(T'\) is obtained from T with an initial unfolding, hence \({\mathsf {topunfold}}(T)={\mathsf {topunfold}}(T')\).
We now prove the Lemma by considering two session types S and T such that  . We have that there exists a path in the subtyping simulation game between T and S that ends in a pair \(T'\) and \(S'\) for which such a game cannot continue. The latter implies that the three properties stated in the Lemma hold for such a pair of session types; in fact, such properties are the negation of corresponding items in the Definition 14, that formalizes the subtyping simulation game. By repeated application of the statement proved above, we have that there exists a computation \([[[T]]]{||}[[[{\overline{S}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) and two session types \(T''\) and \(S''\) such that \(C'=[[T'']]\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S''}}]]\), \({\mathsf {topunfold}}(T')={\mathsf {topunfold}}(T'')\), and \(\exists n. {\mathsf {unfold}}^{n}(S'')=S'\). We have that the three properties stated in the Lemma holds also for \(T''\) and \(S''\). In fact, \({\mathsf {topunfold}}(T')={\mathsf {topunfold}}(T'')\), and \(S''\) is like \(S'\), but possibly less unfolded; this implies that if \(T''\) and \(S''\) have a step in the subtyping simulation game then also \(T'\) and \(S'\) should have a corresponding step. This because one step in the subtyping simulation game can require a minimum amount of unfolding of the r.h.s. type, but additional unfoldings cannot forbid its application. \(\square \)
. We have that there exists a path in the subtyping simulation game between T and S that ends in a pair \(T'\) and \(S'\) for which such a game cannot continue. The latter implies that the three properties stated in the Lemma hold for such a pair of session types; in fact, such properties are the negation of corresponding items in the Definition 14, that formalizes the subtyping simulation game. By repeated application of the statement proved above, we have that there exists a computation \([[[T]]]{||}[[[{\overline{S}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) and two session types \(T''\) and \(S''\) such that \(C'=[[T'']]\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S''}}]]\), \({\mathsf {topunfold}}(T')={\mathsf {topunfold}}(T'')\), and \(\exists n. {\mathsf {unfold}}^{n}(S'')=S'\). We have that the three properties stated in the Lemma holds also for \(T''\) and \(S''\). In fact, \({\mathsf {topunfold}}(T')={\mathsf {topunfold}}(T'')\), and \(S''\) is like \(S'\), but possibly less unfolded; this implies that if \(T''\) and \(S''\) have a step in the subtyping simulation game then also \(T'\) and \(S'\) should have a corresponding step. This because one step in the subtyping simulation game can require a minimum amount of unfolding of the r.h.s. type, but additional unfoldings cannot forbid its application. \(\square \)
We are now ready to prove completeness; actually, we prove the contrapositive statement.
Theorem 2
(Completeness) Given two session types T and S, if  then \([[T]] \not \preceq _s [[S]]\).
then \([[T]] \not \preceq _s [[S]]\).
Proof
Consider two session types T and S such that  . We prove that \([[T]] \not \preceq _s [[S]]\) by showing the existence of a contract C s.t. \([[[S]]]{||}[C]\downarrow \) holds while \([[[T]]]{||}[C]\downarrow \) does not. Such contract C is \([[{\overline{S}}]]\). By Proposition 4 we have that \([[[S]]]{||}[[[{\overline{S}}]]]\downarrow \); it remains to show that
. We prove that \([[T]] \not \preceq _s [[S]]\) by showing the existence of a contract C s.t. \([[[S]]]{||}[C]\downarrow \) holds while \([[[T]]]{||}[C]\downarrow \) does not. Such contract C is \([[{\overline{S}}]]\). By Proposition 4 we have that \([[[S]]]{||}[[[{\overline{S}}]]]\downarrow \); it remains to show that  .
.
Given that Given that  , we can apply Proposition 5. Hence there exist two session types \(T'\) and \(S'\) and a computation \([[[T]]]{||}[[[{\overline{S}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) with \(C = [[T']]\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\) and:
, we can apply Proposition 5. Hence there exist two session types \(T'\) and \(S'\) and a computation \([[[T]]]{||}[[[{\overline{S}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) with \(C = [[T']]\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\) and:
-
1.
if \({\mathsf {topunfold}}(T')={\mathbf {end}}\) then \(\not \exists n\ge 0\) such that \({\mathsf {unfold}}^{n}(S') = {\mathbf {end}}\);
-
2.
if \({\mathsf {topunfold}}(T')=\oplus \{{l}_{i}:{T'}_{i}\}_{i\in I}\) then \(\not \exists n\ge 0,{\mathcal {A}}\) such that
-
\({\mathsf {unfold}}^{n}(S') = \mathcal {A}[{\oplus \{{l}_{j}:{S'_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\) and
-
\(\forall k\in \{1,\ldots , m\}. \, I\subseteq J_k\).
-
-
3.
if \( {\mathsf {topunfold}}(T')={ \& }\{{l}_{i}:{{T'}}_{i}\}_{i\in I}\) then \(\not \exists n\ge 0\) such that \( {\mathsf {unfold}}^{n}(S') = { \& }\{{l}_{j}:{S'}_{j}\}_{j\in J}\) with \(J\subseteq I\).
We now analyse the three above cases showing that we can always extend the computation \([[[T]]]{||}[[[{\overline{S}}]]] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C', {{\mathcal {Q}}}']\) reaching a deadlock, i.e. there exists a computation \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* P\) with P such that it does not hold that \(P\surd \) and there exists no \(P'\) such that \(P {\mathop {\longrightarrow }\limits ^{}} P'\). This implies that  .
.
-
1.
In this case we can extend the computation by considering any of the computations \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* [C, {{\mathcal {Q}}}_1]{||}[C_2, \epsilon ]\) in which \(C'\) consumes all the messages in its queue \({{\mathcal {Q}}}'\). These computations exist because \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,\) is defined. Moreover, given that \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,\) \(= [[{\overline{S'}}]]\) and \(\not \exists n\ge 0\) such that \({\mathsf {unfold}}^{n}(S') = {\mathbf {end}}\), we are in two possible situations: either (i) some outputs have been executed by the r.h.s. session contract during the extension of the computation, or (ii) the r.h.s. session contract \(C''\) is not the terminated process \({{\mathbf {1}}}\) (possibly guarded by some recursive definition).
In the first case (i) we have that the l.h.s. queue \({{\mathcal {Q}}}_1\), at the end of the extended computation, is not empty while the contract C cannot consume such messages because \(C = [[T']]\) and \({\mathsf {topunfold}}(T')={\mathbf {end}}\). Given that the r.h.s. contract cannot perform infinitely many outputs, the computation will eventually terminate in a configuration that is not successful because the l.h.s. queue is not empty.
In the second case (ii) we have that the r.h.s. contract \(C''\) starts with either an input or an output. In the first case, given that the r.h.s. queue is empty, the computation is immediately blocked in a configuration which is not successful because the r.h.s. contract is willing to perform an input on an empty queue. If \(C''\) starts with an output, we can reason as in the above case (i) because the message is introduced in the l.h.s. queue while the l.h.s. contract C is terminated, namely, \(C = [[T']]\) and \({\mathsf {topunfold}}(T')={\mathbf {end}}\).
-
2.
In this case we consider two possibilities: either (i) \(\not \exists n\ge 0,{\mathcal {A}}\) such that \({\mathsf {unfold}}^{n}(S') = \mathcal {A}[{\oplus \{{l}_{j}:{S'_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\) or (ii) there exist such n and \({\mathcal {A}}\) allowing for the decomposition of \(S'\) as an input context filled with output selections.
In the first case (i) we have that the contract \(C'\) has the ability to consume all the messages in its queue \({{\mathcal {Q}}}'\) and then reach the contract \({{\mathbf {1}}}\) (possibly guarded by some recursive definitions). In fact, \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\) guarantees the ability to consume the messages in \({{\mathcal {Q}}}'\). Moreover, the impossibility to decompose \(S'\) as an input context filled with output selections, implies that in \(S'\) there is a sequence of input branching leading to the terminated \({\mathbf {end}}\) type (possibly guarded by some recursive definitions). Symmetrically, besides the inputs for consuming \({{\mathcal {Q}}}'\), \(C'\) has a sequence of outputs selections leading to the terminated process \({{\mathbf {1}}}\) (possibly guarded by some recursive definitions). We now consider the computation \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* [C, {{\mathcal {Q}}}_1]{||}[C_2, \epsilon ] {\mathop {\longrightarrow }\limits ^{}} [C_1, {{\mathcal {Q}}}_1]{||}[C_2, l]\) with \(C_2\) which is the terminated process \({{\mathbf {1}}}\) (possibly guarded by some recursive definitions), and l is one of the labels in the output selection initially present in C. Given that the l.h.s. contract \(C_1\) cannot perform a loop with only outputs, the computation will eventually block in a configuration that cannot be successful because the message l introduced in the r.h.s. queue cannot be consumed, in that the r.h.s. contract \(C_2\) is ended.
In the second case (ii) we have that \(\exists n\ge 0,{\mathcal {A}}\) such that \({\mathsf {unfold}}^{n}(S') = \mathcal {A}[{\oplus \{{l}_{j}:{S'_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\). This implies that \(\exists k\in \{1,\ldots , m\}. \, I\not \subseteq J_k\). From this we have that there exists \(i\in I\) such that \(i \not \in J_k\). We now consider the following extension of the computation \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* [C, {{\mathcal {Q}}}_1]{||}[C_2, \epsilon ] {\mathop {\longrightarrow }\limits ^{}} [C_1, {{\mathcal {Q}}}_1]{||}[C_2, l_i]\) in which the r.h.s. contract \(C'\) consumes all the messages in its queue \({{\mathcal {Q}}}'\), possible because \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\), and then performs outputs corresponding to the inputs that guard the hole \([\,]^k\) in the above context \({\mathcal {A}}\) such that \({\mathsf {unfold}}^{n}(S') = \mathcal {A}[{\oplus \{{l}_{j}:{S'_k}_{j}\}_{j\in J_k}}]^{k\in \{1,\ldots , m\}}\), and then the l.h.s. contract performs the output of \(l_i\), available because \(C=[[T']]\), \({\mathsf {topunfold}}(T')=\oplus \{{l}_{i}:{T'}_{i}\}_{i\in I}\) and \(i \in I\). After this computation, the r.h.s. contract \(C_2\) has a symmetric behaviour w.r.t. the session type \(\oplus \{{l}_{j}:{S'_k}_{j}\}_{j\in J_k}\) filling the hole \([\,]^k\) in the above context \({\mathcal {A}}\); hence, it starts with an input branching and moreover there is no branch labelled with \(l_i\). We can now proceed as in the above case (i) because we have reached a configuration in which the r.h.s. queue contains a message that cannot be consumed by the r.h.s. contract.
-
3.
In this case we consider two possibilities: either (i) the session type \(S'\) does not start with an input branching, or (ii) \(\exists n\ge 0\) such that \( {\mathsf {unfold}}^{n}(S') = { \& }\{{l}_{j}:{S'}_{j}\}_{j\in J}\).
In the first case (i), given that \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\), the r.h.s. contract \(C'\) has the possibility to consume all the messages in its queue \({{\mathcal {Q}}}'\), but it is unable to perform any output (otherwise, symmetrically, \(S'\) should start with an input branching). Hence we can consider the computation \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C_2, \epsilon ]\) in which \(C'\) consumes the messages in \({{\mathcal {Q}}}'\) and then a configuration is reached which is blocked (because no additional transition is possible) and not successful (because C is willing to perform an input because \(C= [[T']]\) and \( {\mathsf {topunfold}}(T')={ \& }\{{l}_{i}:{{T'}}_{i}\}_{i\in I}\)).
In the second case (ii) we have that \(C= [[T']]\), \( {\mathsf {topunfold}}(T')={ \& }\{{l}_{i}:{{T'}}_{i}\}_{i\in I}\), \(\, {\mathsf {ant}}(C',{{\mathcal {Q}}}') \,= [[{\overline{S'}}]]\), \( \exists n\ge 0.\,{\mathsf {unfold}}^{n}(S') = { \& }\{{l}_{j}:{S'}_{j}\}_{j\in J}\) and \(J \not \subseteq I\). The latter implies the existence of \(j \in J\) such that \(j \not \in I\). We can consider the computation \([C, \epsilon ]{||}[C', {{\mathcal {Q}}}'] {\mathop {\longrightarrow }\limits ^{}}^* [C, \epsilon ]{||}[C_2, {{\mathcal {Q}}}''] {\mathop {\longrightarrow }\limits ^{}} [C, l_j]{||}[C_2', {{\mathcal {Q}}}'']\) in which the r.h.s. contract \(C'\) possibly performs inputs until reaching an output that symmetrically corresponds with the input branching \( { \& }\{{l}_{j}:{S'}_{j}\}_{j\in J}\) (let \(C_2\) be the reached contract), and then emits the message \(l_j\) that is not present in any branch of the input branching \( {\mathsf {topunfold}}(T')={ \& }\{{l}_{i}:{{T'}}_{i}\}_{i\in I}\). The latter ensures that in the reached configuration the l.h.s. contract C is blocked because it cannot consume the message \(l_j\). Hence the computation can continue with actions executed by the r.h.s. contract, but it eventually terminate (because the r.h.s. contract has no loops with only outputs) in a configuration which is not successful because C is willing to perform an input.
\(\square \)
As a direct corollary of the two previous Theorems we have the following full abstraction result.
Corollary 1
Given two session types T and S, \(T {\le }S\) if and only if \([[T]] \preceq _s [[S]]\).
5 Related work
In this paper we introduced a behavioural contract theory based on a definition of compliance (correctness of composition of a set of interacting contracts) and refinement (preservation of compliance under any test, i.e. set of interacting contracts): the two basic notions on which behavioural contract theories are usually based [12, 13, 20, 29]. In particular, the definitions of behavioural contracts and compliance considered in this paper have been devised so to formally represent Communicating Finite State Machines (CFSMs) [6, 21], i.e. systems composed by automata performing send and receive actions (the interacting contracts) that communicate by means of FIFO channels. Behavioural contracts with asynchronous communication have been previously considered, see e.g. [14, 17]; however, to the best of our knowledge, this is the first paper defining contracts that formally represent CFSMs. Compared to [14, 17, 19], where at each location an independent FIFO queue of received messages is considered for each channel name “a” (enqueuing only messages of type “a” coming from any location “\(l_1\)”, “\(l_2\)”,...), here we consider a different functioning mechanism for queues. Here, as in CFSMs, at each location an independent FIFO queue of received messages is considered for each sender location “l” (enqueuing only messages coming from “l” and having any type “a” , “b”, ...). Other minor differences w.r.t. [14, 17, 19] concern the syntax of behavioural contracts: while in [14, 17, 19] they include \(\tau \) actions and input actions a with an unspecified sending location, in this paper \(\tau \) actions are disregarded and input actions explicitly specify a required sending location l (thus assuming the form \(a_l\)), so to represent the behaviour of individual machines of CFSMs [6, 21]. Moreover, while in this paper we make use of a notion of compliance that corresponds to absence of deadlocking global CFSM states [6, 21] (globally the system of interacting contracts either reaches successful completion or loops forever), in [14, 17, 19] a totally different definition of compliance is considered, which requires global looping behaviours to be eventually terminated under a fairness assumption. Technically, the definition of compliance considered in this paper is along the lines of that in [4, 5], with the difference that here a general multiparty setting is considered, instead of a client/server one, and that all involved partners are required to reach successful completion (as in [4, 5], though, for the purpose of mapping binary session types, we make use of only two parties). Notice that, in the original definition of CFSMs [6] a notion of well-formedness is assumed that here, instead, we do not impose: this allows us to also consider CFSMs composed of individual machines with potential input actions that are never actually triggered by a received message. Encompassing such CFSMs is fundamental for effectively studying contract refinement with the typical output covariant/input contravariant properties of choices.
Concerning previous work on (variants of) CFSMs, our approach has some commonalities with [30]. In [30] a restricted version of CFSMs is considered w.r.t. [6, 21], by constraining them to be binary (a system is always composed of two CFSMs only) and not to use mixed choice (i.e. choices involving both inputs and outputs). A specific notion of compliance, called compatibility, is considered which, besides guaranteeing absence of deadlocking global CFSM states [6, 21] (i.e. compliance as in this paper) also requires each sent message to be eventually received: thanks to a mapping from the CFSMs of [30] to session types, compatibility of a CFSM A with a CFSM B corresponds to subtyping, as defined in [22], between the mapped session type T(A) and the dual \({\overline{T(B)}}\) of the mapped session type T(B). The approach to compatibility definition in [30] significantly differs from usual contract compliance in that it is based, like for session subtyping, on a co-inductive definition that directly applies to the communicating CFSMs. Contract compliance definition, as considered in this paper, is instead based on the transition system obtained, as for CFSMs [6, 21], by explicitly representing communication among CFSMs via global states that include queues. Moreover, even if [30] makes use of a notion of compliance, it does not consider, as in this paper, a notion of refinement defined in terms of compliance preserving testing (as usual in behavioural contract theories where communicating entities have a syntax). Finally, notice that, as discussed in Sect. 3.1.1, with respect to the subtyping definition used in this paper, [22] adds a requirement (called “orphan message free” constraint) that corresponds to the eventual reception of sent messages considered in the definition of compatibility by [30]. In relation to this, [30] does not exclude, as we do, session types with output divergent or input divergent recursions: under our restriction [22] coincides with subtyping as considered in this paper.
Concerning previous work on session types, our results have some commonalities with those of the above mentioned [22]. The above discussed subtyping variant considered in [22] is shown to correspond to substitutability, in the context of concurrent programs written in a variant of the \(\pi \)-calculus, of a piece of code with session type T with a piece of code with session type \(T'\), while preserving error-freedom. A specific error-freedom notion is formalized for such a language, that corresponds to absence of communication error (similar to our notion of compliance) plus the guaranteed eventual reception of all emitted messages (an orphan-message-free constraint that we do not consider in the definition of compliance). Even if the program (context) in which the piece of code is substituted can be seen as corresponding to a test in contract refinement, the subtyping characterization in [22] is based on a specific programming language, while in this paper we consider as tests a generic, language independent, set of CFSMs and we discuss the conditions on tests under which we can characterize asynchronous session subtyping.
Finally, it is worth mentioning that the connection between session types and CFSMs has been investigated also in [24]. In particular, that paper discusses an encoding of multiparty session types into CFSMs, and vice versa, that preserve a trace-based semantics. The difficult point solved in that encoding is the different way in which session types and CFSMs deal with repetitive behaviour: session types use recursive definitions while CFSMs use cycles. Our approach to deal with the relationship between session types and CFSMs is different; we borrow from the tradition of behavioural contracts a process algebraic denotation of CFSMs that includes recursive definitions. Hence, our translation from session types into CFSMs (see Definition 17) is rather straightforward. Another relevant difference with that paper is that their focus is on the properties preserved by the projection of global into local multiparty session types, while our focus is on the relationship between session subtyping and behavioural contract refinement.
6 Conclusion and future work
6.1 Summary of results
In this paper we have investigated a notion of refinement, intended as compliance preserving replacement of asynchronous behavioural contracts formalized as Communicating Finite State Machines (CSFMs), showing precisely under which conditions it coincides with asynchronous session subtyping. In particular, given that subtyping considers binary session types, we need to restrict to CFSMs composed of two parties. The other significant restrictions for CFSMs that we consider are: (i) we remove mixed choices that involve both input and output actions, and (ii) we remove infinite sequences of only input (or only output) actions. Restriction (i) points out an interesting specificity of session types; they do not naturally model preemption mechanisms like those adopted in many concurrent programming patterns in which time-outs or interrupts are used to avoid waiting for non-incoming messages. In CFSMs, these patterns can be naturally modelled by mixing internal and external choices: the external choices consider the possible incoming messages, while the internal choice models the possibility to stop waiting for such messages. This form of mixed choice is not considered in session types. Restriction (ii) also deals with natural assumptions in binary protocols where the two parties are symmetric, in the sense that they do not play distinct roles like in sensor/collector systems (where the former only sends and the latter only receives) or client/server interactions (for which forms of refinement different from session subtyping are natural, as discussed e.g. in [4, 5]).
6.2 Alternative formalizations of contracts
It is worth to observe that small variations to the formalization of contracts, as well as modifications to the notion of compliance, break our correspondence result.
The main characteristics of asynchronous session subtyping are output anticipation, i.e. the possibility for a subtype to anticipate outputs w.r.t. inputs, and contra/co-variance on input branchings and output selections, i.e. the possibility for a subtype to have more/less branches in inputs/outputs. We now discuss alternative asynchronous communication models for contracts, as well as alternative notions of compliance, that do not accept output anticipation or contra/co-variance on input/outputs as general notions of refinement.
We start by considering a communication model, similar to actor-based communication, in which each location has only one input FIFO channel, instead of one for each potential partner as for CFSMs (or one for each channel name as in [14, 17, 19]). In this model, input actions can be expressed simply with a instead of \(a_l\), indicating that a is expected to be consumed from the unique local input queue. Under this variant, output anticipation is no longer admitted. Consider, e.g.
which is a correct system. If we replace the contract at location \(l_1\) with \({\overline{b}}_{l_2}.a\), that simply anticipates an output, we obtain
which is no longer correct because, in case message b (sent from \(l_1\)) is enqueued at \(l_2\) before message c (sent from \(l_3\)), the entire system is stuck.
Consider now another communication model in which there are many input queues, but instead of naming them implicitly with the sender location, we consider explicit channel names like in CCS [32] or \(\pi \)-calculus [33]. In this case, a send action can be written \({\overline{a}}_{\pi @ l}\), indicating that the message a should be inserted in the input queue \(\pi \) at location l. A receive action can be written \(a_\pi \), indicating that the message a is expected to be consumed from the input queue \(\pi \). Also in this model output anticipation is not admitted. In fact, we can rephrase the above counter-example as follows: the correct system is
while the non-correct one is
where we have applied output anticipation to the contract at location \(l_1\).
We now consider an alternative notion of compliance, like the one discussed in [14, 17, 19]. In those papers, compliance is more restrictive, because it requires, under fair exit from loops, that the computation eventually successfully terminates. In other terms, contracts that can only generate infinite computations are no longer compliant. Consider, for instance, the binary system
It satisfies the condition above because, if we consider only fair computations, the send action \({\overline{a}}\) will be eventually executed, thus guaranteeing successful termination. In this case, output covariance, admitted by synchronous session subtyping, is not correct. If we consider the contract \(rec X.({\overline{b}}.X)\) having less output branches (hence following the output covariance principle), and we use it as a replacement for the first contract above, we obtain the system
that does not satisfy the above definition of compliance because it cannot reach successful termination.
6.3 Future perspectives
We end this section with a presentation of possible future work. The above discussion opens two interesting problems that we plan to investigate. On the one hand, one could study alternative notions of asynchronous session subtyping more appropriate for actor-based communication, multi-channel based communication, or to capture alternative notions of contract compliance/refinement. On the other hand, the undecidability result proved for asynchronous session subtyping may not apply to alternative notions of refinement: one could investigate the possibility to identify decidable refinement notions for contracts/CFSMs.
The notions of asynchronous session subtyping and contract refinement presented in this paper, themselves, could assume different variants if the simplifying assumption about excluding types/contracts with output or input divergent recursion is disregarded. As already discussed in Sect. 3.1.1, when dealing with such types/contracts, a possibility is to consider an “orphan message free” constraint conceptually corresponding to the subtyping of [10, 22]: messages that are sent to a contract cannot remain “orphan”, i.e. they must eventually be read by the contract from its queue in order for a contract composition to be correct. Therefore, a possible line of future research is to adapt Definition 6 (correct contract composition) so to enforce such a constraint: this would yield a technically more involved definition, which no longer corresponds to just absence of deadlock. The obtained notion of refinement should then be shown to correspond to the asynchronous subtyping definition of [10, 22] (which, again, is a technically more involved variant of subtyping as presented in Definition 14). An alternative line of future research could be, on the contrary, not to consider such an “orphan message free” constraint and stick to our simple definition of correct contract composition that just requires absence of deadlock. In this case, as already discussed in Sect. 3.1.1 by means of the two example types \( S=\mu {\mathbf {t}}. \& \{l_1: {\mathbf {t}}, l_2:\oplus \{l: {\mathbf {t}}\}\}\) and \( T=\mu {\mathbf {t}}.\oplus \{l: \& \{l_1: {\mathbf {t}}, l_2:{\mathbf {t}}\}\), subtyping of Definition 14 (i.e. that in [34] and [9]) would be too restrictive, in that it does not consider \(T \, {\le }\, S\) to hold. As we explained in Sect. 3.1.1, this is due to the fact S cannot be decomposed as an input context with holes filled by output branchings: a possible solution could be to extend the syntax of input contexts so to also encompass recursive behaviours. Notice that, on the contrary, if we assumed orphan message freedom, it would be correct for \(T \, {\le }\, S\) not to hold and no extension to the syntax of input contexts would be needed (the subtyping definition in [10, 22] uses non-recursive input contexts as we do here).
Concerning decidability, another possible line of research, we plan to keep investigating, is to devise decidable fragments of the undecidable existing notions of asynchronous session subtyping [9, 10, 22, 34]. This can be done, e.g. by restricting the syntax of session types or limit communication (using forms of bounded asynchrony), as in [9, 10] or, alternatively, by providing algorithmic characterizations of (unrestricted) asynchronous session subtyping that are sound but not complete, as in [8]. More precisely, in [8] an algorithm for checking the orphan message free asynchronous session subtyping of [10, 22] is presented, which is not complete in that in some cases it terminates without returning a decisive verdict. In spite of this limitation, an implementation of this algorithm has been successfully run on many interesting non-trivial examples taken from the literature.
A final interesting line for future research is about multi-party asynchronous session subtyping. The first paper introducing asynchronous session subtyping considered multi-party sessions [35]. Besides allowing for output anticipation w.r.t. inputs (as it happens in the binary case considered in this paper), in [35] also output (resp. input) re-ordering is permitted, when the outputs (resp. inputs) are sent to (resp. received from) different partners. Such re-ordering can be informally justified by observing that the order in which such operations are executed is unobservable in an asynchronous setting because the corresponding messages are placed in distinct FIFO queues. Nevertheless, formalizing such intuitions is not trivial and it is not clear whether the techniques adopted in this paper could be easily adapted. For instance, we use the notion of dual of a session type which is simple to be defined in a binary setting, while it is more complex when moving to a multi-party setting as discussed, for the synchronous case, in [40].
Notes
As for basic CCS [32] finite-stateness is an obvious consequence of the fact that the process algebra does not include static operators, like parallel or restriction.
The correspondence is as follows: the labelled transition systems of the indicated contracts and the corresponding automata in Fig. 1 are isomorphic.
We consider : : to be right associative, as it naturally derives from the syntax of \({{\mathcal {Q}}}\).
Differently from our definitions, in the channel-based approach of Gay and Hole [26] subtyping is covariant on branchings and contra-variant on selections.
We use \({\mathbb {N}}\) to denote the set of natural numbers (excluding 0).
References
Aldini, A., Bravetti, M., Pierro, A.D., Gorrieri, R., Hankin, C., Wiklicky, H.: Two formal approaches for approximating noninterference properties. In: Foundations of Security Analysis and Design II, FOSAD 2001/2002 Tutorial Lectures, volume 2946 of Lecture Notes in Computer Science, pp. 1–43. Springer (2004)
Ancona, D., Bono, V., Bravetti, M., Campos, J., Castagna, G., Deniélou, P., Gay, S.J., Gesbert, N., Giachino, E., Hu, R., Johnsen, E.B., Martins, F., Mascardi, V., Montesi, F., Neykova, R., Ng, N., Padovani, L., Vasconcelos, V.T., Yoshida, N.: Behavioral types in programming languages. Found. Trends Program. Lang. 3(2–3), 95–230 (2016)
Baeten, J.C.M., Bravetti, M.: A ground-complete axiomatisation of finite-state processes in a generic process algebra. Math. Struct. Comput. Sci. 18(6), 1057–1089 (2008)
Barbanera, F., de’Liguoro, U.: Sub-behaviour relations for session-based client/server systems. Math. Struct. Comput. Sci. 25(6), 1339–1381 (2015)
Bernardi, G.T., Hennessy, M.: Modelling session types using contracts. Math. Struct. Comput. Sci. 26(3), 510–560 (2016)
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983)
Bravetti, M.: Reduction semantics in markovian process algebra. J. Log. Algebr. Meth. Program. 96, 41–64 (2018)
Bravetti, M., Carbone, M., Lange, J., Yoshida, N., Zavattaro, G.: A sound algorithm for asynchronous session subtyping. In: Proceedings of 30th International Conference Concurrency Theory, CONCUR’19, volume 140 of Leibniz International Proceedings in Informatics, pp. 38:1–38:16. Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2019)
Bravetti, M., Carbone, M., Zavattaro, G.: Undecidability of asynchronous session subtyping. Inf. Comput. 256, 300–320 (2017)
Bravetti, M., Carbone, M., Zavattaro, G.: On the boundary between decidability and undecidability of asynchronous session subtyping. Theor. Comput. Sci. 722, 19–51 (2018)
Bravetti, M., Lanese, I., Zavattaro, G.: Contract-driven implementation of choreographies. In: Proceedings of 4th International Symposium on Trustworthy Global Computing TGC 2008, volume 5474 of Lecture Notes in Computer Science, pp. 1–18. Springer (2009)
Bravetti, M., Zavattaro, G.: Contract based multi-party service composition. In: Proceedings of International Symposium on Fundamentals of Software Engineering, FSEN’07, volume 4767 of Lecture Notes in Computer Science, pp. 207–222. Springer (2007)
Bravetti, M., Zavattaro, G.: Towards a unifying theory for choreography conformance and contract compliance. In: Proceedings of 6th International Symposium Software Composition, SC’07, volume 4829 of Lecture Notes in Computer Science, pp. 34–50. Springer (2007)
Bravetti, M., Zavattaro, G.: Contract compliance and choreography conformance in the presence of message queues. In: Proceedings of 5th International Workshop on Web Services and Formal Methods, WS-FM’08, volume 5387 of Lecture Notes in Computer Science, pp. 37–54. Springer (2008)
Bravetti, M., Zavattaro, G.: Contract-based discovery and composition of web services. In: Formal Methods for Web Services, 9th International School on Formal Methods for the Design of Computer, Communication, and Software Systems, SFM 2009, Bertinoro, Italy, June 1-6, 2009, Advanced Lectures, volume 5569 of Lecture Notes in Computer Science, pp. 261–295. Springer (2009)
Bravetti, M., Zavattaro, G.: On the expressive power of process interruption and compensation. Math. Struct. Comput. Sci. 19(3), 565–599 (2009)
Bravetti, M., Zavattaro, G.: Foundations of coordination and contracts and their contribution to session type theory. In: Proceedings of 20th IFIP WG 6.1 International Conference on Coordination Models and Languages, COORDINATION 2018, volume 10852 of Lecture Notes in Computer Science, pp. 21–50. Springer (2018)
Bravetti, M., Zavattaro, G.: Relating session types and behavioural contracts: The asynchronous case. In: Proceedings of 17th International Conference on Software Engineering and Formal Methods, SEFM 2019, volume 11724 of Lecture Notes in Computer Science, pp. 29–47. Springer (2019)
Bravetti, M., Zavattaro, G.: Process calculi as a tool for studying coordination, contracts and session types. J. Log. Algebraic Methods Program. 112, 100527 (2020)
Castagna, G., Gesbert, N., Padovani, L.: A theory of contracts for web services. In: Proceedings of 35th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL’08, pp. 261–272. ACM (2008)
Cécé, G., Finkel, A.: Verification of programs with half-duplex communication. Inf. Comput. 202(2), 166–190 (2005)
Chen, T., Dezani-Ciancaglini, M., Scalas, A., Yoshida, N.: On the preciseness of subtyping in session types. Log. Methods Comput. Sci. 13(2), 56 (2017)
de Boer, F.S., Bravetti, M., Lee, M.D., Zavattaro, G.: A petri net based modeling of active objects and futures. Fundam. Inform. 159(3), 197–256 (2018)
Deniélou, P., Yoshida, N.: Multiparty compatibility in communicating automata: Characterisation and synthesis of global session types. In: Fomin, F.V., Freivalds, R., Kwiatkowska, M.Z., Peleg, D. (eds.) Automata, Languages, and Programming-40th International Colloquium, ICALP 2013, Riga, Latvia, July 8-12, 2013, Proceedings, Part II, volume 7966 of Lecture Notes in Computer Science, pp. 174–186. Springer, (2013)
Gay, S.J.: Subtyping supports safe session substitution. In: Lindley, S., McBride, C., Trinder, P.W., Sannella, D. (eds.) A List of Successes That Can Change the World-Essays Dedicated to Philip Wadler on the Occasion of His 60th Birthday, volume 9600 of Lecture Notes in Computer Science, pp. 95–108. Springer, (2016)
Gay, S.J., Hole, M.: Subtyping for session types in the pi calculus. Acta Inf. 42(2–3), 191–225 (2005)
Gay, S.J., Thiemann, P., Vasconcelos, V.T.: Duality of session types: The final cut. In: Balzer, S., Padovani, L. (eds.) Proceedings of the 12th International Workshop on Programming Language Approaches to Concurrency- and Communication-cEntric Software, PLACES@ETAPS 2020, Dublin, Ireland, 26th April 2020, volume 314 of EPTCS, pp. 23–33 (2020)
Hu, R., Yoshida, N.: Hybrid session verification through endpoint API generation. In: Proceedings of 19th International Conference on Fundamental Approaches to Software Engineering FASE 2016, volume 9633 of Lecture Notes in Computer Science, pp. 401–418. Springer (2016)
Laneve, C., Padovani, L.: The Must preorder revisited. In: Proceedings of 18th International Conference Concurrency Theory, CONCUR’07, volume 4703 of Lecture Notes in Computer Science, pp. 212–225. Springer (2007)
Lange, J., Yoshida, N.: On the undecidability of asynchronous session subtyping. In: Proceedings of 20th International Conference on Foundations of Software Science and Computation Structures, FOSSACS’17, volume 10203 of Lecture Notes in Computer Science, pp. 441–457 (2017)
Lindley, S., Morris, J.G.: Embedding session types in Haskell. In: Proceedings of 9th International Symposium on Haskell, Haskell’16, pp. 133–145 (2016)
Milner, R.: Communication and Concurrency. Prentice Hall, London (1989)
Milner, R., Parrow, J., Walker, D.: A calculus of mobile processes. I/II. Inf. Comput. 100(1), 83 (1992)
Mostrous, D., Yoshida, N.: Session typing and asynchronous subtyping for the higher-order \(\pi \)-calculus. Inf. Comput. 241, 227–263 (2015)
Mostrous, D., Yoshida, N., Honda, K.: Global principal typing in partially commutative asynchronous sessions. In: Proceedings of 18th European Symposium on Programming, ESOP’09, volume 5502 of Lecture Notes in Computer Science, pp. 316–332. Springer (2009)
Neykova, R., Hu, R., Yoshida, N., Abdeljallal, F.: A Session Type Provider: Compile-time API Generation for Distributed Protocols with Interaction Refinements in F\(\sharp \). In: Proceedings of 27th International Conference on Compiler Construction, CC 2018. ACM (2018)
Orchard, D.A., Yoshida, N.: Effects as sessions, sessions as effects. In: Proceedings of 43rd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2016, pp. 568–581 (2016)
Padovani, L.: A simple library implementation of binary sessions. J. Funct. Program. 27, e4 (2017)
Scalas, A., Yoshida, N.: Lightweight session programming in scala. In: Proceedings of 30th European Conference on Object-Oriented Programming, ECOOP 2016, volume 56 of LIPIcs, pp. 21:1–21:28. Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2016)
Scalas, A., Yoshida, N.: Multiparty session types, beyond duality. J. Log. Algebr. Methods Program. 97, 55–84 (2018)
Acknowledgements
We would like to thank the anonymous reviewers who provided us with many extremely useful and insightful suggestions. These suggestions allowed us to significantly improve the paper during the revision process.
Funding
Open access funding provided by Alma Mater Studiorum-Università di Bologna within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Gwen Salaün and Peter Csaba Ölveczky.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research partly supported by the H2020-MSCA-RISE project ID 778233 “Behavioural Application Program Interfaces (BEHAPI)”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bravetti, M., Zavattaro, G. Asynchronous session subtyping as communicating automata refinement. Softw Syst Model 20, 311–333 (2021). https://doi.org/10.1007/s10270-020-00838-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-020-00838-x






 (
( such that
such that 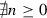 such that
such that  such that
such that