Introduction

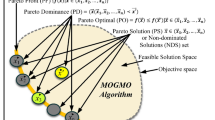
Multi-objective optimization problems (MOPs) with m objectives can be described as Min F(x) = (f1(x), …, fm(x)), x ∈ Ω [29]. The solution x of an MOP is an n-dimensional decision vector x= (x1, …, xn), and F(x) is the phenotype of the solution x in the objective space. A solution u = (u1, …, un) Pareto dominates another solution v = (v1, …, vn) if and only if the objective value of u is less than or equal to that of v on all objectives, and the objective value of u is less than that of v on at least one objective. Solutions that are not dominated by any solution are called non-dominated solutions. The set of all non-dominated solutions is called the Pareto optimal set (PS), and the mapping of the Pareto optimal set in the objective space is called the true Pareto front (PF).

For NP-hard problems, researchers often design customized heuristics to obtain reasonable solutions within a polynomial time. When solving MOPs, the commonly used heuristics are multi-objective evolution algorithms (MOEAs) [5]. One of the major advantages of MOEAs could be that they are population-based algorithms which can obtain a set of solutions approximating the PF in a single run. However, MOEAs sometimes can obtain high performance for several problems but may be ineffective when solving other problems or problems from similar domains [35]. For instance, some dominance-based MOEAs are only effective for MOPs with less than 4 objectives [33]; the decomposition-based MOEAs using fixed reference vectors are not good at solving MOPs with irregular PFs [13, 14].

A hyper-heuristic (HH) is a methodology which has with cross-domain search abilities. This methodology is a high-level strategy by controlling a set of low-level heuristics (LLHs). Instead of solving the problem directly, at each decision point, an HH tries to select one LLH and apply the selected LLH to solve the problem at hand. If an HH is applied to another problem, the high-level strategy does not need to be redesigned [1].

This study proposes an adaptive epsilon-greedy selection based multi-objective hyper-heuristic algorithm (HH_EG) that applies multiple MOEAs as LLHs. In each iteration, HH_EG uses an online-learning strategy to score each LLH and utilizes an adaptive epsilon-greedy selection strategy to select one LLH based on the scores. The selected LLH is then used to solve the problem in this iteration. Specifically, the contribution of this paper consists of the following aspects:

  1. 1.

    An adaptive epsilon-greedy selection strategy is proposed for the hyper-heuristic algorithm to select LLH when solving MOPs. At early stages, the adaptive epsilon-greedy selection strategy prefers to select LLHs randomly while at later stages, the adaptive strategy tends to select the current best LLH using a greedy strategy. The adaptive method updates the probability of using random or greedy algorithms to balance exploration and exploitation.

  2. 2.

    In HH_EG, no parameter is needed to be tuned. Thus, HH_EG could be combined with various indicators to adapt to the preference of users.

  3. 3.

    HH_EG is tested on multiple test suites. We evaluate HH_EG with NSGA-II [9], MOEA/D [37] and, IBEA [40] as LLHs on classical DTLZ [10] and the real-world vehicle crashworthiness problem (VC) [20] test suites. We also conducted an experiment on a challenging IMOP [32] test suite by altering LLHs with NSGA-II, MOEA/D and MSEA [34]. Additionally, the MaF [3] test suite with 5 and 10 objectives are also tested with NSGA-III [8], MOEA/D and MSEA as LLHs. Experimental results show the advantages of HH_EG and its cross-domain search abilities.

Related work

Multi-objective hyper-heuristics

A hyper-heuristic algorithm is an automated methodology for selecting or generating heuristic algorithms to solve computational search problems [1]. There are two main aspects to be considered in the search process of hyper-heuristics: (1) the nature of heuristic search space; (2) the feedback during learning. These factors are orthogonal because heuristic search spaces can be combined with different feedbacks [1]. In terms of the nature of heuristic search space, hyper-heuristics can be divided into selection based hyper-heuristics (methodologies for choosing or selecting existing heuristics) and generation based hyper-heuristics (methodologies for generating new heuristics from components of existing heuristics). In terms of the feedback, hyper-heuristics can be divided into online learning hyper-heuristics, offline learning hyper-heuristics and non-learning hyper-heuristics. In the online learning hyper-heuristics, the learning process occurs at the same time as the algorithm solves the problem instance. The most common example is reinforcement learning [19, 36]. In the offline learning hyper-heuristics, the learning process collects knowledge from a set of training examples in the form of a certain rule or procedure, which can be generalized to solve new examples. Typical offline learning strategies are classifier systems [26], case-based reasoning [27], and genetic programming [15]. The non-learning hyper-heuristics, such as random hyper-heuristics (choosing LLHs randomly), do not deal with the feedback.

In recent years, many studies on hyper-heuristics for solving MOPs have been proposed. Many of these studies focus on online-learning selection hyper-heuristics. In [2], a multi-objective selection hyper-heuristic (TSRoulette Wheel) based on tabu search was proposed. In TSRoulette Wheel, tabu search is used to select LLHs. Experimental results show that TSRoulette Wheel has a good effect on the space allocation and timetabling problems. McClymont and Keedwell [24] proposed an online learning selection hyper-heuristic algorithm (MCHH) based on the Markov chain. Markov chain guides the selection of LLHs, and an online reinforcement learning updates the transfer weights between heuristics. When solving the DTLZ test suite, MCHH performs better than the random hyper-heuristic (HH_RAND) and the TSRoulette Wheel. Subsequently, MCHH was applied to a water distribution networks design problem [25]. In [23], an online learning multi-objective hyper-heuristic algorithm based on choice function (HH_CF) was proposed. HH_CF uses the choice function as the selection method, while employing four indicators and a specific ranking strategy as the learning and feedback strategies. HH_CF uses three well-known MOEAs (NSGA-II, SPEA2 [41], and MOGA [11]) as LLHs. Experiments confirm the ability of HH_CF when solving continuous MOPs. Later, HH_CF is combined with different move acceptance strategies, including the great deluge algorithm and late acceptance in [22].

Li et al. [18] used a multi-objective selection hyper-heuristics to solve the multi-objective wind farm layout optimization problem. Later, Li et al. [19] proposed two novel online learning multi-objective hyper-heuristics (HH_LA and HH_RILA) based on learning automata. Learning automata is used as the learning strategy, and ϵ-RouletteGreedy is proposed to select LLHs from three MOPs (NSGA-II, SPEA2, and IBEA). Experiments on DTLZ, WFG and VC test suites showed that HH_LA and HH_RILA perform better than HH_CF and HH_RAND. Gonçalves et al. [12] used an innovative Restless Multi-Armed Bandit to expand the MOEA/D framework and proposed a multi-objective selection hyper-heuristic algorithm MOEA/D-RMAB. The RMAB strategy is used to select DE operator which should be used by each individual during the operation of the MOEA/D framework to model and process the dynamic behavior of various operators. Yao et al. [36] proposed multi-objective hyper-heuristic algorithms RL-MOHH and RL-PMOHH based on reinforcement learning. By learning and selecting a set of individually designed LLHs, the algorithm is tested on the safety-index map constructed from the historical data of New York City. The results show that the proposed hyper-heuristics have faster convergence speed on the multi-objective route planning in a smart city. Zhang et al. [38] presented a perturbation adaptive pursuit strategy based hyper-heuristic (PAPHH) to manage a set of diversity mechanisms or a set of MOEAs. This method uses a perturbation adaptive pursuit strategy to learn the performance of each LLH, and then use the roulette wheel method to select an LLH based on the selection probability vector. Experimental results show that PAPHH has highly competitive performance in terms of Spacing metric and Hypervolume metric.

Epsilon-greedy

The selection method is important for multi-objective selection hyper-heuristics when taking an action (i.e., selecting an LLH). Several classical selection methods, such as the random algorithm or the greedy algorithm, have been used in the literature. Those methods are different from the function of selection probabilities. A random algorithm takes an action with the same probabilities. This method is easy and has no extra parameter to be considered. The greedy algorithm only selects the best action which is with the highest probabilities. The greedy method has a strong exploitation ability, but always neglects ‘poor’ actions which may perform good in the future. The greedy method easily falls into the local optima.

The Epsilon-greedy method combines the random algorithm and the greedy algorithm to deal with the exploration and exploitation dilemma [16, 28]. The main idea of the Epsilon-greedy is to control the utilization rate of the greedy algorithm or the random algorithm through a small probability ϵ (smaller than 1) with the aim to make the behavior of the Epsilon-greedy to be greedy most of the time, but random once in a while. Specifically, when selecting an action at one decision point, the Epsilon-greedy method first generates a random value rnd in the interval [0, 1], if rnd is larger than ϵ, then the Epsilon-greedy uses the greedy algorithm to select an action, otherwise, the random algorithm is used to select an action.

Adaptive epsilon-greedy selection based multi-objective hyper-heuristic

Framework of HH_EG

HH_EG is a multi-objective selection hyper-heuristic withiniter_total iterations. During each iteration (also called a decision point), an LLH is selected to solve the problem at hand. As shown in Algorithm 1, given a set of LLHs, denoted as H = {h1, h2, …, hl}, HH_EG firstly gets an initial population Pop of size N and initializes the score vector S = (s1, s2, …, sl), where si is the score of hi, i ∈ {1, …, l} (step 1). At each iteration (steps 2–9), HH_EG selects an LLH hcur according to the score vector (step 3) and then uses hcur to evolve the population Pop to generate a new population Pop (step 4). The score vector S is updated according to the degree of improvement after applying hcur (step 5). If the population ′Pop is better than Pop, then Pop is updated (steps 6–8). If the termination criterion is not met, the algorithm goes to step 2.

The framework consists of four key components: initialization (step 1), adaptive epsilon-greedy selection (step 3), score update (step 5) and move acceptance (step 6).

figure a

Initialization strategy

The initialization strategy is used to evaluate the initial performance of each LLH. Beginning with generating a random population, each LLH hi evolves the random population separately with the same number of generations, and obtains a resultant population Popi. The indicator value mpopi evaluated by indicator M for the resultant population Popi obtained by hi is then translated into an initial score si based on the normalized function, as shown in formula (1).

$$ s_{i} = (m_{{{\text{Pop}}_{i} }} - m_{ {\rm min} } )/(m_{ {\rm max} } - m_{ {\rm min} } ) $$
(1)

where mmin and mmax are, respectively, the minimum and maximum indicator values found so far by all LLHs in the initialization strategy. HH_EG can employ various indicators in the framework. If the indicator M is a maximization (or minimization) problem, the larger (or the smaller) score value equals to the better performance. Eventually, the resultant population from the best scoring LLH is then used as the initial population Pop of HH_EG.

Adaptive Epsilon-greedy selection strategy

An adaptive epsilon-greedy selection method is designed as a selection strategy to improve the decision-making ability of HH_EG. The main idea is that the adaptive epsilon-greedy selection strategy first focuses on exploring using the random algorithm to select an LLH. Then, the selection method begins to be greedier using the greedy algorithm. That is, we randomly generate a value in [0, 1]. If the random value is smaller than ϵ, a random LLH from the LLH set is selected to be applied in the next iteration; otherwise, the best scored LLH selected by the greedy algorithm will be applied.

In the traditional Epsilon-greedy algorithm, ϵ is a fixed parameter which is needed to be tuned manually. This paper uses a formula (2) to update the ϵ-value according to the number of iterations:

$$ \epsilon = ({{iter}}\_{{total}} - {{iter}})/{{iter}}\_{{total}}. $$
(2)

The ϵ-value presents a linear decreasing trend. Its value is large at former search processes, so HH_EG has a great probability to randomly select an LLH. At later stages, ϵ-value becomes smaller (down to 0), which means that HH_EG is to select the currently best-scored LLH. This strategy of selection makes the algorithm focusing on exploring different LLHs at early stages and then turns to greedy exploitation gradually as the search progresses.

Score update strategy

As discussed in [17, 38], the LLHs luckily to be chosen at the early stages are easy to get larger improvement values. However, the LLH used at later stages always only brings small improvements even if it is more effective than the rest of LLHs. So the raw indicator value is not able to reflect the actual performance of each LLH throughout the entire search process [38].

In the proposed algorithm, we use the indicator improvement rate with the indicator value of the output population as the baseline to update the score vector S based on the feedback of the selected LLH hcur during searching. If hcur obtains a positive feedback after being applied at one iteration, then its score is rewarded. Otherwise, its score is punished.

Specifically, after applying hcur at one iteration, the input population Pop and the output population Pop′ are evaluated using the indicator M, and then the score value scur of hcur is updated according to Eq. (3):

$$ s_{\text{cur}} = s_{\text{cur}} + (m_{\text{out}} {-}m_{\text{in}} )/m_{\text{out}} $$
(3)

where min and mout denote the indicator values of the input population and the output population. For a maximization indicator M, if the increment (we mean mout − min) is greater than 0, we denote it that an improvement (positive feedback) has obtained after applying hcur. The score scur is rewarded. Otherwise, it means a deteriorated operation (negative feedback) is executed by applying hcur. The score scur is punished. For a minimization indicator M, the situation is reversed.

Move acceptance strategy

In this research, the only-improving acceptance strategy [22] is used to determine whether to accept the output population or not when solving MOPs. At each iteration, the indicator M is used to evaluate the input population Pop and the output population Pop′. We denote min and mout as the indicator values of Pop and Pop′, respectively. The only-improving only accepts the improved new population. For a maximization (or minimization) indicator M, min < mout (or min > mout) indicates that Pop′ is improved compared to Pop, and Pop′ will be the input population of the next iteration; otherwise, Pop is.

Experimental settings

To evaluate the effectiveness, we compare HH_EG with each LLH inside HH_EG and four multi-objective hyper-heuristic algorithms (HH_RAND, HH_CF [23], HH_RILA [19], and PAPHH [38]) on DTLZ (DTLZ1-7) [10], IMOP (IMOP1-8) [32], MaF (MaF1-7) [3] and VC (VC1-4) [20] test suites.

Test suites

DTLZ is a classical test suite which is often used as a baseline to test the performance of multi-objective algorithms. DTLZ1 contains linear and multimodal characteristics. The PFs of DTLZ2-6 are concave. Besides, DTLZ3 is a multimodal problem; DTLZ4 is biased; DTLZ5 is degenerate; and DTLZ6 is a biased and degenerate problem. DTLZ7 has mixed, discontinuous and biased characteristics. These characteristics enable DTLZ to comprehensively test the performance of various algorithms. Experiments are conducted on three-objective DTLZ1-7 test problems.

IMOP is a novel test suite with extremely irregular PFs proposed recently. IMOP1-3 are two-objective MOPs. IMOP1 and IMOP2 have convex and concave PFs with sharptails. The PF of IMOP3 is a multi-segment discontinuous curve. IMOP4-8 are three-objective MOPs with varied shaped PFs. For IMOP4, its PF is a wavy line. The PF of IMOP5 is composed of 8 independent circular faces. The PF of IMOP6 is divided into several grids. The PF of IMOP7 is part of 1/8 sphere, while the PF of IMOP8 looks like a continuous plane, but actually consists of 100 discontinuous small pieces.

MaF is a recently proposed test suite for many-objective optimization. We choose MaF 1–7 with 5 and 10 objectives in the experiments. The seven MaF problems are with diverse properties, such as being multimodal, disconnected, degenerate, and biased. The aim of using MaF is to verify the effectiveness of HH_EG on many-objective optimization problems with various real-world scenarios.

VC is a real-world multi-objective optimization problem referring to the ability of vehicles and components to protect passengers during a collision in the automotive industry. The VC test suite involves the optimization of weight (Mass), acceleration characteristics (Ain), and toe-board intrusion (Intrusion). Four VC problems are used in the experiments, including VC1: min F(x) = [Mass, Ain], VC2: min F(x) = [Mass, Intrusion], VC3: min F(x) = [Ain, Intrusion], and VC4: min F(x) = [Mass, Ain, Intrusion] with VC1-3 from [22] and VC4 from [20].

Performance indicators

In the experiments, IGD [4] and HV [42] are employed in the proposed HH_EG framework as performance indicators to evaluate each LLH during iterations of HH_EG. The main reasons for choosing IGD and HV are that they are commonly used and can evaluate multiple aspects, such as diversity and convergence, of the population. The IGD indicator evaluates the averaged minimum distance between each reference point on PF and the obtained population got by an algorithm. The HV indicator evaluates the objective space covered by a given population. For the two indicators, IGD requires prior knowledge of the PF, while HV does not. But HV is with a slower resolving speed, especially for high-dimensional MOPs. Since DTLZ, IMOP and MaF test suites have known PF, HH_EG incorporates IGD as a performance indicator to serve the high-level online learning strategy as the feedback when solving the two test suites. Aimed at the problems of VC test suite have unknown PFs, HH_EG uses HV instead of IGD as the performance indicator for solving VC test problems.

Low-level heuristics

Five MOEAs are used to form the low-level heuristic set, denoted as h1 (NSGA-II [9]), h2 (MOEA/D [37]), h3 (IBEA [40]), h4 (MSEA [34]), and h5 (NSGA-III [8]). Generally, any population-based MOEAs can be incorporated into HH_EG as LLHs. The main reasons for choosing NSGA-II, MOEA/D, and IBEA are that they are classical and always be the baseline for comparison [31, 39]. MSEA is a recently proposed MOEA for getting better distributed population and NSGA-III is designed for many-objective optimization problems (having four or more objectives). Besides, the five MOEAs are from different categories of MOEAs. Specifically, NSGA-II and IBEA are the dominance-based MOEA and the indicator-based MOEA, respectively, while both MOEA/D and NSGA-III are the decomposition-based MOEA [21]. MSEA is the multi-stage MOEA [34]. Each of the five MOEAs is to promote the approximation population along with the PF, but they are different in utilizing different algorithm components during searching.

h1 (NSGA-II): Each solution in the population is sorted according to its Pareto-optimal level. Only solutions in low levels are selected into the next generation. Besides, the crowding distance assignment strategy is used to maintain the diversity of the population during the selection process.

h2 (MOEA/D): MOEA/D uses a set of uniformly distributed weight vectors to decompose the MOPs into multiple single-objective sub-problems. Each sub-problem is optimized by utilizing the information of neighborhood sub-problems, and the given weight vectors are used to control the diversity.

h3 (IBEA): IBEA uses binary indicators to redefine the optimization goal. The indicator values are used as fitness in the environment selection, and no additional diversity maintaining strategy is needed to control diversity.

h4 (MSEA): MSEA is a multi-stage MOEA for getting better-distributed population. The optimization process is divided into multiple stages according to the population in each generation, and the population is updated by different steady-state selection schemes in different stages. MSEA can solve MOPs with highly irregular PF.

h5 (NSGA-III): NSGA-III is a reference-point-based evolutionary algorithm based on the NSGA-II framework with the aim to solve many-objective optimization problems. Solutions in the population are ranked by the non-dominated sorting method and the reference points are adopted to control the diversity.

Parameter settings

All LLHs use the simulated binary crossover operator and the polynomial distribution operator [7] for recombination and mutation respectively. The crossover probability is set to 1 and the mutation probability is set to 1/n (n is the number of decision variables of a given problem). The crossover and mutation distribution index are both set to 20. MOEA/D uses PBI [37] as the decomposition method. The neighborhood size of MOEA/D is set to 0.1 × N (N indicates the population size), and the maximum number of solutions replaced by each offspring is set to 0.01 × N. The uniformly distributed weight vectors are generated using Das and Dennis’ sampling method [6]. The archive size of IBEA is the same as the population size N, and the fitness scaling factor is set to 0.05. Following the recommendation in [8, 19, 23], the parameter settings of each algorithm on DTLZ, IMOP, MaF, and VC test suites are given in Table 1. Other parameters are the same as used in their original papers.

Table 1 Parameter settings
Full size table

The parameter k in DTLZ1-7 is set to {5, 10, 10, 10, 10, 10, 20} [10]. The parameters of IMOP1–IMOP8 are set to {I = 5, L = 5, a1 = 0.05, a2 = 0.05, a3 = 10} [32], where I and L control the length of decision variables, while a1–a3 control the difficulty of diversity protection.

The indicator IGD is used for DTLZ, IMOP, and MaF test suites. We sample 10,000 uniformly distributed solutions in the objective space from the PF of each DTLZ, IMOP and MaF test problems. The value of IGD ranges in [0, ∞), the smaller value indicating a better performance. HV is used for the VC test suite. Before calculation, the population is normalized. In the measurement of HV, the reference points are set as \( r^{i} = z^{{{\text{nadir}}_{i} }} + 0.5(z^{{{\text{nadir}}_{i} }} - z^{{{\text{ideal}}_{i} }} ) \) for the ith objective [19], where i ∈ 1 …m is the index of the objective and m is the number of objectives, \( z^{{{\text{nadir}}_{i} }} \) and \( z^{{{\text{ideal}}_{i} }} \) are the maximum and minimum values of the ith objective in the population to be calculated respectively. After normalization with the reference point, the value of HV ranges in [0, 1]. The larger HV value indicates a better performance.

All algorithms are run for 30 independent trials and compared using one-tailed Wilcoxon rank-sum test method. ‘+’, ‘−’, and ‘=’ represent the comparing algorithm is “superior to”, “inferior to”, and “similar to” HH_EG at 0.05 significance level. All source codes are implemented with a popular public-domain software named PlatEMO [30] performed on an Intel core i7 3.1 GHz/8G/1T computer.

Experimental results

Experiments in this section are divided into four parts. In “Experimental results on DTLZ”, we evaluate the effectiveness of HH_EG by controlling three LLHs, H = {h1, h2, h3} on the DTLZ test suite. IGD is employed as the indicator since the PFs of DTLZs are known. In “Experimental results on IMOP” and “Experimental results on MaF”, we evaluate the cross-domain ability of HH_EG by solving the two novel test suites, IMOP and MaF. With unchanged high-level framework, HH_EG only replaces LLHs with H = {h1, h2, h4} for low-dimensional IMOP test suite, H = {h2, h4, h5} for high-dimensional MaF test suite. IGD is used as an indicator. In “Experimental results on VC”, we evaluate HH_EG with the real-world multi-objective problem VC with H = {h1, h2, h3} as the LLH set. Since there is no known PFs in VC, HV is incorporated into HH_EG as the indicator.

The mean, standard deviation and ranking performance of HH_EG and the comparing algorithms with respect to IGD or HV indicators got from 30 independent trials on DTLZ, IMOP, MaF, and VC test suites are shown in Tables 2, 3, 4 and 5, respectively. The best mean IGD or HV value on each problem is highlighted in bold. In each table, the ranking values across all test problems are summarized for every algorithm (denoted as “Total”). After the summarization, the final ranking order is displayed sorted by the “Total” value (denoted as “Final Rank”). The corresponding box plots are illustrated in Figs. 1, 2, 3, 4 and 5, where the red lines in each box plot are the median value among 30 trials.

Table 2 The statistical results (mean, standard deviation and ranking) of the IGD values obtained by comparing algorithms and HH_EG on DTLZ1 to DTLZ7
Full size table
Table 3 The statistical results (mean, standard deviation and ranking) of the IGD values obtained by comparing algorithms and HH_EG on IMOP1 to IMOP8
Full size table
Table 4 The statistical results (mean, standard deviation and ranking) of the IGD values obtained by comparing algorithms and HH_EG on MaF1 to MaF7 with 5 and 10 objectives
Full size table
Table 5 The statistical results (mean, standard deviation and ranking) of the HV values obtained by comparing algorithms and HH_EG on VC1 to VC4
Full size table
Fig. 1
figure 1

Box plots of each algorithm on DTLZ test suite from 30 trials with respect to the IGD values

Full size image
Fig. 2
figure 2

Box plots of each algorithm on IMOP test suite from 30 trials with respect to the IGD values

Full size image
Fig. 3
figure 3

Box plots of each algorithm on MaF test suite with 5 objectives from 30 trials with respect to the IGD values

Full size image
Fig. 4
figure 4

Box plots of each algorithm on MaF test suite with 10 objectives from 30 trials with respect to the IGD values

Full size image
Fig. 5
figure 5

Box plots of each algorithm on VC test suite from 30 trials with respect to the HV values

Full size image

Experimental results on DTLZ

From Table 2, we can see from the statistical results of the IGD values on DTLZ test suite from 30 trials that HH_EG works the best on DTLZ2 and DTLZ4–7. HH_EG is significantly better than NSGA-II, IBEA, HH_RAND, HH_RILA, and PAPHH on all DTLZ problems, while HH_EG is significantly better than MOEA/D and HH_CF on five DTLZ problems, including DTLZ2 and DTLZ4–7. For the remaining two problems (DTLZ1, DTLZ3), HH_EG and HH_CF preform similarly. MOEA/D works the best on DTLZ1 and DTLZ3, followed by HH_EG. The superior performance of MOEA/D on DTLZ1 and DTLZ3 is attributed to its uniformly distributed weight vectors which make MOEA/D good at dealing with problems with regular PF. However, HH_EG works better than MOEA/D both on irregular-shaped problems (DTLZ5–7) and the rest regular-shaped problems (DTLZ2 and DTLZ4). Furthermore, HH_EG is relatively stable compared to comparing hyper-heuristics (HH_RAND, HH_CF, HH_RILA, and PAPHH), except DTLZ5 for HH_CF. Corresponding box plots are shown in Fig. 1. According to Total and Final Rank, HH_EG performs the best across all DTLZ test problems in the overall.

Experimental results on IMOP

Table 3 shows that HH_EG is superior to all comparing algorithms on all IMOP test problems with respect to the IGD values, except that HH_EG is inferior to MSEA on IMOP3. From the statistical results of the Wilcoxon rank-sum test, HH_EG is significantly better than NSGA-II, MOEA/D, HH_RAND, and PAPHH on all IMOP test problems. HH_EG is significantly better than MSEA on five instances (IMOP1 and IMOP5–8), and performs similarly to MSEA on IMOP2 and IMOP4. With similar performance on IMOP4–5 for HH_CF and IMOP5 for HH_RILA, HH_EG performs significantly better than HH_CF and HH_RILA on the rest IMOP test problems. Among hyper-heuristics, HH_EG is more stable than HH_RAND and HH_RILA on all test problems. The stability of HH_EG is superior to that of HH_CF and PAPHH except for two test problems (IMOP2 and IMOP4 for HH_CF, IMOP6 and IMOP7 for PAPHH). Figure 2 shows corresponding box plots. The final rank in Table 3 assesses the generality level of each algorithm across IMOP1–8. The rank results show that HH_EG delivers the best performance.

Experimental results on MaF

Experimental results in Table 4 show that HH_EG is the top algorithm on 10 out of 14 MaF test problems except for 5-objective MaF4 and MaF6 test problems, 10-objective MaF4 and MaF7 test problems. On the four MaF test problems, MSEA performs the best. From the statistical results of the Wilcoxon rank-sum test, HH_EG is significantly better than MOEA/D, HH_RAND, and HH_CF on all MaF test problems. HH_EG is significantly better than NSGA-III, HH_RILA, and PAPHH on 13, 12, and 11 MaF test problems respectively, and performs similarly to NSGA-III, HH_RILA, and PAPHH on the rest test problems (10-objective MaF7 for NSGA-III, 10-objective MaF5 and 5-objective MaF7 for HH_RILA, 10-objective MaF1, MaF5, and MaF7 for PAPHH). HH_EG performs significantly better than MSEA on 10 MaF test problems, while MSEA performs significantly better than HH_EG on 3 MaF test problems. From Table 4, HH_EG is more stable among hyper-heuristics, except 5-objective MaF4 for PAPHH and 5-objective MaF5 for HH_RILA. HH_EG ranks first compared with all comparing algorithms according to the final rank, which confirms that HH_EG is effective when solving many-objective MaF test problems. Corresponding box plots of MaF test suite are shown in Figs. 3 and 4.

Experimental results on VC

Table 5 shows the statistical performance comparison of HH_EG and comparing algorithms from 30 independent runs with respect to the HV values for solving VC test problems. For the HV indicator, a higher value indicates better performance, and the box plots of each algorithm are visualized in Fig. 5. From Table 5, we can see that, among the three LLHs, IBEA and NSGA-II perform the best on VC1 and VC2–4, respectively. MOEA/D performs the worst. Besides, HH_EG is significantly better than NSGA-II, MOEA/D, and IBEA on all VC test problems. Compared with the four hyper-heuristics, HH_EG achieves the best mean HV values than HH_RAND, HH_CF, HH_RILA, and PAPHH on VC1–4. In the final rank, HH_EG ranks first.

In general, across the DTLZ, IMOP, MaF, and VC test problems, HH_EG is superior to each LLHs on almost all test problems (except DTLZ1 and DTLZ3 for MOEA/D, IMOP3, 5-objective MaF4, 10-objective MaF4 and MaF7 for MSEA), indicating that HH_EG can combine the advantages of each LLH. Compared with HH_RAND, HH_CF, HH_RILA, and PAPHH, HH_EG performs the best on all DTLZ, IMOP, MaF, and VC test problems, and is more stable. The superiority of HH_EG shows the effectiveness of HH_EG in learning and selection.

Analysis of hyper-heuristics

The average utilization rate of LLHs

Figures 6, 7, 8, 9 and 10 show the average utilization rate of each LLH when HH_EG solves DTLZ, IMOP, MaF and VC test problems (left). The utilization rate of an LLH means the number of invocations of the LLH divided by the number of total iterations of HH_EG in one run. Figures 6, 7, 8, 9 and 10 also show the average indicator values (IGD for DTLZ, IMOP and MaF, HV for VC) of three MOEAs, which are used as LLHs in HH_EG, running independently over 30 trials (right).

Fig. 6
figure 6

The average utilization rate of each LLH by HH_EG (left) and the average IGD values of each LLH run independently (right) over 30 trials on DTLZ test suite

Full size image
Fig. 7
figure 7

The average utilization rate of each LLH by HH_EG (left) and the average IGD values of each LLH run independently (right) over 30 trials on IMOP test suite

Full size image
Fig. 8
figure 8

The average utilization rate of each LLH by HH_EG (left) and the average IGD values of each LLH run independently (right) over 30 trials on MaF test suite with 5 objectives

Full size image
Fig. 9
figure 9

The average utilization rate of each LLH by HH_EG (left) and the average IGD values of each LLH run independently (right) over 30 trials on MaF test suite with 10 objectives

Full size image
Fig. 10
figure 10

The average utilization rate of each LLH by HH_EG (left) and the average HV values of each LLH run independently (right) over 30 trials on VC test suite

Full size image

We conclude our results as follows. Firstly, HH_EG biases to the best performing LLH with respect to the indicator values. As shown in Figs. 6, 7, 8 and 9, the LLH with the lowest IGD value is always selected at the highest frequency by HH_EG on 22 out of 29 problems except for DTLZ4, IMOP5, IMOP7, 5-objective MaF7 and 10-objective MaF2, MaF5–6. Specifically, for the DTLZ and IMOP test suites, HH_EG chooses NSGA-II more frequently on DTLZ5–6, IMOP1, and IMOP4, while providing a bias towards MOEA/D for on DTLZ1–3. HH_EG prefers IBEA on DTLZ7, and MSEA on IMOP2–3, IMOP6, IMOP8. For the high-dimensional MaF test suite, HH_EG gives MOEA/D more chance on 5-objective and 10-objective MaF3. But HH_EG uses MSEA with a high probability on 5-objective MaF1–2, MaF4–6, and 10-objective MaF1, MaF4, MaF7. Figure 10 shows that the LLH with the highest HV (i.e. IBEA for VC1 and NSGA-II for VC2–4) is selected the most by HH_EG when solving all VC test problems. The best performed LLH is always selected more frequently is mainly because that the IGD or HV is served as the feedback guidance in the learning strategy. Secondly, in certain cases, such as DTLZ4, IMOP5, IMOP7, 5-objective MaF7 and 10-objective MaF2, MaF5–6, HH_EG does not give the best performed LLH a higher utilization rate. For DTLZ4, MOEA/D is given more chance instead of NSGA-II. MSEA is selected more than the best performed LLH (i.e. NSGA-II) on IMOP5, while NSGA-II is selected more than the best LLH (i.e. MSEA) on IMOP7. HH_EG prefers MSEA on 5-objective MaF7, 10-objective MaF2, MaF5, and MOEA/D on 10-objective MaF6. This might indicate that combining LLHs together could exploit the potential of ‘poor’ LLH and achieve a better result finally.

The number of invocations of each LLH versus the average indicator values

To further understand the search progress induced by each LLH, Fig. 11 provides plots based on the number of invocations of each LLH at each iteration obtained from HH_EG over 30 trials on DTLZ2 and IMOP5 (left). Each point on the left subplot indicates the total number of trials of the corresponding LLH been selected by HH_EG, with its value ranges in [0, 30]. Figure 11 also plots the average IGD values versus iterations from HH_EG and three MOEAs running alone over 30 trials (right).

Fig. 11
figure 11

The number of invocations of each LLH (left) and the average IGD values of four algorithms (right) versus iterations over 30 trials on DTLZ2 and IMOP5

Full size image

On DTLZ2, in the initial stages, the left subplot shows that the number of invocations of NSGA-II, MOEA/D, and IBEA are similar, which is caused by the randomness of the random algorithm in the adaptive epsilon-greedy selection strategy in the beginning exploration phase. Later, HH_EG slowly reduces the usage of NSGA-II and IBEA, while increasing the usage of MOEA/D. MOEA/D is even predominately used during the final stages. According to the right subplot, MOEA/D is the best performed (with lowest IGD values) algorithm compared to NSGA-II and IBEA. It is not difficult to understand that as the search progresses, the adaptive epsilon-greedy selection strategy becomes more exploitative and prefers invoking the best performed LLH.

On IMOP5, the invocations of NSGA-II, MOEA/D, and MSEA are not dominated with each other, especially in the first ten iterations. After that, the invocations of MSEA is gradually increased with significant superiority to NSGA-II and MOEA/D. But, from the right subplot, it is surprising to find that MSEA is only the second-best LLH when running alone, following the best performing LLH (NSGA-II). Meanwhile, HH_EG obtains the optimal IGD value on IMOP5 (as shown in Table 3 and right subplot of Fig. 11), which also shows that after combining each LLH, HH_EG produces better results than each LLH running alone.

The scores of each LLH versus the IGD values

This section investigates the performance of each LLH in HH_EG from the best trail from 30 trials, as shown in Figs. 12 and 13. The left subplots show the score values of each LLH during the solving of HH_EG. The lower score value indicates a better performance. Correspondingly, the right subplots show the IGD values of HH_EG where each tick in the right plots indicate the IGD value obtained after HH_EG applies the selected LLH during searching.

Fig. 12
figure 12

The score values of each LLH (left) and IGD values of HH_EG (right) versus iterations on DTLZ2 from the trail with the lowest final IGD value among 30 trials

Full size image
Fig. 13
figure 13

The score values of each LLH (left) and IGD values of HH_EG (right) versus iterations on IMOP5 from the trail with the lowest final IGD value among 30 trials

Full size image

Each problem has its own pattern. For example, for DTLZ2 (see Fig. 12), MOEA/D is invoked and applied at the 2nd, 3rd, and 8th iterations, where the IGD values decrease and the corresponding score values of MOEA/D decrease, too. That is the scores of MOEA/D are rewarded. At the 5th, 7th, and 9th iterations, NSGA-II is invoked, while at the 1st, 4th, and 6th iterations, IBEA is invoked. The IGD values at the six iterations are unchanged, but their corresponding score values increase, indicating that un-improved populations are generated. The scores of NSGA-II and IBEA are punished. As we can see, MOEA/D has the lowest scores (performing the best). As the iteration progresses, the adaptive epsilon-greedy selection strategy becomes greedier and MOEA/D has more chance to be selected, which are consistent with the high utilization rate of MOEA/D on DTLZ2 in previous reports in “The average utilization rate of LLHs”.

For IMOP5 (see Fig. 13), NSGA-II is selected at the 1st and 2nd iterations, while MSEA is selected at the 3rd, 7th, 8th and 24th iterations. The IGD values decrease at the six iterations and the corresponding score values decrease. For the rest iterations, the IGD values do not change, but the corresponding score values increase, indicating that the new generated population is not improved after applying LLHs at these iterations. From Fig. 13, the score values of NSGA-II decrease bellow MSEA in the beginning and increase above MSEA later. According to the score values, HH_EG considers that NSGA-II is superior at the early stages, while MSEA works better at later stages. For the adaptive epsilon-greedy selection strategy bias to select the best performed LLH as the search progresses, the probability of selecting MSEA is generally increasing. This explains why MSEA as the second-best LLH is selected the most on IMOP5 (shown in Figs. 7 and 11).

Conclusion

This paper proposes a novel multi-objective hyper-heuristic, HH_EG. This algorithm combines the advantages of existing MOEAs to produce better results on multiple types of problems. Four strategies make up the main high-level framework of HH_EG, including initialization, adaptive epsilon-greedy selection, score update, and move acceptance. Performance indicators are utilized to provide feedback to the high-level online learning strategy. In the proposed algorithm, no parameter is needed to be tuned. This suggests that HH_EG requires little expert intervention. This simplification makes it feasible to incorporate variety of indicators into HH_EG. Experimental results show that HH_EG is more competitive than each LLH running alone and is also superior to four classical hyper-heuristics when dealing with MOPs. Results on DTLZ, IMOP, MaF, and VC show the competitiveness and cross-domain search abilities of the proposed hyper-heuristic.

In future work, we will apply HH_EG to different types of MOPs, such as many-objective, multi-model, or real-world problems, to assess its effectiveness as well as the cross-domain ability. Another research direction is the impact of hyper-heuristics with different algorithm components as LLHs. Besides the IGD and HV indicators in our work, other indicators could be combined with hyper-heuristics. The impact of indicator values as the feedback in learning strategies is also left as future work.