The effects of heterogeneous confidence on cooperation in spatial prisoner's dilemma game

Cooperative behaviors are ubiquitous in both human and animal societies [1]. However, how to understand the evolution of cooperation in real life still remains a challenge. The emergence and maintenance of cooperation among selfish individuals have received considerable attention of researchers from diverse fields during last several decades. Under the theoretical framework of evolutionary games, some typical game models have been widely used to describe the interactions between individuals, such as the prisoner's dilemma game (PDG) [2–4], the stag hunt game (SHG) [5,6], the snowdrift game (SDG) [7,8] and the ultimatum game (UG) [9,10]. Meanwhile, a large variety of mechanisms that facilitate cooperation have been proposed, such as direct and indirect reciprocity [11–14], punishment and reward [15–20], volunteering [21,22], aspiration [23–27], preferential selection [28,29], to name but a few.

In real-world situations, individuals exhibits some personal attributes when they interact with others or make decisions. Considering this, many researchers studied the effects of personal attributes on cooperation in evolutionary games. It has been verified in previous studies that some personal attributes of individuals could promote cooperation effectively such as learning ability [30–32], migration [33,34], memory [35–37], and so on. In a recent work, Szolnoki and Chen considered the way how individuals evaluate their own payoff values by introducing a parameter to characterize the self-deception level [38]. They assumed that the individuals may be underconfident, normal, or overconfident. In particular, when imitation probability is calculated through payoff comparison, an underconfident individual underestimates his own achievement compared to the actual payoff whereas an overconfident one overestimates his own achievement. This means that the underconfident and overconfident individuals use the biased values of payoffs to carry out payoff comparison for the strategy imitation. Therefore, the evolution of cooperation can be affected by the confidence of individuals. The authors found that both underconfident and overconfident individuals are capable of promoting the cooperation level significantly and the presence of overconfident individuals enhances the spatial reciprocity. On the other hand, in previous works, the effects of the heterogeneity in personal attributes have also been intensively studied. Typically, the heterogeneity in degrees of individuals could favor the spreading of cooperation in the population [39]. Heterogeneous teaching ability can also promote cooperation in evolutionary games, in which some individuals have higher influence to spread their strategies [40–43]. In [44], the authors assigned a quenched age distribution to the population and assumed that the strategy transfer capability is related to the age. Their results show that cooperative behavior could be substantially promoted by the heterogeneous age. As another example, in [45], Perc and Szolnozi introduced a heterogeneous parameter as social diversity into the model and assume that individuals can rescale their payoffs. They found that, when the parameter obeys power-law distribution, such society diversity could promote cooperation best.

Meanwhile, considering that individuals' attributes may change over time, the coevolutionary games in which personal attributes of individuals can coevolve with their strategies have received much attention [46]. In an early work [30], Szolnoki and Perc proposed a coevolutionary game, in which the teaching activity of players can evolve with strategy. In their model, each successful strategy adoption process is accompanied by an increase in the donor's teaching activity. They found that, by applying an optimum value of the increment, the coevolution can spontaneously create relevant inhomogeneities in the teaching activities that support the maintenance of cooperation. In [47], Zhang et al. introduced an aspiration-dependent persistence into the spatial prisoner's dilemma game and allowed the persistence level to coevolve with strategy. The results suggest that aspiration-dependent strategy persistence could effectively promote cooperation, and diverse strategy persistence levels among population are formed during the evolution, which ultimately results in the highest cooperation level. In [48], Wu et al. studied the coevolutionary dynamics of aspiration and strategy in spatial repeated public goods games. In [49], Yang et al. treated strategy updating rule as an attribute of players and assumed that the attribute could evolve with time.

Inspired by these previous studies, we propose evolutionary games to study the effects of heterogeneous confidence on cooperation in spatial prisoner's dilemma game by making extensions to the model in [38]. Particularly, the extensions are based on two realistic factors. One is that, as an attribute of individual, the confidence level varies from person to person, instead of having a homogenous value. Thus, we introduce the heterogeneous confidence into evolutionary games, which could well conform to the actual situation, especially for the human society. The other factor is the time-varied confidence levels of individuals. In real life, if an individual gains a higher payoff than his aspiration in one round of game, he might have more confidence in his own choice, and he is less likely to alter his strategy. Contrarily, if his payoff does not reach his aspiration, he might doubt his decision and show lack of confidence. This means that the confidence level may depend on the payoffs that the individuals have obtained in the last round. Considering these, in this work, we will further consider a coevolutionary dynamics, in which the confidence level of individuals coevolve with the strategy.

The rest of this paper is organized as follows. We will describe the model in the next section. Then we will show the main results and discussion in the third section. Finally, the conclusion is summarized in the fourth section.

We consider a structured population located on a square lattice with periodic boundary conditions. The size of the population $N=L\times L$ and we set L = 100 in this work. We adopt the PDG as the fundamental game model to describe the pairwise interaction among the individuals. In a traditional one-shot PDG, two individuals choose one strategy from two choices, cooperation (C) and defection (D), and then their payoffs depend on their choices. Two cooperators both gain reward R through mutual cooperation, while two defectors get payoff P as punishment. If one chooses C and the other chooses D, the cooperator gets the sucker's payoff S while the defector obtains the temptation to defection T. Two inequalities are required for a typical PDG: T > R > P > S and $2R>T+S$. For simplicity, we use the weak PDG, in which $R = 1$, $P = S = 0$ and T > 1 as a tunable game parameter.

We assign the confidence levels to the individuals, which characterize how they perceive their own payoffs. According to the confidence level, the individuals are divided into three types: underconfident, normal and overconfident. Assume that an individual i obtains payoff P_i (t) at time t. During the following strategy imitation, individual i will decide whether to change the strategy or not, according to the imitation probability calculated through payoff comparison. Here, individual i will estimate his payoff value and carry out the payoff comparison by using the estimated payoff value, instead of the actual one. The estimated payoff value of an underconfident individual is lower than the actual one, while an overconfident individual i estimates his payoff value to be higher than the actual payoff. We denote the actual payoff of an individual i obtained at time t by P_i (t) whereas, from his own perspective, the estimated payoff $P'_{i}(t)$ which will be used in the payoff comparison is given by

$$\begin{equation} P'_{i}(t)=[1+\alpha_{i}(t)]P_{i}(t). \end{equation} \tag{ 1 }$$

Here, $\alpha_{i}(t)$, which is in the range of $[-1,1]$, stands for the confidence level of individual i at time t. For an underconfident individual, $\alpha<0$. In contrast, $\alpha>0$ for an overconfident individual. Specifically, a normal individual will use an unbiased payoff (the actual payoff) for the payoff comparison. That is, $\alpha=0$ for a normal individual. In this work, we consider two different cases of α for individuals in the population.

i) Static confidence level. In this case, the confidence levels are different among the population while they remain constant throughout the evolution process. For simplicity, we assume that the confidence level follows the uniform distribution and satisfies the distribution function:

$$\begin{equation} f(\alpha)=\frac{1}{2\gamma}, -\gamma+\alpha_{0}<\alpha<\gamma+\alpha_{0}, \end{equation} \tag{ 2 }$$

where γ represents the half-width of the distribution, indicating the dispersion of confidence level, and $\alpha_{0}$ represents the center (average) of uniform distribution. In addition, we declare that $\gamma=0$ represents the homogeneous confidence level for the players in the population.

ii) Time-varied confidence level. We allow the confidence level to coevolve with the strategy of individuals in this case. Initially, each individual's confidence level is set to be 0 for the initial conditions. Meanwhile, each individual has an aspiration $\beta k$ for his payoff. Following [50], we set β to be 0.5. k is the individual's degree and k = 4 for all the individuals on square lattice. At time t, if the accumulated payoff of individual i, P_i , is higher than $\beta k$, the confidence level of i will be increased by $\Delta \alpha$. Contrarily, if $P_i<\beta k$, the confidence level of i will be decreased by $\Delta \alpha$. If the payoff of individual i is equal to $\beta k$, the confidence level of i remains unchanged. In this way, the evolution of the confidence level could be described as

$$\begin{equation} \alpha_{i}(t+1)=\left\{ \begin{array}{l@{\qquad}l} \alpha_{i}(t)+\Delta \alpha, & P_{i}>\beta k,\\ \alpha_{i}(t), & P_{i}=\beta k, \\ \alpha_{i}(t)-\Delta \alpha, & P_{i}<\beta k. \end{array} \right. \end{equation} \tag{ 3 }$$

Initially, the two strategies of C and D are randomly distributed among the population with equal probability. One elementary evolution procedure includes the following steps: Firstly, an individual i is randomly chosen from the population. Secondly, he accumulates the payoff P_i by playing PDGs with all his neighbors. Thirdly, the individual i selects one neighbor j from his neighbors randomly. And then j accumulates his payoff P_j in the same way as i. Fourthly, individual i updates his strategy s_i by adopting his neighbor j's strategy s_j with the probability

$$\begin{equation} W(s_{j}\leftarrow s_{i})=\frac{1}{1+\exp[(P'_{i}-P_{j})/K]}, \end{equation} \tag{ 4 }$$

where $P'_{i}$ is calculated by eq. (1) and $K=0.1$ denotes the amplitude of noise that quantifies the uncertainty of strategy adoptions. To be noted, for the model with time-varied confidence level, individual i updates his confidence level before the strategy imitation, while for the static confidence level model, $\alpha_i$ does not change.

We study our model by using Monte Carlo simulations. In order to ensure that each individual has one chance on average to be chosen in one time step, one full Monte Carlo step (MCS) includes N elementary procedures described above. All the data in the results are obtained by averaging over the last 1000 MCSs of the whole 20000–50000 time steps and 50 realizations with random initial conditions.

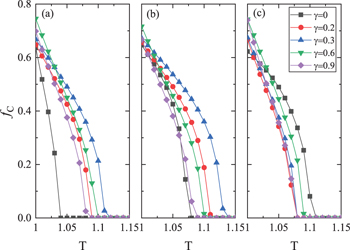
Let us start from the model with static confidence level. We present the frequency of cooperation f_C as a function of the temptation to defection T at different γ and $\alpha_{0}$ in fig. 1. One can find that, f_C decreases with the increase of T for these γ and $\alpha_{0}$. When $\gamma=0$, all individuals in the population have the same confidence level. Comparing the results for $\gamma=0$ (shown by the black curves) in figs. 1(b) and (c) with that in fig. 1(a), one can see that cooperation is significantly promoted by both underconfident and overconfident individuals, which is consistent with the results reported in [38]. Then, we focus on how cooperation is affected by different γ and $\alpha_{0}$. As shown in fig. 1(a) for $\alpha_0=0$, the results for $\gamma\neq0$ are obviously higher than that for $\gamma=0$. Moreover, we can observe that f_C changes non-monotonously with the increase of γ. In particular, for some given T, there exists an optimal γ which is most favorable for cooperation. For $\alpha_0=0.1$ and –0.1 shown by figs. 1(b) and (c), f_C also exhibits non-monotonic behaviors when γ varies. Furthermore, it is worth noting that, for $\alpha_0=0.1$, non-zero γ could lead to higher f_C than $\gamma=0$ in most parameter cases we have considered while, for $\alpha_0=-0.1$, non-zero γ lead to lower f_C than $\gamma=0$. This suggests that, heterogeneous confidence in population with more overconfident individuals facilitates the evolution of cooperation in comparison with population with homogeneous confidence.

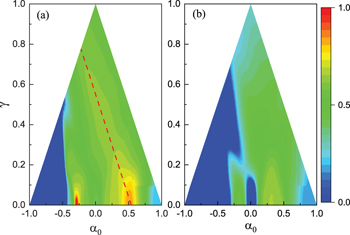
Zoom In Zoom Out Reset image size

To obtain a complete view of the effects of γ and $\alpha_{0}$ on cooperation in the static confidence level model, we present the contour plots for f_C in the plane $\alpha_{0}\text{-}\gamma$ in fig. 2. To be noted, since α is limited to $[-1, 1]$, the ranges of $\alpha_{0}$ and γ are mutually constrained and thus the parameter plane is triangular. At $\gamma=0$, when $\alpha_{0}$ varies from zero towards –1 and 1, f_C first increases and then decreases twice. Two maximized f_C could be obtained at the optimal values of $\alpha_{0}$, that is, $\alpha_{0}=-0.29$ and 0.53, respectively. The double optimization of f_C with $\alpha_{0}$ is kept provided that the dispersion of the confidence level γ is not too strong. When γ is non-zero, we can find that f_C could be locally maximized when $\alpha_0+\gamma$ equals certain values. As an example, when $\alpha_0+\gamma=0.53$, which is marked by a dashed line in fig. 2(a), f_C is significantly higher than that obtained at both sides of the line. Along this line, increasing γ degrades the cooperation level. We show the result for a larger T in fig. 2(b). Similar optimization of f_C could be found, except it is not obvious as that in fig. 2(a) because of overall decline of f_C .

Zoom In Zoom Out Reset image size

To understand the above results, it is instructive to examine the strategy configurations in the population. When the confidence level is introduced into the model, cooperation might be promoted by overconfident cooperators and underconfident defectors. Both of them bring advantages to cooperators in payoffs for strategy updating by raising the probability for converting defectors to cooperators. Given that the strategy alternation occurs only between two neighboring individuals with different strategies, we focus on a pair of neighboring individuals with opposite strategies, that is, a cooperator-defector (CD) pair. Here, there are two possible cases to promote cooperation: strengthening C by $\alpha>0$ and weakening D by $\alpha<0$. Assume that the focal cooperator has N_cc cooperator neighbors and the defector N_cd cooperator neighbors. For $\alpha>0$, the specific condition for which an overconfident cooperator has an advantage in payoff over a defector is $N_{cc}(1+\alpha)R>N_{cd}T$ (strengthening C). Contrarily, for $\alpha<0$, a cooperator can exceed an underconfident defector when $N_{cc}R>N_{cd}(1+\alpha)T$ (weakening D). For the focal pair, N_cc could be 0, 1, 2 or 3, and N_cd could be 1, 2, 3 or 4. Thus, there are 16 possible strategy configurations. The configurations which meet one of the two former inequalities can play roles in improving cooperation. For example, when the game parameter $T=1.02$, for the configuration of $N_{cc}=2$ and $N_{cd}=3$, representing a typical configuration in which a defector is invading cooperators, $\alpha>0.53$ makes the inequality set up. From fig. 2(a), we can observe that, at $\gamma=0$, $\alpha_0=0.53$ exactly corresponds to the optimal value which leads to a maximum f_C . Once $\gamma\neq 0$ when the confidence level becomes heterogeneous and α biases from the center with the half-width γ, the condition turns into $\alpha_0+\gamma>0.53$ to satisfy the inequality. In contrast, cooperation might also be impeded by underconfident cooperators (weakening C by $\alpha<0$) and overconfident defectors (strengthening D by $\alpha>0$). The specific conditions are $N_{cc}(1+\alpha)R<N_{cd}T$ and $N_{cc}R<N_{cd}(1+\alpha)T$, respectively. For example, at $T=1.02$ and $\gamma=0$, $\alpha_0<-0.32$ results in a relatively higher probability for cooperators to alter their strategy in the configuration of $N_{cc}=3$ and $N_{cd}=2$. To be mentioned, the boundaries between the parameter regions for promoting cooperation and those for impeding cooperation are not quite distinct, because the final f_C is generally the outcome of all strategy alternations occurring in various strategy configurations. The fractions of the strategy configurations critically affect the final outcome. Therefore, only when the quantities of some strategy configurations are considerably large, their effects can be manifest.

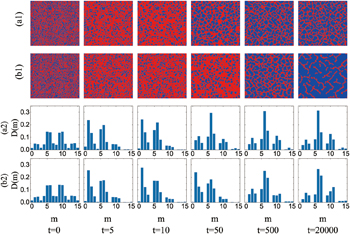
To further verify the above explanations, we present the snapshots of the strategy distributions and the distributions of the 16 possible strategy configurations at several representative times in fig. 3. Two different α have been considered. One leads to a moderate cooperation level, and the other results in a quite high cooperation level. From the snapshots shown in figs. 3(a1) and (b1), we can see that, as time goes on, the boundaries between cooperators and defectors display many tilted branch-like structures. In particular, in the steady state at $\alpha_0=0.53$, defectors always coexist with cooperators only in the form of long tilted strips. By roughly analysing, we can see that such boundaries can be formed by several strategy configurations, and a typical one is $N_{cc}=2$ and $N_{cd}=2$. To further investigate the effects of different $\alpha_0$ from a micro-view, we calculate the frequencies of 16 possible strategy configurations for all the CD pairs in the population, which are denoted by D(m). m represents the index of strategy configuration. The results are shown in figs. 3(a2) and (b2) for two different α, respectively. When compared with the steady state for $\alpha_0=0.25$, there are more strategy configurations of $N_{cc}=3$, $N_{cd}=2$ (denoted by m = 7) and $N_{cc}=3$, $N_{cd}=3$ (denoted by m = 11), but less configurations of $N_{cc}=2$, $N_{cd}=3$ (denoted by m = 10) at $\alpha_0=0.53$. It is worth noting that $\alpha_0=0.53$ is exactly the critical point which leads to a relatively higher probability for defectors inverting the defection strategy in CD pairs with $N_{cc}=2$, $N_{cd}=3$. Therefore, the cooperators embedded in the CD pairs with $N_{cc}=2$, $N_{cd}=3$ get strengthened, which leads to the decrement of the configuration m = 10 and meanwhile the increment of other configurations such as m = 7 and m = 11. These transformations of strategy configurations eventually result in the optimization of cooperation at around $\alpha_0=0.53$ which has been shown in fig. 2(a).

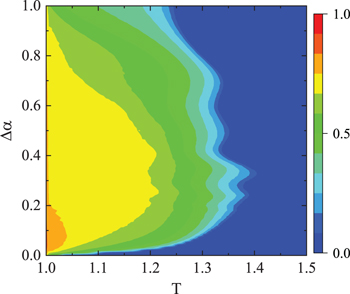
Zoom In Zoom Out Reset image size

Considering that the attributes of individuals usually change over time in real life, we next focus on the model with time-varied confidence level. Initially, we assign the confidence level $\alpha=0$ for the whole population, and then α of each individual coevolves with strategy during the evolution. The contour plot for f_C in the $T\text{-}\Delta \alpha$ plane is presented in fig. 4, in which $\Delta \alpha$ describes the possible increment of α in one elementary step. By comparing with fig. 1, we can find that the parameter region of T which supports the coexistence of cooperators and defectors expands to a larger parameter region when the confidence level coevolves with strategy. As fig. 1 has shown, for a relatively high T (for example, T > 1.14), cooperation goes extinct. In comparison, in fig. 4, the critical T for the extinction of cooperators increases significantly when an appropriate increment $\Delta \alpha$ is adopted in the coevolutionary dynamics. For example, when $\Delta \alpha=0.3$, the critical T can even extend to near 1.4. Furthermore, we can also find that, for a certain T within the range of supporting the coexistence of defectors and cooperators, there always exists an optimal $\Delta \alpha$ (denoted by $\Delta \alpha_{\textit{opt}}$), which leads f_C to the maximal level. Moreover, $\Delta \alpha_{\textit{opt}}$ changes with the variation of T. In particular, f_C reaches the highest value when $\Delta \alpha$ is around 0.1 at $T=1.03$, while $\Delta \alpha_{\textit{opt}}=0.3$ at $T=1.15$. In addition, to test the robustness of the findings, we simulate the coevolutionary model with different initial confidence levels, for example, randomly distributed α in the range of $[-0.5,0.5]$, $[-1,0]$, and $[0,1]$. Similar results of f_C in the $T\text{-}\Delta \alpha$ plane are obtained and the robustness against initial confidence level is confirmed.

Zoom In Zoom Out Reset image size

To further study how $\Delta \alpha$ affects cooperation during the evolution process, we present the distribution of α, denoted by $D(\alpha)$, for different $\Delta \alpha$ at several representative times in fig. 5. Initially, α for all individuals are set to be 0. In the early stage of the coevolutionary dynamics, $D(\alpha)$ is concentrated around 0 for small $\Delta \alpha$, whereas $D(\alpha)$ disperses towards two limits quickly for large $\Delta \alpha$. Furthermore, as shown in figs. 5(a) and (e), if cooperators cannot survive in the steady states and then defector neighbors cannot provide satisfactory payoffs for the defectors to reach their aspiration, α for the whole population are certain to decrease to –1. However, when a coexistent state can be reached (shown in figs. 5(b)–(d)), a large amount of individuals hold an extreme high or low α, and the distribution for the intermediate α displays a valley. It is worth noting that such a coevolutionary dynamics with an optimal $\Delta \alpha$ leads to a larger proportion of cooperators having higher α, when compared with other $\Delta \alpha$. This could be observed from $D(\alpha)$ for different $\Delta \alpha$ shown in fig. 5 and provides an explanation for the optimized f_C at $\Delta \alpha=0.25$. The fraction of cooperators in the individuals with $\alpha=1$ at $\Delta \alpha=0.25$ is higher than that for other $\Delta \alpha$. This provides payoff advantages to cooperators and then favors the evolution of cooperation.

Zoom In Zoom Out Reset image size

In this work, we propose a spatial prisoner's dilemma game in which the individuals might be underconfident, unbiased or overconfident, and we investigate the effects of heterogeneous confidence level on the evolution of cooperation. We consider two cases, static and time-varied confidence level. For the static confidence level model, we find that both underconfidence and overconfidence could promote cooperation, which is consistent with the finding reported in previous studies. More importantly, when the heterogeneous confidence levels are introduced into the model, the two parameters of the uniform distribution, the center $\alpha_0$ and the half-width γ, affect the cooperation level in a specific way. In particular, some values of $\alpha_0+\gamma$ could lead to the optimization of the cooperation level. We provide an analytic explanation from a micro-view based on the strategy configuration. In the time-varied confidence level model, we allow the confidence levels of individuals to coevolve with their strategies. We find that cooperation could be significantly improved by the coevolutionary dynamics. Moreover, for a given parameter T which supports the coexistence of cooperators and defectors, there exists an optimal increment $\Delta \alpha$ which leads to a maximum cooperation level. We study the distribution of α in the steady states and find some relationships between the evolution results of α and the final cooperation level in the population. We hope this work could provide a better understanding for the cooperation in a population in which people may hold heterogeneous confidence levels. The effects of individuals' attributes on cooperation could be further addressed in future research.

This work was supported by the National Natural Science Foundation of China under Grants No. 11805021 and No. 12005043.