User cooperation to mitigate the jamming in OFDMA networks

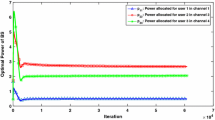
Abstract

In this paper, jamming and anti-jamming in a time slotted orthogonal frequency division multiple access (OFDMA) are investigated. The users of the network cooperate to mitigate the jamming effect. Interactions among the network users and the jammer are modeled by a mixed integer non-cooperative generalized game which is a NP-hard problem. To relax the problem, a new algorithm is proposed based on channel state information (CSI) to determine the transmission channels and the partners of users in the network. To solve the proposed game, an optimization problem is solved for each player considering the best response of the other player. Another generalized game is proposed to model the cooperation among users of the network. The latter game is transformed to an equivalent Quasi Variational Inequality (QVI). Then, a new gradient based algorithm is proposed by utilizing the Karush-Kuhn-Tucker (KKT) conditions to find the solution of the equivalent QVI. Then, solving the latter game and substituting the best related response, the solution of the former generalized game is also obtained. The convergence of the proposed algorithms, and the uniqueness related to the solution of the both generalized games are proven. Finally, the simulation results confirm the effectiveness of the proposed approach.

Appendices

Appendix A: Proof of Theorem 1

Proof

To prove, the convexity of the utility function, and also, the convexity of the constraint should be proved.

Lemma 1

The objective function of problem (28) is a concave function of $(p_{i,1}^{k},p_{i,2}^{k})$.

Proof

The Hessian matrix of objective function in (28) is as:

$$\begin{aligned} \left[ \begin{array}{cc} \left( \frac{h_{i\text {B}}^{k}}{p_{i,1}^{k}h_{i\text {B}}^{k}+j_{1}^{k}g_{0,\text {B}}^{k}+\sigma ^{k}}\right) ^{2} &{} 0 \\ 0 &{} -\left( \frac{h_{i\text {B}}^{k}}{p_{i,2}^{k}h_{i\text {B}}^{k}+j_{2}^{k}g_{0,\text {B}}^{k}+\sigma ^{k}}\right) ^{2} \end{array} \right] , \end{aligned}$$

(48)

which is negative definite, hence, the objective function of (28) is a concave function. $\square$

According to lemma 1, the utility function is convex. Also, since the constraint C1 is an affine function, it is also a convex function. Consequently, the problem (28) is a convex optimization problem. $\square$

Appendix B: Proof of Theorem 3

Proof

In the proposed scenario, the sets $T_{i}$ are composed from the constraint $\mathcal {C}2$. The sets are nonempty, closed and continuous. Since the constraint $\mathcal {C}2$ is affine in terms of $p_{i,1}^{k}$ and $\alpha _{i}$, it is convex. Thus, the sets $T_{i}$ satisfy the condition in the theorem 2. Additionally, for the utility function of players in the game $\tilde{\mathcal {G}}$, we have:

Lemma 2

The objective function of problem (32) is a concave function of $(p_{i,1}^{k},\alpha _{i})$.

Proof

The Hessian matrix of (32) with respect to $(p_{i,1}^{k},\alpha _{i})$ is:

$$\begin{aligned}&\left[ \begin{array}{cc} -\frac{\left( \frac{h_{i\text {B}}^{k}}{\sigma ^{k}+j_{1}^{k}g_{0,\text {B}}^{k} }+ \frac{\alpha _{m}h_{im}^{k}h_{m\text {B}}^{K}}{\alpha _{m}h_{m\text {B}}^{k}(J_{1}^{k})^2+\sigma ^{k}+j_{2}^{k}g_{0,\text {B}}^{k}} \right) ^{2}}{ \left( \frac{p_{i,1}^{k}h_{i\text {B}}^{k}}{\sigma ^{k}+j_{1}^{k}g_{0,\text {B}}^{k} }+ \frac{p_{i,1}^{k}\alpha _{m}h_{im}^{k}h_{m\text {B}}^{K}}{\alpha _{m}h_{m\text {B}}^{k}(J_{1}^{k})^2+\sigma ^{k}+j_{2}^{k}g_{0,\text {B}}^{k}} +1 \right) ^{2} } &{} 0 \\ 0 &{} \Gamma \end{array} \right] , \end{aligned}$$

(49)

$$\begin{aligned}&\begin{array}{rl} \Gamma =&{} - \frac{ \left( h_{\nu i}^{l}h_{i\text {B}}^{l}p_{\nu ,1}^{l}(\sigma ^{l}+g_{0,\text {B}}^{l}J_{2}^{l}) \right) ^{2}}{ \left( \frac{h_{\nu \text {B}}^{l}p_{\nu ,1}^{l}}{\sigma ^{l}+g_{0,\text {B}}^{l}J_{1}^{l}}+ \frac{\alpha _{i}h_{\nu i}^{l}h_{i\text {B}}^{l}p_{\nu ,1}^{l}}{ \sigma ^{l}+g_{0,\text {B}}^{l}J_{2}^{l}+\sigma ^{l}\alpha _{i}h_{i\text {B}}^{l}+ \alpha _{i}h_{i\text {B}}^{l}g_{0,i}^{l}J_{1}^{l} +1 } \right) ^{2} \left( \sigma ^{l}+g_{0,\text {B}}^{l}J_{2}^{l}+\sigma ^{l}\alpha _{i}h_{i\text {B}}^{l}+ \alpha _{i}h_{i\text {B}}^{l}g_{0,i}^{l}J_{1}^{l}\right) ^{4} } - \\ &{} \frac{ 2(h_{\nu i}^{l})^{2}h_{i\text {B}}^{l}p_{\nu ,1}^{l}\left( \sigma ^{l}+g_{0,\text {B}}^{l}J_{2}^{l}\right) \left( \sigma ^{l}+g_{0,i}^{l}J_{1}^{l}\right) }{ \frac{h_{\nu \text {B}}^{l}p_{\nu ,1}^{l}}{\sigma ^{l}+g_{0,\text {B}}^{l}J_{1}^{l}}+ \frac{\alpha _{i}h_{\nu i}^{l}h_{i\text {B}}^{l}p_{\nu ,1}^{l}}{ \sigma ^{l}+g_{0,\text {B}}^{l}J_{2}^{l}+\sigma ^{l}\alpha _{i}h_{i\text {B}}^{l}+ \alpha _{i}h_{i\text {B}}^{l}g_{0,i}^{l}J_{1}^{l} +1 } \left( \sigma ^{l}+g_{0,\text {B}}^{l}J_{2}^{l}+\sigma ^{l}\alpha _{i}h_{i\text {B}}^{l}+ \alpha _{i}h_{i\text {B}}^{l}g_{0,i}^{l}J_{1}^{l}\right) ^{3}}, \end{array} \end{aligned}$$

(50)

which is negative definite. Thus, the problem is concave. $\square$

Since the utility function of all players are convex, and Also, quasi-convex, the conditions of Theorem 2 are fulfilled. It leads that the generalized game $\tilde{\mathcal {G}}$ has a generalized Nash equilibrium. $\square$

Appendix C: Proof of Theorem 5

Proof

To prove the convexity of the jammer problem, it is proven that the objective function and the constraint function are convex.

Lemma 3

The objective function of problem (21) is a convex function of $(j_{1}^{k},j_{2}^{k})$.

Proof

The Hessian of (21) with respect to $(j_{1}^{k},j_{2}^{k})$ is:

$$\begin{aligned} \left[ \begin{array}{cc} \frac{(g_{0,\text {B}}^{k})^{2}h_{1}^{k}p_{1}^{k}(2\sigma +2g_{0,\text {B}}^{k}j_{1}^{k}+h_{1}^{k}p_{1}^{k})}{(\sigma +j_{1}^{k}g_{0,\text {B}}^{k})^{2}(\sigma +j_{1}^{k}g_{0,\text {B}}^{k}+h_{1}^{k}p_{1}^{k})^{2}} &{} 0 \\ 0 &{} \frac{(g_{0,\text {B}}^{k})^{2}h_{2}^{k}p_{2}^{k}(2\sigma +2g_{0,\text {B}}^{k}j_{2}^{k}+h_{2}^{k}p_{2}^{k})}{(\sigma +j_{2}^{k}g_{0,\text {B}}^{k})^{2}(\sigma +j_{2}^{k}g_{0,\text {B}}^{k}+h_{2}^{k}p_{2}^{k})^{2}} \end{array} \right] , \end{aligned}$$

(51)

which is positive definite, hence, the objective function of (21) is a convex one. $\square$

Since the objective function of the jammer is convex, and the constraint $\mathcal {C}3$ is affine, the jammer problem is a convex optimization problem. $\square$

Appendix D: Proof of Theorem 7

Proof

To prove the theorem, consider the following definition and theorem.

Definition 3

The gradient of f is Lipschitz continuous with parameter $L > 0$ if [35]

$$\begin{aligned} \Vert \nabla f(x) -\nabla f(y) \Vert _{2} \le L \Vert x-y \Vert _{2} \quad \forall x,y \in \text {dom}_{f}. \end{aligned}$$

(52)

Theorem 8

To solve (46), the gradient method converges when the utility functions satisfy the following conditions:

• Utility function is convex and differentiable with its domain.

• $\nabla u_{i}$ is Lipschitz continuous with parameter $L \ge 0$.

• Optimal value is finite and attained.

Proof

Please refer to [34]. $\square$

Since the utility functions of both the users and the jammer are logarithmic functions, the related convexity and differentiability are clear. Additionally, the optimal value for both players are finite due to their power constraints and logarithmic form of the utility function. Therefore, if the gradient of utility function is Lipschitz continuous with parameter L, the proposed problem satisfies the above conditions. Thus, the convergence of the proposed algorithm is proven.

Based on Sect. 4, the utility function of all users of the network and the utility of the jammer are the sum of two logarithm functions that is as the logarithm of the product of arguments, which is a logarithm function. As it is proven in the lemma 4, the logarithm function is a gradient Lipschitz function. Note that, in the lemma 4, the proof holds when the argument of the logarithm is in $(1,\infty )$, which is satisfied here. Thus, the utility function of the players are gradient Lipschitz and the proposed algorithm converges. $\square$

Lemma 4

The logarithm function $\log (x)$ is a gradient Lipschitz function.

Proof

Let $d,f \in (1,\infty )$. Based on the mean value theorem, there is a point e such that:

$$\begin{aligned} \frac{1}{d}-\frac{1}{f}=\frac{1}{e}(d-f). \end{aligned}$$

(53)

Hence, we have:

$$\begin{aligned} |\frac{1}{d}-\frac{1}{f}| \le \sup _{e \ge 1} \frac{1}{e} |d-f| \le |d-f|. \end{aligned}$$

(54)

Therefore, the gradient of the $log(\cdot )$ is a Lipschitz function, and then, the $log(\cdot )$ is a gradient Lipschitz function. $\square$