The naturalness in the BLMSSM and B-LSSM

Abstract

In order to interpret the Higgs boson mass and its decays naturally, we hope to examine the BLMSSM and B-LSSM. In the both models, the right-handed neutrino superfields are introduced to better explain the neutrino mass problems. In this paper, we introduce the fine-tuning to acquire the physical Higgs boson mass. Besides, the method of $\chi ^2$ analyses will be adopted in the BLMSSM and B-LSSM to fit the experimental data. Therefore, we can obtain the reasonable theoretical values of the Higgs decays and muon $g-2$ that are in accordance with the experimental results respectively in the BLMSSM and B-LSSM.

1 introduction

The standard model (SM) has been confirmed by many experiments. Especially, the Large Hadron Collider (LHC) have announced a 125.10 GeV SM-like Higgs boson [1,2,3], whose discovery is a great triumph for the SM. Up to now, there are still some problems that can not be naturally explained by SM, such as the masses of neutrinos, the hierarchy problem, the dark matter(DM) candidates, flavor physics and CP-violating problems$\ldots$. Therefore, it is necessary to extend SM, and it happens that Minimal Supersymmetric SM (MSSM) is a highly motivated one [4,5,6,7].

As we know, the mass of the physical Higgs boson in the MSSM at tree level is less than the Z boson mass, and it can be lifted by the top quark-stop quark loop corrections [8,9,10,11,12]. $\delta m_{H_u}^2$ represents one loop radiative correction to the soft supersymmetry breaking mass square of $H_u$: $\delta m_{H_u}^2\simeq -\frac{3y_t^2}{4\pi ^2}m_{\tilde{t}}^2\ln \frac{\Lambda }{m_{\tilde{t}}}\sim m_{\tilde{t}}^2$. Here, $\Lambda$ represents the corresponding new physics (NP) scale while $m_{\tilde{t}}$ corresponds to the scale of the stop quark mass. So, $\delta m_{H_u}^2$ receives a large contribution due to the stop quark masses around TeV region[11,12,13,14,15]. The mass square of physical Higgs boson is deduced as $m_{h^0}^2=-\frac{\bar{m}^2_{h^0}}{2}$ with $\bar{m}^2_{h^0}\simeq |\mu |^2+m_{H_u}^2+\delta m_{H_u}^2$. Therefore, we need to introduce the fine-tuning to obtain relatively light Higgs boson mass, which can be easily accommodated in the MSSM through a certain degree of cancellation between the SUSY parameters. However, MSSM can not explain the existence of the neutrino masses well, which motivates the physicists to study the new model beyond MSSM. Actually, we hope to explain the above problem naturally in the BLMSSM [16,17,18,19,20,21] and B-LSSM [22,23,24,25,26].

The reason why we discuss the BLMSSM is that the baryon(B) and lepton(L) numbers are local gauge symmetries spontaneously broken at the TeV scale. Not only that, broken baryon number can naturally explain the origin of the matter-antimatter asymmetry in the universe. While broken lepton number can explain the neutrino oscillation experiment well by heavy majorana neutrinos contained in the seesaw mechanism [16,17,18,19,20]. Additionally, there is a natural suppression of flavour violation in the quark and leptonic sectors since the gauge symmetries and particle content forbid tree level flavor changing neutral currents involving the quarks or charged leptons [16, 17, 19, 20].

Meanwhile, we also study the B-LSSM whose gauge symmetry group $SU(3)_C\otimes {SU(2)_L}\otimes {U(1)_Y}\otimes {U(1)_{B-L}}$ is introduced with B representing baryon number and L standing for lepton number. Besides, the invariance under $U(1)_{B-L}$ gauge group imposes the R-parity conservation which is assumed in the MSSM to avoid proton decay [27]. In the B-LSSM, due to the introduction of the right-handed neutrino superfields, we can realize type I seesaw mechanism. Thus, B-LSSM provides an elegant solution for the existence and smallness of the light left-handed neutrino masses. Furthermore, additional parameter space in the B-LSSM is released from the LEP, Tevatron and LHC constraints through the additional singlet Higgs states and right-handed (s)neutrinos. It alleviates the hierarchy problem of the MSSM [28]. Other than this, the model can also provide much more DM candidates comparing that in the MSSM [29,30,31,32].

In this paper, we shall both study the natural and realistic BLMSSM and B-LSSM by considering the Higgs masses, Higgs decays and muon anomalous magnetic dipole moment(MDM). We first introduce the corresponding characteristics for BLMSSM and B-LSSM and their fine-tuning in Sect. 2. Meanwhile, we derive the concrete theoretical expressions of Higgs decays and muon MDM in both BLMSSM and B-LSSM in Sect. 3. Considering the $\chi ^2$ analyses, the numerical results will be further illustrated in Sect. 4 to satisfy the phenomenological constraints and the relevant experimental data. Last but not least, we summarize the conclusion in Sect. 5. In appendix A, B and C, we give out the corresponding form factors and couplings used in this paper. Appendix D shows the best fit points for the BLMSSM and B-LSSM particles.

2 The BLMSSM and B-LSSM

At present, DM can be both scalar particles and fermions. The lightest one of left handed sneutrinos in MSSM as a potential DM candidate is excluded by direct LEP searches and cosmological observations due to its large interactions with the Z boson. So the lightest neutralino will be the only viable DM candidate in the MSSM. Besides, the neutrino collision experiment can not be explained well in the MSSM. Not only that, MSSM can not explain the matter-antimatter asymmetry. LHC possesses very strict restrictions on the parameter space of MSSM, which may be excluded by the experiment in the near future. Therefore, we need to extend the MSSM and BLMSSM(B-LSSM) is a favorite choice.

2.1 The BLMSSM

Extending the local gauge group of the SM to $SU(3)_C\otimes {SU(2)_L}\otimes {U(1)_Y}\otimes {U(1)_B}\otimes {U(1)_L}$  [16, 19, 20], we obtain a supersymmetric model where baryon (B) and lepton (L) numbers are local gauge symmetries spontaneously broken at the TeV scale(BLMSSM). Since the new extra fermions have different B and L quantum numbers compared with the quarks and leptons in the first three generations, it is easy to arrange that there are no flavour changing neutral currents at tree level. BLMSSM provides more CP violating phases and flavour violation source. In order to cancel the B and L anomalies, vector-like families are needed, which are $\hat{Q}_4, \hat{U}_4^c, \hat{D}_4^c, \hat{L}_4, \hat{E}_4^c, \hat{N}_4^c$ and $\hat{Q}_5^c, \hat{U}_5, \hat{D}_5, \hat{L}_5^c, \hat{E}_5, \hat{N}_5$. Correspondingly, Higgs superfields $\hat{\Phi }_B$ and $\hat{\varphi }_B$ acquire nonzero vacuum expectation values (VEVs) to break baryon number spontaneously, as well as $\hat{\Phi }_L$ and $\hat{\varphi }_L$ are introduced to break lepton number spontaneously, so the matter-antimatter asymmetry and neutrino mass can be well explained. Other than this, in order to make exotic quarks unstable, the model also introduces superfields $\hat{X}$ and $\hat{X}'$. $\hat{X}$ and $\hat{X}'$ mix together, and the lightest mass eigenstates of X and $\tilde{X}$ can be DM candidates. The lightest sneutrino and neutralino can also be DM candidates.

The superpotential of the BLMSSM is given by [33]

$$\begin{aligned} \mathcal{W}_{BL}= & {} \mathcal{W}_{MSSM}+\mathcal{W}_{B}+\mathcal{W}_{L}+\mathcal{W}_{X}\;, \nonumber \\ \mathcal{W}_{B}= & {} \lambda _{Q}\hat{Q}_{4}\hat{Q}_{5}^c\hat{\Phi }_{B}+\lambda _{U}\hat{U}_{4}^c\hat{U}_{5} \hat{\varphi }_{B}\nonumber \\&+\lambda _{D}\hat{D}_{4}^c\hat{D}_{5}\hat{\varphi }_{B}+\mu _{B}\hat{\Phi }_{B}\hat{\varphi }_{B} \nonumber \\&+Y_{{u_4}}\hat{Q}_{4}\hat{H}_{u}\hat{U}_{4}^c+Y_{{d_4}}\hat{Q}_{4}\hat{H}_{d}\hat{D}_{4}^c\nonumber \\&+Y_{{u_5}}\hat{Q}_{5}^c\hat{H}_{d}\hat{U}_{5}+Y_{{d_5}}\hat{Q}_{5}^c\hat{H}_{u}\hat{D}_{5}, \nonumber \\ \mathcal{W}_{L}= & {} Y_{{e_4}}\hat{L}_{4}\hat{H}_{d}\hat{E}_{4}^c+Y_{{\nu _4}}\hat{L}_{4}\hat{H}_{u}\hat{N}_{4}^c\nonumber \\&+Y_{{e_5}}\hat{L}_{5}^c\hat{H}_{u}\hat{E}_{5}+Y_{{\nu _5}}\hat{L}_{5}^c\hat{H}_{d}\hat{N}_{5} \nonumber \\&+Y_{\nu }\hat{L}\hat{H}_{u}\hat{N}^c+\lambda _{{N^c}}\hat{N}^c\hat{N}^c\hat{\varphi }_{L} +\mu _{L}\hat{\Phi }_{L}\hat{\varphi }_{L}, \nonumber \\ \mathcal{W}_{X}= & {} \lambda _1\hat{Q}\hat{Q}_{5}^c\hat{X}+\lambda _2\hat{U}^c\hat{U}_{5}\hat{X}^\prime \nonumber \\&+\lambda _3\hat{D}^c\hat{D}_{5}\hat{X}^\prime +\mu _{X}\hat{X}\hat{X}^\prime . \end{aligned}$$

(1)

where $\mathcal{W}_{MSSM}$ represents the MSSM superpotential. $\lambda _{Q},\lambda _{U}...$, $Y_{{u_4}},Y_{{d_4}}...$ and $\mu _{B},\mu _{L},\mu _{X}$ are the Yukawa couplings presented in the BLMSSM superpotential. The soft breaking terms in the BLMSSM have been deduced in Refs. [33, 34], which not only introduce the squark, slepton and Higgs soft masses $m_{{\tilde{L}_4}}^2,m_{{\tilde{Q}_4}}^2,m_{{\Phi _{B}}}^2...$, but also consider other parameters, such as $m_{B},m_{L}...$, $A_{{u_4}},A_{{BQ}}...$, $B_{B},B_{L}...$ and $\tan \beta ,\tan \beta _B...$. In our numerical calculation, we adopt the following assumption:

$$\begin{aligned} m_{{\tilde{Q}_1}}= & {} m_{{\tilde{Q}_2}}=m_{{\tilde{U}_1}}=m_{{\tilde{U}_2}}=m_{{\tilde{D}_1}}\nonumber \\= & {} m_{{\tilde{D}_2}} =m_{{\tilde{Q}_4}}=m_{{\tilde{U}_4}}=m_{{\tilde{D}_4}}\nonumber \\= & {} m_{{\tilde{Q}_5}}=m_{{\tilde{U}_5}}=m_{{\tilde{D}_5}}=m_{{\tilde{L}_4}}\nonumber \\= & {} m_{{\tilde{N}_4}}=m_{{\tilde{E}_4}} =m_{{\tilde{L}_5}}=m_{{\tilde{N}_5}}=m_{{\tilde{E}_5}}\equiv m_0^{BL},\nonumber \\ m_{{\tilde{Q}_3}}= & {} m_{{\tilde{U}_3}}=m_{{\tilde{D}_3}}=m_{{\tilde{L}_i}}=m_{{\tilde{R}_i}}\nonumber \\= & {} m_{{\tilde{N}^c_i}}\equiv M_0^{BL},~~~~g_L=g_B\equiv g_{LB},\nonumber \\ A_l= & {} A_l'=A_u=A_u'=A_d=A_d'=A_{{u_4}}=A_{{u_5}}\nonumber \\= & {} A_{{d_4}}=A_{{d_5}}=A_{{\nu _4}}=A_{{e_4}}\nonumber \\= & {} A_{{\nu _5}}=A_{{e_5}}=A_{\nu }=A_{{\nu ^c}}=A_{{BQ}}=A_{{BU}}\nonumber \\= & {} A_{{BD}}\equiv A_0^{BL},m_1=m_2\equiv m_{12}^{BL}. \end{aligned}$$

(2)

2.2 The B-LSSM

In the B-LSSM, one enlarges the local gauge group of the SM to $SU(3)_C\otimes {SU(2)_L}\otimes {U(1)_Y}\otimes {U(1)_{B-L}}$, where the ${U(1)_{B-L}}$ can be spontaneously broken by the chiral singlet superfields $\hat{\eta }_1$ and $\hat{\eta }_2$. Comparing with MSSM, B-LSSM has more superfields with observable consequences at the LHC: $U(1)_{B-L}$ gauge field, righ-handed neutrinos, two $U(1)_{B-L}$ singlet Higgs superfields and their superpartners. The invariance under spontaneously broken $U(1)_{B-L}$ gauge group imposes the R-parity conservation which is assumed in the MSSM to avoid proton decay. Besides, the VEV of $\eta _1$ produces masses to the right-handed neutrinos. The righ-handed neutrinos and left-handed neutrinos mix together through $Y_{\nu ,ij}\hat{L}_i\hat{H}_2\hat{\nu }_j^c$. Then light neutrinos obtain tiny masses through see-saw mechanism. Therefore, the neutrino oscillation experiment can be well explained in the B-LSSM. There are mixing between Higgs doublets $H_u,\;H_d$ and $U(1)_{B-L}$ singlet Higgs superfields $\eta _1,\;\eta _2$, so the mass of the lightest CP-even Higgs will be increased at the tree level. Other than this, the model also provides the lightest right sneutrino as a DM candidate comparing that in the MSSM. The superpotential of the B-LSSM is given by

$$\begin{aligned} W_{B\!-\!L}\! \!=\!\!\mathcal{W}_{MSSM}\!\!-\! {\mu '} \hat{\eta }_1\hat{\eta }_2\!+\!Y_{x,ij}\hat{\nu }_i^c\hat{\eta }_1\hat{\nu }_j^c\!+\!Y_{\nu ,ij}\hat{L}_i\hat{H}_2\hat{\nu }_j^c,\qquad \end{aligned}$$

(3)

where i, j are generation indices, $Y_{x,ij}$ and $Y_{\nu ,ij}$ are the Yukawa couplings in the B-LSSM superpotential. The soft breaking terms presented in the B-LSSM are written as

$$\begin{aligned} \mathcal{L}_{{soft}}^{B-L}= & {} \mathcal{L}_{{soft}}^{MSSM}-m_{\tilde{\eta }_1}^2 |\tilde{\eta }_1|^2-m_{\tilde{\eta }_2}^2 |\tilde{\eta }_2|^2 - m_{\tilde{\nu },{i j}}^{2}(\tilde{\nu }^c_{{i}})^* \tilde{\nu }_{{j}}^c\nonumber \\&+\Big [-{M}_{B B'}\tilde{\lambda }_{B'}\tilde{\lambda }_{B}\nonumber \\&\qquad -\frac{1}{2}{M}_{B'}\tilde{\lambda }_{B'}\tilde{\lambda }_{B'}- B_{\mu '}\tilde{\eta }_1 \tilde{\eta }_2+ T_{\nu }^{i j}H_2 \tilde{\nu }^c_i \tilde{L}_j\nonumber \\&\qquad +T_{x}^{i j}\tilde{\eta }_1 \tilde{\nu }^c_i\tilde{\nu }^c_j+h.c.\Big ], \end{aligned}$$

(4)

where $\mathcal{L}_{{soft}}^{MSSM}$ represents the soft breaking terms of the MSSM and $m_{\tilde{\eta }_1}^2$, $m_{\tilde{\eta }_2}^2$, $m_{\tilde{\nu },{i j}}^{2}...$ are the concrete soft masses. In the B-LSSM, there are other parameters ${M}_{B B'}$, $M_{B'}$, $B_{\mu '}$, $T_{\nu }^{i j},T_{x}^{i j}...$ and $\tan \beta ,\tan \beta '...$. To facilitate numerical discussion, we adopt the following assumption:

$$\begin{aligned} m_{{{\tilde{q},11}}}= & {} m_{{{\tilde{q},22}}}=m_{{{\tilde{u},11}}}=m_{{{\tilde{u},22}}}\nonumber \\= & {} m_{{{\tilde{d},11}}}=m_{{{\tilde{d},22}}}\equiv m_0^{B-L},\nonumber \\ m_{{{\tilde{q},33}}}= & {} m_{{{\tilde{u},33}}}=m_{{{\tilde{d},33}}}=m_{{{\tilde{L},ii}}}=m_{{{\tilde{e},ii}}}\nonumber \\= & {} m_{{{\tilde{\nu },ii}}}\equiv M_0^{B-L},\nonumber \\ T_{e,ii}= & {} T_{x,ii}=T_{\nu ,ii}=T_{u,ii}=T_{d,ii}\nonumber \\\equiv & {} A_0^{B-L},M_1=M_2\equiv m_{12}^{B-L}. \end{aligned}$$

(5)

2.3 The fine-tuning measure

In general weak scale supersymmetric theories, the fine-tuning will be introduced more detail in the Higgs potential. In both the BLMSSM and B-LSSM, the physical Higgs boson $h^0$ is approximately a linear combination of $H_u$ and $H_d$. The effective potential related to $h^0$ can be approximately expressed as: $V=\bar{m}^2_{h^0}|h^0|^2+\frac{\lambda _h}{4}|h^0|^4$. Then the mass square of physical Higgs boson is deduced as $m_{h^0}^2=-\frac{\bar{m}^2_{h^0}}{2}$. In general, $\tan \beta \ge 2$, so $\bar{m}^2_{h^0}$ can be approximately written as $\bar{m}^2_{h^0}\simeq |\mu |^2+m_{H_u}^2+\delta m_{H_u}^2$, where $\mu$ is the supersymmetric mass between $H_u$ and $H_d$. $m_{H_u}^2$ represents the soft supersymmetry breaking mass square for $H_u$, while $\delta m_{H_u}^2$ represents one loop radiative correction to the soft supersymmetry breaking mass square of $H_u$:

$$\begin{aligned} \delta m_{H_u}^2\simeq -\frac{3}{8\pi ^2}y_t^2\Big (m_{\tilde{Q}_3}^2+m_{\tilde{U}_3^c}^2+|A_t|^2\Big )\ln \Big (\frac{\Lambda }{m_{\tilde{t}}}\Big ). \end{aligned}$$

(6)

Here, $y_t$ is top quark Yukawa coupling, $m_{\tilde{Q}_3}$ $m_{\tilde{U}_3}$ and $A_t$ represent the corresponding soft parameters, $\Lambda$ represents the NP scale while $m_{\tilde{t}}$ corresponds to the scale of the stop quark mass.

One needs a certain degree of cancellation between the SUSY parameters to obtain the observed value of $m_{h^0}^{exp}= 125.1$ GeV. To quantitatively evaluate the naturalness, we use the following fine-tuning measure [11, 35, 36]

$$\begin{aligned} \Delta _{FT}\equiv \left| \frac{2\delta m^2_{H_u}}{m_{h^0}^2}\right| . \end{aligned}$$

(7)

where $\delta m_{H_u}^2$ is determined by the $m_{\tilde{Q}_3}$, $m_{\tilde{U}_3}$ and $A_t$. Therefore, the larger $m_{\tilde{Q}_3}$, $m_{\tilde{U}_3}$ and $A_t$, the larger $\Delta _{FT}$ is. Besides, the fine-tuning parameter $\Delta _{FT}=100$ corresponds to $1\%$ fine-tuning. $m_{h^0}^2=-\frac{\bar{m}^2_{h^0}}{2}$ $(\mathrm{with}\;\bar{m}^2_{h^0}\simeq |\mu |^2+m_{H_u}^2+\delta m_{H_u}^2)$ indicates that various contributions meed to be finely tuned to cancel each other, so we hope that $|\mu |^2$, $m_{H_u}^2$ and $\delta m_{H_u}^2$ are relatively small, then the smaller $\Delta _{FT}$ will obtain the physical Higgs boson mass more naturally.

3 The Higgs decays and $(g-2)_{\mu }$ in the BLMSSM and B-LSSM

In the BLMSSM and B-LSSM, we respectively consider the radiative corrections from exotic fermions and corresponding supersymmetric partners to obtain the physical Higgs boson mass. The corrections to Higgs masses in the BLMSSM have been discussed specifically in Ref. [33], while the ones in the B-LSSM have been introduced concretely in Refs. [26, 37]. The corresponding parameter constraints in the BLMSSM and B-LSSM are considered respectively in this paper. Then the Higgs decays and $(g-2)_{\mu }$ will be taken over explicitly as follows.

3.1 The Higgs decays

The LHC produces the Higgs boson chiefly from the gluon fusion. Meanwhile, the leading order(LO) contributions for $h^0\rightarrow gg$ originate from the one-loop diagrams, which can be modified through virtual top quark in the SM. In the BLMSSM and B-LSSM, the LO contributions need to be added by the Higgs-new particle couplings, whose effects are significant. So the decay width of $h^0\rightarrow gg$ can be shown as [33, 38,39,40,41]

$$\begin{aligned} \Gamma _{{NP}}(h^0\rightarrow gg)= & {} {G_{F}\alpha _s^2m_{{h^0}}^3\over 64\sqrt{2}\pi ^3} \Big |\sum \limits _{q}g_{{h^0qq}}A_{1/2}(x_q) \nonumber \\&+\sum \limits _{\tilde{q}}g_{{h^0\tilde{q}\tilde{q}}}{m_{\mathrm{Z}}^2\over m_{{\tilde{q}}}^2}A_{0}(x_{{\tilde{q}}})\Big |^2\;, \end{aligned}$$

(8)

with $x_a=m_{{h^0}}^2/(4m_a^2)$. q and $\tilde{q}$ denote the concrete quarks and squarks in the BLMSSM and B-LSSM. The form factors $A_{1/2}(x)$, $A_0(x)$ and the following $A_1(x)$, F(x) are summarized in the appendix A. In the BLMSSM, the concrete expressions for $g_{{h^0qq}}$, $g_{{h^0\tilde{q}\tilde{q}}}$ and the ones for $g_{{h^0ff}}$, $g_{{h^0H^+H^-}}$, $g_{{h^0\chi _i^+\chi _i^-}}$, $g_{{h^0\tilde{f}\tilde{f}}}$, $g_{{h^0WW}}$, $g_{h^0ZZ}$ mentioned bellow have been discussed in Ref. [33]. The relevant expressions of $g_{{h^0qq}}^{B-L}$ in the B-LSSM are specifically discussed as

$$\begin{aligned} g^{B-L}_{h^0 u u}= & {} -\sum _{k=b=1}^{3}\sum _{j=a=1}^{3}\frac{v}{m_{u_j}} \Big [-\frac{1}{\sqrt{2}} \delta _{\alpha \beta } Y^*_{u,{a b}} U_{R,{j a}}^{u} U_{L,{k b}}^{u} Z_{{1 2}}^{H} \Big ], \nonumber \\ g^{B-L}_{h^0 d d}= & {} -\sum _{k=b=1}^{3}\sum _{j=a=1}^{3}\frac{v}{m_{d_j}}\Big [-\frac{1}{\sqrt{2}} \delta _{\alpha \beta } Y^*_{d,{a b}} U_{R,{j a}}^{d} U_{L,{k b}}^{d} Z_{{1 1}}^{H} \Big ].\nonumber \\ \end{aligned}$$

(9)

In order to save space, $g_{{h^0\tilde{q}\tilde{q}}}^{B-L}$ will be detailed in the following appendix B.

The LO contributions for decay $h^0\rightarrow \gamma \gamma$ also originate from one-loop diagrams. In the SM, the concrete contributions are mainly derived from top quark and charged gauge boson $W^{\pm }$. Due to the Higgs-new particle couplings in the BLMSSM and B-LSSM, the decay width of $h^0\rightarrow \gamma \gamma$ can be expressed as [33, 38,39,40,41,42,43]

$$\begin{aligned}&\Gamma _{{NP}}(h^0\rightarrow \gamma \gamma )\nonumber \\&\quad ={G_{F}\alpha ^2m_{{h^0}}^3\over 128\sqrt{2}\pi ^3} \Big |\sum \limits _fN_cQ_{f}^2g_{{h^0ff}}A_{1/2}(x_f)\nonumber \\&\qquad +\sum \limits _{\tilde{f}}N_cQ_{f}^2g_{{h^0\tilde{f}\tilde{f}}}{m_{ Z}^2\over m_{{\tilde{f}}}^2} A_{0}(x_{{\tilde{f}}}) \nonumber \\&\qquad +g_{{h^0H^+H^-}}{m_{\mathrm{Z}}^2\over m_{{H^\pm }}^2}A_0(x_{{H^\pm }})+g_{{h^0WW}}A_1(x_{\mathrm{W}})\nonumber \\&\qquad +\sum \limits _{i=1}^2g_{{h^0\chi _i^+\chi _i^-}}{m_{\mathrm{W}}\over m_{{\chi _i^{\pm }}}}A_{1/2}(x_{{\chi _i^{\pm }}}) \Big |^2\;, \end{aligned}$$

(10)

with

$$\begin{aligned}&g^{B-L}_{h^0 l l}=-\sum _{k=b=1}^{3}\sum _{j=a=1}^{3}\frac{v}{m_{l_j}}\Big [-\frac{1}{\sqrt{2}} Y^*_{e,{a b}} U_{R,{j a}}^{e} U_{L,{k b}}^{e} Z_{{1 1}}^{H} \Big ], \nonumber \\&g^{B-L}_{h^0WW}=\Big (\cos \beta Z_{{1 1}}^{H} + \sin \beta Z_{{1 2}}^{H} \Big ), \nonumber \\&g^{B-L}_{h^0\chi _i^+\chi _i^-}\!=\!-\sum _{k=i=1}^2\frac{v}{m_{\chi _i^{\pm }}}\left[ -\frac{1}{\sqrt{2}} g_2 \Big (U_{{k 1}} V_{{i 2}} Z_{{1 2}}^{H} \!+\! U_{{k 2}} V_{{i 1}} Z_{{1 1}}^{H} \Big )\right] .\nonumber \\ \end{aligned}$$

(11)

The couplings of $g_{{h^0\tilde{L}\tilde{L}}}^{B-L}$, $g_{{h^0H^+H^-}}^{B-L}$ and the one of $g_{h^0ZZ}^{B-L}$ presented as follows will also be summarized in the appendix B.

The decay widths for $h^0\rightarrow ZZ, WW$ are given by [44, 45]

$$\begin{aligned}&\Gamma (h^0\rightarrow WW)={3e^4m_{{h^0}}\over 512\pi ^3s_{ W}^4}|g_{h^0WW}|^2 F\left( {m_{_\mathrm{W}}\over m_{h^0}}\right) ,\;\nonumber \\&\Gamma (h^0\rightarrow ZZ)={e^4m_{{h^0}}\over 2048\pi ^3s_{W}^4c_{W}^4}|g_{h^0ZZ}|^2\nonumber \\&\quad \quad \quad \quad \qquad \qquad \Big (7-{40\over 3}s_{W}^2+{160\over 9}s_{W}^4\Big )F\left( {m_{Z}\over m_{_{h^0}}}\right) . \end{aligned}$$

(12)

With the Born approximation, the decay width of the physical Higgs into fermion pairs $h^0\rightarrow f\bar{f}$ is written as [46]

$$\begin{aligned}&\Gamma (h^0\rightarrow f\bar{f})=N_c{G_Fm_f^2m_{{h^0}}\over 4\sqrt{2}\pi }|g_{h^0ff}|^2 \left( 1-{4m_f^2\over m_{h^0}^2}\right) ^{3/2}.\;\nonumber \\ \end{aligned}$$

(13)

The signal strengths for the Higgs boson decay channels are quantified by the following ratios [47]

$$\begin{aligned}&\mu _{\gamma \gamma ,VV^*}^{ggF}=\frac{\sigma _{NP}(ggF)}{\sigma _{SM}(ggF)} \frac{BR_{NP}(h^0\rightarrow \gamma \gamma ,VV^*)}{BR_{SM}(h^0\rightarrow \gamma \gamma ,VV^*)},(V=Z,W),\nonumber \\&\quad \mu _{f\bar{f}}^{VBF}=\frac{\sigma _{NP}(VBF)}{\sigma _{SM}(VBF)} \frac{BR_{NP}(h^0\rightarrow f\bar{f})}{BR_{SM}(h^0\rightarrow f\bar{f})},(f=b,\tau ), \end{aligned}$$

(14)

where ggF and VBF stand for gluon-gluon fusion and vector boson fusion respectively. Meanwhile, $\mu _{\gamma \gamma ,VV^*}$ are mainly affected by gluon-gluon fusion and $\mu _{f\bar{f}}$ is more likely to be influenced by vector boson fusion. The Higgs production cross sections can be further simplified as $\frac{\sigma _{NP}(ggF)}{\sigma _{SM}(ggF)}\approx \frac{\Gamma _{NP}(h^0\rightarrow gg)}{\Gamma _{SM}(h^0\rightarrow gg)} ,\frac{\sigma _{NP}(VBF)}{\sigma _{SM}(VBF)}\approx \frac{\Gamma _{NP}(h^0\rightarrow VV^*)}{\Gamma _{SM}(h^0\rightarrow VV^*)}$. Therefore, the ratios of the signal strengths from the Higgs boson decay channels are reduced as

$$\begin{aligned} \mu _{\gamma \gamma }^{ggF}\approx & {} \frac{\Gamma _{NP}(h^0\rightarrow gg)}{\Gamma _{SM}(h^0\rightarrow gg)} \frac{\Gamma _{NP}(h^0\rightarrow \gamma \gamma )/\Gamma _{NP}^{h^0}}{\Gamma _{SM}(h^0\rightarrow \gamma \gamma )/\Gamma _{SM}^{h^0}}\nonumber \\= & {} \frac{\Gamma _{SM}^{h^0}}{\Gamma _{NP}^{h^0}}\frac{\Gamma _{NP}(h^0\rightarrow gg)}{\Gamma _{SM}(h^0\rightarrow gg)} \frac{\Gamma _{NP}(h^0\rightarrow \gamma \gamma )}{\Gamma _{SM}(h^0\rightarrow \gamma \gamma )},\nonumber \\ \mu _{VV^*}^{ggF}\approx & {} \frac{\Gamma _{NP}(h^0\rightarrow gg)}{\Gamma _{SM}(h^0\rightarrow gg)} \frac{\Gamma _{NP}(h^0\rightarrow VV^*)/\Gamma _{NP}^{h^0}}{\Gamma _{SM}(h^0\rightarrow VV^*)/\Gamma _{SM}^{h^0}} \nonumber \\= & {} \frac{\Gamma _{SM}^{h^0}}{\Gamma _{NP}^{h^0}}\frac{\Gamma _{NP}(h^0\rightarrow gg)}{\Gamma _{SM}(h^0\rightarrow gg)}|g_{h^0VV}|^2,(V=Z,W),\nonumber \\ \mu _{f\bar{f}}^{VBF}\approx & {} \frac{\Gamma _{NP}(h^0\rightarrow VV^*)}{\Gamma _{SM}(h^0\rightarrow VV^*)} \frac{\Gamma _{NP}(h^0\rightarrow f\bar{f})/\Gamma _{NP}^{h^0}}{\Gamma _{SM}(h^0\rightarrow f\bar{f})/\Gamma _{SM}^{h^0}}\nonumber \\= & {} \frac{\Gamma _{SM}^{h^0}}{\Gamma _{NP}^{h^0}}|g_{h^0VV}|^2|g_{h^0ff}|^2,(f=b,\tau ). \end{aligned}$$

(15)

Here, $\frac{\Gamma _{NP}(h^0\rightarrow VV^*)}{\Gamma _{SM}(h^0\rightarrow VV^*)}=|g_{h^0VV}|^2$ and $\frac{\Gamma _{NP}(h^0\rightarrow f\bar{f})}{\Gamma _{SM}(h^0\rightarrow f\bar{f})}=|g_{h^0ff}|^2$. $\Gamma _{NP}^{h^0}=\sum _{f}\Gamma _{NP}(h^0\rightarrow f\bar{f}) +\sum _{V}\Gamma _{NP}(h^0\rightarrow VV^*)+\Gamma _{NP}(h^0\rightarrow gg)+\Gamma _{NP}(h^0\rightarrow \gamma \gamma )$ represents the NP total decay width of physical Higg boson.

3.2 The $(g-2)_{\mu }$

The effective Lagrangian for the muon MDM can be actually summarized as follows

$$\begin{aligned}&\mathcal{L}_{MDM}={e\over 4m_{\mu }}\;a_{\mu }\;\bar{l}_{\mu }\sigma ^{\alpha \beta } l_{\mu }\;F_{{\alpha \beta }}, \end{aligned}$$

(16)

where $\sigma _{\alpha \beta }=i[\gamma _\alpha ,\gamma _\beta ]/2$, $F_{\alpha \beta }$ is the electromagnetic field strength. Other than this, $l_{\mu }$ denotes the muon fermion, $m_{\mu }$ represents the corresponding muon mass and $a_\mu$ is the muon MDM. Generally, we obtain the muon MDM through the effective Lagrangian method [7, 48, 49]

$$\begin{aligned}&a_\mu =\frac{4Q_fm_\mu ^2}{(4\pi )^2}\mathfrak {R}(C_2^++C_2^{-*}+C_6^+), \end{aligned}$$

(17)

where $Q_f=-1$, $C_{2,6}^{\pm }$ represent the Wilson coefficients of the corresponding operators $\mathcal {O}_{2,6}^{\mp }$

$$\begin{aligned} \mathcal {O}_2^{\mp }= & {} \frac{eQ_f}{(4\pi )^2}\overline{(i\mathcal {D}_{\mu }l_{\mu })}\gamma ^{\mu } F\cdot \sigma \omega _{\mp }l_{\mu },\nonumber \\&\mathcal {O}_6^{\mp }=\frac{eQ_fm_\mu }{(4\pi )^2}\bar{l}_{\mu }F\cdot \sigma \omega _{\mp }l_{\mu }, \end{aligned}$$

(18)

with $\mathcal {D}_{\mu }=\partial _{\mu }+ieA_{\mu }$ and $\omega _{\mp }=\frac{(1\mp \gamma _5)}{2}$. The BLMSSM and B-LSSM contributions to muon MDM originate from the one-loop triangle diagrams, which are shown in Fig.1. So the relevant one-loop corrections to muon MDM can be expressed as

$$\begin{aligned}&\Delta a_\mu ^{th}=a_\mu (a)+a_\mu (b). \end{aligned}$$

(19)

In the BLMSSM and B-LSSM, the muon MDM corresponding to Fig. 1a can be formulated as

$$\begin{aligned}&a_\mu (a)= -\sum _{F}\sum _{S}\Big [\mathfrak {R}[(\mathcal {A}_1)^I(\mathcal {A}_2)^{I*}] y_S\sqrt{y_Fy_{m_{\mu }}}\;\frac{\partial ^2 \mathcal {B}(y_F,y_S)}{\partial y_S^2} \nonumber \\&+\frac{1}{3}(|(\mathcal {A}_1)^I|^2+|(\mathcal {A}_2)^I|^2)y_Sy_{m_{\mu }} \frac{\partial \mathcal {B}_1(y_F,y_S)}{\partial y_S}\Big ], \end{aligned}$$

(20)

where $y_i$ denote $\frac{m_i^2}{\Lambda ^2}$. $\mathcal {B}(x,y),\;\mathcal {B}_1(x,y)$ are the one-loop functions and given out in appendix A. Similarly, the muon MDM for Fig. 1b is deduced as follows

$$\begin{aligned}&a_\mu (b)= \sum _{F}\sum _{S}\Big [-2\mathfrak {R}[(\mathcal {C}_1)^I(\mathcal {C}_2)^{I*}] \sqrt{y_Fy_{m_{\mu }}}\;\mathcal {B}_1(y_S,y_F) \nonumber \\&+\frac{1}{3}(|(\mathcal {C}_1)^I|^2+|(\mathcal {C}_2)^I|^2)y_Fy_{m_{\mu }} \frac{\partial \mathcal {B}_1(y_S,y_F)}{\partial y_F}\Big ].\nonumber \\ \end{aligned}$$

(21)

In the BLMSSM, the concrete expressions for $(\mathcal {A}_1)^I, (\mathcal {A}_2)^I,(\mathcal {C}_1)^I$ and $(\mathcal {C}_2)^I$ can be found in Ref. [50]. The corresponding expressions that present in the B-LSSM will be specifically discussed in the following appendix C.

Fig. 1

The one-loop diagrams affect $(g-2)_{\mu }$ in the BLMSSM and B-LSSM

4 $\chi ^2$ analyses for the numerical results

In this paper, we will consider the $\chi ^2$ analyses for the corresponding theoretical and experimental data in both BLMSSM and B-LSSM. In general, the expression for $\chi ^2$ can be simplified with $\xi$ data points as [51, 52]

$$\begin{aligned} \chi ^2=\sum _{\xi }\left( \frac{\mu _{\xi }^{th}-\mu _{\xi }^{exp}}{\delta _{\xi }}\right) ^2, \end{aligned}$$

(22)

in which the theoretical values obtained for our model $\mu _{\xi }^{th}$ are confronted with the experimental measurements $\mu _{\xi }^{exp}$, $\delta _{\xi }$ represent the errors which include both statistic and system. Then the the expression for $\chi ^2$ can be deduced specifically as

$$\begin{aligned}&\chi ^2=\left( \frac{\mu _{\gamma \gamma }^{ggF}-\mu _{\gamma \gamma }^{exp}}{\delta _{\mu _{\gamma \gamma }}}\right) ^2 +\left( \frac{\mu _{WW}^{ggF}-\mu _{WW}^{exp}}{\delta _{\mu _{WW}}}\right) ^2 +\left( \frac{\mu _{ZZ}^{ggF}-\mu _{ZZ}^{exp}}{\delta _{\mu _{ZZ}}}\right) ^2 \nonumber \\&\quad +\left( \frac{\mu _{b\bar{b}}^{VBF}-\mu _{b\bar{b}}^{exp}}{\delta _{\mu _{b\bar{b}}}}\right) ^2 +\left( \frac{\mu _{\tau \bar{\tau }}^{VBF}-\mu _{\tau \bar{\tau }}^{exp}}{\delta _{\mu _{\tau \bar{\tau }}}}\right) ^2 +\left( \frac{\Delta a_{\mu }^{th}-\Delta a_{\mu }}{\delta _{\Delta a_{\mu }}}\right) ^2.\nonumber \\ \end{aligned}$$

(23)

The theoretical results $\mu _{\gamma \gamma }^{ggF},\mu _{WW}^{ggF},\mu _{ZZ}^{ggF}\ldots$ have been given out in Sect. 3. The concrete experimental constraints of $\mu _{\gamma \gamma }^{exp},\mu _{WW}^{exp},\mu _{ZZ}^{exp}\ldots$ and $\delta _{\mu _{\gamma \gamma }},\delta _{\mu _{WW}},\delta _{\mu _{ZZ}}\ldots$ will be discussed as follows.

Fig. 2

The fitting results for MSSM and BLMSSM with the $\chi ^2$ analyses

Actually, combining the experimental results from ATLAS, CMS, CDF and D0 collaborations, we adopt the averages for Higgs decays from PDG [3], which are $\mu _{\gamma \gamma }^{exp}=1.11^{+0.10}_{-0.09}$ [53,54,55,56], $\mu _{WW}^{exp}=1.19\pm 0.12$ [53, 55, 56], $\mu _{ZZ}^{exp}=1.20^{+0.12}_{-0.11}$ [53, 55, 57], $\mu _{b\bar{b}}^{exp}=1.04\pm 0.13$ [53, 55, 56, 58, 59] and $\mu _{\tau \bar{\tau }}^{exp}=1.15^{+0.16}_{-0.15}$ [55, 56, 60, 61]. With an improvement in the measured precision of the gluon fusion production rate and the introductions of variants that can effectively couple the photon and gluon, the corresponding results will be more and more compatible with the SM prediction.

Furthermore, the muon MDM possesses $3.7\sigma$ deviation between experimental data and theoretical prediction: $\Delta a_{\mu } =a^{exp}_{\mu }-a^{SM}_{\mu }=(274\pm 73)\times 10^{-11}$ [62, 63]. $a^{exp}_{\mu }$ represents the experiment measurement, which is dominated at the Brookhaven National Laboratory (BNL) [62]. Currently, physicists try to improve the experimental estimate for $(g-2)_{\mu }$ at Fermilab (E989) [64] and the future J-PARC experiment [65]. The E989 experiment follows the principles of the BNL experiment to measure the precession frequency and the magnetic field of muon anomalies. Recently, Run-3 of the E989 experiment has been commenced and we expect for the Run-1 results in the near future.

Fig. 3

The fitting results for B-LSSM with the $\chi ^2$ analyses

Other than this, the Higgs boson mass has been measured in the $H\rightarrow ZZ\rightarrow 4l$ and in the $H \rightarrow \gamma \gamma$ decay channels with $\sqrt{s}$ = 7, 8 and 13 TeV pp collisions by the ATLAS and CMS experiments. The measurements are based on the latest calibrations of muons, electrons, and photons, and on improvements to the analysis techniques used to obtain the previous results from ATLAS Run 1 data. So we obtain the average of Higgs boson mass $m_{h^0}^{exp}=125.1\pm 0.14$ GeV [3, 66,67,68], which possesses strict constraints to the parameter space. In the following numerical discussion, we limit the theoretical Higgs boson mass to be in the range of $3\sigma$. As we know, the squark masses of the first two generations are restricted around or larger than 2 TeV, which are mainly determined by the parameter $m_0^{BL}$($m_0^{B-L}$), so we take $m_0^{BL}=m_0^{B-L}=2$ TeV in our numerical calculation. Besides, parameters $m_{12}^{BL}$($m_{12}^{B-L}$) and $\mu ^{BL}$($\mu ^{B-L}$) affect the masses of chargions and neutralinos. We also consider the constraints from the $b\rightarrow s\gamma$ process. The numerical analyses will be further discussed as follows.

First of all, we analyze the numerical results in the BLMSSM. We propose the $\Delta _{FT}^{BL}$ versus $\tan \beta _{BL}$, $\Delta _{FT}^{BL}$ versus $m_{\tilde{t}_1}^{BL}$, $\mu _{\gamma \gamma }^{ggF}$ versus $\mu _{VV}^{ggF}$ and $\mu _{ff}^{VBF}$ versus $\Delta a_{\mu }^{th}$ in (b1)-(b4) of Fig. 2. The black triangle shows the best-fitted benchmark point with minimal $(\chi ^{BL}_{min})^2$ =9.05121. The green, blue and black regions are respectively $90\%$, $95\%$ and $99\%$ confidence levels with $\chi ^2 < (\chi ^{BL}_{min})^2+ 9.24$, $(\chi ^{BL}_{min})^2 + 11.1$ and $(\chi ^{BL}_{min})^2+ 15.1$. It is clear to see that $\Delta _{FT}^{BL}$ changes from 20 to 45 while $\tan \beta _{BL}$ is in the region $8\sim 50$ within $90\%$ confidence level. $\Delta _{FT}^{BL}$ is mainly influenced by the stop quark mass $m_{\tilde{t}_1}^{BL}$ ($m_{\tilde{t}_2}^{BL}$), and the larger $m_{\tilde{t}_1}^{BL}$ ($m_{\tilde{t}_2}^{BL}$), the larger $\Delta _{FT}^{BL}$ is. Not only that, $\mu _{\gamma \gamma }^{ggF}$ is around $1.0\sim 1.25$, $\mu _{ff}^{VBF}$ is fixed in the range of 0.85 to 1.25, and $\mu _{VV}^{ggF}$ is around $1.18\sim 1.28$. $\Delta a_{\mu }^{th}$ is concentrated in $0.5\times 10^{-9}\sim 1.5\times 10^{-9}$. So $\mu _{\gamma \gamma }^{ggF}$, $\mu _{VV}^{ggF}$, $\mu _{ff}^{VBF}$ and $\Delta a_{\mu }^{th}$ which agree well with the concrete experimental results can naturally be explained in the BLMSSM.

Second, the B-LSSM numerical analyses are also taken over. We present the $g_{B}^{B-L}$ versus $g_{YB}^{B-L}$, $m_{\tilde{t}_1}^{B-L}$ versus $m_{\tilde{t}_2}^{B-L}$, $\Delta _{FT}^{B-L}$ versus $m_{\tilde{t}_1}^{B-L}$, $\Delta _{FT}^{B-L}$ versus $\tan \beta _{B-L}$, $M_0^{B-L}$ versus $\Delta a_{\mu }^{th}$, $\mu _{\gamma \gamma }^{ggF}$ versus $\mu _{WW}^{ggF}$, $\mu _{WW}^{ggF}$ versus $\mu _{ZZ}^{ggF}$ and $\mu _{ff}^{WBF}$ versus $\mu _{ff}^{ZBF}$ in Fig. 3. The black triangle shows the best-fitted benchmark point with minimal $(\chi ^{B-L}_{min})^2$ = 4.05073. The green, blue and black regions are respectively $90\%$, $95\%$ and $99\%$ confidence levels with $\chi ^2 < (\chi ^{B-L}_{min})^2+ 12.02$, $(\chi ^{B-L}_{min})^2 + 14.07$ and $(\chi ^{B-L}_{min})^2+ 18.49$. After limiting the theoretical Higgs boson mass within $3\sigma$ region, fine-tuning $\Delta _{FT}^{B-L}$ is larger than 20, $1.0\;\mathrm{TeV}\lesssim M_0^{B-L}\lesssim 2.3\;\mathrm{TeV}$ and $-0.2\lesssim g_{YB}^{B-L}<0$ with $90\%$ confidence level. Then the stop quark masses satisfy $1.2\;\mathrm{TeV}\lesssim m_{\tilde{t}_1}^{B-L}\simeq m_{\tilde{t}_2}^{B-L}\lesssim 2.5\;\mathrm{TeV}$. And $\Delta _{FT}^{B-L}$ will increase with the enlargement of stop quark masses. Other than these, the $\mu _{\gamma \gamma }^{ggF}$, $\mu _{WW}^{ggF}$ and $\mu _{ZZ}^{ggF}$ can be adjusted in the range of 1.0 to 1.1. The values of $\mu _{ff}^{WBF}$ and $\mu _{ff}^{ZBF}$ are approximately equal and tend to 1.02. And $\Delta a_{\mu }^{th}$ can be well corrected in the range of $0.5\times 10^{-9}$ to $5.0\times 10^{-9}$. Therefore, all of aforementioned results are in good agreement with the corresponding experimental results.

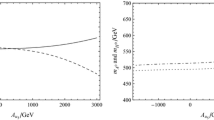
We consider the corresponding comparison of fine-tunings in the Higgs sector between MSSM and B-LSSM(BLMSSM). The models B-LSSM and BLMSSM are better for addressing fine-tunings in the Higgs sector than the MSSM. Considering the constraints of physical Higgs boson mass within $3\sigma$ region and stop quark mass being larger than 1.19 TeV, we obtain the numerical results of $\Delta _{FT}$ versus $m_{\tilde{t}_1}$ from Figs. 2(a3), (b2) and 3(3). We find the fine-tuning measure is $\Delta _{FT}\gtrsim 35(\lesssim 2.9\% \;\mathrm{fine\;tuning})$ according to $m_{\tilde{t}_1}\gtrsim 1.5$ TeV in the MSSM. However, the fine-tuning measure in the B-LSSM or in the BLMSSM is $\Delta _{FT}\gtrsim 19(\lesssim 5.2\% \;\mathrm{fine\;tuning})$ according to $m_{\tilde{t}_1}\gtrsim 1.2$ TeV. We prefer to small fine-tuning measure $\Delta _{FT}$, which can be realized in B-LSSM and BLMSSM. Therefore, the physical Higgs boson mass, which is mainly affected by stop quark masses, will be more naturally obtained in the B-LSSM and BLMSSM.

5 Conclusion

In this paper, we consider the corresponding comparison of fine-tunings in the Higgs sector between MSSM and B-LSSM(BLMSSM), which is strongly influenced by the stop quark masses. Considering the constraints of physical Higgs boson mass within $3\sigma$ region and stop quark mass being larger than 1.19 TeV, we find that the fine-tuning measure is $\Delta _{FT}\gtrsim 35(\lesssim 2.9\% \;\mathrm{fine\;tuning})$ in the MSSM but $\Delta _{FT}\gtrsim 19(\lesssim 5.2\% \;\mathrm{fine\;tuning})$ in the B-LSSM or in the BLMSSM. The smaller $\Delta _{FT}$ will obtain the physical Higgs boson mass more naturally. So the models B-LSSM and BLMSSM are better for addressing fine-tunings in the Higgs sector than the MSSM.

We adopt the method of $\chi ^2$ analyses in the BLMSSM and B-LSSM to calculate the Higgs decays and muon $g-2$. After scanning the parameter space, we point out some sensitive parameters in the BLMSSM and B-LSSM. In the BLMSSM, $\tan \beta _{BL}$ is limited in $8\sim 50$ with $90\%$ confidence level. As well as, we observe that $1.0\;\mathrm{TeV}\lesssim M_0^{B-L}\lesssim 2.3\;\mathrm{TeV}$ and $-0.2\lesssim g_{YB}^{B-L}<0$ in the B-LSSM with $90\%$ confidence level. Then, we can obtain the reasonable theoretical values for Higgs decays and muon $g-2$ respectively in the BLMSSM and B-LSSM, which are all in accordance with the experimental results. Other than this, the best-fitted benchmark points in the BLMSSM and B-LSSM shown in TABLE I give us the suitable particle mass spectrum, which satisfy the present SUSY constraints. Therefore, the BLMSSM and B-LSSM are both natural and realistic.

Appendices

Appendix A: The form factors

The form factors are defined as

$$\begin{aligned} A_{1/2}(x)= & {} 2\Big [x+(x-1)g(x)\Big ]/x^2,\;\;A_0(x)=-(x-g(x))/x^2\;,\nonumber \\ A_1(x)= & {} -\Big [2x^2+3x+3(2x-1)g(x)\Big ]/x^2,\nonumber \\ g(x)= & {} \left\{ \begin{array}{l}\arcsin ^2\sqrt{x},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x\le 1\\ -{1\over 4}\Big [\ln {1+\sqrt{1-1/x}\over 1-\sqrt{1-1/x}}-i\pi \Big ]^2,\;x>1\;,\end{array}\right. \nonumber \\ F(x)= & {} -(1-x^2)(\frac{47}{2}x^2-\frac{13}{2}+\frac{1}{x^2})-3(1-6x^2+4x^4)\ln x \nonumber \\&+\frac{3(1-8x^2+20x^4)}{\sqrt{4x^2-1}}\cos ^{-1}\Big (\frac{3x^2-1}{2x^3}\Big ), \end{aligned}$$

(A1)

$$\begin{aligned} \mathcal {B}(x,y)= & {} \frac{1}{16 \pi ^2}\Big (\frac{x \ln x}{y-x}+\frac{y \ln y}{x-y}\Big ),\nonumber \\&\mathcal {B}_1(x,y)=\left( \frac{\partial }{\partial y}+\frac{y}{2}\frac{\partial ^2 }{\partial y^2}\right) \mathcal {B}(x,y). \end{aligned}$$

(A2)

Appendix B: The expressions for Higgs decays in the B-LSSM

The concrete expressions that present in the B-LSSM are specifically discussed in the following(in this part $i=1$):

1. CP-even Higgs-up squark-up squark contribution

$$\begin{aligned} g^{B-L}_{h^0\tilde{U}\tilde{U}}= & {} \frac{v}{2mz^2}\sum _{j=k=1}^6\Big [\frac{1}{12} \delta _{\beta \gamma } \Big (6 \Big (\sqrt{2} \mu ^* \sum _{b=1}^{3}Z^{U,*}_{j b} \sum _{a=1}^{3}Y_{u,{a b}} Z_{{k 3 + a}}^{U} Z_{{i 1}}^{H} \nonumber \\&\quad +\sqrt{2} \mu \sum _{b=1}^{3}\sum _{a=1}^{3}Y^*_{u,{a b}} Z^{U,*}_{j 3 + a} Z_{{k b}}^{U} Z_{{i 1}}^{H}- \Big (\sqrt{2} \sum _{b=1}^{3}Z^{U,*}_{j b}\nonumber \\&\qquad \times \,\sum _{a=1}^{3}Z_{{k 3 + a}}^{U} T_{u,{a b}} +\sqrt{2} \sum _{b=1}^{3}\sum _{a=1}^{3}Z^{U,*}_{j 3 + a} T^*_{u,{a b}} Z_{{k b}}^{U} \nonumber \\&\quad +2 v_u \Big (\sum _{c=1}^{3}Z^{U,*}_{j 3 + c} \sum _{b=1}^{3}\sum _{a=1}^{3}Y^*_{u,{c a}} Y_{u,{b a}} Z_{{k 3 + b}}^{U} \nonumber \\&\quad + \sum _{c=1}^{3}\sum _{b=1}^{3}Z^{U,*}_{j b} \sum _{a=1}^{3}Y^*_{u,{a c}} Y_{u,{a b}} Z_{{k c}}^{U} \Big )\Big )Z_{{i 2}}^{H} \Big )\nonumber \\&\quad +\sum _{a=1}^{3}Z^{U,*}_{j 3 + a} Z_{{k 3 + a}}^{U} \Big (- \Big (4 g_{1}^{2} + g_{Y B} \Big (4 g_{Y B}\nonumber \\&\quad + g_{B}\Big )\Big )v_d Z_{{i 1}}^{H} +\Big (4 g_{1}^{2} + g_{Y B} \Big (4 g_{Y B} + g_{B}\Big )\Big )v_u Z_{{i 2}}^{H} \nonumber \\&\quad -2 \Big ( 4 g_{Y B} g_{B} + g_{B}^{2} \Big )\Big (-v_{\bar{\eta }} Z_{{i 4}}^{H} + v_{\eta } Z_{{i 3}}^{H} \Big )\Big )\nonumber \\&\quad +\sum _{a=1}^{3}Z^{U,*}_{j a} Z_{{k a}}^{U} \Big (\Big (-3 g_{2}^{2}\nonumber \\&\quad + g_{Y B} g_{B} + g_{1}^{2} + g_{Y B}^{2}\Big )v_d Z_{{i 1}}^{H} \nonumber \\&\quad - \Big (-3 g_{2}^{2} + g_{Y B} g_{B} + g_{1}^{2} + g_{Y B}^{2}\Big )v_u Z_{{i 2}}^{H} +2 \Big (g_{Y B} g_{B} \nonumber \\&\quad + g_{B}^{2}\Big )\Big (- v_{\bar{\eta }} Z_{{i 4}}^{H} + v_{\eta } Z_{{i 3}}^{H} \Big )\Big )\Big )\Big ]; \end{aligned}$$

(B1)

2. CP-even Higgs-down squark-down squark contribution

$$\begin{aligned} g^{B-L}_{h^0\tilde{D}\tilde{D}}= & {} \frac{v}{2mz^2}\sum _{j=k=1}^6\Big [\frac{1}{12} \delta _{\beta \gamma } \Big (-6 \Big (\sqrt{2} \sum _{b=1}^{3} Z^{D,*}_{j b} \sum _{a=1}^{3}Z_{{k 3 + a}}^{D} T_{d,{a b}} Z_{{i 1}}^{H} \nonumber \\&+\,\sqrt{2} \sum _{b=1}^{3}\sum _{a=1}^{3}Z^{D,*}_{j 3 + a} T^*_{d,{a b}} Z_{{k b}}^{D} Z_{{i 1}}^{H} \nonumber \\&+2 v_d \sum _{c=1}^{3}Z^{D,*}_{j 3 + c} \sum _{b=1}^{3} \sum _{a=1}^{3}Y^*_{d,{c a}} Y_{d,{b a}} Z_{{k 3 + b}}^{D} Z_{{i 1}}^{H} \nonumber \\&+\,2 v_d \sum _{c=1}^{3}\sum _{b=1}^{3}Z^{D,*}_{j b} \sum _{a=1}^{3}Y^*_{d,{a c}} Y_{d,{a b}} Z_{{k c}}^{D} Z_{{i 1}}^{H} \nonumber \\&- \sqrt{2} \mu ^* \sum _{b=1}^{3}Z^{D,*}_{j b} \sum _{a=1}^{3}Y_{d,{a b}} Z_{{k 3 + a}}^{D} Z_{{i 2}}^{H} \nonumber \\&- \sqrt{2} \mu \sum _{b=1}^{3}\sum _{a=1}^{3}Y^*_{d,{a b}} Z^{D,*}_{j 3 + a} Z_{{k b}}^{D} Z_{{i 2}}^{H} \Big )\nonumber \\&+\,\sum _{a=1}^{3}Z^{D,*}_{j 3 + a} Z_{{k 3 + a}}^{D} \Big (\Big (2 g_{1}^{2} + g_{Y B} \Big (2 g_{Y B} \nonumber \\&-\, g_{B} \Big )\Big )v_d Z_{{i 1}}^{H} +\Big (-2 g_{1}^{2} + g_{Y B} \Big (-2 g_{Y B} + g_{B}\Big )\Big )v_u Z_{{i 2}}^{H} \nonumber \\&+\,2 \Big (2 g_{Y B} g_{B} - g_{B}^{2}\Big ) \Big (- v_{\bar{\eta }} Z_{{i 4}}^{H} \nonumber \\&+\, v_{\eta } Z_{{i 3}}^{H} \Big )\Big )+\sum _{a=1}^{3}Z^{D,*}_{j a} Z_{{k a}}^{D} \Big (\Big (3 g_{2}^{2} + g_{Y B} g_{B} + g_{1}^{2} + g_{Y B}^{2}\Big )v_d Z_{{i 1}}^{H} \nonumber \\&- \Big (3 g_{2}^{2} + g_{Y B} g_{B} + g_{1}^{2} + g_{Y B}^{2}\Big )v_u Z_{{i 2}}^{H} \nonumber \\&+\,2 \Big ( g_{Y B} g_{B} + g_{B}^{2}\Big )\Big (- v_{\bar{\eta }} Z_{{i 4}}^{H} + v_{\eta } Z_{{i 3}}^{H} \Big )\Big )\Big )\Big ]; \end{aligned}$$

(B2)

3. CP-even Higgs-slepton-slepton contribution

$$\begin{aligned} g^{B-L}_{h^0\tilde{L}\tilde{L}}= & {} \frac{v}{2mz^2}\sum _{j=k=1}^6\Big [\frac{1}{4} \Big ( - 2 \Big (\sqrt{2} \sum _{b=1}^{3}Z^{E,*}_{j b} \sum _{a=1}^{3}Z_{{k 3 + a}}^{E} T_{e,{a b}} Z_{{i 1}}^{H} \nonumber \\&+ \sqrt{2} \sum _{b=1}^{3}\sum _{a=1}^{3}Z^{E,*}_{j 3 + a} T^*_{e,{a b}} Z_{{k b}}^{E} Z_{{i 1}}^{H} \nonumber \\&+2 v_d \sum _{c=1}^{3}Z^{E,*}_{j 3 + c} \sum _{b=1}^{3}\sum _{a=1}^{3}Y^*_{e,{c a}} Y_{e,{b a}} Z_{{k 3 + b}}^{E} Z_{{i 1}}^{H} \nonumber \\&+\,2 v_d \sum _{c=1}^{3}\sum _{b=1}^{3}Z^{E,*}_{j b} \sum _{a=1}^{3}Y^*_{e,{a c}} Y_{e,{a b}} Z_{{k c}}^{E} Z_{{i 1}}^{H} \nonumber \\&- \sqrt{2} \mu ^* \sum _{b=1}^{3}Z^{E,*}_{j b} \sum _{a=1}^{3}Y_{e,{a b}} Z_{{k 3 + a}}^{E} Z_{{i 2}}^{H} \nonumber \\&- \sqrt{2} \mu \sum _{b=1}^{3}\sum _{a=1}^{3}Y^*_{e,{a b}} Z^{E,*}_{j 3 + a} Z_{{k b}}^{E} Z_{{i 2}}^{H} \Big )\nonumber \\&+\,\sum _{a=1}^{3}Z^{E,*}_{j 3 + a} Z_{{k 3 + a}}^{E} \Big (\Big (2 g_{1}^{2} + g_{Y B} \Big (2 g_{Y B} + g_{B}\Big )\Big )v_d Z_{{i 1}}^{H} \nonumber \\&- \Big (2 g_{1}^{2} + g_{Y B} \Big (2 g_{Y B} + g_{B}\Big )\Big )v_u Z_{{i 2}}^{H} \nonumber \\&+\,2 \Big (2 g_{Y B} g_{B} + g_{B}^{2}\Big )\Big (- v_{\bar{\eta }} Z_{{i 4}}^{H} + v_{\eta } Z_{{i 3}}^{H} \Big )\Big )\nonumber \\&+\,\sum _{a=1}^{3}Z^{E,*}_{j a} Z_{{k a}}^{E} \Big (- \Big (- g_{2}^{2} + g_{Y B} g_{B} + g_{1}^{2} + g_{Y B}^{2}\Big )v_d Z_{{i 1}}^{H} \nonumber \\&+\,\Big (- g_{2}^{2} + g_{Y B} g_{B} + g_{1}^{2} + g_{Y B}^{2}\Big )v_u Z_{{i 2}}^{H}\nonumber \\&-\,2 \Big ( g_{Y B} g_{B} + g_{B}^{2}\Big )\Big (- v_{\bar{\eta }} Z_{{i 4}}^{H} + v_{\eta } Z_{{i 3}}^{H} \Big )\Big )\Big )\Big ]; \end{aligned}$$

(B3)

4. CP-even Higgs-charge Higgs-charge Higgs contribution

$$\begin{aligned}&g^{B-L}_{h^0H^{\pm }H^{\pm }}=\frac{v}{2mz^2}\sum _{j=k=1}^2\Big [\frac{1}{4} \Big (-2 g_{YB} g_{B}\Big (- v_{\bar{\eta }} Z_{{i 4}}^{H} + v_{\eta } Z_{{i 3}}^{H} \Big )\nonumber \\&\qquad \Big (Z_{{j 1}}^{+} Z_{{k 1}}^{+} - Z_{{j 2}}^{+} Z_{{k 2}}^{+} \Big )- Z_{{i 1}}^{H} \Big (Z_{{j 2}}^{+} \Big (- \Big (- g_{2}^{2} + g_{1}^{2} + g_{Y B}^{2}\Big )v_d Z_{{k 2}}^{+} \nonumber \\&\qquad +\, g_{2}^{2} v_u Z_{{k 1}}^{+} \Big )+Z_{{j 1}}^{+} \Big (\Big (g_{1}^{2} + g_{Y B}^{2} + g_{2}^{2}\Big )v_d Z_{{k 1}}^{+} + g_{2}^{2} v_u Z_{{k 2}}^{+} \Big )\Big )\nonumber \\&\qquad +\,Z_{{i 2}}^{H} \Big (Z_{{j 1}}^{+} \Big (\Big (- g_{2}^{2} + g_{1}^{2} + g_{Y B}^{2}\Big )v_u Z_{{k 1}}^{+} - g_{2}^{2} v_d Z_{{k 2}}^{+} \Big )\nonumber \\&\qquad - \,Z_{{j 2}}^{+} \Big (\Big (g_{1}^{2} + g_{Y B}^{2} + g_{2}^{2}\Big )v_u Z_{{k 2}}^{+} + g_{2}^{2} v_d Z_{{k 1}}^{+} \Big )\Big )\Big )\Big ]; \end{aligned}$$

(B4)

5. CP-even Higgs-Z boson-Z boson contribution

$$\begin{aligned} g^{B-L}_{h^0ZZ}= & {} \frac{v}{2mz^2}\Big [\frac{1}{2} \Big (v_d \Big (g_1 \cos {\Theta '}_W \sin \Theta _W \nonumber \\&+ g_2 \cos \Theta _W \cos {\Theta '}_W - g_{Y B} \sin {\Theta '}_W \Big )^{2} Z_{{i 1}}^{H} \nonumber \\&+\,v_u \Big (g_1 \cos {\Theta '}_W \sin \Theta _W \nonumber \\&+ g_2 \cos \Theta _W \cos {\Theta '}_W - g_{Y B} \sin {\Theta '}_W \Big )^{2} Z_{{i 2}}^{H} \nonumber \\&+\,4 \Big (- g_{B} \sin {\Theta '}_W \Big )^{2} \Big (v_{\bar{\eta }} Z_{{i 4}}^{H} + v_{\eta } Z_{{i 3}}^{H} \Big )\Big )\Big (g_{\sigma \mu }\Big )\Big ].\nonumber \\ \end{aligned}$$

(B5)

Appendix C: The expressions for muon $(g-2)$ in the B-LSSM

In the B-LSSM, the one-loop corrections for $(g-2)_{\mu }$ are mainly affected by slepton-neutralino, CP-odd sneutrino-chargino and CP-even sneutrino-chargino contributions. The concrete expressions for $(\mathcal {A}_1)^I,(\mathcal {A}_2)^I,(\mathcal {C}_1)^I$ and $(\mathcal {C}_2)^I$ that present in the B-LSSM can be specifically discussed as

$$\begin{aligned} (\mathcal {A}_1^{B-L})^I_{\tilde{L}\chi ^0}= & {} \frac{1}{2}\sum _{i=1}^7\sum _{k=1}^6\Big [\sqrt{2}g_1N_{i1}^*U_{L,22}^{e*}Z_{k2}^E\nonumber \\&+\sqrt{2}g_2N_{i2}^*2U_{L,22}^{e*}Z_{k2}^E +\sqrt{2}g_{YB}N_{i5}^*U_{L,22}^{e*}Z_{k2}^E\nonumber \\&+\sqrt{2}g_BN_{i5}^*U_{L,22}^{e*}Z_{k2}^E -2N_{i3}^*U_{L,22}^{e*}Y_{e,22}Z_{k,5}^E\Big ];\nonumber \\ (\mathcal {A}_2^{B-L})^I_{\tilde{L}\chi ^0}= & {} -\frac{1}{\sqrt{2}}\sum _{i=1}^7\sum _{k=1}^6\Big [Z_{k,5}^EU_{R,22}^{e} (2g_1N_{i1}\nonumber \\&+(2g_{YB}+g_B)N_{i5}) +Y_{e,22}^*U_{R,22}^{e}Z_{k2}^EN_{i3}\Big ]; \end{aligned}$$

(C1)

$$\begin{aligned} (\mathcal {C}_1^{B-L})^I_{\chi ^-\tilde{\nu }^i}= & {} \frac{i}{\sqrt{2}}\sum _{j=1}^2\sum _{k=1}^6U_{j2}^*Z_{k2}^{i,*}U_{R,22}^{e,*}Y_{e,22};\nonumber \\ (\mathcal {C}_2^{B-L})^I_{\chi ^-\tilde{\nu }^i}= & {} -\frac{i}{\sqrt{2}}\sum _{j=1}^2\sum _{k=1}^6\Big [g_2Z_{k2}^{i,*}U_{L,22}^{e}V_{j1}\nonumber \\&- Y_{\nu ,22}^*Z_{k,5}^{i,*}U_{L,22}^eV_{j2}\Big ]; \end{aligned}$$

(C2)

$$\begin{aligned} (\mathcal {C}_1^{B-L})^I_{\chi ^-\tilde{\nu }^R}= & {} \frac{1}{\sqrt{2}}\sum _{j=1}^2\sum _{k=1}^6U_{j2}^*Z_{k2}^{R,*}U_{R,22}^{e,*}Y_{e,22};\nonumber \\ (\mathcal {C}_2^{B-L})^I_{\chi ^-\tilde{\nu }^R}= & {} \frac{1}{\sqrt{2}}\sum _{j=1}^2 \sum _{k=1}^6\Big [-g_2Z_{k2}^{R,*}U_{L,22}^{e}V_{j1}\nonumber \\&+ Y_{\nu ,22}^*Z_{k,5}^{R,*}U_{L,22}^eV_{j2}\Big ]. \end{aligned}$$

(C3)

Appendix D: the best fit masses in the BLMSSM and B-LSSM

Table 1 The best fit masses (in GeV) for the BLMSSM and B-LSSM particles