Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T19:48:35.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Derivatives of symplectic eigenvalues and a Lidskii type theorem

Part of: Basic linear algebra

Published online by Cambridge University Press:  02 December 2020

Tanvi Jain  and
Hemant Kumar Mishra
Tanvi Jain*
Affiliation:
Theoretical Statistics and Mathematics Unit, Indian Statistical Institute, New Delhi, India e-mail: hemant16r@isid.ac.in
Hemant Kumar Mishra
Affiliation:
Theoretical Statistics and Mathematics Unit, Indian Statistical Institute, New Delhi, India e-mail: hemant16r@isid.ac.in
*
e-mail: tanvi@isid.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Associated with every $2n\times 2n$ real positive definite matrix 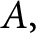$A,$ there exist n positive numbers called the symplectic eigenvalues of 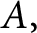$A,$ and a basis of 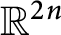$\mathbb {R}^{2n}$ called the symplectic eigenbasis of A corresponding to these numbers. In this paper, we discuss differentiability and analyticity of the symplectic eigenvalues and corresponding symplectic eigenbasis and compute their derivatives. We then derive an analogue of Lidskii’s theorem for symplectic eigenvalues as an application.

Keywords

Positive definite matrixWilliamson’s theoremsymplectic eigenvaluesymplectic eigenvector pairderivativeanalyticitymajorizationLidskii’s theorem

MSC classification

Secondary: 15A18: Eigenvalues, singular values, and eigenvectors 15A45: Miscellaneous inequalities involving matrices 81P45: Quantum information, communication, networks
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 457 - 485
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseevsky, D., Kriegl, A., Losik, M., and Michor, P. W., Choosing roots of polynomials smoothly . Isr. J. Math. 105(1998), 203–233.CrossRefGoogle Scholar
Ando, T., Majorization, doubly stochastic matrices, and comparison of eigenvalues . Linear Algebra Appl. 118(1989), 163–248.CrossRefGoogle Scholar
Bhatia, R., Matrix analysis . Springer, New York, NY, 1997.CrossRefGoogle Scholar
Bhatia, R., Linear algebra to quantum cohomology: the story of Alfred Horn's inequalities . Am. Math. Mon. 108(2001), 289–318.CrossRefGoogle Scholar
Bhatia, R., Perturbation bounds for matrix eigenvalues . Classics in Applied Mathematics, 53 SIAM, Philadelphia, 2007.CrossRefGoogle Scholar
Bhatia, R., Some inequalities for eigenvalues and symplectic eigenvalues of positive definite matrices . Int. J. Math. 30(2019), 1950055.CrossRefGoogle Scholar
Bhatia, R. and Jain, T., On symplectic eigenvalues of positive definite matrices . J. Math. Phys. 56(2015), 112201.CrossRefGoogle Scholar
Bhatia, R., Singh, D., and Sinha, K. B., Differentiation of operator functions and perturbation bounds . Commun. Math. Phys. 191(1998), 603–611.CrossRefGoogle Scholar
Dutta, B., Mukunda, N., and Simon, R., The real symplectic groups in quantum mechanics and optics . Pramana 45(1995), 471–495.Google Scholar
de Gosson, M., Symplectic geometry and quantum mechanics. In: Operator Theory: Advances and applications, 166, Advances in Partial Differential Equations (Basel), Birkhauser Verlag, Basel, 2006.CrossRefGoogle Scholar
Eisert, J., Tyc, T., Rudolph, T., and Sanders, B. C., Gaussian quantum marginal problem . Commun. Math. Phys. 280(2008), 263–280.CrossRefGoogle Scholar
Fulton, W., Eigenvalues of sums of Hermitian matrices . Séminaire Bourbaki 845(1998), 255–269.Google Scholar
Hiroshima, T., Additivity and multiplicativity properties of some Gaussian channels for Gaussian inputs . Phys. Rev. A 73(2006), 012330.CrossRefGoogle Scholar
Idel, M., Gaona, S. S., and Wolf, M. M., Perturbation bounds for Williamson's symplectic normal form . Linear Algebra Appl. 525(2017), 45–58.CrossRefGoogle Scholar
Juang, J. N., Ghaemmaghami, P., and Lim, K. B., Eigenvalue and eigenvector derivatives of a non defective matrix . J. Guid. Control. Dyn. 12(1989), 480–486.CrossRefGoogle Scholar
Kato, T., Perturbation theory for linear operators . Springer, New York, NY, 1997.Google Scholar
Kazdan, J. L., Matrices $A(t)$ depending on a parameter. $t$ University of Pennsylvania, unpublished note 1995.Google Scholar
Kılıç, M., Mengi, E., and Yıldırım, E. A., Numerical optimization of eigenvalues of Hermitian matrix functions . SIAM J. Matrix Anal. A. 35(2014), 699–704.Google Scholar
Koenig, R., The conditional entropy power inequality for Gaussian quantum states . J. Math. Phys. 56(2015), 022201.CrossRefGoogle Scholar
Li, C. K. and Mathias, R., The Lidskii-Mirsky-Wielandt theorem—additive and multiplicative versions . Numer. Math. 81(1999), 377–413.CrossRefGoogle Scholar
Magnus, J. R., On differentiating eigenvalues and eigenvectors . Economet. Theory. 1(1985), 179–191.CrossRefGoogle Scholar
Moral, P. D. and Niclas, A., A Taylor expansion of the square root matrix function . J. Math. Anal. Appl. 465(2018), 259–266.CrossRefGoogle Scholar
Parthasarathy, K. R., Symplectic dilation, Gaussian states and Gaussian channels . Indian J. Pure Ap. Mat. 46(2015), 419–439.CrossRefGoogle Scholar
Rellich, F., Perturbation theory of eigenvalue problems . Lecture notes, New York University, New York, NY, 1954.Google Scholar
Rogers, L. C., Derivatives of eigenvalues and eigenvectors . AIAA J. 8(1970), 943–944.CrossRefGoogle Scholar
Safranek, D. and Fuentes, I., Optimal probe states for the estimation of Gaussian unitary channels . Phys. Rev. A 94(2016), 062313.CrossRefGoogle Scholar
Seyranian, A. P., Kirillov, O. N., and Mailybaev, A. A., Coupling of eigenvalues of complex matrices at diabolic and exceptional points . J. Phys. A Math. Gen. 38(2005), 17–23.CrossRefGoogle Scholar
Xu, Y. and Lai, Y., Derivatives of functions of eigenvalues and eigenvectors for symmetric matrices . J. Math. Anal. Appl. 444(2016), 251–254.CrossRefGoogle Scholar