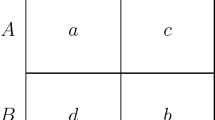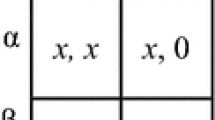Pairwise imitation and evolution of the social contract

Abstract

This paper studies the evolution of conventions in Stag Hunt games when agents’ behaviour depends on pairwise payoff comparisons. The results of two imitative decision rules are compared with each other and with those obtained when agents myopically best respond to the distribution of play. These rules differ in terms of their rationale, their requirements, and the extent to which they make individuals learn from others. Depending on payoffs and the interaction process being considered, best response learning can cause either the rewarding All Stag equilibrium or the inefficient All Hare equilibrium to emerge as the long-run convention. In contrast, pairwise imitation favours the emergence of the Pareto-inferior equilibrium. This result is robust to assuming assortative matching and some heterogeneity in decision rules.

1 Introduction

As Jean-Jacques Rousseau (1762, p. 172) famously argued, ‘[t]here is often a great deal of difference between the will of all and the general will.’ To some extent, this distinction recalls the distinction between social welfare and individual well-being. Rousseau’s general will concerns the common interest aspect of interactions: ‘it is always right’ and aims at the good of all people. Runciman and Sen (1965) view it as always fulfilling the conditions of Pareto-optimality. In contrast, the will of all results from the aggregation of private, particular interests. Despite being aware of this tension, Rousseau had strong faith that individuals could implement the common good: ‘if, when the people, being furnished with adequate information, held its deliberations, the citizens had no communication one with another, the grand total of the small differences would always give the general will, and the decision would always be good’ (p. 173).¹

A less triumphant, yet perhaps more sound, claim can be made with respect to the opposite case: when individuals’ modes of reasoning and learning cause decisions based on inadequate information to be made, the conflict between the general will and the will of all is often resolved in favour of the latter. This paper substantiates this view, examining how myopic comparative judgements can influence cooperative behaviour.

One way of framing the relationship between the two wills is in terms of the contrast between mutual advantage and individual risk. The choice, to be taken independently of other people and without prior knowledge of their decisions, is between risky cooperation and safe defection. Joint cooperation pays the highest possible reward, whereas lone cooperation is less attractive than both lone and joint defection. The game used to represent situations of this type is the Stag Hunt — after a story, again by Rousseau, in which two hunters have to join forces to kill a stag but are tempted to abandon the hunt and catch a hare by themselves instead. The decision to hunt a stag involves a risk of going back home empty-handed, because there is the possibility that the other hunter will go for a hare. Catching a hare involves no such risk but implies forgoing the potential gains from a successful stag hunt. Mutual hare hunting and cooperating by jointly hunting a stag are both Nash equilibria, as each action is a best response to itself.

Following Binmore (1994) and Skyrms (2004, 2014), the Stag Hunt can be seen as a prototypical representation of the social contract, where the state of nature corresponds to the everyone-for-himself equilibrium, or to a nonequilibrium state, and the social contract takes the form of a Pareto-improving reform. Implementing the contract poses a problem of equilibrium selection in that

you can either devote energy to instituting the new social contract or not. If everyone takes the first course, the social contract equilibrium is achieved; if everyone takes the second course, the state of nature equilibrium results. But the second course carries no risk, while the first does (Skyrms 2004, p. 9).

In this paper I study the evolution of cooperation in a population engaged in a Stag Hunt game. Interactions are modelled as pairwise encounters, and individuals are occasionally called to revise their actions. The resulting long-run conventions are derived by applying stochastic stability theory and studying which equilibria are most likely to be observed when agents make mistakes with a small probability (Foster and Young 1990; Kandori et al. 1993; Young 1993). The focus is on the implications of decision rules based on imitation, which has long been recognised as a common form of social learning (Hurley and Chater 2005a, 2005b; Rendell et al. 2010). Imitative heuristics can serve multiple purposes: they are cognitively and informationally undemanding (Gigerenzer and Gaissmaier 2011), and can allow individuals to free ride on the knowledge of others. The tendency to engage in social comparisons and imitation may also stem from a drive for self-evaluation, a desire not to fall behind other people, and other culturally influenced attitudes (Festinger 1954). I consider two different imitative rules. The first makes revising agents compare their payoff with the payoff of their opponent, and then switch to the opponent’s action if and only if it performed better than their own. The second consists in comparing with, and possibly imitating, an individual drawn at random from the population. The results of these rules are contrasted with each other and with those of a third, non-imitative rule, namely best response to the distribution of play in the previous period, which serves as an opposite benchmark. As discussed in Section 3.1 below, best response and pairwise imitation differ in underlying rationale, requirements, and sensitivity to information externalities. Due to its complexity, a best response to the distribution of play is seen as an instance of globally informed, deliberative decision-making. Conversely, pairwise imitation is relatively effortless, relies on local sources of information, and meets needs for quick action.

Depending on payoffs and the matching process being considered, best response learning can select either the rewarding All Stag equilibrium or the inefficient All Hare equilibrium as the stochastically stable state. On the other hand, pairwise imitative rules select the riskless, Pareto-inferior equilibrium; when decisions are made out of short-sighted, me-against-someone-else comparisons, it is very difficult for a society to settle on a social contract. This result is robust to assuming assortative interactions — often regarded as one of the main forces underlying the emergence of cooperation — and some heterogeneity in agents’ decision rules.

The paper is organised as follows. Section 2 reviews the relevant literature and gives some background on imitative rules. Section 3 sets up the model. Section 4 presents the main results and checks their robustness to alternative model specifications. Section 5 contains some concluding remarks.

2 Related literature

In the last three or so decades, game theory has increasingly moved away from the assumption of ideal rationality towards models where agents use simple decision rules. These include success-based imitative rules, which make behaviour depend on interpersonal payoff comparisons.

A common feature of imitative models is that they assume random sampling of references, meaning that whenever an individual receives a revision opportunity, he draws m agents at random from the population as a reference for comparison and imitation. The rules that work under this assumption include imitate-the-best, which consists in imitating the most successful individual in the reference group, and imitate-the-best-average, which prescribes taking the action that yielded the highest average payoff (for an extensive overview, see Alós-Ferrer and Schlag 2009). Models with m = 1 are pairwise-imitative, i.e. they make agents decide whether or not to imitate a randomly chosen individual depending on the difference in their payoffs (Schlag 1998; Sandholm 2010; Izquierdo and Izquierdo 2013).

The random sampling assumption draws a distinction between whom agents meet and interact with, on the one hand, and whom they compare themselves to when given a revision opportunity, on the other hand. An alternative approach is to assume that individuals can only imitate those with whom they interact. For example, in games played on networks, agents typically play and compare with their nearest neighbours (e.g. Fosco and Mengel 2011; Tsakas 2014). Bilancini et al. (2020) study the dynamics of interact-and-imitate behaviours in two-player symmetric games and give a sufficient condition for the convergence of play to a monomorphic equilibrium. Intuitively, if there exists an action a that yields a payoff higher than the payoff received by an opponent playing any action $a^{\prime } \neq a$, then play will eventually converge to the state where all agents choose a. Cabo and García-González (2019) consider the case of a population consisting of two types of agents with the same strategy set but different payoff functions. The resulting evolutionary game lies somewhere between symmetric and asymmetric games, since agents are randomly paired with one another and can imitate their opponent but do not know the opponent’s type.

The interaction-comparison dualism has noteworthy implications. From a learning perspective, separating the matching and comparison processes means assuming that agents do not seek information from within their interaction neighbourhood but from others in the population. From a more general standpoint, it means distinguishing between interaction and competition, with important consequences for evolutionary dynamics. In this vein, Ohtsuki et al. (2007) study cooperative behaviour in a population structured according to two graphs: an interaction graph, which determines matching, and a replacement graph, which describes the geometry of competition. Their results show that depending on the relationship between the graphs, cooperation may or may not be favoured by natural selection.

Regarding the structure of social interactions, evolutionary models of the Stag Hunt frequently consider well-mixed (unstructured) populations and uniform random pairing (Kandori et al. 1993; Young 1993; Ellison 1997; Sugden 2005). This assumption is often made along with the assumptions that agents are expected payoff maximisers and form beliefs based on past play; the resulting long-run equilibrium is the risk-dominant equilibrium, which maximises the product of agents’ losses from unilateral deviation (Harsanyi and Selten 1988). Bilancini and Boncinelli (2020) present a model where each pair of interacting agents has a positive probability of breaking up after every round of play. If agents’ mistakes become less likely as the payoffs obtained increase, then unstable interactions make the inefficient equilibrium emerge in the long run. Other models postulate that agents play with a fixed set of neighbours. In this case, whether or not the payoff-dominant equilibrium is favoured over the risk-dominant equilibrium depends on the topology of the network (Ellison 1993; Skyrms 2004). Yet another approach to modelling interactions is to assume that agents choose which action to take and whom to play with (Goyal and Vega-Redondo 2005; Staudigl and Weidenholzer 2014). When the number of interactions per individual is small, the Pareto-superior equilibrium is usually selected in the long run.

Finally, models with random encounters can either assume assortment or not. Assortative matching captures the tendency of individuals to associate disproportionately with similar others, which can be a strong driver of cooperation (Eshel and Cavalli-Sforza 1982; Bergstrom 2003; Allen and Nowak 2015). Roughly speaking, like-with-like interactions can make cooperative behaviour more attractive to agents by decreasing the likelihood of coordination failure. Assortment may be caused by the sharing of cultural, socio-economic and other individual characteristics (Alger and Weibull 2013, 2016), by similarity in behaviour (Bilancini et al. 2018), or both.

This paper contributes to the literature along several lines. First, it discusses and compares two imitative rules that lie at the extremes of the range of possible interaction-comparison relationships: under one rule, the interaction and comparison structures are independent; under the other, they are perfectly correlated. Second, it examines the differences, and the underlying sources of differences, between pairwise imitative dynamics and the more widely studied best response dynamics, showing that the former bear no relationship to the concept of risk-dominance. Third, it investigates the evolutionary influence of pairwise imitation in more general settings where encounters are not uniformly random and agents have different modes of learning.

3 The model

Consider a finite population $P = \left \lbrace 1, 2, \dots , n \right \rbrace$, where n is an even number. Members of P are repeatedly matched in pairs to play a stage game. Time unfolds discretely and is indexed by $t = 0, 1, 2, \dots$. Assume uniform random matching and denote agent i’s opponent at time t by $\zeta \left (i, t \right ) \in P \smallsetminus \left \lbrace i \right \rbrace$. Thus, for every j≠i ∈ P:

$$ \Pr \left[ \zeta \left( i, t \right) = j \right] = \frac{1}{n - 1} . $$

In every period, agents choose an action $a \in \mathcal {A} = \left \lbrace S, H \right \rbrace$. Let Δ be the simplex of probability distributions on $\mathcal {A}$, and let the function $\pi : \mathcal {A} \times \mathcal {A} \rightarrow \mathbb {R}$ specify the payoff received by an agent playing a against an opponent playing $a^{\prime }$, denoted by $\pi \left (a, a^{\prime } \right )$.

The stage game, represented in Fig. 1, is a two-player Stag Hunt. Throughout the paper it is assumed that α > γ, α > δ, γ >β and δ >β, implying that $\left (H, H\right )$ and $\left (S, S\right )$ are both Nash equilibria, with the latter Pareto-optimal, and that H is the maximin action (i.e. the action that maximises the minimum payoff agents can get). Assume also that α +β ≠γ + δ, meaning that the risk-dominant action can be either S or H. If α+β < γ + δ, then H risk-dominates S; if the opposite holds, then S is both payoff- and risk-dominant.

Fig. 1

The stage game

Let $n_{a} \left (t \right ) \in \left [ 0, n \right ]$ be the number of individuals playing action $a \in \mathcal {A}$ at time t. The aggregate behaviour of the population in each period is described by a state variable $\mathbf {x} \left (t \right ) := \left (x_{S} \left (t \right ), x_{H} \left (t \right ) \right ) \in \mathbf {X} \subset {\varDelta }$, where $x_{a} \left (t \right ) = n_{a} \left (t \right ) / n$ and X are the proportion of individuals playing a and the state space, respectively. By definition, ${\sum }_{a \in \mathcal {A}} x_{a} \left (t \right ) = x_{S} \left (t \right ) + x_{H} \left (t \right ) = 1$. I refer to states $\left (0,1 \right )$ and $\left (1,0 \right )$ as the maximin convention and the payoff-dominant convention, respectively, or as the state of nature and the social contract. The risk-dominant convention can either be All Hare or All Stag, depending on which is the risk-dominant action. I take the initial state, $\mathbf {x} \left (0 \right )$, to be exogenous and study the dynamics resulting from different rules of behaviour.

3.1 Decision rules

After every round of play, each agent has an independent probability $p \in \left (0, 1 \right )$ of being selected for action revision.² A decision rule maps the information available to an individual into the set of possible actions. I consider three rules: myopic best response to the distribution of play in the population (BR), pairwise imitation of a randomly sampled individual (or pairwise random imitation, PRI), and pairwise interaction-and-imitation (PII). These rules all feature bounded memory — they base decisions solely on observations made in the previous round — but have different information and computational requirements.

Definition 1 (myopic best response)

The action chosen at time t + 1 by a revising agent i who best responds to the distribution of play at time t is:

$$ a_{i}^{t+1} \in B_{i} \left( \mathbf{x} \left( t \right) \right), $$

(1)

where

$$ B_{i} \left( \mathbf{x} \left( t \right) \right) := \underset{a \in \mathcal{A}}{\arg \max} \sum\limits_{a^{\prime} \in \mathcal{A}} \pi_{i} \left( a, a^{\prime} \right) x_{a^{\prime}} \left( t \right) \subseteq \mathcal{A}. $$

In case of indifference between actions, $a_{i}^{t+1}$ is determined by tossing a fair coin.

Best responding to a state of play can be difficult; it requires revising agents to adopt a population-level perspective, to know how many times each action was taken by members of P, and to compute expected payoffs based on the distribution of actions. Compared to this, pairwise imitation places a much lighter burden on decision makers, as it simply requires them to observe and possibly imitate another individual. This is most reasonable when agents have limited cognitive abilities and lack strategic sophistication, or when information is costly or time-consuming to acquire. Another way of interpreting the difference between pairwise imitation and best response is to think of them as stylised forms of intuitive and deliberative thinking, respectively (Kahneman 2003). The former is highly accessible, considerably faster and computationally undemanding, whereas the latter involves a more thorough evaluation of the available options.

Following Schlag (1998) and Alós-Ferrer and Schlag (2009), a pairwise imitative rule can be expressed as a mixed action

$$ {\varPsi} \left( a, \pi, a^{\prime}, \pi^{\prime} \right) \in {\varDelta}, $$

with ${\varPsi } \left (a, \pi , a^{\prime }, \pi ^{\prime } \right )_{a^{\prime }}$ the conditional probability that a revising agent will choose action $a^{\prime }$ after playing action a, receiving a payoff of π, and observing another agent playing action $a^{\prime }$ and receiving a payoff of $\pi ^{\prime }$. Let $\xi \left (i, t \right ) \in P \smallsetminus \left \lbrace i \right \rbrace$ denote the individual to whom agent i compares himself at time t — henceforth agent i’s reference. Different assumptions about who can be chosen as reference yield different decision rules. If references are sampled in a uniform random manner, then $\Pr \left [ \xi \left (i, t \right ) = j \right ] = 1 / \left (n - 1 \right )$ for every j≠i ∈ P. Moreover, if i’s opponent and i’s reference are drawn independently of one another, then the probability of $\zeta \left (i, t \right )$ and $\xi \left (i, t \right )$ being the same agent j is:

$$ \Pr \left[ \zeta \left( i, t \right) = \xi \left( i, t \right) = j \right] = \frac{1}{\left( n - 1 \right)^{2}} . $$

The distinction between agent i’s opponent and reference can be emphasised by writing the imitative rule as:

$$ {\varPsi} \left[ {a^{t}_{i}}, \pi_{i} \left( {a^{t}_{i}}, a^{t}_{\zeta \left( i, t \right)} \right), a^{t}_{\xi \left( i, t \right)} , \pi_{\xi \left( i, t \right)} \left( a^{t}_{\xi \left( i, t \right)}, a^{t}_{\zeta \left( \xi \left( i, t \right) , t \right)} \right) \right], $$

(2)

where subscripts and superscripts denote individuals and time, respectively; ${a^{t}_{i}}$ and $\pi _{i} \left (\cdot \right )$ are the action chosen and the payoff received by agent i at time t against an opponent — $\zeta \left (i, t \right )$ — playing $a^{t}_{\zeta \left (i, t \right )}$, whereas $a^{t}_{\xi \left (i, t \right )}$ and $\pi _{\xi \left (i, t \right ) } \left (\cdot \right )$ are the action chosen and the payoff received by agent i’s reference — $\xi \left (i, t \right )$ — against an opponent — $\zeta \left (\xi \left (i, t \right ) , t \right )$ — playing $a^{t}_{\zeta \left (\xi \left (i, t \right ) , t \right )}$. I write ${\varPsi } \left [ \cdot \right ]_{a^{t}_{\xi \left (i, t \right )}}$ to indicate the conditional probability that i has of switching from ${a^{t}_{i}}$ to $a^{t}_{\xi \left (i, t \right )}$, and I assume for simplicity that:

$$ {\varPsi} \left[ {a^{t}_{i}}, \pi_{i} \left( \cdot \right), a^{t}_{\xi \left( i, t \right)} , \pi_{\xi \left( i, t \right)} \left( \cdot \right) \right]_{a^{t}_{\xi \left( i, t \right)}} = \begin{cases}1 & \text{if }\ \pi_{\xi \left( i, t \right) } \left( \cdot \right) > \pi_{i} \left( \cdot \right) \\ 0 & \text{otherwise} \end{cases} . $$

Thus, i will choose action $a^{t}_{\xi \left (i, t \right )}$ at time t + 1 if and only if $\xi \left (i, t \right )$’s payoff at time t is higher than his own. This gives the following definition.

Definition 2 (pairwise random imitation)

Under PRI updating, the action chosen at time t + 1 by a revising agent i is:

$$ a^{t+1}_{i} = \begin{cases} a^{t}_{\xi \left( i, t \right)} & \text{if }\ \pi_{i} \left( {a^{t}_{i}}, a^{t}_{\zeta \left( i, t \right)} \right) < \pi_{\xi \left( i, t \right)} \left( a^{t}_{\xi \left( i, t \right)}, a^{t}_{\zeta \left( \xi \left( i, t \right) , t \right)} \right) \\ {a^{t}_{i}} & \text{otherwise} \end{cases} , $$

(3)

where $\xi \left (i, t \right )$ is sampled, independently of $\zeta \left (i, t \right )$, according to a uniform probability distribution on P.

Pairwise random imitation makes agents ignore, voluntarily or unconsciously, how they perform in relation to their match, and makes them select a third party as a reference for comparison instead. This may be the case, for example, if interactions do not require agents to meet in person, so that it is not possible to observe the opponent’s payoff. However, sometimes people only observe or care about the behaviour of those they interact with. If this is the case, then $\xi \left (i, t \right ) = \zeta \left (i, t \right )$ and $\zeta \left (\xi \left (i, t \right ) , t \right ) = i$, and the rule in (2) can be rewritten as:

$$ {\varPsi} \left[ {a^{t}_{i}}, \pi_{i} \left( {a^{t}_{i}}, a^{t}_{\zeta \left( i, t \right)} \right), a^{t}_{\zeta \left( i, t \right)} , \pi_{\zeta \left( i, t \right)} \left( a^{t}_{\zeta \left( i, t \right)}, {a^{t}_{i}} \right) \right]. $$

(2’)

Revising agents who focus exclusively on how well they do vis-à-vis their opponents are said to follow a pairwise interact-and-imitate rule.

Definition 3 (pairwise interaction-and-imitation)

Under PII updating, the action chosen at time t + 1 by a revising agent i is:

$$ a^{t+1}_{i} = \begin{cases} a^{t}_{\zeta \left( i, t \right)} & \text{if }\ \pi_{i} \left( {a^{t}_{i}}, a^{t}_{\zeta \left( i, t \right)} \right) < \pi_{\zeta \left( i, t \right)} \left( a^{t}_{\zeta \left( i, t \right)}, {a^{t}_{i}} \right) \\ {a^{t}_{i}} & \text{otherwise} \end{cases} , $$

(4)

where $\zeta \left (i, t \right )$ is simultaneously i’s opponent and i’s reference for comparison at time t.

The key characteristic of pairwise imitative rules is that they respond to information about whether or not an agent does better than his reference, rather than information about how well he does in absolute terms. In particular, PII can be viewed as searching for a way of ‘not losing to the opponent’ rather than just ‘doing well.’ Also, and importantly, the three rules considered here differ in the extent to which they look for examples of alternative behaviours (Choi 2008). Best response updating qualifies as an instance of global learning and makes individuals form beliefs that reflect the entire distribution of play. PII relies on information at the local (pair) level and makes individuals evaluate actions according to how they perform against the action of their opponents. This makes revising agents insensitive to information externalities, i.e. prevents them from accessing information from outside their interaction neighbourhood. PRI makes agents learn locally as well, but allows them to look beyond the pair of interacting parties to which they belong.

For every $\mathbf {x}, \mathbf {x}^{\prime } \in \mathbf {X}$ and every $\kappa \in \left \lbrace \text {BR, PRI, PII} \right \rbrace$, let $T^{\kappa }_{\mathbf {x},\mathbf {x}^{\prime }} \in \left [ 0, 1\right ]$ be the probability of moving from state x to state $\mathbf {x}^{\prime }$ in one period under decision rule κ, and let T^κ be the transition matrix with typical element $T^{\kappa }_{\mathbf {x},\mathbf {x}^{\prime }}$. Together, X and T^κ define a discrete-time, unperturbed Markov chain on the state space, denoted by $\left (\mathbf {X}, \mathbf {T}^{\kappa } \right )$. A recurrent class (or absorbing set) is the smallest set $\mathbf {R} \subseteq \mathbf {X}$ such that any state in R is accessible from any other state in R — so there is a positive probability of moving from any state to any other in a finite number of steps — whereas no state outside R is accessible from any state inside it. A singleton recurrent class is called an absorbing state. Conversely, a state that does not belong to any recurrent class is said to be transient.

4 Results

4.1 Unperturbed dynamics

Prior to discussing the main results, it is useful to determine under what conditions agents switch from one action to another. Under best response updating, switching to Stag or to Hare depends on how confident an agent is that the opponent will choose the same action. For every x ∈X such that $\alpha x_{S} + \upbeta \left (1 - x_{S} \right ) > \gamma x_{S} + \delta \left (1 - x_{S} \right )$, the expected payoff from cooperating exceeds that from defecting. This implies that if $x_{S} > \left (\delta - \upbeta \right ) / \left (\alpha - \upbeta - \gamma + \delta \right )$, then a revising agent will best respond by playing Stag; if the opposite inequality holds, the agent will choose Hare.

Under pairwise random imitation, a cooperator who receives a revision opportunity will switch to Hare if and only if his last opponent and his reference both defected. On the other hand, switching from Hare to Stag requires that a defector select a cooperator who received a payoff of $\pi \left (S, S \right ) = \alpha$ as reference. For this to be the case, both the revising agent’s reference and the reference’s opponent must have played Stag. Finally, the interact-and-imitate rule only admits switches from Stag to Hare. Such a switch occurs whenever a cooperator is matched with, and then imitates, a defector. Contrarily, no defector will ever switch to Stag, because the maximin action always yields a payoff greater or equal to that of the opponent.

The single-directionality of switches under PII leads to a sharp result: with the exception of the case where everyone cooperates from the very beginning, play will converge to the maximin convention no matter what the initial state is.

Lemma 1

Under PII updating, the unperturbed process converges with unit probability to $\left (0, 1 \right )$ from every $\mathbf {x} \left (t \right ) \in \mathbf {X} \smallsetminus \left \lbrace \left (1, 0 \right ) \right \rbrace$.

Proof

See text above. □

The following lemma describes the asymptotic behaviour of the three unperturbed processes.

Lemma 2

For every $\kappa \in \left \lbrace \text {\textit {BR, PRI, PII}} \right \rbrace$, the only absorbing states of the unperturbed process $\left (\mathbf {X}, \mathbf {T}^{\kappa } \right )$ are (0,1) and (1,0).

Proof

Consider any action $a \in \mathcal {A}$ and suppose that $x_{a} \left (t \right ) = 1$, meaning that no agent in P played action $a^{\prime } \neq a$ at time t. Since $\pi \left (a, a \right ) > \pi \left (a^{\prime }, a \right )$, a best responder who receives a revision opportunity will always stick to a. Likewise, an imitator will continue to play a because it is impossible to observe a reference who played $a^{\prime }$. This proves that (0,1) and (1,0) are absorbing states under all three decision rules.

Next, I verify that no other absorbing state exists. This requires showing that all states except All Stag and All Hare are transient, meaning that either the payoff-dominant convention or the maximin convention, or both, are accessible from all states in $\mathbf {X} \smallsetminus \left \lbrace \left (1, 0 \right ), \left (0, 1 \right ) \right \rbrace$. To establish the result, it suffices to show that there exists a positive probability path from every such state to All Stag or All Hare. I consider each decision rule in turn.

• BR. Suppose that a is a best response to the distribution of play at time t, and consider an agent i who is playing $a^{\prime } \neq a$. The probability that i has of being the only agent selected for action revision is $p \left (1 - p \right )^{n-1}$, and the conditional probability of i switching to action a is either 1 (if a is the sole best response) or 1/2 (in case of indifference between a and $a^{\prime }$). If the switch occurs, the system moves to a state $\mathbf {x} \left (t +1 \right )$ in which $x_{a} \left (t + 1 \right ) = \left [ n_{a} \left (t \right ) + 1 \right ] / n$ and $x_{a^{\prime }} \left (t + 1 \right ) = \left [ n_{a^{\prime }} \left (t \right ) - 1 \right ] / n$. If $n_{a} \left (t \right ) + 1 = n$, then either $\left (1,0 \right )$ or $\left (0,1 \right )$ has been reached. If not, then a recursive application of this argument shows that the state in which x_a = 1 can be reached with positive probability in a finite number of periods.

• PRI. I first show that All Hare is accessible from every state in $\left \lbrace \mathbf {x} \in \mathbf {X}:\right .$ $\left . n_{H} > 0 \right \rbrace$. Let $m \left (t \right ) \geq 0$ denote the number of cooperators who are matched with a defector at time t. The probability that a cooperator who received a payoff of $\pi \left (S, H \right ) = \upbeta$ has of being the only agent selected for action revision is $m \left (t \right ) p \left (1 - p\right )^{n - 1}$. Moreover, with conditional probability $n_{H} \left (t \right ) / \left (n - 1 \right )$ this agent will select a defector (whose payoff is either γ or δ) as reference. Since $\upbeta < {\min \limits } \left \lbrace \gamma , \delta \right \rbrace$, the revising agent will switch from Stag to Hare with probability 1. The system will then move to a state $\mathbf {x} \left (t +1 \right )$ in which $x_{H} \left (t + 1 \right ) = \left [ n_{H} \left (t \right ) + 1 \right ] / n$ and $x_{S} \left (t + 1 \right ) = \left [ n_{S} \left (t \right ) - 1 \right ] / n$. Applying this argument recursively proves that All Hare can be reached with positive probability.

  Similarly, All Stag is accessible from all states in $\left \lbrace \mathbf {x} \in \mathbf {X}: n_{S} \geq 2 \right \rbrace$. The probability that a defector (who received a payoff of γ or δ) has of being the only agent chosen for action revision is $n_{H} \left (t\right ) p \left (1- p \right )^{n - 1 }$. Furthermore, with conditional probability $\left [ n_{S} \left (t \right ) - \right .$ $\left . m \left (t \right ) \right ] / \left (n - 1 \right )$ this agent will select a cooperator who received a payoff of $\pi \left (S, S \right ) = \alpha$ as reference. Since $\alpha > {\max \limits } \left \lbrace \gamma , \delta \right \rbrace$, the revising agent will switch from Hare to Stag with probability 1. The system will then move to a state $\mathbf {x} \left (t +1 \right )$ in which $x_{S} \left (t + 1 \right ) = \left [ n_{S} \left (t \right ) + 1 \right ] / n$ and $x_{H} \left (t + 1 \right ) = \left [ n_{H} \left (t \right ) - 1 \right ] / n$. A recursive application of this argument proves that All Stag can be reached with positive probability whenever $n_{S} \left (t \right ) \geq 2$. By contrast, if $n_{S} \left (t \right ) = 1$, then All Stag is inaccessible, because it is impossible to ever observe a cooperator who received a payoff of α.

• PII. The result follows from Lemma 1. Since no switch from Hare to Stag can occur, the process will reach All Hare with probability 1.

□

Lemma 2 implies that the unperturbed processes are all nonergodic; eventually they will end up and remain in All Stag or All Hare, but which of the two depends on the initial state of the system.

4.2 Stochastically stable states

Suppose now that whenever an agent receives a revision opportunity, there is a positive probability that he will make a mistake or decide to experiment with a new strategy. I make the standard assumption that, with probability ε, a revising agent chooses the action that is not prescribed by the rule he is following.

Denote by $T^{\kappa ,\varepsilon }_{\mathbf {x},\mathbf {x}^{\prime }}$ the probability of moving from x to $\mathbf {x}^{\prime }$ in one period under decision rule $\kappa \in \left \lbrace \text {BR, PRI, PII} \right \rbrace$ when the system is perturbed by random mutations. Let T^κ,ε be the corresponding transition matrix and $\left (\mathbf {X}, \mathbf {T}^{\kappa ,\varepsilon } \right )$ be the resulting Markov chain. For every ε > 0 this Markov chain is irreducible and regular — meaning that it has exactly one absorbing set consisting of the whole state space and that there exists $v \in \mathbb {N}$ such that $\left (\mathbf {T}^{\kappa ,\varepsilon } \right )^{v}$ has all strictly positive entries, respectively. Since the state space X is finite, regularity of transition probabilities implies that there exists a unique invariant distribution on action profiles, denoted by μ^κ,ε, which describes the asymptotic behaviour of the process. Moreover, irreducibility and regularity imply that the process is ergodic, that is its long-run average behaviour is independent of the initial state. Following Young (1993), a state x is stochastically stable if $\lim _{\varepsilon \rightarrow 0} \mu ^{\kappa ,\varepsilon } \left (\mathbf {x} \right ) > 0$. Simply put, a process that is subject to small but persistent random perturbations will spend most of its time in the stochastically stable states.

If agents follow the best response rule, then the perturbed process exhibits a well-known property: when the probability of mistakes approaches zero, stochastic stability selects the risk-dominant action — which, depending on payoffs, may or may not coincide with the payoff-dominant action — as the long-run conventional way of playing the game.

Proposition 1

Under best response updating, the sole stochastically stable state of the perturbed process is the risk-dominant convention.

Proof

For every $\mathbf {x}, \mathbf {x}^{\prime } \in \mathbf {X}$, define the resistance of a transition from x to $\mathbf {x}^{\prime }$ as the minimum number of mutations needed for the process to move from state x to state $\mathbf {x}^{\prime }$. As ε tends to zero, T^κ,ε approaches T^κ and $T^{\kappa ,\varepsilon }_{\mathbf {x},\mathbf {x}^{\prime }}$ is in the order of $\left (p \varepsilon \right )^{r\left (\mathbf {x},\mathbf {x}^{\prime } \right )}$, where p is the probability of receiving a revision opportunity and $r\left (\mathbf {x},\mathbf {x}^{\prime } \right ) \in \mathbb {N}$ the resistance of the transition. Also, let $\mathcal {R}$ be the set of recurrent classes of the unperturbed process. For any distinct R and $\mathbf {R}^{\prime }$ in $\mathcal {R}$, define a R-to-$\mathbf {R}^{\prime }$ path as a sequence of states that begins in R and ends in $\mathbf {R}^{\prime }$. The resistance of such a path is the sum of the resistances of all points in the sequence, and the stochastic potential of $\mathbf {R}^{\prime }$ is the least resistance over all possible R-to-$\mathbf {R}^{\prime }$ paths. As shown by Young (1993), a state is stochastically stable if and only if it belongs to a recurrent class with minimum stochastic potential. In our model, $\mathcal {R} = \left \lbrace \left (1, 0 \right ), \left (0, 1 \right ) \right \rbrace$. The stochastic potential of $\left (1, 0 \right )$ is the minimum resistance over all paths that go from All Hare to All Stag, and the stochastic potential of $\left (0,1 \right )$ is the minimum resistance over all paths that go from All Stag to All Hare.

Finally, let the basin of attraction of R be a set $\mathbf {B}_{\mathbf {R}} \subseteq \mathbf {X}$ such that, in the unperturbed process, there is a positive probability of moving from any state in B_R to a state in R in a finite number of periods. Note that the least resistance to moving from R to $\mathbf {R}^{\prime }$ equals the least resistance to moving from R to $\mathbf {B}_{\mathbf {R}^{\prime }}$, since no mutation is required to reach $\mathbf {R}^{\prime }$ after entering its basin of attraction.

The least resistant path from All Hare to the basin of attraction of All Stag is found as follows. Suppose that the process is in $\left (0,1 \right )$. For revising agents to switch from Hare to Stag, it must be that $x_{S} > \left (\delta - \upbeta \right ) / \left (\alpha - \upbeta - \gamma + \delta \right ) \equiv \varpi$ (so that the expected payoff from playing S exceeds that from playing H). This will happen if and only if ⌈ϖn⌉ mutations occur, where ⌈⋅⌉ denotes the ceiling function. The probability of this event is in the order of $\left (p \varepsilon \right )^{\lceil \varpi n \rceil }$. As shown in the proof of Lemma 2, from this point onwards there is a positive probability of reaching $\left (1, 0 \right )$ without further mistakes.

Similar reasoning shows that the minimum resistance to moving from All Stag to the basin of attraction of All Hare is $\lceil \left (1 - \varpi \right ) n \rceil$. By Young’s theorem, All Stag is stochastically stable if and only if $\varpi < \left (1 - \varpi \right )$. A simple algebraic manipulation reveals that this is equivalent to α+β > γ + δ, which is the condition for Stag to be risk-dominant. Conversely, All Hare is stochastically stable if and only if α+β < γ + δ, that is if and only if the risk-dominant action is Hare. Taken together, these cases yield the proposition. □

I contrast Proposition 1 with the following.

Proposition 2

Under PRI and PII updating, the sole stochastically stable state of the perturbed process is the maximin convention.

Proof

The two rules are considered in turn.

• PRI. Recall from the proof of Lemma 2 that the basin of attraction of $\left (0, 1\right )$ is $\left \lbrace \mathbf {x} \in \mathbf {X} : n_{H} > 0 \right \rbrace$. In order to reach this set starting from All Stag, a single mutation suffices, implying that the least resistance to moving from All Stag to All Hare is 1. On the other hand, the basin of attraction of $\left (1, 0\right )$ is $\left \lbrace \mathbf {x} \in \mathbf {X} : n_{S} \geq 2 \right \rbrace$. The most likely transition from All Hare to this set requires 2 mistakes, each having a probability of pε. The least resistance to reaching All Stag from All Hare is therefore 2. (If a single mutation occurs, the process will move back to All Hare because of the impossibility of switching from Stag to Hare.) This proves that All Hare is the only stochastically stable state.

• PII. As in the case of random imitation, the basin of attraction of $\left (0, 1\right )$ is $\left \lbrace \mathbf {x} \in \mathbf {X} :\right .$ $\left . n_{H} > 0 \right \rbrace$. Starting from All Stag, this set is reached after a single mutation. The process will then move to $\left (0,1\right )$ in a contagion-like fashion without any need for further mistakes. In contrast, a transition from All Hare to All Stag requires no less than n mutations. Again, All Hare is the only stochastically stable state.

□

Proposition 1 shows that if encounters are random and individuals are calculating enough to behave as expected payoff maximisers, then we get the familiar result of evolution favouring risk-dominance. Put simply, if in state $\left (x_{S}, x_{H} \right ) = \left (\frac {1}{2}, \frac {1}{2} \right )$ agents view the expected reward from a successful stag hunt as sufficiently high to justify the risk of miscoordination, then All Stag will emerge as the long-run convention. Worse news comes from Proposition 2, which states that pairwise imitation makes the maximin convention emerge regardless of which is the risk-dominant action. When decisions are made based on pairwise payoff comparisons, the perturbed process spends most of its time in All Hare irrespective of how large the gains from joint cooperation are.

While it is true that PRI and PII give the same result, there is a noteworthy difference in the dynamics they generate. In short, reaching the Pareto-optimal convention is much less difficult under PRI than under PII. As shown in Fig. 2, the minimum resistance to moving from All Stag to All Hare, denoted by r_SH, is 1 under both rules, meaning that a single defector suffices to reach All Hare with non-zero probability. However, consider the state in which everyone except a single agent is cooperating. Under PRI, there is a positive (and possibly high) probability that this lone defector will receive a revision opportunity, select any of the n − 2 cooperators who received a payoff of α as reference, and then switch to Stag. On the contrary, under PII, the only way for the process to move back to All Stag is for the defector to mutate and start cooperating. As the probability of mutation gets smaller, the probability of this event becomes smaller as well. An even greater difference can be observed when considering the minimum resistance to moving from All Hare to All Stag, denoted by r_HS. Under PII, a transition from the maximin convention to the payoff-dominant convention requires that at least n agents make a mistake; PRI makes this transition relatively easier because it allows All Stag to be reached after only two mutations.

Fig. 2

Least resistant paths under PRI and PII

Figure 3 shows the results from a simulation of 50,000 rounds of play.³ I assume that α = 10, β = 0 and γ = δ = 3, so that S is both payoff- and risk-dominant. The probability of receiving a revision opportunity and the probability of mutation are 0.50 and 0.05, respectively, and the initial state is $\left (x_{S}, x_{H} \right ) = \left (\frac {1}{2}, \frac {1}{2} \right )$. The two panels show the evolution over time of the proportion of cooperators in the population. Starting from the initial state, both processes converge rapidly to a situation in which all non-mutants choose the same action. Under PRI, play can converge either to All Stag or (as is the case in the figure) to All Hare. From that point onwards the process exhibits a punctuated equilibrium-like behaviour, spending the majority of its time in All Hare and occasionally jumping into All Stag. This pattern is due to the accumulation of stochastic mutations, which can dislodge the process from the ruling convention and tip it into the other convention. Everything else being equal, the bigger the population, the longer the periods of stasis. Conversely, the tipping episodes become more frequent as ε increases (Fig. 4 shows an example with ε = 0.10). This alternating pattern is never observed when agents compare themselves with their opponents, because PII makes the maximin convention much more robust to random shocks than does PRI.

Fig. 3

Simulation run — Probability of mutation: 5%. Evolution of cooperation under PRI (top panel) and PII (bottom panel). Payoffs: α = 10, β = 0, γ = δ = 3. Probability of revision: p = 0.50. Probability of mutation: ε = 0.05. Population size: n = 20. Initial proportion of stag hunters: $x_S \left (0 \right ) = 1/2$

Fig. 4

Simulation run — Probability of mutation: 10%. Evolution of cooperation under PRI (top panel) and PII (bottom panel). Payoffs: α = 10, β = 0, γ = δ = 3. Probability of revision: p = 0.50. Probability of mutation: ε = 0.10. Population size: n = 20. Initial proportion of stag hunters: $x_S \left (0\right ) = 1/2$

4.3 Assortative matching

What if interactions were not uniformly random? In some cases it may be more appropriate to assume that individuals meet with one another according to a different rule, which may reflect, among other things, geographic proximity or homophilic group selection. Following Bergstrom (2003; 2013), let $\rho \left (\mathbf {x} \right )$ be the conditional probability for a stag hunter to be matched with another stag hunter and $\tilde {\rho } \left (\mathbf {x} \right )$ be the conditional probability for a hare hunter to be matched with a stag hunter. Thus, the conditional probabilities that a stag hunter is matched with a hare hunter and that a hare hunter is matched with another hare hunter are $1 - \rho \left (\mathbf {x} \right )$ and $1 - \tilde {\rho } \left (\mathbf {x} \right )$, respectively. $\rho \left (\mathbf {x} \right )$ and $1 - \tilde {\rho } \left (\mathbf {x} \right )$ reflect the extent to which those who engage in similar behaviours are more likely than chance to interact.

The expected proportion of pairs in which a stag hunter plays against a hare hunter is $x_{S} \left [ 1 - \rho \left (\mathbf {x} \right ) \right ]$. Since this equals the expected proportion of pairs in which a hare hunter plays against a stag hunter, we have:

$$ \begin{array}{@{}rcl@{}} x_{S} \left[ 1 - \rho \left( \mathbf{x} \right) \right] & =& x_{H} \tilde{\rho} \left( \mathbf{x} \right)\\ & =& \left( 1 - x_{S} \right) \tilde{\rho} \left( \mathbf{x} \right). \end{array} $$

(5)

Bergstrom’s index of assortment, denoted by $\phi \left (\mathbf {x} \right )$, is defined as the difference between the conditional probability that an agent playing a has to meet another agent playing a and the conditional probability that an agent playing $a^{\prime } \neq a$ has to meet an agent playing a:

$$ \phi \left( \mathbf{x} \right) := \rho \left( \mathbf{x} \right) - \tilde{\rho} \left( \mathbf{x} \right). $$

(6)

Equation (6) writes $\phi \left (\mathbf {x} \right )$ as the difference between the probability that a cooperator meets another cooperator and the probability that a defector meets a cooperator. Noting that $\rho \left (\mathbf {x} \right ) - \tilde {\rho } \left (\mathbf {x} \right ) = \left [ 1 - \tilde {\rho } \left (\mathbf {x} \right ) \right ] - \left [ 1 - \rho \left (\mathbf {x} \right ) \right ]$, it is easy to see that this corresponds to the difference between the probabilities that a defector meet another defector and that a cooperator meet a defector. When $\phi \left (\mathbf {x} \right ) > 0$, matching is positively assortative.

Rearranging the terms in Eq. (5) we get $\tilde {\rho } \left (\mathbf {x} \right ) = x_{S} \left [ 1 - \left (\rho \left (\mathbf {x} \right ) - \tilde {\rho } \left (\mathbf {x} \right ) \right ) \right ]$. Then, using (6):

$$ \tilde{\rho } \left( \mathbf{x} \right) = x_{S} \left[1 - \phi \left( \mathbf{x} \right) \right] $$

(7)

and from (6) and (7):

$$ \begin{array}{@{}rcl@{}} \rho \left( \mathbf{x} \right) & =& \phi \left( \mathbf{x} \right) + \tilde{\rho} \left( \mathbf{x} \right)\\ & =& \phi \left( \mathbf{x} \right) + x_{S} \left[1 - \phi \left( \mathbf{x} \right) \right]. \end{array} $$

(8)

As mentioned above, best response updating causes switches from a to $a^{\prime }$ to occur with positive probability if and only if the expected payoff from playing a is greater or equal to the expected payoff from playing $a^{\prime }$. The resulting dynamic is payoff monotone, meaning that in every period the proportions of agents playing Stag and Hare grow at rates that are ordered in the same way as the expected payoffs from the two actions (Weibull 1995). If matching is assortative, then the expected payoff of a stag hunter is:

$$ \begin{array}{@{}rcl@{}} \alpha \rho \left( \mathbf{x} \right) + \upbeta \left[ 1- \rho \left( \mathbf{x} \right) \right] & = &\upbeta + \left( \alpha - \upbeta \right) \rho \left( \mathbf{x} \right) \\ & =& \upbeta + \left( \alpha - \upbeta \right) \left[ \phi \left( \mathbf{x} \right) + x_{S} \left[1 - \phi \left( \mathbf{x} \right) \right] \right] \\ & = &\upbeta + \left( \alpha - \upbeta \right) \phi \left( \mathbf{x} \right) + \left( \alpha - \upbeta \right) x_{S} \left[1 - \phi \left( \mathbf{x} \right) \right], \end{array} $$

(9)

while the expected payoff of a hare hunter is:

$$ \begin{array}{@{}rcl@{}} \gamma \tilde{\rho} \left( \mathbf{x} \right) + \delta \left[ 1- \tilde{\rho} \left( \mathbf{x} \right) \right] & =& \delta + \left( \gamma - \delta \right) \tilde{\rho} \left( \mathbf{x} \right)\\ & =& \delta + \left( \gamma - \delta \right) x_{S} \left[ 1- \phi \left( \mathbf{x} \right) \right]. \end{array} $$

(10)

Subtraction of (10) from (9) gives the difference in the expected gains from cooperating versus defecting when the population state is x:

$$ \upbeta - \delta + \left( \alpha - \upbeta \right) \phi \left( \mathbf{x} \right) + \left( \alpha - \upbeta - \gamma + \delta \right) x_{S} \left[ 1- \phi \left( \mathbf{x} \right) \right]. $$

(11)

For every $\mathbf {x} \in \mathbf {X} \smallsetminus \left \lbrace \left (1, 0 \right ), \left (0, 1 \right ) \right \rbrace$, the rate of growth of x_S and the expression in (11) are of the same sign. In the frequently studied case where the index of assortment is invariant to the state variable (e.g. Cavalli-Sforza and Feldman 1981), switches from Hare to Stag occur only if:

$$ x_{S} \geq \frac{\delta - \upbeta - \left( \alpha - \upbeta \right) \phi }{\left( \alpha - \upbeta - \gamma + \delta \right) \left( 1 - \phi \right)} \equiv \underline{\varpi} , $$

(12)

where $\underline {\varpi }$ is smaller than $\varpi \equiv \frac {\delta - \upbeta }{\alpha - \upbeta - \gamma + \delta }$ for every ϕ > 0. In every state in which $\underline {\varpi } < x_{S} < \varpi$, assortative pairing makes revising agents best respond by playing Stag, whereas uniform random encounters make best responders defect. Put differently, assortment reduces the stochastic potential of All Stag from ⌈ϖn⌉ to $\lceil \underline {\varpi } n \rceil$, and can therefore make the Pareto-superior convention stochastically stable even if Hare is risk-dominant.

Under pairwise imitative dynamics, this result does not hold. PRI and PII do not satisfy payoff monotonicity, because switches do not depend on expected payoffs. For example, suppose that the process is in the state where a single agent cooperates and n − 1 agents defect. If the population is sufficiently small or the gains from mutual cooperation sufficiently high, then the expected payoff from cooperating will still exceed that from defecting. Yet pairwise imitation will drive the process to All Hare, because switches from H to S can occur only when n_S > 1. Keeping in mind that it takes two to catch a Stag, it can be seen that the result of Proposition 2 can be extended to the case of assortative encounters. Under pairwise imitative updating, the stochastic potential of All Hare is 1 regardless of the matching rule being considered. Similarly, the stochastic potential of All Stag is 2 under PRI and n under PII. Thus, the maximin convention continues to be the sole stochastically stable state.

What differentiates the perturbed imitative processes with assortment from those with uniform random encounters is the speed of adjustment from one convention to another. In particular, if cooperators are more likely than chance to meet other cooperators, then the accumulation of random shocks can cause niches of stag hunters to emerge and persist for some time in situations where the prevailing norm is to defect. Also note that under PRI, despite All Hare being the only stochastically stable state, assortment does ease cooperation as compared to the case of uniform random encounters. To see this, recall that a pairwise random imitator will switch from Stag to Hare whenever he interacts with a defector and selects another defector as reference. All other things being equal, the probability of this event is always lower under assortative matching than under uniform random matching. On the other hand, a switch from Hare to Stag requires a defector to select a successful cooperator as reference — an event that is more likely to occur if individuals meet assortatively than if they do not. Thus, assortment increases the probability of a switch from Hare to Stag and reduces the probability of a switch from Stag to Hare. This property does not carry over to the case where agents imitate their opponents, as PII always prevents defectors from switching to Stag.

4.4 Heterogeneous decision rules

So far I have only considered the case where decisions are all based on the same rule of behaviour. However, individuals may have different learning opportunities or decide to follow different rules at different times. One way to account for this is to assume that whenever an agent receives a revision opportunity, he has a positive probability q^κ of following rule $\kappa \in \left \lbrace \text {BR, PRI, PII} \right \rbrace \equiv K$, with ${\sum }_{\kappa \in K} q^{\kappa } = 1$. For simplicity, I restrict myself to the case of uniform random pairing. I write T and $\left (\mathbf {X}, \mathbf {T} \right )$ to denote the transition matrix under heterogeneous rules and the resulting unperturbed Markov chain, respectively, and I write T^ε and $\left (\mathbf {X}, \mathbf {T}^{\varepsilon } \right )$ to indicate their perturbed counterparts.

These assumptions lead to the result below.

Proposition 3

If H is risk-dominant or $n > 2 \big \lfloor \frac {\alpha - \upbeta - \gamma + \delta }{2 \left (\delta - \upbeta \right )}\big \rfloor$, then the sole stochastically stable state of the heterogeneous-population perturbed process is the maximin convention. If S is risk-dominant and $n \leq 2 \big \lfloor \frac {\alpha - \upbeta - \gamma + \delta }{2 \left (\delta - \upbeta \right )}\big \rfloor$, then both the maximin convention and the payoff-dominant convention are stochastically stable.

Proof

Let $\mathbf {B}^{\kappa }_{a}$ denote the basin of attraction of action a under decision rule κ. Since q^κ > 0 for all κ, it is possible that $\left (\mathbf {X}, \mathbf {T} \right )$ will evolve as $\left (\mathbf {X}, \mathbf {T}^{BR} \right )$, $\left (\mathbf {X}, \mathbf {T}^{PRI} \right )$ or $\left (\mathbf {X}, \mathbf {T}^{PII} \right )$ from any initial state. This implies that in the absence of mutations, All Hare is accessible from all states in the set:

$$ \mathbf{B}_{H} = \cup_{\kappa \in K} \mathbf{B}_{H}^{\kappa} = \left\lbrace \mathbf{x} \in \mathbf{X} : n_{H} > 0 \right\rbrace , $$

while All Stag is accessible from all states in:

$$ \mathbf{B}_{S} = \cup_{\kappa \in K} \mathbf{B}_{S}^{\kappa} = \left\lbrace \mathbf{x} \in \mathbf{X} : n_{S} \geq \min \left\lbrace \left\lceil\frac{n \left( \delta - \upbeta \right)}{\alpha - \upbeta - \gamma +\delta}\right\rceil , 2 \right\rbrace \right\rbrace. $$

Starting from All Stag, B_H is reached after a single mutation. From that point it is possible to move into All Hare in a finite number of periods without any further mistake, meaning that the least resistance to moving from All Stag to All Hare is:

$$ r_{SH} = \min \left\lbrace \left( r^{\kappa}_{SH} \right)_{\kappa\in K} \right\rbrace = 1. $$

Similarly, the least resistance to moving from All Hare to All Stag is:

$$ r_{HS} = \min \left\lbrace \left( r^{\kappa}_{HS} \right)_{\kappa\in K} \right\rbrace = \min \left\lbrace \left\lceil{\frac{n \left( \delta - \upbeta \right)}{\alpha - \upbeta - \gamma +\delta}}\right\rceil , 2 \right\rbrace , $$

which, since n is assumed to be even, equals 1 if and only if:

$$ n \leq 2 \left\lfloor\frac{\alpha - \upbeta - \gamma + \delta}{2 \left( \delta - \upbeta \right)}\right\rfloor , $$

(13)

that is if and only if n is smaller than or equal to the largest multiple of 2 not greater than $\left (\alpha - \upbeta - \gamma + \delta \right ) / \left (\delta - \upbeta \right )$. If the condition in (13) does not hold, then r_HS = 2 > r_SH = 1 and All Hare is the sole stochastically stable state. Note that if α+β < γ + δ (so that H is risk-dominant), then $\left (\delta - \upbeta \right ) / \left (\alpha - \upbeta - \gamma + \delta \right ) > 1 / 2$ and the inequality in (13) cannot be satisfied by any positive n. In order for the stochastic potential of All Stag to be 1, the risk-dominant action must therefore be S. If the condition in (13) holds and S risk-dominates H, then r_HS = r_SH = 1 and both All Stag and All Hare are stochastically stable. □

Proposition 3 states that if Hare risk-dominates Stag or the population is sufficiently large, then All Hare is the only stochastically stable state of the perturbed process $\left (\mathbf {X}, \mathbf {T}^{\varepsilon } \right )$. Conversely, if Stag is risk-dominant and the population is small enough, then All Stag and All Hare are both stochastically stable. The intuition here is as follows. Every time an agent receives a revision opportunity, he has a positive probability of following a pairwise imitative rule. Thus, since the stochastic potential of All Hare is 1 under both PRI and PII, there is a possibility (but not a certainty) that the process will transit from the payoff-superior convention to the maximin convention after a single mutation. This is true regardless of which action is risk-dominant. On the contrary, the least resistance to moving from All Hare to All Stag depends both on payoffs and the population size. Specifically, for a single mutation to make best responders cooperate, $1 / n > \left (\delta - \upbeta \right ) / \left (\alpha - \upbeta - \gamma + \delta \right )$ must hold. It follows that in order for All Stag to be stochastically stable along with All Hare, the population cannot exceed the maximum size given in (13). Finally, when Hare risk-dominates Stag, the condition in (13) cannot be satisfied. In this case, the sole long-run convention is the maximin convention.

To make the ideas concrete, let α = 100, β = 0 and γ = δ = 3. From Proposition 3 we see that the two conventions are both stochastically stable if and only if it is payoff-maximising to play Stag when x_S = 1/n. This, in turn, requires that the population consist of at most 32 agents. Ceteris paribus, the bound on the population size becomes less tight as the payoff from mutual cooperation increases, or, put another way, the Pareto-superior convention can emerge in large populations only if the gains from a joint stag hunt exceed those from defection by a considerable extent.

A more general result can be stated as follows. Let $K^{\prime } \equiv \left \lbrace \kappa _{1}, \kappa _{2} \dots , \kappa _{n} \right \rbrace$ be a finite set of decision rules, and let $Q_{K^{\prime }}$ be the probability distribution which describes how likely a revising agent is to follow each rule in $K^{\prime }$. Suppose that $\text {PII} \in K^{\prime }$ and that $Q_{K^{\prime }}$ assigns a strictly positive probability to PII being followed. If there exists $\kappa _{i} \in K^{\prime }$ such that the least resistance to moving from All Hare to All Stag is 1, then both All Stag and All Hare are stochastically stable; if not, then the only stochastically stable state is All Hare. Moreover, since $r_{SH}^{PRI} = r_{SH}^{PII} = 1$, the same is true when PRI belongs to $K^{\prime }$ while PII does not. This allows us to extend the model to cases where, for example, revising agents take action after observing a group of individuals of random size m. Under the random-size sampling assumption, if PRI and BR are the limiting cases of m = 1 and m = n, then a result similar to that of Proposition 3 holds.

5 Concluding remarks

Achievements and behaviours are often assessed on the basis of how they compare with those of other people. With this in mind, this paper presented an evolutionary model of the Stag Hunt where agents’ decisions depend on payoff comparisons.

I considered two different imitate-if-better rules: one which makes individuals compare with a randomly selected agent, the other which makes them focus on how well they do relative to their opponent. The resulting dynamics were compared with that observed when agents follow a myopic best response rule. Under best response updating, it is well-known that evolutionary forces frequently favour the risk-dominant convention. Moreover, if interactions are assortative, the Pareto-superior convention can emerge in the long run even when it is risk-dominant to defect. Under pairwise imitative updating, this is not the case: the Pareto-inferior convention is singled out as the sole stochastically stable state, regardless of how rewarding it can be to cooperate, even when introducing assortment and (under some mildly restrictive conditions) heterogeneous decision rules.

Some general points are worth noting here. First, the model suggests that studying the Stag Hunt through the lens of the payoff/risk-dominance dichotomy is not always appropriate. Pairwise imitation makes risk-dominance play essentially no role, in which case the problem is best understood by contrasting the payoff-dominant and the maximin equilibria. Second, assortment does not necessarily push towards cooperative outcomes: its effect on long-run patterns of behaviour crucially depends on the decision rule considered. Third, whether or not imitation allows Pareto-improvements over the noncooperative equilibrium depends on the information available to and used by agents. Interact-and-imitate rules make individuals forgo the learning opportunities associated with reciprocated cooperation, and permit switches from Stag to Hare only; random imitative rules allow agents to obtain information from elsewhere in the population and learn from successful stag hunts. Clearly, more demanding rules based on larger reference groups would result in a greater likelihood of observing mutual cooperation, thereby making switches from Hare to Stag easier (Khan 2014). For example, in the extreme case where agents imitate the most successful individual in the whole population, a single pair of interacting stag hunters would make everyone cooperate.⁴

These results are in line with those of Alós-Ferrer and Weidenholzer (2014), who, in a different model, show that if information does not circulate among agents, then imitation leads to the emergence of inefficient equilibria. They are also consistent with the experimental findings of Proto et al. (2019) that cognitive abilities and personality traits affect strategic behaviour and the willingness to cooperate in repeated games. As we have seen, if agents judge success in comparative terms and follow informationally undemanding, unsophisticated rules based on imitation of another individual, then it is difficult to sustain cooperation. This is especially so in the case of interact-and-imitate behaviours: when people strive not to fall short of others with whom they interact, the road to establishing a social contract becomes very steep.