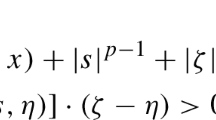On systems of parabolic variational inequalities with multivalued terms

Abstract

In this paper we present an analytical framework for the following system of multivalued parabolic variational inequalities in a cylindrical domain $Q=\varOmega \times (0,\tau )$: For $k=1,\dots , m$, find $u_k\in K_k$ and $\eta _k\in L^{p'_k}(Q)$ such that

$$\begin{aligned}&u_k(\cdot ,0)=0\ \text{ in } \varOmega ,\ \ \eta _k(x,t)\in f_k(x,t,u_1(x,t), \dots , u_m(x,t)), \\&\langle u_{kt}+A_k u_k, v_k-u_k\rangle +\int _Q \eta _k\, (v_k-u_k)\,dxdt\ge 0,\ \ \forall \ v_k\in K_k, \end{aligned}$$

where $K_k$ is a closed and convex subset of $L^{p_k}(0,\tau ;W_0^{1,p_k}(\varOmega ))$, $A_k$ is a time-dependent quasilinear elliptic operator, and $f_k:Q\times \mathbb {R}^m\rightarrow 2^{\mathbb {R}}$ is an upper semicontinuous multivalued function with respect to $s\in {\mathbb R}^m$. We provide an existence theory for the above system under certain coercivity assumptions. In the noncoercive case, we establish an appropriate sub-supersolution method that allows us to get existence and enclosure results. As an application, a multivalued parabolic obstacle system is treated. Moreover, under a lattice condition on the constraints $K_k$, systems of evolutionary variational-hemivariational inequalities are shown to be a subclass of the above system of multivalued parabolic variational inequalities.

1 Introduction

Let $\varOmega \subset \mathbb {R}^N$ be a bounded domain with Lipschitz boundary $\partial \varOmega$, $Q=\varOmega \times (0,\tau )$ a space-time cylindrical domain with base $\varOmega$, and $\varGamma =\partial \varOmega \times (0,\tau )$ its lateral boundary with $\tau >0.$ For $p\in (1,\infty )$, we denote by $W^{1,p}(\varOmega )$ and $W^{1,p}_0(\varOmega )$ the usual Sobolev spaces with dual spaces $(W^{1,p}(\varOmega ))^*$ and $W^{-1,p'}(\varOmega )$, respectively, where $p'$ is the Hölder conjugate of p satisfying $1/p+1/p'=1$. Note that if $2\le p<\infty$, then $W^{1,p}(\varOmega )$ $\subset L^2(\varOmega )\subset (W^{1,p}(\varOmega ))^*$ form an evolution triple with all the imbeddings being dense and compact (see e.g. [18]) .

Let $m\in {\mathbb N}$ and $p_1, \dots , p_m \in [2, \infty )$. We are concerned in this paper with the following system of m multivalued parabolic variational inequalities: For each $k =1 , \dots , m$, find $u_k\in W_{0k}\cap K_k$ and $\eta _k\in L^{p'_k}(Q)$ such that

$$\begin{aligned}&u_k(\cdot ,0)=0\ \text{ in } \varOmega ,\ \ \eta _k(x,t)\in f_k(x,t,u_1(x,t), \dots , u_m(x,t)), \end{aligned}$$

(1.1)

$$\begin{aligned}&\langle u_{kt}+A_k u_k, v_k-u_k\rangle +\int _Q \eta _k\, (v_k-u_k)\,dxdt\ge 0,\ \ \forall \ v_k\in K_k, \end{aligned}$$

(1.2)

where $K_k$ is a closed, convex subset of $X_{0k} := L^{p_k}(0,\tau ; W_0^{1,p_k}(\varOmega ))$, $W_{0k}=\{u_k\in X_{0k} : u_{kt}\in X_{0k}^*\}$, and $\langle \cdot ,\cdot \rangle$ denotes the duality pairing between $X_{0k}^*$ and $X_{0k}$. The operator $A_k: X_{0k}\rightarrow X_{0k}^*$ is a second order quasilinear differential operator of Leray-Lions type, given by

$$\begin{aligned} A_k(u_k)(x,t)=-\sum _{i=1}^N\frac{\partial }{\partial x_i}a_i^{(k)}(x,t, \nabla u_k(x,t)), \end{aligned}$$

and $f_k:Q\times \mathbb {R}^m\rightarrow 2^{\mathbb {R}}$, $(x,t,s_1, \dots , s_m)\mapsto f_k(x,t,s_1, \dots , s_m)\in 2^{\mathbb {R}}$, is an upper semicontinuous multivalued function with respect to $s:=(s_1, \dots , s_m)\in {\mathbb R}^m$, that will be specified later.

The main goal of this article is to present a mathematical theory for systems of parabolic variational inequalities with upper semicontinuous multivalued functions of the form (1.1)–(1.2) in both coercive and noncoercive cases, and to provide existence and enclosure principles when subsolutions and supersolutions of (1.1)–(1.2), defined in certain appropriate sense, exist. To the best of our knowledge, systems of parabolic multivalued variational inequalities have not been studied before in a systematic way by sub-supersolution (lattice) approaches. Moreover, we point out here that the closed and convex sets $K_k$’s that represent constraints in system (1.1)–(1.2) are not supposed to have nonempty interior parts or to satisfy some conditions of similar type. Such assumptions typically allow the application of Rockafellar’s theorem about sums of maximal monotone operators, which facilitates the study of parabolic variational inequalities considerably by the implementation of arguments and results for elliptic variational inequalities to parabolic variational inequalities. However, assumptions of these types would exclude the investigation of certain most important classes of evolutionary variational inequalities such as parabolic obstacles problems, in which the associated closed and convex sets representing the obstacles have empty interior parts. As will be seen later, our approach here applies also to obstacle problems. We also remark that (1.1)–(1.2) covers a wide range of parabolic systems when specifying K and/or f such as the special cases mentioned above including parabolic initial-boundary value problem in the case when $K=X_0$, and $f:Q\times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function. Moreover, under a lattice condition on the constraints $K_k$, systems of evolutionary variational-hemivariational inequalities will be shown to be a subclass of the above system of multivalued parabolic variational inequalities (1.1)–(1.2).

The paper is organized as follows. After introducing necessary assumptions and notations and providing auxiliary results, including one on the pseudomonotonicity of multivalued Nemytskij operators with respect to the graph norm of the time derivative operator, in Sects. 2 and 3, we present our main results in Section 4. In the first part (Sect. 4.1) we treat the coercive case, where some relative growth condition of $A_k$ and $f_k$ for u with large norm is imposed. In this case the existence of solutions of (1.1)–(1.2) follows from penalty arguments and the solvability of systems of equations with multivalued pseudomonotone operators. In the second part (Sect. 4.2), we deal with the noncoercive case where such growth condition is not assumed. We establish in that section a sub-supersolution method that will allow us to prove existence and enclosure results. The concepts of sub- and supersolutions and the arguments in our case here are combinations of those for parabolic multivalued variational inequalities in [5] and those for systems of multivalued elliptic variational inequalities in [10]. In Sect. 5, as an application of the theory developed in the preceding sections, we treat an obstacle problem by explicitly constructing an ordered pair of sub- and supersolutions. Finally, we show in Section 6 that under a lattice condition on the constraints, systems of evolutionary variational-hemivariational inequalities turn out to be only a subclass of system (1.1)–(1.2).

2 Assumptions: setting of the problem

Let us begin with some needed notation and assumptions. Let $\varOmega$, Q, $X_{0k}$, and $W_{0k}$ be defined as in Sect. 1, and $L^0(\varOmega )$ (resp. $L^0(Q)$) be the set of all (equivalent classes of) measurable functions from $\varOmega$ (resp. from Q) to ${\mathbb R}$.

For $k = 1, \dots , m$, let $W_k$ be defined by

$$\begin{aligned} W_k =\{u\in X_k : u_t\in X_k^*\}\,, \end{aligned}$$

where $X_k = L^{p_k}(0,\tau ; W^{1,p_k}(\varOmega ))$ with its dual $X_k^* =L^{p_k'}(0,\tau ; (W^{1,p_k}(\varOmega ))^*)$, and the derivative $u_t:=\partial u/\partial t$ is understood in the sense of vector-valued distributions.

The space $W_k$ endowed with the graph norm of the operator $\partial /\partial t$

$$\begin{aligned} \Vert u\Vert _{W_k} =\Vert u\Vert _{X_k}+\Vert u_t\Vert _{ X_k^*} \end{aligned}$$

is a Banach space which is separable and reflexive due to the separability and reflexivity of $X_k$ and $X_k^*$, where $\Vert \cdot \Vert _{X_k}$ and $\Vert \cdot \Vert _{X_{0k}}$ are the usual norms defined on $X_k$ and $X_{0k}$ (and similarly on $X_k^*$ and $X_{0k}^*$) :

$$\begin{aligned} \Vert u\Vert _{X_k} = \left( \int _0^\tau \Vert u (t)\Vert _{W^{1,p_k}(\varOmega )}^{p_k} \, dt \right) ^{1/{p_k}}, \; \Vert u\Vert _{X_{0k}} = \left( \int _0^\tau \Vert u (t) \Vert _{W^{1,p_k}_0(\varOmega )}^{p_k} \, dt \right) ^{1/p_k}. \end{aligned}$$

For any $k\in \{1, \dots , m\}$, $W_k$ is continuously embedded into $C([0,\tau ],\,L^2(\varOmega ))$. Thus, by Aubin’s lemma, the embedding $W_k\hookrightarrow \hookrightarrow L^{p_k}(Q)$ is compact due to the compact embedding $W^{1,p_k}(\varOmega )\hookrightarrow \hookrightarrow L^{p_k}(\varOmega )$. Similar properties hold true for the space $W_{0k}$,

$$\begin{aligned} W_{0k} =\{u\in X_{0k} : u_t\in X_{0k}^*\}, \end{aligned}$$

introduced in Sect. 1.

For $k = 1, \dots , m$, we denote by $L_k:=\partial /\partial t$, where its domain of definition, $D(L_k)$, is given by

$$\begin{aligned} D(L_k) = \left\{ u\in X_{0k} : u_t\in X_{0k}^* \text{ and } u(\cdot ,0) =0 \right\} . \end{aligned}$$

(2.1)

It is known that the linear operator $L_k: D(L_k)\subset X_{0k}\rightarrow X_{0k}^*$ is closed, densely defined and maximal monotone, e.g., cf. [18, Chap. 32].

For $u,v\in {\mathbb R}^m$, we denote $u\le v$ if $u_k \le v_k,\forall k\in \{1,\dots , m\}$. This ordering is extended to functions $u,v \in [L^0(\varOmega )]^m$ (resp. $u,v \in [L^0(Q)]^m$) in a natural way: $u\le v$ if and only if $u(x) \le v(x)$ for a.e. $x\in \varOmega$ (resp. $u(x,t) \le v(x,t)$ for a.e. $(x,t)\in Q$). If $u_j\in {\mathbb R}$ with $j\in \{1,\dots , m\}{\setminus } \{k\}$, and $t\in {\mathbb R}$, then we denote

$$\begin{aligned}{}[u]_k= & {} (u_1,\dots , u_{k-1}, u_{k+1},\dots , u_m)\in {{\mathbb R}}^{m-1},\\ (t, [u]_k)= & {} (u_1,\dots , u_{k-1}, t, u_{k+1},\dots , u_m)\in \mathbb {R}^m, \end{aligned}$$

For $u\in {\mathbb R}^m$, we also use the same notation $[u]_k$ for $(u_1,\dots , u_{k-1}, u_{k+1},\ldots , u_m)\in {{\mathbb R}}^{m-1}$. Let $u,v\in {\mathbb R}^m$ such that $u\le v$, we put

$$\begin{aligned}{}[u,v] = \{w\in {\mathbb R}^m : u \le w \le v\}. \end{aligned}$$

Similarly, for $k\in \{1,\dots , m\}$ and $[u]_k, [v]_k\in {\mathbb R}^{m-1}$ with $[u]_k \le [v]_k$, we denote

$$\begin{aligned}{}[u,v]_k = [[u]_k, [v]_k] = \{[w]_k \in {\mathbb R}^{m-1} : [u]_k \le [w]_k \le [v]_k\} . \end{aligned}$$

We use the same notation for vector functions, that is, for $u,v\in [L^0(Q)]^m$ or $u,v\in \prod _{j=1}^m X_j$ and for $[u]_k,[v]_k\in [L^0(Q)]^{m-1}$ or $[u]_k , [v]_k\in \prod _{j\in \{1,\dots , m\}{\setminus } \{k\}} X_j$. For example, if $u,v\in \prod _{j=1}^m X_j=X$ and $u\le v$, then

$$\begin{aligned}{}[u,v] = \{w\in X : u \le w \le v\}, \end{aligned}$$

and if $[u]_k , [v]_k\in \prod _{j\in \{1,\dots , m\}{\setminus } \{k\}} X_j$ and $u\le v$, then

$$\begin{aligned}{}[u,v]_k = [[u]_k, [v]_k] = \left\{ [w]_k \in \prod _{j\in \{1,\dots , m\}{\setminus } \{k\}} X_j : [u]_k \le [w]_k \le [v]_k \right\} . \end{aligned}$$

(2.2)

For a normed vector space Z, we denote by ${\mathcal K}(Z)$ the collection of all nonempty, closed, and convex subsets of Z. Let $Z_1, \dots , Z_m$ be Banach spaces with the corresponding norms $\Vert \cdot \Vert _{Z_1}, \dots , \Vert \cdot \Vert _{Z_m}$. The product $Z = \prod _{k=1}^m Z_k$ is a Banach space with the product norm: $\Vert u \Vert _Z = \sum _{k=1}^m \Vert u_k \Vert _{Z_k}$ for $u = (u_1, \dots , u_m)\in Z$.

We use here the standard identification of $u^*\in Z^*$ with $(u_1^*,\dots , u_m^*)\in \prod _{k=1}^m Z_k^*$ by

$$\begin{aligned} \langle u_k^* , u_k\rangle _{Z_k^*, Z_k} = \langle u^* , (u_k , [0]_k)\rangle _{Z^*, Z}, \;\forall u_k\in Z_k , \;\forall k\in \{1, \dots , m\} , \end{aligned}$$

(2.3)

and

$$\begin{aligned} \langle u^* , u\rangle _{Z^*, Z} = \langle (u_1^* , \dots , u_m^*) , (u_1 , \dots , u_m) \rangle _{Z^*, Z} = \sum _{k=1}^m \langle u_k^* , u_k\rangle _{Z_k^*, Z_k} , \;\forall u\in Z . \end{aligned}$$

(2.4)

In this pattern, we consider the following product spaces:

$$\begin{aligned} X = \prod _{k=1}^m X_k, \; X_0 = \prod _{k=1}^m X_{0k}, \; W = \prod _{k=1}^m W_k, \; W_0 = \prod _{k=1}^m W_{0k}, \end{aligned}$$

and their dual spaces,

$$\begin{aligned} X^* \equiv \prod _{k=1}^m X_k^*, \; X_0^* \equiv \prod _{k=1}^m X_{0k}^*, \; W^* \equiv \prod _{k=1}^m W_k^*, \; W_0^* \equiv \prod _{k=1}^m W_{0k}^*. \end{aligned}$$

For simplicity of notation and when there is no confusion, we use $\Vert \cdot \Vert$ for the norms in $X,X_0$, $X_k$, and $X_{0k}$. By the same token, $\langle \cdot , \cdot \rangle$ stands for any of the dual pairings between any of the spaces $X_k$, $X_{0k}$, $W^{1,p_k}(\varOmega )$, $W_0^{1,p_k}(\varOmega )$, X, $X_{0}$, $\prod _{k=1}^m W^{1,p_k}(\varOmega )$, $\prod _{k=1}^m W_0^{1,p_k}(\varOmega )$, and its corresponding dual space. For example, if $u^*\in X^*$ and $u\in X$, then

$$\begin{aligned} \langle u^*,u\rangle =\int _0^\tau \langle u^*(t), u(t) \rangle \, dt = \sum _{k=1}^m \int _0^\tau \langle u_k^*(t), u_k(t) \rangle \, dt. \end{aligned}$$

However, indices will be used in the above norms and dual pairings wherever clarification is needed.

We consider next some assumptions imposed on the principal and lower order terms in (1.1)–(1.2). For $k = 1, \dots , m$, let us assume the following Leray–Lions conditions on the coefficient $a_i^{(k)}$, $i=1,\dots ,N$, of the operator $A_k$.

• (A1) $a_i^{(k)}:Q\times \mathbb {R}^N\rightarrow \mathbb {R}$ are Carathéodory functions, i.e., $a_i^{(k)}(\cdot ,\cdot ,\xi ): Q\rightarrow \mathbb {R}$ is measurable for all $\xi \in \mathbb {R}^N$ and $a_i^{(k)}(x,t, \cdot ): \mathbb {R}^N\rightarrow \mathbb {R}$ is continuous for a.e. $(x,t)\in Q$. In addition, the following growth condition holds:

  $$\begin{aligned} |a_i^{(k)}(x,t,\xi )|\le c_1^{(k)} |\xi |^{p_k-1}+c_2^{(k)}(x,t) \end{aligned}$$

  for a.e. $(x,t)\in Q$ and for all $\xi \in \mathbb {R}^N$, for some constant $c_1^{(k)}>0$ and some function $c_2^{(k)}\in L^{p'_k}_+(Q)$.

• (A2) (Strict monotonicity) For a.e. $(x,t)\in Q\,,$ and for all $\xi ,\xi '\in \mathbb {R}^N$ with $\xi \ne \xi '$ the following monotonicity in $\xi$ holds:

  $$\begin{aligned} \sum _{i=1}^N(a_i^{(k)}(x,t,\xi )-a_i^{(k)}(x,t,\xi '))(\xi _i-\xi '_i)> 0. \end{aligned}$$

• (A3) There is some constant $c_3^{(k)}>0$ such that for a.e. $(x,t)\in Q$ and for all $\xi \in \mathbb {R}^N$ the inequality

  $$\begin{aligned} \sum _{i=1}^Na_i^{(k)}(x,t,\xi )\xi _i\ge c_3^{(k)}|\xi |^{p_k}-c_4^{(k)}(x,t) \end{aligned}$$

  is satisfied for some function $c_4^{(k)}\in L^1(Q).$

In view of (A1), the operator $A_k$ defined by

$$\begin{aligned} \langle A_k u,\varphi \rangle := \int _Q \sum _{i=1}^Na_i^{(k)}(x,t,\nabla u)\frac{\partial \varphi }{\partial x_i}\,dx\,dt,\ \ \forall \varphi \in X_{0k}, \end{aligned}$$

(2.5)

is continuous and bounded from $X_{0k}$ into $X_{0k}^*$.

For functions $w,\ z$ and sets W and Z of functions we use the notations: $w\wedge z=\min \{w,z\},$ $w\vee z=\max \{w, z\},$ $W\wedge Z=\{w\wedge z : w\in W,\ z\in Z\},$ $W\vee Z=\{w\vee z : w\in W,\ z\in Z\},$ and $w\wedge Z=\{w\}\wedge Z,$ $w\vee Z=\{w\}\vee Z.$ In particular, we denote $w^+=w\vee 0$.

For $k = 1, \dots , m$, let us introduce the multivalued Nemytskij operator $F_k$ associated with the multivalued function $f_k:Q\times \mathbb {R}\rightarrow {\mathcal K}({\mathbb {R}})$ by

$$\begin{aligned} \begin{array}{lll} F_k(u) &{} = &{} \{\eta : Q \rightarrow \mathbb {R} : \eta \text { is measurable on}\,\, Q\,\, \hbox {and } \\ &{}&{} \eta (x,t)\in f_k(x,t,u(x,t)) \text{ for } \text{ a.e. }\,\, (x,t)\in Q\}. \end{array} \end{aligned}$$

(2.6)

For each $k\in \{1,\dots , m\}$, we impose the following conditions on $f_k$:

• (F1) $f_k: Q\times \mathbb {R}^m \rightarrow \mathcal {K}(\mathbb {R})$ is graph measurable on $Q\times \mathbb {R}^m$, that is,

  $$\begin{aligned} \mathrm{Gr}(f_k) := \{(x,t , u,\eta ) \in Q\times \mathbb {R}^m\times \mathbb {R} : \eta \in f(x, t , u)\} \end{aligned}$$

  belongs to $[{\mathcal L}(Q)\times {\mathcal B}(\mathbb {R}^m)]\times {\mathcal B}(\mathbb {R})$, where ${\mathcal L}(Q)$ is the family of Lebesgue measurable subsets of Q and ${\mathcal B}(\mathbb {R}^m)$ (resp. ${\mathcal B}(\mathbb {R})$) is the $\sigma$-algebra of Borel sets in $\mathbb {R}^m$ (resp. in $\mathbb {R}$).

• (F2) For a.e. $(x,t)\in Q$, the function $f_k(x,t,\cdot ) : \mathbb {R}^m \rightarrow \mathcal {K}(\mathbb {R})$ is upper semicontinuous.

• (F3) $f_k$ satisfies the growth condition

  $$\begin{aligned} \sup \{|\eta | : \eta \in f_k(x,t ,s)\} \le \alpha _k (x,t) + \beta _k \sum _{j=1}^m |s_j|^{\frac{p_j}{p_k'}} , \end{aligned}$$

  (2.7)

  for a.e. $(x,t)\in Q,\ \forall \ s\in \mathbb {R}^m$, where $\alpha _k \in L^{p'_k}(Q),$ and $\beta _k \ge 0$.

For any $u \in [L^0(Q)]^m$, it follows from (F1) that the function $(x,t)\mapsto f_k(x,t,u(x,t))$ is also a measurable function from Q to $\mathcal {K}(\mathbb {R})$, which implies that $F_k(u) \not =\emptyset$. Moreover, as a consequence of (F3), we see that $F_k(u) \subset L^{p'_k}(Q)$ whenever $u\in \prod _{j=1}^m L^{p_j}(Q)$. Hence, the Nemytskij operator $F_k$ is a well defined mapping from $\prod _{j=1}^m L^{p_j}(Q)$ to $2^{L^{p'_k}(Q)}{\setminus } \{\emptyset \}$.

Let $i_k: X_{0k}\hookrightarrow L^{p_k}(Q)$ be the (continuous) embedding of $X_{0k}$ into $L^{p_k}(Q)$, and let $i_k^* : L^{p_k'}(Q) \hookrightarrow X_{0k}^*$ be its adjoint. The mapping $i_k^*$ is the natural restriction on $X_{0k}$ in the following sense:

$$\begin{aligned} i_k^*(w_k^*) = w_k^*|_{X_{0k}}, \;\forall w_k^*\in L^{p_k'}(Q) (\equiv [L^{p_k}(Q)]^*). \end{aligned}$$

Let $i = i_{1} \times \dots \times i_{m} : X_0 \rightarrow \prod _{k=1}^m L^{p_k}(Q)$, $u \mapsto u$, $\forall u\in X_0$ be the embedding of $X_0$ into $\prod _{k=1}^m L^{p_k}(Q)$. Hence, its adjoint $i^* : \prod _{k=1}^m L^{p_k'}(Q) \rightarrow X_{0}^*$ is the natural restriction on $X_0$, i.e.,

$$\begin{aligned} \begin{array}{lll} i^* (w^*) &{} = &{} i^*(w_1^*, \dots , w_m^*) = (i_1^*(w_1^*), \dots , i_m^*(w_m^*)) = (w_1^*|_{X_{01}}, \dots , w_m^*|_{X_{0m}}) \\ &{} = &{} w^*|_{X_0}. \end{array} \end{aligned}$$

Let us define $F = (F_1, \dots , F_m) : \prod _{k=1}^m L^{p_k}(Q) \rightarrow 2^{\prod _{k=1}^m L^{p_k'}(Q)}$, $F(u) = \prod _{k=1}^m F_k(u)$, and its corresponding composed operator

$$\begin{aligned} \mathcal {F}=i^*\circ F\circ i: X_0\rightarrow 2^{X_0^*} . \end{aligned}$$

(2.8)

In the next step, we shall formulate the system (1.1)–(1.2) as a single variational inequality. Let us define $A : X_0 \rightarrow X_0^*$ by

$$\begin{aligned} A u = (A_1 u_1 , \dots , A_m u_m), \;\forall u = (u_1, \dots , u_m) \in X_0 , \end{aligned}$$

(2.9)

with $A_1 , \dots , A_m$ given by (2.5). It follows from the corresponding property of $A_1 , \dots , A_m$ that A is a continuous and bounded operator from $X_0$ to $X_0^*$. Next, we define

$$\begin{aligned} D(L) = \prod _{k=1}^m D(L_k) , \end{aligned}$$

which can be easily seen as

$$\begin{aligned} D(L) = \left\{ u\in X_{0} : u_t\in X_{0}^* \text{ and } u(\cdot ,0) =0 \right\} . \end{aligned}$$

(2.10)

The time derivative for vector-valued functions is defined by $L : D(L) \rightarrow X_0^*$, $L = L_1\times \dots \times L_k$, that is,

$$\begin{aligned} Lu =(L_1 u_1 , \dots , L_m u_m) = (u_{1t} , \dots , u_{mt}) = u_t \in \prod _{k=1}^m X_{0k}^* \equiv X_0^* , \end{aligned}$$

(2.11)

for all $u = (u_1, \dots , u_m) \in D(L)$.

Lastly, let

$$\begin{aligned} K = \prod _{k=1}^m K_k, \end{aligned}$$

(2.12)

which is a closed and convex subset of $X_0$. With these definitions and settings, we see that the system (1.1)–(1.2) can be formulated as the following multivalued evolutionary variational inequality: Find $u\in D(L)\cap K$ and $\eta \in {\mathcal F}(u)$ such that

$$\begin{aligned} \langle Lu + Au + \eta , v-u \rangle \ge 0, \;\forall v\in K . \end{aligned}$$

We study in the sequel the existence of solutions of this variational inequality in both coercive and noncoercive cases.

3 Auxiliary results

We first have the following simple, yet essential, property of the time derivative operator in the vector case.

Proposition 3.1

The operator L given in (2.11) is a linear, closed, densely defined and maximal monotone operator from $D(L) \subset X_0$ to $X_0^*$.

Proof

By mathematical induction, the above properties of L immediately follow from the corresponding properties of the component operators $L_k$ ($k=1, \dots , m$), which are well known for the time derivative operator. $\square$

We are now ready to state and prove a crucial property of ${\mathcal F}$, which is its pseudo-monotonicity with respect to the graph norm topology of the domain D(L) of L. Let us recall the following definition of a multivalued pseudomonotone operator with respect to the graph norm topology of the domain D(L) (w.r.t. D(L) for short) of a linear, closed, densely defined and maximal monotone operator $L: D(L)\subset Y\rightarrow Y^*$ (cf. [3, 8, 16]).

Definition 3.1

Let Y be a reflexive Banach space, and let $L: D(L)\subset Y\rightarrow Y^*$ be a linear, closed, densely defined and maximal monotone operator. The operator $\mathcal {T}: Y\rightarrow 2^{Y^*}$ is called pseudomonotone w.r.t. D (L) if the following conditions are satisfied:

• (i) The set $\mathcal {T}(u)$ is nonempty, bounded, closed and convex for all $u\in Y.$

• (ii) $\mathcal {T}$ is upper semicontinuous from each finite dimensional subspace of Y to $Y^*$ equipped with the weak topology.

• (iii) If $\{u_n\}\subset D(L)$ with $u_n \rightharpoonup u$ in Y, $Lu_n \rightharpoonup Lu$ in $Y^*$, $u_n^*\in \mathcal {T}(u_n)$ with $u_n^* \rightharpoonup u^*$ in $Y^*$ and $\limsup \langle u_n^*, u_n-u\rangle \le 0,$ then $u^*\in \mathcal {T}(u)$ and $\langle u_n^*,u_n\rangle \rightarrow \langle u^*,u\rangle .$

Similarly, we have the following definition of operators of class $(S_+)$ with respect to the graph norm topology of the domain D(L) (w.r.t. D(L) for short).

Definition 3.2

Let Y be a reflexive Banach space, and let $L: D(L)\subset Y\rightarrow Y^*$ be a linear, closed, densely defined and maximal monotone operator. The operator $\mathcal {T}: Y\rightarrow Y^*$ is said to be of class $(S_+)$ w.r.t. D(L) if for any sequences $\{u_n\} \subset D(L)$, the conditions $u_n \rightharpoonup u$ in $X_0$, $L u_n \rightharpoonup L u$ in $X_0^*$ and $\limsup \langle T u_n, u_n-u \rangle \le 0$ imply that $u_n \rightarrow u$ in $X_0$.

Proposition 3.2

Under conditions (A1)–(A3), the operator $A : X_0 \rightarrow X_0^*$ defined by (2.5) and (2.9) is of class $(S_+)$ w.r.t. D(L), where L and D(L) are given by (2.10)-(2.11).

Proof

It is known (cf. e.g. [1, 2, 4]) that under conditions (A1)–(A3), each operator $A_k$ given by (2.5) is of class $(S_+)$ on $X_{0k}$ w.r.t. $D(L_k)$. By mathematical induction, we see directly from the definition of A in (2.9) that A is also of class $(S_+)$ w.r.t. D(L). $\square$

We have the following result about the pseudomonotonicity of $\mathcal {F}$, which is a vector version of Proposition 2.2, [5].

Proposition 3.3

Under conditions (F1)–(F3), the mapping $\mathcal {F}=i^*\circ F\circ i: X_0\rightarrow 2^{X_0^*}$ is pseudomonotone with respect to D(L), where L and D(L) are given by (2.10)–(2.11).

Proof

The proof of this proposition is divided into three steps.

Step 1: Property (i) of Definition 3.1

We prove in this step that ${\mathcal F}$ is a bounded mapping from $X_0$ to ${\mathcal K}(X_0^*)$.

First, we prove that for any $u\in \prod _{k=1}^m L^{p_k}(Q)$, F(u) is a nonempty, bounded, closed, and convex subset of $\prod _{k=1}^m L^{p'_k}(Q)$ and in particular,

$$\begin{aligned} F(u)\in \mathcal {K}\Big (\prod _{k=1}^m L^{p'_k}(Q)\Big ). \end{aligned}$$

Moreover, we will prove next that the mapping

$$\begin{aligned} F: \prod _{k=1}^m L^{p_k}(Q)\rightarrow \mathcal {K}\Big (\prod _{k=1}^m L^{p'_k}(Q)\Big ) \end{aligned}$$

is bounded. The convexity of F(u) follows from the fact that $f_k (x,t,u)$ is a closed interval in $\mathbb {R}$ for any $k\in \{1, \dots , m\}$. Let $\eta = (\eta _1, \dots , \eta _m)\in F(u)$. As a consequence of (2.7), for each $k\in \{1,\dots , m\}$,

$$\begin{aligned} |\eta _k (x,t)| \le \alpha _k (x,t) + \beta _k \sum _{j=1}^m |u_j (x,t)|^{\frac{p_j}{p_k'}}, \; \text{ a.e. } (x,t)\in Q. \end{aligned}$$

(3.1)

Since $|u_j |^{\frac{p_j}{p_k'}}\in L^{p_k'}(Q)$, we immediately obtain the boundedness of F(u) in $\prod _{k=1}^m L^{p'_k}(Q)$. To prove that F(u) is closed in $\prod _{k=1}^m L^{p'_k}(Q)$, let $\{\eta _n\}$ be a sequence in F(u) such that $\eta _n \rightarrow \eta$ in $\prod _{k=1}^m L^{p'_k}(Q)$. By passing to a subsequence, we can assume without loss of generality that $\eta _n(x,t)\rightarrow \eta (x,t)$ for a.e. $(x,t)\in Q$. Since $\eta _{nk}(x,t)\in f_k(x,t,u(x,t))$ for a.e. $(x,t)\in Q$, all $n\in \mathbb {N}$, all $k\in \{1, \dots , m\}$, and $f_k(x,t,u(x,t))$ is a closed interval in $\mathbb {R}$, we have $\eta _k(x,t)\in f_k(x,t,u(x,t))$, $\forall k\in \{1, \dots , m\}$. As this holds for a.e. $(x,t)\in Q$, it follows that $\eta _k\in F_k(u)$, $\forall k\in \{1, \dots , m\}$, i.e., $\eta \in F(u)$, which proves the closedness of $F_k(u)$ in $L^{p'_k}(Q)$ and thus of F(u) in $\prod _{k=1}^m L^{p'_k}(Q)$. Due to the reflexivity of $L^{p'_k}(Q)$ (resp. of $\prod _{k=1}^m L^{p'_k}(Q)$), we see from these properties that $F_k(u)$ (resp. F(u)) is a weakly closed, and thus a weakly compact subset of $L^{p'_k}(Q)$ (resp. of $\prod _{k=1}^m L^{p'_k}(Q)$).

Inequality (3.1) also implies that if S is a bounded set in $\prod _{k=1}^m L^{p_k}(Q)$ then F(S) is a bounded set in $\prod _{k=1}^m L^{p'_k}(Q)$, that is, F is a bounded mapping from $\prod _{k=1}^m L^{p_k}(Q)$ to $2^{\prod _{k=1}^m L^{p'_k}(Q)}$ and thus to $\mathcal {K}(\prod _{k=1}^m L^{p'_k}(Q))$.

For $u\in X_0$, from the boundedness of $i^*$ and the above arguments we see that $\mathcal {F}(u)$ is a nonempty, convex and bounded subset of $X_0^*$. Moreover, since

$$\begin{aligned} \Vert i^* \eta \Vert _{X_0^*} \le C \Vert \eta \Vert _{\prod _{k=1}^m L^{p'_k}(Q)}, \forall \ \eta \in \prod _{k=1}^m L^{p'_k}(Q) \end{aligned}$$

for some constant $C>0$, it follows from the boundedness of F that $\mathcal {F}$ is also a bounded mapping.

Next, let us prove that $\mathcal {F}(u)$ is closed in $X_0^*$. For this purpose, suppose that $\{\eta _n\} \subset \mathcal {F}(u)$, $\eta _n = i^* \tilde{\eta }_n$ with $\tilde{\eta }_n \in F(iu) = F(u), \;\forall n\in \mathbb {N}$, and that

$$\begin{aligned} \eta _n \rightarrow \eta \text{ in } X_0^* . \end{aligned}$$

(3.2)

Because $\{\tilde{\eta }_n : n \in \mathbb {N}\} \subset F(u)$, $\{\tilde{\eta }_n\}$ is a bounded sequence in $\prod _{k=1}^m L^{p'_k}(Q)$. By passing to a subsequence if necessary, we can assume without loss of generality that

$$\begin{aligned} \tilde{\eta }_n \rightharpoonup \tilde{\eta }_0 \text{ in } \prod _{k=1}^m L^{p'_k}(Q) . \end{aligned}$$

(3.3)

Since F(u) is weakly closed in $\prod _{k=1}^m L^{p'_k}(Q)$, $\tilde{\eta }_0\in F(u)$ and thus $i^* \tilde{\eta }_0\in i^* F(u) = \mathcal {F}(u)$. On the other hand, since $i^*$ is continuous from $\prod _{k=1}^m L^{p'_k}(Q)$ to $X_0^*$ both with weak topologies, we have from (3.3) that

$$\begin{aligned} \eta _n = i^* \tilde{\eta }_n \rightharpoonup i^* \tilde{\eta }_0 \text{ in } X_0^* , \end{aligned}$$

which, combined with (3.2), yields $\eta = i^* \tilde{\eta }_0 \in \mathcal {F}(u)$. Hence, $\mathcal {F}(u)$ is closed in $X_0^*$.

Step 2: Property (ii) of Definition 3.1

Let V be a finite dimensional subspace of $X_0$. We prove in this step that the restriction $\mathcal {F}|_{V}$ of $\mathcal {F}$ on V is upper semicontinuous from V into $2^{X_0^*}$ with respect to the weak topology of $X_0^*$.

In fact, assume $u_0\in V$. To prove the upper semicontinuity of $\mathcal {F}|_{V}$ at $u_0$, we assume by contradiction that there are a weakly open neighborhood U of $\mathcal {F}(u_0)$ in $X_0^*$ and sequences $\{u_n\}\subset V$, $\{\eta _n \}\subset X_0^*$ such that $u_n \rightarrow u_0$ in V and $\eta _n \in \mathcal {F}(u_n){\setminus } U,\;\forall n\in \mathbb {N}$. We see that $\tilde{U} = (i^*)^{-1} (U)$ is a weakly open neighborhood of $F(u_0)$ in $\prod _{k=1}^m L^{p'_k}(Q)$. Moreover, since $\eta _n\in i^* F(u_n)$, there exists $\tilde{\eta }_n \in F(u_n)$ such that

$$\begin{aligned} \eta _n = i^* \tilde{\eta }_n . \end{aligned}$$

(3.4)

We have $\tilde{\eta }_n \notin \tilde{U}$ for all $n\in \mathbb {N}$. As $\{u_n\}$ is a bounded sequence in $\prod _{k=1}^m L^{p_k}(Q)$, it follows from Step 1 that $\{\tilde{\eta }_n\}$ is a bounded sequence in $\prod _{k=1}^m L^{p'_k}(Q)$. Also, as above by passing to a subsequence we can assume that

$$\begin{aligned} \tilde{\eta }_n \rightharpoonup \tilde{\eta }_0 \text{ in } \prod _{k=1}^m L^{p'_k}(Q) . \end{aligned}$$

(3.5)

Since $u_n\rightarrow u_0$ in $\prod _{k=1}^m L^{p_k}(Q)$, we have from conditions (F1)–(F3) that all assumptions of Lemma 3.3, [10], are satisfied. According to this result, we have for all $k\in \{1, \dots , m\}$, $h_{L^{p'_k}(Q)}^*(F_k(u_n),F_k(u_0)) \rightarrow 0$ where

$$\begin{aligned} h^*_{ L^{p'_k}(Q)}(A,B) = \sup _{u\in A}\left( \inf _{v\in B}\Vert u-v \Vert _{L^{p'_k}(Q)} \right) \end{aligned}$$

is the Hausdorff distance between subsets A, B of $L^{p'_k}(Q)$. As

$$\begin{aligned} \begin{array}{lll} h^*_{ L^{p'_k}(Q)}(F_k(u_n),F_k(u_0)) &{} \ge &{} \text{ dist}_{ L^{p'_k}(Q)}(\tilde{\eta }_{nk} , F_k(u_0)) \\ &{} = &{} \inf \{\Vert \tilde{\eta }_{nk} - v \Vert _{ L^{p'_k}(Q)} : v\in F_k(u_0)\}, \end{array} \end{aligned}$$

there is a sequence $\{\overline{\eta }_{n}^{(k)}\} \subset F_k(u_0)$ such that $\Vert \tilde{\eta }_{nk} - \overline{\eta }_n^{(k)} \Vert _{ L^{p'_k}(Q)} \rightarrow 0$. As $F_k(u_0)$ is a convex, closed, and bounded subset of $L^{p_k'}(Q)$, it is weakly compact in $L^{p_k'}(Q)$. Hence, by passing to a subsequence if necessary, we can assume that $\overline{\eta }_{n}^{(k)} \rightharpoonup \overline{\eta }_{0}^{(k)}$ in $L^{p_k'}(Q)$ for some $\overline{\eta }_{0}^{(k)}\in F_k(u_0)$. It follows that $\tilde{\eta }_{nk}\rightharpoonup \overline{\eta }_{0}^{(k)}$ in $L^{p_k'}(Q)$ for all $k = 1, \dots , m$, that is, $\tilde{\eta }_{n}\rightharpoonup (\overline{\eta }_{0}^{(1)}, \dots , \overline{\eta }_{0}^{(m)})$ in $\prod _{k=1}^m L^{p_k'}(Q)$ with $(\overline{\eta }_{0}^{(1)}, \dots , \overline{\eta }_{0}^{(m)}) \in F(u_0)$.

From (3.5), we have $\tilde{\eta }_0 = (\overline{\eta }_{0}^{(1)}, \dots , \overline{\eta }_{0}^{(m)}) \in F(u_0)$ and thus $\tilde{\eta }_0 \in \tilde{U}$. Again from (3.5) we have $\tilde{\eta }_n \in \tilde{U}$ for all n sufficiently large, contradicting (3.4) and the assumption on $\eta _n$, and therefore proving the upper semicontinuity of $\mathcal {F}|_{V}$.

Step 3: Property (iii) of Definition 3.1

First, let us prove that $\mathcal {F}$ is sequentially weakly closed from $D(L)(\subset X_0)$ with respect to the D(L)-graph norm topology into $2^{X_0^*}{\setminus } \{\emptyset \}$ with $X_0^*$ equipped with its weak topology, that is, if $\{u_n\}$ and $\{\eta _n\}$ are sequences in D(L) and $X_0^*$ respectively such that

$$\begin{aligned}&u_n \rightharpoonup u\; \text{ in } \; X_0 , u_{nt} \rightharpoonup u_t\; \text{ in } \; X_0^* , \end{aligned}$$

(3.6)

$$\begin{aligned}&\eta _n \rightharpoonup \eta \; \text{ in } \; X_0^* , \end{aligned}$$

(3.7)

and

$$\begin{aligned} \eta _n \in \mathcal {F}(u_n),\;\forall n\in \mathbb {N}, \end{aligned}$$

(3.8)

then,

$$\begin{aligned} \eta \in \mathcal {F}(u) . \end{aligned}$$

(3.9)

In fact, assume (3.6)–(3.8). From (3.8), for each $n\in \mathbb {N}$, there exists $\tilde{\eta }_n\in F(i (u_n)) = F(u_n)$ such that $\eta _n = i^*(\tilde{\eta }_n)=\tilde{\eta }_n|_{X_0^*}$. From (3.6) and Aubin’s lemma (cf. [13]), we have

$$\begin{aligned} u_n = i(u_n) \rightarrow i(u) = u \; \text{ in } \; \prod _{k=1}^m L^{p_k}(Q) . \end{aligned}$$

(3.10)

As in Step 2, for each $k = 1, \dots , m$, it follows from (F1)–(F3) and Lemma 3.3 in [10] that

$$\begin{aligned} h_{L^{p'_k}(Q)}^*(F_k(u_n), F_k(u)) \rightarrow 0 . \end{aligned}$$

(3.11)

Since $\tilde{\eta }_{nk}\in F_k(u_n)$,

$$\begin{aligned} \inf _{v\in F_k(u)}\Vert \tilde{\eta }_{nk} -v\Vert _{L^{p'_k}(Q)} \le h^*_{L^{p'_k}(Q)}(F_k(u_n) ,F_k(u)) . \end{aligned}$$

Hence, $\inf _{v\in F_k(u)}\Vert \tilde{\eta }_{nk} -v\Vert _{ L^{p'_k}(Q)} \rightarrow 0$ as $n\rightarrow \infty$, and there exists a sequence $\{\eta _n^{(k)}\}\subset F_k(u)$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert \tilde{\eta }_{nk} - \eta _n^{(k)} \Vert _{ L^{p'_k}(Q)} = 0 . \end{aligned}$$

(3.12)

Since $\{\eta _n^{(k)}\}\subset F_k(u)$ and, as noted in Steps 1, $F_k(u)$ is a weakly compact subset of $L^{p'_k}(Q)$, by passing to a subsequence if necessary, we can assume that

$$\begin{aligned} \eta _n^{(k)} \rightharpoonup \eta _0^{(k)} \; \text{ in } L^{p'_k}(Q) \end{aligned}$$

(3.13)

for some $\eta _0^{(k)}\in F_k(u)$. Hence, (3.12) implies that $\tilde{\eta }_{nk} \rightharpoonup \eta _0^{(k)}$ in $L^{p'_k}(Q)$ for $k = 1, \dots , m$. Putting $\eta _0 = (\eta _0^{(1)}, \dots , \eta _0^{(m)})$, we see that $\eta _0 \in F(u)$ and

$$\begin{aligned} \tilde{\eta }_n \rightharpoonup \eta _0 \text{ in } \prod _{k=1}^m L^{p'_k}(Q). \end{aligned}$$

(3.14)

Since $i^*$ is continuous in the weak topologies of both $\prod _{k=1}^m L^{p'_k}(Q)$ and $X_0^*$, it follows from (3.14) that

$$\begin{aligned} \eta _n = i^*(\tilde{\eta }_n) = \tilde{\eta }_n|_{X_0^*} \rightharpoonup i^*({\eta }_0) = {\eta }_0|_{X_0^*} \end{aligned}$$

(3.15)

weakly in $X_0^*$. From (3.7) and (3.15), we have $\eta = i^*(\eta _0)\in i^* F(u)$, since $\eta _n \rightharpoonup \eta$ and $\eta _n \rightharpoonup i^*(\eta _0)$ both in the sense of distribution. The inclusion (3.9) is thus verified, which completes our proof of the weakly closed property of $\mathcal {F}$.

Next, we prove that if $\{u_n\}\subset D(L)$, $\{\eta _n\}\subset X_0^*$ are sequences satisfying (3.6)-(3.8) then

$$\begin{aligned} \langle \eta _n, u_n\rangle _{X_0^*, X_0} \rightarrow \langle \eta , u \rangle _{X_0^*, X_0} . \end{aligned}$$

(3.16)

In fact, let $\{\tilde{\eta }_n\}$ and $\eta _0$ be as above. We have

$$\begin{aligned} \begin{array}{lll} \langle \eta _n , u_n\rangle _{X_0^*, X_0} &{} = &{} \langle \tilde{\eta }_n|_{X_0^*} , u_n\rangle _{X_0^*, X_0} \\ &{} = &{} \langle i^*(\tilde{\eta }_n ), u_n\rangle _{X_0^*, X_0} \\ &{} = &{} \langle \tilde{\eta }_n , i(u_n)\rangle _{\prod _{k=1}^m L^{p'_k}(Q), \prod _{k=1}^m L^{p_k}(Q)} \\ &{} = &{} \langle \tilde{\eta }_n , u_n\rangle _{\prod _{k=1}^m L^{p'_k}(Q), \prod _{k=1}^m L^{p_k}(Q)} . \end{array} \end{aligned}$$

(3.17)

From (3.10) and (3.14), we have

$$\begin{aligned} \begin{array}{lll} \langle \tilde{\eta }_n , u_n\rangle _{\prod _{k=1}^m L^{p'_k}(Q), \prod _{k=1}^m L^{p_k}(Q)} &{} \rightarrow &{} \langle {\eta }_0 , u \rangle _{\prod _{k=1}^m L^{p'_k}(Q), \prod _{k=1}^m L^{p_k}(Q)} \\ &{} = &{} \langle {\eta }_0 , i(u) \rangle _{\prod _{k=1}^m L^{p'_k}(Q), \prod _{k=1}^m L^{p_k}(Q)} \\ &{} = &{} \langle i^*(\eta _0 ), u \rangle _{X_0^*, X_0} \\ &{} = &{} \langle \eta , u \rangle _{X_0^*, X_0} . \end{array} \end{aligned}$$

This limit, together with (3.17), proves (3.16).

The weakly closed property of $\mathcal {F}$ and (3.16) show that $\mathcal {F}$ satisfies condition (iii) in Definition 3.1, which together with the results proved in Steps 1 and 2, shows that $\mathcal {F}$ is pseudomonotone from $X_0$ to $\mathcal {K}(X_0^*)$ with respect to D(L). $\square$

4 Main results

In this section we prove our main results about problem (1.1)–(1.2), which is equivalently rewritten in Sect. 2 as the following evolutionary multivalued variational inequality: Find $u\in D(L)\cap K$ and $\eta \in \mathcal {F}(u)$ such that

$$\begin{aligned} \langle Lu + Au + \eta , v-u \rangle \ge 0, \;\forall v\in K , \end{aligned}$$

(4.1)

where $L, D(L), A, \mathcal {F}$, and K are defined in (2.10), (2.11), (2.5), (2.9), (2.8), and (2.12).

By identifying $\eta = (\eta _1, \dots , \eta _m)\in \prod _{k=1}^m L^{p'_k}(Q)$ with $i^*\eta = \eta |_{X_0} \in X_0^*$, we see that (4.1) is also written in the form: Find $u\in D(L)\cap K$ and an $\eta \in F(u)$ such that

$$\begin{aligned} \eta \in F(u),\ \langle Lu+Au, v-u\rangle +\int _Q \eta \, (v-u)\,dxdt\ge 0,\ \ \forall \ v\in K . \end{aligned}$$

(4.2)

In Sect. 4.1 we deal with the coercive case for (4.1) and in Sect. 4.2 a version of the method of sub-supersolution for (4.1) is established to treat the noncoercive case.

We first recall the following definition of a penalty operator associated with a convex set.

Definition 4.1

Let $C\ne \emptyset$ be a closed and convex subset of a reflexive Banach space Y. A bounded, hemicontinuous and monotone operator $P: Y\rightarrow Y^*$ is called a penalty operator associated with $C\subset Y$ if

$$\begin{aligned} P(u)=0 \Longleftrightarrow u\in C. \end{aligned}$$

In what follows, we assume that for each $k\in \{1, \dots , m\}$, there exists a penalty operator $P_k : X_{0k} \rightarrow X_{0k}^*$ associated with $K_k\subset X_{0k}$ with the following properties:

• (P) For each $u_k\in D(L_k)$, there exists $w_k=w_k(u_k)\in X_{0k}$ such that

  $$\begin{aligned} \begin{array}{rl} \text{(i) } &{} \langle u_{kt} + {A_k} u_k , w_k \rangle \ge 0 ,\; \text{ and }\\ \text{(ii) } &{} \langle P_k u_k , w_k \rangle \ge D_k \Vert P_k u_k\Vert _{X_{0k}^*} \Vert w_k\Vert _{L^{p_k}(Q)} , \end{array} \end{aligned}$$

  (4.3)

  for some constant $D_k>0$ independent of $u_k$ and $w_k$.

For $u \in X_0$, let

$$\begin{aligned} P u = (P_1 u_1, \dots , P_m u_m)\in X_0^* . \end{aligned}$$

(4.4)

It is clear that P is a penalty operator associated with K.

4.1 Coercive case

In this subsection, we prove the existence of solutions of (4.1) under certain coercivity condition. More precisely, we have the following result.

Theorem 4.1

Assume (A1)–(A3) and that f satisfies hypotheses (F1)–(F3). Suppose $D(L) \cap K \not = \emptyset$ and $u_0\in D(L) \cap K$, and assume the existence of a penalty operator associated with K satisfying (P). Then, under the coercivity condition

$$\begin{aligned} \lim _{\Vert u\Vert _{X_0}\rightarrow \infty } \left[ \inf _{\eta \in \mathcal {F}(u)}\frac{\langle A u + \eta , u- u_0 \rangle }{\Vert u\Vert _{X_0}}\right] = \infty , \end{aligned}$$

(4.5)

the multivalued parabolic variational inequality (4.1) has solutions.

Proof

For $\varepsilon >0$, let us consider the following penalized equation:

$$\begin{aligned} u\in D(L) , \eta \in \mathcal {F} (u) : \langle u_t , v\rangle + \langle A(u) + \eta , v\rangle + \frac{1}{\varepsilon } \langle Pu,v\rangle = 0, \;\forall v\in X_0 , \end{aligned}$$

(4.6)

where P is a penalty operator (associated to K) defined in (4.4).

From Proposition 3.3, $\mathcal {F}$ is pseudomonotone with respect to D(L). Since A and $\varepsilon ^{-1}P$ are monotone and hemicontinuous, they are pseudomonotone and thus pseudomonotone with respect to D(L) (cf. e.g. Proposition 27.6, [18]). As a consequence, $A + \mathcal {F} + \varepsilon ^{-1}P$ is pseudomonotone with respect to D(L). Moreover, it is bounded since A, P and $\mathcal {F}$ are bounded mappings. From the coercivity condition (4.5) and the monotonicity of $\varepsilon ^{-1}P$, it is easy to see that $A + \mathcal {F} + \varepsilon ^{-1}P$ is coercive on $X_0$ in the following sense:

$$\begin{aligned} \lim _{\Vert u\Vert _{X_0}\rightarrow \infty } \left[ \inf _{\eta \in \mathcal {F}(u)}\frac{\langle (A+\varepsilon ^{-1}P)(u) + \eta , u- u_0 \rangle }{\Vert u\Vert _{X_0}}\right] = \infty . \end{aligned}$$

(4.7)

According to the surjectivity result of [8, Theorem 1.3.73, p. 62], (4.6) has solutions for each $\varepsilon >0$. Let $u_{\varepsilon }\in D(L)$ and $\eta _{\varepsilon } \in {\mathcal F}(u_{\varepsilon })$ satisfy (4.6). Let us show that the family $\{u_{\varepsilon }: \varepsilon > 0, \text{ small }\}$ is bounded with respect to the graph norm of D(L). In fact, let $u_0$ be a (fixed) element of $D(L)\cap K$. Putting $v=u_{\varepsilon } - u_0$ into (4.6) (with $u_{\varepsilon }$) and noting the monotonicity of L and that $P u_0 =0$, one gets

$$\begin{aligned} \langle - u_{0t}, u_\varepsilon - u_0 \rangle= & {} \langle u_{\varepsilon t} - u_{0t}, u_\varepsilon - u_0 \rangle + \langle A u_\varepsilon + \eta _{\varepsilon }, u_{\varepsilon } - u_0 \rangle \\&+ \frac{1}{\varepsilon } \langle P u_{\varepsilon } - P u_0 , u_{\varepsilon } - u_0 \rangle \\\ge & {} \langle A u_\varepsilon + \eta _{\varepsilon } , u_\varepsilon - u_0 \rangle . \end{aligned}$$

Thus,

$$\begin{aligned} \frac{\langle A u_\varepsilon + \eta _{\varepsilon }, u_\varepsilon - u_0 \rangle }{\Vert u_\varepsilon - u_0 \Vert _{X_0}} \le \Vert u_{0t}\Vert _{X_0^*} , \end{aligned}$$

for all $\varepsilon >0$. From (4.5), we have that the set $\{\Vert u_\varepsilon \Vert _{X_0} : \varepsilon > 0\}$ is bounded. As a consequence, we see that $A u_\varepsilon$ stays bounded in $X_0^*$. Moreover, from the growth condition (2.7), we see that the set $\{\eta _{\varepsilon } : {\varepsilon } >0\}$ is bounded in $\prod _{k=1}^m L^{p_k'}(Q)$.

Next, let us check that the set $\{(\varepsilon ^{-1} Pu_\varepsilon ) : \varepsilon > 0\}$ is also bounded in $X_0^*$. To see this, for each $k=1,\dots , m$ and $\varepsilon >0$, we choose $w_k=w_{\varepsilon k}$ to be an element satisfying (4.3) with $u_k=u_{\varepsilon k}$. From (4.6) with $v = (w_{\varepsilon k} , [0]_k)$, we obtain

$$\begin{aligned} \langle u_{\varepsilon k t} , w_{\varepsilon k} \rangle + \langle A_k u_{\varepsilon k} + \eta _{\varepsilon k} , w_{\varepsilon k} \rangle + \frac{1}{\varepsilon } \langle P_k u_{\varepsilon k} , w_{\varepsilon k} \rangle = 0. \end{aligned}$$

From (4.3)(i), we see that $\langle u_{\varepsilon k t}, w_{\varepsilon k} \rangle + \langle A_k u_{\varepsilon k} , w_{\varepsilon k} \rangle \ge 0$. Therefore,

$$\begin{aligned} \frac{1}{\varepsilon } \langle P_k u_{\varepsilon k}, w_{\varepsilon k} \rangle \le \langle -\eta _{\varepsilon k} , w_{\varepsilon k}\rangle . \end{aligned}$$

(4.8)

Since the set $\{\Vert \eta _{\varepsilon }\Vert _{\prod _{k=1}^m L^{p_k'}(Q)} : \varepsilon >0\}$ is bounded, there exists a constant $c >0$ such that

$$\begin{aligned} |\langle \eta _{\varepsilon k} , w_{\varepsilon k} \rangle | \le c \Vert w_{\varepsilon k}\Vert _{L^{p_k}(Q)},\; \forall \varepsilon . \end{aligned}$$

This and (4.3)(ii) imply that for all $k\in \{1, \dots , m\}$,

$$\begin{aligned} \frac{1}{\varepsilon } \Vert P_k u_{\varepsilon k}\Vert _{X_{0k}^*}\le \frac{c}{D_k} , \;\forall \varepsilon >0 , \end{aligned}$$

which proves the boundedness of the set $\{(\varepsilon ^{-1} Pu_\varepsilon ) : \varepsilon > 0\}$ in $X_0^*$. On the other hand, since

$$\begin{aligned} u_{\varepsilon t} = - (A + \varepsilon ^{-1} P)(u_\varepsilon ) - \eta _{\varepsilon } \end{aligned}$$

in $X^*_0$, the above estimate implies that $( u_{\varepsilon t})$ is also bounded in $X_0^*$. Thus, we have shown that $\{u_\varepsilon : \varepsilon >0\}$ is bounded with respect to the graph norm of D(L). Hence, there exist $u\in X_0$, with $u_t\in X_0^*$, and a sequence $\{u_{\varepsilon _n}\}$, which is still denoted by $\{u_\varepsilon \}$, for simplicity of notation, such that

$$\begin{aligned} u_\varepsilon \rightharpoonup u \text{ in } X_0,\; u_{\varepsilon t} \rightharpoonup u_t \text{ in } X_0^* \; (\varepsilon \rightarrow 0^+) . \end{aligned}$$

(4.9)

Since D(L) is closed in $W_0$ and convex, it is weakly closed in $W_0$, and thus $u\in D(L)$. Now, let us prove that u is a solution of the variational inequality (4.1). First, note that $Pu=0$. In fact, we have $P u_\varepsilon \rightarrow 0$ in $X_0^*$. It follows from the monotonicity of P that

$$\begin{aligned} \langle Pv, v-u \rangle \ge 0,\;\forall v\in X_0 . \end{aligned}$$

As in the proof of Minty’s lemma (cf. [9]), one obtains from this inequality that

$$\begin{aligned} \langle Pu, v \rangle \ge 0,\;\forall v\in X_0 . \end{aligned}$$

Hence, $Pu=0$ in $X_0^*$, that is, $u\in K$. On the other hand, (4.9) and Aubin’s lemma imply that

$$\begin{aligned} u_\varepsilon \rightarrow u \; \text{ in } \prod _{k=1}^m L^{p_k}(Q). \end{aligned}$$

(4.10)

As a consequence, we have

$$\begin{aligned} \langle \eta _{\varepsilon } , u_\varepsilon -u \rangle \rightarrow 0 \text{ as }\,\, \varepsilon \rightarrow 0^+. \end{aligned}$$

(4.11)

For $w\in K$, letting $v=w-u_\varepsilon$ in (4.6) (with $u=u_\varepsilon$), one gets

$$\begin{aligned} \langle u_{\varepsilon t}, w-u_\varepsilon \rangle + \langle A u_\varepsilon + \eta _{\varepsilon } , w-u_\varepsilon \rangle = \frac{1}{\varepsilon } \langle - Pu_\varepsilon , w-u_\varepsilon \rangle \ge 0. \end{aligned}$$

(4.12)

By choosing $w=u$ in (4.12), we have

$$\begin{aligned} \langle A u_\varepsilon , u-u_\varepsilon \rangle\ge & {} -\langle \eta _{\varepsilon } , u-u_\varepsilon \rangle - \langle u_{t}, u-u_\varepsilon \rangle + \langle u_t - u_{\varepsilon t}, u-u_\varepsilon \rangle \\\ge & {} - \langle \eta _{\varepsilon } , u-u_\varepsilon \rangle - \langle u_{t}, u-u_\varepsilon \rangle . \end{aligned}$$

As a consequence, one gets

$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0^+} \langle A u_\varepsilon , u-u_\varepsilon \rangle \ge 0 . \end{aligned}$$

Note that A is of class $(S_+)$ with respect to D(L), according to Proposition 3.2, we deduce from (4.9) and the above limit that

$$\begin{aligned} u_\varepsilon \rightarrow u \text{ in } X_0 . \end{aligned}$$

(4.13)

On the other hand, since $\{\eta _{\varepsilon } : \varepsilon > 0\}$ is bounded in $X_0^*$, by passing to a subsequence still denoted by $\{\eta _{\varepsilon }\}$ for simplicity of notation, we have

$$\begin{aligned} \eta _{\varepsilon } \rightharpoonup \eta \text{ in } X_0^*. \end{aligned}$$

(4.14)

From (4.9) and the weak closedness of the mapping $\mathcal {F}$ with respect to D(L) proved in Step 3 of Proposition 3.3, we have

$$\begin{aligned} \eta \in \mathcal {F}(u). \end{aligned}$$

(4.15)

Letting $\varepsilon \rightarrow 0$ in (4.12) and taking (4.9), (4.13), (4.14) and the continuity of the operator A into account, we obtain

$$\begin{aligned} \langle u_{t}, w-u \rangle + \langle A u + \eta , w-u \rangle \ge 0. \end{aligned}$$

This holds for all $w\in K$ which together with (4.15) proves that u is in fact a solution of (4.1).$\square$

Penalty operators associated with obstacle problems

For $k=1,\dots , m$, let $A_k=-\varDelta _{p_k}$ ($p_k\ge 2$) be the $p_k$-Laplacian. For an upward obstacle constraint, the convex set $K_k$ is given by

$$\begin{aligned} K_k =\{u_k\in X_{0k} : u_k\le \psi _k \; \text{ a.e. } \text{ on } \; Q\}, \end{aligned}$$

(4.16)

with $\psi _k$ a given function in $W_k$ such that $\psi _k(\cdot , 0)\ge 0$ on $\varOmega$, $\psi _k\ge 0$ on $\varGamma$, and $\psi _{kt} +A_k \psi _k \ge 0$ in $X_{0k}^*$, in the sense that

$$\begin{aligned} \langle \psi _{kt} +A_k \psi _k, v_k \rangle \ge 0,\;\forall v_k\in X_{0k}\cap L^{p_k}_+(Q). \end{aligned}$$

In other words, the obstacle function $\psi _k$ is assumed to be a (weak) supersolution of the following parabolic initial boundary value problem:

$$\begin{aligned} w_{kt}-\varDelta _{p_k} w_k=0, \ \ w_k(\cdot , 0)=0 \text{ on } \varOmega ,\ \ w_k=0 \text{ on } \varGamma . \end{aligned}$$

Then the operator $P_k$ given by

$$\begin{aligned} \langle P_ku_k,v_k \rangle = \int _Q [(u_k-\psi _k)^+]^{p_k-1}\,v_k \,dx dt, \ \ \forall \ u_k,v_k\in X_{0k}, \end{aligned}$$

is easily seen to be a penalty operator, and, moreover, property (P) can be verified with $w_k(u_k)=(u_k-\psi _k)^+$.

Analogously, for a downward obstacle constraint, the convex set $K_k$ is given by

$$\begin{aligned} K_k =\{u_k\in X_{0k} : u_k\ge \vartheta _k \; \text{ a.e. } \text{ on } \; Q\}, \end{aligned}$$

(4.17)

with $\vartheta _k\in W_k$, $\vartheta _k(\cdot , 0)\le 0$ on $\varOmega$, $\vartheta _k\le 0$ on $\varGamma$, and $\vartheta _{kt} +A_k \vartheta _k \le 0$ in $X_{0k}^*$, i.e.,

$$\begin{aligned} \langle \vartheta _{kt} +A_k \vartheta _k, v_k \rangle \le 0,\;\forall v_k\in X_{0k}\cap L^{p_k}_+(Q). \end{aligned}$$

In the case of a lower obstacle constraint, the operator $P_k$ given by

$$\begin{aligned} \langle P_ku_k,v_k \rangle = -\int _Q [(u_k-\vartheta _k)^-]^{p_k-1}\,v_k \,dx dt, \ \ \forall \ u_k,v_k\in X_{0k}, \end{aligned}$$

is a penalty operator for $K_k$ that satisfies property (P), where $w_k = w_k(u_k)$ corresponding to $u_k\in D(L_k)$ is chosen as $w_k(u_k)=-(u_k-\vartheta _k)^-$.

We note that in an upward (resp. downward) obstacle system, all constraint sets $K_k$ in (1.2) are of the form (4.16) (resp. (4.17)), while in mixed system of upward-downward obstacle problems, some of constraint sets $K_k$ in (1.2) are given by (4.16), while the others are given by (4.17).

4.2 Noncoercive case

Note that when the growth condition (2.7) or the coercivity condition (4.5) is not fulfilled then the inequality (4.1) may not have solutions. However, without these conditions, we can still have the existence and other properties of solutions of (4.1) if sub- and supersolutions of (4.1), defined in a certain appropriate sense, exist. In this subsection we establish a sub-supersolution method for (4.1), which will allow us to derive existence and enclosure results for (4.1).

Let us first introduce our basic notion of sub-supersolution for the system of parabolic MVI (1.1)–(1.2). Let $\underline{u}, \overline{u}\in X_0$ be a pair of functions such that $\underline{u}\le \overline{u}$. For $k=1, \dots , m$, we use the notation $Q_k = Q_{k, \underline{u}, \overline{u}}$ for the cylinder based on Q and lying between $[\underline{u}]_k$ and $[\overline{u}]_k$:

$$\begin{aligned} Q_k = \{ (x , t , [s]_k) \in Q\times {\mathbb R}^{m-1} : [\underline{u}(x,t)]_k \le [s]_k \le [\overline{u}(x,t)]_k \; \text{ for } \text{ a.e. } \; (x,t)\in Q\}. \end{aligned}$$

Definition 4.2

A pair of functions $\underline{u}, \overline{u}\in W$ is said to form an ordered pair of subsolution–supersolution of (4.1) if $\underline{u} \le \overline{u}$ and the following conditions are satisfied.

• (i) $\underline{u}\vee K \subset K$, $\overline{u}\wedge K \subset K$,

• (ii) $\underline{u}_k (\cdot ,0)\le 0 \text{ in } \varOmega$, $\overline{u}_k(\cdot ,0)\ge 0 \text{ in } \varOmega$ ($k=1,\dots , m$), and

• (iii) for each $k\in \{1,\dots , m\}$, there exist functions $\underline{\eta }_{k} , \overline{\eta }_{k}: Q_k \rightarrow {\mathbb R}$ such that for any $[w]_k \in [\underline{u} , \overline{u}]_k$, the functions $(x,t) \mapsto \underline{\eta }_{k} (x,t, [w(x,t)]_k)$ and $(x,t) \mapsto \overline{\eta }_{k} (x,t, [w(x,t)]_k)$ belongs to $L^{p'_k}(Q)$,

  $$\begin{aligned}&\underline{\eta }_{k} (x,t, [w(x,t)]_k) \in f_k (x, t, \underline{u}_k(x,t), [w(x,t)]_k) , \end{aligned}$$

  (4.18)
  $$\begin{aligned}&\overline{\eta }_{k} (x,t, [w(x,t)]_k) \in f_k (x, t, \overline{u}_k(x,t), [w(x,t)]_k) , \end{aligned}$$

  (4.19)

  for a.e. $(x,t)\in Q$, and

  $$\begin{aligned} \langle \underline{u}_{kt}+A_k\underline{u}_k,v_k-\underline{u}_k\rangle + \int _{Q}\underline{\eta }_{k} (\cdot ,\cdot , [w]_k)\,(v_k-\underline{u}_k)\,dxdt \ge 0,\,\forall v_k\in \underline{u}_k\wedge K_k , \end{aligned}$$

  (4.20)

  and

  $$\begin{aligned} \langle \overline{u}_{kt}+A_k\overline{u}_k,v_k-\overline{u}_k\rangle + \int _{Q}\overline{\eta }_k (\cdot ,\cdot , [w]_k)\,(v_k-\overline{u}_k)\,dxdt \ge 0, \,\forall v_k\in \overline{u}_k\vee K_k. \end{aligned}$$

  (4.21)

Throughout this subsection instead of the growth condition (F3) of the preceding section we assume the following local growth assumption with respect to the ordered interval of sub-supersolutions.

• (F4) Assume that there exists a pair of sub-supersolutions $\underline{u}$ and $\overline{u}$ of (4.1) such that for all $k\in \{1, \dots , m\}$, $f_k$ has the following growth between $\underline{u}$ and $\overline{u}$:

  $$\begin{aligned} | \eta | \le c_5^{(k)} (x,t),\ \ \forall \ \eta \in f_k (x,t,s), \end{aligned}$$

  (4.22)

  for a.e. $(x,t)\in Q$, and all $s\in [\underline{u}(x,t) , \overline{u}(x,t)]$, for some $c_5^{(k)}\in L^{p_k'}(Q)$.

We note that (F3) implies (F4), that is, the local growth condition (F4) is a weaker condition.

We are now ready to state and prove our main existence and enclosure result.

Theorem 4.2

Assume (A1)–(A3) and that (4.1) has an ordered pair of sub- and supersolutions $\underline{u}$ and $\overline{u}$, and that (F1)–(F2), (F4) are satisfied. Suppose furthermore that $D(L)\cap K\not =\emptyset$, and that there exists a penalty operator associated with K satisfying (P). Then, (4.1) has a solution u such that $\underline{u} \le u\le \overline{u}$.

Proof

For $k = 1, \dots ,m$, we define the following cut-off function $b_k: Q\times \mathbb {R}\rightarrow \mathbb {R}$:

$$\begin{aligned} b_k(x,t,s) = \left\{ \begin{array}{lll} [s-\overline{u}_k(x,t)]^{p_k-1} &{} \text{ if } &{} s > \overline{u}_k(x,t) \\ 0 &{} \text{ if } &{} \underline{u}_k (x,t) \le s \le \overline{u}_k(x,t) \\ -[\underline{u}_k(x,t) - s]^{p_k-1} &{} \text{ if } &{} s < \underline{u}_k(x,t) , \end{array} \right. \end{aligned}$$

for $(x,t,s)\in Q\times \mathbb {R}$. It is easy to check that $b_k$ is a Carathéodory function with the growth condition

$$\begin{aligned} | b_k(x,t,s) | \le c_6^{(k)} (x,t) + c_7^{(k)} |s |^{p_k-1}, \; \text{ for } \text{ a.e. }\, (x,t)\in Q,\, \hbox {all}\,\, s\in \mathbb {R}, \end{aligned}$$

(4.23)

with $c_6^{(k)}\in L^{p_k'}(Q), \; c_7^{(k)} >0$. Hence, the Nemytskij operator $B_k : u \mapsto b_k(\cdot , \cdot , u)$ is a continuous and bounded mapping from $L^{p_k}(Q)$ to $L^{p_k'}(Q)$ and $\mathcal {B}_k = i_k^*\circ B_k\circ i_k : X_{0k} \rightarrow X_{0k}^*$ is given by

$$\begin{aligned} \langle \mathcal {B}_k u , v\rangle = \int _Q b_k(\cdot ,\cdot ,u) \,v \, dx dt , \; \forall u,v\in X_{0k} . \end{aligned}$$

(4.24)

Moreover, there are $c_8^{(k)}, c_9^{(k)}>0$ such that

$$\begin{aligned} \int _Q b_k(\cdot ,\cdot ,u)u \, dx dt \ge c_8^{(k)} \Vert u\Vert ^{p_k}_{L^{p_k}(Q)} - c_9^{(k)} , \;\forall u\in L^{p_k}(Q). \end{aligned}$$

(4.25)

Let $\mathcal {B} : X_0 \rightarrow X_0^*$ be defined by $\mathcal {B} u = (\mathcal {B}_1 u_1 , \dots , \mathcal {B}_m u_m)$ for $u\in X_0$. We have from (4.25) that

$$\begin{aligned} \langle \mathcal {B} u , u \rangle \ge c_8 \sum _{k=1}^m \Vert u\Vert ^{p_k}_{L^{p_k}(Q)} - c_9 , \;\forall u\in X_0, \end{aligned}$$

(4.26)

for some constants $c_8 , c_9 >0$. For $k\in \{1,\dots , m\}$, $(x,t)\in Q$, $u_k\in {\mathbb R}$, let us define the truncation function $T_k$ as follows:

$$\begin{aligned} (T_k u_k)(x,t)=\left\{ \begin{array}{lll} \overline{u}_k(x,t) &{} \text{ if } &{} u_k>\overline{u}_k(x,t),\\ u_k &{} \text{ if } &{} \underline{u}_k(x,t)\le u_k \le \overline{u}_k(x,t),\\ \underline{u}_k(x,t) &{} \text{ if } &{} u_k <\underline{u}_k(x,t) . \end{array}\right. \end{aligned}$$

(4.27)

In other words,

$$\begin{aligned} (T_k u_k)(x,t) = [u_k \wedge \overline{u}_k(x,t)]\vee \underline{u}_k(x,t) = [u_k \vee \underline{u}_k(x,t)]\wedge \overline{u}_k(x,t). \end{aligned}$$

Straightforward calculations show that $T_k$ is continuous and bounded from $L^{p_k}(Q)$ (resp. $X_{0k}$) into itself. The corresponding truncated vector function for $u=(u_1,\dots , u_m)\in {\mathbb R}^m$, Tu is given by

$$\begin{aligned} (Tu)(x,t)=((T_1u_1)(x,t),\dots ,(T_m u_m)(x,t)) , \end{aligned}$$

(4.28)

and as above,

$$\begin{aligned}{}[ Tu ]_k (x,t) = ((T_j u_j)(x,t) : j\in \{1,\dots m\}{\setminus } \{k\}) . \end{aligned}$$

(4.29)

For $k = 1, \dots , m$, we define next the truncated function $f_{0k} : Q\times \mathbb {R}^m \rightarrow 2^{\mathbb {R}}$ of $f_k$ as follows:

$$\begin{aligned} f_{0k}(x,t,u) = \left\{ \begin{array}{lll} \{ \underline{\eta }_{k}(x,t, [T u(x,t)]_k) \} &{} \text{ if } &{} u_k < \underline{u}_k(x,t) \\ f_k (x,t ,u_k,[T u(x,t)]_k) &{} \text{ if } &{} \underline{u}_k(x,t) \le u_k \le \overline{u}_k(x,t)\\ \{\overline{\eta }_{k}(x,t, [T u(x,t)]_k)\} &{} \text{ if } &{} u_k > \overline{u}_k(x,t) , \end{array} \right. \end{aligned}$$

(4.30)

for $(x,t,u)\in Q\times \mathbb {R}^m$, where $\underline{\eta }$ and $\overline{\eta }$ correspond to $\underline{u}$ and $\overline{u}$ as in Definition 4.2.

Let $f_0 = (f_{01}, \dots , f_{0m})$. Since f satisfies (F1) and (F2), in view of (4.18) and (4.19), we can check that $f_0$ satisfies (F1) and (F2) as well. Moreover, as a consequence of (4.27), (4.18), (4.19), and the growth condition (4.22) in (F4), $f_0$ also satisfies (2.7) of (F3) with $\beta _k = 0$ and $\alpha _k = c_5^{(k)}\in L^{p_k'}(Q)$. For $u : Q \rightarrow \mathbb {R}$ measurable, let

$$\begin{aligned} F_{0k} (u) = \{\eta : Q \rightarrow \mathbb {R} : \eta \text{ is } \text{ measurable } \text{ on }\,\, Q\,\, \hbox {and } \eta (x,t)\in f_{0k}(x,t,u(x,t))\} , \end{aligned}$$

for $k = 1,\dots , m$, and

$$\begin{aligned} \begin{array}{lll} F_0 (u) &{} = &{} \displaystyle \prod _{k=1}^m F_{0k} (u) \\ &{} = &{} \{\eta : Q \rightarrow \mathbb {R}^m : \eta \in [L^0(Q)]^m \text{ and } \eta (x,t)\in f_0(x,t,u(x,t))\}. \end{array} \end{aligned}$$

From (F4) it follows that $F_0(u)\subset \prod _{k=1}^m L^{p_k'}(Q)$ for any measurable function u defined on Q, which allows us to define the Nemytskij operator of $f_0$,

$$\begin{aligned} F_0 : \prod _{k=1}^m L^{p_k}(Q) \rightarrow 2^{\prod _{k=1}^m L^{p_k'}(Q)},\ \ u\mapsto F_0(u), \end{aligned}$$

and its related mapping

$$\begin{aligned} \mathcal {F}_0 : X_0 \rightarrow 2^{X_0^*}, \ \ \mathcal {F}_0 = i^* \circ F_0 \circ i. \end{aligned}$$

For any $u\in X_0$, we have $\mathcal {F}_0 (u) = \prod _{k=1}^m \mathcal {F}_{0k} (u)$, where $\mathcal {F}_{0k} = i_k^* \circ F_{0k} \circ i_k$. We see that $\mathcal {F}_0$ is pseudomonotone with respect to D(L), according to Proposition 3.3. Let us consider the following auxiliary variational inequality:

$$\begin{aligned} u\in D(L)\cap K , \eta \in \mathcal {F}_0 (u) : \langle Lu + A u + \mathcal {B}u + \eta , v-u\rangle \ge 0 , \;\forall v\in K . \end{aligned}$$

(4.31)

It is clear from its definition that $\mathcal {B}$ is a (single-valued) pseudomonotone mapping w.r.t. D(L) from $X_0$ to $X_0^*$. Moreover, $f_1 = b + f_0$ satisfies (F1)–(F3), and thus $\mathcal {F}_1 = \mathcal {B} + \mathcal {F}_0$ is pseudomonotone with respect to D(L) according to Proposition 3.3.

Now, let us verify that $A+ \mathcal {B} + \mathcal {F}_0$ is coercive on $X_0$ in the following sense:

$$\begin{aligned} \lim _{\Vert u\Vert _{X_0}\rightarrow \infty } \left[ \inf _{\eta \in \mathcal {F}_0(u)}\frac{\langle A u+ \mathcal {B}u + \eta , u-\varphi \rangle }{\Vert u\Vert _{X_0}}\right] = \infty , \end{aligned}$$

(4.32)

for any (fixed) $\varphi \in X_0$. In fact, from (A3), we have

$$\begin{aligned} \langle A u , u \rangle \ge c_3 \sum _{k=1}^m \Vert \, |\nabla u_k | \,\Vert ^{p_k}_{L^{p_k}(Q)} - c_{10} , \;\forall u\in X_0 , \end{aligned}$$

(4.33)

with some constants $c_3, c_{10}>0$. For $\eta \in \mathcal {F}_0(u)$, $\eta = i^* \tilde{\eta } i$ with $\tilde{\eta }\in F_0(u)$, we have

$$\begin{aligned} \begin{array}{lll} |\langle \eta , u \rangle | &{} \le &{} \displaystyle \sum _{k=1}^m \left| \int _Q \tilde{\eta }_k u_k \,dx dt\right| \\ &{} \le &{} \displaystyle \sum _{k=1}^m \Vert c_5^{(k)} \Vert _{L^{p_k'}(Q)} \Vert u_k \Vert _{L^{p_k}(Q)} . \end{array} \end{aligned}$$

(4.34)

Combining (4.26) with (4.33) and (4.34), one gets for all $u\in X_0$

$$\begin{aligned} \begin{array}{lll} \langle (A u + \mathcal {B}u + \eta , u\rangle &{}\ge &{}\displaystyle c_3 \sum _{k=1}^m \Vert \, |\nabla u_k | \,\Vert ^{p_k}_{L^{p_k}(Q)} + c_8 \sum _{k=1}^m \Vert u\Vert ^{p_k}_{L^{p_k}(Q)} \\ &{}&{}\displaystyle - \sum _{k=1}^m \Vert c_5^{(k)} \Vert _{L^{p_k'}(Q)} \Vert u_k \Vert _{L^{p_k}(Q)}- c_9 -c_{10} . \end{array} \end{aligned}$$

(4.35)

For $\varphi \in X_0$ fixed, it is inferred from (A1), (4.23), and (4.22) that

$$\begin{aligned} |\langle A u + \mathcal {B}u + \eta ,\varphi \rangle | \le c_{11} \left( \sum _{k=1}^m \Vert u\Vert _{X_{0k}}^{p_k-1} +1 \right) ,\;\forall u\in X_0 , \end{aligned}$$

(4.36)

for some constant $c_{11} >0$. From (4.35) and (4.36), we obtain (4.32). Let $u_0\in D(L)\cap K$ be fixed. With the particular choice of $\varphi = u_0$, we see that all conditions of Theorem 4.1 are fulfilled with $\mathcal {F}_1 = \mathcal {B} + \mathcal {F}_0$ in place of $\mathcal {F}$. According to Theorem 4.1, (4.31) has solutions.

Next, we show that any solution u of (4.31) satisfies: $\underline{u}\le u\le \overline{u}$ a.e. in Q. We verify that $\underline{u}\le u$, the second inequality is proved in the same way. Let u be a solution of (4.31), which is equivalent to the system

$$\begin{aligned} u_k\in D(L_k)\cap K_k , \eta _k \in \mathcal {F}_{0k} (u) : \langle u_{kt} + A_k u_k + \mathcal {B}_ku_k + \eta _k , v_k-u_k\rangle \ge 0 , \;\forall v_k\in K_k , \end{aligned}$$

(4.37)

with $k =1, \dots ,m$. Because $u_k\in K_k$, it follows that

$$\begin{aligned} u_k+ (\underline{u}_k -u_k)^+ = \underline{u}_k \vee u_k \in K_k . \end{aligned}$$

Letting $v_k=u_k+(\underline{u}_k-u_k)^+$ into (4.37), one gets

$$\begin{aligned} \langle u_{kt} , (\underline{u}_k-u_k)^+ \rangle + \langle A_k u_k + \mathcal {B}_k u_k + \eta _k , (\underline{u}_k-u_k)^+ \rangle \ge 0. \end{aligned}$$

(4.38)

On the other hand, let $\underline{\eta }$ be associated with the subsolution $\underline{u}$ as in Definition 4.2. For $[w]_k = [Tu]_k \in [\underline{u}, \overline{u}]_k$, and

$$\begin{aligned} v_k= \underline{u}_k-(\underline{u}_k -u_k)^+ = \underline{u}_k\wedge u_k \in \underline{u}_k\wedge K_k , \end{aligned}$$

we have from (4.20) that

$$\begin{aligned} - \langle \underline{u}_{kt} , (\underline{u}_k-u_k)^+ \rangle - \langle A_k \underline{u}_k , (\underline{u}_k-u_k)^+ \rangle - \langle i_k^* \underline{\eta }_{k}(\cdot , \cdot , [Tu]_k) , (\underline{u}_k-u_k)^+ \rangle \ge 0. \end{aligned}$$

(4.39)

Adding (4.38) and (4.39) yields

$$\begin{aligned} \begin{array}{l} \langle (u_k-\underline{u}_k)_t , (\underline{u}_k-u_k)^+ \rangle + \langle A_k u_k - A_k\underline{u}_k + \mathcal {B}_k u_k , (\underline{u}_k-u_k)^+ \rangle \\ \quad + \langle \eta _k-i_k^* \underline{\eta }_{k}(\cdot , \cdot , [Tu]_k) , (\underline{u}_k-u_k)^+ \rangle \ge 0 . \end{array} \end{aligned}$$

(4.40)

We have $\underline{u}_k-u_k \in W_k$ and $(\underline{u}_k-u_k)^+(\cdot ,0) =0$, and thus

$$\begin{aligned} \langle (\underline{u}_k-u_k)_t , (\underline{u}_k-u_k)^+ \rangle = \frac{1}{2}\Vert (\underline{u}_k-u_k)^+(\cdot ,\tau )\Vert _{L^2(\varOmega )}^2 \ge 0. \end{aligned}$$

(4.41)

On the other hand, it is easy to check from (A2) that

$$\begin{aligned} \langle A_k\underline{u}_k - A_k u_k , (\underline{u}_k-u_k)^+ \rangle \ge 0 . \end{aligned}$$

(4.42)

Moreover, with $\eta _k = i_k^* \tilde{\eta }_k i_k$, $\tilde{\eta }_k \in F_{0k}(u)$, we have

$$\begin{aligned} \begin{aligned}&\displaystyle \langle \eta _k - i_k^* \underline{\eta }_{k}(\cdot , \cdot , [Tu]_k), (\underline{u}_k-u_k)^+ \rangle \\&\quad = \displaystyle \int _{Q}(\tilde{\eta }_k (x,t) - \underline{\eta }_{k}(x,t , [Tu(x,t)]_k)) (\underline{u}_k (x,t)-u_k(x,t))^+ \, dx dt \\&\quad = \displaystyle \int _{\{\underline{u}_k>u_k\}}(\tilde{\eta }_k (x,t) - \underline{\eta }_{k}(x,t , [Tu(x,t)]_k)) (\underline{u}_k(x,t)-u_k(x,t)) \, dx dt , \end{aligned} \end{aligned}$$

where $\{\underline{u}_k>u_k\}=\{ (x,t)\in Q : \underline{u}_k(x,t) > u_k(x,t) \}$. But because of (4.30), we have

$$\begin{aligned} \tilde{\eta }_k (x,t) = \underline{\eta }_{k}(x,t , [Tu(x,t)]_k)) \text{ for } \text{ a.e. }\,\, (x,t) \in \{\underline{u}_k>u_k\}. \end{aligned}$$

Therefore

$$\begin{aligned} \langle \eta _k - i_k^* \underline{\eta }_{k}(\cdot , \cdot , [Tu]_k), (\underline{u}_k-u_k)^+ \rangle = 0 . \end{aligned}$$

(4.43)

Combining (4.41)–(4.43) with (4.40), we obtain

$$\begin{aligned} 0 \le \langle \mathcal {B}_k u_k , (\underline{u}_k-u_k)^+ \rangle = -\int _{\{\underline{u}_k>u_k\}} (\underline{u}_k - u_k)^{p_k} \, dx dt \le 0. \end{aligned}$$

This proves that $\underline{u}_k-u_k=0$ a.e. on $\{\underline{u}_k>u_k\}$, i.e., $\{\underline{u}_k>u_k\}$ has measure zero, and thus $\underline{u}_k\le u_k$ a.e. on Q. Since this holds true for all $k = 1, \dots , m$, we have $\underline{u}\le u$. A similar proof shows that $u\le \overline{u}$. From $\underline{u}\le u\le \overline{u}$, we have $\mathcal {B}u=0$ and $\mathcal {F}_0(u)\subset \mathcal {F}(u)$. Consequently, a solution u of (4.31) is also a solution of (4.1).$\square$

5 Application: obstacle problem

In this section we deal with the system of multivalued parabolic variational inequalities (1.1)–(1.2) with $A_k=-\varDelta _{p_k}$ ($p_k\ge 2$) being the $p_k$-Laplacian, and under upward obstacle constraints $K_k$ given by (4.16), that is,

$$\begin{aligned} K_k =\{u_k\in X_{0k} : u_k\le \psi _k \; \text{ a.e. } \text{ on } \; Q\}, \end{aligned}$$

(5.1)

with $\psi _k$ a given function in $W_k$ such that $\psi _k(\cdot , 0)\ge 0$ on $\varOmega$, $\psi _k\ge 0$ on $\varGamma$, and $\psi _{kt} +A_k \psi _k \ge 0$ in $X_{0k}^*$, in the sense that

$$\begin{aligned} \langle \psi _{kt} +A_k \psi _k, v_k \rangle \ge 0,\;\forall v_k\in X_{0k}\cap L^{p_k}_+(Q). \end{aligned}$$

In other words, the obstacle function $\psi _k$ is assumed to be a (weak) supersolution of the parabolic initial boundary value problem:

$$\begin{aligned} v_t-\varDelta _{p_k} v=0, \ \ v(\cdot , 0)=0 \text{ on } \varOmega ,\ \ v=0 \text{ on } \varGamma . \end{aligned}$$

Thus, by comparison we have $\psi _k(x,t)\ge 0$ for a.a. $(x,t)\in Q$. Moreover, it has been shown in Sect. 4 that there exists a penalty operator $P_k$ associated with $K_k$ satisfying property (P).

Assuming hypotheses (F1)–(F3) for the multivalued lower order terms $f_k: Q\times \mathbb {R}^m\rightarrow 2^{\mathbb {R}}{\setminus }\{\emptyset \}$, our main goal is to construct an ordered pair of sub-supersolutions for the obstacle problem. Only for simplifying the presentation in this section, we assume $\varOmega =B(0,1)$ with B(0, 1) being the unit ball in $\mathbb {R}^N$. Further, let $\varOmega _R=B(0,R)$ be the ball with radius $R>1$. For $k=1,\dots , m$, let $h_k\in W^{1,p_k}_0(\varOmega _R)$ be the unique weak solution of

$$\begin{aligned} -\varDelta _{p_k} h_k=1\ \ \text{ in } \varOmega _R,\quad h_k=0\ \ \text{ on } \partial \varOmega _R, \end{aligned}$$

(5.2)

which means

$$\begin{aligned} h_k\in W^{1,p_k}_0(\varOmega _R): -\varDelta _{p_k} h_k=1\ \ \text{ in } (W^{1,p_k}_0(\varOmega _R))^*. \end{aligned}$$

(5.3)

Let $s^-=\max \{-s,0\}$ for $s\in \mathbb {R}$, and using $-h_k^-\in W^{1,p_k}_0(\varOmega _R)$ as a test function in (5.3), we see that

$$\begin{aligned} \langle -\varDelta _{p_k}\, h_k,-h_k^-\rangle =\Vert \nabla h_k^-\Vert ^p_{L^p(\varOmega _R)}=-\int _{\varOmega _R} h_k^-(x)\,dx\le 0, \end{aligned}$$

which implies that $h_k^-=0$, and thus $h_k\ge 0$. From the nonlinear regularity theory (cf., e.g. [12]) we have $h_k\in C^1_0(\overline{\varOmega _R})$, and from the nonlinear strong maximum principle due to Vazquez (see [17]) we infer that $h_k\in \mathrm{int\,}(C^1_0(\overline{\varOmega _R})_+)$. Here $\mathrm{int\,} (C^1_0(\overline{\varOmega _R})_+)$ denotes the interior of the positive cone $C^1_0(\overline{\varOmega _R})_+=\{u\in C^1_0(\overline{\varOmega _R})\,: \ u(x)\ge 0,\ \forall x\in \varOmega _R\}$ in the Banach space $C^1_0(\overline{\varOmega _R})=\{u\in C^1(\overline{\varOmega _R})\,: \ u(x)= 0,\ \forall x\in \partial \varOmega _R\}$, given by

$$\begin{aligned} \mathrm{int\,} (C^1_0(\overline{\varOmega _R})_+)=\left\{ u\in C^1_0(\overline{\varOmega _R})\,: \ u(x)> 0, \ \forall x\in \varOmega _R, \text{ and } \frac{\partial u}{\partial n}(x)<0,\ \forall x\in \partial \varOmega _R\right\} , \end{aligned}$$

where $n=n(x)$ is the outer unit normal at $x\in \partial \varOmega _R$. We are going to construct a pair of sub-supersolutions by means of the solutions $h_k$ of the Dirichlet problem (5.3) on $\varOmega _R=B(0,R)$ with $R>0$. Since the lower order multivalued nonlinearities $f_k: Q\times \mathbb {R}^m\rightarrow \mathcal {K}(\mathbb {R})$ satisfy (F1)–(F3), we have the following representation of $f_k$ for a.a. $(x,t)\in Q=B(0,1)\times (0,\tau )$ and for all $s\in \mathbb {R}^m$

$$\begin{aligned} f_k(x,t,s) = [\underline{f_k}(x,t,s), \overline{f_k}(x,t,s)]. \end{aligned}$$

(5.4)

By means of [11, Proposition 4.2] we see that the (single-valued) functions $\underline{f_k},\ \overline{f_k}: Q\times \mathbb {R}^m\rightarrow \mathbb {R}$ have the following properties for a.a. $(x,t)\in Q$ and for all $s\in \mathbb {R}^m$:

$$\begin{aligned}&(x,t)\mapsto \underline{f_k}(x,t,s),\ (x,t)\mapsto \overline{f_k}(x,t,s) \text{ are } \text{ measurable } \text{ on } Q,\\&s\mapsto \underline{f_k}(x,t,s) \text{ is } \text{ lower } \text{ semicontinuous } \text{ on } \mathbb {R}^m, \\&s\mapsto \overline{f_k}(x,t,s) \text{ is } \text{ upper } \text{ semicontinuous } \text{ on } \mathbb {R}^m. \end{aligned}$$

Thus $\underline{f_k},\ \overline{f_k}: Q\times \mathbb {R}^m\rightarrow \mathbb {R}$ belong to a Baire–Carathéodory class, and are therefore superpositionally measurable, that is, the associated Nemytskij operators $\underline{F_k}(u)(x,t)= \underline{f_k}(x,t,u(x,t))$, and $\overline{F_k}(u)(x,t)=\overline{f_k}(x,t,u(x,t))$ map measurable functions into measurable functions. We now make the following assumption on the (single-valued) functions $\underline{f_k},\ \overline{f_k}: Q\times \mathbb {R}^m\rightarrow \mathbb {R}$:

• (H) There exist functions $\underline{c_k}\in L^\infty (Q)$ and $\overline{c_k}\in L^\infty (Q)$ such that for a.a. $(x,t)\in Q$ and for all $s\in \mathbb {R}^m$ we have

  $$\begin{aligned} \underline{f_k}(x,t,s) \le \underline{c_k}(x,t),\quad \overline{f_k}(x,t,s) \ge \overline{c_k}(x,t),\ \ k=1,\dots ,m. \end{aligned}$$

  (5.5)

  Assume $0 \notin f_i(x,t,0)$ for at least one $i\in \{1,\dots ,m\}$.

We note that hypothesis (H) excludes the trivial solution, and the one-sided bounds in (5.5) still allow the multi-valued functions $f_k$ to be unbounded.

We are now in the position to explicitly construct an ordered pair of sub-supersolution for the (upward) obstacle problem (1.1)–(1.2) with $A_k=-\varDelta _{p_k}$ ($p_k\ge 2$), and $K_k$ given by (5.1).

Theorem 5.1

Assume (F1)–(F3) for the multivalued lower order terms $f_k$ and let hypothesis (H) on the single-valued functions $\underline{f_k},\, \overline{f_k}$ generating $f_k$ through (5.4) be satisfied. Then

$$\begin{aligned}&\underline{u}(x,t)=(-M_1\phi _1(t)h_1(x),\dots , -M_m\phi _m(t)h_m(x)) \ \text{ and } \\&\overline{u}(x,t)=(M_1\phi _1(t)h_1(x),\dots , M_m\phi _m(t)h_m(x)), ~~(x,t)\in Q , \end{aligned}$$

form an ordered pair of sub- and supersolution for $M_k>0$ sufficiently large, where $h_k$ are the positive solutions of problem (5.2) on $\varOmega _R$, and $\phi _k\in C^1([0,\tau ])$ are supposed to satisfy $\phi _k(0)=0$, and $\phi _k(t)\ge 0$, $\phi _k'(t)\ge d_k>0$, $\forall \ t\in [0,\tau ]$, $k=1,\dots ,m$.

Proof

Let us verify that $\underline{u}$ and $\overline{u}$ satisfy Definition 4.2. Clearly, we have $\underline{u}\le \overline{u}$ and properties (i) and (ii) of Definition 4.2 with $K_k$ given by (5.1) are satisfied. So it remains to check property (iii) in Definition 4.2, that is, we need to show the existence of functions $\underline{\eta }_{k} , \overline{\eta }_{k}: Q_k \rightarrow {\mathbb R}$ such that for any $[w]_k \in [\underline{u} , \overline{u}]_k$, the functions $(x,t) \mapsto \underline{\eta }_{k} (x,t , [w(x,t)]_k)$ and $(x,t) \mapsto \overline{\eta }_{k} (x,t , [w(x,t)]_k)$ belong to $L^{p'_k}(Q)$, and

$$\begin{aligned}&\underline{\eta }_{k} (x,t, [w(x,t)]_k) \in f_k (x, t, \underline{u}_k(x,t), [w(x,t)]_k) , \end{aligned}$$

(5.6)

$$\begin{aligned}&\overline{\eta }_{k} (x,t, [w(x,t)]_k) \in f_k (x, t, \overline{u}_k(x,t), [w(x,t)]_k) , \end{aligned}$$

(5.7)

for a.e. $(x,t)\in Q$, and

$$\begin{aligned} \langle \underline{u}_{kt}-\varDelta _{p_k}\underline{u}_k,v_k-\underline{u}_k\rangle + \int _{Q}\underline{\eta }_{k} (\cdot ,\cdot , [w]_k)\,(v_k-\underline{u}_k)\,dxdt \ge 0,\,\forall \ v_k\in \underline{u}_k\wedge K_k , \end{aligned}$$

(5.8)

and

$$\begin{aligned} \langle \overline{u}_{kt}-\varDelta _{p_k}\overline{u}_k,v_k-\overline{u}_k\rangle + \int _{Q}\overline{\eta } (\cdot ,\cdot , [w]_k)\,(v_k-\overline{u}_k)\,dxdt \ge 0, \,\forall \ v_k\in \overline{u}_k\vee K_k, \end{aligned}$$

(5.9)

where $\underline{u}_k(x,t) =-M_k\phi _k(t)h_k(x)$ and $\overline{u}_k(x,t)=M_k\phi _k(t)h_k(x)$. Let $\varphi _k\in K_k$, then $v_k\in \underline{u}_k\wedge K_k$ has the representation $v_k=\underline{u}_k-(\underline{u}_k-\varphi _k)^+$, and thus (5.8) becomes

$$\begin{aligned} \langle \underline{u}_{kt}-\varDelta _{p_k}\underline{u}_k,(\underline{u}_k-\varphi _k)^+\rangle + \int _{Q}\underline{\eta }_{k} (\cdot ,\cdot , [w]_k)\,(\underline{u}_k-\varphi _k)^+\,dxdt \le 0,\,\forall \ \varphi _k\in K_k. \end{aligned}$$

(5.10)

Similarly, $v_k\in \overline{u}_k\vee K_k$ can be written as $v_k=\overline{u}_k+(\varphi _k-\overline{u}_k)^+$ with $\varphi _k\in K_k$, and thus (5.9) becomes

$$\begin{aligned} \langle \overline{u}_{kt}-\varDelta _{p_k}\overline{u}_k,(\varphi _k-\overline{u}_k)^+\rangle + \int _{Q}\overline{\eta } (\cdot ,\cdot , [w]_k)\,(\varphi _k-\overline{u}_k)^+\,dxdt \ge 0, \,\forall \ \varphi _k\in K_k. \end{aligned}$$

(5.11)

We are going to verify (5.10) with $\underline{\eta }_{k}$ given by

$$\begin{aligned} \underline{\eta }_{k} (x,t, [w(x,t)]_k)=\underline{f_k}(x,t,-M_k\phi _k(t)h_k(x), [w(x,t)]_k) \text{ for } (x,t)\in Q. \end{aligned}$$

(5.12)

Since $\underline{f_k}$ is superpositionally measurable, the growth condition (F3) on $f_k$ implies that $\underline{\eta }_{k}$ given by (5.12) belongs to $L^{p_k'}(Q)$. Applying hypothesis (H) we have for all $[w(x,t)]_k$

$$\begin{aligned} \underline{f_k}(x,t,-M_k\phi _k(t)h_k(x), [w(x,t)]_k)\le \underline{c_k}(x,t), \end{aligned}$$

and thus we get the following inequalities (in the weak sense)

$$\begin{aligned}&\underline{u}_{kt}-\varDelta _{p_k}\underline{u}_k +\underline{\eta }_{k} (\cdot ,\cdot , [w]_k)\\&\quad =-M_k\phi '_kh_k-(M_k\phi _k)^{p_k-1}+\underline{f_k}(x,t,-M_k\phi _k(t)h_k(x), [w(x,t)]_k)\\&\quad \le -M_kd_kh_k+\underline{c_k}(x,t) \end{aligned}$$

We note that $h_k$ is the positive solution on the bigger ball $\varOmega _R$ with $R>1$, and therefore the restriction of $h_k$ on $\overline{\varOmega }=\overline{B(0,1)}$ has a positive minimum, that is,

$$\begin{aligned} \min _{x\in \overline{B(0,1)}}h_k(x)=\delta _k>0, \end{aligned}$$

which yields the estimate

$$\begin{aligned}&\underline{u}_{kt}-\varDelta _{p_k}\underline{u}_k +\underline{\eta }_{k} (\cdot ,\cdot , [w]_k)\\&\quad =-M_k\phi '_kh_k-(M_k\phi _k)^{p_k-1}+\underline{f_k}(x,t,-M_k\phi _k(t)h_k(x), [w(x,t)]_k)\\&\quad \le -M_kd_kh_k+\underline{c_k}(x,t)\\&\quad \le -M_kd_k \delta _k+\Vert \underline{c_k}\Vert _{L^\infty (Q)}\le 0, \ \text{ for } \,\,M_k\,\, \hbox {large} \end{aligned}$$

and thus (5.10) is verified. Let us next check (5.11). To this end we take

$$\begin{aligned} \overline{\eta }_{k} (x,t, [w(x,t)]_k)=\overline{f_k}(x,t,M_k\phi _k(t)h_k(x), [w(x,t)]_k) \text{ for } (x,t)\in Q. \end{aligned}$$

(5.13)

By the same arguments as for $\underline{\eta }_{k}$ we have that $\overline{\eta }_{k}\in L^{p_k'}(Q)$, and from hypothesis (H) we get, for all $[w(x,t)]_k$,

$$\begin{aligned} \overline{f_k}(x,t,M_k\phi _kh_k, [w(x,t)]_k)\ge \overline{c_k}(x,t). \end{aligned}$$

Using the definition of $h_k$ we obtain the following inequalities (in the weak sense) with $\overline{u}_k(x,t)=M_k\phi _k(t)h_k(x)$

$$\begin{aligned}&\overline{u}_{kt}-\varDelta _{p_k}\overline{u}_k+ \overline{\eta } (\cdot ,\cdot , [w]_k)\\&\quad =M_k\phi '_kh_k+(M_k\phi _k)^{p_k-1}+\overline{f_k}(x,t,M_k\phi _kh_k, [w(x,t)]_k)\\&\quad \ge M_kd_kh_k -\Vert \overline{c_k}\Vert _{L^\infty (Q)}\ge 0, \ \text{ for } M_k \text{ large }, \end{aligned}$$

which proves (5.11). This completes the proof of Theorem 5.1.$\square$

An immediate consequence is the following corollary.

Corollary 5.1

Under the hypotheses of Theorem 5.1 there exists a solution u of the (upward) obstacle problem (1.1)–(1.2) with $A_k=-\varDelta _{p_k}$ ($p_k\ge 2$), and $K_k$ given by (5.1) satisfying

$$\begin{aligned} \underline{u}\le u\le \overline{u}\wedge \psi , \end{aligned}$$

for $M_k>0$ sufficiently large, where $\underline{u}$ and $\overline{u}$ are as in Theorem 5.1, and $\psi$ is the obstacle function.

Proof

Since $(\underline{u},\overline{u})$ is an ordered pair of sub-supersolution, by Theorem 4.2 there exists a solution $u\in [\underline{u},\overline{u}]$ of the obstacle problem with $K_k$ given by (5.1), and thus $\underline{u}\le u\le \overline{u}\wedge \psi$.$\square$

6 Systems of evolutionary variational-hemivariational inequalitiesl

Variational-hemivariational inequalities have been proved a powerful tool to describe relevant models in mechanical engineering, and have been first introduced by Panagiotopoulos see e.g. [14, 15]. With the notations of the preceding sections, in this section we consider the following system of evolutionary variational-hemivariational inequalities: Find $u\in D(L)\cap K$ such that

$$\begin{aligned} \langle Lu+Au, v-u\rangle +\int _Q\sum _{k=1}^m j^o_k(x,t,u_k,[u]_k; v_k-u_k)\,dxdt\ge 0,\ \ \forall \ v\in K, \end{aligned}$$

(6.1)

which is equivalent to ($k=1,\dots ,m$)

$$\begin{aligned} \langle u_{kt}+A_ku_k, v_k-u_k\rangle +\int _Qj^o_k(x,t,u_k,[u]_k; v_k-u_k)\,dxdt\ge 0,\ \ \forall \ v_k\in K_k. \end{aligned}$$

(6.2)

The functions $j_k: Q\times \mathbb {R}^m\rightarrow \mathbb {R}$, $k=1,\dots ,m$, are supposed to be Carathéodory functions with $s_k\mapsto j_k(x,t, s_k, [s]_k)$ being locally Lipschitz for a.a. $(x,t)\in Q$ and for all $[s]_k\in \mathbb {R}^{m-1}$, and $s_k\mapsto j^o_k(x,t,s_k,[s]_k; \varrho _k)$ denotes Clarke’s partial generalized directional derivative with respect to the $s_k$ component of $s\in \mathbb {R}^m$ in the direction $\varrho _k\in \mathbb {R}$, which is defined by

$$\begin{aligned} j_k^o(x,t,s_k, [s]_k;\varrho _k)=\limsup _{h\rightarrow s_k,\ \varepsilon \downarrow 0} \frac{j_k(x,t,h+\varepsilon \,\varrho _k, [s]_k)-j_k(x,t,h, [s]_k)}{\varepsilon }, \end{aligned}$$

(6.3)

(cf., e.g., [7, Chap. 2]). Further, let us introduce Clarke’s partial generalized gradient $\partial _kj_k$ of the locally Lipschitz function $s_k\mapsto j_k(x,t, s_k, [s]_k)$ given by

$$\begin{aligned} \partial _kj_k(x,t,s)=\{\eta \in \mathbb {R}: j_k^o(x,t,s_k, [s]_k;\varrho _k)\ge \eta \,\varrho _k,\ \ \forall \ \varrho _k\in \mathbb {R}\}. \end{aligned}$$

(6.4)

We assume the following hypotheses on $j_k$.

• (J1) The functions $j_k: Q\times \mathbb {R}^m\rightarrow \mathbb {R}$, $k=1,\dots ,m$, are supposed to be Carathéodory functions, that is, $(x,t)\mapsto j_k(x,t,s)$ is measurable in Q for all $s\in \mathbb {R}^m$, and $s\mapsto j_k(x,t,s)$ is continuous in $\mathbb {R}^m$ for a.a. $(x,t)\in Q$, and $s_k\mapsto j_k(x,t, s_k, [s]_k)$ is locally Lipschitz for a.a. $(x,t)\in Q$ and for all $[s]_k\in \mathbb {R}^{m-1}$.

• (J2) The functions $s\mapsto j_k^o(x,t,s_k, [s]_k;\varrho _k)$, $k=1,\dots ,m$, are upper semicontinuous for $\varrho _k=\pm 1$.

• (J3) Clarke’s partial generalized gradient $\partial _kj_k$ satisfies the growth condition

  $$\begin{aligned} \sup \{|\eta | : \eta \in \partial _kj_k(x,t ,s)\} \le \alpha _k (x,t) + \beta _k \sum _{j=1}^m |s_j|^{\frac{p_j}{p_k'}} , \end{aligned}$$

  for a.e. $(x,t)\in Q,\ \forall \ s\in \mathbb {R}^m$, where $\alpha _k \in L^{p'_k}(Q),$ and $\beta _k \ge 0$.

Remark 6.1

Regarding assumption (J2) on Clarke’s partial generalized directional derivative $s\mapsto j_k^o(x,t,s_k,[s]_k;\varrho _k)$ a few comments are in order. One may ask for sufficient conditions on the function $j_k=j_k(x,t,s)$ itself such that the general condition (J2) is satisfied. Here, we provide such sufficient conditions for functions $j_k: Q\times \mathbb {R}^m\rightarrow \mathbb {R}$ of the following class:

$$\begin{aligned} j_k(x,t,s)= g_{k}\left( x, t, s_{k}\right) h_{k}\left( x, t,[s]_{k}\right) , \end{aligned}$$

(6.5)

for $(x, t) \in Q,$ $s=\left( s_{k},[s]_{k}\right) \in \mathbb {R}^{m}$.

Corollary 6.1

Assume that $g_{k}: Q \times \mathbb {R} \rightarrow \mathbb {R}$ and $h_{k}: Q \times \mathbb {R}^{m-1} \rightarrow \mathbb {R}$ are Carathéodory functions such that for a.e. $(x, t) \in Q$, $s_k\rightarrow g_{k}(x, t, s_k)$ is locally Lipschitz, and $h_{k}(x, t,[s]_{k}) \ge 0$ for a.e. $(x,t) \in Q$, all $[s]_{k}\in \mathbb {R}^{m-1}$. Then $j_k$ given by (6.5) fulfills (J2), that is, $s\mapsto j_k^o(x,t,s_k,[s]_k;\varrho _k)$ is upper semicontinuous for $\varrho _k=\pm 1$.

Proof

Let $(s^{(j)})\subset \mathbb {R}^m$ such that $s^{(j)}\rightarrow s$ as $j\rightarrow \infty$. To prove that $s\mapsto j_k^o(x,t,s_k,[s]_k;\varrho _k)$ is upper semicontinuous, we need to show that

$$\begin{aligned} \limsup _{j\rightarrow \infty }j_k^o(x,t,s_k^{(j)},[s^{(j)}]_k;\varrho _k)\le j_k^o(x,t,s_k,[s]_k;\varrho _k). \end{aligned}$$

(6.6)

In fact, we have, for any $\varrho _k\in \mathbb {R}$,

$$\begin{aligned} \begin{array}{lll} j_k^o(x,t,s_k, [s]_k;\varrho _k) &{} = &{}\displaystyle \limsup _{h\rightarrow s_k,\ \varepsilon \downarrow 0} \frac{j_k(x,t,h+\varepsilon \,\varrho _k, [s]_k)-j_k(x,t,h, [s]_k)}{\varepsilon }\\ &{} = &{}\displaystyle \limsup _{h\rightarrow s_k,\ \varepsilon \downarrow 0} \left[ \frac{g_k(x,t,h+\varepsilon \,\varrho _k)-g_k(x,t,h)}{\varepsilon } h_{k}\left( x, t,[s]_{k}\right) \right] \\ &{} = &{}\displaystyle \limsup _{h\rightarrow s_k,\ \varepsilon \downarrow 0} \left[ \frac{g_k(x,t,h+\varepsilon \,\varrho _k)-g_k(x,t,h)}{\varepsilon }\right] h_{k}\left( x, t,[s]_{k}\right) \\ &{} = &{} g_k^o(x,t,s_k;\varrho _k) h_{k}\left( x, t,[s]_{k}\right) . \end{array} \end{aligned}$$

As $s^{(j)}\rightarrow s$ in $\mathbb {R}^m$, it follows that $s^{(j)}_k \rightarrow s_k$ in $\mathbb {R}$ and $[s^{(j)}]_k \rightarrow [s]_k$ in $\mathbb {R}^{m-1}$. Thus for a.e. $(x,t)\in Q$, all $\varrho _k\in \mathbb {R}$, we have from a basic property of Clarke’s generalized directional derivative (see [7, Chap. 2]) that

$$\begin{aligned} \limsup _{j\rightarrow \infty } g_k^o(x,t,s^{(j)}_k;\varrho _k) \le g_k^o(x,t,s_{k};\varrho _k). \end{aligned}$$

By the Carathéodory property we have

$$\begin{aligned} \lim _{j\rightarrow \infty } h_k(x,t, [s^{(j)}]_k) = h_k(x,t, [s]_k) , \end{aligned}$$

and along with $h_{k}(x, t,[s]_{k}) \ge 0$ we obtain

$$\begin{aligned} \begin{array}{lll} \displaystyle \limsup _{j\rightarrow \infty } j_k^o(x,t,s^{(j)}_{k}, [s^{(j)}]_k;\varrho _k) &{} = &{}\displaystyle \limsup _{j\rightarrow \infty }[g_k^o(x,t,s^{(j)}_{k};\varrho _k) h_k(x,t, [s^{(j)}]_k)]\\ &{} = &{} \displaystyle \limsup _{j\rightarrow \infty }g_k^o(x,t,s^{(j)}_{k};\varrho _k) \lim _{j\rightarrow \infty }h_k(x,t, [s^{(j)}]_k)] \\ &{} \le &{} \displaystyle g_k^o(x,t,s_{k};\varrho _k) h_k(x,t, [s]_k) \\ &{} = &{} \displaystyle j_k^o(x,t,s_k, [s]_k;\varrho _k) \end{array} \end{aligned}$$

which proves (6.6).$\square$

We note that these arguments also hold when $j_k$ is a finite sum of functions of the above form.

Let us introduce the multivalued functions $f_k: Q\times \mathbb {R}^m\rightarrow 2^\mathbb {R}{\setminus }\{\emptyset \}$ defined by

$$\begin{aligned} f_k(x,t,s)=\partial _kj_k(x,t ,s). \end{aligned}$$

(6.7)

Our main goal in this section is to show that under some lattice condition on the constraint K and assuming (J1)–(J3), the system of evolutionary variational-hemivariational inequalities (6.1) is equivalent to the system of multi-valued parabolic variational inequalities (1.1)–(1.2) with $f_k$ specified by (6.7). Thus, system (6.1) is only a particular case of system (1.1)–(1.2).

To this end, first we are going to show the following lemma.

Lemma 6.1

Under the assumptions (J1)–(J3), the multivalued functions $f_k: Q\times \mathbb {R}^m\rightarrow 2^\mathbb {R}{\setminus }\{\emptyset \}$ defined by (6.7) satisfy hypotheses (F1)–(F3).

Proof

Clearly, (F3) follows directly from (J3). As for the proof of the graph measurability of $f_k$ and the upper semicontinuity of $s\mapsto f_k(x,t,s)$ we follow an idea from [6, Sect.5].

By definition of Clarke’s gradient $\partial _kj_k(x,t ,s)$ and the positive homogeneity of the mapping $\varrho _k \mapsto j^o_k(x,t,s_k,[s]_k;\varrho _k)=j^o_k(x,t,s;\varrho _k)$, we see that for almost all $(x,t)\in Q$, and all $s\in {\mathbb {R}^m}$,

$$\begin{aligned} \partial _k j_k(x,t,s) = [- j^o_k(x,t,s;-1) , j^o_k(x,t,s;1)] . \end{aligned}$$

Hence,

$$\begin{aligned} \begin{array}{ll} \mathrm{Gr}(f_k) &{}= \{ (x,t, s, \eta ) \in Q\times {\mathbb {R}^m}\times {\mathbb {R}} : \eta \in \partial _k j_k(x,t,s)\} \\ &{}= \{ (x,t, s, \eta ) \in Q\times {\mathbb {R}^m}\times {\mathbb {R}} : - j^o_k(x,t,s;-1) \le \eta \le j^o_k(x,t,s;1) \} \\ &{}= \{ (x,t, s, \eta ) \in Q\times {\mathbb {R}^m}\times {\mathbb {R}} : \eta \ge - j^o_k(x,t,s;-1) \} \\ &{} \ \quad \bigcap \{ (x,t, s, \eta ) \in Q\times {\mathbb {R}^m}\times {\mathbb {R}} : \eta \le j^o_k(x,t,s;1) \} . \end{array} \end{aligned}$$

For each $\varrho _k \in \mathbb {R}$, it follows from (J1) that the function $(x,t,s) \mapsto j^o_k(x,t,s;\varrho _k)$ is measurable on $Q\times \mathbb {R}^m$ with respect to the measure $\mathcal {L}(Q) \times \mathcal {B}(\mathbb {R}^m) \times \mathcal {B}(\mathbb {R})$, as “countable limit superior” of measurable functions there. Hence the functions $(x,t, s) \mapsto j^o_k(x,t,s;1)$ and $(x,t, s) \mapsto j^o_k(x,t,s;-1)$ are measurable on $Q\times \mathbb {R}^m$ with respect to the measure $\mathcal {L}(Q) \times \mathcal {B}(\mathbb {R}^m)$. This implies that $\mathrm{Gr}(f_k)$ belongs to $[\mathcal {L}(Q) \times \mathcal {B}(\mathbb {R}^m)]\times \mathcal {B}(\mathbb {R})$, i.e., $f_k$ satisfies (F1).

As for the proof of (F2), let $(x,t)\in Q$ be a point such that the functions $s\mapsto j^o_k(x,t,s;\pm 1)$ are upper semicontinuous on $\mathbb {R}^m$. Let $s_0\in \mathbb {R}^m$ and U be an open neighborhood of $\partial _k j_k(x,t,s_0)$. Then there exists $\varepsilon >0$ such that

$$\begin{aligned} ( -j^o_k(x,t,s_0;-1) - \varepsilon , j^o_k(x,t,s_0;1)+\varepsilon ) \subset U . \end{aligned}$$

From the upper semicontinuity of the (single-valued) functions $s\mapsto j^o_k(x,t,s;\pm 1)$ at $s_0$, there exists an open neighborhood O of $s_0$ such that

$$\begin{aligned} \left\{ \begin{array}{l} j^o_k(x,t,s; 1)< j^o_k(x,t,s_0; 1) + \varepsilon , \text{ and } \\ j^o_k(x,t,s; -1) < j^o_k(x,t,s_0; -1) + \varepsilon ,\;\forall s\in O . \end{array} \right. \end{aligned}$$

Hence, for all $s\in O$,

$$\begin{aligned} \begin{array}{lll} \partial _k j_k(x,t,s) &{} = &{} [- j^o_k(x,t,s;-1) , j^o_k(x,t,s;1)] \\ &{} \subset &{} ( - j^o_k(x,t,s_0;-1) - \varepsilon , j^o_k(x,t,s_0;1)+\varepsilon ) \\ &{} \subset &{} U . \end{array} \end{aligned}$$

which shows the upper semicontinuity of $f_k$ at $s_0$.$\square$

With the multivalued functions $f_k$ specified by (6.7), let us consider the system (1.1)–(1.2), that is, we consider the following system of multivalued parabolic variational inequalities: For each $k =1 , \dots , m$, find $u_k\in W_{0k}\cap K_k$ and $\eta _k\in L^{p'_k}(Q)$ such that

$$\begin{aligned}&u_k(\cdot ,0)=0\ \text{ in } \varOmega ,\ \ \eta _k(x,t)\in f_k(x,t,u_1(x,t), \dots , u_m(x,t)), \end{aligned}$$

(6.8)

$$\begin{aligned}&\langle u_{kt}+A_k u_k, v_k-u_k\rangle +\int _Q \eta _k\, (v_k-u_k)\,dxdt\ge 0,\ \ \forall \ v_k\in K_k, \end{aligned}$$

(6.9)

The following equivalence result of system (6.1) and (6.8)–(6.9) holds true.

Theorem 6.1

Let (A1)–(A3) and (J1)–(J3) be satisfied and assume the following lattice condition for the constraint K:

$$\begin{aligned} K\vee K\subset K\ \text{ and } \ K\wedge K\subset K. \end{aligned}$$

(6.10)

Then u is a solution of the system of evolutionary variational-hemivariational inequalities (6.1) if and only if u is a solution of the system of multi-valued parabolic variational inequalities (6.8)–(6.9) with the multi-functions $f_k$ given by (6.7).

Proof

Let u be a solution of (6.8)–(6.9) , which means $u\in D(L)\cap K$ and there are $\eta _k\in L^{p'_k}(Q)$ with

$$\begin{aligned} \eta _k(x,t)\in f_k(x,t,u_1(x,t), \dots , u_m(x,t))=\partial _kj_k(x,t, u_1(x,t), \dots , u_m(x,t)) \end{aligned}$$

such that

$$\begin{aligned} \langle u_{kt}+A_k u_k, v_k-u_k\rangle +\int _Q \eta _k\, (v_k-u_k)\,dxdt\ge 0,\ \ \forall \ v_k\in K_k, \end{aligned}$$

(6.11)

By definition of $\partial _kj_k(x,t, u)$ we get for any $v\in K_k$

$$\begin{aligned} j^o_k(x,t,u_k,[u]_k; v_k-u_k)\ge \eta _k(x,t)(v_k-u_k). \end{aligned}$$

(6.12)

From (J1) and (J3) it follows that the left-hand side of inequality (6.12) is integrable, which by combining with (6.11) yields (6.2) or equivalently (6.1). We have seen by this way that any solution of (6.8)–(6.9) is a solution of the system of evolutionary variational-hemivariational inequalities (6.1).

Now let us show the reverse, and assume u is a solution of (6.1). In order to show that u is a solution of (6.8)–(6.9), we are going to show that u is both a subsolution and a supersolution for (6.8)–(6.9) which, via Theorem 4.2, completes the proof. In fact, according to Theorem 4.2, there exists a solution $\hat{u}$ within the interval of sub- and supersolutions, that is, $u\le \hat{u}\le u$, and therefore $u=\hat{u}$ must be a solution of (6.8)–(6.9), completing the proof. We note that Theorem 4.2 can be applied in this situation, since by Lemma 6.1 the hypotheses (F1)–(F3) for $f_k$ (defined by (6.7)) are fulfilled and (F3) implies (F4).

Let u be a solution of (6.1), that is, of (6.2). By assumption, K has the lattice property (6.10), so $K_k$ has the same property. In particular, we can use in (6.2) $v_k\in u_k\wedge K_k\subset K_k$, i.e., $v_k=u_k\wedge \varphi _k=u_k-(u_k-\varphi _k)^+$ with $\varphi _k\in K_k$, which yields for all $\varphi _k\in K_k$,

$$\begin{aligned} \langle u_{kt}+A_ku_k, -(u_k-\varphi _k)^+\rangle +\int _Q j^o_k(x,t, u_k,[u]_k;-(u_k-\varphi _k)^+)\,dxdt \ge 0. \end{aligned}$$

Because $\varrho \mapsto j^o_k(x,t, u_k,[u]_k;\varrho _k)$ is positively homogeneous, the last inequality is equivalent to

$$\begin{aligned} \langle u_{kt}+A_ku_k, -(u_k-\varphi _k)^+\rangle +\int _Q j^o_k(x,t, u_k,[u]_k;-1)(u_k-\varphi _k)^+\,dxdt \ge 0, \end{aligned}$$

for all $\varphi _k\in K_k$. Using again $v_k=u_k\wedge \varphi _k=u_k-(u_k-\varphi _k)^+$, the last inequality is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&\langle u_{kt}+A_ku_k, v_k-u_k\rangle +\int _Q -j^o_k(x,t, u_k,[u]_k;-1)(v_k-u_k)\,dxdt \ge 0,\\&\forall \ v_k\in u_k\wedge K_k. \end{aligned} \right. \end{aligned}$$

(6.13)

In view of [7, Proposition 2.1.2] we have

$$\begin{aligned} \begin{aligned}&j^o_k(x,t,u_k(x,t),[u(x,t)]_k;-1)\\ =&\max \{-\theta _k(x,t): \theta _k(x,t)\in \partial _k j_k(x,t,u_k(x,t),[u(x,t)]_k)\}\\ =&-\min \{\theta _k(x,t): \theta _k(x,t)\in \partial _k j_k(x,t,u_k(x,t),[u(x,t)]_k)\}\\ =&:-\underline{\eta }_k(x,t), \end{aligned} \end{aligned}$$

(6.14)

where

$$\begin{aligned} \underline{\eta }_k(x,t) \in \partial _k j_k(x,t,u_k(x,t),[u(x,t)]_k)=f_k(x,t,u_1(x,t),\dots , u_m(x,t)). \end{aligned}$$

(6.15)

Since $(x,t)\mapsto j^o_k(x,t,u_k(x,t),[u(x,t)]_k;-1)$ is measurable, it follows that $(x,t)\mapsto \underline{\eta }_k(x,t)$ is measurable in Q as well. Thus, in view of the growth conditions (J3) on the Clarke’s gradients, we infer that $\underline{\eta }_k\in L^{p_k'}(Q)$. Taking (6.14)–(6.15) into account, from (6.13) we get ($k=1,\dots ,m$)

$$\begin{aligned} \left\{ \begin{aligned}&\langle u_{kt}+A_ku_k, v_k-u_k\rangle +\int _Q \underline{\eta }_k(x,t)(v_k-u_k)\,dxdt \ge 0,\\&\forall \ v_k\in u_k\wedge K_k. \end{aligned} \right. \end{aligned}$$

(6.16)

which shows that u is a subsolution for (6.8)–(6.9)(with respect to the interval [u, u]). By similar arguments one shows that u is also a supersolution, which completes the proof.$\square$