Abstract
A complete theoretical analysis of the C- conserving semileptonic decays \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^\prime \rightarrow \eta l^+l^-\) (\(l=e\) or \(\mu \)) is carried out within the framework of the Vector Meson Dominance (VMD) model. An existing phenomenological model is used to parametrise the VMD coupling constants and the associated numerical values are obtained from an optimisation fit to \(V\rightarrow P\gamma \) and \(P\rightarrow V\gamma \) radiative decays (\(V=\rho ^0\), \(\omega \), \(\phi \) and \(P=\pi ^0\), \(\eta \), \(\eta ^{\prime }\)). The decay widths and dilepton energy spectra for the two \(\eta \rightarrow \pi ^0l^+l^-\) processes obtained using this approach are compared and found to be in good agreement with other results available in the published literature. Theoretical predictions for the four \(\eta ^{\prime }\rightarrow \pi ^0l^+l^-\) and \(\eta ^\prime \rightarrow \eta l^+l^-\) decay widths and dilepton energy spectra are calculated and presented for the first time in this work.
Similar content being viewed by others
1 Introduction
The electromagnetic and strong interactions conserve parity (P) and charge conjugation (C) within the well-established and well-tested Standard Model of particle physics (SM). In this framework, the \(\eta \) and \(\eta ^{\prime }\) pseudoscalar mesons are specially suited for the study of rare decay processes, for instance, in search of C, P and CP violations, as these mesons are C and P eigenstates of the electromagnetic and strong interactions [1].
Specifically, the semileptonic decays \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^\prime \rightarrow \eta l^+l^-\) (\(l=e\) or \(\mu \)) are of special interest given that they can be used as fine probes to assess if new physics beyond the Standard Model (BSM) is at play. This is because any contribution from BSM physics ought to be relatively smallFootnote 1 and the above decay processes only get a contribution from the SM through the C-conserving exchange of two photons that is highly suppressed, as there is no contribution at tree-level but only corrections at one-loop and higher orders. This small SM contribution would presumably be of the same order of magnitude as that of physics BSM, which, in turn, means that the \(\eta \)-\(\eta ^{\prime }\) phenomenology might play an interesting role and be an excellent arena for stress testing SM predictions [1, 2]. As an example, the \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^\prime \rightarrow \eta l^+l^-\) decays could be mediated by a single intermediate virtual photon, but this would entail that the electromagnetic interactions violate C-invariance (e.g. [3, 4]) and, therefore, would represent a departure from the SM.
Early theoretical studies of semileptonic decays of pseudoscalar mesons date back to the late 1960s. A very significant contribution was made by Cheng in Ref. [5] where he analysed the \(\eta \rightarrow \pi ^0e^+e^-\) decay mediated by a C-conserving, two-photon intermediate state within the Vector Meson Dominance (VMD) framework. By setting the electron mass to \(m_e=0\) and neglecting in the numerator of the amplitude terms that were second or higher order in the electron or positron 4-momenta, he found theoretical estimations for the decay width  eV, the relative branching ratio
eV, the relative branching ratio  , as well as the associated decay energy spectrum. This was an enormous endeavour given the very limited access to computer algebra systems at the time. For this reason, a number of strong assumptions had to be made, as pointed out above, which may have had an undesired effect on the accuracy of Cheng’s estimates. A different approach was followed by Smith [6] also in the late 1960s, whereby an S-wave \(\eta \pi ^0\gamma \gamma \) coupling and unitary boundsFootnote 2 were used for the calculation of the C-conserving modes associated to both \(\eta \rightarrow \pi ^0l^+l^-\) decay processes. By neglecting p-wave contributing terms to simplify the calculations and noting that the unknown \(\eta \pi ^0\gamma \gamma \) coupling constant cancels out when calculating relative branching ratios, Smith was able to find
, as well as the associated decay energy spectrum. This was an enormous endeavour given the very limited access to computer algebra systems at the time. For this reason, a number of strong assumptions had to be made, as pointed out above, which may have had an undesired effect on the accuracy of Cheng’s estimates. A different approach was followed by Smith [6] also in the late 1960s, whereby an S-wave \(\eta \pi ^0\gamma \gamma \) coupling and unitary boundsFootnote 2 were used for the calculation of the C-conserving modes associated to both \(\eta \rightarrow \pi ^0l^+l^-\) decay processes. By neglecting p-wave contributing terms to simplify the calculations and noting that the unknown \(\eta \pi ^0\gamma \gamma \) coupling constant cancels out when calculating relative branching ratios, Smith was able to find  and
and  , after estimating the real part of the matrix element from a single dispersion relation and employing a cut-off \(\varLambda = 2m_{\eta }\). The calculation of the latter ratio was possible due to the fact that Smith did not approximate the lepton mass to zero.
, after estimating the real part of the matrix element from a single dispersion relation and employing a cut-off \(\varLambda = 2m_{\eta }\). The calculation of the latter ratio was possible due to the fact that Smith did not approximate the lepton mass to zero.
Ng et al. [8] also found in the early 1990s lower limits for the decay widths of the two \(\eta \rightarrow \pi ^0l^+l^-\) processes by making use of unitary bounds and the decay chain \(\eta \rightarrow \pi ^0\gamma \gamma \rightarrow \pi ^0l^+l^-\). The transition form factors associated to the \(\eta \rightarrow \pi ^0\gamma \gamma \) decay, which are required to perform the above calculation, were obtained using the VMD model supplemented by the exchange of an \(a_0\) scalar meson. The lower bounds that they found are  eV and
eV and  eV, making use of VMD only. By adding the \(a_0\) exchangeFootnote 3 to the latter process, they obtained
eV, making use of VMD only. By adding the \(a_0\) exchangeFootnote 3 to the latter process, they obtained  eV and
eV and  eV for a constructive and destructive interference, respectively. The real parts of the amplitudes were estimated by means of a cut-off dispersive relation and the authors argued that the expected dispersive contribution should be no larger than 30% of the absorptive one. Only a few months later, Ng and Peters provided in Ref. [9] new estimations for the unitary bounds of the \(\eta \rightarrow \pi ^0l^+l^-\) decay widths. This new contribution was two-fold; on one hand, they calculated the \(\eta \rightarrow \pi ^0\gamma \gamma \) decay width within a constituent quark model framework; on the other hand, they recalculated the VMD transition form factors from Ref. [8] by performing a Taylor expansion and keeping terms linear in \(M_{\eta }^2/M_V^2\), \(x_1\) and \(x_2\) (\(x_i\equiv P_{\eta }\cdot q_{\gamma _i}/M_{\eta }^2\)), which had been neglected in their previous work. Their new findings were: (i)
eV for a constructive and destructive interference, respectively. The real parts of the amplitudes were estimated by means of a cut-off dispersive relation and the authors argued that the expected dispersive contribution should be no larger than 30% of the absorptive one. Only a few months later, Ng and Peters provided in Ref. [9] new estimations for the unitary bounds of the \(\eta \rightarrow \pi ^0l^+l^-\) decay widths. This new contribution was two-fold; on one hand, they calculated the \(\eta \rightarrow \pi ^0\gamma \gamma \) decay width within a constituent quark model framework; on the other hand, they recalculated the VMD transition form factors from Ref. [8] by performing a Taylor expansion and keeping terms linear in \(M_{\eta }^2/M_V^2\), \(x_1\) and \(x_2\) (\(x_i\equiv P_{\eta }\cdot q_{\gamma _i}/M_{\eta }^2\)), which had been neglected in their previous work. Their new findings were: (i)  eV and
eV and  eV for a constituent quark mass \(m=330\) MeV\(/c^2\); and (ii)
eV for a constituent quark mass \(m=330\) MeV\(/c^2\); and (ii)  eV and
eV and  eV. It is important to highlight that their estimations using the quark-box mechanism were strongly dependent on the specific constituent quark mass selected, especially for the electron mode.
eV. It is important to highlight that their estimations using the quark-box mechanism were strongly dependent on the specific constituent quark mass selected, especially for the electron mode.
On the experimental front, new upper limits have recently been established by the WASA-at-COSY collaboration for the \(\eta \rightarrow \pi ^0e^+e^-\) decay width [10]. This is a very useful contribution, as the previous available empirical measurements date back to the 1970s which provided an upper limit for the relative branching ratio of the above process that was many orders of magnitude larger than the corresponding theoretical estimations at the time. In particular, Adlarson et al. [10] found from the analysis of a total of \(3\times 10^7\) events of the reaction \(\text {pd}\rightarrow \!^3\!\text {He}\eta \), with a recorded excess energy of \(Q=59.8\) MeV, that the results are consistent with no C-violating single-photon intermediate state event being recorded. Based on their analysis, the new upper limits  and
and  (CL \(=90\%\)) have been established for the C-violating \(\eta \rightarrow \pi ^0\gamma ^*\rightarrow \pi ^0e^+e^-\) decay. In addition, the WASA-at-COSY Collaboration is currently analysing additional data from the \(\text {pp}\rightarrow \text {pp}\eta \) reaction collected over three periods in 2008, 2010 and 2012 which should put more stringent upper limits on the \(\eta \rightarrow \pi ^0e^+e^-\) branching ratio. The experimental state of play is expected to be further improved in the near future with the advent of new experiments such as the REDTOP Collaboration, which will focus on rare decays of the \(\eta \) and \(\eta ^{\prime }\) mesons, providing increased sensitivity in the search for violations of SM symmetries by several orders of magnitude beyond the current experimental state of the art [11].
(CL \(=90\%\)) have been established for the C-violating \(\eta \rightarrow \pi ^0\gamma ^*\rightarrow \pi ^0e^+e^-\) decay. In addition, the WASA-at-COSY Collaboration is currently analysing additional data from the \(\text {pp}\rightarrow \text {pp}\eta \) reaction collected over three periods in 2008, 2010 and 2012 which should put more stringent upper limits on the \(\eta \rightarrow \pi ^0e^+e^-\) branching ratio. The experimental state of play is expected to be further improved in the near future with the advent of new experiments such as the REDTOP Collaboration, which will focus on rare decays of the \(\eta \) and \(\eta ^{\prime }\) mesons, providing increased sensitivity in the search for violations of SM symmetries by several orders of magnitude beyond the current experimental state of the art [11].
The present work is structured as follows: In Sect. 2, we present the detailed calculations for the decay widths associated to the six \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\) processes. In Sect. 3, numerical results from theory for the decay widths and the corresponding dilepton energy spectra are presented and discussed for the six reactions. Some final remarks and conclusions are given in Sect. 4.
2 Calculations of \(\pmb {\eta ^{(\prime )}\rightarrow \pi ^0 l^+ l^-}\) and \(\pmb {\eta ^{\prime }\rightarrow \eta l^+ l^-}\)
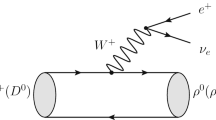
The calculations in this work assume that the \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\) decays processes are dominated by the exchange of vector resonancesFootnote 4 [5]; that is, they proceed through the C-conserving virtual transition \(\eta ^{(\prime )}\rightarrow V\gamma ^*\) (with \(V = \rho ^0\), \(\omega \) or \(\phi \)), followed by \(V\rightarrow \pi ^0\gamma ^*\) (or \(V\rightarrow \eta \gamma ^*\)) and \(2\gamma ^{*}\rightarrow l^+l^-\) (see Fig. 1 for details).Footnote 5
In order to perform the calculations, one first needs to select an effective vertex that contains the appropriate interacting terms. The \(VP\gamma \) interaction amplitude consistent with Lorentz, P, C and electromagnetic gauge invariance can be written as [13]
where \(g_{VP\gamma }\) is the coupling constant for the \(VP\gamma \) transition involving on-shell photons, \(\epsilon _{\mu \nu \alpha \beta }\) is the totally antisymmetric Levi-Civita tensor, \(\epsilon _{(V)}\) and \(p_V\) are the polarisation and 4-momentum vectors of the initial V, \(\epsilon _{(\gamma )}^*\) and q are the corresponding ones for the final \(\gamma \), and \({\hat{F}}_{VP\gamma }(q^2)\equiv F_{VP\gamma }(q^2)/F_{VP\gamma }(0)\) is a normalised form factor to account for off-shell photons mediating the transition.Footnote 6 In addition to this, the usual QED vertex is used to describe the subsequent \(2\gamma ^{*}\rightarrow l^+l^-\) transition. Accordingly, there are six diagrams contributing to each one of the six semileptonic decay processes and the corresponding Feynman diagrams are shown in Fig. 1.
The invariant decay amplitude in momentum space can, therefore, be written as follows

where \(q=p_{+}+p_{-}\) is the sum of lepton-antilepton pair 4-momenta, e is the electron charge, and \(g_{V\eta ^{(\prime )}\gamma }\) and \(g_{V\pi ^0(\eta )\gamma }\) are the corresponding coupling constants in Eq. (1). Noting that the Levi-Civita tensors are antisymmetric under the substitutions  and
and  , whilst the products of loop momenta \(k^{\mu }k^{\alpha }\) and \(k^{\rho }k^{\delta }\) are symmetric under these substitutions, one finds that the terms in Eq. (2) containing these combinations vanish and that the superficial degree of divergence for the loop integrals of the two diagrams in Fig. 1 is \(-1\). Accordingly, both diagrams are convergent individually.
, whilst the products of loop momenta \(k^{\mu }k^{\alpha }\) and \(k^{\rho }k^{\delta }\) are symmetric under these substitutions, one finds that the terms in Eq. (2) containing these combinations vanish and that the superficial degree of divergence for the loop integrals of the two diagrams in Fig. 1 is \(-1\). Accordingly, both diagrams are convergent individually.
The numerator of \({\mathcal {M}}\) can be simplified using the usual Dirac algebra manipulations and the equations of motion. For these calculations, the mass of the leptons are not approximated to zero, as we are interested in both the electron and muon modes for the six decay processes; as a result, the task of manipulating and simplifying the algebraic expressions would be daunting should computer algebra packages not be available. In the present work, use of the Mathematica package FeynCalc 9.2.0 [14, 15] is made for this purpose.
Let us now proceed to calculate the loop integral. As usual, one first introduces the Feynman parametrisation and completes the square in the new denominators \(\varDelta _{iV}\) (\(i=1,2\) and  ) by shifting to a new loop momentum variable \(\ell \) [16]. Hence, the denominators become
) by shifting to a new loop momentum variable \(\ell \) [16]. Hence, the denominators become
Rewriting the numerators of the Feynman diagrams 1 and 2 (i.e. t-channel and u-channel diagrams, respectively, in Fig. 1) in terms of the new momentum variable \(\ell \), one finds

where the explicit expressions for the parameters \(A_i\), \(B_i\), \(C_i\) and \(D_i\) (\(i=1,2\)) are provided in Appendix A. Finally, we perform a Wick rotation and change to four-dimensional spherical coordinates [16, 17] to carry out the momentum integral. The following expressions for the amplitudes of the Feynman diagrams are found

where \(m_l\) is the corresponding lepton mass, and the parameters  ,
,  in Eq. (5) are defined as
in Eq. (5) are defined as

with x, y and z being the Feynman integration parameters. Therefore, the full amplitude can now be expressed as

where \(\varOmega \) and \(\Sigma \) are defined as follows
and the unpolarised squared amplitude is
Finally, the differential decay rate for a three-body decay can be written as [18]
where \(m_{ij}^2=(p_i+p_j)^2\).
3 Theoretical results
Making use of the theoretical expressions that have been presented in Sect. 2, one can find numerical predictions for the decay widths of the \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\) decay processes, as well as their associated dilepton energy spectra. Both, the integral over the Feynman parameters as well as the integral over phase space, must be carried out numerically, as algebraic expressions cannot be obtained. In addition, the numerical integrals over the Feynman parameters are to be performed using adaptive Monte Carlo methods [19]; this is driven by the complexity of the expressions to be integrated and their multidimensional nature.
In the conventional VMD model, pseudoscalar mesons do not couple directly to photons but through the exchange of intermediate vectors. Thus, in this framework, a particular \(VP\gamma \) coupling constant times its normalised form factor, cf. Eq. (1), is given byFootnote 7
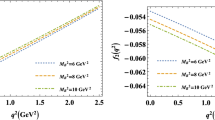
where \(g_{VV^\prime P}\) are the vector-vector-pseudoscalar couplings, \(g_{V^\prime \gamma }\) the vector-photon conversion couplings, and \(M_{V^\prime }\) the intermediate vector masses. In the SU(3)-flavour symmetry and OZI-rule respecting limits, one could express all the \(g_{VP\gamma }\) in terms of a single coupling constant and SU(3)-group factors [20]. However, to account for the unavoidable SU(3)-flavour symmetry-breaking and OZI-rule violating effects, we make use of the simple, yet powerful, phenomenological quark-based model first presented in Ref. [21], which was developed to describe \(V\rightarrow P\gamma \) and \(P\rightarrow V\gamma \) radiative decays. According to this model, the decay couplings can be expressed as
where g is a generic electromagnetic constant, \(\phi _P\) is the pseudoscalar \(\eta \)-\(\eta ^{\prime }\) mixing angle in the quark-flavour basis, \(\phi _V\) is the vector \(\omega \)-\(\phi \) mixing angle in the same basis, \({\overline{m}}/m_s\) is the quotient of constituent quark masses, and \(z_{\text {NS}}\) and \(z_{\text {S}}\) are the non-strange and strange multiplicative factors accounting for the relative meson wavefunction overlaps [21, 22]. By performing an optimisation fit to the most up-to-date \(VP\gamma \) experimental data [18], one can find values for the above parameters
Given the very wide decay width associated to the \(\rho ^0\) resonance, which, in turn, is linked to its very short lifetime, the use of the usual Breit-Wigner approximation for the \(\rho ^0\) propagator is not justified. Instead, an energy-dependent approximation for the vector propagator must be used. This can be written for the t-channel process (cf. t-channel diagram in Fig. 1) as follows
where \(\theta (x)\) is the Heaviside step function. Likewise, for the u-channel process (cf. u-channel diagram in Fig. 1), one only needs to substitute \(t\leftrightarrow u\) in Eq. (14). The energy dependent propagator is not needed, though, for the \(\omega \) and \(\phi \) resonances, as their associated decay widths are narrow and, therefore, use of the usual Breit-Wigner approximation suffices.
Using the most recent empirical data for the meson masses and total decay widths from Ref. [18], together with all the above considerations, one arrives at the decay width results shown in Table 1 for the six \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\) processes. The total decay widths associated to the electron modes turn out to be larger than the ones corresponding to the muon modes despite the second and third terms in the unpolarised squared amplitude (cf. Eq. (9)) being helicity suppressed for the electron modes. This suppression, though, does not overcome the phase space suppression for the muon modes, yielding  and
and  .
.
Let us now look at the contributions from the different vector meson exchanges to the total decay widths. For the first decay, i.e. \(\eta \rightarrow \pi ^0e^+e^-\), we find that the contribution from the \(\rho ^0\) exchange is \(\sim 25\%\), the contribution from the \(\omega \) is \(\sim 22\%\), whilst the one from the \(\phi \) is negligible, i.e. \(\sim 0\%\). The interference between the \(\rho ^0\) and the \(\omega \) is constructive, accounting for the \(\sim 47\%\); similarly, the interference between the \(\rho ^0\) and the \(\omega \) with the \(\phi \) is constructive and about \(\sim 6\%\). The contributions to the second decay, i.e. \(\eta \rightarrow \pi ^0\mu ^+\mu ^-\), are \(\sim 26\%\), \(\sim 22\%\) and \(\sim 0\%\) from the \(\rho ^0\), \(\omega \), and \(\phi \) exchanges, respectively. As before, the interference between the \(\rho ^0\) and the \(\omega \) is constructive, weighing \(\sim 49\%\), and the interference between the \(\rho ^0\) and the \(\omega \) with the \(\phi \) is constructive and accounts for approximately the \(\sim 3\%\). For the third decay, i.e. \(\eta ^{\prime }\rightarrow \pi ^0e^+e^-\), the contributions from the \(\rho ^0\), \(\omega \) and \(\phi \) turn out to be \(\sim 17\%\), \(\sim 36\%\) and \(\sim 0\%\), respectively; the interference between the \(\rho ^0\) and the \(\omega \) exchanges is constructive and accounts for the \(\sim 51\%\), whilst the interference between the \(\rho ^0\) and \(\omega \) with the \(\phi \) is destructive and weighs approximately \(\sim 4\%\). The contributions to the fourth decay, i.e. \(\eta ^{\prime }\rightarrow \pi ^0\mu ^+\mu ^-\), from the \(\rho ^0\), \(\omega \) and \(\phi \) exchanges are \(\sim 21\%\), \(\sim 32\%\) and \(\sim 0\%\), respectively. The interference between the \(\rho ^0\) and the \(\omega \) is constructive, representing a \(\sim 52\%\) contribution, whilst the interference between the \(\rho ^0\) and the \(\omega \) with the \(\phi \) is destructive and accounts for the \(\sim 5\%\). The fifth decay, i.e. \(\eta ^{\prime }\rightarrow \eta e^+e^-\), gets contributions from the exchange of \(\rho ^0\), \(\omega \) and \(\phi \) resonances of approximately \(\sim 79\%\), \(\sim 1\%\) and \(\sim 2\%\), respectively; the interference between the \(\rho ^0\) and the \(\omega \) is constructive weighing \(\sim 26\%\), and the interference between the \(\rho ^0\) and the \(\omega \) with the \(\phi \) is destructive and contributes with roughly the \(\sim 8\%\). Finally, for the sixth decay, i.e. \(\eta ^{\prime }\rightarrow \eta \mu ^+\mu ^-\), we find that the contribution from the \(\rho ^0\) exchange is \(\sim 93\%\), the contribution from the \(\omega \) is \(\sim 2\%\) and the one from the \(\phi \) is \(\sim 3\%\); the interference between the \(\rho ^0\) and the \(\omega \) is constructive and accounts for the \(\sim 26\%\), whilst the interference between the \(\rho ^0\) and the \(\omega \) with the \(\phi \) is destructive weighing close to \(\sim 24\%\). The tiny contribution from the \(\phi \) exchange to the decay widths of the six processes is explained by the relatively small product of VMD \(VP\gamma \) coupling constants. Likewise, the comparatively minute contribution from the \(\omega \) exchange to the decay widths of the last two reactions is down to the significantly smaller product of coupling constants, if compared to that of the \(\rho ^0\) exchange.
In order to assess a systematic error associated to the model dependency of our predictions, we repeat all the above calculations in the context of Resonance Chiral Theory (RChT). In this framework, the \(VP \gamma \) effective vertex is made of two contributions, a local \(VP\gamma \) vertex weighted by a coupling constant, \(h_V\), and a non-local one built from the exchange of an intermediate vector which, again, is weighted by a second coupling constant, \(\sigma _V\), times the vector-photon conversion factor \(f_V\). For a given \(VP\gamma \) transition, this effective vertex can be written in the SU(3)-flavour symmetry limit as [13]
where \(C_{VP\gamma }\) are SU(3)-group factors and, depending on the process, the exchanged vector is or is not the same as the initial vector (see Refs. [13, 23] for each particular case). To fix the \(VP\gamma \) couplings in this second approach, we make use of the extended Nambu–Jona-Lasinio (ENJL) model, where \(h_V\) is found to be \(h_V=0.033\) [13]. The VVP coupling \(\sigma _V\) obtained using the ENJL model turns out to be \(\sigma _V=0.28\). However, \(\sigma _V\) can also be obtained from the analysis of the dilepton mass spectrum in \(\omega \rightarrow \pi ^0\mu ^+\mu ^-\) decays, where one finds \(\sigma _V \approx 0.58\) [24]. Due to the fact that \(\sigma _V\) is poorly known and the dispersion of the above estimations is large, we do not consider the \(q^2\) dependence of the form factors in the subsequent calculations. An alternative model to fix \(g_{VP\gamma }\), the normalisation of the form factors, is the Hidden Gauge Symmetry (HGS) model [25], where the vector mesons are considered as gauge bosons of a hidden symmetry. Within this model, a \(VP\gamma \) transition proceeds uniquely through the exchange of intermediate vector mesons. In this sense, it is equivalent to the conventional VMD model with the relevant exception of including direct \(\gamma P^3\) terms (P being a pseudoscalar meson), which are forbidden in VMD [26]. Due to this similarity, we will not make use of the HGS model to assess the systematic model error and refer the interested reader to Ref. [20] for a detailed calculation of the \(g_{VP\gamma }\) couplings in this model.
Next, our results for the semileptonic decays \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^\prime \rightarrow \eta l^+l^-\) in the conventional VMD framework using the \(VP\gamma \) couplings from the phenomenological quark-based model in Eq. (12) are discussed and, if available, compared with previous literature. These predictions include a first experimental error ascribed to the propagation of the parametric errors in Eq. (13), a second error down to the numerical integration, and a third systematic error associated to the model dependence of our approach. The latter is calculated as the absolute difference between the predicted central values obtained from the VMD and RChT frameworks (cf. Table 1).
Our prediction for the decay width  eV is about an order of magnitude smaller than the one provided by Cheng in Ref. [5] (cf. Sect. 1), i.e.
eV is about an order of magnitude smaller than the one provided by Cheng in Ref. [5] (cf. Sect. 1), i.e.  eV; however, by plugging into our expressions the couplings that Cheng used in his work, we find a decay width
eV; however, by plugging into our expressions the couplings that Cheng used in his work, we find a decay width  eV, which is less than a factor of two larger than Cheng’s result, and the difference might be down to the simplifications that he had to carry out in his calculations, as well as the more sophisticated propagators that have been employed in the present work.Footnote 8 In addition, from our calculations one can also get a prediction for the ratio of branching ratiosFootnote 9
eV, which is less than a factor of two larger than Cheng’s result, and the difference might be down to the simplifications that he had to carry out in his calculations, as well as the more sophisticated propagators that have been employed in the present work.Footnote 8 In addition, from our calculations one can also get a prediction for the ratio of branching ratiosFootnote 9 , which is very approximate to Cheng’s model independent estimation of
, which is very approximate to Cheng’s model independent estimation of  , but more than two orders of magnitude larger than Smith’s resultFootnote 10
, but more than two orders of magnitude larger than Smith’s resultFootnote 10 [6]; as well as this, for the muon mode we find the relative branching ratioFootnote 11
[6]; as well as this, for the muon mode we find the relative branching ratioFootnote 11 , which is roughly an order of magnitude smaller than Smith’s estimation
, which is roughly an order of magnitude smaller than Smith’s estimation  [6]. Moreover, our decay widths for both the \(\eta \rightarrow \pi ^0e^+e^-\) and \(\eta \rightarrow \pi ^0\mu ^+\mu ^-\) processes are consistent with the lower bounds provided by Ng et al. in Ref. [8], i.e.
[6]. Moreover, our decay widths for both the \(\eta \rightarrow \pi ^0e^+e^-\) and \(\eta \rightarrow \pi ^0\mu ^+\mu ^-\) processes are consistent with the lower bounds provided by Ng et al. in Ref. [8], i.e.  eV and
eV and  eV making use of VMD, and
eV making use of VMD, and  eV and
eV and  eV using VMD supplemented by the exchange of an \(a_0\) scalar meson. Using the quark-box diagram and a constituent quark mass \(m=330\) MeV\(/c^2\), Ng et al. provided in Ref. [9] an estimation for the electron mode,
eV using VMD supplemented by the exchange of an \(a_0\) scalar meson. Using the quark-box diagram and a constituent quark mass \(m=330\) MeV\(/c^2\), Ng et al. provided in Ref. [9] an estimation for the electron mode,  eV, which is in accordance with our result, and an estimate for the muon mode,
eV, which is in accordance with our result, and an estimate for the muon mode,  eV, which in this case is incompatible with our calculation.Footnote 12 Additionally, Ng et al. also presented in Ref. [9] a recalculation of their previous VMD results from Ref. [8], yielding
eV, which in this case is incompatible with our calculation.Footnote 12 Additionally, Ng et al. also presented in Ref. [9] a recalculation of their previous VMD results from Ref. [8], yielding  eV and
eV and  eV, which are consistent with our results if one considers the associated errors. Our decay width calculations for the other four processes, i.e. \(\eta ^{\prime }\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\), cannot be compared with any previously published theoretical results, as these decays have been calculated, to the best of our knowledge, for the first time in the present work. Likewise, comparison with the most up-to-date empirical data provides limited value given that the corresponding current experimental upper bounds, though consistent with our theoretical predictions, are many orders of magnitude larger (cf. Table 1).
eV, which are consistent with our results if one considers the associated errors. Our decay width calculations for the other four processes, i.e. \(\eta ^{\prime }\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\), cannot be compared with any previously published theoretical results, as these decays have been calculated, to the best of our knowledge, for the first time in the present work. Likewise, comparison with the most up-to-date empirical data provides limited value given that the corresponding current experimental upper bounds, though consistent with our theoretical predictions, are many orders of magnitude larger (cf. Table 1).
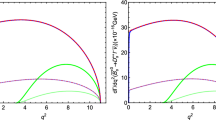
Finally, theoretical results for the dilepton energy spectra of the six C-conserving semileptonic decays are presented in Fig. 2. The energy spectra for the three electron modes, which are displayed in Fig. 2a, c, e, take off as the dilepton invariant mass \(q^2\) approaches zero. This is in line with Cheng’s and Ng et al.’s energy spectra for the \(\eta \rightarrow \pi ^0 e^+e^-\) (Refs. [5] and [8], respectively), which exhibit the same behaviour at low \(q^2\). It appears as though the electron modes prefer to proceed through the emission of (relativistic) collinear electron-positron pairs (i.e. \(\theta _{e^+e^-}\simeq 0\), where \(\theta _{e^+e^-}\) is the electron-positron angle). The reason for this can easily be understood from dynamicsFootnote 13 if one assumes the electron and positron to be massless, \(m_e\approx 0\); then, by inspection of Eq. (9), one can determine that the unpolarised squared amplitude is maximised when \(q^2\rightarrow 0\), which occurs when \(\theta _{e^+e^-}\simeq 0\)Footnote 14. Physically, it may be explained to some extent by the fact that the diphoton invariant spectra for the three \(\eta ^{(\prime )}\rightarrow \pi ^0\gamma \gamma \) and \(\eta ^{\prime }\rightarrow \eta \gamma \gamma \) peak at low \(m_{\gamma \gamma }^2\) (cf., e.g., Ref. [12] and references therein). On the other hand, the dilepton energy spectra for the muon modes, shown in Fig. 2b, d, f, are bell-shaped, which is driven by the kinematics of the processes. This, once more, seems to be consistent with Ng et al.’s [8] energy spectrum for the \(\eta \rightarrow \pi ^0 \mu ^+\mu ^-\). It is interesting to observe that the energy spectra for the \(\eta \rightarrow \pi ^0\mu ^+\mu ^-\) and \(\eta ^{\prime }\rightarrow \pi ^0 \mu ^+\mu ^-\) are skewed to the left (i.e. small values for \(\theta _{\mu ^+\mu ^-}\) are favoured, where \(\theta _{\mu ^+\mu ^-}\) is the muon-antimuon angle), whilst the energy spectrum for the \(\eta ^{\prime }\rightarrow \eta \mu ^+\mu ^-\) is skewed to the right (i.e. somewhat larger values for \(\theta _{\mu ^+\mu ^-}\) are preferred). This is more difficult to explainFootnote 15 given that this effect, which is connected to the fact that \(m_{\eta }>m_{\pi ^0}\), is a consequence of the complex dynamical interplay between the different terms in Eq. (9). Surprisingly, the kinematics of the reactions do not seem to play a significant role in this difference in skewness.
4 Conclusions
In this work, the C-conserving decay modes \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\) (\(l=e\) or \(\mu \)) have been analysed within the theoretical framework of the VMD model. The associated decay widths and dilepton energy spectra have been calculated and presented for the six decay processes. To the best of our knowledge, the theoretical predictions for the four \(\eta ^{\prime }\rightarrow \pi ^0l^+l^-\) and \(\eta ^{\prime }\rightarrow \eta l^+l^-\) reactions that we have provided in this work are the first predictions from theory that have been published.
The decay width results that we have obtained from our calculations, which are summarised in Table 1, have been compared with those available in the published literature. In general, the agreement is reasonably good considering that the previous analysis either contain important approximations or consist of unitary lower bounds. Predictions for the dilepton energy spectra have also been presented for all the above processes, cf. Fig. 2.
Experimental measurements to date have provided upper limits to the decay processes studied in this work. These upper limits, though, are still many orders of magnitude larger than the theoretical results that we have presented. For this reason, we would like to encourage experimental groups, such as the WASA-at-COSY and REDTOP Collaborations, to study these semileptonic decays processes, as we believe that they can represent a fruitful arena in the search for new physics beyond the Standard Model.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The present work is theoretical and does not have any associated data to be deposited.]
Change history
24 August 2022
An Erratum to this paper has been published: https://doi.org/10.1140/epjc/s10052-022-10717-y
09 February 2021
An Erratum to this paper has been published: https://doi.org/10.1140/epjc/s10052-021-08864-9
Notes
Otherwise, they would have already been detected.
As it is well known, the Cutkovsky rules [7] allow one to calculate the imaginary part of a transition amplitude by putting the intermediate virtual particles on-shell.
The \(a_0\eta \pi ^0\) and \(a_0\gamma \gamma \) couplings needed to perform this calculation were roughly estimated and the authors acknowledged to be poorly known. As well as this, their signs were not unambiguously fixed.
It is worth highlighting that contributions from the exchange of scalar resonances can be safely discarded as they ought to be negligible for the first four \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) decays and relatively small for the last two \(\eta ^{\prime }\rightarrow \eta l^+l^-\) processes. The interested reader is referred to the in-depth analysis carried out in Ref. [12] where scalar exchanges were introduced under the framework of the Linear Sigma Model for the \(\eta ^{(\prime )}\rightarrow \pi ^0\gamma \gamma \) and \(\eta ^{\prime }\rightarrow \eta \gamma \gamma \) decays.
Note that any C-violating contributions to these processes, such as e.g. the single-photon exchange channel, would be associated to BSM physics. In this work, though, the focus is on the SM contribution from the C-conserving two-photon exchange channel.
For simplicity of the calculation, we neglect the \(q^2\) dependence of the transition form factor in Eq. (1). This is not fully rigorous but, we understand, it is a tolerable approximation given that these form factors are usually determined from on-shell photon processes.
Should \(q^2\) be timelike, that is, \(q^2>0\), then an imaginary part would need to be added to the propagator; this introduces the associated resonance width effects and rids the propagator from its divergent behaviour.
Note that in Ref. [5] Cheng used vector propagators without total decay widths (i.e. Feynman propagators) for the vector exchanges whilst we are using an energy dependent propagator for the \(\rho ^0\) exchange and usual Breit-Wigner propagators for the \(\omega \) and \(\phi \) exchanges.
The discrepancy with Smith’s relative branching ratio might be explained, though, by the effect of p-wave terms that he neglected after admitting that they are not necessarily small.
Once more, should we have used the theoretical prediction from Ref. [12]
 eV, we would have obtained
eV, we would have obtained 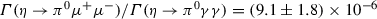 .
.Note, however, that, as part of their calculation, they had to estimate the decay width of the \(\eta \rightarrow \pi ^0\gamma \gamma \) process using their quark-box model and found
 eV for a constituent quark mass \(m=330\) MeV\(/c^2\), which is approximately a factor of two larger than the current experimental measurement. Therefore, it is no surprise that their estimates for the associated \(\eta \rightarrow \pi ^0 l^+l^-\) processes are at the upper end of the spectrum of estimations.
eV for a constituent quark mass \(m=330\) MeV\(/c^2\), which is approximately a factor of two larger than the current experimental measurement. Therefore, it is no surprise that their estimates for the associated \(\eta \rightarrow \pi ^0 l^+l^-\) processes are at the upper end of the spectrum of estimations.It must be noted, though, that the kinematics of the electron modes also contribute to this particular shape of the energy spectra, producing a somewhat synergistic effect.
Note that \(q^2\simeq 2p_{e^+}p_{e^-}\simeq 2|\varvec{p_{e^+}}||\varvec{p_{e^-}}|(1-\cos {\theta _{e^+e^-}})\) in the leptonic massless limit, i.e. \(m_e\approx 0\).
A qualitative explanation could be given from a statistical mechanics viewpoint, whereby high momentum \(\eta \) mesons in the final state would be Boltzmann suppressed compared to high momentum \(\pi ^0\) states.
References
L. Gan, B. Kubis, E. Passemar, S. Tulin, arXiv:2007.00664 [hep-ph]
S.s. Fang, A. Kupsc, D.h. Wei, Chin. Phys. C 42, no. 4, 042002 (2018) arXiv:1710.05173 [hep-ex]
J. Bernstein, G. Feinberg, T.D. Lee, Phys. Rev. 139, B1650 (1965)
T.D. Lee, Phys. Rev. 140, B959 (1965)
T.P. Cheng, Phys. Rev. 162, 1734 (1967)
J. Smith, Phys. Rev. 166, 1629 (1968)
R. Cutkosky, J. Math. Phys. 1, 429–433 (1960)
J.N. Ng, D.J. Peters, Phys. Rev. D 46, 5034 (1992)
J.N. Ng, D.J. Peters, Phys. Rev. D 47, 4939 (1993)
P. Adlarson et al., WASA-at-COSY Collaboration. Phys. Lett. B 784, 378 (2018). arXiv:1802.08642 [hep-ex]
C. Gatto [REDTOP], arXiv:1910.08505 [physics.ins-det]
R. Escribano, S. Gonzàlez-Solís, R. Jora, E. Royo, Phys. Rev. D 102 (2020) no.3, 034026 arXiv:1812.08454 [hep-ph]
J. Prades, Z. Phys. C 63 (1994), 491-506 [erratum: Z. Phys. C 11 (1999), 571] arXiv:hep-ph/9302246 [hep-ph]
V. Shtabovenko, R. Mertig, F. Orellana, Comput. Phys. Commun. 207, 432 (2016). arXiv:1601.01167 [hep-ph]
R. Mertig, M. Bohm, A. Denner, Comput. Phys. Commun. 64, 345 (1991)
M.E. Peskin, D.V. Schroeder, Westview Press (1995)
M.D. Schwartz, Cambridge University Press, Cambridge (2014)
P.A. Zyla et al. [Particle Data Group], PTEP 2020 (2020) no.8, 083C01
W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Cambridge University Press, Cambridge (2007)
A. Bramon, A. Grau, G. Pancheri, Phys. Lett. B 344, 240–244 (1995)
A. Bramon, R. Escribano, M. Scadron, Phys. Lett. B 503 (2001), 271-276. arXiv:hep-ph/0012049 [hep-ph]
R. Escribano, E. Royo, Phys. Lett. B 807, 135534 (2020). arXiv:2003.08379 [hep-ph]
S. Eidelman, S. Ivashyn, A. Korchin, G. Pancheri, O. Shekhovtsova, Eur. Phys. J. C 69, 103–118 (2010). arXiv:1003.2141 [hep-ph]
S. Ivashyn, Prob. Atom. Sci. Technol. 2012N1 (2012), 179-182 arXiv:1111.1291 [hep-ph]
M. Bando, T. Kugo, K. Yamawaki, Phys. Rep. 164, 217–314 (1988)
T. Fujiwara, T. Kugo, H. Terao, S. Uehara, K. Yamawaki, Prog. Theor. Phys. 73 (1985), 926 LaTeX (EU)
Acknowledgements
We would like to thank Sergi Gonzàlez-Solís for suggesting us to work on this particular topic and Pablo Roig for recommending relevant literature on Resonance Chiral Theory. As well as this, we are very grateful to Pablo Sanchez-Puertas for a thorough read of the manuscript and for checking some of the numerical results. Finally, this work is supported by the Secretaria d’Universitats i Recerca del Departament d’Empresa i Coneixement de la Generalitat de Catalunya under the grant 2017SGR1069, by the Ministerio de Economía, Industria y Competitividad under the grant FPA2017-86989-P, from the Centro de Excelencia Severo Ochoa under the grant SEV-2016-0588, and from the EU STRONG-2020 project under the H2020-INFRAIA-2018-1 programme, grant agreement No. 824093. IFAE is partially funded by the CERCA program of the Generalitat de Catalunya.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original online version of this article was revised: the authors were only affiliated to one affiliation in the published version. They are however affiliated to both affiliations.
Appendix A: Definition of parameters \(\pmb {A_i}\), \(\pmb {B_i}\), \(\pmb {C_i}\) and \(\pmb {D_i}\)
Appendix A: Definition of parameters \(\pmb {A_i}\), \(\pmb {B_i}\), \(\pmb {C_i}\) and \(\pmb {D_i}\)
The parameters \(A_i\), \(B_i\), \(C_i\) and \(D_i\) (\(i=1,2\)) from Eq. (4) are defined as follows
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
About this article
Cite this article
Escribano, R., Royo, E. A theoretical analysis of the semileptonic decays \(\eta ^{(\prime )}\rightarrow \pi ^0l^+l^-\) and \(\eta ^\prime \rightarrow \eta l^+l^-\). Eur. Phys. J. C 80, 1190 (2020). https://doi.org/10.1140/epjc/s10052-020-08748-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08748-4





 provided in Ref. [
provided in Ref. [ eV to obtain
eV to obtain  .
. eV, we would have obtained
eV, we would have obtained 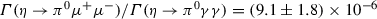 .
. eV for a constituent quark mass
eV for a constituent quark mass