Measurement of exclusive ${\varvec{{{{\pi ^+\pi ^-}}}}}$ and ${\varvec{{{{\rho ^0}}}}}$ meson photoproduction at HERA

Abstract

Exclusive photoproduction of ${{\rho ^0}} (770)$ mesons is studied using the H1 detector at the ep collider HERA. A sample of about 900,000 events is used to measure single- and double-differential cross sections for the reaction $\gamma p \rightarrow \pi ^{+}\pi ^{-}Y$. Reactions where the proton stays intact (${{{m_Y}} {=}m_p}$) are statistically separated from those where the proton dissociates to a low-mass hadronic system ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$). The double-differential cross sections are measured as a function of the invariant mass $m_{\pi \pi }$ of the decay pions and the squared 4-momentum transfer t at the proton vertex. The measurements are presented in various bins of the photon–proton collision energy ${{W_{\gamma p}}}$. The phase space restrictions are $0.5\le m_{\pi \pi } \le 2.2~{{\text {GeV}}}$, $\vert t\vert \le 1.5~{{\text {GeV}^2}}$, and $20 \le W_{\gamma p} \le 80~{{\text {GeV}}}$. Cross section measurements are presented for both elastic and proton-dissociative scattering. The observed cross section dependencies are described by analytic functions. Parametrising the ${m_{\pi \pi }}$ dependence with resonant and non-resonant contributions added at the amplitude level leads to a measurement of the ${{\rho ^0}} (770)$ meson mass and width at $m_\rho = 770.8{}^{+2.6}_{-2.7}~({\text {tot.}})~{{\text {MeV}}}$ and $\Gamma _\rho = 151.3 {}^{+2.7}_{-3.6}~({\text {tot.}})~{{\text {MeV}}}$, respectively. The model is used to extract the ${{\rho ^0}} (770)$ contribution to the $\pi ^{+}\pi ^{-}$ cross sections and measure it as a function of t and ${W_{\gamma p}}$. In a Regge asymptotic limit in which one Regge trajectory $\alpha (t)$ dominates, the intercept $\alpha (t{=}0) = 1.0654\ {}^{+0.0098}_{-0.0067}~({\text {tot.}})$ and the slope $\alpha ^\prime (t{=}0) = 0.233 {}^{+0.067 }_{-0.074 }~({\text {tot.}}) ~{{\text {GeV}^{-2}}}$ of the t dependence are extracted for the case $m_Y{=}m_p$.

1 Introduction

Diffractive hadron interactions at high scattering energies are characterised by final states consisting of two systems well separated in rapidity, which carry the quantum numbers of the initial state hadrons. Most diffractive phenomena are governed by soft, large distance processes. Despite being dominated by the strong interaction, they remain largely inaccessible to the description by Quantum Chromodynamics (QCD) in terms of quark and gluon interactions. In many cases, perturbative QCD calculations are not applicable because the typical scales involved are too low. Instead, other models have to be employed, such as Regge theory [1], in which interactions are described in terms of the coherent exchange of reggeons and the pomeron.

Fig. 1

Diffractive vector meson electroproduction

Exclusive vector meson (VM) electroproduction $e+p \rightarrow e + {\text {VM}} + Y$ is particularly suited to study diffractive phenomena. This process is illustrated in Fig. 1. In leading order QED, the interaction of the electron with the proton is the exchange of a virtual photon which couples to the proton in a diffractive manner to produce a VM (${{\rho ^0}}$, $\omega$, $\phi$, $J/\psi , \ldots )$ in the final state. The proton is scattered into a system Y, which can be a proton (elastic scattering) or a diffractively excited system (diffractive proton dissociation). Scales for the process are provided by the vector meson mass squared $m^2_{{\text {VM}}}$, the photon virtuality $Q^2 = -q^2$, and the squared 4-momentum transfer at the proton vertex t, the dependence on each of which can be studied independently.

In this paper, elastic and proton-dissociative photoproduction ($Q^2=0$) of ${{\rho ^0}}$ mesons is studied using electroproduction data at small $Q^2 < 2.5~{{\text {GeV}^2}}$. Electroproduction of ${\rho ^0}$ mesons has been studied previously at HERA in both the photoproduction regime and for large $Q^2\gg \Lambda _\mathrm {QCD}^2$ (the perturbative cut-off in QCD), as well as for elastic and proton-dissociative scattering [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Measurements at lower photon–proton centre-of-mass energy ${W_{\gamma p}}$ have been published in fixed-target interactions [20,21,22,23,24,25]. Most recently, a measurement of exclusive ${\rho ^0}$ photoproduction has been performed at the CERN LHC in ultra-peripheral lead-proton collisions [26].

The present measurement is based on a data set collected during the 2006/2007 HERA running period by the H1 experiment. Since ${\rho ^0}$ mesons decay almost exclusively into a pair of charged pions, the analysis is based on a sample of ${\pi ^+\pi ^-}$ photoproduction events. Compared with previous HERA results, the size of the sample makes possible a much more precise measurement with a statistical precision at the percent level. It is then possible to extract up to three-dimensional kinematic distributions as a function of the invariant mass of the ${\pi ^+\pi ^-}$ system ${{m_{\pi \pi }}}$, of ${{W_{\gamma p}}}$, and of t. However, the size of the dataset is such that the systematic uncertainties of the modelling of the H1 experiment are important.

The structure of the paper is as follows: Theoretical details of ${\rho ^0}$ meson photoproduction are discussed in Sect. 2 with a focus on the description of ${\pi ^+\pi ^-}$ photoproduction in terms of Regge theory (Sect. 2.1), cross section definitions (Sect. 2.2), and Monte Carlo modelling of relevant processes (Sect. 2.3). In Sect. 3, the experimental method is detailed, including a description of the H1 detector (Sect. 3.1), the dataset underlying the analysis (Sect. 3.2), the unfolding procedure applied to correct detector level distributions (Sect. 3.3), and systematic uncertainties of the measurement (Sect. 3.4). Results are presented in Sect. 4. They encompass a measurement of the integrated ${\pi ^+\pi ^-}$ production cross section in the fiducial phase space (Sect. 4.1), a study of the invariant ${m_{\pi \pi }}$ distributions (Sect. 4.2), measurements of the scattering energy (Sect. 4.3) and t dependencies of the ${\rho ^0}$ meson production cross sections (Sect. 4.4), as well as the extraction of the leading Regge trajectory from the two-dimensional t and ${W_{\gamma p}}$ dependencies (Sect. 4.5).

2 Theory

2.1 ${\pi ^+\pi ^-}$ and ${\rho ^0}$ meson photoproduction

In electron¹–proton collisions, ${\pi ^+\pi ^-}$ and ${\rho ^0}$ meson photoproduction is studied in the scattering process

$$\begin{aligned} e(e) + p(p) \rightarrow e(e^\prime ) + \pi ^+(k_1) + \pi ^-(k_2) + Y(p^\prime )\, , \end{aligned}$$

(1)

where the 4-momenta of the participating particles are given in parentheses. The relevant kinematic variables are the electron–proton centre-of-mass energy squared

$$\begin{aligned} s = (e+p)^2 , \end{aligned}$$

(2)

the photon virtuality, i.e., the negative squared 4-momentum transfer at the electron vertex

$$\begin{aligned} Q^2 = -q^2 = (e-e^\prime )^2 , \end{aligned}$$

(3)

the inelasticity

$$\begin{aligned} y= (q \cdot p)/(e\cdot p) \,\mathrm , \end{aligned}$$

(4)

the $\gamma p$ centre-of-mass energy squared

$$\begin{aligned} W_{\gamma p}^2 = (q+p)^2 , \end{aligned}$$

(5)

the invariant mass of the ${\pi ^+\pi ^-}$ system squared

$$\begin{aligned} {{m_{\pi \pi }^2}} = (k_1+k_2)^2\mathrm , \end{aligned}$$

(6)

the squared 4-momentum transfer at the proton vertex

$$\begin{aligned} t = (p-p^\prime )^2\mathrm , \end{aligned}$$

(7)

and the invariant mass squared of the (possibly dissociated) final state proton system

$$\begin{aligned} {{m_Y^2}} = (p^\prime )^2. \end{aligned}$$

(8)

In general, diffractive photoproduction of (light) vector mesons shares the characteristics of soft hadron–hadron scattering: In the high energy limit, the total and elastic cross sections are observed to rise slowly with increasing centre-of-mass energy. Differential cross sections ${\text {d}}\sigma /{\text {d}}t$ are peripheral, favouring low |t|, forward scattering. With increasing scattering energy, the typical |t| of elastic cross sections becomes smaller, i.e. forward peaks appear to shrink.

In vector dominance models (VDM) [27,28,29,30,31], the photon is modelled as a superposition of (light) vector mesons which can interact strongly with the proton to subsequently form a bound VM state. Like hadron–hadron interactions in general, VM production is dominated by colour singlet exchange in the t-channel. The lack of a sufficiently hard scale makes these exchanges inaccessible to perturbative QCD in a large portion of the phase space. Empirical and phenomenological models are used instead to describe the data. At low $|t| \ll 1~{{\text {GeV}^2}}$, differential cross sections are observed to follow exponential dependencies ${\text {d}}\sigma / {\text {d}}t \propto \exp (bt)$. In the optical interpretation, the exponential slope b is related to the transverse size of the scattered objects. Towards larger |t|, cross section dependencies change into a less steep power-law dependence ${\text {d}}\sigma / {\text {d}}t \propto |t|^a$. In Regge theory [1], the dependence of hadronic cross sections on the scattering energy ${{W_{\gamma p}}}$ and the shrinkage of the forward peak are characterised by Regge trajectories $\alpha (t)$. The contribution of a single Regge pole to the differential elastic cross section is ${\text {d}}\sigma _{{\text {el}}} / {\text {d}}t({{W_{\gamma p}}}) \propto W_{\gamma p}^{4 (\alpha (t)-1)}$ [1]. At low energies ${{W_{\gamma p}}} \lesssim 10~{{\text {GeV}}}$, reggeon trajectories $\alpha _{{I\!\!R}}(t)$ dominate which are characterised by intercepts $\alpha _{{I\!\!R}}(0) < 1$, i.e., they result in cross sections that fall off with increasing energy [32]. In the high energy limit, only the contribution of what is known as the pomeron Regge pole remains because its trajectory $\alpha _{{I\!\!P}}(t)$ has a large enough intercept $\alpha _{{I\!\!P}}(0) \gtrsim 1$ for it not to have decreased to a negligible level. The shrinkage of the elastic forward peak with increasing energy is the result of a positive slope $\alpha _{{I\!\!P}}^\prime > 0$ of the trajectory $\alpha (t)$ at $t=0$.

Fig. 2

Diagram of ${\rho ^0}$ meson production and decay in elastic (left) and proton-dissociative (right) ep scattering in the VDM and Regge picture, where the interaction is governed by soft pomeron exchange in the high energy limit

Feynman-like diagrams which illustrate the interpretation of ${\rho ^0}$ meson photoproduction in the VDM/Regge picture are given in Fig. 2. In the diagrams, the ${\rho ^0}$ meson is shown to decay into a pair of charged pions. This is the dominant decay channel with a branching ratio ${{{\mathcal {BR}}}} ({{\rho ^0}} \rightarrow {{\pi ^+\pi ^-}}) \simeq 99\%$ [33]. The decay structure of the ${\rho ^0}$ meson into ${\pi ^+\pi ^-}$ is described by two decay angles [34]. These also give insight into the production mechanism of the ${\rho ^0}$ meson. Contributions with s-channel helicity conservation are expected to dominate, such that the ${\rho ^0}$ meson retains the helicity of the photon, i.e., in photoproduction the ${\rho ^0}$ meson is transversely polarised [15].

While vector mesons dominate photon–proton interactions, the VDM approach does not provide a complete picture. This is particularly evident for ${\rho ^0}$ meson production where in the region of the ${\rho ^0}$ meson resonance peak also non-resonant ${\pi ^+\pi ^-}$ production plays an important role. The non-resonant ${\pi ^+\pi ^-}$ amplitude interferes with the resonant ${\rho ^0}$ meson production amplitude to produce a skewing of the Breit–Wigner resonance profile in the ${\pi ^+\pi ^-}$ mass spectrum [35]. Newer models thus aim to take a more general approach, e.g., a recently developed model for ${\pi ^+\pi ^-}$ photoproduction based on tensor pomeron exchange [36]. That model seems to be in fair agreement with H1 data when certain model parameters are adjusted [37]. A more detailed investigation is beyond the scope of this paper.

2.2 Cross section definition

2.2.1 Photon flux normalisation

In this paper, photoproduction cross sections $\sigma _{{{\gamma p}}}$ are derived from the measured electron–proton cross sections $\sigma _{ep}$. At low $Q^2$, these can be expressed as a product of a flux of virtual photons $f^{T/L}_{\gamma /e}$ and a virtual photon–proton cross section $\sigma ^{T/L}_{\gamma ^* p}$:

$$\begin{aligned}&\dfrac{{\text {d}}^2 \sigma _{ep}}{{\text {d}}y {\text {d}}Q^2} =f^T_{\gamma /e}(y, Q^2) \, \sigma ^T_{\gamma ^* p}({{W_{\gamma p}}} (y,Q^2), Q^2) \nonumber \\&\quad + f^L_{\gamma /e}(y, Q^2) \, \sigma ^L_{\gamma ^* p}({{W_{\gamma p}}} (y,Q^2), Q^2). \end{aligned}$$

(9)

A distinction is made between transversely and longitudinally polarised photons, as indicated by the superscripts T and L, respectively. In the low $Q^2$ regime studied here, the transverse component is dominant. The transverse and longitudinal photon fluxes are given in the Weizsäcker–Williams approximation [38,39,40] by

$$\begin{aligned} f^T_{\gamma /e}(y,Q^2)&= \dfrac{\alpha _\mathrm {em}}{2\pi } \dfrac{1}{yQ^2}\left( 1 + (1-y)^2 - 2(1-y) \dfrac{Q^2_\mathrm {min}}{Q^2} \right) \end{aligned}$$

(10)

and

$$\begin{aligned} f^L_{\gamma /e}(y,Q^2)&= \dfrac{\alpha _\mathrm {em}}{\pi } \dfrac{1}{yQ^2}\left( 1-y\right) , \end{aligned}$$

(11)

respectively, where $\alpha _\mathrm {em}$ is the fine structure constant, $m_e$ the mass of the electron, and $Q^2_\mathrm {min} = m_e^2 y^2/(1-y)$ is the smallest kinematically accessible $Q^2$ value.

In vector meson production in the VDM approach, the cross section for virtual photon interactions ($Q^2>0$) can be related to the corresponding photoproduction cross section $\sigma _{\gamma p}$ at $Q^2=0$:

$$\begin{aligned} \sigma ^T_{\gamma ^* p}({{W_{\gamma p}}}, Q^2)&= \sigma _{\gamma p}({{W_{\gamma p}}}) \, \left( 1 + \frac{Q^2}{m^2_{{\text {VM}}}} \right) ^{-2}, \end{aligned}$$

(12)

$$\begin{aligned} \sigma ^L_{\gamma ^* p}({{W_{\gamma p}}}, Q^2)&= \sigma ^T_{\gamma ^* p}({{W_{\gamma p}}}, Q^2) \, \dfrac{Q^2}{m^2_{{\text {VM}}}} \xi ^2. \end{aligned}$$

(13)

In the equations, $m_{{\text {VM}}}$ denotes the mass of the considered vector meson and $\xi ^2$ is a proportionality constant, that in the following is set to unity. The real photoproduction cross section can then be factored out of Eq. (9) according to

$$\begin{aligned} \dfrac{{\text {d}}^2 \sigma _{ep}}{{\text {d}}y {\text {d}}Q^2} = \sigma _{\gamma p}( {{W_{\gamma p}}} (y) )\, \varphi _{\mathrm {eff}}(y, Q^2), \end{aligned}$$

(14)

were the so-called effective photon flux is given by

$$\begin{aligned}&\varphi _{\mathrm {eff}}(y, Q^2) = \dfrac{\alpha _\mathrm {em}}{2\pi } \dfrac{1}{yQ^2}\nonumber \\&\quad \times \left[ 1 + (1-y)^2 - 2(1-y) \left( \dfrac{Q^2_\mathrm {min}}{Q^2}-\dfrac{Q^2}{m^2_{{\text {VM}}}} \right) \right] \nonumber \\&\quad \times \left( 1 + \frac{Q^2}{m^2_{{\text {VM}}}} \right) ^{-2}. \end{aligned}$$

(15)

In practice, measurements of $\sigma _{ep}$ are evaluated as integrals over finite regions in $Q^2$ and ${{W_{\gamma p}}}$. In order to extract corresponding photoproduction cross sections at $Q^2=0$ and for an appropriately chosen average energy $\langle {{W_{\gamma p}}} \rangle$, the measured values are normalised by the effective photon flux integrated over the corresponding $Q^2$ and ${{W_{\gamma p}}}$ ranges:

$$\begin{aligned} \sigma _{\gamma p}\left( \langle {{W_{\gamma p}}} \rangle \right) = \dfrac{ \sigma _{ep} }{{\Phi _{\gamma /e}}} , \end{aligned}$$

(16)

with

$$\begin{aligned} {\Phi _{\gamma /e}} = \int _{\begin{array}{c}Q^2_{\min }<Q^2<Q^2_{\max } \\ W_{\min }<{{W_{\gamma p}}} <W_{\max }\end{array}} \varphi _{\mathrm {eff}}(y, Q^2) \, {\text {d}}y{\text {d}}Q^2. \end{aligned}$$

(17)

2.2.2 ${\rho ^0}$ meson photoproduction cross section

With the H1 detector, ${\pi ^+\pi ^-}$ photoproduction is measured. In the kinematic region studied, there are significant contributions from the ${\rho ^0}$ meson resonance, non-resonant ${\pi ^+\pi ^-}$ production, the $\omega$ meson resonance and excited $\rho$ meson states [33, 36]. Photoproduction of ${\rho ^0}$ mesons has to be disentangled from these processes by analysis of the ${\pi ^+\pi ^-}$ mass spectrum. Here, a model is used which parametrises the spectrum in terms of ${\rho ^0}$ and $\omega$ meson, as well as non-resonant amplitudes [37], similar to the original proposal made by Söding [35].

The contributions are added at the amplitude level, and interference effects are taken into account. The model is defined as

$$\begin{aligned} \dfrac{{\text {d}}\sigma _{\pi \pi }}{{\text {d}}{{m_{\pi \pi }}}}({{m_{\pi \pi }}}) = A\ \dfrac{q^3({{m_{\pi \pi }}})}{q^3(m_\rho )} \ \bigg \vert A_{\rho ,\omega }({{m_{\pi \pi }}}) + A_{{\text {nr}}}({{m_{\pi \pi }}}) \bigg \vert ^2,\nonumber \\ \end{aligned}$$

(18)

where A is a global normalisation factor and $q^3({{m_{\pi \pi }}})$ describes the phase space, with $q({{m_{\pi \pi }}}) = \frac{1}{2} \sqrt{{{m_{\pi \pi }^2}}- 4m_\pi ^2}$ being the momentum of one of the pions in the ${\pi ^+\pi ^-}$ centre-of-mass frame [41]. It is normalised to the value $q^3(m_\rho )$ at the ${\rho ^0}$ mass. The amplitude $A_{\rho ,\omega }$ takes into account the ${{\rho ^0}}$ and $\omega$ meson resonance contributions, whereas the non-resonant component is modelled by $A_{{\text {nr}}}({{m_{\pi \pi }}})$. The components are considered to be fully coherent. Since additional resonances with masses above 1 ${\text {GeV}}$ are neglected, the model can only be applied to the region near the ${\rho ^0}$ meson mass peak. Models of this form have been widely used in similar past analyses because they preserve the physical amplitude structure while being parametric and thus easily applicable. More sophisticated models are designed to preserve unitarity [42] or are regularised by barrier factors at higher masses [43].

The combined ${{\rho ^0\text {-}\omega }}$ amplitude is modelled following a parametrisation given by [44]

$$\begin{aligned} A_{\rho ,\omega }({{m_{\pi \pi }}}) = {\mathcal {BW}}_{\rho }({{m_{\pi \pi }}}) \ \left( 1 + f_\omega {\text {e}}^{{\text {i}}\phi _{\omega } } \dfrac{ {{m_{\pi \pi }^2}}}{ m_\omega ^2 } {\mathcal {BW}}_{\omega }({{m_{\pi \pi }}}) \right) ,\nonumber \\ \end{aligned}$$

(19)

where $f_\omega$ and $\phi _\omega$ are a normalisation factor and a mixing phase for the $\omega$ contribution, respectively. The $\omega$ meson is not expected to decay into a pair of charged pions directly because of the conservation of G-parity by the strong interaction. However, electromagnetic $\omega \rightarrow {{\rho ^0}}$-mixing with a subsequent ${{\rho ^0}} \rightarrow {{\pi ^+\pi ^-}}$ decay is possible [45]. Both resonances are modelled by a relativistic Breit–Wigner function [46]:

$$\begin{aligned} {\mathcal {BW}}_{{\text {VM}}}({{m_{\pi \pi }}}) = \dfrac{ m_{{\text {VM}}} \Gamma _{{{\text {VM}}}} }{ m^2_{\pi \pi } - m_{{\text {VM}}}^2 + {\text {i}}\, m_{{\text {VM}}} \Gamma ({{m_{\pi \pi }}}) }. \end{aligned}$$

(20)

The parameters $m_{{\text {VM}}}$ and $\Gamma _{{{\text {VM}}}}$ are the respective vector meson’s Breit–Wigner mass and width. The Breit–Wigner function is normalised to $|{\mathcal {BW}}_{{\text {VM}}}(m_{{\text {VM}}})|=1$. For the ${\rho ^0}$ resonance a p-wave mass-dependent width [41] is used:

$$\begin{aligned} \Gamma ({{m_{\pi \pi }}}) = \Gamma _{{{\text {VM}}}} \dfrac{q^3({{m_{\pi \pi }}})}{q^3(m_{{\text {VM}}})} \dfrac{m_{{\text {VM}}}}{{{m_{\pi \pi }}}}\mathrm {,} \end{aligned}$$

(21)

whereas a constant width is assumed for the very narrow $\omega$ resonance.

The unknown non-resonant amplitude is parametrised by the function

$$\begin{aligned} A_{{\text {nr}}}({{m_{\pi \pi }}}) = \dfrac{f_{{\text {nr}}}}{ \left( {{m_{\pi \pi }^2}}- 4m_\pi ^2 + \Lambda ^2_{{\text {nr}}} \right) ^{\delta _{{\text {nr}}}}} \mathrm {,} \end{aligned}$$

(22)

where the relative normalisation is given by $f_{{\text {nr}}}$, while $\Lambda _{{\text {nr}}}$ and $\delta _{{\text {nr}}}$ are free model parameters. They can shape the amplitude for the modelling of a possible internal structure of the non-resonant $\gamma \pi \pi$-coupling. In similar past analyses, typically a purely real non-resonant amplitude has been assumed. Following that assumption, $f_{{\text {nr}}}$ is set to be real. For $\delta _{{\text {nr}}} > \frac{3}{4}$, the non-resonant contribution to the cross section (cf. Eq. (18)) has a local maximum at

$$\begin{aligned} m_{{\text {nr}}}^{\text {max}} = \dfrac{ \sqrt{\Lambda ^2_{{\text {nr}}} + (\frac{4}{3}\delta _{{\text {nr}}}-1)\, 4m_\pi ^2} }{\sqrt{\frac{4}{3}\delta _{{\text {nr}}}-1}}\mathrm , \end{aligned}$$

(23)

and falls proportionally to $\left( 1/{{m_{\pi \pi }^2}} \right) ^{2\delta _{{\text {nr}}}-3}$ in the high mass region.

In order to extract the ${\rho ^0}$ meson contribution to the ${\pi ^+\pi ^-}$ photoproduction cross section, the measured ${\pi ^+\pi ^-}$ mass distributions are fitted using Eq. (18). The ${\rho ^0}$ meson Breit–Wigner contribution is then conventionally defined by the integral

$$\begin{aligned} \sigma (\gamma p \rightarrow {{\rho ^0}} Y) = \dfrac{A}{q^3(m_\rho )} \int _{2m_\pi }^{m_\rho + 5 \Gamma _{\rho } } \big \vert {\mathcal {BW}}_{\rho }(m) \big \vert ^2 q^3(m) {\text {d}}m.\nonumber \\ \end{aligned}$$

(24)

As the ${\rho ^0}$ meson resonance decays almost exclusively into two charged pions, this is taken to be equal to the total ${\rho ^0}$ meson photoproduction cross section without correcting for the ${{\rho ^0}} \rightarrow {{\pi ^+\pi ^-}}$ branching fraction.

Kinematic dependencies of the ${\rho ^0}$ meson production cross section on the variables ${W_{\gamma p}}$, t, and ${m_Y}$ are measured by fitting the mass distributions in bins of the respective variables, such that all model parameters may have kinematic dependencies. Physical considerations and statistical and technical limitations affect the assumed dependencies. Physical parameters, i.e., $m_{{\text {VM}}}$, $\Gamma _{{{\text {VM}}}}$, and $\delta _{{\text {nr}}}$ are assumed to be constants. The small width of the $\omega$ meson cannot be constrained by the present data and the PDG value $\Gamma _{\omega }=8.5~{{\text {MeV}}}$ [33] is assumed and kept fixed in all fits. Dependencies of $f_\omega$, $\phi _\omega$, and $f_{{\text {nr}}}$ on t or ${W_{\gamma p}}$ cannot be constrained with the present data. However, these parameters are allowed to depend on ${m_Y}$, i.e., to be different for elastic and proton-dissociative distributions. The non-resonant background is observed to change with t. This is modelled by a t dependence of the parameter $\Lambda _{{\text {nr}}}$, which also can be different for elastic and proton-dissociative distributions. The normalisation A is a free parameter in each kinematic bin. All fit set-ups with the corresponding parameter assumptions are summarised in Table 1.

Table 1 Parameter assumptions and resulting number of parameters used to fit Eq. (18) to the invariant ${\pi ^+\pi ^-}$ mass distributions. The number of parameters depends on the number of bins in the extracted cross sections. The number of bins in which a parameter is fitted freely is given and the corresponding distribution indicated by sub- and superscripts. For the fits of the ${m_{\pi \pi }}$ distributions in multiple ${W_{\gamma p}}$ or t bins, the $\omega$ meson model parameters are fixed to the values obtained from the fit to the one-dimensional distributions. The $\omega$ meson width is always fixed to the PDG value

2.3 Monte Carlo modelling

For the purpose of quantifying detector effects, the data are modelled using Monte Carlo (MC) simulations of elastic and proton-dissociative electroproduction of ${{\rho ^0}}$, $\omega (782)$, $\phi (1020)$, $\rho (1450)$, and $\rho (1700)$ vector mesons, as well as for non-resonant diffractive photon dissociation. The samples are all generated using the DIFFVM event generator [47] that models VM production on the principles of equivalent photon approximation [38,39,40], VDM [27,28,29,30,31], and pomeron exchange [48,49,50,51]. Proton dissociation is modelled by DIFFVM assuming the following dependence of the cross section on the mass of the dissociated system:

$$\begin{aligned} \dfrac{{\text {d}}\sigma _{{\gamma p}}}{{\text {d}}{{m_Y^2}}} = \dfrac{f({{m_Y}})}{ ({{m_Y^2}})^{1+\epsilon _Y} }\mathrm {.} \end{aligned}$$

(25)

Here, $\epsilon _Y = 0.0808$ and $f({{m_Y}})$ is a phenomenological function that is fitted to the experimental data [52, 53] to parametrise the low-mass resonance structure in the region $m_p< {{m_Y}} < 1.9~{{\text {GeV}}}$. For ${{m_Y}} >1.9~{{\text {GeV}}}$, the function $f({{m_Y}})=1$ becomes constant. In the low mass region the dissociative system is treated as an $N^*$ resonance and decays are modelled according to measured branching fractions [33]. For higher masses the decay is simulated using the Lund fragmentation model as implemented in JETSET [54]. Non-resonant photon dissociation is modelled analogously by assuming a dissociative mass $m_X$ spectrum ${\text {d}}\sigma _{{{\gamma p}}}/{\text {d}}m_X^2 = 1/(m_X^2)^{1+\epsilon _X}$ with $\epsilon _X = \epsilon _Y$, and simulating the decay using the Lund model.

Table 2 DIFFVM MC samples used to model the ${\pi ^+\pi ^-}$ photoproduction dataset. All decay modes with a branching fraction $\gtrsim 1\%$ are simulated [47]. For the $\rho (1450)$ and $\rho (1700)$ samples a ratio of 1:1 is assumed. The ${\pi ^+\pi ^-}$ final states are removed from background samples and included in the signal definition

In Table 2, details on the samples and in particular on the simulated decay modes are listed.² Several of the considered processes result in an exclusive ${\pi ^+\pi ^-}$ final state. They are simulated by DIFFVM independently, so that interference effects are not considered. However, these can be significant. For example, the interference between the ${\rho ^0}$ meson resonance and non-resonant ${\pi ^+\pi ^-}$ production causes a strong skewing of the resonance lineshape. To consider these interference effects, the ${{\rho ^0}}$ meson samples are reweighted to describe exclusive ${\pi ^+\pi ^-}$ production including contributions from ${\rho ^0}$, $\omega$, and a single ${\rho ^\prime }$ meson resonance and non-resonant production, that are all added at the amplitude level. For the reweighting, a t and ${m_{\pi \pi }}$ dependent lineshape is used, which is similar to the model introduced in Sect. 2.2.2 but is extended by an additional ${\rho ^\prime }$ Breit–Wigner amplitude [37].

All generated events are passed through the full GEANT-3 [55] based simulation of the H1 apparatus and are reconstructed using the same program chain as used for the data. Trigger scaling factors are applied to correct differences in the trigger performance between data and simulation. They are obtained from a ${\pi ^+\pi ^-}$ electroproduction sample, that is triggered independently of the tracking devices [37].

A template is constructed from all MC samples to describe the data. For a better description of the ${W_{\gamma p}}$ and t distributions, all samples are tuned to data [37]. An additional background contribution from beam-gas events is estimated in a data driven method. The MC normalisations are obtained from data control regions that are enriched with events from a given process through modified event selection requirements as described below. The $\rho (1450)$ and $\rho (1700)$ samples cannot be well distinguished experimentally in this analysis. They are thus combined at a 1 : 1 ratio and treated as a single MC sample. In order to obtain normalisations for the elastic and proton-dissociative samples independently, information from the forward detector components is used as described below.

Neither initial and final state radiation of real photons from the electron, nor vacuum polarisation effects are simulated. Consequently, these effects are not corrected for in the present measurement. In a comparable phase space, their effect on the overall cross section has been estimated to be smaller than 2% [56].

3 Experimental method and data analysis

3.1 H1 detector

A detailed description of the H1 detector is given elsewhere [57, 58]. The components that are relevant for the present analysis are briefly described in the following. A right-handed Cartesian coordinate system is used with the origin at the nominal ep interaction point. The proton beam direction defines the positive z-axis (forward direction). Transverse momenta are measured in the x–y plane. Polar ($\theta$) and azimuthal ($\phi$) angles are measured with respect to this frame of reference.

The interaction point is surrounded in the central region ($15^\circ< \theta < 165^\circ$) by the central tracking detector. Two large coaxial cylindrical jet chambers (CJC1 and CJC2) for precise track reconstruction form its core. They are supported by the central inner proportional chamber (CIP) used for the reconstruction of the primary vertex position on the trigger level, a z-drift chamber for an improved reconstruction of z coordinates, and a silicon vertex detector for the reconstruction of secondary decay vertices [59]. In the forward direction (${7^\circ< \theta < 30^\circ }$), additional coverage is provided by the forward tracking detector, a set of planar drift chambers. The tracking detectors are operated in a solenoidal magnetic field of 1.16 T. For offline track reconstruction, track helix parameters are fitted to the inner detector hits in a general broken lines fit [60]. The procedure considers multiple scattering and corrects for energy loss by ionisation in the detector material. The primary vertex position is calculated from all tracks and optimised as part of the fitting procedure. Transverse track momenta are measured with a resolution of ${\sigma (p_T)/p_T \simeq 0.002~p_T/{{\text {GeV}}} \oplus 0.015}$. The CJCs also provide a measurement of the specific energy loss of charged particles by ionisation ${{{\text {d}}E/{\text {d}}x}}$ with a relative resolution of 6.5% for long tracks.

The tracking detectors are surrounded by the liquid argon (LAr) sampling calorimeter [61]. It provides coverage in the region ${4^\circ< \theta < 154^\circ }$ and over the full azimuthal angle. The inner electromagnetic section of the LAr is interlaced with lead, the outer hadronic section with steel absorbers. With the LAr, the energies of electromagnetic and hadronic showers are measured with a precision of ${\sigma (E)/E \simeq 12\%/\sqrt{E/{{\text {GeV}}}} \oplus 1\%}$ and $\sigma (E)/E \simeq 50\%/\sqrt{E/{{\text {GeV}}}}\oplus 2\%$, respectively [62, 63]. In the backward region (${153^\circ< \theta < 178^\circ }$), energies are measured with a spaghetti calorimeter (SpaCal) of lead absorbers interlaced with scintillating fibres [58].

Detector components positioned in the very forward direction are used in this analysis to identify proton dissociation events. These are the forward muon detectors (FMD), the PLUG calorimeter and the forward tagging system (FTS). The lead-scintillator plug calorimeter is positioned around the beampipe at $z=4.9~{{\text {m}}}$ to measure the energies of particles in the pseudorapidity region $3.5< \eta < 5.5$. The FMD is a system of six drift chambers positioned outside of the LAr and covering the range $1.9< \eta < 3.7$. Particles at larger pseudorapidity up to $\eta \lesssim 6.5$ can still induce spurious signals via secondary particles produced in interactions with the beam transport system and detector support structures [64]. The very forward region, $6.0< \eta < 7.5$, is covered by an FTS station of scintillation detectors positioned around the beampipe at $z=28~{{\text {m}}}$.

The H1 trigger is operated in four stages. The first trigger level (L1) is implemented in dedicated hardware reading out fast signals of selected sub-detector components. Those signals are combined and refined at the second level (L2). A third, software-based level (L3) combines L1 and L2 information for partial event reconstruction. After full detector read-out and full event reconstruction, events are subject to a final software-based filtering (L4). The data used for the present analysis are recorded using mainly information from the fast track trigger (FTT) [65,66,67]. The FTT makes it possible to measure transverse track parameters at the first trigger level and complete three-dimensional tracks at L2. This is achieved through applying pattern recognition and associative memory technology to identify predefined tracks in the hit-patterns produced by charged particles in a subset of the CJC signal wires.

The instantaneous luminosity is measured by H1 with a dedicated photon detector located close to the beampipe at $z=-103~{{\text {m}}}$. With it, the rate of the Bethe–Heitler process $ep \rightarrow ep\gamma$ is monitored. The integrated luminosity is measured more precisely with the main H1 detector using the elastic QED Compton process. In this process, the electron and photon in the $ep\gamma$ final state have large transverse momenta and can be reconstructed in a back-to-back topology in the SpaCal. The integrated luminosity has been measured with a total uncertainty of $2.7\%$ [68] that is dominated by systematic effects.

3.2 Data sample

The present analysis is based on data collected by the H1 experiment during the 2006/2007 HERA running period. In that period, the accelerator was operated with positrons having an energy of $E_e = 27.6~{{\text {GeV}}}$ and protons with an energy of $E_p = 920~{{\text {GeV}}}$. Due to bandwidth limitations, only a subset of the H1 dataset is available for the trigger conditions relevant for this analysis, corresponding to an effective integrated luminosity of ${\mathcal {L}}_\mathrm {int} = 1.3~{{\text {pb}^{-1}}}$. In the kinematic range considered in this analysis, the pions from ${{\rho ^0}} \rightarrow {{\pi ^+\pi ^-}}$ photoproduction are produced within the acceptance of the CJC and with low transverse momenta $p_T \lesssim 0.5~{{\text {GeV}}}$. In the diffractive photoproduction regime, both the outgoing proton and electron avoid detection by escaping through the beampipe.³

3.2.1 Trigger

A dedicated, track-based ${\pi ^+\pi ^-}$ photoproduction trigger condition was used for online event selection. Track information within the 2.3 $\upmu$s decision time of the L1 trigger was available through the FTT. For a positive trigger decision, at least two FTT tracks above a transverse momentum threshold of 160 ${\text {MeV}}$ and at most three tracks above a threshold of 100 ${\text {MeV}}$ were required. The sum of the charges of these tracks was restricted to $\pm 1$ elementary electric charge. In addition, trigger information from the CIP was used to ensure a low multiplicity interaction within the nominal interaction region along the z-axis. Vetoes on the inner forward part of the LAr calorimeter and on a scintillator wall in the forward direction were applied to suppress non-diffractive inelastic interactions. Further SpaCal and timing vetoes rejected events from beam-gas and beam-machine interactions. To keep under control the expected rate from the large ${\rho ^0}$ meson production cross section, the trigger was scaled down by an average factor of $\sim 100$.

3.2.2 Event reconstruction and selection

In order to select a sample of ${\pi ^+\pi ^-}$ photoproduction events, a set of offline selection cuts is applied on top of the trigger requirements:

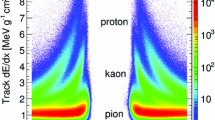
• The ${\pi ^+\pi ^-}$ topology is ensured by requiring exactly two primary-vertex fitted, central tracks to be reconstructed. They need to satisfy some additional quality requirements, have opposite charge, and be within the acceptance region⁴ defined as $25^\circ< \theta < 155^\circ$ and $p_T>0.16~{{\text {GeV}}}$. Low-momentum kaons, protons, and deuterons are suppressed using the difference between the measured energy loss ${{{\text {d}}E/{\text {d}}x}}$ of the tracks in the CJC and the expected loss for the respective particle hypothesis in a likelihood-based approach. The two tracks are then taken to be the pion candidates, and their 4-momentum vectors are calculated with the corresponding mass hypothesis.

• The photoproduction kinematic regime is ensured by vetoing events with a scattered electron candidate in the SpaCal or LAr. The SpaCal acceptance then limits the photon virtuality to $Q^2\lesssim 2.5~{{\text {GeV}^2}}$.

• The diffractive topology is ensured by requiring a large rapidity gap between the central tracks and any forward detector activity. Events with LAr clusters above a noise level of 0.6 ${\text {GeV}}$ in the forward region $\theta < 20^\circ$ are rejected. Information from the FTD is used to reconstruct forward tracks, and events with more than one forward track that cannot be matched to one of the central tracks are also rejected. The presence of a single unmatched track is permitted to reduce the sensitivity on the modelling of the forward energy flow in the forward detectors. This rapidity gap selection in particular also limits the mass of the proton-dissociative system to approximately ${{m_Y}} \lesssim 10~{{\text {GeV}}}$.

• Background processes with additional neutral particles or charged particles outside of the central tracker acceptance are suppressed by cuts on the LAr and SpaCal energy. LAr and SpaCal clusters above respective noise levels of 0.6 and 0.3 ${\text {GeV}}$ are geometrically matched to the two central tracks: A cluster is associated to a track if it is within a cylinder of a 60 ${\text {cm}}$ radius in the direction of the track upon calorimeter entry. The energies from clusters not associated to either track are summed up. Events are rejected if the total unassociated LAr or SpaCal energies exceed thresholds of 0.8 ${\text {GeV}}$ or 0.4 ${\text {GeV}}$, respectively. This allows for a small amount of unassociated energy to account for residual noise or secondary particles produced in interactions of the pion candidates with the detector material. A further suppression of background events with additional final state particles is achieved by requiring a transverse opening angle between the two pion tracks $\Delta \phi > 50^\circ$.

• For a reliable trigger performance and MC modelling thereof, the difference in the FTT track angles⁵ must exceed $\Delta \phi _\mathrm {FTT} > 20^\circ$.

• The background is further reduced by rejecting out-of-time events via cuts on the LAr and CJC event timing information. Background events from beam-gas and beam-wall interactions are suppressed by restricting the z coordinate of the primary vertex to be within 25 ${\text {cm}}$ of the nominal interaction point.

Fig. 3

Control distributions of the reconstructed ${m_{\pi \pi }^\text {rec}}$ on a linear (a) and logarithmic y-scale (b), of ${W_{\gamma p}^{\text {rec}}}$ (c), and of ${t^\text {rec}}$ (d). The black data points are compared to the MC simulation including various signal and background components as given in the legends. The dotted red bands denote the total uncertainty of the simulation including normalisation uncertainties

Fig. 4

Zero- (a), single- (b), and multi-tag fraction (c) using tagging information from the FMD, the FTS, and the PLUG as a function of $|{t^\text {rec}} |$. The fraction measured in data is given by the black points. The orange bands show the corresponding fraction predicted by the MC simulation. The tagging fractions of the simulated elastic and proton-dissociative exclusive ${\pi ^+\pi ^-}$ signal channels are also shown. The dotted bands denote the total uncertainty of the simulation

The reaction $ep \rightarrow e {{\pi ^+\pi ^-}} Y$ is kinematically underconstrained since only the two pions in the final state are reconstructed. The mass of the ${\pi ^+\pi ^-}$ system ${m_{\pi \pi }^\text {rec}}$ is reconstructed from the 4-momenta of the two tracks under pion hypothesis. The momentum transfer at the proton vertex t and the scattering energy ${{W_{\gamma p}}}$ are reconstructed from the two pion 4-momenta:

$$\begin{aligned} {t^\text {rec}}&= -{{\left( p_{T,\pi \pi }^{\text {rec}}\right) ^2}} \end{aligned}$$

(26)

and

$$\begin{aligned} {{W_{\gamma p}^{\text {rec}}}}&= \sqrt{2E_p \left( {{E_{\pi \pi }^{\text {rec}}}}- {{p_{z,\pi \pi }^{\text {rec}}}} \right) }\,. \end{aligned}$$

(27)

Here, $E_p$ denotes the proton-beam energy and ${{E_{\pi \pi }^{\text {rec}}}}$, ${{p_{T,\pi \pi }^{\text {rec}}}}$, and ${{p_{z,\pi \pi }^{\text {rec}}}}$ are the measured energy, transverse, and longitudinal 4-momentum components of the ${\pi ^+\pi ^-}$ system. These two equations are approximations to Eqs. (5) and (7), respectively. In some regions of the probed phase space, $Q^2$ may be similar in size to t, or ${{m_Y}}$ may be similar in size to ${W_{\gamma p}}$, such that these approximations are poor. Such effects are corrected for in the unfolding procedure discussed later in the text (cf. Sect. 3.3).

The analysis phase space probed by this measurement is explicitly defined by detector-level cuts $15< {{W_{\gamma p}^{\text {rec}}}} <90~{{\text {GeV}}}$, ${t^\text {rec}} < 3~{{\text {GeV}^2}}$, and $0.3<{{m_{\pi \pi }^\text {rec}}} < 2.3~{{\text {GeV}}}$. The exclusivity requirements, which veto events with detector activity not related to the ${\pi ^+\pi ^-}$ pair, further restrict the phase space to $Q^2 \lesssim 2.5~{{\text {GeV}^2}}$ and ${{m_Y}} \lesssim 10~{{\text {GeV}}}$. The mean and median $Q^2$ in that phase space are approximately $0.02~{{\text {GeV}^2}}$ and $8\times 10^{-6}~{{\text {GeV}^2}}$, respectively, as evaluated in the MC simulation.

A total of 943,962 ${\pi ^+\pi ^-}$ photoproduction event candidates pass all selection requirements. In Fig. 3, the selected number of events is shown as a function of ${m_{\pi \pi }^\text {rec}}$, ${W_{\gamma p}^{\text {rec}}}$, and ${t^\text {rec}}$. The distributions are compared to the MC model introduced in Sect. 2.3. The ${\rho ^0}$ meson resonance at a mass of $\sim 770~{{\text {MeV}}}$ clearly dominates the sample. Background contamination amounts to about 11% and is investigated in the next section.

3.2.3 Background processes

The ${\pi ^+\pi ^-}$ photoproduction sample includes various background contributions, even after the full event selection. The dominant background processes are the decays of diffractively produced $\omega \rightarrow {{\pi ^+\pi ^-}} \pi ^0$, $\phi \rightarrow K^+K^-$, or $\rho ^\prime \rightarrow 4\pi$, as well as diffractive photon dissociation. Another source of background originates from interactions of the electron and proton beams with residual gas. Such reducible background events are wrongly selected when charged kaons or protons are misidentified as pions or additional charged or neutral particles escape detection, e.g., by being outside the central tracker acceptance or having energies below the calorimeter noise threshold. In addition to the ${\rho ^0}$ meson, some other vector mesons also decay to an exclusive ${\pi ^+\pi ^-}$ state (cf. Table 2). Rather than being treated as irreducible background, these are included in the signal for the analysis of the ${\pi ^+\pi ^-}$ production cross section.

To study the reducible background contributions in more detail, multiple dedicated control regions are introduced:

• $\omega (782)$ mesons predominantly decay into the ${{\pi ^+\pi ^-}} \pi ^0$ final state. The $\pi ^0$ meson can be identified via energy deposits in the calorimeters that are not associated with either of the two pion tracks. An $\omega$ control region is defined by replacing the empty calorimeter selection by a cut $E_\mathrm {LAr}^\mathrm {!assoc} > 0.8~{{\text {GeV}}}$ on the unassociated energy deposited in the LAr. Events with an $\omega$ meson are distinguished from those with a ${\rho ^\prime }$ meson by cuts on ${{m_{\pi \pi }}} < 0.55~{{\text {GeV}}}$ and on the invariant mass of both tracks (assumed to be pions) and all unassociated clusters $m_\mathrm {evt} < 1.2~{{\text {GeV}}}$. The $\omega$ meson purity achieved in this region is roughly 54%.

• $\phi (1020)$ mesons predominantly decay into pairs of charged kaons. A $\phi$ control region is defined by replacing the ${\text {d}}E/{\text {d}}x$ pion identification selection cuts by a kaon selection and requiring the invariant $K^+K^-$ mass to be within 15 ${\text {MeV}}$ of the $\phi$ meson mass. Also the cut on the opening angle between the two tracks at the vertex is removed. The $\phi$ meson purity achieved in this region is roughly 89%.

• The excited ${{\rho ^\prime }}$ meson dominantly decay into 4 pions in various charge configurations. Due to the track veto in the trigger, additional tracks cannot be used to identify ${{\rho ^\prime }} \rightarrow 4\pi$ events. Instead, unassociated energy deposits in the LAr $E_\mathrm {LAr}^\mathrm {!assoc} > 0.8~{{\text {GeV}}}$ are required in place of the empty LAr signal selection. Events with a ${{\rho ^\prime }}$ meson are distinguished from those with an $\omega$ meson by requiring $m_\mathrm {evt}>1.2~{{\text {GeV}}}$. The ${{\rho ^\prime }}$ meson purity achieved in this region is roughly 48%.

• Particles from photon dissociation emerge primarily in the backwards direction. A photon dissociation control region is thus defined by replacing the empty SpaCal signal requirement by a cut $4< E_\mathrm {SpaCal}^\mathrm {!assoc} < 10~{{\text {GeV}}}$ on the unassociated energy deposit in the SpaCal. The lower cut removes $\omega$ and ${{\rho ^\prime }}$ events, the upper cut is retained as a veto against the scattered electron. The photon dissociation purity achieved in this region is roughly 78%.

For the ${\rho ^0}$ meson photoproduction cross section measurement, reducible background processes are subtracted in the unfolding procedure, where the templates for the respective diffractive background processes are taken from the DIFFVM MC samples, as described in Sect. 2.3. The respective normalisation factors are determined by making use of the control regions in the unfolding process. The residual beam-gas induced background is modelled in a data driven approach, using events from electron and proton pilot bunches. For electron (proton) pilot bunches, there is a corresponding gap in the proton (electron) beam bunch structure, such that only interactions with rest-gas atoms may occur. The beam gas background shape predictions estimated from pilot bunch events are scaled to match the integrated beam current of the colliding bunches. The beam-gas induced background amounts to about 2%.

3.2.4 Proton dissociation tagging

In proton-dissociative events, the proton remnants are produced in the very forward direction where the H1 detector is only sparsely instrumented. Consequently, the remnants cannot be fully reconstructed, and elastic and proton-dissociative scattering cannot be uniquely identified on an event-by-event basis. However, in many cases some of the remnants do induce signals in the forward instruments, either directly or via secondary particles that are produced in interactions with the detector or machine infrastructure. These signals are used to tag proton-dissociative events (tagging fraction). At a much lower level, such signals can also be present in elastic scattering events (mistagging fraction), e.g. in the presence of detector noise or when the elastically scattered proton produces secondaries in interactions with the beam transport system. By simulating the respective tagging and mistagging fractions of proton-dissociative and elastic scattering, the respective proton-dissociative and elastic contributions to the cross section can be determined.

The forward detectors used for tagging in this analysis are the FMD, the PLUG, and the FTS. An event is considered to be tagged by the FMD if there is at least one hit in any of the first three FMD layers, by the PLUG if there is more than one cluster above a noise level of 1.2 ${\text {GeV}}$, or by the FTS if it produces at least one hit. A small contribution to the FTS signal, induced by secondary particles produced by the elastically scattered proton hitting a beam collimator, is discarded by applying acceptance cuts depending on ${t^\text {rec}}$ and the location of hits in the FTS [37].

The tagging information from the three detectors is combined by summing the total number of tags in an event: $0 \le N_\mathrm {tags} \le 3$. In turn, three tagging categories are defined: a zero-tag ($N_\mathrm {tag} = 0$), single-tag ($N_\mathrm {tag} = 1$), and multi-tag ($N_\mathrm {tag} \ge 2$) category. The respective tagging fractions for events passing the standard selection cuts are shown in Fig. 4 as a function of ${t^\text {rec}}$. The tagging categories are used to split the dataset into 3 tagging control regions. The zero-tag region is dominated by $\sim 90\%$ elastic events, in the single-tag region their fraction is reduced to $\sim 64\%$, and in the multi-tag region proton dissociation dominates at $\sim 91\%$.

3.3 Unfolding

An unfolding procedure is applied to correct binned reconstructed detector-level distributions for various detector effects. The unfolding corrects the data for reducible background contributions, the finite resolution of reconstructed variables, and efficiency and acceptance losses. Furthermore, it is set up to separate elastic and proton-dissociative scattering events. This makes possible the determination of elastic and proton-dissociative particle level distributions from which the corresponding differential ${\pi ^+\pi ^-}$ photoproduction cross sections are derived. The cross sections are measured in a fiducial phase space that is slightly smaller than the analysis phase space defined by the event selection. This makes it possible to account for contributions migrating into and out of the fiducial phase space. The fiducial and analysis phase space cuts are summarised in Table 3.

Table 3 Analysis and fiducial measurement phase space. At detector level, the respective cuts are applied to ${W_{\gamma p}^{\text {rec}}}$, ${t^\text {rec}}$, and ${m_{\pi \pi }^\text {rec}}$, the $Q^2$ cut is replaced by the veto on the reconstruction of the scattered electron, and the ${{m_Y}}$ cut is replaced by the rapidity gap requirement as detailed in the text

Fig. 5

Response matrix for unfolding the one-dimensional ${m_{\pi \pi }^\text {rec}}$ distributions. The matrix depicts migration probabilities from bins of the truth-level distributions along the y axis into bins of the detector-level distributions along the x axis. On detector-level, ${m_{\pi \pi }^\text {rec}}$ distributions in the forward tagging categories are considered, and on truth-level, ${m_{\pi \pi }}$ distributions from the elastic and proton-dissociative ${\pi ^+\pi ^-}$ signal processes are considered, as indicated. Migrations from outside the fiducial phasespace are accounted for in dedicated bins in each region. Background processes are considered in separate truth-level bins to be normalised in corresponding detector-level control regions

3.3.1 Regularised template fit

Differential cross section measurements are performed for various distributions of the variables ${{m_{\pi \pi }}}$, ${W_{\gamma p}}$, and t, and combinations thereof. The beam-gas background template is subtracted from the considered data distribution and the result is used as input to the unfolding. The unfolding is performed by means of a regularised template fit within the TUnfold framework [71]. A response matrix ${\varvec{A}}$ is introduced, with elements $A_{ij}$ describing the probability that an event generated in bin j of a truth-level distribution $\vec {x}$ is reconstructed in bin i of a detector-level distribution $\vec {y}$. In the definition of the response matrix, elastic and proton-dissociative signal and background MC processes are included as dedicated sub-matrices. This makes it possible to separate the elastic and proton-dissociative signal components in the unfolding. Also, background subtraction is implicitly performed during the unfolding where the normalisation of the backgrounds is determined in the fit. At detector level, the response matrix is split into signal and background control regions as defined above. The signal region is further split into three and the background regions into two orthogonal forward tagging categories. This constrains the respective MC contributions in the template fit. Migrations into and out of the fiducial phase space are considered by including side bins in each sub-matrix both at detector and at truth level [37]. These contain events passing the analysis phase space cuts but failing the fiducial cuts (cf. Table 3). As an illustration, the response matrix used for unfolding the one-dimensional ${m_{\pi \pi }^\text {rec}}$ distributions is given in Fig. 5. For all response matrices, most truth bins are found to have good constraints by at least one reconstruction level bin with a purity above 50%. As a result, the statistical correlations between bins of the unfolded one-dimensional distributions are small. The somewhat larger statistical correlations in the unfolding of multi-dimensional distributions are reduced by introducing a Tikhonov regularisation term on the curvature into the template fit [71,72,73]. The truth-level MC distributions, that are adjusted to data as explained in Sect. 2.3, are used as a bias in the regularisation. However, regularisation is not used in the unfolding of the one-dimensional ${m_{\pi \pi }}$ distributions. This makes possible the measurement of the $\omega$ meson mass and production cross section, which were found to be very sensitive to any sort of regularisation.

3.3.2 ${\pi ^+\pi ^-}$ cross section definition

Differential ${\pi ^+\pi ^-}$ photoproduction cross sections are calculated from the number of unfolded ${\pi ^+\pi ^-}$ events. The double-differential cross section in ${m_{\pi \pi }}$ and t is defined as

$$\begin{aligned}&\left[ \dfrac{{\text {d}}^{2} \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y) ({{m_{\pi \pi }}}, t; {{W_{\gamma p}}})}{ {\text {d}}t \, {\text {d}}{{m_{\pi \pi }}}} \right] _j\nonumber \\&\quad =\dfrac{ {\hat{x}}_j }{ \Delta t \, \Delta {{m_{\pi \pi }}}} \dfrac{1}{ {\mathcal {L}}\, {\Phi _{\gamma /e}} \left( {{W_{\gamma p}}} \right) } \end{aligned}$$

(28)

in bin j of an unfolded distribution and with ${{\hat{x}}}_j$ being the number of unfolded events. Differentiation is approximated by dividing the event yields by the ${m_{\pi \pi }}$ and t bin widths, $\Delta t$ and $\Delta {{m_{\pi \pi }}}$, respectively. No bin centre correction is performed for the variables ${m_{\pi \pi }}$ and t. Instead, predictions or fit functions are integrated over the respective bin width when comparing to data. The event yields are normalised by the integrated ep luminosity ${\mathcal {L}}$. Photoproduction cross sections are calculated by normalising the ep cross sections by means of the integrated effective photon flux ${\Phi _{\gamma /e}}$, that is calculated for the relevant ${W_{\gamma p}}$ ranges according to Eq. (17).

3.4 Cross section uncertainties

The measured cross sections are subject to statistical and systematic uncertainties. Statistical uncertainties originate from the limited size of the available data and MC samples. Systematic uncertainties originate from the MC modelling of the signal and background processes and their respective kinematic distributions, as well as from the simulation of the detector response. Detector uncertainties are estimated by either varying the simulated detector response to MC events or by modifying the event selection procedure simultaneously in both the MC samples and data. Model uncertainties are estimated by varying the generation and reweighting parameters of the MC samples.

3.4.1 Statistical uncertainties

Two sources of statistical uncertainties are considered: uncertainties of the data distributions and uncertainties of the unfolding factors obtained from the MC samples. The data uncertainties include contributions from the subtraction of the beam-gas background. Statistical uncertainties are propagated through the unfolding as described in the TUnfold documentation [71]. The finite detector resolution imposes correlations on the statistical uncertainties after the unfolding.

3.4.2 Experimental systematic uncertainties

In order to estimate uncertainties related to the knowledge of the H1 detector response, the unfolding is repeated with systematically varied response matrices. Two types of variations are considered for different sources of uncertainty. Variations of the MC samples on detector level are introduced and are propagated to the cross sections by repeating the unfolding with varied response matrices. Other uncertainties are estimated by modifying the selection procedure. Such variations affect both the migration matrices and the input data distributions simultaneously. For two-sided variations, the full absolute shifts between the nominal and varied unfolded distributions are used to define up and down uncertainties. For one-sided variations, the full shift is taken as a two-sided uncertainty [37].

Concerning the trigger, the following uncertainties are considered:

• The trigger scale factors for the CIP and FTT correction are varied to account for statistical and shape uncertainties. A further uncertainty is estimated to cover the propagation of the correction factors from the electroproduction regime, where they are derived, to photoproduction [37].

• The trigger scale factors for the correction of the forward vetoes are varied to account for statistical and shape uncertainties [37].

• Pions in the very backward direction may potentially interfere with the SpaCal trigger veto via secondary particles produced in nuclear interactions. Nuclear interactions of the pions with the beam transport system and detector material are not modelled perfectly by the simulation. To estimate a potential impact, the cut on the upper track polar angle acceptance is varied between $150^\circ$ and $160^\circ$.

Concerning the track reconstruction and simulation, the following uncertainties are considered:

• The uncertainty of the modelling of the geometric CJC acceptance in $p_T$ is estimated by varying the acceptance cut to $p_T >0.18~{{\text {GeV}}}$.

• The uncertainty for potential mismodelling of the forward tracking detectors is estimated by varying the veto on the number of forward tracks to allow either none or up to two tracks in the selection.

• The uncertainty of the MC z-vertex distribution is estimated by varying the MC distribution to cover small discrepancies in the mean and tails relative to the observed z-vertex distribution in data.

• In the particle identification, the cuts on the kaon, proton, and deuteron ${{\text {d}}E/{\text {d}}x}$ rejection likelihoods are varied up and down while simultaneously varying the pion ${{\text {d}}E/{\text {d}}x}$ selection likelihood down and up.

• Inhomogeneities in the magnetic field may not be fully modelled in the simulation. Nor may the modelling of nuclear interactions of the pions with the detector material be completely accurate. These effects are estimated to result in an uncertainty on the modelled track $p_T$ resolution of 20%. Their impact is evaluated by smearing the reconstructed track $p_{T,\mathrm {rec}} \rightarrow p_{T,\mathrm {rec}} \pm 0.2\, \left( p_{T,\mathrm {rec}}-p_{T,\mathrm {gen}} \right)$ with respect to the generated true $p_{T,\mathrm {gen}}$ in the signal ${\pi ^+\pi ^-}$ MC samples. The result is propagated to all kinematic variables reconstructed from the two pion 4-momenta.

• Similarly, a 20% uncertainty is assumed on the resolution of the track $\theta$ measurement to cover potential mismodellings in the simulation.

Concerning the track momentum scale, the following uncertainties are considered:

• The field strength of the H1 solenoid is known to a level of 0.3% [57] or better. To estimate a potential impact on the absolute track $p_T$ scale, the reconstructed MC $p_T$ values are varied up and down by $\pm 0.3\%$. The variation is performed simultaneously for both tracks.

• The energy loss correction depends on a precise knowledge of the material budget, which is known at a level of 7%. Through the energy loss correction in the track reconstruction, this uncertainty results in an average track $p_T$ uncertainty of $0.4~{{\text {MeV}}}$.

Concerning the calorimeters, the following uncertainties are considered:

• The noise cuts on LAr and SpaCal energy clusters are independently varied up and down by $\pm 0.2~{{\text {GeV}}}$ and $\pm 0.1~{{\text {GeV}}}$, respectively.

• The energy scales of the LAr and SpaCal clusters are independently varied by $\pm 10\%$. These variations are applied prior to the respective cluster noise cut.

• A mismodelling of nuclear interactions may also affect the calorimeter response. A potential impact is estimated by varying the cut applied for associating calorimeter clusters to tracks by $\pm 10~{{\text {cm}}}$.

Concerning the forward detectors, the following tagging uncertainties are considered:

• The tagging and mistagging fractions of the forward detectors are varied independently. The FTS tagging fraction is varied by $\pm 5\%$ in the proton-dissociative MC samples and the mistagging fraction by $\pm 50\%$ in the elastic samples. Similarly, these fractions in the FMD are varied by $\pm 5$ and $\pm 5\%$ and in the PLUG by $\pm 5$ and $\pm 100\%$, respectively. The sizes of the variations are estimated to cover observed mismodellings in the tagging fractions of the respective detectors.

3.4.3 Model uncertainties

In order to estimate model uncertainties, the MC samples are modified on generator-level. Model uncertainties are propagated to the cross sections by repeating the unfolding with the varied migration matrices and MC bias distributions. Cross section uncertainties are then calculated from the shifted unfolded spectra in the same manner as for the experimental uncertainties. Generally, the unfolding approach is rather insensitive to many aspects of the MC modelling. The following model variations are considered:

• Uncertainties on the $Q^2$ and ${{m_Y}}$ dependencies of the MC samples are estimated [74]. The $Q^2$ dependence of the MC samples is varied by applying an event weight ${(1+Q^2/m_{{\text {VM}}}^2)^{\pm 0.07}}$ in agreement with experimental uncertainties [3]. The ${{m_Y}}$ dependence of the proton-dissociative sample is varied by applying a weight ${(1/{{m_Y^2}})^{\pm 0.15}}$.

• The tuning parameters of the MC samples derived to describe the kinematic data distributions (Sect. 2.3) are independently varied up and down [37].

• For the ${{\rho ^\prime }}$ background MC samples, an uncertainty on the relative ratio of $\rho (1450)$ and $\rho (1700)$ is estimated by varying it from 1 : 1 up and down to 2 : 1 and 1 : 2, respectively. An uncertainty on the ${{\rho ^\prime }}$ decay modes is estimated by varying ${{{{\mathcal {BR}}}} ({{\rho ^\prime }} \rightarrow \rho ^\pm \pi ^\mp \pi ^0) = (50\pm 25)\%}$ while simultaneously scaling all other decay modes proportionally.

• A shape uncertainty on the mass distribution of the photon-dissociative mass is estimated by reweighting the distribution by $(1/m_{X}^2)^{\pm 0.15}$.

3.4.4 Normalisation uncertainties

Normalisation uncertainties are directly applied to the unfolded cross sections. The following uncertainties are considered:

• The uncertainty of the track reconstruction efficiency due to modelling of the detector material is 1% per track, leading to a 2% normalisation uncertainty.

• The integrated luminosity of the used dataset is known at a precision of 2.7%.

• Higher order QED effects have been estimated to be smaller than 2% [56] which is taken as a normalisation uncertainty.

This results in a combined 3.9% normalisation uncertainty on the measured cross sections.

3.5 Cross section fits

For the analysis, various parametric models are fitted to the measured cross section distributions. Fits are performed by varying model parameters to minimise a $\chi ^2$ function. Parametrisations of differential distributions are integrated over the respective kinematic bins and divided by their bin widths in order to match the differential cross section definition (cf. Eq. (28)). The $\chi ^2$ function takes into account only the statistical uncertainties, represented by the covariance matrix. Nominal fit parameters are obtained by fitting the nominal measured cross section distributions. The corresponding $\chi ^2$ value relative to the number of degrees of freedom ${\chi _\text {stat}^2/\text {n}_\text {dof}}$ is used as a measure of the quality of a fit. Systematic uncertainties are then propagated through a fit via an offset method, where each systematic cross section variation is fitted independently. The resulting shifts in the fit parameters relative to the nominal parameters are used to define the systematic parameter uncertainties.

4 Results

Elastic and proton-dissociative ${\pi ^+\pi ^-}$ photoproduction cross sections are measured. The measurement is presented integrated over the fiducial phase space and as one-, two-, and three-dimensional cross section distributions as functions of ${m_{\pi \pi }}$, ${W_{\gamma p}}$, and t. Subsequently, ${\rho ^0}$ meson photoproduction cross sections as functions of ${W_{\gamma p}}$ and t are extracted via fits to the invariant ${\pi ^+\pi ^-}$ mass distributions (cf. Eq. (18)). The procedure is exemplified with the differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ as functions of ${m_{\pi \pi }}$. One- and two-dimensional ${\rho ^0}$ meson photoproduction cross section distributions are then parametrised and interpreted using fits. In particular, a Regge fit of the elastic ${\rho ^0}$ meson production cross section as a function of ${W_{\gamma p}}$ and t makes possible the extraction of the effective leading Regge trajectory $\alpha (t)$.

4.1 Fiducial ${\pi ^+\pi ^-}$ photoproduction cross sections

The fiducial ${\pi ^+\pi ^-}$ electroproduction cross section is measured in the phase space defined in Table 3 by unfolding one-dimensional ${m_{\pi \pi }^\text {rec}}$ distributions, integrating the event yield over all bins, and normalising the result by the integrated luminosity. It is subsequently turned into a photoproduction cross section by normalisation to the integrated effective photon flux. In the phase space considered, the integrated effective flux calculated with Eq. (17) is ${\Phi _{\gamma /e}}$ = 0.1368. This yields a ${\pi ^+\pi ^-}$ photoproduction cross section of

$$\begin{aligned} {\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)}= & {} 16.20 \pm 0.05\ ({\text {stat.}})\ {}^{+1.11}_{-1.15}\nonumber \\&\quad ({\text {syst.}})\ \mu b, \nonumber \\&\quad \text {for }\ m_p \le {{m_Y}} < 10~{{\text {GeV}}}. \end{aligned}$$

(29)

The cross section is measured at an average energy $\langle {{W_{\gamma p}}} \rangle \simeq 43~{{\text {GeV}}}$ as estimated from the MC simulation. The elastic and proton-dissociative components of the cross section are separated through the unfolding which yields

$$\begin{aligned} {\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} p)}&= 11.52 \pm 0.06\ ({\text {stat.}})\ {}^{+0.76}_{-0.78}\nonumber \\&\quad ({\text {syst.}})\ {\upmu \text {b}} \text { and} \end{aligned}$$

(30)

$$\begin{aligned} {\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)}&= 4.68 \pm 0.06\ ({\text {stat.}})\ {}^{+0.62}_{-0.64}\ ({\text {syst.}})\ {\upmu \text {b}}, \nonumber \\&\qquad \text {for }\ m_p< {{m_Y}} < 10~{{\text {GeV}}}, \end{aligned}$$

(31)

respectively.⁶ The uncertainties of the two components are correlated with a statistical and symmetrised total Pearson correlation coefficient of $\rho _\mathrm {stat} = -0.59$, and $\rho _\mathrm {tot} = +0.30$, respectively. The measurements are statistically very precise at a level of 0.5% (1.2%) but have large systematic uncertainties of 6.3% (13.2%) for the elastic (proton-dissociative) component. The uncertainty of the elastic component is dominated by the trigger and the normalisation uncertainties of 4.1 and 3.9%, respectively, whereas the uncertainties associated with the tagging and the calorimeter dominate the proton-dissociative component at 8.4 and 7.3%, respectively. A more detailed breakdown of the cross section uncertainties is given in Table 4.

Table 4 Summary of the combined impact of systematic uncertainties on the fiducial ${\pi ^+\pi ^-}$ photoproduction cross sections. The numbers are obtained by unfolding the one-dimensional ${m_{\pi \pi }}$ distribution and with symmetrised systematic uncertainties

Photoproduction of ${\pi ^+\pi ^-}$ mesons has a fairly large cross section and forms a sizeable contribution to the total $\gamma p$ cross section, which is known for similar ${W_{\gamma p}}$ from cosmic ray experiments [75, 76]. Within the restrictions of the fiducial phase space in ${m_{\pi \pi }}$, t, and ${m_Y}$, the elastic and proton-dissociative processes contribute to the total cross section by about 9 and 4%, respectively. The elastic ${\pi ^+\pi ^-}$ photoproduction cross section has been measured before in ep collisions at slightly higher ${W_{\gamma p}}$ [9, 15]. Considering the differences in ${W_{\gamma p}}$ and the energy dependence of the elastic cross section (see below), the measurements are found to be consistent. There has not been a previous measurement of the proton-dissociative ${\pi ^+\pi ^-}$ photoproduction cross section in a comparable phase space.

4.2 Differential ${\pi ^+\pi ^-}$ photoproduction cross sections

The elastic and proton-dissociative differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ are measured as functions of ${m_{\pi \pi }}$ by unfolding one-dimensional ${m_{\pi \pi }^\text {rec}}$ distributions. Numerical results are given in Appendix A and the cross section distributions are displayed in Fig. 6. The photoproduction of ${\pi ^+\pi ^-}$ mesons is dominated by the ${\rho ^0}$ meson resonance peaking at a mass of around 770 ${\text {MeV}}$. The differential cross sections fall off steeply towards higher masses with a second broad excited $\rho ^\prime$ meson resonance appearing at around 1600 ${\text {MeV}}$. At the ${\rho ^0}$ meson resonance peak, the proton-dissociative cross section is around 40% of the elastic cross section with the difference becoming smaller towards higher masses. The uncertainties of the measurement vary slowly with ${m_{\pi \pi }}$. At the ${\rho ^0}$ meson peak the statistical and systematic uncertainty of the elastic differential cross section are roughly 1 and 7%, respectively. At the position of the $\rho ^\prime$ peak they have grown to 7 and 13%, respectively. The corresponding uncertainties of the differential proton-dissociative cross section are about twice as large.

Fig. 6

Elastic (${{m_Y}} {=}m_p$) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}}$ as functions of ${m_{\pi \pi }}$. The black points and error bars show the measured cross section values with statistical uncertainties. The red and green bands show the total uncertainties of the elastic and proton-dissociative components, respectively

4.2.1 Fit of the ${m_{\pi \pi }}$ dependence

In order to extract the ${\rho ^0}$ meson contributions to the ${\pi ^+\pi ^-}$ photoproduction cross sections, the ${m_{\pi \pi }}$ lineshape defined in Eq. (18) is fitted to the data. As this paper focusses on the analysis of ${\rho ^0}$ meson production, the fit is only performed in the analysis range $0.6~{{\text {GeV}}} \le {{m_{\pi \pi }}} \le 1.0~{{\text {GeV}}}$ where contributions from excited $\rho ^\prime$ meson states can be neglected. The parametrisation is fitted simultaneously to the elastic and proton-dissociative distributions with the parameter settings described in Table 1. The model describes the data well with the fit yielding ${\chi _\text {stat}^2/\text {n}_\text {dof}} = 24.6/24$. The resulting model parameters are presented in Table 5. The fitted curves are shown in Fig. 7, where they are compared to the measured data.

Table 5 Free parameters for the fit of the single-differential elastic and proton-dissociative cross section ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ as a function of ${m_{\pi \pi }}$. The nominal fit values and statistical and systematic uncertainties are given. A full uncertainty breakdown and statistical correlations are provided [77]. The corresponding fit is shown in Fig. 7

Fig. 7

Elastic (${{m_Y}} {=}m_p$) (a) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) (b) differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ as functions of ${m_{\pi \pi }}$. Equation (18) is fitted to the distributions in the mass region $0.6~{{\text {GeV}}} \le {{m_{\pi \pi }}} \le 1.0~{{\text {GeV}}}$ as described in the text. The model and its components are displayed as indicated in the legend. In the ratio panel, the data are compared to the bin-averaged fit function values as they entered in the $\chi ^2$ calculation for the fit

Within the fit model, the differential ${\pi ^+\pi ^-}$ photoproduction cross sections obtain significant contributions from the ${\rho ^0}$ meson resonance and non-resonant ${\pi ^+\pi ^-}$ production. The two corresponding amplitudes give rise to large interference terms that result in a skewing of the resonance lineshapes. At the measured ${\rho ^0}$ meson mass, the relative contributions of the ${\rho ^0}$ resonance and non-resonant ${\pi ^+\pi ^-}$ production to the elastic differential ${\pi ^+\pi ^-}$ photoproduction cross section are $[79.1 \pm 3.2~({\text {stat.}})~{}^{+4.4}_{-1.4}~({\text {syst.}})]\%$ and $[7.1 \pm 0.6~({\text {stat.}})~{}^{+0.7}_{-0.5}~({\text {syst.}})]\%$, respectively. The corresponding contributions to the proton-dissociative cross section are $[85.9 \pm 3.8~({\text {stat.}})~{}^{+3.8}_{-3.2}~({\text {syst.}})]\%$ and $[4.8 \pm 0.6~({\text {stat.}})~{}^{+0.6}_{-0.5}~({\text {syst.}})]\%$, respectively. Most noticeably, the relative non-resonant contribution is smaller for proton-dissociative than for elastic scattering resulting in a weaker skewing. In the analysed mass range, the non-resonant differential cross section exhibits little dependence on ${m_{\pi \pi }}$. For this reason the two fit parameters $\delta _{{\text {nr}}}$ and $\Lambda _{{\text {nr}}}$ are strongly correlated and cannot be constrained very well individually. Qualitatively the result of the fit is similar to past HERA ${\pi ^+\pi ^-}$ photoproduction analyses [15]. Quantitative comparisons of fit parameters are not possible because different parametrisations were used. Variants of the fit were also explored but did not significantly improve the compatibility with data. When including a possible admixture of incoherent background, the respective contribution is found to be compatible with zero. This conclusion is largely independent of the assumed incoherent background shape. Models including barrier factors [43] also can be fitted well by the data. Obviously, all extracted particle masses and widths are model dependent. A detailed discussion of these effects is beyond the scope of this paper.

Table 6 Comparison of measured ${{\rho ^0}}$ and $\omega$ meson properties to the PDG values [33]. Only the total uncertainties are given. The last column gives the mass differences between the PDG $e^+e^-$ and the present measurement

The rich structure of the interference term near 770 ${\text {MeV}}$, visible in Fig. 7, originates from the $\omega$ resonance. In the fit model, the $\omega$ resonance amplitude prevents the net interference contribution from vanishing at the ${\rho ^0}$ meson mass and shifts the position of the sign change of the interference term towards the $\omega$ meson mass. In the ${\pi ^+\pi ^-}$ production cross section this is visible as a characteristic step. The impact of the $\omega$ meson on the measured differential cross sections is similar in size to observations made in $e^+e^- \rightarrow {{\pi ^+\pi ^-}}$ production [79,80,81,82]. In the present analysis, this effect is measured for the first time at HERA.

The masses of the ${{\rho ^0}}$ and $\omega$ mesons and the width of the ${{\rho ^0}}$ meson obtained from the fit are compared to the world average PDG values [33] in Table 6. The PDG lists two sets of ${\rho ^0}$ parameters from ${\rho ^0}$ meson photoproduction and production in $e^+e^-$ scattering, respectively. The value measured for the ${\rho ^0}$ mass is compatible with previous photoproduction measurements [15, 19, 78], confirming a slightly lower ${\rho ^0}$ mass parameter as compared to typical $e^+e^-$ measurements [79,80,81,82]. The mass uncertainty is dominated by the uncertainties in the magnetic field and the material in the detector affecting the track $p_T$ scale. The precision of the presented value is similar to the most precise previous photoproduction measurements. The ${\rho ^0}$ width is consistent with both PDG values and offers an uncertainty as good as previous photoproduction measurements. The $\omega$ mass is also compatible with the PDG value but has a sizeable uncertainty. The observed difference between the measured and the PDG $\omega$ mass is similar to that of the ${{\rho ^0}}$ mass relative to the $e^+e^-$ measurement.

Fig. 8

Elastic (${{m_Y}} {=}m_p$) differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} p)/{\text {d}}{{m_{\pi \pi }}}}$ in bins of ${W_{\gamma p}}$ and as functions of ${m_{\pi \pi }}$. The model that is fitted to the data as described in the text and its components are also shown

Fig. 9

Proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ in bins of ${W_{\gamma p}}$ and as functions of ${m_{\pi \pi }}$. The model that is fitted to the data as described in the text and its components are also shown

4.2.2 Fiducial ${\rho ^0}$ and $\omega$ meson photoproduction cross sections

The result of the fit is used to calculate the ${\rho ^0}$ meson contributions to the fiducial ${\pi ^+\pi ^-}$ photoproduction cross sections. This is achieved by integrating the ${\rho ^0}$ meson resonance amplitude in the range $2m_\pi< {{m_{\pi \pi }}} < 1.53~{{\text {GeV}}}$ as discussed in Sect. 2.2.2. The integration yields

$$\begin{aligned} {\sigma (\gamma p \rightarrow \rho ^0 p)}&=\ 10.97 \pm 0.18\ ({\text {stat.}})\ {}^{+0.72}_{-0.73}\ ({\text {syst.}})\ {\upmu \text {b}} \text { and} \end{aligned}$$

(32)

$$\begin{aligned} {\sigma (\gamma p \rightarrow \rho ^0 Y)}&=\ 4.71 \pm 0.09\ ({\text {stat.}})\ {}^{+0.60}_{-0.59}\ ({\text {syst.}})\ {\upmu \text {b}}, \nonumber \\&\qquad \text {for }\ m_p< {{m_Y}} < 10~{{\text {GeV}}}, \end{aligned}$$

(33)

for the elastic and proton-dissociative ${{\rho ^0}}$ meson photoproduction cross sections, respectively. The ratio of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections in the measurement phase space is

$$\begin{aligned}&\dfrac{{\sigma (\gamma p \rightarrow \rho ^0 Y)}}{{\sigma (\gamma p \rightarrow \rho ^0 p)}} = 0.429 \pm 0.009\ ({\text {stat.}})\ {}^{+0.056}_{-0.053}\ ({\text {syst.}}) , \nonumber \\&\qquad \text {for }\ m_p< {{m_Y}} < 10~{{\text {GeV}}}, \end{aligned}$$

(34)

taking into account correlations. The measured elastic ${\rho ^0}$ meson photoproduction cross section is consistent with previous HERA measurements [9, 15, 17], when accounting for ${W_{\gamma p}}$ differences between the measurements. Suitable reference measurements for the proton-dissociative cross section are not available. However, the ratio of the proton-dissociative to the elastic ${\rho ^0}$ meson photoproduction cross section is consistent with a previous measurement [15], assuming that phase space differences are covered by the large uncertainties.

With the fit model Eq. (18), also the indirect measurement of the fiducial $\omega$ meson photoproduction cross sections is possible by integrating the $\omega$-${\rho ^0}$ mixing amplitude over the range $2m_\pi \le {{m_{\pi \pi }}} \le 0.82~{{\text {GeV}}}$. The result is corrected for the $\omega \rightarrow {{\pi ^+\pi ^-}}$ branching fraction ${\mathcal {BR}}(\omega \rightarrow {{\pi ^+\pi ^-}}) = 0.0153 \pm 0.0006\ ({\text {tot.}})$ [33] to yield the cross sections

$$\begin{aligned} \sigma (\gamma p \rightarrow \omega p)&=\ 1.06 \pm 0.26\ ({\text {stat.}})\ {}^{+0.13}_{-0.30}\ ({\text {syst.}})\ {\upmu \text {b}}\ \text { and} \end{aligned}$$

(35)

$$\begin{aligned} \sigma (\gamma p \rightarrow \omega Y)&=\ 0.31 \pm 0.23\ ({\text {stat.}})\ {}^{+0.19}_{-0.16}\ ({\text {syst.}})\ {\upmu \text {b}}, \nonumber \\&\qquad \text {for }\ m_p< {{m_Y}} < 10~{{\text {GeV}}}. \end{aligned}$$

(36)

The uncertainty of the branching fraction is included in the systematic uncertainty. The ratios of the $\omega$ meson to the ${{\rho ^0}}$ meson photoproduction cross sections are then determined to be

$$\begin{aligned} \dfrac{ \sigma (\gamma p \rightarrow \omega p)}{{\sigma (\gamma p \rightarrow \rho ^0 p)}}= & {} 0.097 \pm 0.020\ ({\text {stat.}})\ {}^{+0.011}_{-0.026}\ ({\text {syst.}}) \text { and}\nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned} \dfrac{ \sigma (\gamma p \rightarrow \omega Y)}{{\sigma (\gamma p \rightarrow \rho ^0 Y)}}= & {} 0.065 \pm 0.041\ ({\text {stat.}})\ {}^{+0.042}_{-0.032}\ ({\text {syst.}}),\nonumber \\&\quad \text {for }\ m_p< {{m_Y}} < 10~{{\text {GeV}}}. \end{aligned}$$

(38)

The elastic $\omega$ photoproduction cross section has been directly measured at HERA in the $\omega \rightarrow {{\pi ^+\pi ^-}} \pi ^0$ channel by the ZEUS collaboration. In a similar phase space, a compatible value for the cross section was observed [83]. The present value is also consistent with the expectation that the ${\rho ^0}$ and $\omega$ meson photoproduction cross sections differ by a factor $c_{\omega }/c_{\rho } \simeq 1/9$ that originates from SU(2) flavour symmetry and the quark electric charges.

Table 7 Elastic (${{m_Y}} {=}m_p$) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) ${\rho ^0}$ meson photoproduction cross sections ${\sigma (\gamma p \rightarrow \rho ^0 Y)}$ in bins of ${W_{\gamma p}}$. The cross sections are obtained by analysing the ${\pi ^+\pi ^-}$ photoproduction cross sections given in Tables 18 and 19 with the fit model defined in Eq. (18). The effective photon flux factors ${\Phi _{\gamma /e}}$ for each ${W_{\gamma p}}$ bin are given. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 10

Fig. 10

Elastic (${{m_Y}} {=}m_p$) (a) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) (b) ${\rho ^0}$ meson photoproduction cross sections ${\sigma (\gamma p \rightarrow \rho ^0 Y)}$ as functions of ${{W_{\gamma p}}}$. The vertical lines indicate the total uncertainties. The statistical uncertainties are indicated by the inner error bars, which however are mostly covered by the data markers. The distributions are parametrised with fits as described in the text, and the fitted curves are also shown. In the ratio panels, the data are compared to the fit function values at the geometric bin centres as they entered the $\chi ^2$ calculation in the fit

4.3 Energy dependence of ${\rho ^0}$ meson photoproduction

The energy dependencies of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections are obtained by unfolding two-dimensional distributions ${{W_{\gamma p}^{\text {rec}}}} \otimes {{m_{\pi \pi }^\text {rec}}}$ and calculating the corresponding two-dimensional ${\pi ^+\pi ^-}$ cross sections. Numerical results are presented in Appendix A and the cross section distributions are displayed in Figs. 8 and 9 for the elastic and proton-dissociative components, respectively. To extract the ${\rho ^0}$ meson contributions, Eq. (18) is fitted simultaneously to the ${m_{\pi \pi }}$ distributions in every unfolded ${W_{\gamma p}}$ bin with the parameter settings described in Table 1. In particular, the $\omega$ meson model parameters cannot be constrained well by the fit and are fixed to the values obtained in the fit to the one-dimensional mass distributions. The fit gives ${\chi _\text {stat}^2/\text {n}_\text {dof}} = 222.0/188$. The fitted curves are also shown Figs. 8 and 9.

The fit results are used to calculate the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections ${\sigma (\gamma p \rightarrow \rho ^0 Y)}$ as a function of ${W_{\gamma p}}$. The results are given in Table 7 and displayed in Fig. 10. The cross sections only have weak dependencies on ${W_{\gamma p}}$, as is expected for diffractive processes at such energies. Many sources of uncertainty considered here are observed to vary with ${W_{\gamma p}}$. For the elastic cross section, the full systematic uncertainty is about 6% in the centre of the considered phase space and increases to 10% and 8% at the lowest and highest considered ${W_{\gamma p}}$, respectively. The corresponding-proton dissociative uncertainties are about twice as large.

Table 8 Fit parameters for the fit of the energy dependence of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections ${\sigma (\gamma p \rightarrow \rho ^0 Y)}$ in the range ${20<{{W_{\gamma p}}} < 80~{{\text {GeV}}}}$. The nominal fit values and statistical and systematic uncertainties are given. A full uncertainty breakdown and statistical correlations are provided [77]. The corresponding fit is shown in Fig. 10

4.3.1 Fit of the energy dependence

The energy dependencies of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections in the range ${20< {{W_{\gamma p}}} < 80~{{\text {GeV}}}}$ are parametrised by a simple power law:

$$\begin{aligned} {{\sigma _{\rho }}} ({{W_{\gamma p}}}) = {{\sigma _{\rho }}} (W_0)\ \left( \dfrac{{{W_{\gamma p}}}}{W_0} \right) ^\delta \,. \end{aligned}$$

(39)

The parametrisation is fitted simultaneously to the measured elastic and proton-dissociative distributions assuming independent elastic and proton-dissociative fit parameters. The function is evaluated at the geometric bin centres, and the reference energy is set to $W_0 = 40~{{\text {GeV}}}$. The fit yields a very poor ${\chi _\text {stat}^2/\text {n}_\text {dof}} = 33.0 / 11$, where however systematic uncertainties are not considered. The resulting fit parameters are presented in Table 8. The fitted curves are compared to the data in Fig. 10.

Fig. 11

Elastic (${{m_Y}} {=}m_p$) ${\rho ^0}$ meson photoproduction cross section ${\sigma (\gamma p \rightarrow \rho ^0 Y)}$ as a function of ${W_{\gamma p}}$. The present data are compared to measurements by fixed-target [20,21,22,23,24,25], HERA [9, 15, 17], and LHC [26] experiments as indicated in the legend. Only total uncertainties are shown. The solid line shows the fit of a sum of two power-law functions to the fixed-target and HERA data. The respective contributions are shown as dotted lines. The fit uncertainty is indicated by a band

The fitted power parameter $\delta _{{\text {el}}}=0.171\pm 0.009~({\text {stat.}}) {}^{+0.039}_{-0.026}~({\text {syst.}})$ characterises the slow rise of the elastic cross section with increasing scattering energy. The measured value is compatible with previous measurements, e.g., by the ZEUS collaboration [15] or the CMS Collaboration (pPb) [26], but is more precise. The fit results in a proton-dissociative parameter $\delta _{{\text {pd}}}=-0.156\pm 0.026~({\text {stat.}}) {}^{+0.081}_{-0.079}~({\text {syst.}})$ that is significantly different from the elastic parameter and suggests a decrease of the proton-dissociative cross section with increasing energy. However, the proton-dissociative cross section is expected to be strongly shaped by the restriction of the fiducial phase space; most notably by the requirement ${{m_Y}} < 10~{{\text {GeV}}}$. Since energy is required to excite high masses ${m_Y}$, the cut suppresses the cross section more strongly for high than for low ${W_{\gamma p}}$. The phase space is not accounted for in Eq. (39) so that the proton-dissociative result $\delta _{{\text {pd}}}$ cannot be interpreted directly in terms of a scattering amplitude.

Table 9 Fit parameters for the fit of the energy dependence of the elastic ${\rho ^0}$ meson photoproduction cross section in the range ${2<{{W_{\gamma p}}} < 200~{{\text {GeV}}}}$. The nominal fit values and statistical and systematic uncertainties are given. A full uncertainty breakdown and statistical correlations are provided [77]. The corresponding fit is shown in Fig. 11

Fig. 12

Elastic (${{m_Y}} {=}m_p$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} p)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of t and as functions of ${m_{\pi \pi }}$. The model that is fitted to the data as described in the text and its components are also shown

Fig. 13

Proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of t and as functions of ${m_{\pi \pi }}$. The model that is fitted to the data as described in the text and its components are also shown

In Fig. 11, the measured elastic ${\rho ^0}$ meson photoproduction cross section data are compared to selected measurements by fixed-target [20,21,22,23,24,25], HERA [9, 15, 17], and LHC [26] experiments.⁷ The present elastic data are in agreement with other measurements and connect the fixed-target data with the high energy regime. The combination of data makes possible the study of the region of reggeon exchange at small scattering energies and of pomeron exchange at large energies simultaneously. For describing the energy range $2< {{W_{\gamma p}}} < 200~{{\text {GeV}}}$, the energy dependence of the elastic cross section is parametrised by the sum of two power-law functions:

$$\begin{aligned} {{\sigma _{\rho }}} ({{W_{\gamma p}}}) = {{\sigma _{\rho }}} (W_0)\ \left( \left( \dfrac{{{W_{\gamma p}}}}{W_0} \right) ^{\delta _{{I\!\!P}}} + f_{{I\!\!R}} \left( \dfrac{{{W_{\gamma p}}}}{W_0} \right) ^{\delta _{{I\!\!R}}} \right) . \end{aligned}$$

(40)

The two parameters $\delta _{{I\!\!P}}$ and $\delta _{{I\!\!R}}$ are associated with pomeron exchange at high and reggeon exchange at low ${W_{\gamma p}}$, respectively. The parametrisation is fitted to the HERA data [9, 15, 17] together with data from fixed-target experiments [20,21,22,23,24,25] as shown in Fig. 11. In the fit, previous measurements enter with their respective uncorrelated and normalisation uncertainties. For the H1 [9] and ZEUS measurements [15], normalisation uncertainties of 8% and 9%, respectively, are extracted from the total uncertainties. Correlations between experiments are not considered. The uncorrelated uncertainties are accounted for in the data covariance, together with the statistical uncertainties of the present measurement. The normalisation uncertainties are included by offsetting the data and repeating the fit, as is also done for systematic and normalisation uncertainties of the present data.

The fit yields ${\chi _\text {stat}^2/\text {n}_\text {dof}} = 84.3/43$ and results in $\delta _{{I\!\!P}} = 0.207 \pm 0.015~({\text {stat.}}) ^{+0.053}_{-0.033}~({\text {syst.}})$ and $\delta _{{I\!\!R}} = -1.45 \pm 0.12~({\text {stat.}}) ^{+0.35}_{-0.21} ~({\text {syst.}})$. All fit parameters are given in Table 9.

The fitted curve is compared to the data in Fig. 11. The extracted parameters are consistent with the broader picture of vector meson electroproduction, in particular with the observed dependence of $\delta _{{I\!\!P}}$ on the vector meson mass [84]. The fit further suggests a small reggeon contribution of ${f_{{I\!\!R}} = [2.0 \pm 0.7~({\text {stat.}})\ {}^{+2.9}_{-1.3}~({\text {syst.}})]\%}$ at $W_0=40~{{\text {GeV}}}$. For this reason, the parameter $\delta _{{\text {el}}}$ from the fit with a single power-law function (Table 8, ${{m_Y}} =m_p$) is interpreted as an effective parameter describing both pomeron and reggeon exchange contributions.

Table 10 Elastic (${{m_Y}} {=}m_p$) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) differential ${\rho ^0}$ meson photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}$ in bins of t. The cross sections are obtained by analysing the ${\pi ^+\pi ^-}$ photoproduction cross sections given in Tables 20 and 21 with the fit model defined in Eq. (18). The t bin centres $t_{bc}$ are calculated as described in the text. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 14

4.4 t dependence of ${\rho ^0}$ meson photoproduction

The t dependencies of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections are obtained by unfolding two-dimensional distributions ${t^\text {rec}} \otimes {{m_{\pi \pi }^\text {rec}}}$ and calculating the corresponding two-dimensional ${\pi ^+\pi ^-}$ cross sections. Numerical results are presented in Appendix A and the cross section distributions are displayed in Figs. 12 and 13 for the elastic and proton-dissociative component, respectively. To extract the ${\rho ^0}$ meson contributions, Eq. (18) is fitted simultaneously to the ${m_{\pi \pi }}$ distributions in every unfolded t bin with the parameter settings described in Table 1. The fit yields ${{\chi _\text {stat}^2/\text {n}_\text {dof}} = 353.4/247}$. The fitted curves are also shown Figs. 12 and 13.

The fit results are used to calculate the elastic and proton-dissociative differential ${\rho ^0}$ meson photoproduction cross sections ${{{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}}$ as a function of t. The results are given in Table 10 and displayed in Fig. 14. The cross sections fall of exponentially with t as is expected for diffractive processes. The relative systematic uncertainties of roughly 6% for the elastic distribution vary little with t and increase moderately to 11% in the highest |t| bin. For the proton-dissociative distribution, the uncertainties increase from roughly 13% at intermediate |t| to 17% in both the highest and lowest considered |t| bins.

Fig. 14

Elastic (${{m_Y}} {=}m_p$) (a) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) (b) differential ${\rho ^0}$ meson photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}$ as functions of t. The distributions are parametrised with fits as described in the text, and the fitted curves are also shown. In the ratio panels, the data are compared to the bin-averaged fit function values as they entered in the $\chi ^2$ calculation for the fit. The depicted bin centres are evaluated using the fit functions as described in the text

4.4.1 Fit of the t dependence

Table 11 Fit parameters for the fit of the t dependencies of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}$. The nominal fit values and statistical and systematic uncertainties are given. A full uncertainty breakdown and statistical correlations are provided [77]. The corresponding fit is shown in Fig. 14

The t dependencies of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections are parametrised by the function

$$\begin{aligned} \dfrac{{\text {d}}{{\sigma _{\rho }}}}{{\text {d}}t}(t) = \dfrac{{\text {d}}{{\sigma _{\rho }}}}{{\text {d}}t}(t=0)\ \left( 1 - \dfrac{ b\, t}{a} \right) ^{-a} . \end{aligned}$$

(41)

It interpolates between an exponential ${\text {d}}{{\sigma _{\rho }}}/{\text {d}}t \propto \exp \left( b\, t \right)$ at low |t| and a power-law ${\text {d}}{{\sigma _{\rho }}}/ {\text {d}}t \propto |t|^{-a}$ at large |t|. The function is fitted simultaneously to the elastic and proton-dissociative distributions assuming independent elastic and proton-dissociative model parameters. To match the cross section definition, the function is integrated over each bin and divided by the respective bin width in the fit. The proton-dissociative distribution is affected by phase space restrictions that are not accounted for in the parametrisation. The impact is particularly large at small |t| because excitations with large ${{m_Y}}$ require a minimal⁸ |t|. For this reason, the lowest |t| bin of the proton-dissociative distribution is not included in the fit. The fit yields ${{\chi _\text {stat}^2/\text {n}_\text {dof}} = 15.3 / 14 }$. The resulting fit parameters are presented in Table 11. The fitted curves are compared to data in Fig. 14.

Fig. 15

Elastic (${{m_Y}} {=}m_p$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} p)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of ${W_{\gamma p}}$ and t and as functions of ${m_{\pi \pi }}$. The model that is fitted to the data as described in the text and its components are also shown

Fig. 16

Proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of ${W_{\gamma p}}$ and t and as functions of ${m_{\pi \pi }}$. The model that is fitted to the data as described in the text and its components are also shown

The exponential t dependencies of the elastic and proton-dissociative cross sections at small |t| are quantified by the parameters ${b_{{\text {el}}} = 9.61\pm 0.15~({\text {stat.}})\ {}^{+0.20}_{-0.15}~({\text {syst.}})~{{\text {GeV}^{-2}}}}$ and ${b_{{\text {pd}}} = 4.81\pm 0.24~({\text {stat.}})\ {}^{+0.39}_{-0.37}~({\text {syst.}})~{{\text {GeV}^{-2}}}}$, respectively. With $b_{{\text {pd}}} \sim 1/2\, b_{{\text {el}}}$, the elastic spectrum falls off much more steeply than the proton-dissociative spectrum. The difference between the exponential slope parameters is $b_{{\text {el}}} - b_{{\text {pd}}} = 4.80 \pm 0.29~({\text {stat.}})\ {}^{+0.41}_{-0.40}~({\text {syst.}})$, taking into account correlations. In the optical interpretation (or in an eikonal model approach [85]), this difference reflects the difference in the size of the respective target, i.e., proton in elastic vs parton in proton-dissociative interactions. The measured value is consistent with HERA measurements in ${\rho ^0}$ meson electroproduction [3]. There is evidence for a deviation from the purely exponential behaviour given by the finite values for $a_{{\text {el}}} = 20.4\pm 3.7~({\text {stat.}})\ {}^{+6.8}_{-5.1}~({\text {syst.}})$ and $a_{{\text {pd}}} = 8.5\pm 1.7~({\text {stat.}})\ {}^{+2.7}_{-2.1}~({\text {syst.}})$. The smaller $a_{{\text {pd}}}$ indicates a stronger deviation for the proton-dissociative than for the elastic cross section. The present measurements of the t dependencies of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections can be compared with other HERA measurements [9, 15]. The measured values for the elastic slope $b_{{\text {el}}}$ are somewhat lower than observed previously but seem compatible within uncertainties when taking into account the differences in energy and the thus expected shrinkage. The present value is the most precise of these measurements. The observed deviation of the elastic slope from the exponential behaviour is compatible with the ZEUS measurement [15]. Similar to the elastic case, the slopes $b_{{\text {pd}}}$ in proton-dissociative scattering are compatible with earlier measurements. The present measurement is more precise and does account for deviations from the exponential form. Differences in the definition of the proton-dissociative phase space were not considered in these comparisons.

4.5 ${\rho ^0}$ meson photoproduction as a function of t and ${W_{\gamma p}}$

The two-dimensional t and ${W_{\gamma p}}$ dependencies of the elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections are obtained by unfolding three-dimensional distributions ${t^\text {rec}} \otimes {{W_{\gamma p}^{\text {rec}}}} \otimes {{m_{\pi \pi }^\text {rec}}}$ and calculating the corresponding ${\pi ^+\pi ^-}$ cross sections.⁹ Numerical results are presented in Appendix A and the cross section distributions are displayed in Figs. 15 and 16 for the elastic and proton-dissociative component, respectively. To extract the ${\rho ^0}$ meson contributions, Eq. (18) is fitted simultaneously to the ${m_{\pi \pi }}$ distributions in every unfolded ${W_{\gamma p}}$ and t bin with the parameter settings described in Table 1. The fit yields ${\chi _\text {stat}^2/\text {n}_\text {dof}} = 804.0/607$. The fitted curves are also shown in Figs. 15 and 16 .

The fit results are used to calculate the elastic and proton-dissociative differential ${\rho ^0}$ meson photoproduction cross sections ${{{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}}$ as a function of t and ${W_{\gamma p}}$. The results are given in Tables 12 and 13 for the elastic and proton-dissociative component, respectively, and are shown in Fig. 17.

4.5.1 Regge fit of the t and ${{W_{\gamma p}}}$ dependence

The elastic and proton-dissociative ${\rho ^0}$ meson photoproduction cross sections are parametrised by the function

$$\begin{aligned} \dfrac{{\text {d}}{{\sigma _{\rho }}}}{{\text {d}}t}(t;{{W_{\gamma p}}}) = \dfrac{{\text {d}}{{\sigma _{\rho }}}}{{\text {d}}t}(t;W_0) \left( \dfrac{{{W_{\gamma p}}}}{W_0} \right) ^{4 (\alpha (t)-1) } , \end{aligned}$$

(42)

with an energy dependence predicted by Regge theory and with a single leading trajectory $\alpha (t)$. The t dependence at the reference energy $W_0=40~{{\text {GeV}}}$ is parametrised according to Eq. (41). Regge trajectories are expected to continue linearly only in the region of small |t|. Since the analysis extends to $|t| \le 1.5~{{\text {GeV}^2}}$, a modified parametrisation based on a Fermi function is used:

$$\begin{aligned} \alpha (t) = \alpha _0 + \beta \, \left( \left( {\text {e}}^{ - \frac{4\alpha _1 t}{\beta } }+1\right) ^{-1} -\dfrac{1}{2}\right) \text{. } \end{aligned}$$

(43)

It approximates a linear function $\alpha _0 + \alpha _1\, t$ for small |t| and approaches a constant value ${\alpha _0 - \beta /2}$ for ${t \rightarrow -\infty }$. Such a lower bound is expected for large |t| from QCD calculations [87,88,89,90] but deviations from a linear behaviour have not been observed yet in this reaction in the t range considered here. The parametrisation in Eq. (42) is fitted simultaneously to the elastic and proton-dissociative cross sections assuming independent elastic and proton-dissociative fit parameters. In the $\chi ^2$ calculation, the function is integrated over each t bin and evaluated at the geometric ${W_{\gamma p}}$ bin centres to match the cross section definition. Following the argumentation discussed above, the respective lowest |t| bins of the proton-dissociative cross sections are excluded from the fit. The fit yields ${\chi _\text {stat}^2/\text {n}_\text {dof}} =31.7/32$. The resulting fit parameters are presented Table 14. The fitted curves are compared to data in Fig. 17.

Table 12 Elastic (${{m_Y}} {=}m_p$) differential ${\rho ^0}$ meson photoproduction cross section ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}$ in bins of ${W_{\gamma p}}$ and t. The cross section is obtained by analysing the ${\pi ^+\pi ^-}$ photoproduction cross section given in Table 22 with the fit model defined in Eq. (18). The effective photon flux factors ${\Phi _{\gamma /e}}$ for each ${W_{\gamma p}}$ bin are given. The t bin centres $t_{bc}$ are calculated as described in the text. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 17

Table 13 Proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) differential ${\rho ^0}$ meson photoproduction cross section ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}$ in bins of ${W_{\gamma p}}$ and t. The cross section is obtained by analysing the ${\pi ^+\pi ^-}$ photoproduction cross section given in Table 23 with the fit model defined in Eq. (18). The effective photon flux factors ${\Phi _{\gamma /e}}$ for each ${W_{\gamma p}}$ bin are given. The t bin centres $t_{bc}$ are calculated as described in the text. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 17

4.5.2 Shrinkage of the elastic differential cross section

The fit parameters in Table 14 that describe the t dependencies of the differential ${\rho ^0}$ meson photoproduction cross sections at $W_0=40~{{\text {GeV}}}$ are in agreement with the parameters from the one-dimensional fit of the t dependencies that is described above. For the elastic differential cross section, the finite slope of the measured trajectory $\alpha (t)$ (see below) results in a shrinkage of the forward peak with increasing ${W_{\gamma p}}$. At small |t|, where the differential cross section ${{{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} p)/{\text {d}}t}}$ falls exponentially with t and the trajectory is linear, the shrinkage can be expressed in terms of a ${W_{\gamma p}}$ dependence of the exponential slope parameter

$$\begin{aligned} b_{{\text {el}}}({{W_{\gamma p}}}) = b_{{\text {el}}}\left( W_0\right) + 4\alpha _{1} \log \left( \dfrac{{{W_{\gamma p}}}}{W_0} \right) . \end{aligned}$$

(44)

The function is plotted in Fig. 18 using the parameters extracted for the elastic cross section in the two-dimensional fit (cf. Table 14, $m_Y{=}m_p$). For comparison, $b({{W_{\gamma p}}})$ is measured in every ${W_{\gamma p}}$ bin by fitting the parametrisation Eq. (41) with free fit parameters $b_t$ to the t dependencies in all ${W_{\gamma p}}$ bins. Deviations from the exponential form are accounted for by including a single parameter a common to all four ${W_{\gamma p}}$ bins. The result is presented in Table 15 and also shown in Fig. 18. Further data from previous HERA [9, 15, 17] and fixed-target [20,21,22,23,24,25] measurements are included in the figure, as well. The present slope values are somewhat lower than those from previous HERA measurements but are much more precise. The present data alone clearly indicate that there is shrinkage of the elastic peak with increasing energy.

Fig. 17

Elastic (${{m_Y}} {=}m_p$) (a) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) (b) differential ${\rho ^0}$ meson photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}$ in bins of ${W_{\gamma p}}$ and as functions of t. Individual distributions are scaled for visual separation, as indicated. The depicted t bin centres are evaluated as described in the text. The quoted average ${W_{\gamma p}}$ correspond to the geometrical bin centres. The cross sections are parametrised and fitted as described in the text, and the fitted curves are also shown

4.5.3 Effective leading Regge trajectory

For visualisation of the Regge trajectory parameters, $\alpha (t)$ is measured separately in each t bin by fitting a simple power law $\propto {{W_{\gamma p}}} ^{4(\alpha _t - 1)}$ with free fit parameters $\alpha _t$ to the ${W_{\gamma p}}$ distributions in all t bins. The resulting parameters $\alpha _t$ are presented in Table 16 and displayed as a function of the t bin centres $t_{bc}$¹⁰ in Fig. 19. The data are compared to the parametrisations $\alpha (t)$ obtained in the two-dimensional fit and to other curves as discussed below. A direct fit of a parametrisation $\alpha (t)$ to the so extracted $\alpha _t$ is ambiguous because of the definition of the bin centres $t_{bc}$.

For the elastic cross section, the measured trajectory is linear at small |t|. The intercept and slope parameters are measured at ${\alpha _{0}=1.0654 \pm 0.0044~({\text {stat.}})\ {}^{+0.0088}_{-0.0050}~({\text {syst.}})}$ and ${\alpha _{1} = 0.233 \pm 0.064~({\text {stat.}})\ {}^{+0.020 }_{-0.038 }~({\text {syst.}}) ~{{\text {GeV}^{-2}}}}$, respectively. Potential non-linearities start occurring for $t\lesssim -0.2~{{\text {GeV}^2}}$ and the trajectory is compatible with approaching a constant asymptotic value of approximately $0.98 \pm 0.04~({\text {tot.}})$ for $t \rightarrow -\infty$. However, a linear trajectory over the full considered t range is also able to describe the elastic cross section. The resulting intercept and slope parameters are ${\alpha _{0,\mathrm {lin}} = 1.0624 \pm 0.0033~({\text {stat.}})~{}^{+0.0083}_{-0.0052}~({\text {syst.}})}$ and $\alpha _{1,\mathrm {lin}} = 0.175 \pm 0.026~({\text {stat.}})~{}^{+0.021}_{-0.027}~({\text {syst.}})~{{\text {GeV}^{-2}}}$, respectively. For comparison, the linear trajectory is also included in Fig. 19. In contrast, the proton-dissociative cross section is not compatible with a linear trajectory $\alpha (t)$. The fitted parametrisation falls off steeply at low |t| but is constant with a value of approximately ${0.93 \pm 0.03~({\text {tot.}})}$ for $t \lesssim -0.2~{{\text {GeV}^2}}$. However, significant shaping effects are expected from the phase space restrictions, as discussed earlier. No attempt is made here to relate these fit parameters with the underlying amplitude.

Fig. 18

Fit parameters $b_W$ as a function of ${{W_{\gamma p}}}$ for the elastic (${{m_Y}} {=}m_p$) differential ${\rho ^0}$ meson photoproduction cross section ${{{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}} (t;{{W_{\gamma p}}})$. The parameters are obtained from fits of modified exponential functions to the t distributions in all ${{W_{\gamma p}}}$ bins, as described in the text. Corresponding measurements by HERA [9, 15, 17] and fixed-target [20,21,22,23,24,25] experiments are also shown. The plotted curve depicts the dependence $b({{W_{\gamma p}}})$ expected from the leading Regge trajectory parameters that are extracted from the present data as described in the text

In the high energy limit, the elastic cross section is expected to be governed by the soft pomeron trajectory. The canonical pomeron trajectory has been determined by Donnachie and Landshoff from pp and $p{\bar{p}}$ scattering data as $\alpha _\mathrm {DL}(t) = 1.0808 + 0.25\,t/{{\text {GeV}^2}}$ [91, 92]. The trajectory parameters have been investigated in various vector meson photo- and electroproduction measurements. A recent analysis of HERA data with a two tensor pomeron model furthermore has lead to a precise measurement of the soft pomeron intercept using inclusive DIS cross sections at low Bjorken-x and total photoproduction cross sections [93]. In ${\rho ^0}$ meson photoproduction, the trajectory has previously been directly extracted [13] in an analysis of the energy dependence of the differential cross section ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} p)/{\text {d}}t}$ in the range $8.2< {{W_{\gamma p}}} < 94~{{\text {GeV}}}$ as measured by various experiments [9, 13, 15, 16, 25]. The present analysis has the advantage that it measures the leading trajectory from a single dataset. In Fig. 20, the measured intercept and slope at $t=0$ are compared to the canonical pomeron trajectory parameters and those measured by the cited works [13, 93]. The measured intercept seems to be comparatively low. The analysis of the one-dimensional energy dependence (Sect. 4.3) suggests the presence of a subleading reggeon contribution that indeed may have lowered the measured effective trajectory by about 0.01 units. For the measured slope, good agreement is observed with the canonical DL value. However, there is some tension with previous HERA measurements, such as the cited ZEUS measurement. A potential explanation could arise from possible deviations from the linear form of the trajectory, which are taken into account in the present analysis. For proton-dissociative ${\rho ^0}$ meson photoproduction, a constant trajectory has been previously measured at HERA for higher |t| than are considered here [11].

Table 14 Fit parameters of the Regge fit of the t and ${W_{\gamma p}}$ dependencies of the ${\rho ^0}$ meson photoproduction cross sections in the range $20< {{W_{\gamma p}}} < 80~{{\text {GeV}}}$ and $|t|<1.5~{{\text {GeV}^2}}$. The nominal fit values and statistical and systematic uncertainties are given. A full uncertainty breakdown and statistical correlations are provided [77]. The corresponding fit is shown in Fig. 17

Table 15 Fit parameters $b_W$ for the fit of t dependencies of the elastic differential ${\rho ^0}$ photoproduction cross sections ${{{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} p)/{\text {d}}t}}$ in bins of ${{W_{\gamma p}}}$ (cf. Table 12). The statistical and full systematic uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 18

Table 16 Fit parameters $\alpha _t$ for the fit of simple power-law functions to the energy dependencies of the elastic and proton-dissociative differential ${\rho ^0}$ cross sections ${{{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}}$ in bins of t (cf. Tables 12 and 13). The t bin centres $t_{bc}$ are calculated as described in the text. The statistical and full systematic uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 19

5 Summary

Elastic and proton-dissociative ${\pi ^+\pi ^-}$ and ${\rho ^0}$ meson photoproduction cross sections are measured as a function of the invariant ${\pi ^+\pi ^-}$ mass ${m_{\pi \pi }}$, the scattering energy ${W_{\gamma p}}$, and the squared momentum transfer at the proton vertex t. The measurement covers a phase space of $0.5< {{m_{\pi \pi }}} < 2.2~{{\text {GeV}}}$, $20< {{W_{\gamma p}}} < 80~{{\text {GeV}}}$, and $|t|<1.5~{{\text {GeV}^2}}$. The cross sections are obtained by unfolding up to three-dimensional ${\pi ^+\pi ^-}$ distributions. In the procedure, the elastic and proton-dissociative components are extracted simultaneously. The results are more precise than previous measurements, in particular the measurement of the proton-dissociative cross sections.

Fig. 19

Fit parameters $\alpha _t$ as functions of t for the elastic (${{m_Y}} {=}m_p$) (a) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) (b) differential ${\rho ^0}$ meson photoproduction cross sections ${{{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} Y)/{\text {d}}t}} (t;{{W_{\gamma p}}})$. The parameters are obtained from fits of a power law to the energy dependencies of the cross sections in all t bins, as described in the text. The trajectories extracted from a Regge model fit to the ${W_{\gamma p}}$ and t dependencies are shown as solid curved lines (non-linear ansatz) and as a dashed line (linear ansatz). In panel a, the Donnachie–Landshoff trajectory is also shown

Fig. 20

Comparison of the soft pomeron intercept (a) and slope (b) according to Donnachie and Landshoff (DL) [91, 92] with measurements of the leading trajectory in ${\rho ^0}$ meson photoproduction in the present paper and from an analysis of previous data [13], as well as with a measurement of the intercept from inclusive DIS and photoproduction data [93]. The shaded bands show the total statistical and systematic uncertainties of the respective measurements. For the present data points, the statistical uncertainties alone are indicated by the error bars

The ${\pi ^+\pi ^-}$ mass spectra are analysed with a model in which the skewing of the ${\rho ^0}$ meson resonance peak is attributed to interference with non-resonant ${\pi ^+\pi ^-}$ production, as originally proposed by Söding in 1966. A fit of the model to the data yields $m_\rho = 770.8 \pm 1.3~({\text {stat.}})\ {}^{+2.3}_{-2.4}~({\text {syst.}})\ \,\, {{\text {MeV}}}$ and $\Gamma _\rho = 151.3 \pm 2.2~({\text {stat.}})\ {}^{+1.6}_{-2.8} ({\text {syst.}})\, {{\text {MeV}}}$ for the mass and width of the ${\rho ^0}$ meson, respectively. For the first time at HERA, the sensitivity of the data is sufficient to constrain the $\omega$ meson contribution to ${\pi ^+\pi ^-}$ photoproduction and measure the $\omega$ meson mass at $m_\omega = 777.9 \pm 2.2~({\text {stat.}})\ {}^{+4.3}_{-2.2}~({\text {syst.}}) ~{{\text {MeV}}}$.

The fit is used to extract the ${\rho ^0}$ meson contributions to the elastic and proton-dissociative ${\pi ^+\pi ^-}$ photoproduction cross sections. One- and two-dimensional ${\rho ^0}$ meson photoproduction cross sections as functions of ${W_{\gamma p}}$ and t are presented and subsequently interpreted with phenomenological models in the context of Regge theory. Precise parameters describing the t and ${W_{\gamma p}}$ dependencies are measured. The slope parameters describing the exponential drop of the cross sections with t are measured at an average energy of $\langle {{W_{\gamma p}}} \rangle = 43~{{\text {GeV}}}$ as ${b_{{\text {el}}} = 9.61\pm 0.15~({\text {stat.}})\ {}^{+0.20}_{-0.15}~({\text {syst.}})~{{\text {GeV}^{-2}}}}$ and $b_{{\text {pd}}} = 4.81\pm 0.24~({\text {stat.}})\ {}^{+0.39}_{-0.37}~({\text {syst.}})~{{\text {GeV}^{-2}}}$ for the elastic and proton-dissociative components, respectively. From the analysis of the elastic cross section ${{\text {d}}\sigma (\gamma p \rightarrow {{\rho ^0}} p)/{\text {d}}t}$ as a function of ${W_{\gamma p}}$ and t the effective leading Regge trajectory is extracted. Allowing for deviations from the linear form at large |t|, an intercept of $\alpha (t{=}0) = 1.0654 \pm 0.0044~({\text {stat.}})\ {}^{+0.0088}_{-0.0050}~({\text {syst.}})$ and a slope of $\alpha ^\prime (t{=}0) = 0.233 \pm 0.064~({\text {stat.}})\ {}^{+0.020 }_{-0.038 }~({\text {syst.}}) ~{{\text {GeV}^{-2}}}$ are measured. Since the probed energies are low, the intercept measurement may be obscured somewhat by sub-leading reggeon contributions that cannot be constrained by the present data alone. There are some indications that the trajectory deviates from a linear behaviour for $t < -0.2~{{\text {GeV}^2}}$. Within uncertainties, the data are compatible with the trajectory becoming equal to unity for large |t|.

Appendix A: \({\pi ^+\pi ^-}\) photoproduction cross section tables

Unfolded ${\pi ^+\pi ^-}$ photoproduction cross sections are presented in tabular form. A full breakdown of systematic uncertainties and all statistical correlations is available [77].

• The differential cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ in bins of ${m_{\pi \pi }}$ and for elastic and proton-dissociative production are given in Table 17.

• The differential cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ in bins of ${W_{\gamma p}}$ and ${m_{\pi \pi }}$ are given in Tables 18 and 19 for elastic and proton-dissociative production, respectively.

• The double-differential cross sections ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of t and ${m_{\pi \pi }}$ are given in Tables 20 and 21 for elastic and proton-dissociative production, respectively.

• The double-differential cross sections ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of t, ${W_{\gamma p}}$, and ${m_{\pi \pi }}$ are given in Tables 22 and 23 for elastic and proton-dissociative production, respectively.

Table 17 Unfolded elastic (${{m_Y}} {=}m_p$) and proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) differential ${\pi ^+\pi ^-}$ photoproduction cross sections ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ in bins of ${{m_{\pi \pi }}}$. The cross sections are measured in the fiducial phasespace defined in Table 3 and calculated according to Eq. (28). The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 6

Table 18 Unfolded elastic (${{m_Y}} {=}m_p$) differential ${\pi ^+\pi ^-}$ photoproduction cross section ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ in bins of ${{m_{\pi \pi }}}$ and ${W_{\gamma p}}$. The cross section is measured in the fiducial phasespace defined in Table 3 and calculated according to Eq. (28). The effective photon flux factors ${\Phi _{\gamma /e}}$ are given for each ${W_{\gamma p}}$ bin. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 8

Table 19 Unfolded proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) differential ${\pi ^+\pi ^-}$ photoproduction cross section ${{\text {d}}\sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}}}$ in bins of ${{m_{\pi \pi }}}$ and ${W_{\gamma p}}$. The cross section is measured in the fiducial phasespace defined in Table 3 and calculated according to Eq. (28). The effective photon flux factors ${\Phi _{\gamma /e}}$ are given for each ${W_{\gamma p}}$ bin. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 9

Table 20 Unfolded elastic (${{m_Y}} {=}m_p$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross section ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of ${{m_{\pi \pi }}}$ and t. The cross section is measured in the fiducial phasespace defined in Table 3 and calculated according to Eq. (28). The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 13

Table 21 Unfolded proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross section ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of ${{m_{\pi \pi }}}$ and t. The cross section is measured in the fiducial phasespace defined in Table 3 and calculated according to Eq. (28). The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 13

Table 22 Unfolded elastic (${{m_Y}} {=}m_p$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross section ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of ${{m_{\pi \pi }}}$, ${W_{\gamma p}}$, and t. The cross section is measured in the fiducial phasespace defined in Table 3 and calculated according to Eq. (28). The effective photon flux factors ${\Phi _{\gamma /e}}$ for each ${W_{\gamma p}}$ bin are given. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown in Fig. 15

Table 23 Unfolded proton-dissociative ($m_p{<}{{m_Y}} {<}10~{{\text {GeV}}}$) double-differential ${\pi ^+\pi ^-}$ photoproduction cross section ${{\text {d}}^2 \sigma (\gamma p \rightarrow {{\pi ^+\pi ^-}} Y)/{\text {d}}{{m_{\pi \pi }}} {\text {d}}t}$ in bins of ${{m_{\pi \pi }}}$, ${W_{\gamma p}}$, and t. The cross section is measured in the fiducial phasespace defined in Table 3 and calculated according to Eq. (28). The effective photon flux factors ${\Phi _{\gamma /e}}$ for each ${W_{\gamma p}}$ bin are given. The statistical and full systematic uncertainties including normalisation uncertainties are given by $\Delta _{{\text {stat.}}}$ and $\Delta _{{\text {syst.}}}$, respectively. A full uncertainty breakdown and statistical correlations are provided [77]. The data are shown Fig. 16