1 Introduction

Due to their superior load-carrying capabilities, the mechanical analysis of shells is of great interest in engineering. A large literature body exists on the formulation of shell models. We refer to [8, 34, 41] and references therein for an overview. In the present paper, we consider the classical Koiter model [14, 32], which is one of the most popular models for thin shells. The Koiter shell model has been justified by asymptotic analysis in [15], in the sense of being a reasonable approximation to the full 3D problem of a thin shell-like body. Existence and uniqueness results can be found in [9, 14].

Classically, for theoretical treatment it is assumed that the shell mid-surface is represented by a global parametrization. However, for the numerical treatment typically the mid-surface is approximated by, possibly curved, finite elements, i.e. represented by a collection of local parametrizations. In contrast to these representations, we consider the case where the mid-surface is represented implicitly as the zero-level set of a scalar function \(\phi ({{\mathbf {x}}})\), see Fig. 1 for the illustration of some examples. We refer to the review article [21] for an overview of finite element methods for problems on such surfaces. In the classical surface finite element method the discretization of the unknown field relies on the higher order or exact meshing (local parametrization) of the surface [19, 26]. In contrast to this, in the proposed method the discretization of the displacement field does not rely on parametrizations. Therefore, we provide a throughout derivation of the governing equations in strong form based on first principles of continuum mechanics independent of a parametrization. This allows a natural implementation of the method and also the construction of manufactured solutions for code verification on arbitrary geometries. Equivalent derivations relying on a parametrization can be found in e.g. [3] and [45]. We remark that membrane and equivalent thin shell formulations without relying on a parametrization with a mathematical focus can be found in [18, 28]. For a treatment from an engineering perspective we refer to [39, 48]. However, in [39] only the weak formulation is reformulated in a parametrization free way and no strong form is given. Although in [48] both the strong and the weak forms are provided, no derivations/ proofs are presented. Furthermore, in the author’s opinion, the notation used in the present paper is more direct and thus traceable.

Fig. 1
figure 1

Examples of implicitly defined surfaces. The surfaces are defined by the level-set functions a \(\phi =x^2+y^2+\) \( z^2-r^2, \mathbf{b} \phi = (x^2+y^2+z^2+R^2-r^2)^2- 4R^2(x^2+y^2)\), c \(\phi = x^2+y^2 - r^2\), d \(\phi = \sin x\cos y+\sin y\cos z+\sin z\cos x\)

Full size image

One of the main difficulties in developing finite element methods for thin shells is the construction of \(C^1\)-continuous approximation spaces. For general unstructured meshes it is not possible to ensure \(C^1\)-continuity with only local polynomial shape functions and the nodal degrees of freedom consist of displacements and slopes only [49]. However, different non-standard triangular elements developed for thin plate bending are the Argyris element [2, 20], the Bell element [5] or the Clough-Tocher macrotriangle [17]. A further possibility to construct \(C^1\)-continuous approximation spaces on general space triangulation relies on sophisticated techniques from subdivision surfaces [16]. However, on a structured quadrilateral mesh the Bogner-Fox-Schmit element [10] is a simple conforming element. The constraint of a structured quadrilateral mesh can be partially overcome by introducing a smooth mapping of the geometry [24]. This idea can be realized in an isoparametric way by the use of splines for the geometry mapping and for the discretization of the displacement field [31]. The general difficulty of constructing \(C^1\)-continuous approximation spaces led to approaches where the \(C^1\)-continuity requirement is circumvented. Among them we mention discrete Kirchhoff elements [1, 4] where the Kirchhoff constraint is enforced only at discrete points, the use of shear-deformable (Reissner-Mindlin) shell theory, were only \(C^0\)-continuity approximation spaces are required, mixed methods [35, 43], continuous/discontinuous Galerkin methods [23, 29] and others.

In the present paper, we combine ideas from unfitted finite element methods and the Bogner-Fox-Schmit element. Following the idea of the TraceFEM [36, 37] (see also CutFEM [11, 13]) the approximation of the displacement field is constructed by restricting shape functions defined on a background mesh on the shell surface. In particular, we follow the idea of the Finite-Cell-Method [40, 47] and use a structured grid where the simple tensor product of three uni-variant cubic spline shape functions leads to a \(C^1\)-continuous approximation in 3D (like the Bogner-Fox-Schmit element in 2D). Therefore, the shape functions for approximation of the displacement field on the shell mid-surface are \(C^1\)-continuous. We remark that cut Bogner-Fox-Schmit elements for thin plates were proposed and analyzed in [12]. Therefore, the proposed method can be seen as an extension of the work [12] from plates to curved shells.

One challenge in unfitted finite element methods is the efficient integration on the problem domain [38]. During the preparation of the present paper it turned out that due to a growing number of constraints for finer meshes the strategy developed in [25] is not applicable in the present situation. Therefore, we have implemented the quadrature strategy developed in [46].

The implementation of the proposed method is verified by a convergence analysis where the error is computed with an exact manufactured solution. Furthermore, the capabilities of the method are shown in two standard and two non-standard benchmark tests.

2 Notation and geometric preliminaries

Fig. 2
figure 2

Illustration and notation of the geometric setting

Full size image

The underlying assumption in shell analysis is that the computational domain has a small extension with respect to one coordinate. Thus, we assume that it is located around a two-dimensional mid-surface \(\varOmega \) which is embedded in \({\mathbb {R}}^3\). In the present paper we assume that the mid-surface is defined implicitly as the zero-level set of a function \(\phi : {\mathbb {R}}^3 \rightarrow {\mathbb {R}}\) inside a cuboid \(B\subset {\mathbb {R}}^3\),

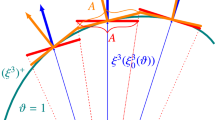
$$\begin{aligned} \varOmega = \{{{\mathbf {x}}}\in B|\,\phi ({{\mathbf {x}}}) = 0 \}. \end{aligned}$$
(1)

The boundary of \(\varOmega \) is denoted \(\varGamma \), the surface normal vector is denoted by \(\pmb {\nu }\), and the normal vector tangential to the surface on a boundary point is denoted by \(\pmb \mu \), see Fig. 2. We assume that \(\varOmega \) is regular (smooth) such that

$$\begin{aligned} \nabla \phi ({{\mathbf {x}}}) \ne {\mathbf {0}}, \end{aligned}$$
(2)

holds in the neighborhood of \(\varOmega \), where \(\nabla \) denotes the usual gradient of some scalar-valued function \(f:{\mathbb {R}}^3\rightarrow {\mathbb {R}}\),

$$\begin{aligned} \nabla f({{\mathbf {x}}}) = f_{,i} \,{\mathbf {e}}^i := \frac{\partial f({\mathbf {x}})}{\partial x_i} {\mathbf {e}}^i \end{aligned}$$
(3)

with the Cartesian coordinates \({{\mathbf {x}}}= (x_1,x_2,x_3)\) and the standard Cartesian orthonormal basis \(\{{\mathbf {e}}^1,\,{\mathbf {e}}^2,\,{\mathbf {e}}^3\}\). Here, and in the following, the Einstein summation convention applies. Whenever an index occurs once in an upper position and in a lower position we sum over this index, where Latin indices \(i,j,\dots \) take the values 1, 2, 3 whereas Greek indices \(\alpha , \beta ,\dots \) take the values 1, 2. Let \({\mathcal {T}}\) be some tensor space of the form \({\mathbb {R}}^3\otimes \dots \otimes {\mathbb {R}}^3\). In the following we also use the generalization of the gradient for scalar-valued functions (3) to tensor-valued functions \({{\mathbf {T}}}: {\mathbb {R}}^3 \rightarrow {\mathcal {T}}\),

$$\begin{aligned} \nabla {{\mathbf {T}}}({{\mathbf {x}}}) = {{\mathbf {T}}}_{,i} \otimes {\mathbf {e}}^i. \end{aligned}$$
(4)

2.1 Differential geometry of implicitly defined surfaces

Given a implicit representation (1) of the surface \(\varOmega \), we can compute the unit normal vector to the surface by

$$\begin{aligned} \pmb {\nu }({{\mathbf {x}}}) = \frac{\nabla \phi ({{\mathbf {x}}})}{||\nabla \phi ({{\mathbf {x}}})||}, \end{aligned}$$
(5)

and are able to define the tangential projector,

$$\begin{aligned} {{\mathbf {P}}}= {\mathbf {I}} - \pmb {\nu }\otimes \pmb {\nu }. \end{aligned}$$
(6)

Furthermore, the extended Weingarten map is given by

$$\begin{aligned} {{{\mathbf {H}}}}= - \nabla \pmb {\nu }\cdot {{\mathbf {P}}}= -\frac{{\mathbf {P}} \cdot \nabla \nabla \phi \cdot {\mathbf {P}}}{||\nabla \phi ||}, \end{aligned}$$
(7)

and the mean curvature H is defined as

$$\begin{aligned} H = \text {tr}({{{\mathbf {H}}}}) = {{{\mathbf {H}}}}: {{\mathbf {P}}}. \end{aligned}$$
(8)

2.2 Differential geometry of parametrized surfaces

We briefly review the differential geometry of parametrized surfaces. For details we refer to e.g. [14]. Although the mid-surface \(\varOmega \) is assumed to be given implicitly, at least a local parametric representation is guaranteed to exist by the implicit function theorem. This justifies to consider parametrizations \(\hat{{\mathfrak {g}}}:\;U\subset {\mathbb {R}}^2 \rightarrow \varOmega \) with the parameter domain \(U\) for theoretical considerations (see [21, Lemma 2.2]). Given the parametrization \(\hat{{\mathfrak {g}}}(\theta ^1,\theta ^2)\), we can define the two covariant base vectors \(\hat{{\mathbf {g}}}_\alpha := \frac{\partial \hat{{\mathfrak {g}}} }{\partial \theta ^\alpha } \), which span the tangent plane to \(\varOmega \). With the base vectors we can define the unit normal vector

$$\begin{aligned} \hat{\pmb {\nu }}(\theta ^1,\theta ^2) = \frac{\hat{{\mathbf {g}}}_1(\theta ^1,\theta ^2) \times \hat{{\mathbf {g}}}_2(\theta ^1,\theta ^2)}{||\hat{{\mathbf {g}}}_1(\theta ^1,\theta ^2) \times \hat{{\mathbf {g}}}_2(\theta ^1,\theta ^2)||}, \end{aligned}$$
(9)

and the covariant coefficients of the metric \(\hat{ G}_{\alpha \beta } = \hat{{\mathbf {g}}}_\alpha \, \cdot \, \hat{{\mathbf {g}}}_\beta \). The contravariant coefficients of the metric are given by \([\hat{ G}^{\alpha \beta }]=[\hat{ G}_{\alpha \beta }]^{-1}\), where \([\hat{ G}_{\alpha \beta }]\) is the coefficient matrix. The contravariant base vectors can then be computed by \({\hat{{\mathbf {g}}}}^\alpha = \hat{ G}^{\alpha \beta } \hat{{\mathbf {g}}}_\beta \). The covariant coefficients of the Weingarten map \({\hat{{\mathbf {H}}}}= {\hat{h}}_{\alpha \beta } \, \hat{{\mathbf {g}}}^\alpha \otimes \hat{{\mathbf {g}}}^\beta \) are given by

$$\begin{aligned} {\hat{h}}_{\alpha \beta } = - \hat{{\mathbf {g}}}_{\alpha } \cdot \hat{\pmb {\nu }}_{,\beta }, \end{aligned}$$
(10)

and obey the symmetry relation \({\hat{h}}_{\alpha \beta } = {\hat{h}}_{\beta \alpha }\). The mean curvature \({\hat{H}}\) is given by

$$\begin{aligned} {\hat{H}} = {\hat{h}}_{\alpha }^{\alpha } = {\hat{h}}_{\alpha \beta } \hat{ G}^{\beta \alpha }. \end{aligned}$$
(11)

Furthermore, the derivatives of the base vectors are given by

$$\begin{aligned} \begin{aligned} \hat{{\mathbf {g}}}_{\alpha ,\beta } = \varGamma _{\alpha \beta }^\gamma \hat{{\mathbf {g}}}_{\gamma } + {\hat{h}}_{\alpha \beta } \hat{\pmb {\nu }}, \\ \hat{{\mathbf {g}}}_{,\beta }^{\alpha } = -\varGamma _{\beta \gamma }^\alpha \hat{{\mathbf {g}}}^{\gamma } + {\hat{h}}^{\alpha }_{\beta } \hat{\pmb {\nu }}, \end{aligned} \end{aligned}$$
(12)

with the surface Christoffel symbols of the second kind defined by

$$\begin{aligned} {\hat{\varGamma }}_{\alpha \beta }^{\gamma } = \hat{{\mathbf {g}}}^\gamma \cdot \hat{{\mathbf {g}}}_{\alpha ,\beta }. \end{aligned}$$
(13)

Remark

In our notion a hat over a quantity refers to a dependency on the parametric coordinates \((\theta ^1,\theta ^2)\in U\), whereas no hat refers to a dependency on \({{\mathbf {x}}}\in {\mathbb {R}}^3\).

2.3 Relations between parameter space and embedding space

The field \({\hat{{\mathbf {u}}}}(\theta ^1,\theta ^2)\) defined on the parameter space is related to the field \({{\mathbf {u}}}({{\mathbf {x}}})\) defined on the embedding space \({\mathbb {R}}^3\) by

$$\begin{aligned} \begin{aligned} {\hat{{\mathbf {u}}}}(\theta ^1,\theta ^2)&= {{\mathbf {u}}}({{\mathbf {x}}})\circ \hat{{\mathfrak {g}}}(\theta ^1,\theta ^2) = {{\mathbf {u}}}(\hat{{\mathfrak {g}}}(\theta ^1,\theta ^2)) \end{aligned} \end{aligned}$$
(14)

By applying the chain rule we find that the first and second derivatives are related by

$$\begin{aligned} \begin{aligned} {\hat{{\mathbf {u}}}}_{,\theta }&= (\nabla {{\mathbf {u}}}\circ \hat{{\mathfrak {g}}}) \cdot \hat{{\mathbf {g}}}_\theta , \end{aligned} \end{aligned}$$
(15)

and

$$\begin{aligned} \begin{aligned} {\hat{{\mathbf {u}}}}_{,\theta \tau }&= (\nabla \nabla {{\mathbf {u}}}\circ \hat{{\mathfrak {g}}})\cdot \hat{{\mathbf {g}}}_\tau \cdot \hat{{\mathbf {g}}}_\theta + (\nabla {{\mathbf {u}}}\circ \hat{{\mathfrak {g}}}) \cdot \hat{{\mathbf {g}}}_{\theta ,\tau } \\&= (\nabla \nabla {{\mathbf {u}}}\circ \hat{{\mathfrak {g}}}): (\hat{{\mathbf {g}}}_\tau \otimes \hat{{\mathbf {g}}}_\theta ) + (\nabla {{\mathbf {u}}}\circ \hat{{\mathfrak {g}}}) \cdot (\varGamma _{\theta \tau }^\alpha \, \hat{{\mathbf {g}}}_\alpha + h_{\theta \tau } \,\pmb {\nu }). \end{aligned} \end{aligned}$$
(16)

Furthermore, we have the following relations summarized in the following lemma.

Lemma 1

The metric tensor \(\hat{{\mathbf {G}}}= \hat{ G}_{\alpha \beta } \,\hat{{\mathbf {g}}}^\alpha \otimes \hat{{\mathbf {g}}}^\beta = \hat{{\mathbf {g}}}_\alpha \otimes \hat{{\mathbf {g}}}^\alpha \) and the projector \({\mathbf {P}}\) are related by

$$\begin{aligned} \hat{{\mathbf {G}}}= {\mathbf {P}} \circ \hat{{\mathfrak {g}}}. \end{aligned}$$
(17)

For the Weingarten map we have the relation

$$\begin{aligned} {\hat{{\mathbf {H}}}}= {{\mathbf {H}}}\circ \hat{{\mathfrak {g}}}. \end{aligned}$$
(18)

The proof can be found in “Appendix A”.

2.4 Surface gradient

The surface gradient of a tensor-valued function represented with respect to parametric coordinates by the map \({\hat{\mathbf {f}}}:U\rightarrow {\mathcal {T}}\) is given by

$$\begin{aligned} \nabla _\varOmega \hat{{\mathbf {f}}} = \hat{{\mathbf {f}}}_{,\alpha } \otimes \hat{{\mathbf {g}}}^\alpha . \end{aligned}$$
(19)

Lemma 2

For the representation \({{\mathbf {f}}}:{\mathbb {R}}^3\rightarrow {\mathcal {T}}\) the surface gradient is given by

$$\begin{aligned} \nabla _\varOmega {{\mathbf {f}}} = \nabla {\mathbf {f}} \cdot {{\mathbf {P}}}. \end{aligned}$$
(20)

Proof

Using the relation between the projector and the metric tensor and (15) we have

$$\begin{aligned} \nabla _\varOmega {{\mathbf {f}}} \circ \hat{{\mathfrak {g}}}= (\nabla {\mathbf {f}} \circ \hat{{\mathfrak {g}}}) \cdot (\hat{{\mathbf {g}}}_\alpha \otimes \hat{{\mathbf {g}}}^\alpha ) = \hat{{\mathbf {f}}}_{,\alpha } \otimes \hat{{\mathbf {g}}}^\alpha . \end{aligned}$$
(21)

\(\square \)

We remark that many definitions of the surface gradient found in literature apply only to a scalar field [21, 44]. If the surface gradient of a vector field is needed, a separate definition is given [28, 30, 48]. In contrast to this, (19) and (20) apply to tensors of arbitrary order.

2.5 Surface divergence

We define the surface divergence as the adjoint operator to the surface gradient [44]. Therefore, on an Riemannian manifold we have in local coordinates

$$\begin{aligned} \text {div} \hat{{\mathbf {T}}}= \frac{1}{\sqrt{\det \hat{{\mathbf {G}}}}} \left( \hat{{\mathbf {T}}}\cdot \hat{{\mathbf {g}}}^\alpha \sqrt{\det \hat{{\mathbf {G}}}}\right) _{,\alpha }, \end{aligned}$$
(22)

where we use the notation \(\det \hat{{\mathbf {G}}}= \det ([\hat{ G}_{\alpha \beta }])\). The next lemma gives the simpler representation for the surface divergence in case of a surface embedded in \({\mathbb {R}}^3\).

Lemma 3

On a surface \(\varOmega \subset {\mathbb {R}}^3\) parametrized by \(\hat{{\mathfrak {g}}}:U\rightarrow \varOmega \) the surface divergence of a tensor-valued function represented by \(\hat{{\mathbf {T}}}:U\rightarrow {\mathcal {T}}\) is given by

$$\begin{aligned} \text{ div }\hat{{\mathbf {T}}}= \hat{{\mathbf {T}}}_{,\alpha }\cdot \hat{{\mathbf {g}}}^\alpha + H \, \hat{{\mathbf {T}}}\cdot \hat{\pmb {\nu }}. \end{aligned}$$
(23)

Furthermore, for the representation \({{\mathbf {T}}}:{\mathbb {R}}^3\rightarrow {\mathcal {T}}\) we have

$$\begin{aligned} \text{ div } {\mathbf {T}} = \nabla {\mathbf {T}}:{{\mathbf {P}}}+ H\,{\mathbf {T}} \cdot \pmb {\nu }. \end{aligned}$$
(24)

The proof can be found in “Appendix A”.

In the following lemma we collect product rules for the divergence operator [28].

Lemma 4

Let \({\mathbf {v}}\times {\mathbf {T}}\) be the cross product of a vector \({\mathbf {v}} = v_i {\mathbf {e}}^i\) and a second order tensor \({\mathbf {T}} = T_{lk} {\mathbf {e}}^l \otimes {\mathbf {e}}^k\) defined by

$$\begin{aligned} {\mathbf {v}}\times {\mathbf {T}} = v_iT_{lk} ({\mathbf {e}}^i\times {\mathbf {e}}^l) \otimes {\mathbf {e}}^k, \end{aligned}$$
(25)

and \({\mathbf {V}} \cdot \!\!\times {\mathbf {T}}\) the scalar-cross product of two second order tensors \({\mathbf {V}} = V_{ij} {\mathbf {e}}^i \otimes {\mathbf {e}}^j\) and \({\mathbf {T}} = T_{lk} {\mathbf {e}}^l \otimes {\mathbf {e}}^k\) defined by

$$\begin{aligned} {\mathbf {V}}\cdot \!\!\times {\mathbf {T}} = V_{ij}T_{lk} ({\mathbf {e}}^j\cdot {\mathbf {e}}^l)({\mathbf {e}}^i\times {\mathbf {e}}^k). \end{aligned}$$
(26)

Then, the following product rules hold

$$\begin{aligned} \text{ div }({\mathbf {v}}\times {\mathbf {T}})&= {\mathbf {v}}\times \text{ div }({\mathbf {T}}) + \nabla _\varOmega {\mathbf {v}}\cdot \!\!\times {\mathbf {T}}^\top , \end{aligned}$$
(27)
$$\begin{aligned} \text{ div }({\mathbf {v}}\cdot {\mathbf {T}})&= {\mathbf {v}}\cdot \text{ div }({\mathbf {T}}) + \nabla _\varOmega {\mathbf {v}}:{\mathbf {T}}^\top . \end{aligned}$$
(28)

The proof can be found in “Appendix A”.

2.6 Integral identities

For further use we introduce the surface divergence theorem for a tensor-valued function \({{\mathbf {T}}}\) [28]

$$\begin{aligned} \begin{aligned} \int _\varOmega \text {div} \,{{\mathbf {T}}}\;\mathrm {d} {{\mathbf {x}}}= \int _{\varGamma } {{\mathbf {T}}}\cdot \pmb \mu \;\mathrm {d} s_{{\mathbf {x}}}. \end{aligned} \end{aligned}$$
(29)

Using (28) and (29), the integration by parts formula for a vector \({\mathbf {v}}\) and a second order tensor \({{\mathbf {T}}}\) reads [28]

$$\begin{aligned} \begin{aligned} \int _\varOmega {\mathbf {v}}\cdot \text {div}{\mathbf {T}} \;\mathrm {d} {{\mathbf {x}}}= \int _{\varGamma } {\mathbf {v}} \cdot {\mathbf {T}} \cdot \pmb \mu \;\mathrm {d} s_x - \int _\varOmega \nabla _\varOmega {\mathbf {v}} : {\mathbf {T}}^\top \;\mathrm {d} {{\mathbf {x}}}. \end{aligned} \end{aligned}$$
(30)

3 The linear thin shell problem

In this section, we derive the governing equations of linear thin shells from first principles of continuum mechanics [3, 45]. Furthermore, we show the equivalence to the linear Koiter model formulated as a minimization problem.

3.1 Shell kinematics

The kinematics of the surface \(\varOmega \) is described by the change in metric tensor and the change in curvature tensor. In the present paper we focus on the linear theory and use the linearized change in metric tensor \({\hat{\pmb \gamma }}= {\hat{ \gamma }}_{\alpha \beta } \,\hat{{\mathbf {g}}}^\alpha \otimes \hat{{\mathbf {g}}}^\beta \) and the linearized change in curvature tensor \({\hat{\pmb \rho }}= {\hat{ \rho }}_{\alpha \beta } \,\hat{{\mathbf {g}}}^\alpha \otimes \hat{{\mathbf {g}}}^\beta \). The respective covariant components are given by [9, 14]

$$\begin{aligned} {\hat{ \gamma }}_{\alpha \beta }({\hat{{\mathbf {u}}}}) = \frac{1}{2} ({\hat{{\mathbf {u}}}}_{,\beta } \cdot \hat{{\mathbf {g}}}_\alpha + {\hat{{\mathbf {u}}}}_{,\alpha } \cdot \hat{{\mathbf {g}}}_\beta ), \end{aligned}$$
(31)

and

$$\begin{aligned} {\hat{ \rho }}_{\alpha \beta }({\hat{{\mathbf {u}}}}) = \hat{\pmb {\nu }}\cdot \left( {\hat{{\mathbf {u}}}}_{,\alpha \beta } - \varGamma _{\alpha \beta }^\sigma {\hat{{\mathbf {u}}}}_{,\sigma }\right) . \end{aligned}$$
(32)

The next lemma establishes the representations for \({{\pmb \gamma }}= {\hat{\pmb \gamma }}\circ \hat{{\mathfrak {g}}}^{-1}\) and \({{\pmb \rho }}= {\hat{\pmb \rho }}\circ \hat{{\mathfrak {g}}}^{-1}\).

Lemma 5

For the linearized change in metric tensor we have the representation [28]

$$\begin{aligned} {{\pmb \gamma }}({{\mathbf {u}}}) = \frac{1}{2} {{\mathbf {P}}}\cdot (\nabla {{\mathbf {u}}}+ (\nabla {{\mathbf {u}}})^\top ) \cdot {{\mathbf {P}}}, \end{aligned}$$
(33)

and for the linearized change in curvature tensor we have the representation

$$\begin{aligned} \pmb \rho ({{\mathbf {u}}}) ={{\mathbf {P}}}\cdot (\pmb {\nu }\cdot \nabla \nabla {\mathbf {u}})\cdot {{\mathbf {P}}}- ( \pmb {\nu }\cdot \nabla {{\mathbf {u}}}\cdot \pmb {\nu }) {{{\mathbf {H}}}}. \end{aligned}$$
(34)

The proof can be found in “Appendix A”.

3.2 Stress and moment tensors

We define the traction vector \({\mathbf {t}}(\pmb \mu )\) on a cut defined by the boundary normal \(\pmb \mu \) tangential to the surface. Due to Cauchy’s theorem, we have the representation

$$\begin{aligned} {\mathbf {t}}(\pmb \mu ) = \pmb \sigma \cdot \pmb \mu , \end{aligned}$$
(35)

with the stress tensor \(\pmb \sigma \). We decompose the stress tensor \(\pmb \sigma \) in a tangential and a normal part,

$$\begin{aligned} \pmb \sigma = {\mathbf {N}} + \pmb {\nu }\otimes {\mathbf {S}}, \end{aligned}$$
(36)

with the tangential stress tensor \({\mathbf {N}} = N^{\alpha \beta } {{\mathbf {g}}}_\alpha \otimes {{\mathbf {g}}}_\beta \) and the vector \({\mathbf {S}} = S^{\alpha } {{\mathbf {g}}}_\alpha \) related to transverse shear. Analogously, we have a moment vector \({\mathbf {m}}(\pmb \mu )\) on the cut defined by \(\pmb \mu \), which can be expressed as

$$\begin{aligned} {\mathbf {m}}(\pmb \mu ) = \pmb {\nu }\times ({\mathbf {M}} \cdot \pmb \mu ), \end{aligned}$$
(37)

with the tangential moment tensor \({\mathbf {M}}\).

3.3 Equilibrium of forces

The equilibrium of forces states that the sum of the resulting force of boundary traction and the resultant force from the surface loading vanishes,

$$\begin{aligned} \begin{aligned} \int _{\varGamma } {\mathbf {t}} \;\mathrm {d} s_{{\mathbf {x}}}+ \int _\varOmega {\mathbf {b}} \;\mathrm {d} {{\mathbf {x}}}= {\mathbf {0}}. \end{aligned} \end{aligned}$$
(38)

Applying the surface divergence theorem (29) results in

$$\begin{aligned} \begin{aligned} \int _{\varOmega } \text {div}\,\pmb \sigma + {\mathbf {b}}\;\mathrm {d} {{\mathbf {x}}}= {\mathbf {0}}. \end{aligned} \end{aligned}$$
(39)

Due to the fact that \(\varOmega \) is arbitrary, the local force equilibrium reads

$$\begin{aligned} \text {div}\,\pmb \sigma + {\mathbf {b}} = {\mathbf {0}}. \end{aligned}$$
(40)

3.4 Equilibrium of moments

The equilibrium of moments states that the sum of boundary moments, the moments of boundary tractions, and the moments due to surface loads vanishes,

$$\begin{aligned} \begin{aligned} \int _{\varGamma }{\mathbf {m}} + {\mathbf {x}} \times {\mathbf {t}} \;\mathrm {d} s_x + \int _{\varOmega }{\mathbf {x}} \times {\mathbf {b}} \;\mathrm {d} {{\mathbf {x}}}= {\mathbf {0}}. \end{aligned} \end{aligned}$$
(41)

The following lemma summarizes the consequences of the equilibrium of moments.

Lemma 6

For \({{\mathbf {T}}}= {T}_{ij} {\mathbf {e}}^i \otimes {\mathbf {e}}^j\) let \([{{\mathbf {T}}}]_{\times } = {T}_{ij}{\mathbf {e}}^i \times {\mathbf {e}}^j\). The equilibrium of moments is fulfilled if

$$\begin{aligned}{}[-{\mathbf {H}}\cdot {\mathbf {M}} + {\mathbf {N}}^\top ]_{\times } = {\mathbf {0}}, \end{aligned}$$
(42)

and

$$\begin{aligned} {\mathbf {S}} = {{\mathbf {P}}}\cdot \text{ div }({\mathbf {M}}). \end{aligned}$$
(43)

The proof can be found in “Appendix A”.

The statement of Lemma 6 using local coordinates implied by a parametrization can also be found in [3, 45].

3.5 Constitutive equations

In the present paper we assume linear constitutive equations of the form

$$\begin{aligned} {\mathbf {M}} = -\frac{t^3}{12}\,{\mathcal {E}} : \pmb \rho , \end{aligned}$$
(44)

and

$$\begin{aligned} {\mathbf {N}} = t\,{\mathcal {E}} : \pmb \gamma - {\mathbf {H}}\cdot {\mathbf {M}}. \end{aligned}$$
(45)

The fourth order elasticity tensor \({\mathcal {E}}\) is given by

$$\begin{aligned} \begin{aligned} {\mathcal {E}} = \lambda ({\mathbf {P}} \otimes {\mathbf {P}}) + 2 \mu {\mathcal {P}}^s,\qquad \text {with} \quad \lambda =\frac{4{\bar{\lambda }}\mu }{{\bar{\lambda }}+2\mu }, \end{aligned} \end{aligned}$$
(46)

where \({\bar{\lambda }}\) and \(\mu \) are the Lamé constants of the elastic material constituting the shell and \({\mathcal {P}}^s\) the symmetric part of the tangential fourth order identity tensor. The Lamé constants are related to the Young’s modulus E and Poisson’s ratio \(\nu \) by

$$\begin{aligned} \begin{aligned} {\bar{\lambda }} = \frac{E\nu }{(1+\nu )(1-2\nu )}, \qquad \mu = \frac{E}{2(1+\nu )}. \end{aligned} \end{aligned}$$
(47)

The constitutive equations can also be written as

$$\begin{aligned} \begin{aligned} {\mathbf {N}}&= \bar{{\mathbf {N}}} - {\mathbf {H}} \cdot {\mathbf {M}}, \\ {\mathbf {M}}&= -\frac{t^3}{12}(\lambda \, {{\mathbf {P}}}\,\text {tr}\,\pmb \rho + 2\mu \,\pmb \rho ), \\ \bar{{\mathbf {N}}}&= t(\lambda \, {{\mathbf {P}}}\,\text {tr}\,\pmb \gamma + 2\mu \,\pmb \gamma ). \end{aligned} \end{aligned}$$
(48)

We remark that with (45) the condition (42) is fulfilled identically.

3.6 Weak form of the governing equations

The weak form of the governing equations is given by

$$\begin{aligned} \begin{aligned} t\int _\varOmega&\pmb \gamma ({\mathbf {v}}):{\mathcal {E}} : \pmb \gamma ({\mathbf {u}}) \;\mathrm {d} {{\mathbf {x}}}+ \frac{t^3}{12} \int _\varOmega \pmb \rho ({\mathbf {v}}):{\mathcal {E}} : \pmb \rho ({\mathbf {u}}) \\&\;\mathrm {d} {{\mathbf {x}}}= \int _\varOmega {\mathbf {v}} \cdot {\mathbf {b}} \;\mathrm {d} {{\mathbf {x}}}\\&+ \int _{\varGamma _{N_i}} v_i \, N^N_i \;\mathrm {d} s_x - \int _{\varGamma _{N_t}} \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}) \cdot {\mathbf {t}} \; M^N_t \;\mathrm {d} s_x \\&- \int _{\varGamma _{N_\mu }} \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}) \cdot \pmb \mu \; M^N_\mu \;\mathrm {d} s_x, \end{aligned} \end{aligned}$$
(49)

where \({\mathbf {v}}\) are appropriate test functions, see “Appendix B”. The boundary conditions which can be prescribed are given by,

$$\begin{aligned} \begin{aligned} {\mathbf {u}} \cdot {\mathbf {e}}_i&= u^D_i \quad&\text {or} \quad&{\mathbf {e}}_i\cdot (\bar{{\mathbf {N}}} + \pmb {\nu }\otimes {\mathbf {S}}) \cdot \pmb \mu&= N^N_i, \\ \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {u}})\cdot {\mathbf {t}}&= \omega _{t} \quad&\text {or} \quad&{\mathbf {t}} \cdot {\mathbf {M}} \cdot \pmb \mu&= M^N_t, \\ \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {u}}) \cdot \pmb \mu&= \omega _{\mu } \quad&\text {or} \quad&\pmb \mu \cdot {\mathbf {M}} \cdot \pmb \mu&= M^N_\mu , \end{aligned} \end{aligned}$$
(50)

where \(u^D_i\) is a given displacement in the direction of \({\mathbf {e}}_i\), \(\omega _{t}\) and \(\omega _{\mu }\) are given rotations, \(N^N_i\) is a given force in the direction of \({\mathbf {e}}_i\), \(M^N_t\) and \(M^N_\mu \) are given moments. If \({\mathbf {u}}\) is prescribed on the boundary, the derivative along the boundary \(d_{\mathbf {t}} (\pmb {\nu }\cdot {\mathbf {u}} ) = \nabla _\varOmega (\pmb {\nu }\cdot {{\mathbf {u}}})\cdot {\mathbf {t}}\) is also prescribed [3]. Thus, in this case, only the normal derivative \(d_{\pmb \mu } (\pmb {\nu }\cdot {\mathbf {u}} ) = \nabla _\varOmega (\pmb {\nu }\cdot {{\mathbf {u}}})\cdot \pmb \mu \) can be independently prescribed by \(\omega _{\mu }\).

3.7 Equivalence to the Koiter model

In this section, the equivalence of the classical linear Koiter model [14, 32] and (49) is outlined. To this end, we define the energy functional

$$\begin{aligned} \begin{aligned} {\mathcal {E}}({\mathbf {v}}) = \frac{1}{2}&\left[ \int _{\varOmega } t \,\pmb \gamma ({\mathbf {v}}) :{\mathcal {E}}:\pmb \gamma ({\mathbf {v}})+ \frac{t^3}{12}\pmb \rho ({\mathbf {v}}):{\mathcal {E}}:\pmb \rho ({\mathbf {v}}) \;\mathrm {d} {{\mathbf {x}}}\right] \\&- \int _{\varOmega } {\mathbf {b}}\cdot {\mathbf {v}} \;\mathrm {d} {{\mathbf {x}}}\\&- \int _{\varGamma _{N_i}} v_i \, N^N_i \;\mathrm {d} s_x + \int _{\varGamma _{N_t}} \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}) \cdot {\mathbf {t}} \; M^N_t \;\mathrm {d} s_x \\&+ \int _{\varGamma _{N_\mu }} \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}) \cdot \pmb \mu \; M^N_\mu \;\mathrm {d} s_x. \end{aligned} \end{aligned}$$
(51)

Then, the linear Koiter shell model reads: Find \({\mathbf {u}}\in {\mathcal {V}}\) such that

$$\begin{aligned} \begin{aligned} {\mathcal {E}}({\mathbf {u}}) = \inf _{{\mathbf {v}} \in {\mathcal {V}}} {\mathcal {E}}({\mathbf {v}}). \end{aligned} \end{aligned}$$
(52)

Since the variational equations of (51) are the equations given in (49) we have established the equivalence. Therefore, we conclude that the Koiter model proposed out of purely mechanical and geometrical intuitions can be derived from first principles of continuum mechanics.

4 \(C^1\)-Trace-Finite-Cell-Method

For the discretization of the weak form (49), we propose a \(C^1\)-continuity version of the TraceFEM. Following the TraceFEM concept the ansatz space on the surface is defined as the restriction (trace) of an outer ansatz space defined on a background mesh. We label the present method also a Finite-Cell method because we use as a background mesh a Cartesian grid. On this structured grid we are able to construct \(C^1\)-continuity shape functions by the tensor product of univariate cubic Hermite form functions. Locally, they are defined on the on the unit interval by (see Fig. 3)

$$\begin{aligned} \begin{aligned} \varphi _1(\xi )&= 1 + \xi ^2(2\xi -3), \\ \varphi _2(\xi )&= \xi (\xi (\xi -2)+1), \\ \varphi _3(\xi )&= -\xi ^2(2\xi -3), \\ \varphi _4(\xi )&= \xi ^2(\xi -1). \end{aligned} \end{aligned}$$
(53)
Fig. 3
figure 3

Local univariate cubic Hermite form functions

Full size image

The local functions (53) are pieced together to global \(C^1\) shape functions \(N^i({{\mathbf {x}}})\) by the standard finite element procedure of relating local degrees of freedom and global degrees of freedom. The degrees of freedom are the values and the first derivatives at the vertices of the background grid. Thus, at each vertex we have \(2^3=8\) degrees of freedom for the discretization of a scalar field and 24 degrees of freedom for the vector-valued displacement field. Thus, on a background cell we have 64 local form functions and 192 local degrees of freedom for the displacement field. We denote the vector-valued finite element space on the background grid by \(V_h\). Then, the discrete problem is given by: Find \({\mathbf {u}}_h \in V_h\) such that

$$\begin{aligned} M_h({\mathbf {u}}_h,{\mathbf {w}}_h) = f_D({\mathbf {w}}_h), \end{aligned}$$
(54a)

holds for all \({\mathbf {w}}_h\in V_h\) and

$$\begin{aligned} K_h({\mathbf {u}}_h,{\mathbf {v}}_h) = f_N({\mathbf {v}}_h), \end{aligned}$$
(54b)

holds for all \({\mathbf {v}}_h\) with \(M_h({\mathbf {v}}_h, {\mathbf {w}}_h)=0\) for all \({\mathbf {w}}_h \in V_h\). The linear and bi-linear forms are given by

$$\begin{aligned} M_h({\mathbf {u}}_h,{\mathbf {v}}_h)&= \int _{\varGamma _{D_i}} {\mathbf {v}}_h \cdot {\mathbf {u}}_h \;\mathrm {d} s_{{\mathbf {x}}}\nonumber \\&\quad + \int _{\varGamma _{D_c}} [\nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}_h) \cdot \pmb \mu ] [\nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {u}}_h) \cdot \pmb \mu ] \;\mathrm {d} s_{{\mathbf {x}}}, \end{aligned}$$
(55a)
$$\begin{aligned} f_D({\mathbf {v}}_h)&= \int _{\varGamma _{D_i}} {\mathbf {v}}_h \cdot {\mathbf {u}}_{D_i} \;\mathrm {d} s_{{\mathbf {x}}}\nonumber \\&+ \int _{\varGamma _{D_c}} [\nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}_h) \cdot \pmb \mu ] \; u_{D_c} \;\mathrm {d} s_{{\mathbf {x}}}, \end{aligned}$$
(55b)
$$\begin{aligned} K_h({\mathbf {u}}_h,{\mathbf {v}}_h)&= t\int _\varOmega \pmb \gamma ({\mathbf {v}}_h):{\mathcal {E}} : \pmb \gamma ({\mathbf {u}}_h) \;\mathrm {d} {{\mathbf {x}}}\nonumber \\&+ \frac{t^3}{12} \int _\varOmega \pmb \rho ({\mathbf {v}}_h):{\mathcal {E}} : \pmb \rho ({\mathbf {u}}_h) \;\mathrm {d} {{\mathbf {x}}}, \end{aligned}$$
(55c)
$$\begin{aligned} f_N({\mathbf {v}}_h)&=\int _\varOmega {\mathbf {v}}_h \cdot {\mathbf {b}} \;\mathrm {d} {{\mathbf {x}}}+ \int _{\varGamma _{N_i}} v_{h,i} \, N^N_i \;\mathrm {d} s_x \nonumber \\&- \int _{\varGamma _{N_t}} \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}) \cdot {\mathbf {t}} \; M^N_t \;\mathrm {d} s_x \nonumber \\&- \int _{\varGamma _{N_\mu }} \nabla _\varOmega (\pmb {\nu }\cdot {\mathbf {v}}) \cdot \pmb \mu \; M^N_\mu \;\mathrm {d} s_x. \end{aligned}$$
(55d)

In (54a) the solution \({\mathbf {u}}_h\) gets fixed to prescribed values at the Dirichlet boundary. In (54b) the test functions \({\mathbf {v}}_h\) are restricted to the null-space of \(M_h\). However, the matrix \(M_h\) (and also \(K_h\)) is singular by definition because of two reasons. First, in order to avoid further notation, we take \({\mathbf {w}}_h\in V_h\) resulting in zero rows and columns, which can easily be identified. Secondly, since we define the shape functions by restriction of the shape functions defined on the background mesh, they are not linearly independent. In the standard setting of a fitted finite element method the respective degrees of freedom in (54a) are easy to identify and can be determined by interpolation. Here, in the case of an unfitted method a linear independent basis is not known explicitly in general and have to be determined. In order to illustrate the linear dependency of the basis functions on the surface we consider a simple example, see Fig. 4. For simplicity we investigate a two-dimensional background cell on which bi-linear shape functions are defined (instead of cubic Hermite functions (53)). In Fig. 4e a linear combination of basis functions is shown, which vanishes on the considered one-dimensional line \(\varOmega ^{1d}\). Therefore, the basis functions are not linearly independent on \(\varOmega ^{1d}\) and form only a frame (instead of a basis). We remark that this situation is different from the one in the Finite-Cell-Method for volume problems. There, the basis functions are linearly independent, however the condition number blows up for bad cut situations, see e.g. [42].

Fig. 4
figure 4

Illustration of the linear dependency of the basis functions. The 1D domain \(\varOmega ^{1d}\) in the 2D background cell \([0,1]^2\) is given by \(\phi (x,y) = 2y - 2x + 1\)(blue line): a–d bi-linear shape functions \(\varphi ^{lin}_1 \dots \varphi ^{lin}_4\) on the background cell, e linear combination of shape functions such that \(\varphi ^\star (x,y)=0\) for \((x,y)\in \varOmega ^{1d}\). (Color figure online)

Full size image

In the discrete method the integrals in (55) are evaluated by quadrature, which is described in the next section.

4.1 Integral evaluation

In order to evaluate the surface and line integrals in (55) we use the quadrature schema developed in [46]. Here, we outline only the main ingredients and refer to [46] for technical details. Following the standard finite element procedure the integrals are evaluated by summing up background cell (face) contributions where the shape functions are smooth. The individual contributions are evaluated by Gaussian quadrature. The main idea from [46] is to subdivide the background cells (faces) until it is possible to convert the implicitly defined geometry into the graph of an implicitly defined height function. Then, a recursive algorithm which requires only one-dimensional root finding and one-dimensional Gaussian quadrature can be set up. In order to choose suitable height function directions we have to be able to ensure the monotonicity of the level-set function in that direction. This can be done by showing that the derivative in that direction is uniform in sign, i.e. place bounds on the values attainable by the derivative. In contrast to [46] we use interval arithmetic for this task.

4.2 Solution strategy and stabilization

In order to solve (54) we consider the null-space method with and without a stabilization term. We first solve

$$\begin{aligned} {\mathbf {M}}_h {\mathbf {u}}^D_h = {\mathbf {f}}_D, \end{aligned}$$
(56)

and compute the null-space of \(M_h\). We denote the null-space basis by \({\mathbf {Z}}_h\). In the approach without stabilization the solution \(u^0_h\) of

$$\begin{aligned} ({\mathbf {Z}}_h^\top {\mathbf {K}}_h {\mathbf {Z}}_h) {\mathbf {u}}^0_h = {\mathbf {Z}}_h^\top ({\mathbf {f}}_N - {\mathbf {K}}_h {\mathbf {u}}^D_h) \end{aligned}$$
(57)

is computed. The overall solution is then given by

$$\begin{aligned} {\mathbf {u}}_h = {\mathbf {Z}}_h {\mathbf {u}}^0_h + {\mathbf {u}}^D_h. \end{aligned}$$
(58)

In the case of the stabilized method we replace \({\mathbf {K}}_h\) in (57) by \({\mathbf {K}}_h + {\mathbf {S}}_h\) where the stabilization matrix \({\mathbf {S}}_h\) results from the bi-linear form

$$\begin{aligned} S_h({\mathbf {u}}_h,{\mathbf {v}}_h) = \alpha _S E \int _{B} (\nabla {\mathbf {v}}_h \cdot \pmb {\nu }) \cdot (\nabla {\mathbf {u}}_h \cdot \pmb {\nu }) \;\mathrm {d} s_{{\mathbf {x}}}, \end{aligned}$$
(59)

with the stabilization parameter \(\alpha _S\) and Young’s modulus E. The stabilization in (59) is known as volume normal stabilization in thr literature [13, 27]. We refer to [36] for an overview of different stabilization possibilities.

Fig. 5
figure 5

Problem geometries of the verification

Full size image

4.3 Implementation

The proposed method has been implemented in Matlab. Within the method the exact level-set function \(\phi ({{\mathbf {x}}})\) is used. For the evaluation of the surface normal vector (5) and the Weingarten map (7), the first and second order derivatives of the level-set function are necessary. In the implementation we use symbolic differentiation of \(\phi ({{\mathbf {x}}})\) to provide these derivatives.

When no stabilization is used, in both system of Eqs. (56) and (57) the system matrix is singular by definition. In numerical experiments we have observed that the Matlab backslash operator does not give satisfactory results in this case. Therefore, we use the direct qr solver suitable for under-determined linear equation systems from the SuiteSparseFootnote 1 project in the non-stabilized method. In the stabilized method, i.e. when the stabilization (59) is used, the Matlab backslash operator can be used, provided the stabilization parameter is large enough.

5 Numerical results

In this section, numerical results are presented. First, we verify the implementation of the proposed method against exact manufactured solutions. Secondly, we demonstrate that the method works by testing it with two benchmark problems (one cylindrical shell and one spherical shell) of the well-known shell obstacle course [6]. Finally, in two more examples, complex shell geometries are investigated. All computations are performed on a personal computer with an AMD Ryzen 7 3700X 8-Core processor, which uses an Ubuntu 18.04 operating system.

5.1 Verification example

The implementation of the proposed method is verified. We have successfully run the method on various geometries, displacement fields and boundary condition combinations, but present only the results of two configurations. In all verification examples we used \(B=[-0.4,0.8]\times [0,1]\times [-0.3,1]\) and a shell thickness \(t=0.25\). The material parameters are \(E=10\) and \(\nu =0.4\). The considered geometries are defined by the zero level-set of the functions

$$\begin{aligned} \phi _1(x,y,z)&= x + z - 0.7, \end{aligned}$$
(60a)
$$\begin{aligned} \phi _2(x,y,z)&= 4x^2 + 0.25y^2 + z^2 - 0.7, \end{aligned}$$
(60b)

and are illustrated in Fig. 5. The level-set function (60a) implies a flat geometry, whereas (60b) implies a surface with varying curvature.

As manufactured solutions we consider the two displacement fields

$$\begin{aligned} {\mathbf {u}}^{ex}_1(x,y,z)&= x^3{\mathbf {e}}_x +y \,x^3{\mathbf {e}}_y +(xzy^2+x(x-1)y(y-1)){\mathbf {e}}_z, \end{aligned}$$
(61a)
$$\begin{aligned} {\mathbf {u}}^{ex}_2(x,y,z)&= \sin (16y)\cos (16x\,z){\mathbf {e}}_x+\cos (16x\,y\,z){\mathbf {e}}_y\nonumber \\&\quad +2\sin (16x\,y\,z){\mathbf {e}}_z. \end{aligned}$$
(61b)

Using (40), we compute symbolically the necessary surface force \({\mathbf {b}}\) such that (61) is the respective exact solution of the shell problem. The displacement field \({\mathbf {u}}_1\) is chosen as a third order polynomial such that the solution can be represented exactly in the discrete space, whereas \({\mathbf {u}}_2\) can only be approximated.

Fig. 6
figure 6

Errors for the geometry induced by \(\phi _1\) and displacement \({\mathbf {u}}_1\)

Full size image
Fig. 7
figure 7

Errors for the geometry induced by \(\phi _1\) and displacement \({\mathbf {u}}_2\)

Full size image

In the following, we study the behavior of the error

$$\begin{aligned} e = \sqrt{\frac{\int _\varOmega ({\mathbf {u}}_h - {\mathbf {u}}^{ex})^2 \;\mathrm {d} {{\mathbf {x}}}}{\int _\varOmega ({\mathbf {u}}^{ex})^2 \;\mathrm {d} {{\mathbf {x}}}}} \end{aligned}$$
(62)

under uniform mesh refinement for the non-stabilized method and the stabilized method described in Section 4.2. Furthermore, for comparison, we also consider the Hermite interpolation \({\mathbf {u}}^{int}_h\) of the solution on the background grid and the surface \(L_2\)-projection: Find \({\mathbf {u}}^{L_2}_h \in V_h\) such that

$$\begin{aligned} \int _\varOmega ({\mathbf {u}}^{ex}-{\mathbf {u}}^{L_2}_h)^2 \;\mathrm {d} {{\mathbf {x}}}\quad \rightarrow \quad \text {min}. \end{aligned}$$
(63)

We remark that the Hermite interpolation and the \(L_2\)-projection are only possible if the solution is known, and is thus only computed for the verification examples in this section. Furthermore, all solutions apart from the Hermite interpolation require the solution of a system of linear equations. The numerical results for the flat plate defined in (60a) and displacement field \({\mathbf {u}}_1\) are visualized in Fig. 6. The refinement level 0 refers to a single background cell, whereas level 4 has 4096 background cells. We remark that for this flat geometry the numerical integration is exact up to round of errors. Therefore, for \({\mathbf {u}}_1\) the sources for errors are the error due to round off errors in the numerical computations. In Fig. 6a the error for different stabilization parameters is given. We observe that the optimal parameter choice depends on the discretization level. Furthermore, if the stabilization parameter is chosen too low, instabilities occur. In Fig. 6b the results for the different methods are given. For the results of the stabilized method the lowest error values from Fig. 6a are taken. As no system of equation has to be solved for the interpolation on the background grid (volume interpolation) the error is around \(10^{-16}\) for all refinement levels. In contrast to this the other results require the solution of a system of equations and therefore the errors are between \(10^{-8}\) and \(10^{-4}\) due to round off errors.

Fig. 8
figure 8

Errors for on the geometry induced by \(\phi _2\) for displacement \({\mathbf {u}}_2\)

Full size image
Fig. 9
figure 9

Influence of the stabilization parameter on the condition number and the elapsed computation time

Full size image

The numerical results for the flat geometry and displacement field \({\mathbf {u}}_2\) are visualized in Fig. 7. Since \({\mathbf {u}}_2\) cannot be represented exactly in the discrete space an approximation error limits the overall error. In Fig. 7a the error for different stabilization parameters is given. The results obtained by the different methods are illustrated in Fig. 7b. For the stabilized method we used the lowest errors of the results shown in Fig. 7a. For \({\mathbf {u}}_2\) we observe the convergence of all methods with optimal rate. Here, by definition the \(L_2\)-projection gives the lowest error, whereas the Hermite volume interpolation results in the highest error for a fixed refinement level. Here, we do not observe an influence of the stabilization.

We omit the results for the curved geometry and displacement field \({\mathbf {u}}_1\) field because they are similar to the results in Fig. 6 The numerical results for the part of the ellipse defined in (60b) and displacement field \({\mathbf {u}}_2\) are visualized in Fig. 8. In Fig. 8a the results for different stabilization parameters are given. We observe that \(\alpha _s \approx 10^{-10}\) yield the lowest errors. The results obtained by the non-stabilized method, the stabilized method, the Hermite volume interpolation and the \(L_2\)-projection are illustrated in Fig. 8b. Again, for the stabilized method we used the lowest errors of the results shown in Fig. 8a. We observe the convergence of all methods with optimal rate. Here, we observe that the stabilized method with optimal parameter choice yields the lowest errors. Furthermore, the influence of the stabilization on the condition number and on the elapsed computation time is illustrated in Fig. 9. However, we observe that the lowest condition numbers are obtained for a stabilization parameter around \(10^5\) in this example. Regarding the computation times we observe that larger stabilization parameters yield faster computations. For parameters \(\alpha _S<1\) the computation times for the non-stabilized method and the stabilized method are similar. Nonetheless, for \(\alpha _S>1\) the elapsed times are significantly lower.

Fig. 10
figure 10

Problem description of the Scordelis-Lo roof problem

Full size image
Table 1 Vertical displacements of the classical Scordelis-Lo roof at point A. Reference: \(u_z^A = -0.3006\)
Full size table
Fig. 11
figure 11

Deformed configurations of the Scordelis-Lo roof (displacements scaled by a factor of 20)

Full size image

5.2 Classical and modified Scordelis-Lo roof

We consider the classical Scordelis-Lo roof problem, which is one example from the shell obstacle course [6]. It is a popular benchmark test to assess the performance of finite elements regarding complex membrane strain states. Furthermore, a modified version of the problem with an re-entrant corner is considered. The cylindrical roof (radius \(r=25\), thickness \(t =0.25\)) is supported by rigid diaphragms at the ends (\(x=0\) and \(x=50\)), i.e. \(u_y=u_z=0\). The straight edges are free. The geometries are depicted in Fig. 10. We describe the classical problem geometry by

$$\begin{aligned} \phi (x,y,z) = y^2 + z^2 - r^2, \end{aligned}$$
(64)

and \(B = [0,50] \times [-r\sin (\frac{40}{180}\pi ),r \sin (\frac{40}{180}\pi )]\times [10,31.25]\). For the modified roof problem we have extended the geometry description (1) slightly, such that background cells can be excluded from the analysis. This simple approach allows us to remove one quarter of the shell surface. The material parameters are \(E =4.32 \cdot 10^8\) and \(\nu =0\). The structure is subjected to gravity loading with \({\mathbf {b}}=-90\,{\mathbf {e}}_z\).

Table 2 Vertical displacements of the modified Scordelis-Lo roof at point B
Full size table
Fig. 12
figure 12

Problem description of the pinched hemisphere problem

Full size image
Table 3 Displacements of the pinched hemisphere at one loading point. Reference: \(u_r = 0.0924\)
Full size table

For the classical roof, we study the vertical displacement of point A, which is located in the middle of one free edge. As a reference solution we use the overkill solution \(u_z^A = -0.3006\) from [7] obtained by an isogeometric formulation using fifth-order NURBS and a mesh of 48 control points in each direction. The results for different meshes obtained with the presented method are given in Table 1 and the deformed geometry is depicted in Fig. 11a. We observe that the method is able to reproduce the reference displacement found in the literature accurately. In this example we hardly see a effect of the stabilization (\(\alpha _s = 10^{-7}\)). Only on level 0 there is an slight difference in the displacement and no significant deviation in the computation times can be found.

For the modified roof, we study the vertical displacement of point B, which is located at the re-entrant corner. The results for different number of background cells are given in Table 2 and the deformed geometry is depicted in Fig. 11b. Basically, here the observations are the same as for the classical version. The stabilization has only little influence on the results and on the computation times. However, in contrast to the results in Table 1, no monotone convergence can be observed. We conjecture that this is due to a singularity at the re-entrant corner.

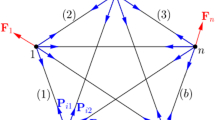
5.3 Pinched hemisphere

In this example, we consider the pinched hemisphere problem from the shell obstacle course in [6]. We describe the spherical mid-surface by

$$\begin{aligned} \begin{aligned} \phi (x,y,z) = x^2 + y^2 + z^2 - R^2, \end{aligned} \end{aligned}$$
(65)

with \(R=10\) and \(B = [-12.5,12.5] \times [-12.5,12.5]\times [0,12.5]\). The material properties and the general problem setup are shown in Fig. 12. The edge of the hemisphere is unconstrained and the four radial forces have alternating signs such that the sum of the applied forces is zero. We investigate the radial displacement at the loaded points. In [6], the reference displacement of \(u_r = 0.0924\) is given. The results obtained by the presented methods are given in Table 3 and the deformed configuration is depicted in Fig. 13. We observe that the results are in very good agreement with the reference value found in literature. The chosen stabilization (\(\alpha _s=10^{-7}\)) reduces the accuracy only minimal. Regarding the computation times, no clear observation can be made. While the stabilization significantly increases the elapsed time for levels 3 and 4, the elapsed time for level 5 is only \(44\%\) in comparison with no stabilization.

Fig. 13
figure 13

Deformed configuration of the pinched hemisphere (displacements scaled by a factor of 40)

Full size image

5.4 Gyroid

In this example, we consider the deformation of a shell structure with a complex geometry. The mid-surface is part of a gyroid which is given by the level-set function

$$\begin{aligned} \phi (x,y,z)= & {} \sin (\pi x)\cos (\pi y)+\sin (\pi y)\cos (\pi z)\nonumber \\&+\sin (\pi z)\cos (\pi x). \end{aligned}$$
(66)
Fig. 14
figure 14

Geometry of the gyroid problem. The structure is clamped at the gray plane

Full size image

The considered shell lies in the cuboid \(B= [0,2]\times \) \([-0.5,0.5]\times \) \([-0.5,0.5]\). The geometry and the material parameters are depicted in Fig. 14. The shell structure is clamped at the boundary curve which is in the plane \(x=0\). We assume a thickness \(t= 0.03\). We study the vertical deflection due to a volume load \({\mathbf {b}}=-10^7 {\mathbf {e}}_z \, \) at the point \([2,0.5,-0.25]\). The deformed geometry is depicted in Fig. 15. The displacement results for different numbers of background cells are summarized in Table 4. We observe that the results obtained for levels 2, 3, and 4 with and without stabilization are nearly the same and that they are in good agreement with the reference displacement \(u_z = -1.8812\) given in [26]. We remark that the reference solution was obtained for a seven-parameter shell model including more physical effects and thus leading to a slightly larger displacement. Therefore, the deviation in the deflection is acceptable. However, for level 0 the result for the chosen stabilization (\(\alpha _s=10^{-7}\)) is unusable. Here, a larger stabilization parameter would be necessary. Nevertheless, the stabilized method is superior regarding computation times. On level 4 the elapsed time is only \(13\%\) in comparison with the non-stabilized method.

Fig. 15
figure 15

Deformed configuration of the gyroid

Full size image
Table 4 Displacements \(u_z\) of the gyroid at the point \([2,0.5,-0.25]\)
Full size table
Fig. 16
figure 16

Undeformed and deformed configuration of the channel problem

Full size image
Table 5 Displacements \(u_z\) of the channel problem at the point \([0,-1.7,0]\)
Full size table

5.5 Channel

In this last example we study the deformation of a channel. The construction consists of a cylindrical channel with spherical end-caps and a cylindrical downpipe (all radius \(R=0.2\)), see Fig. 16a. The geometry of the two cylinders and the two spheres is described by

$$\begin{aligned} c_1(x,y,z)&= x^2+y^2 - R^2, \end{aligned}$$
(67)
$$\begin{aligned} c_2(x,y,z)&= x^2+z^2 - R^2, \end{aligned}$$
(68)
$$\begin{aligned} s_1(x,y,z)&= (y-1.5)^2+x^2+z^2-R^2, \end{aligned}$$
(69)
$$\begin{aligned} s_2(x,y,z)&= (y+1.5)^2+x^2+z^2-R^2. \end{aligned}$$
(70)

In order to state the final level set function of the problem we introduce a smooth approximation of the min-function,

$$\begin{aligned} \text {smin}_{k}(a,b) = -\frac{1}{k}\log \left( e^{-ka} + e^{-kb} \right) , \end{aligned}$$
(71)

with a parameter k controlling the shape of the approximation. Furthermore, we introduce a combination of the horizontal cylinder and the spheres,

$$\begin{aligned}&{\hat{c}}_2(x,y,z) = H(\tfrac{3}{2}+y)H(\tfrac{3}{2}-y) c_2(x,y,z)\nonumber \\&\quad + H(y-\tfrac{3}{2})s_1(x,y,z) + H(-\tfrac{3}{2}-y)s_2(x,y,z) \end{aligned}$$
(72)

where \(H(\cdot )\) denotes the Heaviside-function. The geometry is now described by

$$\begin{aligned} \phi (x,y,z) = \text {smin}_{10}\left( c_1(x,y,z),{\hat{c}}_2(x,y,z)\right) \end{aligned}$$
(73)

and \(B= [-0.5,0.5]\times [-2,2]\times [-1,0]\). The material parameters are the same as in Section 5.4, whereas the shell thickness is \(t = 0.005\). Furthermore, the structure is fixed at the plane \(z=-1\). In this problem two loads are considered simultaneously. These are a volume load \({\mathbf {b}}=-10^7 {\mathbf {e}}_z \, \) and a concentrated load \({\mathbf {F}} = [10^4,0,0]\) acting at the point \([0,-1.7,0]\). The deformed geometry is depicted in Fig. 16b. We also evaluate the absolute value of the displacement at the force application point for different numbers of background cells. The results are given in Table 5. Regarding the displacement results the non-stabilized method delivers slightly more accurate results than the stabilized method. However, the computational times are significantly reduced for the stabilized method.

6 Conclusions

We have developed a \(C^1\)-continuous finite element method for thin shells with mid-surface given as the zero level-set of a scalar function. In order to achieve the continuity of the discretization, concepts of the TraceFEM and the Finite-Cell-Method are combined. In particular the shape functions on the shell surface are obtained by restriction of tensor-product cubic Hermite splines on a structured background mesh. In order to allow a natural implementation, the underlying shell model is formulated in a parametrization-free way. Furthermore, the strong form of the governing equations are given. This allows to obtain manufactured solutions on arbitrary geometries. Thus, the implementation of the proposed method is verified by a convergence analysis where the error is computed with an exact manufactured solution.

In the present method, the shape functions on the shell surface are linearly dependent. In order to avoid a singular system matrix, the so-called normal volume stabilization is used. Furthermore, also the singular system is solved by the direct qr-solver suitable for under-determined linear equation systems from the SuiteSparse project. In the numerical experiments we have observed that the non-stabilized and the stabilized method give reliable results, provided the stabilization parameter is large enough.

A major assumption in the present paper is that the surface is smooth (regular). Therefore, kinks within the shell surfaces are not allowed for the presented method. If one describes the geometry with a bunch of level set functions then they have to be smoothly connected. In future work, it would be interesting to extend the presented approach to geometries with sharp intersections of several surfaces.

In contrast to thin shells, for Reissner-Mindlin shells only \(C^0\)-continuous shape functions are commonly used. In order to avoid transverse shear locking, in [22, 33] an hierarchic concept of shell models is presented. This approach has the advantage that transverse shear locking is eliminated on the continuous formulation level, independent of a particular discretization, but requires \(C^1\)-continuous shape functions. An extension of the present work to Mindlin-Reissner shells with implicitly defined mid-surface seems possible and would be worth to investigate.