The nodal-based floating frame of reference formulation with modal reduction

Abstract

In a recent paper of the authors, a novel nodal-based floating frame of reference formulation (FFRF) for solid finite elements has been proposed. The nodal-based approach bypasses the unhandy inertia shape integrals ab initio, i.e. they neither arise in the derivation nor in the final equations of motion, leading to a surprisingly simple derivation and computer implementation without a lumped mass approximation, which is conventionally employed within commercial multibody codes. However, the nodal-based FFRF has so far been presented without modal reduction, which is usually required for efficient simulations. Hence, the aim of this follow-up paper is to bring the nodal-based FFRF into a suitable form, which allows the incorporation of modal reduction techniques to reduce the overall system size down to the number of modes included in the reduction basis, which further reduces the computational complexity significantly. Moreover, this exhibits a way to calculate the so-called FFRF invariants, which are constant “ingredients” required to set up the FFRF mass matrix and quadratic velocity vector, without integrals and without a lumped mass approximation.

1 Introduction

The floating frame of reference formulation (FFRF) is one of the most widely used methods to analyse flexible multibody systems and is implemented in most commercial flexible multibody dynamics codes. The formulation is applicable to flexible multibody systems subjected to large rigid body translations and rotations but small strains and flexible deformations with respect to the floating frame, such as vehicles, aircraft, robots, and machines.

The FFRF is conventionally derived from a continuum mechanics point of view [10, 11, 14, 18, 19], which yields so-called inertia shape integrals. These unhandy volume integrals depend not only on the degrees of freedom (DOFs) but also on the finite element (FE) shape functions, which makes computer implementations and the derivation of the conventional FFRF error-prone and laborious. Nevertheless, this circuitous approach has become a standard in the multibody literature [17]. To circumvent the evaluation of these integrals, commercial flexible multibody packages like ADAMS (MSC Software Corporation) or RecurDyn (FunctionBay, Inc.) resort to a lumped mass approach according to [17], see [3, 13]. Within this approximative approach, a so-called nodal mass (for translational DOFs) or a nodal inertia (for rotational DOFs) $m_{\mathrm {n}}^j$ is assigned to each FE nodal DOF $q_{\mathrm {fe}}^j$. Hence, the kinetic energy T of each flexible body is in turn approximately calculated by the sum of all N nodal DOF contributions according to particle dynamics theory, i.e. [13, 17]

$$\begin{aligned} T \approx \frac{1}{2} \sum _{j=1}^{N} \dot{q}_{\mathrm {fe}}^j \, m_{\mathrm {n}}^j \, \dot{q}_{\mathrm {fe}}^j. \end{aligned}$$

(1)

Hence, all FFRF integrals are replaced and approximated by sums. This significant simplification enables commercial multibody packages to calculate the so-called FFRF invariants, which are constant “ingredients” required to set up the FFRF mass matrix and quadratic velocity vector—approximately. These invariants may be found in the documentations of commercial multibody packages, see, for example, [3, 13].

In recent papers of the authors [20, 21], a novel nodal-based FFRF for solid FEs has been proposed. This nodal-based approach bypasses the inertia shape integrals ab initio, i.e. the integrals arise neither in the derivation nor in the final expression of the equations of motion (EOMs), leading to a surprisingly simple derivation and computer implementation without a lumped mass approximation. The key idea is to treat a flexible body as a collection of discrete points, i.e. the FE nodes, to describe the kinematics and to define the system energies on a semi-discrete nodal-based level. In doing so, [20] presented a derivation via the absolute coordinate formulation (ACF) (see [6] for early work on the ACF), and [21] an even more elegant and concise way via Lagrange’s equation for a general mechanical system, whereas [22] formed the basis of the nodal-based treatment to derive the generalized component mode synthesis (GCMS) EOMs (see [5, 15] for early work on the GCMS). However, the governing EOMs of the nodal-based FFRF have so far been presented without modal reduction, i.e. the approximation of the flexible DOFs as a linear combination of component modes, which is usually required to efficiently simulate flexible multibody systems, but is not trivial to incorporate, since the so far presented equations involve undesired matrix operations during time integration with “large” matrices depending on the DOFs. Hence, the aim of this follow-up paper is to bring the nodal-based FFRF into a suitable form, which allows the incorporation of modal reduction techniques to reduce the overall system size down to the number of modes included in the reduction basis and to render the aforementioned matrix operations unnecessary, which further reduces the computational complexity significantly. This will reveal a possibility to calculate the FFRF invariants without a lumped mass approximation and, of course, without inertia shape integrals. Please note that the inertia shape integrals are replaced by matrix multiplications with the consistent (constant) FE mass matrix, which itself could be considered as an inertia shape integral; however, this is no burden, since the FE mass matrix can be exported from any FE package and is, furthermore, anyway required to calculate the eigenmodes included in the reduction basis¹.

The remainder of this paper is structured as follows: Sect. 2 provides a brief summary of the derivation of the non-reduced nodal-based FFRF EOMs according to [21]. In Sects. 3 and  4, which is the main part and the novelty of this paper, the modally reduced nodal-based FFRF is derived in 3D and 2D space, respectively. Then, Sect. 5 shows the convergence of the modally reduced nodal-based FFRF to its non-reduced counterpart and the dangers of the lumped mass approximation using a flexible slider–crank mechanism, which should reinforce that the presented model order reduction and EOMs within this paper are reliable. Finally, the paper is concluded in Sect. 6.

2 Non-reduced equations of motion of the nodal-based FFRF

As already mentioned in Sect. 1, two approaches have been presented so far to derive the nodal-based FFRF, i.e. a direct derivation via Lagrange’s equation for a general mechanical system [21] and a derivation via the ACF [20]. We briefly summarize the main steps required to obtain the nodal-based EOMs according to [21]; for the detailed steps, the reader is referred to the mentioned literature.

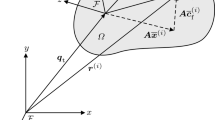
Let us consider a representative FE-discretized body of a 3D system with $n_{\mathrm {n}}$ nodes and an attached floating frame $\overline{\mathcal {F}}$, i.e. a body-fixed coordinate system; the origin of $\overline{\mathcal {F}}$ is translated by ${\varvec{q}}_{\mathrm {t}} \in \mathbb {R}^{3 \times 1}$ with respect to (w.r.t.) the origin of the global inertial frame $\mathcal {F}$ and their orientations are related by the rotation matrix ${\varvec{A}}={\varvec{A}}({\varvec{\theta }}) \in \mathbb {R}^{3 \times 3}$, where ${\varvec{\theta }} \in \mathbb {R}^{n_{\mathrm {r}} \times 1}$ denotes a proper rotational parametrization with $n_{\mathrm {r}}$ rotational DOFs.

The first step is to split the global nodal displacements ${\varvec{c}} \in \mathbb {R}^{3 n_{\mathrm {n}} \times 1}$ into their translational (${\varvec{c}}_{\mathrm {t}}$), rotational (${\varvec{c}}_{\mathrm {r}}$) and flexible (${\varvec{c}}_{\mathrm {f}}$) parts, i.e.

$$\begin{aligned} {\varvec{c}}={\varvec{c}}_{\mathrm {t}}+{\varvec{c}}_{\mathrm {r}}+{\varvec{c}}_{\mathrm {f}} , \end{aligned}$$

(2)

and relate them to the FFRF generalized coordinates

$$\begin{aligned} {\varvec{q}} =\left[ \begin{matrix} {\varvec{q}}_{\mathrm {t}}^{\mathrm {T}}&{\varvec{\theta }}^{\mathrm {T}}&\overline{{\varvec{c}}}_{\mathrm {f}}^{\mathrm {T}} \end{matrix} \right] ^{\mathrm {T}} , \end{aligned}$$

(3)

i.e.

$$\begin{aligned} {\varvec{c}} = {\varvec{\varPhi }}_{\mathrm {t}} {\varvec{q}}_{\mathrm {t}} + \left( {\varvec{A}}_{\mathrm {bd}}-{\varvec{I}}_{\mathrm {bd}}\right) {\varvec{\overline{x}}} + {\varvec{A}}_{\mathrm {bd}} \overline{{\varvec{c}}}_{\mathrm {f}} , \end{aligned}$$

(4)

with

$$\begin{aligned} {\varvec{\varPhi }}_{\mathrm {t}}&=\left[ \begin{matrix} {{\varvec{I}}}&\dots&{\varvec{I}} \end{matrix} \right] ^{\mathrm {T}} \in \mathbb {R}^{3 n_{\mathrm {n}} \times 3} , \end{aligned}$$

(5)

$$\begin{aligned} {\varvec{A}}_{\mathrm {bd}}&=\mathrm {diag}({\varvec{A}},\dots ,{\varvec{A}}) \in \mathbb {R}^{3 n_{\mathrm {n}} \times 3 n_{\mathrm {n}}} , \end{aligned}$$

(6)

$$\begin{aligned} {\varvec{I}}_{\mathrm {bd}}&={\mathrm {diag}}({\varvec{I}},\dots ,{\varvec{I}}) \in \mathbb {R}^{3 n_{\mathrm {n}} \times 3 n_{\mathrm {n}}} , \end{aligned}$$

(7)

where ${\varvec{I}} \in \mathbb {R}^{3 \times 3}$ denotes the identity matrix and ${\varvec{\overline{x}}} \in \mathbb {R}^{3n_{\mathrm {n}} \times 1}$ as well as ${\varvec{\overline{c}}}_{\mathrm {f}} \in \mathbb {R}^{3n_{\mathrm {n}} \times 1}$ denote the undeformed (reference) nodal coordinates and the flexible nodal displacements w.r.t. the floating frame, respectively. Differentiating Eq. (4) w.r.t. time $t \, (\dot{\;})$ and exploiting some inherent properties of the involved matrices as well as some basic kinematic relationships, see [20, 21], yields

$$\begin{aligned} \dot{{\varvec{c}}}={\varvec{L}}({\varvec{q}}) \dot{{\varvec{q}}}, \end{aligned}$$

(8)

with

$$\begin{aligned} {\varvec{L}}=\left[ \begin{matrix} {{\varvec{\varPhi }}_{\mathrm {t}}} \;&\; - {\varvec{A}}_{\mathrm {bd}} \widetilde{\overline{{\varvec{r}}}}_{\mathrm {f}} \overline{{\varvec{G}}} \;&\; {\varvec{A}}_{\mathrm {bd}} \end{matrix} \right] , \end{aligned}$$

(9)

where $\overline{{\varvec{G}}} \in \mathbb {R}^{3 \times n_{\mathrm {r}}}$ is implicitly defined by the local angular velocity $\overline{{\varvec{\omega }}} \in \mathbb {R}^{3 \times 1}$ and rotational parametrization as $\overline{{\varvec{\omega }}}=\overline{{\varvec{G}}}\dot{{\varvec{\theta }}}$, and $\widetilde{\overline{{\varvec{r}}}}_{\mathrm {f}}$ comprises the $n_{\mathrm {n}}$ skew-symmetric matrices²$\widetilde{\overline{{\varvec{r}}}}_{\mathrm {f}}^{(i)} \in \mathbb {R}^{3 \times 3}$ of all FE nodes associated with the nodal position vectors

$$\begin{aligned} \overline{{\varvec{r}}}_{\mathrm {f}}^{(i)}= {\varvec{\overline{x}}}^{(i)} + \overline{{\varvec{c}}}_{\mathrm {f}}^{(i)} \in \mathbb {R}^{3 \times 1} \; \Leftrightarrow \; \overline{{\varvec{r}}}_{\mathrm {f}}= {\varvec{\overline{x}}} + \overline{{\varvec{c}}}_{\mathrm {f}} \in \mathbb {R}^{3 n_{\mathrm {n}} \times 1} \end{aligned}$$

(10)

after elastic deformation, relative to the body frame, i.e.

$$\begin{aligned} {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}=\left[ \begin{matrix} {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{(1)} \\ \vdots \\ {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{(n_{\mathrm {n}})} \end{matrix} \right] \in \mathbb {R}^{3 n_{\mathrm {n}} \times 3}. \end{aligned}$$

(11)

The coordinate mappings, Eqs. (4) and  (8), are required to derive the EOMs via Lagrange’s equation, i.e.

$$\begin{aligned} \underbrace{\frac{\mathrm {d}}{\mathrm {d} t} \bigg ( \frac{\partial {T}}{\partial \dot{{\varvec{q}}}^{\mathrm {T}} } \bigg ) - \frac{\partial {T}}{\partial {\varvec{q}}^{\mathrm {T}}}}_{\begin{array}{c} {\text {inertia}} \\ {\text {forces}} \end{array}} + \underbrace{\frac{\partial {V}}{\partial {\varvec{q}}^{\mathrm {T}}}}_{\begin{array}{c} {\text {elastic}} \\ {\text {forces}} \end{array}} + \underbrace{\frac{\partial {\varvec{\lambda }}^{\mathrm {\! T}} {\varvec{g}}}{\partial {\varvec{q}}^{\mathrm {T}}}}_{\begin{array}{c} {\text {constraint}} \\ {\text {forces}} \end{array}} = \underbrace{\frac{\partial {W}}{\partial {\varvec{q}}^{\mathrm {T}}}}_{\begin{array}{c} {\text {applied}} \\ {\text {forces}} \end{array}} , \end{aligned}$$

(12)

since [20, 21]

$$\begin{aligned} {T}(\dot{{\varvec{c}}}({\varvec{q}},\dot{{\varvec{q}}}))&=\frac{1}{2} \dot{\varvec{c}}^{\mathrm {T}} \overline{{\varvec{M}}} \dot{\varvec{c}}, \end{aligned}$$

(13)

$$\begin{aligned} {V}({\varvec{q}})&=\frac{1}{2} {\varvec{\overline{c}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{K}}} {\varvec{\overline{c}}}_{\mathrm {f}} , \end{aligned}$$

(14)

$$\begin{aligned} {W}({\varvec{c}}({\varvec{q}}),t)&={\varvec{c}}^{\mathrm {T}} {\varvec{f}} , \end{aligned}$$

(15)

$$\begin{aligned} {\varvec{g}}({\varvec{q}},t)&={\varvec{0}} , \end{aligned}$$

(16)

with the kinetic energy T, the strain energy V, the work W done by applied nodal forces ${\varvec{f}}$, the holonomic constraint equations ${\varvec{g}}={\varvec{0}}$, and the Lagrange multipliers ${\varvec{\lambda }}$. Note that $\overline{{\varvec{M}}}$ and $\overline{{\varvec{K}}}$ denote the constant mass and stiffness matrix from the underlying linear FE model, respectively. It has been shown by [21] that combining Eq. (4), Eq. (8) and Eqs. (12) to (16) and carrying out differentiation in a very elegant way yields

$$\begin{aligned} {\varvec{L}}^{\mathrm {T}} {\varvec{M}} {\varvec{L}} \ddot{{\varvec{q}}} + {\varvec{L}}^{\mathrm {T}} {\varvec{M}} \dot{{\varvec{L}}} \dot{{\varvec{q}}} + {\varvec{\widehat{K}}} {\varvec{q}} + {\varvec{\widehat{J}}}^{\mathrm {T}} {\varvec{\lambda }} = {\varvec{L}}^{\mathrm {T}} {\varvec{f}} , \end{aligned}$$

(17)

i.e. slightly rearranged,

$$\begin{aligned}&\left[ \begin{matrix} {{\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}}} \overline{{\varvec{M}}} {\varvec{\varPhi }}_{\mathrm {t}} \quad &{} \quad -{\varvec{A}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \overline{{\varvec{G}}} \quad &{} \quad {\varvec{A}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \\ \quad &{} \quad \overline{{\varvec{G}}}^{\mathrm {T}}{\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \overline{{\varvec{G}}} \quad &{} \quad -\overline{{\varvec{G}}}^{\mathrm {T}}{\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \\ {\text {sym.}} \quad &{} \quad \quad &{} \quad \overline{{\varvec{M}}} \end{matrix} \right] \left[ \begin{matrix} {\ddot{{\varvec{q}}}_{\mathrm {t}}} \\ \ddot{{\varvec{\theta }}} \\ \ddot{\overline{{\varvec{c}}}}_{\mathrm {f}} \end{matrix} \right] = - \left[ \begin{matrix} {{\varvec{0}}} &{} {\varvec{0}} &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} &{} \overline{{\varvec{K}}} \\ \end{matrix} \right] \left[ \begin{matrix} {{\varvec{q}}_{\mathrm {t}}} \\ {\varvec{\theta }} \\ {\varvec{\overline{c}}}_{\mathrm {f}} \end{matrix} \right] \nonumber \\&\qquad + \left[ \begin{matrix} - {\varvec{A}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \left( {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\overline{{\varvec{r}}}}_{\mathrm {f}} + 2 {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}\dot{{\overline{{\varvec{c}}}}}_{\mathrm {f}} - {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \right) \\ \overline{{\varvec{G}}}^{\mathrm {T}}{\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \left( {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\overline{{\varvec{r}}}}_{\mathrm {f}} + 2 {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}\dot{{\overline{{\varvec{c}}}}}_{\mathrm {f}} - {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \right) \\ -\overline{{\varvec{M}}} \left( {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\overline{{\varvec{r}}}}_{\mathrm {f}} + 2 {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}\dot{{\overline{{\varvec{c}}}}}_{\mathrm {f}} - {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \right) \end{matrix} \right] \nonumber \\&\qquad + \left[ \begin{matrix} {{\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}}} \\ - {\varvec{\overline{G}}}^{\mathrm {T}} {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} {\varvec{A}}_{\mathrm {bd}}^{\mathrm {T}} \\ {\varvec{A}}_{\mathrm {bd}}^{\mathrm {T}} \end{matrix} \right] {\varvec{f}} - \dfrac{\partial {\varvec{g}}}{\partial {\varvec{q}}^{\mathrm {T}}} {\varvec{\lambda }} , \end{aligned}$$

(18)

where

$$\begin{aligned} {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}={\mathrm {diag}}({\widetilde{\overline{{\varvec{\omega }}}}},\dots ,\widetilde{\overline{{\varvec{\omega }}}}) \in \mathbb {R}^{3 n_{\mathrm {n}} \times 3 n_{\mathrm {n}}}. \end{aligned}$$

(19)

Please not that the nodal-based FFRF presented in here is valid if (see [20, 21] for further discussions) ...

• flexible deformations and strains with respect to each body frame are small³,

• the coordinates ${\varvec{q}}$ are sorted alternating for x, y and z components of an underlying orthogonal coordinate system,

• the mass matrix is invariant to rotations, i.e. $\overline{{\varvec{M}}}={\varvec{A}}_{\mathrm {bd}}^{\mathrm {T}} {\varvec{M}} {\varvec{A}}_{\mathrm {bd}}={\varvec{M}}$, which also implies that the matrices ${\varvec{A}}_{\mathrm {bd}}$ and ${\varvec{M}}=\overline{{\varvec{M}}}$ commute, which is, for example, the case for displacement-based FEs with identical shape functions used to interpolate all coordinate directions such as, using ABAQUS (Dassault Systèmes) terminology, C3D4, C3D8, C3D10, C3D20 elements.

3 Modally reduced nodal-based FFRF in 3D space

3.1 A suitable form of the nodal-based FFRF to enable a proper modal reduction

It is usually required to reduce the number of flexible DOFs due to limited computation resources or efficiency reasons. The well-established component mode synthesis (CMS), where the flexible deformation is approximated by a linear combination of $n_{\mathrm {m}}$ component modes, such as vibration eigenmodes and static modes, is a widely used approach to do so, see, for example, the pioneering work of [1, 8, 9, 12, 16].

Within the CMS the flexible deformation is approximated by⁴

$$\begin{aligned} {\varvec{\overline{c}}}_{\mathrm {f}} \approx {\varvec{\overline{\varPsi }}} {\varvec{\zeta }} \quad {\text {with}} \quad n_{\mathrm {m}}={\mathrm {dim}}({\varvec{\zeta }}) \ll {\mathrm {dim}}({\varvec{\overline{c}}}_{\mathrm {f}})=3 n_{\mathrm {n}} , \end{aligned}$$

(20)

where ${\varvec{\overline{\varPsi }}} \in \mathbb {R}^{3n_{\mathrm {n}} \times n_{\mathrm {m}}}$ contains column-wise the modes included in the reduction basis, i.e. a low-dimensional solution subspace, and ${\varvec{\zeta }} \in \mathbb {R}^{n_{\mathrm {m}} \times 1}$ are the associated modal coordinates. From Eqs. (3) and  (20), it is obvious to define a reduction matrix for all generalized coordinates, not only for ${\varvec{\overline{c}}}_{\mathrm {f}}$, i.e.

$$\begin{aligned} {\varvec{q}} = {\varvec{H}} {\varvec{p}} \quad \Leftrightarrow \quad \left[ \begin{matrix} {{\varvec{q}}_{\mathrm {t}}} \\ {\varvec{\theta }} \\ \overline{{\varvec{c}}}_{\mathrm {f}} \end{matrix} \right] = \left[ \begin{matrix} {{\varvec{I}}} &{} {\varvec{0}} &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{I}}_{ \theta } &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} &{} \overline{{\varvec{\varPsi }}} \end{matrix} \right] \left[ \begin{matrix} {{\varvec{q}}_{\mathrm {t}}} \\ {\varvec{\theta }} \\ {\varvec{\zeta }} \end{matrix} \right] , \end{aligned}$$

(21)

where ${\varvec{I}}_{ \theta } \in \mathbb {R}^{n_{\mathrm {r}} \times n_{\mathrm {r}}}$ is an identity matrix of proper size.

Substituting Eq. (21) into Eq. (18) and left-multiplying the result with ${\varvec{H}}^{\mathrm {T}}$ yield

$$\begin{aligned}&\left[ \begin{matrix} {{\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}}} \overline{{\varvec{M}}} {\varvec{\varPhi }}_{\mathrm {t}} \quad &{} \quad -{\varvec{A}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}}\, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \overline{{\varvec{G}}} \quad &{} \quad {\varvec{A}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \, \overline{{\varvec{\varPsi }}} \\ \quad &{} \quad \overline{{\varvec{G}}}^{\mathrm {T}}{\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}}\, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \overline{{\varvec{G}}} \quad &{} \quad -\overline{{\varvec{G}}}^{\mathrm {T}}{\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \, \overline{{\varvec{\varPsi }}} \\ {\text {sym.}} \quad &{} \quad \quad &{} \quad {\varvec{\overline{\varPsi }}}^{\mathrm {T}} \overline{{\varvec{M}}} \, \overline{{\varvec{\varPsi }}} \end{matrix} \right] \left[ \begin{matrix} {\ddot{{\varvec{q}}}_{\mathrm {t}}} \\ \ddot{{\varvec{\theta }}} \\ \ddot{{\varvec{\zeta }}} \end{matrix} \right] =- \left[ \begin{matrix} {{\varvec{0}}} \;\; &{} {\varvec{0}} \;\; &{} {\varvec{0}} \\ {\varvec{0}} \;\; &{} {\varvec{0}} \;\; &{} {\varvec{0}} \\ {\varvec{0}} \;\; &{} {\varvec{0}} \;\; &{} {\varvec{\overline{\varPsi }}}^{\mathrm {T}} {\varvec{\overline{K}}} \, \overline{{\varvec{\varPsi }}} \\ \end{matrix} \right] \left[ \begin{matrix} {{\varvec{q}}_{\mathrm {t}}} \\ {\varvec{\theta }} \\ {\varvec{\zeta }} \end{matrix} \right] \nonumber \\&\qquad + \left[ \begin{matrix} - {\varvec{A}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \left( {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\overline{{\varvec{r}}}}_{\mathrm {f}} + 2 {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}\dot{{\overline{{\varvec{c}}}}}_{\mathrm {f}} - {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \right) \\ \overline{{\varvec{G}}}^{\mathrm {T}}{\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \left( {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\overline{{\varvec{r}}}}_{\mathrm {f}} + 2 {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}\dot{{\overline{{\varvec{c}}}}}_{\mathrm {f}} - {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \right) \\ - {\varvec{\overline{\varPsi }}}^{\mathrm {T}} \overline{{\varvec{M}}} \left( {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\overline{{\varvec{r}}}}_{\mathrm {f}} + 2 {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}\dot{{\overline{{\varvec{c}}}}}_{\mathrm {f}} - {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \right) \end{matrix} \right] \nonumber \\&\qquad + \left[ \begin{matrix} {{\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}}} \\ - {\varvec{\overline{G}}}^{\mathrm {T}} {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} {\varvec{A}}_{\mathrm {bd}}^{\mathrm {T}} \\ {\varvec{\overline{\varPsi }}}^{\mathrm {T}} {\varvec{A}}_{\mathrm {bd}}^{\mathrm {T}} \end{matrix} \right] {\varvec{f}} - \dfrac{\partial {\varvec{g}}}{\partial {\varvec{p}}^{\mathrm {T}}} {\varvec{\lambda }} , \end{aligned}$$

(22)

i.e. in a more convenient form for further considerations,

$$\begin{aligned} \underbrace{\left[ \begin{matrix} {{\varvec{\widehat{M}}}_{\mathrm {tt}}} &{} {\varvec{\widehat{M}}}_{\mathrm {tr}} &{} {\varvec{\widehat{M}}}_{\mathrm {tf}} \\ &{} {\varvec{\widehat{M}}}_{\mathrm {rr}} &{} {\varvec{\widehat{M}}}_{\mathrm {rf}} \\ {\text {sym.}} &{} &{} {\varvec{\widehat{M}}}_{\mathrm {ff}} \end{matrix} \right] }_{\begin{array}{c} {\text {FFRF mass}} \\ {\text {matrix}} \end{array}} \left[ \begin{matrix} {\ddot{{\varvec{q}}}_{\mathrm {t}}} \\ \ddot{{\varvec{\theta }}} \\ \ddot{{\varvec{\zeta }}} \end{matrix} \right] = \underbrace{\left[ \begin{matrix} {{\varvec{\widehat{Q}}}_{\mathrm {e_t}}} \\ {\varvec{\widehat{Q}}}_{\mathrm {e_r}} \\ {\varvec{\widehat{Q}}}_{\mathrm {e_f}} \end{matrix} \right] }_{\begin{array}{c} {\text {elastic}} \\ \text {forces} \end{array}} + \underbrace{\left[ \begin{matrix} {{\varvec{\widehat{Q}}}_{\mathrm {v_t}}} \\ {\varvec{\widehat{Q}}}_{\mathrm {v_r}} \\ {\varvec{\widehat{Q}}}_{\mathrm {v_f}} \end{matrix} \right] }_{\begin{array}{c} \text {quadratic} \\ {\text {vel. vector}} \end{array}} + \underbrace{\left[ \begin{matrix} {{\varvec{\widehat{Q}}}_{\mathrm {a_t}}} \\ {\varvec{\widehat{Q}}}_{\mathrm {a_r}} \\ {\varvec{\widehat{Q}}}_{\mathrm {a_f}} \end{matrix} \right] }_{\begin{array}{c} {\text {applied}} \\ {\text {forces}} \end{array}} + \underbrace{\left[ \begin{matrix} {{\varvec{\widehat{Q}}}_{\mathrm {c_t}}} \\ {\varvec{\widehat{Q}}}_{\mathrm {c_r}} \\ {\varvec{\widehat{Q}}}_{\mathrm {c_f}} \end{matrix} \right] }_{\begin{array}{c} {\text {constraint}} \\ {\text {forces}} \end{array}} , \end{aligned}$$

(23)

where, clearly,

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {e}}=- \left[ \begin{matrix} {{\varvec{0}}} \\ {\varvec{0}} \\ {\varvec{\overline{K}}}_{\! {\psi } {\psi }} {\varvec{\zeta }} \end{matrix} \right] , \end{aligned}$$

(24)

with the reduced FE stiffness matrix known from linear elastodynamics, i.e.

$$\begin{aligned} {\varvec{\overline{K}}}_{\! {\psi } {\psi }} = {\varvec{{\overline{\varPsi }}}}^{\mathrm {T}} {\varvec{\overline{K}}} \, {\varvec{{\overline{\varPsi }}}} \in \mathbb {R}^{n_{\mathrm {m}} \times n_{\mathrm {m}}}. \end{aligned}$$

(25)

Nevertheless, the following problems still remain: (i) the EOMs contain the quantity $\widetilde{\overline{{\varvec{c}}}}_{\mathrm {f}}$, which has not been defined in terms of $\overline{{\varvec{\varPsi }}}$ and ${\varvec{\zeta }}$, and (ii) the aim of a proper model reduction is to reduce the overall “size” of the governing system of equations; however, Eq. (22) still contains operations with “large” $\mathbb {R}^{3n_{\mathrm {n}} \times 3n_{\mathrm {n}}}$ matrices depending on the DOFs. That is why the main purpose of this contribution is to rearrange Eq. (22) in a way, such that all matrix terms of size $3 n_{\mathrm {n}}$ are condensed to “small” constant terms in the order of $n_{\mathrm {m}}$. However, it is mentioned beforehand that the derivations presented below do not introduce any further approximations or simplifications besides the modal reduction, i.e. the following manipulations are exact.

To obtain the desired expression of $\widetilde{\overline{{\varvec{c}}}}_{\mathrm {f}}$ in terms of $\overline{{\varvec{\varPsi }}}$ and ${\varvec{\zeta }}$, we resort to an equivalent expression of Eq. (20), i.e.

$$\begin{aligned} {\varvec{\overline{c}}}_{\mathrm {f}} = \sum _{m=1}^{n_{\mathrm {m}}} \overline{{\varvec{\psi }}}_m \zeta _m \quad \Rightarrow \quad \widetilde{\overline{{\varvec{c}}}}_{\mathrm {f}} = \sum _{m=1}^{n_{\mathrm {m}}} \widetilde{\overline{{\varvec{\psi }}}}_m \zeta _m , \end{aligned}$$

(26)

where ${\varvec{\overline{\psi }}}_m \in \mathbb {R}^{3 n_{\mathrm {n}} \times 1}$ denotes the mth mode included in the reduction basis, $\zeta _m \in \mathbb {R}^{1 \times 1}$ the corresponding modal coordinate, and $\widetilde{\overline{{\varvec{\psi }}}}_m \in \mathbb {R}^{3 n_{\mathrm {n}} \times 3}$ the corresponding matrix generated from ${\varvec{\overline{\psi }}}_m$ according to Eq. (11). The right part of Eq. (26) may be written in matrix notation as

$$\begin{aligned} {\widetilde{\overline{{\varvec{c}}}}}_{\mathrm {f}} = \widetilde{\overline{{\varvec{\varPsi }}}} \big ( {\varvec{\zeta }} \otimes {\varvec{I}} \big ) , \end{aligned}$$

(27)

where

$$\begin{aligned} \widetilde{\overline{{\varvec{\varPsi }}}}=\left[ \begin{matrix} {\widetilde{\overline{{\varvec{\psi }}}}_1}&\dots&\widetilde{\overline{{\varvec{\psi }}}}_{n_{\mathrm {m}}} \end{matrix} \right] \in \mathbb {R}^{3 n_{\mathrm {n}} \times 3 n_{\mathrm {m}}} , \end{aligned}$$

(28)

and $\otimes$ denotes Kronecker’s product.

The next step is to bring the quadratic velocity vector in a suitable form to avoid multiplications with “large” matrices depending on the DOFs, i.e.

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {v}}=\left[ \begin{matrix} {{\varvec{A}}} \Big ( \widetilde{\overline{{\varvec{\omega }}}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} {\varvec{\overline{\omega }}} + 2 {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \, \dot{{\widetilde{\overline{{\varvec{c}}}}}}_{\mathrm {f}} \overline{{\varvec{\omega }}} + {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \Big ) \\ - \overline{{\varvec{G}}}^{\mathrm {T}} \Big ( \widetilde{\overline{{\varvec{\omega }}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} {\varvec{\overline{\omega }}} + 2 {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}}\overline{{\varvec{M}}} \, \dot{{\widetilde{\overline{{\varvec{c}}}}}}_{\mathrm {f}} {\varvec{\overline{\omega }}} + {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \Big ) \\ \big ( {\varvec{I}}_{\zeta } \otimes {\varvec{\overline{\omega }}} \big )^{\mathrm {T}} \widetilde{\overline{{\varvec{\varPsi }}}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} {\varvec{\overline{\omega }}} + 2{\varvec{\overline{\varPsi }}}^{\mathrm {T}}\overline{{\varvec{M}}} \, \dot{{\widetilde{\overline{{\varvec{c}}}}}}_{\mathrm {f}} {\varvec{\overline{\omega }}} +{\varvec{\overline{\varPsi }}}^{\mathrm {T}} \overline{{\varvec{M}}}\, \widetilde{\overline{{\varvec{r}}}}_{\mathrm {f}} \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} \end{matrix} \right] . \end{aligned}$$

(29)

Equation (29) follows from the commutativity and anticommutativity properties of the involved matrices derived in [20, 21], i.e.

$$\begin{aligned} {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}\overline{{\varvec{M}}}&= \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}, \end{aligned}$$

(30)

$$\begin{aligned} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}&= \widetilde{\overline{{\varvec{\omega }}}} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} , \end{aligned}$$

(31)

$$\begin{aligned} {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\varvec{\overline{r}}}_{\mathrm {f}}&=- \widetilde{\overline{{\varvec{r}}}}_{\mathrm {f}} \overline{{\varvec{\omega }}} , \end{aligned}$$

(32)

and since

$$\begin{aligned} \widetilde{\overline{{\varvec{r}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \,{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\overline{{\varvec{r}}}}_{\mathrm {f}} = - \widetilde{\overline{{\varvec{\omega }}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{M}}} \, {\widetilde{\overline{{\varvec{r}}}}}_{\mathrm {f}} {\varvec{\overline{\omega }}} , \end{aligned}$$

(33)

which follows from the generic $\mathbb {R}^{3 \times 1}$ vector identity $\widetilde{{\varvec{z}}}^{\mathrm {T}}\widetilde{{\varvec{y}}} \, \widetilde{{\varvec{z}}}{\varvec{y}}=\widetilde{{\varvec{y}}} \, \widetilde{{\varvec{z}}}^{\mathrm {T}}\widetilde{{\varvec{z}}}{\varvec{y}}$, see [19], and from the fact that the consistent FE mass matrix is composed out of $m_{ij} {\varvec{I}}$-blocks, where $m_{ij}$ are scalars. Furthermore, the relationship

$$\begin{aligned} {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}{\varvec{\overline{\varPsi }}} = - \widetilde{\overline{{\varvec{\varPsi }}}} \big ( {\varvec{I}}_{ \zeta } \otimes {\varvec{\overline{\omega }}} \big ) \end{aligned}$$

(34)

with an identity matrix ${\varvec{I}}_{ \zeta } \in \mathbb {R}^{n_{\mathrm {m}} \times n_{\mathrm {m}}}$ of proper size, which follows from the anticommutativity of the cross product in combination with the fact that ${\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}$ is a skew symmetric matrix, see Eq. (19), i.e.

$$\begin{aligned} {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}^{\mathrm {T}} = - {\widetilde{\overline{{\varvec{\omega }}}}}_{\mathrm {bd}}, \end{aligned}$$

(35)

has been used to obtain Eq. (29). Note that Eq. (32) is valid for any $\mathbb {R}^{3 n_{\mathrm {n}} \times 1}$ block nodal vector, such as ${\varvec{c}}$, $\overline{{\varvec{x}}}$, $\overline{{\varvec{c}}}_{\mathrm {f}}$, $\dots$ $\in \mathbb {R}^{3n_{\mathrm {n}} \times 1}$, not only for ${\varvec{\overline{r}}}_{\mathrm {f}}$.

3.2 Nodal-based FFRF invariants without a lumped mass approximation

It may be shown, via the definition of the total mass and of the FE mass matrix, that the total mass of the body m is calculated from the quantities arising in the rearranged modally reduced nodal-based FFRF as (see Appx. A)

$$\begin{aligned} m {\varvec{I}}={\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} {\varvec{\varPhi }}_{\mathrm {t}} \in \mathbb {R}^{3 \times 3}. \end{aligned}$$

(36)

Likewise, the definition of the centre of mass and that of the FE mass matrix yield the centre of mass position of the undeformed body ${\varvec{\overline{\chi }}}_{\mathrm {u}}$ w.r.t. the floating frame and the associated skew-symmetric matrix $\widetilde{\overline{{\varvec{\chi }}}}_{\mathrm {u}}$ as (see Appx. A)

$$\begin{aligned} {\varvec{\overline{\chi }}}_{\mathrm {u}}&= \frac{1}{m} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} {\varvec{\overline{M}}}\, {\varvec{\overline{x}}} \in \mathbb {R}^{3 \times 1} , \end{aligned}$$

(37)

$$\begin{aligned} \widetilde{\overline{{\varvec{\chi }}}}_{\mathrm {u}}&= \frac{1}{m} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} {\varvec{\overline{M}}} \, \widetilde{\overline{{\varvec{x}}}} \in \mathbb {R}^{3 \times 3}. \end{aligned}$$

(38)

In addition, the definition of the inertia tensor and of the FE mass matrix yields the inertia tensor of the undeformed body ${\varvec{\overline{\varTheta }}}_{\mathrm {u}}$ expressed in the floating frame, which is given by (see Appx. A)

$$\begin{aligned} {\varvec{\overline{\varTheta }}}_{\mathrm {u}}= \widetilde{\overline{{\varvec{x}}}}^{\mathrm {T}} {\varvec{\overline{M}}} \, \widetilde{\overline{{\varvec{x}}}} \in \mathbb {R}^{3 \times 3} . \end{aligned}$$

(39)

Furthermore, let us define the following reduced and constant “inertia-like” matrices:

$$\begin{aligned} {\varvec{\overline{M}}}_{\! {\psi } {\psi }}&= {\varvec{{\overline{\varPsi }}}}^{\mathrm {T}} {\varvec{\overline{M}}} \, {\varvec{{\overline{\varPsi }}}} \in \mathbb {R}^{ n_{\mathrm {m}} \times n_{\mathrm {m}}} , \end{aligned}$$

(40)

$$\begin{aligned} {\varvec{\overline{M}}}_{\! \widetilde{\psi } {\psi }}&= \widetilde{\overline{{\varvec{\varPsi }}}}^{\mathrm {T}} {\varvec{\overline{M}}} \, {\varvec{{\overline{\varPsi }}}} \in \mathbb {R}^{3n_{\mathrm {m}} \times n_{\mathrm {m}}} , \end{aligned}$$

(41)

$$\begin{aligned} {\varvec{\overline{M}}}_{\! \widetilde{\psi } \widetilde{\psi }}&= \widetilde{\overline{{\varvec{\varPsi }}}}^{\mathrm {T}} {\varvec{\overline{M}}} \, \widetilde{\overline{{\varvec{\varPsi }}}} \in \mathbb {R}^{ 3n_{\mathrm {m}} \times 3n_{\mathrm {m}}} , \end{aligned}$$

(42)

$$\begin{aligned} {\varvec{\overline{M}}}_{\! \phi {\psi }}&= {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} {\varvec{\overline{M}}} \, {\varvec{{\overline{\varPsi }}}} \in \mathbb {R}^{ 3 \times n_{\mathrm {m}}} , \end{aligned}$$

(43)

$$\begin{aligned} {\varvec{\overline{M}}}_{\! \phi \widetilde{\psi }}&= {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} {\varvec{\overline{M}}} \, \widetilde{\overline{{\varvec{\varPsi }}}} \in \mathbb {R}^{ 3 \times 3n_{\mathrm {m}}} , \end{aligned}$$

(44)

$$\begin{aligned} {\varvec{\overline{M}}}_{\! \widetilde{x} {\psi }}&= \widetilde{\overline{{\varvec{x}}}}^{\mathrm {T}} {\varvec{\overline{M}}} \, {\varvec{\overline{\varPsi }}} \in \mathbb {R}^{ 3 \times n_{\mathrm {m}}}, \end{aligned}$$

(45)

$$\begin{aligned} {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }}&= \widetilde{\overline{{\varvec{x}}}}^{\mathrm {T}} {\varvec{\overline{M}}} \, \widetilde{\overline{{\varvec{\varPsi }}}} \in \mathbb {R}^{ 3 \times 3n_{\mathrm {m}}} , \end{aligned}$$

(46)

where the first matrix (Eq. (40)) is the reduced FE mass matrix known from linear elastodynamics. These constant matrices from Eqs. (36) to (46) represent the nodal-based FFRF invariants without integrals and without a lumped mass approach, which is usually employed by commercial multibody codes, see, for example, [3, 13].

3.3 Nodal-based modally reduced FFRF mass matrix and quadratic velocity vector

We may now express the sub-matrices ${\varvec{\widehat{M}}}_{\mathrm {tt}}$, ${\varvec{\widehat{M}}}_{\mathrm {tr}}$, ${\varvec{\widehat{M}}}_{\mathrm {tf}}$, ${\varvec{\widehat{M}}}_{\mathrm {rr}}$, ${\varvec{\widehat{M}}}_{\mathrm {rf}}$, and ${\varvec{\widehat{M}}}_{\mathrm {ff}}$ of the FFRF mass matrix, see Eqs. (22) to (23), as well as the terms of the rearranged quadratic velocity vector, see Eq. (29), in terms of the constant and reduced matrices—the nodal-based FFRF invariants—defined in Eqs. (36) to (46) and in terms of the reduced DOFs in order to avoid the undesired “large” matrix operations during time integration. Hence, using Eqs. (10) to (11), Eq. (20) and Eq. (27), the nodal-based FFRF mass sub-matrices read

$$\begin{aligned} {\varvec{\widehat{M}}}_{\mathrm {tt}}&= m {\varvec{I}}, \end{aligned}$$

(47)

$$\begin{aligned} {\varvec{\widehat{M}}}_{\mathrm {ff}}&= {\varvec{\overline{M}}}_{\! {\psi } {\psi }}, \end{aligned}$$

(48)

$$\begin{aligned} {\varvec{\widehat{M}}}_{\mathrm {tf}}&= {\varvec{A}} {\varvec{\overline{M}}}_{\! \phi {\psi }} , \end{aligned}$$

(49)

$$\begin{aligned} {\varvec{\widehat{M}}}_{\mathrm {tr}}&= - {\varvec{A}} \left[ m \widetilde{\overline{{\varvec{\chi }}}}_{\mathrm {u}} + {\varvec{\overline{M}}}_{\! \phi \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \overline{{\varvec{G}}} , \end{aligned}$$

(50)

$$\begin{aligned} {\varvec{\widehat{M}}}_{\mathrm {rf}}&=- {\varvec{\overline{G}}}^{\mathrm {T}} \left[ {\varvec{\overline{M}}}_{\! \widetilde{x} \psi } + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{\psi } \psi } \right] , \end{aligned}$$

(51)

$$\begin{aligned} {\varvec{\widehat{M}}}_{\mathrm {rr}}&= {\varvec{\overline{G}}}^{\mathrm {T}} \! \left[ {\varvec{\overline{\varTheta }}}_{\mathrm {u}} + {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }}^{\mathrm {T}} + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{\psi } \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \overline{{\varvec{G}}} , \end{aligned}$$

(52)

see also Eqs. (22) to (23) and Eqs. (36) to (46).

Furthermore, the translational, rotational and flexible parts of the quadratic velocity vector, see Eq. (29), may be expressed as

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {v_t}}=&{\varvec{A}} \widetilde{\overline{{\varvec{\omega }}}} \left[ m \widetilde{\overline{{\varvec{\chi }}}}_{\mathrm {u}} + {\varvec{\overline{M}}}_{\! \phi \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \overline{{\varvec{\omega }}} + 2 {\varvec{A}} {\varvec{\overline{M}}}_{\! \phi \widetilde{\psi }} \left( \dot{{\varvec{\zeta }}} \otimes {\varvec{I}} \right) \overline{{\varvec{\omega }}} \nonumber \\&+ \underbrace{{\varvec{A}} \left[ m \widetilde{\overline{{\varvec{\chi }}}}_{\mathrm {u}} + {\varvec{\overline{M}}}_{\! \phi \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}}}_{=0,\,{\text {if Euler parameters are used}}} , \end{aligned}$$

(53)

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {v_r}}=&- {\varvec{\overline{G}}}^{\mathrm {T}} \widetilde{\overline{{\varvec{\omega }}}} \left[ {\varvec{\overline{\varTheta }}}_{\mathrm {u}} + {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }}^{\mathrm {T}} + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{\psi } \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \overline{{\varvec{\omega }}} \nonumber \\&-2 {\varvec{\overline{G}}}^{\mathrm {T}} \left[ {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }} \left( \dot{{\varvec{\zeta }}} \otimes {\varvec{I}} \right) + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{\psi } \widetilde{\psi }} \left( \dot{{\varvec{\zeta }}} \otimes {\varvec{I}} \right) \right] \overline{{\varvec{\omega }}} \\ &-\underbrace{{\varvec{\overline{G}}}^{\mathrm {T}} \left[ {\varvec{\overline{\varTheta }}}_{\mathrm {u}} + {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }}^{\mathrm {T}} + \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) ^{\mathrm {T}} {\varvec{\overline{M}}}_{\! \widetilde{\psi } \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}} ,}_{=0,\,{\text {if Euler parameters are used}}} \end{aligned}$$

(54)

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {v_f}}=&\big ( {\varvec{I}}_{ \zeta } \otimes \overline{{\varvec{\omega }}} \big )^{\mathrm {T}} \left[ {\varvec{\overline{M}}}_{\! \widetilde{x} \widetilde{\psi }}^{\mathrm {T}} + {\varvec{\overline{M}}}_{\! \widetilde{\psi } \widetilde{\psi }} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \overline{{\varvec{\omega }}} + 2 {\varvec{\overline{M}}}_{\! \widetilde{\psi } \psi }^{\mathrm {T}} \big ( \dot{{\varvec{\zeta }}} \otimes {\varvec{I}} \big ) \overline{{\varvec{\omega }}} \nonumber \\&+ \underbrace{\left[ {\varvec{\overline{M}}}_{\! \widetilde{x} \psi }^{\mathrm {T}} + {\varvec{\overline{M}}}_{\! \widetilde{\psi } \psi }^{\mathrm {T}} \left( {\varvec{\zeta }} \otimes {\varvec{I}} \right) \right] \dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}}}_{=0,\,{\text {if Euler parameters are used}}} , \end{aligned}$$

(55)

where Eqs. (10) to (11), Eqs. (20), (27), and

$$\begin{aligned} \dot{\widetilde{\overline{{\varvec{c}}}}}_{\mathrm {f}} = \widetilde{\overline{{\varvec{\varPsi }}}} \big ( \dot{{\varvec{\zeta }}} \otimes {\varvec{I}} \big ) , \end{aligned}$$

(56)

since $\widetilde{\overline{{\varvec{\varPsi }}}}, \, {\varvec{I}} = \mathrm {const.}$, have been used. Note that $\dot{\overline{{\varvec{G}}}} \dot{{\varvec{\theta }}}={\varvec{0}}$ if Euler parameters are used for the rotational parametrization, see, for example, [17].

3.4 Nodal-based modally reduced FFRF applied generalized forces

The last step is to bring the applied forces in a slightly more efficient form. The applied nodal forces ${\varvec{f}}={\varvec{f}}(t)$ are known functions of time. Furthermore, forces are only applied to specific nodes of the discretized body. Hence, it is possible to express the nodal forces as “small” sums—compared to the unreduced model size of $3n_{\mathrm {n}}$—as

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {a_t}}&= \sum _{\begin{array}{c} i=1 \\ {\varvec{f}}^{(i)}\ne 0 \end{array}}^{n_{\mathrm {n}}} {\varvec{f}}^{(i)} , \end{aligned}$$

(57)

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {a_r}}&= {\varvec{\overline{G}}}^{\mathrm {T}} \sum _{\begin{array}{c} i=1 \\ {\varvec{f}}^{(i)}\ne 0 \end{array}}^{n_{\mathrm {n}}} \left[ \widetilde{\overline{{\varvec{x}}}}^{(i)} + \sum _{m=1}^{n_{\mathrm {m}}} \widetilde{\overline{{\varvec{\psi }}}}^{(i)}_m \zeta _m \right] {\varvec{A}}^{\mathrm {T}} {\varvec{f}}^{(i)} , \end{aligned}$$

(58)

$$\begin{aligned} {\varvec{\widehat{Q}}}_{\mathrm {a_f}}&= \sum _{\begin{array}{c} i=1 \\ {\varvec{f}}^{(i)}\ne 0 \end{array}}^{n_{\mathrm {n}}} \left[ \begin{matrix} {\overline{{\varvec{\psi }}}^{{(i)}^{\mathrm {T}}}_1} \\ \vdots \\ \overline{{\varvec{\psi }}}^{{(i)}^{\mathrm {T}}}_{n_{\mathrm {m}}} \end{matrix} \right] {\varvec{A}}^{\mathrm {T}} {\varvec{f}}^{(i)} , \end{aligned}$$

(59)

see Eqs. (5) to (6), Eqs. (10) to (11), Eq. (20), Eqs. (22) to (23) and Eq. (26). Furthermore, the fact that the transposed of a skew-symmetric matrix is its negative has been used.

Note that ${\varvec{\widehat{Q}}}_{\mathrm {a_t}}={\varvec{f}}_{\mathrm {res}}$ is the resultant of all nodal forces, and ${\varvec{A}}^{\mathrm {T}} {\varvec{f}}^{(i)}=\overline{{\varvec{f}}}^{(i)}$ is the applied force on node i expressed in the body frame.

3.5 From 3D to 2D spaces

The 2D modally reduced nodal-based FFRF is obtained in analogy to the 3D case shown in this section, but in a much more straightforward fashion, since the unreduced 2D FFRF, originally derived in [21], neither involve the quantity $\widetilde{\overline{{\varvec{c}}}}_{\mathrm {f}}$ nor operations with “large” matrices depending on the DOFs; the modally reduced nodal-based FFRF in 2D space is the topic of Sect. 4.

4 Modally reduced nodal-based FFRF in 2D space

The non-reduced 2D FFRF is derived in a similar fashion as outlined for the 3D case in Sect. 2. For clarity, the quantities are underlined in the planar case, leading to the EOMs [21]

$$\begin{aligned}&\left[ \begin{matrix} {{\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}}} &{} \quad {_{\theta }\! \! \; {\varvec{\underline{A}}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \, \overline{{\varvec{\underline{r}}}}_{\mathrm {f}} &{} \quad {\varvec{\underline{A}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \\ &{} \quad \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \, \overline{{\varvec{\underline{r}}}}_{\mathrm {f}} \quad &{} \quad \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} \, \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} \overline{{\varvec{\underline{M}}}} \\ {\text {sym.}} &{} \quad &{} \quad \overline{{\varvec{\underline{M}}}} \end{matrix} \right] \left[ \begin{matrix} {\ddot{{\varvec{\underline{q}}}}_{\mathrm {t}}} \\ \ddot{{\underline{\theta }}} \\ \ddot{\overline{{\varvec{\underline{c}}}}}_{\mathrm {f}} \end{matrix} \right] =- \left[ \begin{matrix} {{\varvec{0}}} &{} {\varvec{0}} &{} {\varvec{0}} \\ {\varvec{0}} &{} 0 &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} &{} \overline{{\varvec{\underline{K}}}} \\ \end{matrix} \right] \left[ \begin{matrix} {{\varvec{\underline{q}}}_{\mathrm {t}}} \\ \underline{\theta } \\ {\varvec{\overline{\underline{c}}}}_{\mathrm {f}} \end{matrix} \right] \nonumber \\&\quad + \left[ \begin{matrix} {_{\theta }\! \! \; {\varvec{\underline{A}}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \left( \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\overline{{\varvec{\underline{r}}}}}_{\mathrm {f}} \dot{\underline{\theta }}^2 - 2 \dot{{\overline{{\varvec{\underline{c}}}}}}_{\mathrm {f}} \dot{\underline{\theta }} \right) \\ \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \left( \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\overline{{\varvec{\underline{r}}}}}_{\mathrm {f}} \dot{\underline{\theta }}^2 - 2 \dot{{\overline{{\varvec{\underline{c}}}}}}_{\mathrm {f}} \dot{\underline{\theta }} \right) \\ \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \left( \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\overline{{\varvec{\underline{r}}}}}_{\mathrm {f}} \dot{\underline{\theta }}^2 - 2 \dot{{\overline{{\varvec{\underline{c}}}}}}_{\mathrm {f}} \dot{\underline{\theta }} \right) \end{matrix} \right] + \left[ \begin{matrix} {{\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}}} \\ \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} {_\theta \! \! \;{\varvec{\underline{A}}}_{\mathrm {bd}}^{\mathrm {T}}} \\ {\varvec{\underline{A}}}_{\mathrm {bd}}^{\mathrm {T}} \end{matrix} \right] {\varvec{\underline{f}}} - \dfrac{\partial {\varvec{g}}}{\partial {\varvec{\underline{q}}}^{\mathrm {T}}} {\varvec{\lambda }} , \end{aligned}$$

(60)

with $\underline{\theta }$ denoting the only (scalar) rotational parameter in 2D,

$$\begin{aligned} _{\theta }\!\! \;{\varvec{\underline{A}}}=\frac{\partial {\varvec{\underline{A}}}}{\partial \underline{\theta }}=- {\varvec{\underline{A}}} \, \widetilde{\underline{{\varvec{I}}}} \quad {\text {with}} \quad \widetilde{\underline{{\varvec{I}}}}=- \widetilde{\underline{{\varvec{I}}}}^{\mathrm {T}}=\left[ \begin{matrix} \; \; 0 \; &{} \; 1 \\ -1 \; &{} \; 0 \end{matrix} \right] , \end{aligned}$$

(61)

and the corresponding block diagonal matrices $_{\theta }\!\! \;{\varvec{\underline{A}}}_{\mathrm {bd}}$, $\widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}}$. Note that underlined quantities represent the associated 2D counterparts of the quantities defined for the 3D case and are, therefore, different in size. Employing a (flexible) coordinate reduction according to Eq. (21) yields

$$\begin{aligned}&\left[ \begin{matrix} {{\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}}} \overline{{\varvec{\underline{M}}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}} &{} \quad {_{\theta }\! \! \;{\varvec{\underline{A}}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}}\, \overline{{\varvec{\underline{r}}}}_{\mathrm {f}} &{} \quad {\varvec{\underline{A}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \, \underline{\overline{{\varvec{\varPsi }}}} \\ &{} \quad \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \, \overline{{\varvec{\underline{r}}}}_{\mathrm {f}} \quad &{} \quad \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} \, \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} \overline{{\varvec{\underline{M}}}} \, \underline{\overline{{\varvec{\varPsi }}}} \\ {\text {sym.}} &{} \quad &{} \quad {\varvec{\underline{\overline{\varPsi }}}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \, \underline{\overline{{\varvec{\varPsi }}}} \end{matrix} \right] \left[ \begin{matrix} {\ddot{{\varvec{\underline{q}}}}_{\mathrm {t}}} \\ \ddot{{\underline{\theta }}} \\ \ddot{{\varvec{\zeta }}} \end{matrix} \right] =- \left[ \begin{matrix} {{\varvec{0}}} \;\;&{} {\varvec{0}} \;\;&{} {\varvec{0}} \\ {\varvec{0}} \;\;&{} 0 \;\;&{} {\varvec{0}} \\ {\varvec{0}} \;\;&{} {\varvec{0}} \;\;&{} {\varvec{\underline{\overline{\varPsi }}}}^{\mathrm {T}} \overline{{\varvec{\underline{K}}}} \, {\varvec{\underline{\overline{\varPsi }}}} \\ \end{matrix} \right] \left[ \begin{matrix} {{\varvec{\underline{q}}}_{\mathrm {t}}} \\ \underline{\theta } \\ {\varvec{\zeta }} \end{matrix} \right] \nonumber \\&\quad + \left[ \begin{matrix} {}_{\theta }\!\! \;{\varvec{\underline{A}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \left( \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\overline{{\varvec{\underline{r}}}}}_{\mathrm {f}} \dot{\underline{\theta }}^2 - 2 \dot{{\overline{{\varvec{\underline{c}}}}}}_{\mathrm {f}} \dot{\underline{\theta }} \right) \\ \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \left( \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\overline{{\varvec{\underline{r}}}}}_{\mathrm {f}} \dot{\underline{\theta }}^2 - 2 \dot{{\overline{{\varvec{\underline{c}}}}}}_{\mathrm {f}} \dot{\underline{\theta }} \right) \\ {\varvec{\underline{\overline{\varPsi }}}}^{\mathrm {T}} \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}}^{\mathrm {T}} \overline{{\varvec{\underline{M}}}} \left( \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\overline{{\varvec{\underline{r}}}}}_{\mathrm {f}} \dot{\underline{\theta }}^2 - 2 \dot{{\overline{{\varvec{\underline{c}}}}}}_{\mathrm {f}} \dot{\underline{\theta }} \right) \end{matrix} \right] + \left[ \begin{matrix} {{\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}}} \\ \overline{{\varvec{\underline{r}}}}_{\mathrm {f}}^{\mathrm {T}} {_\theta \!\! \; {\varvec{\underline{A}}}_{\mathrm {bd}}^{\mathrm {T}}} \\ {\varvec{\underline{\overline{\varPsi }}}}^{\mathrm {T}} {\varvec{\underline{A}}}_{\mathrm {bd}}^{\mathrm {T}} \end{matrix} \right] {\varvec{\underline{f}}} - \dfrac{\partial {\varvec{g}}}{\partial {\varvec{\underline{p}}}^{\mathrm {T}}} {\varvec{\lambda }}. \end{aligned}$$

(62)

In line with Eq. (23) and Sect. 3, we obtain—in a straightforward manner since the 2D equations are simpler and do neither involve the quantity $\widetilde{\overline{{\varvec{c}}}}_{\mathrm {f}}$ nor “large” matrices depending on the DOFs,

$$\begin{aligned} {\varvec{\widehat{\underline{M}}}}_{\mathrm {tt}}&= m \underline{{\varvec{I}}} , \end{aligned}$$

(63)

$$\begin{aligned} {\varvec{\widehat{\underline{M}}}}_{\mathrm {ff}}&= {\varvec{\overline{\underline{M}}}}_{ \psi {\psi }} , \end{aligned}$$

(64)

$$\begin{aligned} {\varvec{\widehat{\underline{M}}}}_{\mathrm {tf}}&= {\varvec{\underline{A}}} \, {\varvec{\overline{\underline{M}}}}_{ \phi {\psi }} , \end{aligned}$$

(65)

$$\begin{aligned} {\varvec{\widehat{\underline{M}}}}_{\mathrm {rf}}&= -{\varvec{\overline{\underline{m}}}}_{\widetilde{\psi } x }^{\mathrm {T}} + {\varvec{\zeta }}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}}_{ \widetilde{\psi } \psi } , \end{aligned}$$

(66)

$$\begin{aligned} {\varvec{\widehat{\underline{M}}}}_{\mathrm {tr}}&= {_{\theta }\!\! \;{\varvec{\underline{A}}}} \left( m {\varvec{\underline{\overline{\chi }}}}_{\mathrm {u}} + {\varvec{\overline{\underline{M}}}}_{ \phi {\psi }} {\varvec{\zeta }} \right) , \end{aligned}$$

(67)

$$\begin{aligned} \widehat{\underline{M}}_{\mathrm {rr}}&= \overline{\underline{\varTheta }}_{\mathrm {u}} + 2 {\varvec{\overline{\underline{m}}}}_{\psi x}^{\mathrm {T}} {\varvec{\zeta }} + {\varvec{\zeta }}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}}_{\psi \psi } {\varvec{\zeta }} , \end{aligned}$$

(68)

and

$$\begin{aligned} {\varvec{\widehat{\underline{Q}}}}_{\mathrm {v}}=\left[ \begin{matrix} {{\varvec{\underline{A}}}} \left( m {\varvec{\overline{\underline{\chi }}}}_{\mathrm {u}} + {\varvec{\overline{\underline{M}}}}_{\phi \psi } {\varvec{\zeta }} \right) \dot{\underline{\theta }}^2 - 2 \, {_\theta \!\! \;{\varvec{\underline{A}}}} \, {\varvec{\overline{\underline{M}}}}_{\phi \psi } \dot{{\varvec{\zeta }}} \dot{\underline{\theta }} \\ {\varvec{\zeta }}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}}_{\widetilde{\psi } \psi } {\varvec{\zeta }} \dot{\underline{\theta }}^2 - 2 \left( {\varvec{\overline{\underline{m}}}}_{\psi x}^{\mathrm {T}} + {\varvec{\zeta }}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}}_{\psi \psi } \right) \dot{{\varvec{\zeta }}} \dot{\underline{\theta }} \\ \left( {\varvec{\overline{\underline{m}}}}_{\psi x} + {\varvec{\overline{\underline{M}}}}_{\psi \psi } {\varvec{\zeta }} \right) \dot{\underline{\theta }}^2 - 2 {\varvec{\overline{\underline{M}}}}_{\widetilde{\psi } \psi } \dot{{\varvec{\zeta }}} \dot{\underline{\theta }} \end{matrix} \right] , \end{aligned}$$

(69)

with

$$\begin{aligned} m \underline{{\varvec{I}}}&= {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\underline{\varPhi }}}_{\mathrm {t}} \in \mathbb {R}^{2 \times 2} , \end{aligned}$$

(70)

$$\begin{aligned} {\varvec{\overline{\underline{\chi }}}}_{\mathrm {u}}&= \frac{1}{m} {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\overline{\underline{x}}}} \in \mathbb {R}^{2 \times 1}, \end{aligned}$$

(71)

$$\begin{aligned} \overline{\underline{\varTheta }}_{\mathrm {u}}&= {\varvec{\overline{\underline{x}}}}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\overline{\underline{x}}}} \in \mathbb {R}^{1 \times 1}, \end{aligned}$$

(72)

$$\begin{aligned} {\varvec{\overline{\underline{M}}}}_{\psi \psi }&= {\varvec{\overline{\underline{\varPsi }}}}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\overline{\underline{\varPsi }}}} \in \mathbb {R}^{n_{\mathrm {m}} \times n_{\mathrm {m}}} , \end{aligned}$$

(73)

$$\begin{aligned} {\varvec{\overline{\underline{M}}}}_{\widetilde{\psi } \psi }&= {\varvec{\overline{\underline{\varPsi }}}}^{\mathrm {T}} \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\overline{\underline{\varPsi }}}} \in \mathbb {R}^{n_{\mathrm {m}} \times n_{\mathrm {m}}} , \end{aligned}$$

(74)

$$\begin{aligned} {\varvec{\overline{\underline{M}}}}_{\phi \psi }&= {\varvec{\underline{\varPhi }}}_{\mathrm {t}}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\overline{\underline{\varPsi }}}} \in \mathbb {R}^{2 \times n_{\mathrm {m}}} , \end{aligned}$$

(75)

$$\begin{aligned} {\varvec{\overline{\underline{m}}}}_{\psi x}&= {\varvec{\overline{\underline{\varPsi }}}}^{\mathrm {T}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\overline{\underline{x}}}} \in \mathbb {R}^{n_{\mathrm {m}} \times 1} , \end{aligned}$$

(76)

$$\begin{aligned} {\varvec{\overline{\underline{m}}}}_{\widetilde{\psi } x}&= {\varvec{\overline{\underline{\varPsi }}}}^{\mathrm {T}} \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}} {\varvec{\overline{\underline{M}}}} \, {\varvec{\overline{\underline{x}}}} \in \mathbb {R}^{n_{\mathrm {m}} \times 1 } , \end{aligned}$$

(77)

since

$$\begin{aligned} {\varvec{\overline{\underline{M}}}}^{\mathrm {T}}&={\varvec{\overline{\underline{M}}}} , \end{aligned}$$

(78)

$$\begin{aligned} {\varvec{\overline{\underline{M}}}} \, \widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}}&=\widetilde{\underline{{\varvec{I}}}}_{\mathrm {bd}}{\varvec{\overline{\underline{M}}}}, \end{aligned}$$

(79)

$$\begin{aligned} {\varvec{\overline{\underline{x}}}}^{(i)^{\mathrm {T}}} \widetilde{\underline{{\varvec{I}}}} \, {\varvec{\overline{\underline{x}}}}^{(i)}&= 0. \end{aligned}$$

(80)

Furthermore, Eq. (61) and the fact that $\widetilde{{\varvec{\underline{I}}}}$ is an orthogonal matrix have been used to obtain Eq. (69). Note that the tilde operator has a different “meaning” in 2D, see Eq. (61). This depicts how to calculate the nodal-based FFRF invariants for 2D problems, i.e. without integrals and without a lumped mass approximation.

The elastic forces have exactly the same form as in the 3D case, but involve, of course, the 2D stiffness and modal matrix, see Eqs. (24) to (25).

Likewise, the applied forces may be also written as “small” sums in line with the 3D case, where ${\varvec{\widehat{\underline{Q}}}}_{\mathrm {a_t}}$ and ${\varvec{\widehat{\underline{Q}}}}_{\mathrm {a_f}}$ have again exactly the same form but involve the 2D rotation matrix, modes, and nodal force vectors, see Eqs. (57) and (59). Finally,

$$\begin{aligned} \widehat{\underline{Q}}_{\mathrm {a_r}} = \sum _{\begin{array}{c} i=1 \\ {\varvec{\underline{f}}}^{(i)}\ne 0 \end{array}}^{n_{\mathrm {n}}} \left[ {\varvec{\overline{\underline{x}}}}^{(i)^{\mathrm {T}}} + \sum _{m=1}^{n_{\mathrm {m}}} \underline{\overline{{\varvec{\psi }}}}^{(i)^{\mathrm {T}}}_m \zeta _m \right] {_\theta \!\! \;{\varvec{\underline{A}}}^{\mathrm {T}}} \underline{{\varvec{f}}}^{(i)} , \end{aligned}$$

(81)

see Eqs. (58) and (62).

5 Numerical example

5.1 Slider–crank mechanism

It has been shown by [20] that the non-reduced nodal-based FFRF and the conventional FFRF—the inertia shape integral formulation—can be derived from one another without any approximations, which confirms the validity of the nodal-based framework and derivations presented in [20, 21]. The following comparison between the modally reduced and non-reduced nodal-based FFRF should reinforce that the presented model order reduction and EOMs within this paper are equally reliable.

The underlying FE models of the flexible bodies with their floating frames are displayed in Fig. 1a. The bodies (con rod/crank) were discretized with 136/104 quadratic hexahedral elements yielding 935/665 nodes in total; their dimensions are listed in Table 1 and their mechanical properties are as follows:

$\bullet$:

Rayleigh damping matrix⁵, $\overline{{\varvec{D}}}= 10^{-4} \cdot \overline{{\varvec{M}}} + 10^{-5} \cdot \overline{{\varvec{K}}} \,\mathrm {N} \mathrm {s} \mathrm {m}^{-1}$

$\bullet$:

Young’s modulus, $E=70\,\mathrm {GPa}$

$\bullet$:

Poisson’s ratio, $\nu =0.3$

$\bullet$:

density, $\rho =2710\,\mathrm {kg} \mathrm {m}^{-3}$

The flexible bodies are connected to other components via standard interpolation constraint elements (RBE3s), since the definition of constraints is not influenced by the modal reduction approach. Using this kind of multipoint constraints (MPCs), the average of the nodal displacements of the edge nodes of the bearing bolts and holes define the motion of a reference point, which is located at each centre of the corresponding circle (edge). These reference points are then constrained via spherical joints (six in total, i.e. one for each MPC or two for each connection between two bodies) to connect the bodies to each other or to the ground. The node sets included for the two MPCs used to connect the crank to the ground are shown in Fig. 1b⁶ (grey cubes).

Fig. 1

Flexible multibody system employed in the numerical example: a The meshed con rod (left) and the meshed crank (right) are shown with their local floating frames and their dimensions are listed in Table 1. b The assembled system consists out of the flexible con rod, the flexible crank, and the rigid piston; a drive torque is applied to the floating frame of the crank (red arrows). Please note the simplified visualization of sub-figure (b), where only the corner nodes of the elements are connected with flat surfaces

Note that in order to attach the floating frames to the flexible bodies in the non-reduced formulation, Tisserand constraints, i.e.

$$\begin{aligned} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \, \overline{{\varvec{c}}}_{\mathrm {f}}&= {\varvec{0}} , \end{aligned}$$

(82)

$$\begin{aligned} \widetilde{\overline{{\varvec{x}}}}^{\mathrm {T}} \overline{{\varvec{M}}} \, \overline{{\varvec{c}}}_{\mathrm {f}}&= {\varvec{0}} , \end{aligned}$$

(83)

are used, and in the modally reduced formulation, the rigid body modes are excluded from the reduction basis.

Table 1 Dimensions of the flexible bodies (see Fig. 1a) employed in the numerical example

The rigid piston (see grey cylinder in Fig. 1b) is simply modelled as a point mass of 0.1 kg, which is constrained to move along a straight line.

A drive torque (see red arrows in Fig. 1b) of 2.5 Nm is then applied to the floating frame of the crank for the first 0.025 s; after that time, the torque drops to zero. No gravity is considered during the simulation.

The proposed formulation, with and without modal reduction, has been implemented in the open source flexible multibody research code EXUDYN; the code itself as well as the slider–crank example presented in this paper may be downloaded from GitHub (https://github.com/jgerstmayr/EXUDYN), where the interested reader can find the thorough model set-up.

The system is integrated with Newmark’s method, where the constraints are fulfilled on the velocity level (index two), and the step size is $h=2.5 \times 10^{-5}$ s; see the documentation of EXUDYN [4] for further information. The simulation time is 0.07 s, which corresponds to almost 6 crank revolutions; see Fig. 2a and b for a better understanding of the piston’s translational displacement magnitude $q_{\mathrm {t,p}}$ and the angular velocity magnitude $\overline{\omega }_{\mathrm {c}}$ of the crank’s floating frame.

Figure 2c depicts the flexible nodal displacement magnitude $\overline{c}_{\mathrm {f,r}}^{(190)}$ of the con rod’s mid node ($\overline{{\varvec{x}}}_{\mathrm {r}}^{(190)}=[0 \; 40 \; 5]^{\mathrm {T}}$ mm, see Fig. 1a and Table 1). The figure shows the convergence of the modally reduced nodal-based FFRF to the non-reduced version with an increasing number of flexible modes included in the reduction basis. It can be seen that already the first eight eigenmodes (see Table 2) capture the deformation behaviour qualitatively; however, the magnitude of the deformation is smaller, as expected, due to the incomplete solution basis, which makes the problem stiffer than the non-reduced one. Figure 2c also illustrates that the deformation increases if more modes are included in the reduction basis, and that the reduced formulation will eventually converge to the non-reduced one. It shall be noted, however, that a better convergence may be obtained using, for example, Hurty/Craig–Bampton modes, since only free vibration modes are included in the reduction basis in this example, and it is well known that free modes are a poor choice for constrained systems and add artificial stiffness to the problem. Nevertheless, the example serves its purpose, i.e. the validation of the algebraic manipulations required to derive the FFRF invariants without a lumped mass approach.

Fig. 2

Time histories of representative quantities associated with the slider–crank mechanism; calculated with an increasing number of flexible modes included in the reduction basis (CMS-8, CMS-16, CMS-256) and without modal reduction (FFRF-full)

Figure 2 also shows that the rigid body motion is less affected by the number of modes included in the reduction basis than the flexible deformation (compare Figs. 2a and b with Fig. 2c).

Note that the paper is mainly devoted to the novel derivation of the modally reduced FFRF without inertia shape integrals and without a lumped mass approach; a thorough analysis of the differences between the lumped and consistent mass approach, as well as the investigation of various benchmark examples is the scope of future research. Nevertheless, a brief presentation of the dangers of the lumped mass approach is illustrated in Sect. 5.2.

5.2 A short note on the consequences of a lumped mass approach

There are several lumping techniques available, such as nodal quadrature, row-sum lumping, or the so-called special lumping technique, where only the latter ensures that the arising lumped FE mass matrix is positive definite for any element type [2], which is important since negative nodal masses are physically absurd and their presence may lead to numerical troubles⁷. The special lumping technique [7] also yields, by construction, the correct total mass of the underlying body; the method is usually defined on an element level; however, we use a global equivalent, which enables us to calculate the global lumped FE mass matrix from the global consistent FE mass matrix as follows:

$$\begin{aligned} {\varvec{\overline{M}}}_{\mathrm {lump}} = \mu \, \mathrm {diag}\left( \mathrm {diag}\left( \overline{{\varvec{M}}}\right) \right) \quad {\text {such that}} \quad m = m_{\mathrm {lump}} , \end{aligned}$$

(84)

where $\mathrm {diag}\left( \mathrm {diag}\left( \overline{{\varvec{M}}}\right) \right)$ is a diagonal matrix with the diagonal elements of $\overline{{\varvec{M}}}$. The scaling parameter $\mu$ follows from the requirement of equal total masses $m = m_{\mathrm {lump}}$, i.e.

$$\begin{aligned} m ={\varvec{\phi }}_{\mathrm {t}l}^{\mathrm {T}} \overline{{\varvec{M}}} {\varvec{\phi }}_{\mathrm {t}l} {\mathop {=}\limits ^{!}} m_{\mathrm {lump}} = {\varvec{\phi }}_{\mathrm {t}l}^{\mathrm {T}} \overline{{\varvec{M}}}_{\mathrm {lump}} {\varvec{\phi }}_{\mathrm {t}l} \quad {\mathop {\Rightarrow }\limits ^{(84)}} \quad \mu = \frac{{\varvec{\phi }}_{\mathrm {t}l}^{\mathrm {T}} \overline{{\varvec{M}}} {\varvec{\phi }}_{\mathrm {t}l}}{{\varvec{\phi }}_{\mathrm {t}l}^{\mathrm {T}} \mathrm {diag}\left( \mathrm {diag}\left( \overline{{\varvec{M}}}\right) \right) {\varvec{\phi }}_{\mathrm {t}l}} , \end{aligned}$$

(85)

where

$$\begin{aligned} {\varvec{\phi }}_{\mathrm {t}l}=\left[ \varvec{e}_l^{\mathrm {T}} \quad \varvec{e}_l^{\mathrm {T}} \quad \dots \quad \varvec{e}_l^{\mathrm {T}} \right] ^{\mathrm {T}} \quad {\text {with}} \quad l=1,2,3, \end{aligned}$$

(86)

is a rigid body translation mode in any coordinate direction, i.e. any column of ${\varvec{\varPhi }}_{\mathrm {t}}$, see Eq. (5).

We can now compare characteristic quantities to identify the influence of the lumped mass approach. The rigid body motion is characterized by the total mass m, the local position of the centre of mass ${\varvec{\overline{\chi }}}_{\mathrm {u}}$, and the local inertia tensor ${\varvec{\overline{\varTheta }}}_{\mathrm {u}}$, and the mass and stiffness distribution of the flexible bodies can be characterized by the eigenfrequencies $\omega _m$. Hence, the percentage error $e_{\%}$ of these characteristic quantities are compared for the con rod (see Fig. 1a).

The eigenfrequencies are obtained via the generalized eigenvalue problem, i.e.

$$\begin{aligned} \omega ^2_m \overline{{\varvec{M}}}\, \overline{{\varvec{\psi }}}_m =\overline{{\varvec{K}}} \, \overline{{\varvec{\psi }}}_m , \end{aligned}$$

(87)

and the deviations between the frequencies obtained with the consistent and lumped FE mass matrix, see Eqs. (84) to (85), are depicted in Fig. 3 for the first 50 flexible modes; the model assurance criterion (MAC) was used to ensure that the frequencies of corresponding modes are compared.

Fig. 3

Percentage error $e_{\%}$ between the eigenfrequencies of the flexible modes calculated with the consistent and lumped FE mass matrix, see Eqs. (84) to (85)

Figure 3 reveals that the error grows with increasing frequency; the “zigzag” behaviour can be attributed to the types of the modes (bending, torsion, axial), see also Table 2. For example, the error of the second torsion frequency is higher than the error of the first torsion frequency, but the errors of the first $x-$ and $z-$bending frequencies (mode number 1 and 2) are smaller than the error of the first torsion frequency (mode number 3); within each mode type, the deviation increases monotonically.

Table 2 First ten flexible eigenmodes of the con rod calculated with the consistent FE mass matrix

Table 3 shows the errors of the rigid body inertia quantities, see Eqs. (36) to (39), between the lumped and consistent mass approach, see Eqs. (84) to (85). The total mass is, by construction of the lumped mass matrix, the same in both cases, as already mentioned; hence, the error is zero within machine precision. The largest error in the centre of mass position is approximately three percent, and the significant errors in the inertia tensor components are approximately three, seven, and 57 percent. The large errors here can be attributed to the relatively coarse mesh employed for the simulations⁸.

Table 3 Percentage error $e_{\%}$ between the total mass m, the centre of mass position ${\varvec{\overline{\chi }}}_{\mathrm {u}}$, and the inertia tensor ${\varvec{\overline{\varTheta }}}_{\mathrm {u}}$ calculated with the consistent and lumped FE mass matrix, see Eqs. (36) to (39) and Eqs. (84) to (85)

6 Conclusions

The present paper extended the recently developed nodal-based floating frame of reference formulation, which avoids inertia shape integrals and does not rely on a lumped mass approximation, by the proper modal reduction to reduce the overall system size down to order of the number of modes included in the reduction basis. The presented inertia-integral-free modally reduced nodal-based equations are now given in a similar form as implemented by commercial flexible multibody packages, i.e. in terms of so-called floating frame invariants, but without the necessity of a lumped mass approximation. The invariants can now be calculated directly—without approximations—by simple (offline) matrix multiplications between the modal reduction matrix, the nodal coordinate vector, and the consistent finite element mass matrix prior time integration. The derived equations are given in a simple and explicit form ready for computer implementations for 2D and 3D spaces.

Appendix A Rigid body inertia quantities extracted from the FE mass matrix

To describe the dynamics of a rigid body, we need three constant inertia quantities, i.e. the total mass

$$\begin{aligned} m= \int _{\mathcal {V}} \rho {\mathrm {d}} \mathcal {V} , \end{aligned}$$

(88)

the position of the centre of mass w.r.t. the body frame

$$\begin{aligned} \overline{{\varvec{\chi }}}_{\mathrm {u}}= \frac{1}{m}\int _{\mathcal {V}} \rho \overline{{\varvec{\chi }}} \mathrm {d} \mathcal {V} , \end{aligned}$$

(89)

and the inertia tensor w.r.t. the body frame

$$\begin{aligned} \overline{{\varvec{\varTheta }}}_{\mathrm {u}}= \int _{\mathcal {V}} \rho \widetilde{\overline{{\varvec{\chi }}}}^{\mathrm {T}} \widetilde{\overline{{\varvec{\chi }}}} {\mathrm {d}} \mathcal {V} , \end{aligned}$$

(90)

with the density $\rho$, the volume $\mathcal {V}$, and the continuous position $\overline{{\varvec{\chi }}}$ of a material point of the body w.r.t. the floating frame. This section briefly shows that all three quantities may be calculated with the consistent FE mass matrix $\overline{{\varvec{M}}}$ and the vector of nodal coordinates $\overline{{\varvec{x}}}$.

To do so, we first recall the expression of the FE mass matrix

$$\begin{aligned} \overline{{\varvec{M}}}=\int _{\mathcal {V}} \rho \overline{{\varvec{S}}}^{\mathrm {T}} \overline{{\varvec{S}}} \,{\mathrm {d}} \mathcal {V} , \end{aligned}$$

(91)

with the global FE shape function matrix

$$\begin{aligned} \overline{{\varvec{S}}} =\left[ \begin{matrix} {\overline{S}^{(1)} {\varvec{I}}}&\dots&\overline{S}^{(n_{\mathrm {n}})} {\varvec{I}} \end{matrix} \right] \in \mathbb {R}^{3 \times 3 n_{\mathrm {n}}} , \end{aligned}$$

(92)

where partition of unity holds, i.e.

$$\begin{aligned} \sum _{i=1}^{n_{\mathrm {n}}} \overline{S}^{(i)} \equiv 1 \quad {\mathop {\Rightarrow }\limits ^{(5)}_{(92)}} \quad \overline{{\varvec{S}}} {\varvec{\varPhi }}_{\mathrm {t}} \equiv {\varvec{I}}. \end{aligned}$$

(93)

Since the same shape functions are used to interpolate the nodal coordinates,

$$\begin{aligned} \overline{{\varvec{\chi }}} =\overline{{\varvec{S}}} \,\overline{{\varvec{x}}} \end{aligned}$$

(94)

holds, and since $\overline{{\varvec{S}}}$ is composed out of $\overline{S}^{(i)}{\varvec{I}}$-blocks,

$$\begin{aligned} \widetilde{\overline{{\varvec{\chi }}}} =\overline{{\varvec{S}}}\, \widetilde{\overline{{\varvec{x}}}}. \end{aligned}$$

(95)

Given this information and the fact that

$$\begin{aligned} \overline{{\varvec{x}}} , {\varvec{\varPhi }}_{\mathrm {t}} = {\text {const.,}} \end{aligned}$$

(96)

and can therefore be brought inside the integrals, it is easy to show that

$$\begin{aligned} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} {\varvec{\varPhi }}_{\mathrm {t}}&\;{\mathop {=}\limits ^{(91)}} \;{\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \int _{\mathcal {V}} \rho \overline{{\varvec{S}}}^{\mathrm {T}} \overline{{\varvec{S}}} \, {\mathrm {d}} \mathcal {V} \, {\varvec{\varPhi }}_{\mathrm {t}} \end{aligned}$$

(97)

$$\begin{aligned}&{\mathop {=}\limits ^{(96)}} \int _{\mathcal {V}} \rho {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{S}}}^{\mathrm {T}} \overline{{\varvec{S}}} {\varvec{\varPhi }}_{\mathrm {t}} \,\mathrm {d} \mathcal {V} \end{aligned}$$

(98)

$$\begin{aligned}&{\mathop {=}\limits ^{(93)}}\int _{\mathcal {V}} \rho \, {\mathrm {d}} \mathcal {V} {\varvec{I}} \end{aligned}$$

(99)

$$\begin{aligned}&{\mathop {=}\limits ^{(88)}}\; m {\varvec{I}} , \end{aligned}$$

(100)

and

$$\begin{aligned} {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{M}}} \overline{{\varvec{x}}}& \;{\mathop {=}\limits ^{(91)}} \; {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \int _{\mathcal {V}} \rho \overline{{\varvec{S}}}^{\mathrm {T}} \overline{{\varvec{S}}} \mathrm {d} \mathcal {V} \, \overline{{\varvec{x}}} \end{aligned}$$

(101)

$$\begin{aligned}&{\mathop {=}\limits ^{(96)}}\int _{\mathcal {V}} \rho {\varvec{\varPhi }}_{\mathrm {t}}^{\mathrm {T}} \overline{{\varvec{S}}}^{\mathrm {T}} \overline{{\varvec{S}}} \overline{{\varvec{x}}}\, {\mathrm {d}} \mathcal {V} \end{aligned}$$

(102)

$$\begin{aligned}& {\mathop {= }\limits ^{(93)}_{(94)}} \int _{\mathcal {V}} \rho \overline{{\varvec{\chi }}} \, {\mathrm {d}} \mathcal {V} \end{aligned}$$

(103)

$$\begin{aligned}&{\mathop {=}\limits ^{(89)}} \;m \overline{{\varvec{\chi }}}_{\mathrm {u}}, \end{aligned}$$

(104)

and

$$\begin{aligned} \widetilde{\overline{{\varvec{x}}}}^{\mathrm {T}} \overline{{\varvec{M}}} \, \widetilde{\overline{{\varvec{x}}}}&\; {\mathop {=}\limits ^{(91)}}\; \widetilde{\overline{{\varvec{x}}}}^{\mathrm {T}} \! \int _{\mathcal {V}} \rho \overline{{\varvec{S}}}^{\mathrm {T}} \overline{{\varvec{S}}} \, {\mathrm {d}} \mathcal {V} \, \widetilde{\overline{{\varvec{x}}}} \end{aligned}$$

(105)

$$\begin{aligned}&{\mathop {=}\limits ^{(96)}} \int _{\mathcal {V}} \rho \widetilde{\overline{{\varvec{x}}}}^{\mathrm {T}} \overline{{\varvec{S}}}^{\mathrm {T}} \overline{{\varvec{S}}} \, \widetilde{\overline{{\varvec{x}}}} \,{\mathrm {d}} \mathcal {V} \end{aligned}$$

(106)

$$\begin{aligned}&{\mathop {=}\limits ^{(95)}}\int _{\mathcal {V}} \rho \widetilde{\overline{{\varvec{\chi }}}}^{\mathrm {T}} \widetilde{\overline{{\varvec{\chi }}}}\, {\mathrm {d}} \mathcal {V} \end{aligned}$$

(107)

$$\begin{aligned}&{\mathop {=}\limits ^{(90)}}\; \overline{{\varvec{\varTheta }}}_{\mathrm {u}}. \end{aligned}$$

(108)