1 Introduction

Already in their edited volume on Mathematics Teacher Noticing in 2011, Sherin, Jacobs, and Philipp raised the question about the context specificity of noticing as one of the key considerations in corresponding research. Regarding different content areas within mathematics, they asked in particular: “If a mathematics teacher has expertise in noticing, will he or she have noticing expertise for all mathematical areas and instructional contexts? For example, do the teaching of algebra and the teaching of fractions require different noticing skills?” (Sherin, Jacobs, and Philipp 2011, p. 11). How teacher noticing regarding different mathematical content areas is related appears to be an essential question for the development of noticing as well as for corresponding research.

Until today, mathematics teacher noticing has been investigated in a broad range of contexts, also regarding mathematical content areas and different grades (e.g., early numeracy, geometry, fractions, algebra, linear functions, etc.; cf. Stahnke, Schueler, and Roesken-Winter 2016; Schack, Fisher, and Wilhelm 2017). There is a broad consensus that what teachers attend to and how they make sense of it is an important prerequisite for providing students with adequate learning situations and learning support (e.g., Sherin et al. 2011; Schoenfeld 2011). Several studies provide evidence that teacher noticing informs teaching decisions (Schoenfeld 2011) and is therefore highly relevant for instructional quality and student learning (e.g., Kersting et al. 2012). However, there is still a lack of empirical studies that allow a systematic comparison of how teachers’ noticing regarding different mathematical content areas is related. The question of whether teachers need different noticing abilities for different mathematical content areas has, therefore, remained largely unanswered. Investigating the role of context for teacher noticing, however, does not involve only considerations on the level of different mathematical content areas. On a more fine-grained level, namely the level of the classroom situation with the help of which teacher noticing is investigated, context might also play a critical role for the investigation of teacher noticing: different lessons contain different contexts in the sense of varying tasks, mathematical content, representations, teacher-student interaction, etc. Considering context on this level raises the question of whether teachers draw on the same noticing abilities independently from different classroom situations so that a more general competence construct can be inferred.

In our prior studies (Friesen and Kuntze 2016, 2018, 2020; Friesen 2017), we have conducted research related to an aspect of mathematics teacher noticing focusing on the use of multiple representations in classroom situations, in particular on how representations of mathematical objects are dealt with in student–teacher interaction. We have used the term “teachers’ analysing of classroom situations” for describing the knowledge-based process, in which relevant observations in a classroom situation (here: related to the use of multiple representations) have to be connected with professional knowledge (here: on using multiple representations) in order to make sense of what has been observed (Kuntze, Dreher, and Friesen 2015). There is thus a clear parallelism to the concept of teacher noticing introduced by Sherin, Jacobs, and Philipp (2011), encompassing teachers’ selective attention and knowledge-based reasoning as parts of a cyclical and interrelated process (van Es and Sherin 2002). However, since the notion of noticing has been conceptualised in very different ways until today (Sherin 2017), we use the term teachers’ analysis of classroom situations in our research to highlight that teachers have to connect their observations to professional knowledge under a specific focus (here: multiple representations).

In prior studies, we investigated secondary teachers’ analyses using classroom situations from the content area of fractions in grade six (e.g., Friesen and Kuntze 2016, 2018). Since the integration of multiple representations of fractions is regarded as particularly significant for students’ conceptual understanding of fractions (e.g., Charalambous and Pitta-Pantazi 2007), we were particularly interested in how teachers analyse vignettes of classroom practice where students are not sufficiently supported in connecting multiple representations of fractions to one other. Following up on the question of whether teacher noticing is context specific regarding mathematical content areas, we report here on our expanded research in which we included functions. Functions provide another content area in which the integration of multiple representations plays a crucial role for students’ conceptual understanding (e.g., Nitsch et al. 2015). Accordingly, we complemented the vignette-based test instrument we designed for the content area of fractions (e.g., Friesen 2017) by adding classroom vignettes from the content area of functions.

Since this study examines an aspect of teacher noticing regarding the use of multiple representations in the context of fractions and functions, we first outline the corresponding theoretical background. We then derive our research questions, describe the design and methods we used in the study, report on results, and discuss them in a concluding section.

2 Theoretical background

2.1 Using multiple representations in different contexts: fractions and functions

The flexible use of multiple representations plays a crucial role for the learning of mathematics (Acevedo Nistal et al. 2009). As mathematical objects are abstract in nature, they can be accessed only by using representations such as: formulae, graphs, diagrams, tables, written and spoken language (e.g., Goldin and Shteingold 2001). Numerous studies show that using multiple representations of a mathematical object and changing among them involve high cognitive demands for the learners (Ainsworth 2006; Duval 2006). Changes among different representations, so-called conversions, can consequently lead to serious problems in understanding when students fail to see that different representation registers (e.g., a verbal explanation, specific written symbols, or a drawing) represent the same mathematical object (Duval 2006; Lesh, Post, and Behr 1987). Since the present study is situated in the learning of fractions and functions, the role of multiple representations is specifically described for these two mathematical content areas in the following.

Fractions are among the most difficult concepts learners of mathematics encounter in their school life and children’s errors in fraction learning have been investigated for many years (Charalambous and Pitta-Pantazi 2007; Hansen et al. 2017). One issue contributing to students’ difficulty with learning fractions is confusion regarding the various conceptual interpretations including fractions as a part of a whole, part of a set of objects, a measure on a number line, a ratio, an operator and a quotient (Morano, Riccomini, and Lee 2019; Behr et al. 1992). Different visual representations are often used in teaching the different conceptual interpretations of fractions: For example, area models and set models are typically used to teach the part-whole interpretation of fractions, and number lines are recommended for teaching the measurement interpretation (Siegler, Thompson, and Schneider 2011). Beyond visual representations, students have to deal with different symbolic representations of fractions, including fractional notation and decimal notation. The integration of these multiple representations of fractions is regarded as particularly significant for students’ conceptual understanding of fractions (e.g., Charalambous and Pitta-Pantazi 2007). However, research in the field shows that students often struggle in changing among the different forms of fraction representations (Morano, Riccomini, and Lee 2019).

Comparable to the learning of fractions, a student’s ability to translate from one representation to another is considered a crucial factor for developing a holistic concept of mathematical functions (Nitsch et al. 2015). Four representation registers play a key role in this content area, namely, graph, table of values, algebraic equation and situational description (Nitsch et al. 2015). A systematic examination of translations among graph, numerical table, algebraic equation and situational description provided evidence that students should be given the opportunity to familiarise themselves with all kinds of translations in order to develop broad skills in the field of functional relationships (Nitsch et al. 2015). Studies in the field show also that students often struggle with the use of representations when investigating functions (e.g., Adu-Gyamfi, Stiff, and Bossé 2012) since they often fail to integrate information across multiple registers of representation (e.g., Adu-Gyamfi and Bossé 2014; Yerushalmy 1991).

Numerous studies emphasise the significant role of the teacher for supporting students in integrating multiple representations: In the case of functions, encouraging students to make explicit links between different representations of a functional relationship has been found to lessen learners’ difficulties (e.g., Thomas et al. 2010). In the case of fractions, it has been shown that students can benefit from the use of multiple representations only when they are supported in relating them to one other and to the key concepts they depict (Rau, Aleven, and Rummel 2015).

2.2 Analysing classroom situations in different contexts

In order to meet the professional demands related to the use of multiple representations described above, teachers not only need corresponding professional knowledge (Goldin and Shteingold 2001; Ball, Thames, and Phelps 2008; Mitchell, Charalambous, and Hill 2014). They also have to link that knowledge to relevant observations in the classroom to make sense of what has been observed. This process has been described as the dynamic interaction of selective attention and knowledge based reasoning in the framework of teacher noticing (Sherin 2017; Sherin, Jacobs, and Philipp 2011). In our prior studies related to teacher noticing (e.g., Friesen and Kuntze 2016, 2018; Friesen 2017), we used the term “competence of analysing” to describe to which extent mathematics teachers are able to notice in the content area of fractions.

As can be seen from the theoretical background on multiple representations in the case of fractions and functions, context on the level of the mathematical content area can be expected to play an important role for teachers’ analysis of the use of representations. When teachers analyse classroom situations regarding the use of multiple representations in different mathematical content areas (here: fractions and functions), they might draw on different professional knowledge related to that particular content area in order to make sense of what they observe. As outlined above, professional knowledge on multiple representations and their use can encompass more general aspects (e.g., the significant role of multiple representations for the development of mathematical concepts), together with knowledge aspects related to the particular content area (e.g., the key role of graph, table of values, algebraic equation and situational description in the case of learning functions).

However, examining the role of context for teachers’ analysis does also involve considerations on a more fine-grained level, namely the level of the individual classroom situations, as used, e.g., in vignette-based test instruments. From a methodological perspective, it is crucial to obtain results from teachers’ analysis in the context of several classroom situations in order to infer a more general competence construct (Shavelson 2013), so that teacher noticing can be seen as more than a classroom situation-dependent phenomenon. Studies comprising several classroom vignettes mostly enclose also different lessons with different teachers and different students in their test instruments (e.g., Kaiser et al. 2015) to avoid interaction effects related to these context aspects. However, this approach leads inevitably to the fact that the participants of a study are required to analyse classroom situations with different contexts regarding tasks, mathematical content, representations in use, teacher-student-interaction, etc. Considering context aspects on this level raises the methodological question of whether teachers can draw on the same noticing abilities independently from different classroom situations so that a more general competence construct can be inferred.

The assumptions regarding the role of context for teachers’ analysis of classroom situation can be substantiated by a model of teachers’ professional knowledge by Kuntze (2012). It distinguishes components of professional knowledge on different levels of situatedness: As teachers’ professional knowledge is often organised episodically (Leinhardt and Greeno 1986); components of such knowledge can, for example, be considered on the level of the mathematical content area (here: fractions, functions) and also on the level of particular classroom situations. Based on this model, Dreher and Kuntze (2015) have reported, for example, cases showing that teachers draw on professional knowledge from different levels of situatedness when they analyse classroom situations regarding the use of multiple representations.

There is a large body of research showing that teacher noticing is positively influenced by teaching experience (cf. Stahnke, Schueler, and Roesken-Winter 2016; Schack, Fisher, and Wilhelm 2017). However, since context-aware measures for teacher noticing are still scarce, not much is known about whether teachers’ degree of teaching experience plays a role for their competence in analysing the use of representations in different mathematical content areas. We consequently aimed at exploring this issue with teachers of different but (in Germany) typical degrees of teaching experience in this study.

3 Research questions

With the aim of examining the so far largely unexplored role of context for teacher noticing related to the use of multiple representations, we focus on context regarding two levels. Using a vignette-based test instrument, we examined whether the participants’ analysis can be described empirically through a more general competence construct that is independent from the specific context elements (tasks, representations, etc.) contained in the individual classroom situations. We also aimed to investigate how teachers’ analyses regarding the use of multiple representations in the content area of fractions are related to their corresponding analyses in the content area of functions. In particular, we asked the following questions:

  1. 1.

    To what extent do the data allow to infer an overarching competence dimension based on the teachers’ analyses of the individual classroom situations? Is it necessary to introduce sub-dimensions for the content areas?

  2. 2.

    What effect does the content area have when teachers analyse the use of multiple representations in classroom situations from the content areas of fractions and functions?

  3. 3.

    What is the role of the teachers’ degree of teaching experience for their competence in analysing the use of multiple representations in the two content areas, and for its relation between the two content areas?

4 Sample and methods

The sample in this study consists of N = 175 secondary mathematics teachers, teaching or preparing to teach mathematics in secondary schools (grades 5–10). Four subsamples represent typical degrees of teacher education and teaching experience in Germany: The participating student teachers (n = 35; 68.6% female) were at the beginning of their university studies (Mage = 20.9, SDage = 1.8; Msemester = 1.4, SDsemester = 0.7) and were enrolled in courses preparing to teach mathematics in secondary schools (grades 5–10). They came from different Universities of Education in the State of Baden-Wuerttemberg, Germany, and participated during a course at their home universities on a voluntary basis. The first subsample of pre-service teachers (n = 82; 63.4% female; Mage = 26.3, SDage = 3.7) had just finished the university part of teacher education and were just about to start the 18-month induction phase at secondary schools (teaching grades 5–10). The induction phase includes the observation of experienced teachers’ teaching, weekly seminars and their own teaching of classes in mathematics. The second subsample of pre-service teachers (n = 30; 60.0% female; Mage = 28.3, SDage = 3.9) were already at the end of their induction phase. Both subsamples of pre-service teachers participated on a voluntary basis in their respective weekly seminars. The in-service teachers (n = 28; 67.9% female; Mage = 39.0, SDage = 10.1) came from seven different secondary schools and volunteered to participate in the study. They were contacted via e-mail to the headmasters of their schools. They completed the test after classes at their schools in the presence of the first author of this study. Their experience in teaching mathematics in secondary schools ranged from two to thirty-one years after having finished their 18-month induction phase (Mexp = 9.4; SDexp = 6.4).

In order to find answers to the research questions of this study, we extended a vignette-based test instrument developed in our prior research (Friesen 2017; Friesen and Kuntze 2016, 2018; Kuntze and Friesen 2016). The existing test instrument was comprised of six classroom situations in the context of learning fractions in grade 6. Based on the advocatory approach (Oser, Salzmann, and Heinzer 2009), the participants were asked to observe other teachers teaching their classes and were asked to evaluate the observed teaching behaviour focusing on the use of multiple representations. These evaluations were then taken as indicators of the observing teachers’ own competence in analysing the use of multiple representations. The classroom situations were represented in three different vignette formats: text, comic and video. We designed the vignettes in a strictly parallel way so that the represented classroom situations would contain the same student–teacher dialogues and use of representations in each format.

In a prior study involving N = 298 mathematics teachers with different degrees of teaching experience, we found that the participants’ analysis of and engagement with the classroom situations did not significantly differ in the three formats (see Friesen 2017, for more details on that study) so that comic, video and text-based vignettes were comparably suitable to elicit teachers’ analyses.

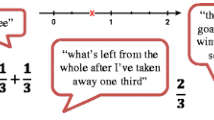
Expanding the instrument, we designed and added a comparable set of classroom situations in the context of learning functions in grade 8. We aimed at allowing the participants of the study to analyse various classroom situations within each of the two mathematical content areas (fractions, functions) and also making it possible to compare their analyses between the two content areas. Therefore, the 12 vignettes in the two content areas under investigation (fractions, functions) contain similarly structured narratives: Each classroom situation presents teacher behaviour that is likely to be obstructive for students’ conceptual learning due to a lack of support in integrating multiple representations. Providing mathematics teachers with vignettes containing such disruptive elements has been found to provoke deeper analysis of the represented classroom situations than vignettes containing examples of best practice (e.g., Chieu, Aaron, and Herbst 2018). Figure 1 shows two text-based sample vignettes for the content area of fractions (on the left) and functions (on the right), respectively.

Fig. 1
figure 1

Vignette examples in text format; left—vignette #5 on learning fractions; right—vignette #6 on learning functions

Full size image

The classroom situation from the content area of fractions (Fig. 1, on the left; Friesen 2017, p. 58) shows a group of students struggling with the task of rewriting an improper fraction as a mixed number. The students ask the teacher for help and show her their notes where they have started to divide the numerator by the denominator. The teacher’s first approach is a verbal explanation about writing the remainder of the division as a fraction. Since the students still do not comprehend, the teacher changes the register of representation and uses a situational description (putting together pizza slices) together with a visual representation (pie charts). The teacher does, however, not help to connect the situational description to the students’ division and the task is finally solved by the teacher using the situational description and the pie charts. Due to this unconnected change of representations, the teacher’s reaction to the students’ question can be described as a potential learning obstacle rather than a support for the students’ learning of the fraction concept.

In the classroom situation from the content area of functions (Fig. 1, on the right), a group of students struggles with determining the intersection of a function graph with the x-axis. They have already used the algebraic equation of the function and started to solve the task by creating a table of values, however, they appear not to understand that they need to extend their table of values to receive the coordinates of the point of intersection. Already here, the students might have a problem related to connecting among different representations standing for the intersection of the function graph with the x-axis, in particular, the verbal description relating to the graphical representation (“where the graph intersects the x-axis”) and the representation in the table of values (“y = 0”). The teacher tries to help by giving them the hint that “some values are still missing” in the table, however, the students do still not understand that they have to extend their table of values. In order to demonstrate the missing “crucial value”, the teacher changes the registers of representation and uses a situational description together with a sketch of a candle to represent the given values. However, the teacher misses connecting this new representation (situational description, sketch of the candle) to the students’ approach (table of values); the explanation can therefore be considered as a potential learning obstacle rather than a support for students’ learning of functions.

Although all of the vignettes contain classroom situations in which the teacher misses supporting his or her students in integrating the multiple representations in use, each of the vignettes contains also specific context information on both levels, the content area (fractions, functions) and the classroom situation itself. Regarding the two content areas under investigation, each set of fraction and function vignettes contained student questions related to the learning of corresponding concepts and involved registers of representation playing a key role in this content area (e.g., graph, table of values, algebraic equation and situational description in the content area of functions).

Regarding the level of the classroom situation, each situation was designed to take place in a different classroom involving different student and teacher characters. Also within a content area, each of the six classroom situations contained a different problem about which the students asked, as well as different registers of representation used by students and teachers. In the content area of fractions, the participating teachers were asked to analyse classroom situations involving, for example, students’ questions about multiplying or simplifying fractions and the use of varied fraction representations, such as area models or the number line.

In order to examine the participants’ analyses regarding the use of representations in the 12 classroom situations, each of the vignettes was followed by the same open-ended question: How appropriate is the teacher’s response in order to help the students? Please evaluate regarding the use of representations and give reasons for your answer. (cf. Friesen 2017, p. 63). This open-ended question explicitly prompted the participants to evaluate the classroom situation by taking into account the use of representations by both the teacher (“the teacher’s response”) and the students (“in order to help the students”), and to provide reasons for their evaluation.

The vignettes in the different formats (text, comic, video) were randomly assigned to the participants in six different test booklets, so that each test-taker analysed the same 12 classroom situations receiving always four situations in the format text, comic or video (see Fig. 2). The test booklets were administered as paper-and-pencil tests and each booklet started with a short introduction to the common setting of the presented classroom situations (practice lesson with small-group work in the context of learning fractions in grade 6 or learning functions in grade 8). One part of the booklet contained the six fraction vignettes, the other part the six function vignettes. Each test-taker was provided with earphones and a laptop or tablet computer for watching the video vignettes included in his or her test booklet. It was possible to pause the video clips or watch them again. Thus, each participant was enabled to analyse the 12 classroom situations according to his or her individual pace of work, which took around 120–150 min altogether.

Fig. 2
figure 2

Vignette example from the content area of functions: screenshots from video and comic versions of vignette #6 (shown in Fig. 1)

Full size image

5 Data analysis and results

The participants’ answers were coded dichotomously in order to examine whether or not they were able to analyse the potentially obstructive change of representations caused by the lack of teacher support in the classroom situations. A methodological reason for choosing a dichotomous coding in this study was also that we aimed at analysing the obtained data using the dichotomous Rasch model in order to find answers to our research questions (see more detailed explanation below). Answers indicating that a participant had successfully analysed the corresponding classroom situation were coded 1 and accordingly assigned one point. This coding resulted in a maximum sum score of 12 points, with a maximum of six points in each of the content areas (corresponding to six vignettes in the content areas of fractions and functions, respectively). More than 80% of the test booklets (144 out of 175 booklets, randomly selected) were coded twice, by independent raters, reaching a good inter-rater reliability of κ ≥ 0.89 (Cohen’s kappa).

Figure 3 shows two sample answers from an in-service teacher. Her answer to the fraction vignette was coded 0 whereas one point (Code 1) was assigned for her answer to the vignette from the content area of functions. Analysing the fraction vignette, the in-service teacher evaluated the use of the teacher’s verbal explanation and the visual representation as “coherent”; she wrote that the students will therefore understand the picture and the explanation. The in-service teacher’s answer, however, does not relate the teacher’s response to the students’ approach and therefore the potentially obstructive change of representations is not mentioned. In her analysis of the function vignette, the in-service teacher wrote that the change of representations involving the candle does not help here, but is confusing for the students. She provided an alternative approach suggesting that the teacher should first explain with the help of the graph. Accordingly, she drew a graph and marked in green the intersection of the graph with the x-axis. She additionally explained how the different registers of representation should be connected in this situation: the graphical representation showing the intersection with the graph and the x-axis and the corresponding algebraic representation (y = 0). Moreover, she suggested going back to the students’ approach with the table of values in order to connect the different registers of representations that were used in her alternative explanation.

Fig. 3
figure 3

Sample answer (in-service teacher); at the top—analysing result from fraction vignette #5; at the bottom—analysing result from function vignette #6 (both shown in Fig. 1)

Full size image

Figure 4 shows two sample answers from a pre-service teacher at the beginning of his induction phase at secondary schools. Both answers (above—content area of fractions; below—content area of functions) were coded 0. In his analysis of the fraction vignette, the pre-service teacher evaluated the teacher’s response as helpful for the students. He justified his evaluation by drawing on knowledge that “pizza or cake models can represent the whole very well”. The pre-service teacher’s evaluation does not address the change of representations but concentrates only on the representation used by the teacher; the students’ approach with its specific representation is not taken into account. Analysing the classroom situation in the content area of functions, the pre-service teacher evaluated the teacher’s representation as positive and explained that it illustrates the given problem well. There is evidence that the change of representations has been observed (“problem is illustrated”, “a transfer is made”) but the pre-service teachers’ answer does not indicate that this change is not sufficiently supported by the teacher and could therefore be potentially obstructive for the students’ learning.

Fig. 4
figure 4

Sample answers from the two content areas (by pre-service teacher I); above—answer to fraction vignette #5; below—answer to function vignette #6 (both vignettes are shown in Fig. 1)

Full size image

We addressed our first research question in the next step of data analysis and examined what model could be specified in order empirically to describe teachers’ analyses of different classroom situations as an overarching competence construct. As mentioned above, we used the opportunities of binary coding for analysing the obtained data using the dichotomous Rasch model. Specific item characteristics, such as the content of a specific classroom situation, can play a role in the solution of an item, as they can increase or decrease the demands that are required in order to solve it (Hartig 2008). For this reason, the role of specific item characteristics should be taken into account when test scores are computed. IRT (item response theory) models are supposed to be highly applicable in this context, since they account for both the ability of the test-takers as well as specific situational demands caused by item characteristics (Hartig et al. 2012; Blömeke, Gustafsson, and Shavelson 2015). Accordingly, the scores obtained by the coding described above were analysed using the dichotomous Rasch model in order to check for unidimensionality, i.e., that all items (here, classroom vignettes) measure the same underlying latent construct (here, competence in analysing regarding the use of multiple representations) (cf. Bond and Fox 2015). Unidimensionality as assumed by the Rasch model is also a necessary requirement for summarising a test by means of its overall sum score. Since the sum score is the sufficient statistic for the latent subject ability in the Rasch model (Andrich 1988), there is a one-to-one correspondence between a person’s estimated ability and his/her raw score on a test (Wu, Tam, and Yen 2016). It is consequently possible to use the participants’ raw scores for summarising a test when the data fit the Rasch model.

We estimated and compared two Rasch models in order to account for assumed dependencies between the items from the same content area, since they could lead to a violation of local independence (cf. Brandt 2008; Wu et al. 2016). In the first model, all 12 items load on the same underlying dimension (competence in analysing regarding the use of multiple representations). In the second model, all 12 items load on the same underlying dimension (competence in analysing regarding the use of multiple representations) and always six items are additionally grouped into a subdimension (subdimension 1—group of fraction items; subdimension 2—group of function items). In the second model, we thus explicitly considered possible local item dependencies (cf. Brandt 2008) among the six items belonging to the same mathematical content area (fractions or functions).

The analysis of the data using the software ConQuest 2.0 revealed good fit values for both Rasch models (model with subdimensios, 0.96 ≤ wMNSQ ≤ 1.04; -0.9 ≤ T ≤ 1.2; model without subdimension, 0.96 ≤ wMNSQ ≤ 1.04; -0.9 ≤ T ≤ 1.2; cf. Bond and Fox 2015). The results indicate that each item contributed in a meaningful way to the latent construct under investigation (here, competence of analysing regarding the use of multiple representations). The comparison between the two Rasch models (with and without subdimensions) showed that taking into account assumed local dependencies among the items of the same content area led to a significant improvement of the model fit [χ2(2) = 7.578, p = 0.023].

In the next step of data analysis, we addressed the second research question asking what effect the content area has when teachers analyse the use of multiple representations in classroom situations from the content areas of fractions and functions. We computed the empirical item difficulties of the 12 vignettes to investigate the effect of the content area on the empirical solution rate. Figure 5 displays the empirical item difficulties of the vignettes (1–6 in each content area) as obtained by computing the Rasch model, with subdimensions in ascending order (Table 1). The graphical representation (Fig. 5) indicates that the items in the two content areas (fractions and functions) have on average comparable item difficulties. Comparing the means with an analysis of variance (ANOVA) revealed no significant effect of the content area on the item difficulties [F(1) = 0.002, p = 0.968] As can also be seen in the graphical representation of the item difficulties (Fig. 5), there are significant differences within the content area of functions [M = 0.821, SE = 0.246, t(5) = 3.33, p = 0.021], and marginally significant differences within the content area of fractions [M = 0.838, SE = 0.328, t(5) = 2.55, p = 0.051].

Fig. 5
figure 5

Rasch item difficulties for the two content areas in ascending order

Full size image
Table 1 Empirical item difficulties (in ascending order) and standard errors for the vignettes in both content areas
Full size table

The next steps of analysis addressed our third research question on the role of the teachers’ degree of teaching experience for their competence of analysing in the two content areas, and how such competence is related. Since good fit values of the data were found for the Rasch model, the participants’ raw scores were used for summarising the test and for the following data analyses (cf. Wu, Tam, and Yen, 2016). As described above, the maximum score was six points in each of the content areas, corresponding to the six vignettes that the participants analysed related to fractions or functions, respectively. Table 2 summarises the descriptive statistics and contains the means and standard deviations for the participants’ scores in the two content areas under investigation.

Table 2 Sum scores on the four degrees of teaching experience: mean values and standard deviations (maximum score = 6 in the area of fractions or functions, respectively)
Full size table

The student teachers reached on average the lowest scores for their analyses in both content areas (see also Fig. 6 for a graphical illustration of the findings). In the content area of fractions, the highest scores were reached by the subsample of pre-service teachers at the beginning of their induction phase. In the content area of functions, the in-service teachers reached the highest scores.

Fig. 6
figure 6

Sum scores (mean values) for teachers’ competence of analysing in the two content areas

Full size image

In order to investigate the relationship between teachers’ competence of analysing in the two content areas, we calculated the correlations between the scores obtained for the fraction and function vignettes. The table of correlations (Table 3) shows a significant positive relationship (r = 0.409, p = 0.000) between the scores of the two content areas for the complete sample. Correlational analyses of the subsamples indicate also a significant positive relationship for the student teachers at the beginning of their university studies and for the pre-service teachers at the beginning of their induction phase (Table 3). The scores were not significantly related between the two content areas in case of the other two degrees of teaching experience, namely, pre-service teachers at the end of their induction phase and in-service teachers.

Table 3 Correlations (Pearson) between the analysing scores in the content area of fractions and functions; ns = not significant, *p > 0.05; **p < 0.01
Full size table

In order to further investigate the effect of the content area on the participants’ scores, we computed an analysis of variance (ANOVA) with the score of the participants as dependent variable and the content area and degree of teaching experience as fixed factors. Preliminary analyses using Levene’s test indicated the homogeneity of variance in the different subgroups, an important prerequisite for running ANOVAs (Field 2013). The findings showed that there was no significant effect of the content area on the participants’ scores [F(1) = 0.84, p = 0.361], but a significant effect of the participants’ degree of teaching experience [F(3) = 3.04, p = 0.029]. The results of the ANOVA also revealed a significant interaction between the factors content area and degree of teaching experience on the participants’ score [F(3) = 2.72, p = 0.045], as indicated in the case of the in-service teachers in Fig. 6. We consequently ran a multivariate analysis of variance (MANOVA) with the participants’ scores in the content area of fractions and functions as two separate dependent variables and the degree of teaching experience as fixed factor. The tests of between-subjects effects showed that there was a significant effect of the participants’ degree of teaching experience on their score in the content area of functions [F(3) = 3.81, p = 0.011], but not in the content area of fractions [F(3) = 1.55, p = 0.203]. In the post hoc tests, we used Games–Howell procedures to account for the unequal group sizes of the subsamples in the study (Field 2013). The findings showed that for the content area of functions, the subsample of in-service teachers reached on average higher scores than the other subsamples with less teaching experience (Fig. 6). This difference was significant only in the case of student teachers (p = 0.007).

6 Discussion and conclusions

In his conclusion to the edited volume Mathematics Teacher Noticing (Sherin, Jacobs, and Philipp 2011), Alan Schoenfeld resumes the editors’ question of how context specific noticing expertise is, and states that this question will “require significant unpacking” (Schoenfeld 2011, p. 237). The study presented in this paper can be seen as a step towards unpacking that question by comparing teachers’ competence of analysing regarding the use of multiple representations in two different mathematical content areas: fractions and functions. We took another step forward by additionally looking at the question of context on the level of particular classroom situations, as implemented in the vignette-based test-instrument used in this study.

Regarding our first research question, we found that our data fit the Rasch model, indicating that each of the 12 classroom situations contributed in a meaningful way to an overarching competence construct with key relevance for mathematics teachers’ content-related noticing, namely, teachers’ competence in analysing the use of multiple representations. It can therefore be assumed that the set of vignettes used in our test instrument allowed us to elicit a test result from which the participants’ competence of analysing can be inferred (Shavelson 2013). We thus conclude that our measure is context-aware regarding the level of different specific classroom situations: the teachers’ answers allow both insight into their situation-specific analysis, as well as inferring their overarching competence of analysing with respect to the use of representations.

Regarding our second research question, no effect of the content area on teachers’ competence of analysing the use of representations could be found: The mean scores attained by the participating teachers for their analyses in each of the content areas (fractions and functions) were almost equal. The related Rasch analyses showed at the same time that an improved model fit could be gained when the items were additionally grouped for each of the content areas. The findings can be taken as evidence that the vignette-based test instrument provided the possibility of a context–aware measure regarding the two content areas, since related items (vignettes) were not only theoretically but also empirically linked to one other. Taken together, these findings suggest that analysing the use of multiple representations can be seen as an overarching competence construct linking teachers’ corresponding competence specific to the content areas of fractions and functions. However, the findings also imply that including items from different mathematical content areas can bring in methodological challenges for (vignette-based) measures of teacher noticing. Although such challenges are widely discussed for large-scale studies (cf. Brandt 2008), also studies with smaller samples might benefit from considering the issue of context-specificity.

Whereas we did not find significant differences between the average scores for teachers’ analysis of the fraction and function vignettes, the related data analyses revealed substantial differences regarding the item difficulties within each of the content areas (see Fig. 5). These results are consistent with findings from a prior study in which we explicitly investigated the role of different item characteristics (vignette format and question format) for teachers’ competence of analysing (Friesen 2017). Already in this study, we found evidence that the content of the classroom situations (here, vignettes on learning fractions) was more strongly associated (η = 0.83) with the empirical items difficulties than the question format (η = 0.45) or the vignette format (η = 0.15). These findings encourage further research into the question of context for teacher noticing and suggest in-depth studies of the content provided in vignette-based test instruments.

The results for the third research question revealed a positive effect of the participants’ degree of teaching experience on their competence of analysing (cf. Jacobs et al. 2010), but only in the case of functions (cf. Fig. 6). The participants’ degree of teaching experience appeared also to play a role for the relation between their competence of analysing in the two content areas under investigation: for the two subsamples with less teaching experience, significant positive correlations could be found between their competence of analysing in the content areas of fractions and functions. This was, however, not the case for the two subsamples of teachers with more experience in teaching. According to the model of teachers’ professional knowledge by Kuntze (2012) introduced above, it could be argued that the subsamples might have drawn differently on their (potentially different) professional knowledge when analysing the vignettes regarding the use of multiple representations. Student teachers and pre-service teachers who have just finished the university part of their teacher education should have developed a systematic and therefore similar level of professional knowledge in different mathematical content areas (here, fractions and functions). In contrast, more experienced teachers might increasingly draw on knowledge gained in daily teaching practice which is related to particular classroom situations in particular content areas (here, functions). For the sample of this study, we can say only that the participating teachers have experience in teaching the grades where fractions and functions are normally taught according to the federal curriculum. Explicitly collecting data regarding teachers’ actual hours of teaching experience in a particular mathematical content area should consequently be taken into account in future studies.

Although we can provide answers to our research questions, we would also like to consider the limitations of our study that might make it necessary to interpret our findings with caution. The study is not representative for German teachers: Our aim to explore teachers in four different degrees of teaching experience led to rather small subsamples and also to varying sample sizes. Even if we were able to compare teachers’ competence of analysing in two different content areas where the use of multiple representations is highly relevant for students’ learning and therefore well researched, the question of context specificity remains open for other mathematical areas. A promising methodological approach for research into mathematics teachers’ noticing appears to be the systematic comparison of teachers’ analyses between different content areas but under a common area-spanning perspective (here, the use of multiple representations). Comparable overarching perspectives could be derived from other professional demands teachers have to master in the mathematics classroom, such as dealing with students’ errors and misconceptions, dealing with heterogeneous learning conditions, dealing with students’ engagement, etc. Corresponding follow-up questions will be addressed in the ERASMUS + strategic partnership coReflect@maths (http://www.coreflect.eu). Through the collaboration between scholars from universities in Germany, England, Czech Republic and Spain, this project will also provide the opportunity to address the question of context specificity on the level of culture, allowing researchers to compare teachers’ analyses of classroom situations among different cultural contexts.