Optimal selling mechanisms with crossholdings

Abstract

We characterize the optimal selling mechanism when bidders have ownership links among them (crossholdings). This mechanism discriminates against bidders who enjoy a value comparative advantage resulting from the extent to which they appropriate their own surplus. It is shown that since crossholdings improve the seller’s ability to selectively extract surplus from bidders, expected seller revenue is increasing with the asymmetry in these stakes. The optimal mechanism is implemented by a hybrid procedure that combines an auction with price preferences and a possible exclusive deal. An alternative negotiation procedure replicates some properties of the optimal one, and revenue-dominates most commonly used auction formats.

Appendices

Appendix

The optimal mechanism problem

The optimal mechanism solves the following problem:

$$\begin{aligned} \max _{x_{i}\in {\mathbb {R}} ,~p_{i}\in \left[ 0,1\right] ,~\varphi ^{i}\in \left[ 0,1 \right] ^{2}}~U_{0} \end{aligned}$$

(A1)

$$\begin{aligned}&\qquad s.t. \\&V_{i}(t_{i}) \,\ge \varphi ^{i}{\overline{u}}^{i}~\forall t_{i}\in \left[ {\underline{t}},{\overline{t}}\right] ,~i=1,2,3 \end{aligned}$$

(A2)

$$\begin{aligned} V_{i}(t_{i})~\ge U_{i}(\widehat{t_{\begin{array}{c} i \\ ~ \end{array}}} ,t_{i})~\forall t_{i},\widehat{t_{i}}\in \left[ {\underline{t}}, {\overline{t}}\right] ,~i=1,2,3 \end{aligned}$$

(A3)

$$\begin{aligned} \sum _{i=1}^{3}p_{i}(t)\le 1\text { and }p_{i}(t)\ge 0,~ i=1,2,3,\forall t\in T, \end{aligned}$$

(A4)

where (A1) is the seller’s expected revenue, (A2) and (A3) represent bidders’ participation constraints and incentive compatibility constraints, respectively, and (A4) represents the feasibility constraints of this problem. First, notice that since there exist crossholdings, the original participation constraints consider endogenous reservation utilities that depend on the allocation rule adopted by the seller in case of non-participation of a bidder. This rule is represented by $\varphi ^{i}=(\varphi _{j}^{i},\varphi _{k}^{i})$, the vector of probabilities with which the seller assigns the object to bidder j or k if bidder i does not participate in the auction. Similarly, ${\overline{u}} ^{i}=(\overline{u_{j}}^{i},\overline{u_{k}}^{i})$ represents the vector of outside opportunity utilities of bidder i when bidder j or k gets the object. Given the cross-ownership structure assumed, it is clear that $\overline{u_{2}}^{1}>\overline{u_{3}}^{1}$, $\overline{u_{1}}^{2}>\overline{ u_{3}}^{2}$ and $\overline{u_{1}}^{3}=\overline{u_{2}}^{3}$. Hence, it must be optimal that $\varphi ^{1}=(\varphi _{2}^{1},\varphi _{3}^{1})=(0,1)$ and $\varphi ^{2}=(\varphi _{1}^{2},\varphi _{3}^{2})=(0,1)$. As we normalize $\overline{u_{3}}^{1}=\overline{u_{3}}^{2}=\overline{u_{1}}^{3}=\overline{ u_{2}}^{3}=0$, all of this implies that the zero reservation utility for all bidders is optimal as well.

Second, following Myerson (1981), it is possible to show that the incentive compatibility constraints are satisfied if and only if

• (i) $\frac{\partial V_{i}(t_{i})}{\partial t_{i}}=(1-\theta _{j})Q_{i}(t_{i})$ for $i,j=1,2$ and $i\ne j$,

• (ii) $\frac{\partial V_{3}(t_{3})}{\partial t_{3}}=Q_{3}(t_{3})$,

• (iii) $\frac{\partial Q_{i}(t_{i})}{\partial t_{i}}\ge 0$ for all i .

Using these conditions, straightforward computations allow us to rewrite the seller’s expected payoff and simplify the maximization problem as presented in Sect. 3.

Proofs

Proof of Lemma 1

Clearly from (2), it is in the seller’s interest to make $V_{i}({\underline{t}})=0$ for all i because $V_{i}({\underline{t}})>0$ is suboptimal and setting $V_{i}({\underline{t}})<0$ violates the participation constraint. Moreover, $H^{\prime }(t_{i})>0$ implies $m_{i}^{\prime }(t_{i})>0$ and thus $\frac{\partial p_{i}(t)}{ \partial t_{i}}\ge 0$ , so that $Q_{i}^{\prime }(t_{i})\ge 0$ is satisfied for all i. Finally, since $t_{0}=0$, the optimal allocation rule is found by comparing for a given t $=(t_{1},t_{2},t_{3})$ the terms $m_{1}(t_{1})$ , $m_{2}(t_{2})$ and $m_{3}(t_{3})$ whenever they are positive. The solution sets $p_{i}(t)=1$ iff $m_{i}(t_{i})>\max \left\{ 0,\max _{j\ne i}m_{j}(t_{j})\right\} .$ $\square$

Proof of Lemma 2

• (i) We only show the claim for $z_{31}$; the remaining cases are similar and hence omitted. Notice that by definition, $z_{31}(t_{1})\equiv$ $m_{3}^{-1}(m_{1}(t_{1}))$. Then, $z_{31}^{\prime }(t_{1})=m_{3}^{-1\prime }(m_{1}(t_{1}))m_{1}^{\prime }(t_{1})>0$ follows from the fact that both $m_{i}$ and its inverse are strictly increasing functions for all i.

• (iii) By definition, $z_{12}({\underline{t}})\equiv m_{1}^{-1}(m_{2}( {\underline{t}}))>m_{1}^{-1}(m_{3}({\underline{t}}))\equiv z_{13}({\underline{t}})$ , where the inequality follows from the fact that $m_{2}({\underline{t}} )>m_{3}({\underline{t}})$ and the inverse of $m_{1}$ is a strictly increasing function. Notice, however, that $z_{13}({\underline{t}})\equiv m_{1}^{-1}(m_{3}({\underline{t}}))<m_{1}^{-1}(m_{1}({\underline{t}}))=\underline{ t}$, which is not possible and so, we must impose a truncation such that we define

  $$\begin{aligned} z_{13}(t_{3})=\left\{ \begin{array}{ll} {\underline{t}} &{} \text {if }{\underline{t}}\le t_{3}<z_{31}({\underline{t}}) \\ m_{1}^{-1}(m_{3}(t_{3})) &{} \text {otherwise} \end{array} .\right. \end{aligned}$$

  Using the same arguments, one can verify that the other cases also hold, which includes the following definition for bidder 2

  $$\begin{aligned} z_{2j}(t_{j})=\left\{ \begin{array}{ll} {\underline{t}} &{} \text {if }{\underline{t}}\le t_{j}<z_{j2}({\underline{t}}) \\ m_{2}^{-1}(m_{j}(t_{j})) &{} \text {otherwise} \end{array} \text {,}\right. \end{aligned}$$

  for all $j\ne 2.$

• (ii) According to definitions of the discrimination policy functions provided in the proof of (iii), and using the same arguments applied in (i), the desired result follows directly.

• (iv) The claim is only proved for $z_{31}$. First, from (iii) we know that $z_{31}({\underline{t}})>{\underline{t}}$. Second, notice that $z_{31}(\overline{t })\equiv m_{3}^{-1}(m_{1}({\overline{t}}))={\overline{t}}$, where the last equality follows from the fact that $m_{1}({\overline{t}})=m_{3}({\overline{t}})$ . Third, from (i), we know that $z_{31}$ is a strictly increasing function. Fourth, it is easy to check that the condition $H^{\prime \prime }(t_{3})\ge 2(H^{\prime }(t_{3}))^{2}/H(t_{3})$ guarantees that $m_{3}$ is a convex function, and hence, $z_{31}$ is a concave function. All of that implies that $z_{31}$ has a unique fixed point $\sigma ={\overline{t}}.$

• (v) This is a direct consequence of results (i)-(iv).

$\square$

Proof of Proposition 1

Let us define $J_{i}(t_{i})\equiv \frac{ H(t_{i})}{\psi _{i}}$, the modified hazard rate of bidder i’s value distribution function, where $\psi _{i}$ is the fraction in which bidder i appropriates his own surplus, i.e., $\psi _{1}=1-\theta _{2}$, $\psi _{2}=1-\theta _{1}$ and $\psi _{3}=1$. Let $G_{i}$ denote its corresponding c.d.f. Since $m_{i}(s)$ is increasing with s then $z_{ij}(s) > reqqless s$ iff $m_{i}(s)\lesseqqgtr m_{i}(z_{ij}(s))=m_{j}(s)$, where the last equality follows from the implicit definition of $z_{ij}$. It is easy to check that this inequality is equivalent to $J_{j}(s) > reqqless J_{i}(s)$ for all s, and for all $i\ne j$, which means that $z_{ij}(s)<s$  iff $G_{j}\succ _{HRD}G_{i}$ (i.e., $G_{j}$ hazard rate dominates $G_{i}$). As $\psi _{3}>\psi _{1}>\psi _{2}$ implies that $G_{3}\succ _{HRD}G_{1}\succ _{HRD}G_{2}$, the desired result follows. $\square$

Proof of Proposition 2

From (2) and Lemma 1, let us define $V_{0}$, the seller’s expected revenue evaluated according to the optimal mechanism, as follows

$$\begin{aligned} V_{0}=\sum _{i=1}^{3}\int _{T}m_{i}(t_{i})p_{i}(t)f(t)dt. \end{aligned}$$

(A5)

From this, when $\theta _{1}=\theta _{2}=\theta >0$, and after applying the envelope theorem, we get

$$\begin{aligned} \frac{\partial V_{0}}{\partial \theta }=\sum _{i=1}^{2}\int _{T}\frac{1}{ H(t_{i})}p_{i}(t)f(t)dt\ge 0 \end{aligned}$$

because $H(t_{i})>0$ and $p_{i}(t)\ge 0$ for all t and i. $\square$

Proof of Proposition 3

Let k be a positive constant such that $\theta _{1}+\theta _{2}=k$, and thus, $\theta _{2}=k-\theta _{1}$ . Using this substitution to rewrite $V_{0}$, from (A5) we obtain

$$\begin{aligned} \frac{\partial V_{0}}{\partial \theta _{1}}&=\int _{T}\frac{1}{H(t_{2})} p_{2}(t)f(t)dt-\int _{T}\frac{1}{H(t_{1})}p_{1}(t)f(t)dt \\&=\int _{t_{2}}\frac{1}{H(t_{2})}\left( \int _{T-2}p_{2}(t)f(t_{-2})dt_{t-2}\right) f(t_{2})dt_{2} \\&\quad -\int _{t_{1}}\frac{1}{H(t_{1})}\left( \int _{T-1}p_{2}(t)f(t_{-1})dt_{t-1}\right) f(t_{1})dt_{1} \\&=\int _{t_{2}}\frac{1}{H(t_{2})}Q_{2}(t_{2})f(t_{2})dt_{2}-\int _{t_{1}} \frac{1}{H(t_{1})}Q_{1}(t_{1})f(t_{1})dt_{1}, \\&=\int _{s}\frac{Q_{2}(s)-Q_{1}(s)}{H(s)}f(s)ds. \end{aligned}$$

(A6)

According to our optimal allocation rule, $Q_{i}(s)=\Pr (t_{j}<z_{ji}(s))\Pr (t_{i}^{*}<s)$ for $i,j=1,2$, $i\ne j$. Note that $t_{1}^{*}>t_{2}^{*}$ implies that $\Pr (t_{2}^{*}<s)$ $\ge \Pr (t_{1}^{*}<s)$, and that from Lemma 2 it follows that $F(z_{21}(s))<F(z_{12}(s))$ for all $s\in \left[ {\underline{t}},{\overline{t}}\right)$. All of that implies that $Q_{1}(s)\le Q_{2}(s)$ for a given value s. Since the exclusion of both bidders is not possible for all s, the last result implies from (A6) that $\frac{\partial V_{0}}{\partial \theta _{1}}\ge 0$. $\square$

Proof of Proposition 4

We first need to state the next auxiliary result.

Lemma B1

Let us define $\Theta _{i}\equiv \frac{\theta _{i}}{1-\theta _{j}}$ for $i,j=1,2,$ $i\ne j$; and $L(s)=F^{1-\Theta _{2}}(z_{12}(s))F(z_{32}(s))$ and $L_{1}(s)=F^{1-\Theta _{2}}(z_{12}(s))$ for all $s\in \left[ {\underline{t}},{\overline{t}}\right]$.²⁵ A Bayesian Nash equilibrium of the auction-based selling procedure is the following one:

Bidder 3’ strategy Accept participation in Stage II if and only if $t_{3}\ge z_{32}({\underline{t}})$; and in Stage II bid:

$$\begin{aligned} b_{3}^{{\textit{II.1}}}(t_{3})=E\left[ \max \left\{ z_{32}(t_{2}),z_{31}(t_{1})\right\} |\max \left\{ z_{12}(t_{2}),t_{1}\right\} <z_{13}(t_{3})\right] \end{aligned}$$

and

$$\begin{aligned} b_{3}^{{\textit{II.2}}}(t_{3})=E\left[ z_{32}(t_{2})|t_{2}<z_{23}(t_{3}) \right] . \end{aligned}$$

Bidder 1’ strategy Accept participation in Stage II if and only if $t_{1}\ge z_{12}({\underline{t}})$; and in Stage II bid:

$$\begin{aligned} b_{1}^{{\textit{II.1}}}(t_{1})=E\left[ \max \left\{ \frac{ z_{12}(t_{2})-\Theta _{1}t_{2}}{1-\Theta _{1}},z_{13}(t_{3})\right\} |\max \left\{ t_{2},z_{23}(t_{3})\right\} <z_{21}(t_{1})\right] \end{aligned}$$

and

$$\begin{aligned} b_{1}^{{\textit{II.3}}}(t_{1})=E\left[ \frac{z_{12}(t_{2})-\Theta _{1}t_{2}}{1-\Theta _{1}}|t_{2}<z_{21}(t_{1})\right] . \end{aligned}$$

Bidder 2’ strategy Accept the offer to pay $\underline{b_{2}}$ in Stage I; and in Stage II bid:

$$\begin{aligned} b_{2}^{{\textit{II.1}}}(t_{2})&=\frac{{\underline{t}}L({\underline{t}}){ }}{L(t_{2})}+E\left[ \max \left\{ \frac{z_{21}(t_{1})-\Theta _{2}t_{1}}{ 1-\Theta _{2}},z_{23}(t_{3})\right\} |\max \left\{ t_{1},z_{13}(t_{3})\right\}<z_{12}(t_{2})\right] \\ b_{2}^{{\textit{II.2}}}(t_{2})&=\frac{{\underline{t}}F(z_{32}({\underline{t}} )) ~}{F(z_{32}(t_{2}))}+E\left[ z_{23}(t_{3})|t_{3}<z_{32}(t_{2}) \right] \\ b_{2}^{{\textit{II.3}}}(t_{2})&=\frac{{\underline{t}}L_{1}({\underline{t}})}{ L_{1}(t_{2})}+E\left[ \frac{z_{21}(t_{1})-\Theta _{2}t_{1}}{1-\Theta _{2}} |t_{1}\in \left[ z_{12}({\underline{t}}),z_{12}(t_{2})\right] \right] . \end{aligned}$$

These are equilibrium strategies if the seller designs a modified FPA with the following characteristics:

• (i) $\underline{b_{3}}=z_{32}({\underline{t}}),$

• (ii) $\underline{b_{1}}=z_{12}({\underline{t}}),$

• (iii) $\underline{b_{2}}$ such that $\Gamma _{2}({\underline{t}})=0,$ and

• (iv) $\widetilde{z_{ij}}(b)=b_{i}(z_{ij}(b_{j}^{-1}(b))),$

where $\Gamma _{i}(\cdot )$ represents bidder i’s expected truthtelling payoff (i.e. the average across all stages) in this sequential mechanism.

Proof of Lemma B1

We only demonstrate that these candidate bidding functions constitute an equilibrium for the most general case: bidder 1. Let us define:

$b_{1}^{k}(t_{1})$, the candidate bidding function for bidder 1 in Stage k, as follows

$$\begin{aligned} b_{1}^{k}(t_{1})=\left\{ \begin{array}{ll} b_{1}^{II.1}(t_{1}) &{} \quad \text {if }t_{1}>z_{12}({\underline{t}})\text { and } t_{3}>z_{32}({\underline{t}})\text { (Stage II.1)} \\ b_{1}^{II.3}(t_{1}) &{}\quad \text {if }t_{1}>z_{12}({\underline{t}})\text { and } t_{3}<z_{32}({\underline{t}})\text { (Stage II.3)} \\ 0 &{} \quad \text {otherwise (Stage II.2 or Stage I)} \end{array} \right. \text {,} \end{aligned}$$

$q_{i}^{k}(t_{i},t_{-i})$ as the probability that bidder i gets the object in Stage k,

$\Lambda _{1}^{k}(\widehat{t_{1}},t_{1})$, bidder 1’s expected payoff in Stage k when he observes $t_{1}$, but plays a strategy as if his value were $\widehat{t_{1}}$, as follows

$$\begin{aligned} \int _{T_{-1}}\left\{ (1-\theta _{2})\left[ t_{1}-b_{1}^{k}(\widehat{t_{1}}) \right] q_{1}^{k}(\widehat{t_{1}},t_{-1})+\theta _{1}\left[ t_{2}-b_{2}^{k}(t_{2})\right] q_{2}^{k}(\widehat{t_{1}},t_{-1})\right\} f(t_{-1})dt_{-1}\text {,} \end{aligned}$$

$\Gamma _{1}^{k}(t_{1})\equiv \Lambda _{1}^{k}(t_{1},t_{1})$, bidder 1’s truthtelling payoff in Stage k, and$P_{1}^{k}(t_{1})\equiv \int _{T_{-1}}q_{1}^{k}(t_{1},t_{-1})f(t_{-1})dt_{-1}$ , bidder 1’s probability of winning in Stage k, conditional on value realization $t_{1}$.

Let us organize this proof in two steps.

Step 1. Notice that the payoff function $\Gamma _{1}^{k}$ corresponds to the particular case of the truthtelling payoff function $V_{1}$ defined in Sect. 3 when the optimal payment is $x_{1}(t_{1},t_{-1})=b_{1}^{k}(t_{1})$ and the optimal allocation rule is $p_{1}(t_{1},t_{-1})=q_{1}^{k}(t_{1},t_{-1})$.²⁶ It follows then directly from conditions (i) and (iii) of “Appendix A” that the incentive compatibility constraint $\Gamma _{1}^{k}(t_{1})$ $\ge \Lambda _{1}^{k}( \widehat{t_{1}},t_{1})$ for all $t_{1},\widehat{t_{1}} \in \left[ {\underline{t}},{\overline{t}}\right]$ and k, is satisfied if $\frac{\partial \Gamma _{1}^{k}(t_{1})}{\partial t_{1}} =(1-\theta _{2})P_{1}^{k}(t_{1})$ and $\frac{\partial P_{1}^{k}(t_{1})}{ \partial t_{1}}\ge 0$ for all k.

Step 2. We show now that the strategy $b_{1}^{k}(t_{1})$ satisfies these two sufficient conditions and therefore is an equilibrium bidding strategy of this game. First, given that $b_{1}^{k}(t_{1})$ is increasing for stages II.1 and II.3, and, since by construction $\widetilde{z_{ji}}$ implements the optimal allocation rule, we have that

$$\begin{aligned} P_{1}^{k}(t_{1})=\left\{ \begin{array}{ll} F(z_{21}(t_{1}))F(z_{31}(t_{1})) &{} \quad \text {if }t_{1}>z_{12}({\underline{t}}) \text { and }t_{3}>z_{32}({\underline{t}})\text { (Stage II.1)} \\ F(z_{21}(t_{1})) &{}\quad \text {if }t_{1}>z_{12}({\underline{t}})\text { and } t_{3}<z_{32}({\underline{t}})\text { (Stage II.3)} \\ 0 &{}\quad \text {otherwise (Stage II.2 or Stage I)} \end{array} \text {.}\right. \end{aligned}$$

(A7)

Also, notice that $\frac{\partial P_{1}^{k}(t_{1})}{\partial t_{1}}\ge 0$ is satisfied both for each stage and across stages, as by assumption $f(z_{i1}(t_{1}))>0$, $F(z_{i1}(t_{1}))>0$ and by Lemma 2$z_{i1}^{\prime }(t_{1})$ $>0$, for all $t_{1}>z_{12}({\underline{t}})$. We prove now that the second sufficient condition also holds. If $t_{1}>z_{12}({\underline{t}})$ and $t_{3}>z_{32}({\underline{t}})$ (Stage II.1), it can be checked after some computations that $\frac{\partial \Gamma _{1}^{II.1}(t_{1})}{\partial t_{1}} =(1-\theta _{2})F(z_{21}(t_{1}))F(z_{31}(t_{1}))=(1-\theta _{2})P_{1}^{k}(t_{1})$, where the second equality follows from (A7). Using the same argument, a similar result holds for Stage II.3. Lastly, when $t_{1}<z_{12}({\underline{t}})$, bidder 1 does not participate in the auction. By noting that $z_{21}(t_{1})={\underline{t}}$ for all $t_{1}<z_{12}( {\underline{t}})$, one can verify that $\frac{\partial \Gamma _{1}^{k}(t_{1})}{ \partial t_{1}}=0=(1-\theta _{2})P_{1}^{k}(t_{1})$, where the second equality follows from (A7). $\square$

We are now prepared to demonstrate Proposition 4. From Lemma 1, we know that a selling procedure is optimal if it satisfies two conditions: (1) the bidder with the lowest possible value realization gets his reservation payoff (which in “Appendix A” we have showed to be optimally the same for all bidders and normalized to zero), and (2) it uses the optimal allocation rule. Notice that by construction, the sequential selling procedure satisfies both conditions. First, the payoff for either bidder with value ${\underline{t}}$ is zero: (i) bidder 3 does not participate in Stage II (because $z_{32}({\underline{t}})>{\underline{t}}$) and thus, he gets $\Gamma _{3}^{k}({\underline{t}})=0$ for all stage k; (ii) bidder 2 loses the auction for sure if some other bidder agrees to participate in Stage II and thus, he has a positive expected payoff. Otherwise, he pays $\underline{b_{2} }$ in the exclusive deal, which by construction, guarantees that the average payoff across all stages in the sequential mechanism for the lowest-type is $\Gamma _{2}({\underline{t}})=0$; and (iii) bidder 1 neither participates in Stage II (because $z_{12}({\underline{t}})>{\underline{t}}$), and result (ii) also ensures that he gets in expected terms (as average across all stages) $\Gamma _{1}({\underline{t}})=0$. Second, the allocation rule is the optimal one as we can check that $b_{i}>\widetilde{z_{ij}}(b_{j})$ iff $t_{i}>z_{ij}(t_{j})$ using the definition of $\widetilde{z_{ij}}(\cdot )$. $\square$

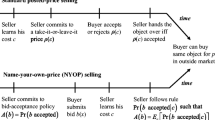
Proof of Proposition 5

Applying backward induction, we first need to characterize the Nash equilibrium resulting from Stage II. In this stage, bidder 1 accepts the offer if $(1-\theta _{2})(t_{1}-\rho _{1})>0$, i.e., if $t_{1}>\rho _{1}$, and rejects otherwise. The seller therefore has to optimally choose the offer given by $\rho _{1}^{*}=\arg \max _{\rho _{1}}(1-\rho _{1})\rho _{1}$. After solving, we get that $\rho _{1}^{*}=1/2$ and the optimal seller’s expected revenue from this stage is equal to 1/4.

In Stage I, bidder 2 accepts any seller’s offer if his payoff is larger than the expected payoff at the equilibrium of stage II. That is, if

$$\begin{aligned} (1-\theta _{1})(t_{2}-\rho _{2})> & {} E_{t_{1}}\left[ \theta _{2}(t_{1}-\rho _{1}^{*})|t_{1}>\rho _{1}^{*}\right] \Pr (t_{1}>\rho _{1}^{*}) \\= & {} \frac{\theta _{2}}{8}, \end{aligned}$$

which is equivalent to the condition $t_{2}>\rho _{2}+\theta _{2}/8(1-\theta _{1})$. Thus, the seller’s optimal offer is characterized by

$$\begin{aligned} \rho _{2}^{*}=\arg \max _{\rho _{2}}\left[ \left( 1-\left( \rho _{2}+ \frac{\theta _{2}}{8(1-\theta _{1})}\right) \right) \rho _{2}+\left( \rho _{2}+\frac{\theta _{2}}{8(1-\theta _{1})}\right) \frac{1}{4}\right] . \end{aligned}$$

The solution is given by $\rho _{2}^{*}=5/8-\theta _{2}/16(1-\theta _{1})$, which yields an optimal seller’s expected revenue equal to $V_{0}^{N}=(100-\lambda (12-\lambda ))/256$, where $\lambda \equiv \theta _{2}/(1-\theta _{1})$ and N highlights that this is the revenue generated by the negotiation mechanism. Since $\lambda \le 1$, it is easy to verify that $\rho _{2}^{*}>\rho _{1}^{*}$, which proves the first statement of the proposition.

In order to show the second result, notice that in the presence of asymmetric crossholdings it is not possible to find an analytical expression for the equilibrium bidding strategy in both FPA and SPA, and thereby, it is neither possible to obtain a closed expression for the seller’s revenue (see Dasgupta and Tsui 2004, Section 5). However, we can alternatively perform a comparison between the proposed mechanism with crossholdings and the FPA and SPA without crossholdings. It is well known that without crossholdings these two auction formats yield larger expected revenues than their versions with crossholdings, as these ownership stakes hurt the seller (see, for instance, Chillemi 2005, and Ettinger 2008). So, it suffices to show that expected revenues of our sequential mechanism exceeds that of standard FPA and SPA. Thanks to the revenue equivalence theorem, the last expected revenue is the same for both auction formats and equal to 1/3. Since $V_{0}^{N}$ is decreasing in $\lambda$, the worst case for our sequential negotiation mechanism arises when $\lambda$ is equal to its upper bound. Under the symmetric case, since $\partial \lambda /\partial \theta >0$, $\lambda$ reaches its upper bound at 1 when $\theta _{1}=\theta _{2}=\theta$ converges to 1/2, situation in which the expected revenue is equal to $89/256>1/3$. Under the asymmetric case, since $\partial \lambda /\partial \theta _{1}<0$ (with $\theta _{1}+\theta _{2}=1/2$ ), $\lambda$ converges to an upper bound of 1/3 when $\theta _{1}\downarrow 1/4$ and $\theta _{2}\uparrow 1/4$, situation in which the seller’s expected revenue converges to $0.375>1/3$. In both cases, the respective result implies that the second part of the proposition holds. $\square$