Description of the newly observed $\Xi _c^{0}$ states as molecular states

Abstract

Very recently, three new structures $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ at the invariant mass spectrum of $\Lambda _c^{+}K^{-}$ observed by the LHCb Collaboration trigger a hot discussion about their inner structure. In this work, we study the strong decay mode of the newly observed $\Xi ^0_c$ assuming that the $\Xi ^0_c$ is a $\bar{D}\Lambda -\bar{D}\Sigma$ molecular state. With the possible quantum numbers $J^p=1/2^{\pm }$ and $3/2^{\pm }$, the partial decay widths of the $\bar{D}\Lambda -\bar{D}\Sigma$ molecular state into the $\Lambda _c^{+}K^{-}$, $\Sigma _c^{+}K^{-}$,and $\Xi _c^{+}\pi ^{-}$ final states through hadronic loop are calculated with the help of the effective Lagrangians. By comparison with the LHCb observation, the current results of total decay width support the $\Xi _c(2923)^0$ as $\bar{D}\Lambda -\bar{D}\Sigma$ molecule while the decay width of the $\Xi _c(2938)^0$ and $\Xi _c(2964)^0$ can not be well reproduced in the molecular state picture. In addition, the calculated partial decay widths with S wave $\bar{D}\Lambda -\bar{D}\Sigma$ molecular state picture indicate that allowed decay mode, $\Xi _c^{+}\pi ^{-}$, may have the biggest branching ratio for the $\Xi _c(2923)^0$. The experimental measurements for this strong decay process could be a crucial test for the molecule interpretation of the $\Xi _c(2923)^0$.

1 Introduction

Thanks to the great progress of the experiment in past several decades, many narrow baryons with a heavy charm quark, a light up or down quark, and a strange quark have been reported by the LHCb,CDF Collaboration and so on [1]. Very recently, three other neutral resonances $\Xi _c^{*0}$ named $\Xi _c(2923)^0$, $\Xi _c(2939)^0$, and $\Xi _c(2965)^0$ have been observed in the $K^{-}\Lambda _c^{+}$ mass spectra by the LHCb Collaboration [2]. The observed resonance masses and widths are

$$\begin{aligned}&\mathrm{M}=2923.04\pm {0.25}(stat)\pm 0.20(syst)\pm {}0.14(\Lambda ^+_c)~ \mathrm{MeV}\\&\Gamma =7.1\pm 0.8(stat)\pm 1.8(syst)~\mathrm{MeV},\\&\mathrm{M}=2938.55\pm {0.21}(stat)\pm 0.17(syst)\pm {}0.14(\Lambda ^+_c)~ \mathrm{MeV}\\&\Gamma =10.2\pm 0.8(stat)\pm 1.1(syst)~\mathrm{MeV},\\&\mathrm{M}=2964.88\pm {0.26}(stat)\pm 0.14\pm {}(syst)0.14(\Lambda ^+_c)~ \mathrm{MeV}\\&\Gamma =14.1\pm 0.9(stat)\pm 1.3(syst)~\mathrm{MeV}, \end{aligned}$$

respectively. From the observed decay mode, the isospin of these three states is 1/2. Although the quantum numbers remain undetermined, it is very helpful to understand the spectroscopy of the heavy baryon containing c and s quarks.

From the $K^{-}\Lambda _c^{+}$ decay mode, the new structures $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ contain at least three different valence quarks. In other words, they may be candidates of conventional three-quark state. Indeed, the QCD sum rule suggests that the newly observed states $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ are most likely to be considered as the P-wave $\Xi _c^{'}$ baryons with the spin parity $J^p=1/2^{-}$ or $J^p=3/2^{-}$ [3]. The $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ are also suggested to be 1P $\Xi _c^{'}$ state with spin parity $J^P = 3/2^-$ or $J^P = 5/2^-$ in the chiral quark model [4]. In Ref. [5] the two-body strong decays of the $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ were calculated by employing the $^3P_0$ approach with the conclusion that the $\Xi _c(2923)^0$ and $\Xi _c(2938)^0$ can be 1P $\Xi _c^{'}$ states, while the $\Xi _c(2964)^0$ can be regarded as the 2S $\Xi _c^{'}$ state. The lattice QCD calculation was also performed and tried to determine their quantum numbers [6].

Although the authors in Refs. [3,4,5,6] try to assign these states into the conventional three-quark frame, at present we cannot fully exclude the other additional configurations such as molecule explanation of these three states due to the uncertainty of the quark pair creation model is not under control [5]. Indeed, it is shown in Refs. [7,8,9] that the interaction between D meson and $\Lambda$ or $\Sigma$ baryon is strong enough to form a bound state with a mass about 2930 MeV that can be associated to the $\Xi _c(2923)^0$ or $\Xi _c(2938)^0$.

The key point in this work is to explain whether the $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ can be considered as a molecular state. Here, we will consider the strong $\Xi _c^{*}\rightarrow \Lambda _c^+K^{-}$,$\Sigma _c^+K^{-}$, and $\Xi _c^{+}\pi ^{-}$ decays of the $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ with the possible quantum numbers $J^p=1/2^{\pm }$ and $3/2^{\pm }$ using an effective Lagrangian approach. The approach is based on the hypothesis that the $\Xi _c^{*}$ is a hadronic molecular state of $D\Lambda -D\Sigma$. The coupling of the $\Xi _c^{*}$ to the constituents is described by the effective Lagrangian. The corresponding coupling constants $g_{\Xi _c^{*}\Lambda {}D}$ and $g_{\Xi _c^{*}\Sigma {}D}$ are determined by the compositeness condition $Z=0$ [10,11,12,13,14], which implies that the renormalization constant of the hadron wave function is set to zero. By constructing a phenomenological Lagrangian including the couplings of the bound state to its constituents and the constituents with other particles we calculated one-loop diagram describing different decays of the molecular states.

This work is organized as follows. The theoretical formalism is explained in Sect. 2. The predicted partial decay widths are presented in Sect. 3, followed by a short summary in the last section.

2 Formalism and ingredients

Fig. 1

Self-energy of the $\Xi _c^{*}$ states

In the molecular scenario, the details of the calculations for $\Xi _c^{*}\rightarrow \Lambda _c^{+}K^{-}$, $\Xi _c^{*}\rightarrow \Sigma _c^{+}K^{-}$, and $\Xi _c^{*}\rightarrow \Xi _c^{+}\pi ^{-}$ are presented for $\Xi ^{*}_c$ state with two different total angular momentum $J=1/2,3/2$. The molecular structure of the $\Xi _c^{*}$ baryon with quantum numbers $J^p=1/2^{\pm }$ is described by the Lagrangian [14]

$$\begin{aligned} \mathcal{{L}}_{\Xi _c^{*}}(x)&=\bar{\Xi }_c^{*}(x)\int {}d^4y\Phi (y^2)\nonumber \\&\quad \times {}\Bigg \{g_{\Xi _c^{*}D\Lambda }D^0(x+\omega _{\Lambda }y)\Gamma \Lambda (x-\omega _{D^0}y)\nonumber \\&\quad +g_{\Xi _c^{*}D\Sigma }\Bigg [\sqrt{\frac{2}{3}}D^0(x+\omega _{\Sigma ^0}y)\Gamma \Sigma ^0(x-\omega _{D^0}y)\nonumber \\&\quad -\sqrt{\frac{1}{3}}D^{+}(x+\omega _{\Sigma ^{-}}y)\Gamma \Sigma ^{-}(x-\omega _{D^{+}}y)\Bigg ]\Bigg \}, \end{aligned}$$

(1)

while for the choice $J^p=3/2^{\pm }$ the Lagrangian take the form of

$$\begin{aligned} \mathcal{{L}}_{\Xi _c^{*}}(x)&=\bar{\Xi }_c^{*\mu }(x)\int {}d^4y\Phi (y^2)\nonumber \\&\quad \times {}\Bigg \{g_{\Xi _c^{*}D\Lambda }D^0(x+\omega _{\Lambda }y)\Gamma \partial _{\mu }\Lambda (x-\omega _{D^0}y)\nonumber \\&\quad +g_{\Xi _c^{*}D\Sigma }\Bigg [\sqrt{\frac{2}{3}}D^0(x+\omega _{\Sigma ^0}y)\Gamma \partial _{\mu }\Sigma ^0(x-\omega _{D^0}y)\nonumber \\&\quad -\sqrt{\frac{1}{3}}D^{+}(x+\omega _{\Sigma ^{-}}y)\Gamma \partial _{\mu }\Sigma ^{-}(x-\omega _{D^{+}}y)\Bigg ]\Bigg \}. \end{aligned}$$

(2)

Where the $\Gamma$ is the corresponding Dirac matrix reflecting the spin-parity of $\Xi _c^{*}$. In particular, for $J^{p}=1/2^{+}$ and $3/2^{-}$,$\Gamma =\gamma _5$, while for $J^{p}=1/2^{-}$ and $3/2^{+}$, $\Gamma =1$. In the above Lagrangian, an effective correlation function $\Phi (y^2)$ is introduced to reflect the distribution of the two constituents in the hadronic molecular $\Xi _c^{*}$ states. The introduced correlation function also serves the purpose of making the Feynman diagrams ultraviolate finite. Here we choose the Fourier transformation of the correlation in the Gaussian form [10,11,12,13,14],

$$\begin{aligned} \Phi (p_E^2)\doteq \exp (-p_E^2/\alpha ^2) \end{aligned}$$

(3)

with $p_E$ being the Euclidean Jacobi momentum and $\alpha$ being the size parameter which characterize the distribution of components inside the molecule. The value of $\alpha =1.0$ is determined by fitting to experimental data [10,11,12,13,14] (and references therein).

The coupling constants $g_{\Xi _c^{*}\Lambda \bar{D}}$ ($g_{\Xi _c^{*}\Sigma {}D}$) in Eq. 1 (Eq. 2) is determined by the compositeness condition [15, 16]. It implies that the renormalization constant of the hadron wave function is set to zero with

$$\begin{aligned} Z_{\Xi _c^{*}}=X_{D\Lambda }+X_{D\Sigma }-\frac{d\Sigma ^{1/2,3/2-T}_{\Xi _c^{*}}}{dk\!\!\!/_0}|_{k\!\!\!/_0=m_{\Xi ^{*}_{c}}}=0. \end{aligned}$$

(4)

where the $X_{AB}$ is the probability to find the $\Xi _c^*$ in the hadronic state AB with the normalization $X_{D\Lambda }+X_{D\Sigma }=1.0$. And the $\Sigma ^{3/2-T}_{\Xi _c^{*}}$ is the transverse part of the self-energy operator $\Sigma ^{3/2}_{\Xi _c^{*}}$, related to $\Sigma ^{3/2}_{\Xi _c^{*}}$ via

$$\begin{aligned} \Sigma ^{3/2}_{\Xi _b^{*}}(k_0)= \Bigg (g_{\mu \nu }-\frac{k_0^{\mu }k_0^{\nu }}{k_0^2}\Bigg )\Sigma ^{3/2-T}_{\Xi _c^{*}}+\cdots . \end{aligned}$$

(5)

With the help of the above effective Lagrangians, the $\Sigma ^{1/2}_{\Xi _c^{*}}$ and $\Sigma ^{3/2}_{\Xi _c^{*}}$ can be computed as follow

$$\begin{aligned} \Sigma ^{1/2}_{\Xi _c^{*}}(k_0)&= \int \frac{d^4k_1}{(2\pi )^4}\Bigg \{g^2_{\Xi _c^{*}\Lambda {D}}\Phi ^2[(k_1-k_0\omega _{\Lambda })^2]\nonumber \\&\quad \times \Gamma \frac{k\!\!\!/_1+m_{\Lambda }}{k_1^2-m^2_{\Lambda }}\Gamma \frac{1}{(k_1-k_0)^2-m^2_{D^{0}}}\nonumber \\&\quad +g^2_{\Xi _c^{*}\Sigma {}D}\Bigg [\frac{2}{3}\Phi ^2[(k_1-k_0\omega _{\Sigma ^0})^2]\nonumber \\&\quad \times \Gamma \frac{k\!\!\!/_1+m_{\Sigma ^0}}{k_1^2-m^2_{\Sigma ^0}}\Gamma \frac{1}{(k_1-k_0)^2-m^2_{D^{0}}}\nonumber \\&\quad +\frac{1}{3}\Phi ^2[(k_1-k_0\omega _{\Sigma ^{-}})^2]\nonumber \\&\quad \times \Gamma \frac{k\!\!\!/_1+m_{\Sigma ^{-}}}{k_1^2-m^2_{\Sigma ^{-}}}\Gamma \frac{1}{(k_1-k_0)^2-m^2_{D^{+}}}\Bigg ]\Bigg \}, \end{aligned}$$

(6)

$$\begin{aligned} \Sigma ^{3/2}_{\Xi _c^{*}}(k_0)&=\int \frac{d^4k_1}{(2\pi )^4}\Bigg \{g^2_{\Xi _c^{*}\Lambda {D}}\Phi ^2[(k_1-k_0\omega _{\Lambda })^2]\nonumber \\&\quad \times {}\Gamma \frac{k\!\!\!/_1+m_{\Lambda }}{k_1^2-m^2_{\Lambda }}\Gamma \frac{1}{(k_1-k_0)^2-m^2_{D^{0}}}\nonumber \\&\quad +g^2_{\Xi _c^{*}\Sigma {}D}\Bigg [\frac{2}{3}\Phi ^2[(k_1-k_0\omega _{\Sigma ^0})^2]\nonumber \\&\quad \times \Gamma \frac{k\!\!\!/_1+m_{\Sigma ^0}}{k_1^2-m^2_{\Sigma ^0}}\Gamma \frac{1}{(k_1-k_0)^2-m^2_{D^{0}}}\nonumber \\&\quad +\frac{1}{3}\Phi ^2[(k_1-k_0\omega _{\Sigma ^{-}})^2]\nonumber \\&\quad \times \Gamma \frac{k\!\!\!/_1+m_{\Sigma ^{-}}}{k_1^2-m^2_{\Sigma ^{-}}}\Gamma \frac{1}{(k_1-k_0)^2-m^2_{D^{+}}}\Bigg ]\Bigg \}k_1^{\mu }k_1^{\nu }, \end{aligned}$$

(7)

where $k_0^2=m^2_{\Xi _c^{*}}$ with $k_0, m_{\Xi ^{*}_c}$ denoting the four momenta and mass of the $\Xi _c^{*}$, respectively, $k_1$, $m_{D}$, and $m_{Y}(Y=\Lambda ,\Sigma )$ are the four-momenta, the mass of the D meson, and the mass of the Y baryon, respectively.

Fig. 2

Feynman diagrams for the $\Xi _c^{*}\rightarrow {}\Lambda _c^{+}K^{-}$,$\Xi _c\pi$, and $\Sigma _c\bar{K}$ decay process

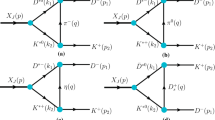
Figure 2 shows the hadronic decay of the $\Lambda {}D-\Sigma {D}$ molecular state into the $\Lambda _c^{+}K^{-}$,$\Xi _c^{+}\pi ^{-}$, and $\Sigma _c^{+}K^{-}$ final states occuring by exchanging nucleon, $D_s^{*}$ meson, and $D^{*}$ meson. To compute the amplitude of these Feynman diagrams, we need the effective Lagrangian density for the relevant interaction vertex. The following effective Lagrangians, responsible for vector mesons and pseudoscalar mesons interactions are needed as well [17]

$$\begin{aligned} \mathcal{{L}}_{PPV}=\frac{i}{4}g_{h}\langle [\partial ^{\mu }P,P]V_{\mu }\rangle , \end{aligned}$$

(8)

where P is the SU(4) pseudoscalar meson matrices, and $\langle ...\rangle$ in the trace over the SU(4) matrices. The meson matrices are [17]

$$\begin{aligned} P=\sqrt{2} \left( \begin{array}{cccc} \frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}+\frac{\eta ^{'}}{\sqrt{3}} &{}\pi ^{+} &{}K^{+} &{} D^0 \\ \pi ^{-} &{} -\frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}+\frac{\eta ^{'}}{\sqrt{3}} &{}K^{0} &{}-D^{-} \\ K^{-} &{} \bar{K}^{0} &{} -\sqrt{\frac{2}{3}}\eta +\frac{\eta ^{'}}{\sqrt{3}} &{} D^{-}_s\\ D^0 &{} -D^{+} &{}D_s^{+} &{}\eta _c \\ \end{array} \right) . \end{aligned}$$

(9)

The coupling $g_h$ is fixed from the strong decay width of $K^{*}\rightarrow {}K\pi$. With the help of Eq. (9), the two-body decay width $\Gamma (K^{*+}\rightarrow {}K^{0}\pi ^{+})$ is related to $g_h$ as

$$\begin{aligned} \Gamma (K^{*+}\rightarrow {}K^{0}\pi ^{+})=\frac{g_h^2}{6\pi {}m^2_{K^{*+}}}\mathcal{{P}}^3_{\pi {}K^{*}}=\frac{2}{3}\Gamma _{K^{*+}}, \end{aligned}$$

(10)

where $\mathcal{{P}}_{\pi {}K^{*}}$ is the three-momentum of the $\pi$ in the rest frame of the $K^{*}$. Using the experimental strong decay width($\Gamma _{K^{*+}}=50.3\pm 0.8$ MeV) and the masses of the particles needed in the present work are listed in Table 1 we obtain $g=4.64$ [1].

Table 1 Masses of the particles needed in the present work (in units of MeV)

In Refs. [17, 18], coupling of the vector meson to charm baryon is described from effective Lagrangians, which is obtained using the hidden gauge formalism and assuming SU(4) symmetry:

$$\begin{aligned} \mathcal{{L}}_{VBB}=\frac{g_1}{4}\sum _{i,j,k,l=1}^{4}\bar{B}_{ijk}\gamma ^{\mu }(V^{K}_{\mu ,l}B^{ijl}+2V^{j}_{\mu ,l}B^{ilk}), \end{aligned}$$

(11)

where the coupling constant $g=6.6$ is got from Ref. [17]. The symbol $V_{\mu }$ represents the vector fields of the 16-plet of the $\rho$, given by

$$\begin{aligned} V_{\mu }= \left( \begin{array}{cccc} \frac{1}{\sqrt{2}}(\rho ^{0}+\omega ) &{} \rho ^{+} &{} K^{*+} &{} \bar{D}^{*0} \\ \rho ^{-} &{} \frac{1}{\sqrt{2}}(-\rho ^{0}+\omega ) &{} K^{*0} &{} -D^{*-} \\ K^{*-} &{} \bar{K}^{*0} &{} \phi &{} D^{*-}_s \\ D^{*0} &{} -D^{*+} &{} D^{*+}_{s} &{} J/\psi \\ \end{array} \right) _{\mu }, \end{aligned}$$

(12)

and B is the tensor of baryons belonging to the 20-plet of p

$$\begin{aligned}&B^{121}=p, \quad B^{122}=n,\quad B^{132}=\frac{1}{\sqrt{2}}\Sigma ^{0}-\frac{1}{\sqrt{6}}\Lambda ,\nonumber \\&B^{213}=\sqrt{\frac{2}{3}}\Lambda ,\quad B^{231}=\frac{1}{\sqrt{2}}\Sigma ^{0}+\frac{1}{\sqrt{6}}\Lambda ,\quad B^{232}=\Sigma ^{-},\nonumber \\&B^{233}=\Xi ^{-},B^{311}=\Sigma ^{+},\quad B^{313}=\Xi ^{0},\quad B^{141}=-\Sigma _c^{++},\nonumber \\&B^{142}=\frac{1}{\sqrt{2}}\Sigma ^{+}_{c}+\frac{1}{\sqrt{6}}\Lambda _c,\quad B^{143}=\frac{1}{\sqrt{2}}\Xi ^{'+}_c-\frac{1}{\sqrt{6}}\Xi _c^{+},\nonumber \\&B^{241}=\frac{1}{\sqrt{2}}\Sigma _c^{+}-\frac{1}{\sqrt{6}}\Lambda _c,\quad B^{242}=\Sigma _c^{0},\nonumber \\&B^{243}=\frac{1}{\sqrt{2}}\Xi ^{'0}_c+\frac{1}{\sqrt{6}}\Xi _c^{0},\quad B^{341}=\frac{1}{\sqrt{2}}\Xi ^{,+}_c+\frac{1}{\sqrt{6}}\Xi _c^{+},\nonumber \\&B^{124}=\sqrt{\frac{2}{3}}\Lambda _c,\quad B^{234}=\sqrt{\frac{2}{3}}\Xi _c^{0},\quad B^{314}=\sqrt{\frac{2}{3}}\Xi _c^{+},\nonumber \\&B^{342}=\frac{1}{\sqrt{2}}\Xi ^{'0}_c-\frac{1}{\sqrt{6}}\Xi _c^{0},\quad B^{343}=\Omega _c^{0},\nonumber \\&B^{144}=\Xi ^{++}_{cc},\quad B^{244}=-\Xi ^{+}_{cc},\quad B^{344}=\Omega _{cc}, \end{aligned}$$

(13)

where the indices i, j, k of $B^{ijk}$ denote the quark content of the baryon fields with the identification $1\leftrightarrow {u},2\leftrightarrow {d},3\leftrightarrow {}s$,and $4\leftrightarrow {}c$.

The vertexes for the meson–baryon interaction are needed and the form in the SU(3) sector is given by the chiral Lagrangian [19]

$$\begin{aligned} {\mathcal {L}}_{\phi {\mathcal {B}}{\mathcal {B}}}&=\frac{F}{2}\langle {\bar{\mathcal {B}}} \gamma _{\mu }\gamma _5[u^{\mu },{\mathcal {B}}]\rangle +\frac{D}{2}\langle {\bar{\mathcal {B}}}\gamma _{\mu }\gamma _5\{u^{\mu },{\mathcal {B}}\}\rangle , \end{aligned}$$

(14)

where $F=0.51$, $D=0.75$ [19] and at lowest order in the pseudoscalar field $u^{\mu }=-\sqrt{2}\partial ^{\mu }\phi /f$, with $f=93$ MeV. $\mathcal{{B}}$ and $\phi$ are now the SU(3) matrix of the baryon octet and meson, respectively,

$$\begin{aligned} \mathcal{{B}}= & {} \left( \begin{array}{ccc} \frac{1}{\sqrt{2}}\Sigma ^{0}+\frac{1}{\sqrt{6}}\Lambda &{} \Sigma ^{+} &{} p \\ \Sigma ^{-} &{} -\frac{1}{\sqrt{2}}\Sigma ^{0}+\frac{1}{\sqrt{6}}\Lambda &{} n \\ \Xi ^{-} &{} \Xi ^{0} &{} -\frac{2}{\sqrt{6}}\Lambda \\ \end{array} \right) , \end{aligned}$$

(15)

$$\begin{aligned} \phi= & {} \left( \begin{array}{ccc} \frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{} \pi ^{+} &{} K^{+}\\ \pi ^{-} &{} -\frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{} K^{0}\\ K^{-} &{} \bar{K}^{0} &{} -\frac{2}{\sqrt{6}}\eta \end{array} \right) . \end{aligned}$$

(16)

Moreover, the effective Lagrangians for the $DN\Lambda _c$ and $DN\Sigma _c$ couplings are [20, 21]

$$\begin{aligned}&\mathcal{{L}}_{DN\Lambda _c}=ig_{\Lambda _cpD}\bar{\Lambda }_c\gamma _5pD^0, \end{aligned}$$

(17)

$$\begin{aligned}&\mathcal{{L}}_{DN\Sigma _c}=-ig_{\Sigma _cpD}\bar{N}\gamma _5\mathbf {\tau }\cdot \mathbf {\Sigma }_cD, \end{aligned}$$

(18)

with $\mathbf {\tau }$ being the usual Pauli matrix. The coupling constants $g_{\Lambda _cpD}=10.7^{+5.3}_{-4.3}$ and $g_{\Sigma _cpD}=-2.69$ are borrowed from Refs. [20,21,22], where we take the central value $g_{\Lambda _cpD}=10.7$ in our calculation.

With the above vertices, the amplitudes of the triangle diagrams of Fig. 2, evaluated in the center of mass frame of final states, are

$$\begin{aligned} \mathcal{{M}}_{a}&=(i)^3\frac{g_1g_hg_{\Xi _c^{*}\Lambda {D^0}}}{2}\int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{\Lambda }-k_2\omega _{D})^2]\nonumber \\&\quad \times \bar{u}(p_2)\gamma _{\mu }\frac{(k\!\!\!/_2+m_{\Lambda })}{k_2^2-m^2_{\Lambda }}\Gamma {}\{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\nonumber \\&\quad \times {}\frac{1}{k^2_1-m^2_{D^0}}(p_1^{\nu }+k_1^{\nu })\frac{(-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{D_s^{*+}})}{q^2-m^2_{D_s^{*+}}}, \end{aligned}$$

(19)

$$\begin{aligned} \mathcal{{M}}_{b}&=-(i)^3\frac{(D+3F)g_{\Lambda _cpD}g_{\Xi _c^{*}\Lambda {D^0}}}{2\sqrt{3}f}\int \frac{d^4q}{(2\pi )^4}\nonumber \\&\quad \times \Phi [(k_1\omega _{\Lambda }-k_2\omega _{D})^2]\bar{u}(p_2)\frac{(q\!\!\!/-m_{N})}{q^2-m^2_{N}}p\!\!\!/_1\nonumber \\&\quad \times {}\frac{k\!\!\!/_2+m_{\Lambda }}{k_2^2-m^2_{\Lambda }}\Gamma {}\{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\frac{1}{k^2_1-m^2_{D^0}}, \end{aligned}$$

(20)

$$\begin{aligned} \mathcal{{M}}_{c}&=-(i)^3\frac{g_1g_hg_{\Xi _c^{*}\Lambda {D^0}}}{4}\int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{\Lambda }-k_2\omega _{D})^2]\nonumber \\&\quad \times {}\bar{u}(p_2)\gamma _{\mu }\frac{(k\!\!\!/_2+m_{\Lambda })}{k_2^2-m^2_{\Lambda }}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\nonumber \\&\quad \times {}\frac{1}{k^2_1-m^2_{D^0}}(p_1^{\nu }+k_1^{\nu })\frac{(-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{D^{*+}})}{q^2-m^2_{D^{*+}}}, \end{aligned}$$

(21)

$$\begin{aligned} \mathcal{{M}}_{d}&=-(i)^3\frac{(D+3F)g_{\Sigma _cpD}g_{\Xi _c^{*}\Lambda {D^0}}}{2\sqrt{3}f}\int \frac{d^4q}{(2\pi )^4}\nonumber \\&\quad \times \Phi [(k_1\omega _{\Lambda }-k_2\omega _{D})^2]\bar{u}(p_2)\frac{(q\!\!\!/-m_{N})}{q^2-m^2_{N}}p\!\!\!/_1\nonumber \\&\quad \times {}\frac{k\!\!\!/_2+m_{\Lambda }}{k_2^2-m^2_{\Lambda }}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\frac{1}{k^2_1-m^2_{D^0}}, \end{aligned}$$

(22)

$$\begin{aligned} \mathcal{{M}}_{e1}&=(i)^3\frac{(F-D)g_{\Lambda _cpD}g_{\Xi _c^{*}\Sigma ^0D^0}}{2\sqrt{3}f}\int \frac{d^4q}{(2\pi )^4}\nonumber \\&\quad \times \Phi [(k_1\omega _{\Sigma ^0}-k_2\omega _{D^0})^2]\bar{u}(p_2)\frac{(q\!\!\!/-m_{p})}{q^2-m^2_{p}}p\!\!\!/_1\nonumber \\&\quad \times {}\frac{k\!\!\!/_2+m_{\Sigma ^0}}{k_2^2-m^2_{\Sigma ^0}}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\frac{1}{k^2_1-m^2_{D^0}}, \end{aligned}$$

(23)

$$\begin{aligned} \mathcal{{M}}_{e2}&=-(i)^3\frac{(F-D)g_{\Lambda _cpD}g_{\Xi _c^{*}\Sigma ^-D^+}}{\sqrt{6}f}\int \frac{d^4q}{(2\pi )^4}\nonumber \\&\quad \times \Phi [(k_1\omega _{\Sigma ^-}-k_2\omega _{D^+})^2]\bar{u}(p_2)\frac{(q\!\!\!/-m_{n})}{q^2-m^2_{n}}p\!\!\!/_1\nonumber \\&\quad \times {}\frac{k\!\!\!/_2+m_{\Sigma ^-}}{k_2^2-m^2_{\Sigma ^-}}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\frac{1}{k^2_1-m^2_{D^+}}, \end{aligned}$$

(24)

$$\begin{aligned} \mathcal{{M}}_{f1}&=(i)^3\frac{g_1gg_{\Xi _c^{*}\Sigma ^0{D^0}}}{4}\int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{\Sigma ^0}-k_2\omega _{D^0})^2]\nonumber \\&\quad \times {}\bar{u}(p_2)\gamma _{\mu }\frac{(k\!\!\!/_2+m_{\Sigma ^0})}{k_2^2-m^2_{\Sigma ^0}}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\nonumber \\&\quad \times \frac{1}{k^2_1-m^2_{D^0}}(p_1^{\nu }+k_1^{\nu })\frac{(-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{D^{*+}})}{q^2-m^2_{D^{*+}}}, \end{aligned}$$

(25)

$$\begin{aligned} \mathcal{{M}}_{f2}&=-(i)^3\frac{g_1gg_{\Xi _c^{*}\Sigma ^-{D^+}}}{2}\int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{\Sigma ^-}-k_2\omega _{D^+})^2]\nonumber \\&\quad \times {}\bar{u}(p_2)\gamma _{\mu }\frac{(k\!\!\!/_2+m_{\Sigma ^-})}{k_2^2-m^2_{\Sigma ^-}}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\nonumber \\&\quad \times {}\frac{1}{k^2_1-m^2_{D^+}}(p_1^{\nu }+k_1^{\nu })\frac{(-g^{\mu \nu }+q^{\mu }q^{\nu }/m^2_{D^{*0}})}{q^2-m^2_{D^{*0}}}, \end{aligned}$$

(26)

$$\begin{aligned} \mathcal{{M}}_{g1}&=-(i)^3\frac{(F-D)g_{\Sigma _cpD}g_{\Xi _c^{*}\Sigma ^0{D^0}}}{\sqrt{6}f}\int \frac{d^4q}{(2\pi )^4}\nonumber \\&\quad \times \Phi [(k_1\omega _{\Sigma ^0}-k_2\omega _{D})^2]\bar{u}(p_2)\frac{(q\!\!\!/-m_{N})}{q^2-m^2_{N}}p\!\!\!/_1\nonumber \\&\quad \times {}\frac{k\!\!\!/_2+m_{\Sigma ^0}}{k_2^2-m^2_{\Sigma ^0}}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\frac{1}{k^2_1-m^2_{D^0}}, \end{aligned}$$

(27)

$$\begin{aligned} \mathcal{{M}}_{g2}&=(i)^3\frac{\sqrt{6}(F-D)g_{\Sigma _cpD}g_{\Xi _c^{*}\Sigma ^-{D^+}}}{3f}\int \frac{d^4q}{(2\pi )^4}\nonumber \\&\quad \times {}\Phi [(k_1\omega _{\Sigma ^-}-k_2\omega _{D^+})^2]\bar{u}(p_2)\frac{(q\!\!\!/-m_{N})}{q^2-m^2_{N}}p\!\!\!/_1\nonumber \\&\quad \times {}\frac{k\!\!\!/_2+m_{\Sigma ^-}}{k_2^2-m^2_{\Sigma ^-}}\Gamma \{u(k_0),ik_{2\rho }u^{\rho }(k_0)\}\frac{1}{k^2_1-m^2_{D^+}}. \end{aligned}$$

(28)

where $\{u(p)$, and $ik_2^{\rho }u_{\rho }(p)\}$ are $J^P=1/2$ and $J^P=3/2$ $\Xi _c^{*}$ fields,respectively.

Once the amplitudes are determined, the corresponding partial decay widths can be obtained, which read,

$$\begin{aligned} \Gamma (\Xi _c^{*}\rightarrow MB)=\frac{1}{2J+1}\frac{1}{8\pi }\frac{|\mathbf {p}_1|}{m^2_{\Xi _c^{*}}}\overline{|\mathcal{{M}}|^2}, \end{aligned}$$

(29)

where J is the total angular momentum of the $\Xi _c^{*}$ state, the $|\mathbf {p}_1|$ is the three-momenta of the decay products in the center of mass frame, the overline indicates the sum over the polarization vectors of the final hadrons, and MB denotes the decay channel of MB, i.e.,$\Lambda _c\bar{K}$, $\Xi _c\pi$, $\Sigma _c\bar{K}$.

3 Results and discussions

Fig. 3

The coupling constants of the $\Xi _c^*$ state with different $J^P$ assignments as a function of the parameter $X_{D\Lambda }$. And the $X_{D\Lambda }$ is the probability to find the $\Xi _c^{*}$ in the hadronic state $D\Lambda$

In this work, we try to explain whether the $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ can be considered as a $D\Lambda -D\Sigma$ molecular state by calculating allowed two body strong decay modes. Before calculating the two body decay width, we need to determine the coupling constants relevant to the effective Lagrangians listed in Eqs. (1) and (2). According to the compositeness condition that we introduced in Eq. (4), the $X_{D\Lambda }$ dependence of the coupling constants $g_{\Xi _c^*\Lambda {}D}$ and $g_{\Xi _c^*\Sigma {}D}$ are computed. With a value of the $X_{D\Lambda }=0.0-1.0$, these coupling constants are shown in Fig. 3. We note that the coupling constant $g_{\Xi _c^*\Sigma {}D}$ monoto-nously decreases with increasing $X_{D\Lambda }$, while the coupling constant $g_{\Xi _c^*\Lambda {}D}$ increases with increasing $X_{D\Lambda }$. The opposite trend can be easily understood, as the coupling constants $g_{\Xi _c^*\Lambda {}D}$ and $g_{\Xi _c^*\Sigma {}D}$ are directly proportional to the corresponding molecular compositions. We also find that the dependence on $X_{D\Lambda }$ is the largest for the $J^p=3/2^{-}$ case, is intermediate for the $J^p=1/2^{+}$ and $J^p=3/2^{+}$ cases, and is the smallest for the $J^p=1/2^{-}$ case.

Fig. 4

The total decay width with different spin-parity assignments for the various $\Xi _c^{*}$ as a function of the parameter $X_{D\Lambda }$. The cyan band denotes the experimental total width [2]

We show the dependence of the total decay width on the $X_{D\Lambda }$ in Fig. 4. The total decay widths increase with $X_{D\Lambda }$ for the $J^P=1/2^{+}$ and $J^P=3/2^{\pm }$ assignments. For the $J^P=1/2^-$ assignment, we found that the line shape of the total decay width is huge different and the total decay width is the biggest than total decay width in other three cases. A possible explanation for this may be that for an S-wave loosely impure bound state the effective coupling strength of the impure bound state to its components is more sensitive to the inner structure than the effective coupling strength of another possible molecular state, such as P-wave molecular state, relative to their inner component. However, a completely different conclusion was drawn in Refs. [10,11,12,13,14] (and their references) that for an S-wave loosely pure bound state the effective coupling strength of the bound state to its components is insensitive to its inner structure. This may be why people often focus on the impure bound state from S-wave interaction and assume the P- and D-wave bound state should be difficult to form from hadron–hadron interaction [23].

From the Fig. 4, one find that the predicted total decay widths for the $\Xi _c(2964)^0$ state and $\Xi _c(2938)^0$ state in the four spin-parity assignments are all smaller than the experimental total width. Such results disfavor the assignment of these two states as $D\Lambda -D\Sigma$ molecular state. For the $\Xi _c(2923)^0$ state, the predicted total decay width is much smaller than the experimental total width in the case of $J^P=1/2^{+}$, which disfavors such a spin-parity assignment for the $\Xi _c(2923)^0$ in the $D\Lambda -D\Sigma$ molecular picture. For the case of $J^P=3/2^{+}$, since the estimated total decay width is much smaller than the experimental total width, this case can be completely excluded as well. The $J^P=3/2^-$ case is also disfavored due to the smallest width predicted. Hence, only the assignment as a S- wave $D\Lambda -D\Sigma$ molecular state for the $\Xi _c(2923)^0$ is consistent with the LHCb data [2].

The individual contributions of the $D\Sigma$ and $D\Lambda$ components for the decays $\Xi _c(2923)^0\rightarrow {}K^{-}\Lambda _c^{+}$ and $\Xi _c(2923)^0\rightarrow {}\pi \Xi _c^{+}$ in the case of the $J^P=1/2^{-}$ are calculated and presented in Fig. 5. Our result shows that the $D\Lambda$ component contribution can become larger than the $D\Sigma$ component contribution when $X_{D\Lambda }$ is lager than 0.59. We also find that the total decay width of the $\Xi _c(2923)^0$ can not be well reproduced in a pure $D\Lambda$ or pure $D\Sigma$ molecular state. However, the interference among the two channels is sizable, leading to a total decay width consistent with the experimental data. In other words, the $D\Lambda$ channel strongly couples to the $D\Sigma$ channel.

Fig. 5

Decomposed contributions to the decay width of the $\Xi _c(2923)$ into $\Lambda _c^{+}K^{-}$ and $\pi \Xi$. The cyan bands denote the experimental total width [2]

Fig. 6

Partial decay widths of $\Xi _c(2923)^0\rightarrow \Lambda _c^+K^-$ (red solid line) and $\Xi _c(2923)^0\rightarrow \Xi _c\pi$ (black dash line) with $J^P=1/2^{-}$ as a function of the parameter $X_{D\Lambda }$. The cyan bands denote the experimental total width [2]

The partial decay widths of $\Xi _c(2923)^0\rightarrow \Lambda _c^+K^-$ and $\Xi _c(2923)^0\rightarrow \Xi _c\pi$ with $J^P=1/2^{-}$ assignment as a function of the parameter $X_{D\Lambda }$ are presented in Fig. 6. It is found that the transition $\Xi _c(2923)^0\rightarrow \Xi _c\pi$ is main decay channel, which almost saturates the total width of $\Xi _c(2923)^0$. However, the transition $\Xi _c(2923)^0\rightarrow \Lambda _c^+K^-$ give minor contributions. The decay width $\Xi _c(2923)^0\rightarrow \Xi _c\pi$ is very different from that in the constituent quark model [3,4,5] if we assign $\Xi _c(2923)^0$ as a S-wave $D\Lambda -D\Sigma$ bound state. Future experimental measurement of such process can be quite useful to test the different interpretations of the $\Xi _c(2923)^0$.

We found that the decay widths of the three new narrow $\Xi _c^{*}$ baryon are almost the same under the $D\Lambda -D\Sigma$ molecular state assignment. It means that the interaction between the $D\Lambda$ channel and the $D\Sigma$ channel can only form a bound state with mass about 2923 MeV and $J^P=1/2^{-}$. In order to prove, we show the dependence of the total decay width on the masses of the bound state $\Xi _c^{*}$ in Fig. 7. One can see that the total decay width decreases slightly with the mass of the bound state $\Xi _c^{*}$ from 2.90 GeV to 2.97 GeV. The predicted total decay width is small and find it can be comparable with that of $\Xi _c(2923)^0$ experimental total width.

Fig. 7

Total decay width of the $\Xi _c^{*}$ as a function of the mass of bound state $\Xi _c^{*}$ and $X_{D\Lambda }$. The cyan bands denote the experimental total width of $\Xi _c(2923)$ [2]

In evaluating the amplitudes shown in Fig. 2, phenomenological form factors should be included because hadrons are not pointlike particles. A monopole form factor is introduced to depict the off-shell effect of the exchanged meson (or baryon), which is often adopted in many previous works,

$$\begin{aligned} \mathcal{{F}}=\frac{\Lambda ^2-m^2}{\Lambda ^2-q^2}. \end{aligned}$$

(30)

Here the q and m are the four momentum and the mass of the t-channel exchanged meson (or baryon), respectively. The $\Lambda =m+\alpha \Lambda _{QCD}$ with $\Lambda _{QCD}=0.22$ GeV. To make a reliable prediction for the decay width of the $\Xi _c^{0}\rightarrow \Lambda _c^{+}K^{-}$, $\Xi _c^{0}\rightarrow \Sigma _c^{+}K^{-}$, and $\Xi _c^{0}\rightarrow \Xi _c^{+}\pi ^{-}$, it is crucial to know the value of the $\alpha$. At present, the value of $\alpha$ still could not be accurately determined from first principles, therefore it can only be determined from experimental data. As the free parameter, $\alpha =0.91$–1.0 is fixed by fitting the experimental decay data on possible baryon–antibaryon bound states within the same theoretical framework adopted in the current work in Ref. [24]. This result is too uncertain to be used in the further analysis. Since only two of five states, i.e., the $\Omega _c^{*}(3119)$ and $\Omega _c^{*}(3050)$, newly observed by LHCb can be interpreted as molecules [25] with the $\alpha$ values adopted in above. In other words, abundant experimental data are needed to verify its reliability. Within the same theoretical framework adopted in the current work, the experimental total widths of more than thirty states that can be considered as molecules can be well explained without adopting any phenomenological form factor. In other words, the results of our method are reliable without considering any phenomenological form factor.

4 Summary

In this work, the S-wave $D\Lambda -D\Sigma$ molecular states were studied by calculating their allowed two body strong decay to investigate whether the three new narrow $\Xi _c^*$ baryons, $\Xi _c(2923)^0$, $\Xi _c(2938)^0$, and $\Xi _c(2964)^0$ can be understood as $D\Lambda -D\Sigma$ molecules. With the coupling constants obtained by the composition condition, the decays through hadronic loops are calculated in a phenomenological effective Lagrangian approach. The total decay widths can be well reproduced with the assumption that the $\Xi _c(2923)^0$ as S-wave $D\Lambda -D\Sigma$ bound state with $J^P=1/2^{-}$, which decay channels are $\Lambda _c^+K^-$ and $\Xi _c\pi$. The other newly reported $\Xi _c^*$ states cannot be accommodated in the current molecular picture. If the $\Xi _c(2923)^0$ is pure $D\Lambda -D\Sigma$ molecule, the transition strength of $\Xi _c(2923)^0\rightarrow \Xi _c\pi$ is quite different from that in the constituent quark model [3,4,5] and the decay width almost saturates the total width of $\Xi _c(2923)^0$. Future experimental measurements of such a process can be quite useful to test the different interpretations of the $\Xi _c(2923)^0$.