On the drawback of local detrending in universal kriging in conditions of heterogeneously spaced regional TEC data, low-order trends and outlier occurrences

Abstract

The study intercompares three stochastic interpolation methods originating from the same geostatistical family: least-squares collocation (LSC) known from geodesy, as well as ordinary kriging (OKR) and universal kriging (UKR) known from geology and other geosciences. The objective of this work is to assess advantages and drawbacks of fundamental differences in modeling between these methods in imperfect data conditions. These differences primarily refer to the treatment of the reference field, commonly called ‘mean value’ or ‘trend’ in geostatistical language. The trend in LSC is determined globally before the interpolation, whereas OKR and UKR detrend the observations during the modeling process. The approach to detrending leads to the evident differences between LSC, OKR and UKR, especially in severe conditions such as far from the optimal data distribution. The theoretical comparisons of LSC, OKR and UKR often miss the numerical proof, while numerical prediction examples do not apply cross-validation of the estimates, which is proven to be a reliable measure of the prediction precision and a validation of empirical covariances. Our study completes the investigations with precise parametrization of all these methods by leave-one-out validation. It finds the key importance of the detrending schemes and shows the advantage of LSC prior global detrending scheme in unfavorable conditions of sparse data, data gaps and outlier occurrence. The test case is the modeling of vertical total electron content (VTEC) derived from GNSS station data. This kind of data is a challenge for precise covariance modeling due to weak signal at higher frequencies and existing outliers. The computation of daily set of VTEC maps using the three techniques reveals the weakness of UKR solutions with a local detrending type in imperfect data conditions.

1 Introduction

An important aspect in TEC estimation at a regional or global scale is the appropriate interpolation strategy. GNSS dual-frequency observations provide TEC point measurements at the so-called ionosphere pierce points (IPPs), whose density substantially differs across the globe, e.g., due to the large gaps over the oceans. Therefore, it is expected that any interpolation method will render some larger differences in the modeling over the regions of sparse data. Global TEC models are often approximated by relatively low degrees of the spherical orthogonal functions, e.g., spherical harmonics (Alizadeh et al. 2011; Liu et al. 2018) or other empirical orthogonal functions (Mao et al. 2008). These functions are very sensitive to data gaps, and additionally, the regions with denser data suffer from the high-frequency cutoff of the signal in case of lower-order functions. A better representation of the resolution, in comparison with spherical harmonics, may be provided by spherical splines (Schmidt et al. 2011; Erdogan et al. 2017). However, one should keep in mind that every sum of orthogonal functions applies signal cutoff at the spatial resolution equivalent to the maximum degree of the applied base functions. Together with the development of GNSS remote sensing, a need has arisen for the employment of precise modeling techniques in the interpolation of atmospheric parameters. Particularly, the local applications of GNSS positioning rely on the stochastic parametric methods of the interpolation like least-squares collocation (LSC) (Odijk 2002; Krypiak-Gregorczyk et al. 2017) or the ordinary kriging (OKR) (Odijk 2002; Wielgosz et al. 2003). Sayin et al. (2008) present a comparison of OKR and universal kriging (UKR) and assess these techniques together, in a study of local TEC phenomena. Other local studies of TEC and other parameters related to the ionosphere with the use of kriging can be found in Stanisławska et al. (1996, 2002). The atmospheric effects like ionospheric or tropospheric delays are nowadays commonly modeled globally, using a large number of GNSS stations and other additional data. In order to enhance the spatial resolution and accuracy of local and global TEC models, Orùs et al. (2005, 2007) conducted research on the application of the OKR to global ionosphere mapping. It has been shown there that kriging based on the assumption of an error decorrelation function with distance and direction was the optimal interpolation method for GNSS data. This approach can provide improvements of up to 10% or more, in comparison with other popular techniques. The evidence of the stochastic approach improvement is thus demonstrated globally; however, many factors contribute to compromising this advantage like sparse and irregular global GNSS data, noise of these data or noise of the validation data such as altimetry-derived TEC (Li et al. 2019).

The majority of the stochastic parametric techniques apply the least-squares (LS) rule in linear models. The advantages of the parametric techniques of interpolation and extrapolation result from accurate signal covariance models estimated from real data. These modeling techniques can allocate data noise in noise covariance matrix, separating it from the signal. Different kinds of these techniques may have different detrending schemes, correlation approximations and parametrization methods. This study compares two groups of methods, which substantially differ with respect to the detrending rule. These two methods are compared using the same covariance model and the same parametrization rule, which preserves detrending rule as the only difference. This approach enables the comparison of the influence of prior detrending and synchronous detrending on the modeling results. Two general names can be found among the parametric spatial domain techniques based on the LS rule: LSC and kriging. The former one originates from geodesy and gravity field modeling and can be generalized from the interpolation/extrapolation alone, to the transformation between physically dependent quantities, e.g., physical quantities and their gradients (Moritz 1980, Tscherning and Rapp 1974, Sansó et al. 1999). The latter term has its roots in geology and refers to different forms of interpolation, which have different detrending schemes and names (Olea 1999; Wackernagel 2003; Diggle and Ribeiro 2007; Lichtenstern 2013). LSC and kriging correspond to each other, in particular when LSC has only an interpolation form (Hofmann-Wellenhof and Moritz 2005, p. 361) and kriging has a form of simple kriging (SKR) (Ligas and Kulczycki 2010). Three selected techniques are assessed in this work: LSC as interpolation that is comparable to SKR, OKR and UKR. Three orders of trends are applied in LSC, which forms the group of three approaches using prior detrending. OKR and two orders of trend applied in UKR compose the second group of methods, which detrend the data synchronously with the interpolation process.

There are some examples in the literature of the common assessment and comparison of LSC and kriging, or different kinds of kriging. Many of the existing works aiming at the evaluation of similarities or differences of LSC/SKR and OKR or UKR are theoretical comparisons. Numerical studies, in turn, often have no detailed parametrization of the covariance matrices, regarding especially the noise variance. Too little attention is also paid to the fact that detrending in kriging has a local character, when the range of interpolation data is limited, which is common in local applications. A synthesis of kriging methods is given by Blais (1982) and includes OKR and UKR theory, as well as an extension to nonstationary problems and nonlinear modeling. Dermanis (1984) mathematically compares LSC and kriging, employing OKR and UKR. His conclusions point to the differences between LSC and kriging resulting from the difference in the detrending approach related to the scaled mean in kriging and differences in linearity conditions. Another theoretical comparison with a numerical example is given by Reguzzoni et al. (2005). That study compares a generalized form of kriging with LSC and discusses known application areas of both methods, and also existing limitations of their use in geodesy and other geosciences. The examples of LSC, OKR and additional linear methods used for the interpolation of atmospheric effects for real-time kinematic GNSS positioning can be found in Al-Shaery et al. (2011). The authors assess horizontal and vertical positioning errors after the applications of LSC and OKR in spatial interpolation of the vertical reference station (VRS) data in GNSS real-time kinematic (RTK) positioning. They find some advantage of LSC interpolation in the vertical accuracy, but the errors are not further analyzed. Many geophysical problems suffer from a deficiency of lower-order models of the analyzed phenomena or from inadequate knowledge of the mean. The problem of unbiasedness appears, therefore, as one of the most investigated issues, and it makes a difference between the LSC/SKR and OKR, which together with UKR applies constraints for unbiasedness. Thus, kriging with constrained averages like OKR and UKR is often more willingly applied (Daya and Bejari 2015; Malvić and Balić 2009; Wackernagel 2003). Malvić and Balić (2009) investigate Lagrange multiplier significance in OKR and indicate advantages of OKR related to the Lagrange multiplier application. They also find some rules for the Lagrange multiplier choice in OKR. The presented study, therefore, completes the above-mentioned investigations with a precise parametrization of LSC and kriging prior to their common assessment. Additionally, the same three selected orders of the polynomial trend are applied in our investigations, respectively, in both groups of methods. We decided to start the comparisons with the lowest trend orders, as they are most often used. The third detrend order, which is the second-order polynomial, as a curved shape, is expected to behave in a different way in global detrending used in LSC and local detrending applied in UKR.

The parametrization, i.e., the estimation of the optimal parameters of LSC and kriging, is a crucial stage prior to the modeling. The effects of the parameter change on the modeling results are widely discussed in the literature (Brooker 1986; Arabelos and Tscherning 1998; O’Dowd 1991; Sadiq et al. 2010). The oldest and well-known method of the parameter selection is the fitting of analytical model into its corresponding empirical representation (Posa 1989; Barzaghi et al. 2003; Samui and Sitharam 2011). This method is quite effective for the signal parameters; however, supplementary investigations have been undertaken in order to determine noise parameters more accurately (Marchenko et al. 2003; Peng and Wu 2014; Jarmołowski 2016, 2017). The estimates of signal and noise covariance parameters are very often achieved by different cross-validation techniques, e.g., hold-out (HO) validation (Arlot and Celisse 2010; Kohavi 1995) or leave-one-out (LOO) validation (Kohavi 1995; Behnabian et al. 2018). Another solution that can be applied in the parametrization procedures is maximum likelihood estimation (MLE) of parameters for kriging (Pardo-Igúzquiza et al. 2009; Todini 2001; Zimmermann 2010) or for LSC (Jarmołowski 2015, 2017).

This study assesses LSC and kriging (OKR and UKR) after implementing the same C⁴-Wendland covariance models, parametrized in exactly the same way by LOO in case of all six approaches. Therefore, the only remaining difference tested in the study is prior detrending in LSC in comparison with synchronous detrending in OKR and UKR. The data conditions are far from the ideal distribution, both from the spatial and from the statistical point of view. By preserving data gaps and outliers, we expect to reveal weak points of one or the other method. Particularly, this study can show strong and weak points of the detrending schemes, as the most evident differences between the corresponding methods are their rules of trend removal. The differences between the models created under rigorous parametrization conditions are analyzed with the use of cross-validation techniques, such as LOO, and comparison with independent data set. Hence, this work aims at revealing the advantages and drawbacks of global and local detrending schemes using unfavorable to severe data conditions.

2 Algorithms and applied covariance

As it was mentioned in Sect. 1, in general LSC and kriging terms may refer to different algorithms, which cannot be compared, and these terms can also refer to individual applications. A generalized LSC can employ different data types in one process of interpolation combined with the integration. For instance, gravity anomalies together with deflections of the vertical can be used in geoid modeling with the help of appropriate Stokes kernels (Moritz 1980). Kriging, on the contrary, is usually modified to various forms that, for example, handle higher-order trends existing in the data or work with anisotropic data (Wackernagel 2003). Therefore, we compare collocation and kriging in their most common and most comparable forms referring exactly to the same problem—the interpolation of spatially correlated data with expected values approximated by lower-order trends and covariance expressed by an isotropic covariance model. This kind of interpolation model stems from general LS estimation, typically applied in LS adjustment (Teunissen 2003, p. 5):

$$ {\user2{Z}} = \user2{F\beta } + {\varvec{e}} $$

(1)

where ${\user2{Z}}$ is the observation vector, ${\varvec{F}}$ is the design matrix, which will be explained in the next paragraphs, ${\varvec{\beta}}$ is a vector including parameters and ${\varvec{e}}$ is the vector of errors also called noise vector. The stochastic fundamentals of this type of model are explained in details in Koch (1999 p. 153–161). The noise vector often stores uncorrelated random values, and since $\user2{F\beta }$ is deterministic, in order to interpolate correlated quantities, general LS must be extended to LSC (Moritz 1980, p. 111):

$$ {\user2{Z}} = \user2{F\beta } + {\varvec{s}} + {\varvec{n}} $$

(2)

where ${\varvec{s}}$ is the vector of correlated signal interpolated by LSC, OKR or UKR, and ${\varvec{n}}$ is the vector of uncorrelated noise. Equation (2) is the representative for LSC, OKR and UKR. However, the deterministic part $\user2{F\beta }$ will be separated from the observations in different ways, which is explained in Sects. 2.1–2.3. One should keep in mind that SKR is especially close or even equivalent to LSC, and, therefore, its results are assumed to be equal to those of LSC (Dermanis 1984). LSC works with detrended data, whereas OKR and UKR determine mean or higher-order trend by the constraints applied to the modeling process. LSC with a zero-order trend, which is simply the mean, corresponds to OKR, which uses a scaled mean in theory. For instance, the scaled mean is applied locally in practical formulas. The LSC based on the residuals after first- and second-order polynomial trends removal corresponds to UKR, which also uses the same higher-order polynomials. Nevertheless, there is a slightly larger difference in the detrending between LSC and UKR, than in the former case. The trend in LSC is applied globally, as based on the whole dataset, whereas UKR applies the trend locally for the selected data subset defined by the maximum sampling distance. Also, the approximation of the signal variance is different for different estimation methods. The UKR method, in contrast to LSC, applies the detrending based on the observations in the covariance matrix used in the single prediction, and therefore it handles the existing non-stationarity in the analyzed stochastic field to a certain level. Hence, the aim of this study is the confrontation of LSC with OKR and UKR in order to empirically inspect the advantages and drawbacks of detrending prior to the modeling or when the trend removal is combined with modeling process in point prediction.

2.1 Least-squares collocation (LSC)/simple kriging (SKR)

It is assumed in LSC that the mean or trend of data Z(x) is known, i.e.,

$$ \mu = {\mathbb{E}}\left( {Z\left( x \right)} \right), $$

(3)

where ${\mathbb{E}}$ denotes the expectation operator. Furthermore, Z(x) is assumed to be second-order stationary and having known covariance function

$$ C\left( h \right) = {\mathbb{E}}\left( {Z\left( x \right)Z\left( {x + h} \right)} \right) - \mu^{2}. $$

(4)

The empirical covariance function calculation rule is explained in Hofmann-Wellenhof and Moritz (2005, p. 347). In case of LSC, the unbiasedness condition is assumed to be provided automatically by the trend removal, i.e.,

$$ \begin{aligned} {\mathbb{E}}\left( {\tilde{Z}_{\text{LSC}} \left( {x_{p} } \right) - Z\left( {x_{p} } \right)} \right) & = \mu + \mathop \sum \limits_{i = 1}^{n} \omega_{i}^{LSC} {\mathbb{E}}\left( {Z\left( {x_{i} } \right) - \mu } \right) \\ &\quad - {\mathbb{E}}\left( {Z\left( {x_{p} } \right)} \right) = \mu - \mu = 0, \end{aligned} $$

(5)

and therefore any additional constraints on weights $\omega_{i}^{LSC}$ are not necessary. $Z\left( {x_{i} } \right)$ denotes the arbitrary data value, $Z\left( {x_{p} } \right)$ is data in some selected position and $\tilde{Z}_{\text{LSC}} \left( {x_{p} } \right)$ is the LSC estimate at this selected position. The term μ is expanded later (Eq. 8–10) to the polynomial case, as the detrending in this study is based on zero-, first- and second-order polynomials removed prior to LSC prediction. However, one should keep in mind that the trend in LSC can be also derived from the other sources or functions of higher orders, e.g., spherical harmonic expansion, popular in the case of gravity and geoid modeling (Sadiq et al. 2010; Jarmołowski 2019). The assumption of the minimum prediction variance (Hofmann-Wellenhof and Moritz 2005) provides the condition for LSC weights ω_j^LSC and enables the creation of the system of equations, which in matrix form reads.

$$ \user2{C{\varvec\omega }_{{{\text{LSC}}}}} ={\varvec {\user2{c}}_{{\user2{p}}}} , $$

(6)

where ${\varvec{\omega}}_{{{\varvec{LSC}}}}$ denotes the vector of LSC weights. Finally, with the use of matrices, the prediction is

$$ \tilde{Z}_{\text{LSC}} \left( {x_{p} } \right) = \mu + {\varvec{\user2{c}}}_{{\user2{p}}}^{T} {\user2{C}}^{ - 1} \left( {{\user2{Z}} - \mu {\user2{I}}} \right) = {\varvec{\user2{c}}}_{{\user2{p}}}^{T} {\user2{C}}^{ - 1} {\user2{Z}} + \mu \left( {1 - {\varvec{\user2{c}}}_{{\user2{p}}}^{T} {\user2{C}}^{ - 1} {\user2{I}}} \right) $$

(7)

where ${\varvec{\user2{c}}_{{\user2{p}}}}$ preserves the covariances prediction-data, ${\user2{C}}$ is the data covariance matrix and Z is the data vector of n points. The variable $\mu$ denotes the mean as the simplest form of the trend function removed in the numerical study. In order to remove a higher-order trend, we must determine a set of deterministic functions of the coordinates f₀, f₁… f_L, as follows:

$$ {\varvec{F}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {f_{1} \left( {x_{1} } \right)} \\ 1 & {f_{1} \left( {x_{2} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {f_{L} \left( {x_{1} } \right)} \\ \cdots & {f_{L} \left( {x_{2} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ 1 & {f_{1} \left( {x_{n} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} \cdots & \vdots \\ \cdots & {f_{L} \left( {x_{n} } \right)} \\ \end{array} } \\ \end{array} } \right] $$

(8)

${\varvec{F}}$ is in fact previously introduced design matrix (Eqs. 1–2). Two successive orders of the trend are applied in the study as first- and second-order polynomials. They are removed before LSC interpolation and implemented intrinsically in the UKR method. The second-order polynomial trend applied locally reads:

$$ {\varvec{F}} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & {\varphi_{1} } & {\lambda_{1} } & {\varphi_{1}^{2} } & {\lambda_{1}^{2} } & {\varphi_{1} \lambda_{1} } \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & {\varphi_{n} } & {\lambda_{n} } & {\varphi_{n}^{2} } & {\lambda_{n}^{2} } & {\varphi_{n} \lambda_{n} } \\ \end{array} } \right]. $$

(9)

Note that the first three columns correspond to first-order trend. In LSC trend matrix, F can be applied to compose the so-called projection matrix ${\user2{P}}$ (Pardo-Igúzquiza et al. 2009) or orthogonal projection operator (Koch 1999, p. 65; Teunissen 2003, p. 8).

$$ {\user2{P}} = {\user2{I}}_{n} - {\varvec{F}}\left[ {{\varvec{F}}^{T} {\varvec{F}}} \right]^{ - 1} {\varvec{F}}^{T} $$

(10)

which multiplied by the data vector ${\user2{Z}}$ replaces ${\user2{Z}} - \mu {\user2{I}}$ and removes a higher-order trend. This removal is principally related with Eq. (2), and in practice is equal to LS adjustment of the polynomial surface of arbitrary order, determined by the base functions such as those in Eq. (9). The relation of P with general LS solution can be found in Koch (1999, pp. 153–154), where two solutions of the parameter vector ${\varvec{\beta}}$ (Eq. 2) can also be found. The simplified, unweighted projection operator based on unweighted LS solution is applied here. This is because the covariance matrix is not directly available before detrending process, and because a very similar unbiasedness of Eq. (10) with low-order trends was previously proven in practice (Jarmołowski and Bakuła 2014; Pardo-Igúzquiza et al. 2009). The variance of the prediction, i.e., a posteriori error at selected point p, can be calculated from

$$ {\sigma ^{\prime}_{{{\text{LSC}}}}}^{2} = C_{0} + {\varvec{\omega}}_{{{\text{LSC}}}}^{T} {\user2{C}}{\varvec{\omega }_{{{\text{LSC}}}}} - 2{\varvec{\omega}}_{{{\text{LSC}}}}^{T} {\user2{c}}_{{\varvec{\user2{p}}}} = C_{0} - {\user2{c}}_{{\varvec{\user2{p}}}}^{T} {\user2{C}}^{ - 1} {\user2{c}}_{{\varvec{\user2{p}}}} $$

(11)

with $C_{0}$ referring to signal covariance at distance equal to zero. The above a posteriori error (Eq. 11), in case of noisy data, is strongly related to a priori noise that together with the signal covariance contributes to the covariance matrix C. Therefore, a realistic estimate of a priori noise must be introduced to the noise covariance matrix. In the LSC theory, the total covariance matrix C is composed of the signal covariance matrix C_s and the noise covariance matrix C_n (Moritz 1980, p. 102):

$$ {\user2{C}} = {\user2{C}}_{{\varvec{s}}} + {\user2{C}}_{{\varvec{n}}} $$

(12)

where C_s is based on the selected signal covariance model, and C_n, under the assumption of non-correlated noise, is a diagonal matrix based on data a priori noise standard deviation ($\sigma_{\text{LSC}}$) in the following way:

$$ {\user2{C}}_{{\varvec{n}}} = \sigma_{{{\text{LSC}}}}^{2} \cdot {\user2{I}}_{n}. $$

(13)

Therefore finally, introducing a priori noise variance of the data gives an extended form of the a posteriori error (Moritz 1980, p. 105):

$$ {\sigma ^{\prime}_{{{\text{LSC}}}}}^{2} = C_{0} + \sigma_{{{\text{LSC}}}}^{2} - {\user2{c}}_{{\user2{p}}}^{T} {\user2{C}}^{ - 1} {\user2{c}}_{{\user2{p}}}. $$

(14)

Different covariance models and corresponding variograms can be applied in the modeling process. Isotropic covariance models are the most popular and easy to apply. Some theoretical considerations about the positive definiteness and other properties of the selected models for the spheres can be found in Huang et al. (2011), Gneiting (2013) or in Guinness and Fuentes (2016). This numerical study applies C⁴-Wendland covariance function in LSC and C⁴-Wendland variogram in OKR and UKR. The C⁴-Wendland covariance function applied in LSC is

$$ C^{C4W} \left( \psi \right) = C_{0} \cdot \left( {1 + \tau \frac{\psi }{{\alpha_{{{\text{LSC}}}} }} + \frac{{\tau^{2} - 1}}{3}\frac{{\psi^{2} }}{{\alpha_{{{\text{LSC}}}}^{2} }}} \right)\left( {1 - \frac{\psi }{{\alpha_{{{\text{LSC}}}} }}} \right)_{ + }^{\tau } $$

(15)

where ψ is the spherical distance, and α_LSC is named correlation length in LSC theory (Hofmann-Wellenhof and Moritz 2005). The shape parameter $\tau$ has to be ≥ 6 in order to guarantee positive-definiteness on the sphere (Gneiting 2013). Therefore, this parameter is equal 6.5 in the study.

2.2 Ordinary kriging (OKR)

The theory of OKR method starts without the mean or trend removal before the covariance estimation (Olea 1999; Wackernagel 2003; Lichtenstern 2013). Instead, the mean is eliminated by the subtraction in the estimation of the semivariogram:

$$ \gamma \left( h \right) = \frac{1}{2}{\mathbb{E}}\left( {\left( {Z\left( {x + h} \right) - Z\left( x \right)} \right)^{2} } \right). $$

(16)

The calculation of empirical semivariogram is given by Wackernagel (2003, p. 47). The unbiasedness of OKR must be forced by the equality

$$ \mathop \sum \limits_{i = 1}^{n} \omega_{i}^{{{\text{OKR}}}} = 1. $$

(17)

Therefore, the bias in OKR also converges to zero, as follows:

$$ {\mathbb{E}}\left( {\tilde{Z}_{{{\text{OKR}}}} \left( {x_{p} } \right) - Z\left( {x_{p} } \right)} \right) = {\mathbb{E}}\left( {\mathop \sum \limits_{i = 1}^{n} \omega_{i}^{{{\text{OKR}}}} Z\left( {x_{i} } \right) - Z\left( {x_{p} } \right)\mathop \sum \limits_{i = 1}^{n} \omega_{i}^{{{\text{OKR}}}} } \right) = \mathop \sum \limits_{i = 1}^{n} \omega_{i}^{{{\text{OKR}}}} {\mathbb{E}}\left( {Z\left( {x_{i} } \right) - Z\left( {x_{p} } \right)} \right) = 0. $$

(18)

The system of equations similar to Eq. (6), which leads to the solution of ω_i values, is extended to

$$ \user2{ \Gamma \omega }_{{{\text{OKR}}}} + \lambda_{{{\text{OKR}}}} {\user2{I}} = {\varvec{\gamma}}_{{\user2{p}}} $$

(19)

$$ {\varvec{\omega}}_{{{\text{OKR}}}}^{{\varvec{T}}} {\user2{I}} = 1 $$

(20)

where $\lambda_{{{\text{OKR}}}}$ is the so-called Lagrange multiplier. The solution must be additionally supported by the condition in Eq. (17).

The block matrix of variogram between the data $\overline{\user2{\Gamma }}$ and data prediction vector of variogram $\overline{\user2{\gamma }}_{{\user2{p}}}$ are therefore composed as follows:

$$ \overline{\user2{\Gamma }} = \left[ {\begin{array}{*{20}c}{\varvec{\varGamma}}& {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \end{array} } \\ {\begin{array}{*{20}c} 1 & \cdots & 1 \\ \end{array} } & 0 \\ \end{array} } \right]\quad {\text{and}}\quad \overline{\user2{\gamma }}_{p} = \left[ {\begin{array}{*{20}c} {{\varvec{\gamma}}_{{\user2{p}}} } \\ \vdots \\ 1 \\ \end{array} } \right],\,{\text{as}}\,{\text{well}}\,\overline{\user2{Z}} = \left[ {\begin{array}{*{20}c} {\user2{Z}} \\ \vdots \\ 0 \\ \end{array} } \right]. $$

(21)

Consequently, the final OKR prediction reads (Olea 1999, p. 48)

$$ \tilde{Z}_{{{\text{OKR}}}} \left( {x_{p} } \right) = \overline{\user2{Z}}^{T} \overline{\user2{\Gamma }}^{ - 1} \overline{\user2{\gamma }}_{{\user2{p}}}. $$

(22)

Contrary to LSC, a posteriori error estimate at the selected point p can be derived from a slightly different equation (Olea 1999, p. 48):

$${\sigma ^{\prime}_{{{\text{OKR}}}}}^{2} = - {\varvec{\omega}}_{{{\text{OKR}}}}^{T} \user2{\Gamma \omega }_{{{\text{OKR}}}} + 2{\varvec{\omega}}_{{{\text{OKR}}}}^{T} {\varvec{\gamma}}_{{\user2{p}}} = {\varvec{\omega}}_{{{\text{OKR}}}}^{T} \left( {2{\varvec{\gamma}}_{{\user2{p}}} - \user2{\Gamma \omega }_{{{\text{OKR}}}} } \right) = \overline{\user2{\gamma }}_{{\user2{p}}}^{T} \overline{\user2{\Gamma }}^{ - 1} \overline{\user2{\gamma }}_{{\user2{p}}}. $$

(23)

It was mentioned in Sect. 2 that covariance models are equivalent for all predictions in the study. The C⁴-Wendland variogram selected for the analysis of signal model parameters in OKR and UKR reads:

$$ \gamma^{C4W} \left( \psi \right) = C_{0} \cdot \left( {1 - \left( {1 + \tau \frac{\psi }{{\alpha_{K} }} + \frac{{\tau^{2} - 1}}{3}\frac{{\psi^{2} }}{{\alpha_{K}^{2} }}} \right)\left( {1 - \frac{\psi }{{\alpha_{K} }}} \right)_{ + }^{\tau }} \right), $$

(24)

and all the parameters have the same meaning as in Eq. (15); however, α_K is often called range in relation to kriging methods. The shape parameter $\tau$ in the variograms applied in the study is also equal to 6.5, as well as in the covariance function case. The noise is introduced in OKR equations by the nugget parameter ($\sigma_{K}$) and applied in the following way:

$$ \begin{array}{*{20}c} {\gamma \left( {x_{i} ,x_{j} } \right) = \gamma^{C4W} + \sigma_{K}^{2} } & {if} & {i \ne j} \\ \end{array} $$

(25)

with $\sigma_{K}$ referring to natural surveying conditions, where the signal is not the only quantity that contributes to data, as there is no measurement device that can provide errorless observations. The signal variance $C_{0}$ is often called a partial sill in the kriging theory.

2.3 Universal kriging (UKR)

In UKR modeling, the signal can be decomposed into a deterministic trend function µ(x) of the order $l$, and a residual function $Y\left( {x_{i} } \right)$, such that

$$ Z\left( {x_{i} } \right) = \mu \left( {x_{i} } \right) + Y\left( {x_{i} } \right) = \mathop \sum \limits_{l = 0}^{L} a_{l} f_{l} \left( {x_{i} } \right) + Y\left( {x_{i} } \right). $$

(26)

The unbiasedness condition is satisfied from

$$ \begin{aligned} {\mathbb{E}}\left( {\tilde{Z}_{{{\text{UKR}}}} \left( {x_{p} } \right) - Z\left( {x_{p} } \right)} \right) & = \mathop \sum \limits_{i = 1}^{n} \omega_{i}^{{{\text{UKR}}}} \left( {{\mathbb{E}}\left( {\mu \left( {x_{i} } \right)} \right) + {\mathbb{E}}\left( {Y\left( {x_{i} } \right)} \right)} \right) \\ &\quad - \left( {{\mathbb{E}}\left( {\mu \left( {x_{p} } \right)} \right) + {\mathbb{E}}\left( {Y\left( {x_{p} } \right)} \right)} \right) \\ & = \mathop \sum \limits_{i = 1}^{n} \omega_{i}^{{{\text{UKR}}}} \mu \left( {x_{i} } \right) - \mu \left( {x_{p} } \right) = 0 \\ &\quad { \Leftrightarrow }\mathop \sum \limits_{l = 0}^{L} a_{l} \left( {\mathop \sum \limits_{i = 1}^{n} \omega_{i}^{{{\text{UKR}}}} f_{l} \left( {x_{i} } \right) - f_{l} \left( {x_{p} } \right)} \right) = 0 \\ \end{aligned} $$

(27)

where $a_{l}$ are the coefficients of the deterministic trend. If we denote the vector of this trend by a, and the matrix of deterministic functions by F, we can apply the first- or second-order trend based on Eq. (9). The matrix F is implemented intrinsically in UKR for the local correlated data sample selected for the prediction in point p.

Using the matrix notation, we obtain the following system:

$${\varvec{\varGamma}}_{{\varvec{Y}}} {\varvec{\omega}}_{{{\text{UKR}}}} + \user2{F\lambda }_{{{\text{UKR}}}} = {\varvec{\gamma}}_{{{\varvec{Y}}p}} $$

(28)

$$ {\varvec{F}}^{{\varvec{T}}} {\varvec{\omega}}_{{{\text{UKR}}}} = {\varvec{f}}_{p} , $$

where ${\varvec{\lambda}}_{{{\text{UKR}}}}$ is Lagrange parameter vector. The block matrix form of these equations, similarly to OKR, gives the solution of the UKR prediction (Olea 1999, p. 105, Wackernagel 2003, pp. 68–69):

$$ \left[ {\begin{array}{*{20}c} {{\varvec{\omega}}_{{{\text{UKR}}}} } \\ {\lambda_{{{\text{UKR}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{\varGamma}}_{{\varvec{Y}}} } & {\varvec{F}} \\ {{\varvec{F}}^{{\varvec{T}}} } & 0 \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {{\varvec{\gamma}}_{{{\varvec{Y}}p}} } \\ {{\varvec{f}}_{p} } \\ \end{array} } \right] = \overline{\user2{\Gamma }}^{ - 1} \overline{\user2{\gamma }}_{{{\varvec{Yp}}}} $$

(29)

where matrix ${\varvec{\varGamma}}_{{\varvec{Y}}}$ is based on C⁴-Wendland variogram and matrix F is expressed by Eq. (9). ${\varvec{\gamma}}_{{{\varvec{Y}}p}}$ and ${\varvec{f}}_{p}$ are vectors calculated from the variogram and deterministic functions for the point of interest p, respectively. Summarizing, the prediction can be written in a similar way to OKR (Olea 1999, p. 103):

$$ \tilde{Z}_{{{\text{UKR}}}} \left( {x_{p} } \right) = \overline{\user2{Z}}^{T} {\overline{\user2{\Gamma }}}_{{\varvec{Y}}}^{ - 1} \overline{\user2{\gamma }}_{{{\varvec{Yp}}}}. $$

(30)

The variance of the prediction error will be then (Olea 1999, p. 103):

$$ {\sigma ^{\prime}_{{{\text{UKR}}}}}^{2} = - {\varvec{\omega}}_{{{\text{UKR}}}}^{T}{\varvec{\varGamma}}_{{\varvec{Y}}} {\varvec{\omega}}_{{{\text{UKR}}}} + 2{\varvec{\omega}}_{{{\text{UKR}}}}^{T} {\varvec{\gamma}}_{{{\varvec{Yp}}}} = \overline{\user2{\gamma }}_{{{\varvec{Yp}}}}^{T} \overline{\user2{\Gamma }}_{{\varvec{Y}}}^{ - 1} \overline{\user2{\gamma }}_{{{\varvec{Yp}}}}. $$

(31)

The $\sigma_{K}$ parameter is implemented in the variogram in an analogous way as in the case of OKR in the previous section.

3 LOO validation

LOO validation is based on the prediction in the position of data point, with exclusion of this point value from the dataset being used for the prediction (Kohavi 1995). The differences between n data values and the predictions made in the same positions are used as a measure of reliable prediction precision. The difference in case of LSC is calculated between the residual ${\user2{Z}}_{P}^{r} = {\user2{Z}}_{{\user2{p}}} - \mu {\user2{I}}$ in point P and its estimate excluding this single compared value, i.e.,

$$ {\text{LOO}}_{P} \left( {C_{0} ,CL,\sigma {|}{\user2{Z}}_{n \times 1}^{r} } \right) = \left\{ {\begin{array}{c} {\left. {Z_{P}^{r} - \tilde{Z}_{P}^{r} } \right|} \\ {\tilde{Z}_{P}^{r} = {\user2{c}}_{{\user2{p}}}{^T_{{\left( {n - 1} \right) \times 1}}}\cdot \left( {{\varvec{Cs}}_{{\left( {n - 1} \right) \times \left( {n - 1} \right)}} + {\varvec{Cn}}_{{\left( {n - 1} \right) \times \left( {n - 1} \right)}} } \right)^{ - 1} } \\ {Z_{P}^{r} \not\in {\user2{Z}}_{{\left( {n - 1} \right) \times 1}}^{r} } \\ \end{array} \cdot {\user2{Z}}_{{\left( {n - 1} \right) \times 1}}^{r} \wedge } \right\}, $$

(32)

where $Z_{P}^{r}$ is the point residual value and $\tilde{Z}_{P}^{r}$ is the LSC estimate in the same location. The root mean square of all n differences (RMSLOO) calculated by Eq. (32) is a measure of the quality of the estimated model. RMSLOO is affected by the noise present in the dataset, as it comes from the comparison with noisy data. Therefore, if the prediction is optimal in least-squares sense, RMSLOO can be assessed as an empirical measure of the noise. In the proposed study, LOO differences are calculated for some range of parameters CL and σ. Equation (32) describes the validation for LSC, whereas OKR and UKR have analogous rule for comparison of ${\user2{Z}}_{{\user2{p}}}$ and its estimates.

4 VTEC test data

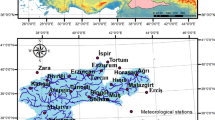
The study uses point VTEC values calculated from GNSS observations from the Crustal Movement Observation Network of China (CMONOC). The CMONOC network includes around 1000 permanent stations distributed almost homogeneously over most of China’s territory. This number of stations provides dense local coverage of ionosphere piercing points (IPPs) (Chen et al. 2017), which is quite a challenging dataset for testing of local data modeling by stochastic techniques.

The estimation of VTEC at IPPs is derived using the precise point positioning (PPP) approach. The PPP method and the related VTEC estimation procedure are based on the same algorithm as PPP implementation in previous works of the authors, investigating the calculation of ionospheric maps (Jarmołowski et al. 2019; Ren et al. 2016). This article, in turn, is focused on the extended analysis of the parametric spatial stochastic modeling of the VTEC signal resulting from the PPP method. The noise coming from the PPP VTEC estimation is a useful property of the data, and it is thoroughly investigated and estimated by LOO validation in the individual modeling methods. Additionally, the datasets are cleaned of large outliers and intentionally sparsed out in relation to the original set of IPPs with the use of 1° grid for selection of the closest data. The selected datasets for the successive data epochs are distributed approximately homogeneously in the horizontal direction. This is made intentionally for the purpose of the study on the stochastic methods, in order to help the parameter estimation, especially if we assume the stationarity of the process and average uncorrelated value of the noise. The estimation of the parameters by LOO is difficult, as we deal with low residual signal variance with respect to the noise in case of VTEC observations. Most of the signal referring to equatorial TEC anomaly is preserved at lower frequencies and removed with the polynomial deterministic trend. Figure 1 shows all epochs of the data used in the numerical study, separated by 2 h. This relatively large interval was selected to shorten the time of estimation; however, it is also known that many of global ionospheric maps (GIMs) have the same interval (Roma-Dollase et al. 2018). Figure 1 presents the IPPS after the removal of the outliers and sparsing with 1° grid, used in LOO estimation of the parameters. The red line in Fig. 1 separates the rectangular area of the compact, enclosed region of approximately homogeneous spatial distribution, and data at the margins, where the estimation can suffer from gaps and sparsity. These two sets of unequal size will be investigated separately in further numerical tests.

Fig. 1

Datasets in sample GPS epochs, red rectangle separates approximately homogeneous data from sparse data at the margins of the area

Figure 2a presents the removal of the outliers, which is done by a specific application of LOO validation (Tscherning 1991). The LSC estimation with some roughly assumed, overestimated a priori noise variance has been made at data points. Then, the data values furthest from the predictions were removed, if these differences extended some assumed threshold. This threshold was quite rigorous in the study, and it was set to 3 TECU, as the amount of data was large enough to allow us to freely discard the outliers. Figure 2b reveals more clearly the effect of data sparsing, which is mostly noticeable in the center of the area, as IPPs are always concentrated mostly in the center due to the GNSS satellites tracks alignment.

Fig. 2

Example data epoch describing sparsing and outliers removal: a outlier spatial distribution is visible and b sparsing effect is better visible in a horizontal view

5 Comparison of covariance parameters and accuracy indicators between LSC, OKR and UKR

The numerical analysis comprises a few associated items:

LOO estimation of $\sigma$ and $\alpha$ parameters in LSC with zero-, first- and second-order polynomial removal, and in OKR and UKR after first- and second-order polynomial removal (Figs. 3, 5, and 6). A posteriori errors $\sigma ^{\prime}$ are presented jointly in Fig. 6.

Fig. 3

Example epoch (January 1, 2016, 8:00 AM) of $\alpha_{{{\text{LSC}}}}$/$\alpha_{K}$ and $\sigma_{{{\text{LSC}}}}$/$\sigma_{K}$ parameter estimation by LOO for: a LSC after mean removal, b LSC after first-order trend removal, c LSC after second-order trend removal, d OKR, e UKR with first-order trend, f UKR with second-order trend. The contours with interval of 0.02 TECU indicate minima of RMSLOO. The black dot indicates minimum RMS in LOO and corresponding $\alpha_{{{\text{LSC}}}}$/$\alpha_{K}$ and $\sigma_{{{\text{LSC}}}}$/$\sigma_{K}$ estimates. The red dot indicates alternative $\alpha_{{{\text{LSC}}}}$/$\alpha_{K}$ estimate from the manual covariance function fitting in Fig. 4

Empirical covariance and semi-variance calculation for the same six approaches, and comparative $\alpha$ estimation by analytical model fitting (Fig. 4).

Fig. 4

Covariance functions and variograms for the six modeling schemes. The dots describe empirical covariance/variogram estimates, the black line is the C⁴-Wendland model with parameters from LOO, and the red line is manual fit of the same model

Comparison of minimum empirical accuracy of the prediction from LOO process, for all six approaches in terms of RMSLOO (Figs. 7, 8, 9).

Comparison of gridded models predicted with optimal estimated parameters, including various data conditions, i.e., sparse data regions, extrapolated regions, outlier occurrences and different solar conditions (Fig. 10, 11, 12).

This study applies precise LOO parametrization before the comparison of the two detrending approaches, different in LSC, OKR and UKR (Fig. 3). The estimation of $\alpha_{\text{LSC}}$ and $\alpha_{K}$ parameters by the covariance function fitting has been also compared to that coming from LOO (Fig. 4). The optimal parameters in the modeling are crucial if we want to be sure that we analyze and compare the best possible solutions of LSC to those from OKR and UKR. The RMSLOO parameter, as coming from the best solution, is also a kind of relative measure of the obtained accuracy. It is also used to find the most accurate and robust way of the trend removal (Figs. 7, 8, 9). Additionally, the unused data from the dataset remaining after data selection are applied in additional comparisons and provide another measures of accuracy differences (Figs. 10, 11, 12). Therefore, the process of the validation can appear as combined together with the parametrization step, as it uses similar techniques based on cross-validation.

The parametrizations of LSC, OKR and UKR often assume homogeneous uncorrelated noise, and therefore a single value of $\sigma_{{{\text{LSC}}}}$ or $\sigma_{K}$ is determined for a single stationary process. The theory of LSC uses a priori noise as a name of this parameter, while it is named nugget in kriging techniques. Generally, they are corresponding parameters. However, technically their implementation in the covariance matrices differs, and therefore they are denoted by different symbols in this work: $\sigma_{\text{LSC}}$ in LSC and $\sigma_{K}$ in both kriging methods, as OKR and UKR are based on the same variogram and noise model (Eqs. 24 and 25). The second pair of parameters corresponding one to another is correlation length in LSC ($\alpha_{\text{LSC}}$) and range in kriging techniques ($\alpha_{K}$). There is a third covariance parameter present in both Eqs. (15) and (24), denoted as $C_{0}$. This parameter stands for the signal variance, and it is approximated by the residual data variance in this study. This way we limit LOO parametrization to two parameters and make it more reliable in practical computation. This simplification introduces some uncertainty of $\sigma_{{{\text{LSC}}}}$/$\sigma_{K}$ parameters. However, its insignificancy on the modeling results is proven later in this section. The parametrization of $C_{0}$ together with $\sigma_{{{\text{LSC}}}}$ or $\sigma_{K}$ is difficult by LOO, as these parameters are dependent in the applied kind of covariance models (Jarmołowski and Bakuła 2014).

This study is based on LOO method of parametrization, which is composed of interpolation in the positions of data points with the use of 100 nearest points that are located at most 20° from the investigation point, excluding the data in the place of interest. The 60 points are the closest points, and the remaining 40 points are a sparsed subset selected from more distant points located up to 20° from the investigated point. This way we can assure the influence of the distant signal and limit the calculation time. The spherical distance of 20° was empirically selected as the smallest that enables the calculation of the covariance parameters in case of zero-order trend. This is because it approximately corresponds to the distance at which the covariance model for zero-order detrended data is noticeably larger than zero (Fig. 4a). Subsequently, the estimate is compared to the data value and renders a single LOO value. Then, the RMS of all LOO differences (RMSLOO) in data points is calculated for the selected parameters, and the procedure is repeated for the selected range of parameters in order to find their best set with the minimum value of RMSLOO (Behnabian et al. 2018; Krypiak-Gregorczyk et al. 2017; Jarmołowski 2016). The estimation of $C_{0}$ in LSC is always based on the whole set of residual data, so the covariance function (Eq. 15) is parametrized globally for the whole residual dataset. In the same way, we estimate $C_{0}$ and variogram (Eq. 24) in OKR, as its estimation in OKR is based on the residuals detrended by the mean value only. This does not change the residuals variance regardless of whether the mean is estimated from the whole dataset or its subset. The residuals of the whole dataset are more representative from the statistical point of view, as more Gaussian-distributed data can be applied in variogram parametrization. The $C_{0}$ parameter in UKR cannot be calculated for the whole dataset, as detrending is applied locally in the variogram matrix (Eq. 29), which is created using local points, and the remaining data cannot be included in the detrending. Of course, the point prediction could involve all the data in UKR; however, such inclusion would make the prediction equivalent to LSC. This study, however, refers to the local prediction, where the residuals are correlated within some spatial distance only, and the limitation of the sampling is crucial for practical implementation in the engineering and science applications. The detailed illustrations of the parametrizations for the selected time epoch are shown in Fig. 3, and the estimated parameters for the whole day at 2-h intervals are presented in Figs. 5 and 6.

Fig. 5

$\alpha_{{{\text{LSC}}}}$/$\alpha_{K}$ parameter estimated for, January 1, 2016, at 2-h intervals. The methods are in the same order as in Fig. 4

Fig. 6

$\sigma_{{{\text{LSC}}}}$/$\sigma_{K}$ parameter (bars) and minima (solid line) and maxima (dashed line) of $\sigma ^{\prime}_{{{\text{LSC}}}}$/$\sigma ^{\prime}_{{{\text{OKR}}}}$/$\sigma ^{\prime}_{{{\text{UKR}}}}$ estimated at points for January 1, 2016, at 2-h intervals

Fig. 7

RMSLOO minima estimated for January 1, 2016, at 2-h intervals. White bars show the values for data inside the red rectangle from Fig. 1, black bars show values at points outside the red zone

The minima of the RMSLOO surfaces drawn for the selected parameters ranges, i.e., $\alpha_{\text{LSC}}$ = $\alpha_{K}\,{\in}\,${0.5:1:24.5}° and $\sigma_{{{\text{LSC}}}}$ = $\sigma_{K}\,{\in}\,${0.1:0.2:5} TECU, indicate the optimal parameters on the axes of the parameters, depending on the method (Fig. 3) and also on the epoch (Figs. 5 and 6). However, the minima of RMSLOO calculated with the use of these optimal parameters differ significantly only between the epochs, but not between the methods (Fig. 7). This strongly indicates a minor difference between the methods, and the differences in specific cases will be observed later, in relation to Figs. 8, 9, 10 and 11. It can be noted in Fig. 1 that the removal of the mean cannot produce Gaussian residuals, nor even close to Gaussian from local VTEC data, and the parametrization and modeling are biased. An insufficient detrending with the use of mean in LSC and OKR produces the largest RMSLOO at two edges of the parameter space, i.e., for small $\alpha_{{{\text{LSC}}}}$/$\alpha_{K}$ and small $\sigma_{\text{LSC}}$/$\sigma_{K}$ (Fig. 3a, d). This automatically requires a larger $\alpha_{\text{LSC}}$/$\alpha_{K}$ and $\sigma_{\text{LSC}}$/$\sigma_{K}$ with the lowest-order trend (mean) in order to keep the same accuracy as for the higher orders of detrending in LSC or UKR (Fig. 3b, c, e, f). Additionally, as it seems from all parametrizations in Fig. 3, it is even better to overestimate these parameters, rather than underestimate. Moreover, the surface of RMSLOO in Fig. 3f indicates that the parameters for UKR with the second-order trend must be determined with particular accuracy. This is because an overestimation of the noise $\sigma_{K}$ increases the RMSLOO and significantly decreases the model accuracy. This happens due to the problems with the local detrending in Eq. (30), when the limited number of data and the use of large noise cause a significantly worse fit of the polynomial trend of the second order.

Fig. 8

Differences of RMSLOO minima for LSC and between different six modeling approaches for the data inside the red zone from Fig. 1

Fig. 9

Differences of RMSLOO minima for LSC and between different six modeling approaches for the data outside the red zone from Fig. 1

Fig. 10

Example epoch (January 1, 2016, 8:00 AM) of VTEC interpolated by six methods and differences between respective trend orders in LSC and kriging for data free of outliers

Fig. 11

Example epoch (January 1, 2016, 8:00 AM) of VTEC interpolated by the six methods and differences between respective trend orders in LSC and kriging for data with restored outliers

In addition to the LOO parametrization, the calculation of empirical covariance functions (Hofmann-Wellenhof and Moritz 2005, p. 347) and empirical semivariograms (Wackernagel 2003, p. 47) is done for the same six approaches as in Fig. 3. The sampling interval of the empirical functions was set to 3°, in order to make it larger than average data resolution, which is not everywhere close to 1°. The empirical variograms have been calculated from the residual data, as well as empirical covariance functions in order to keep them consistent. This way the covariance (Eq. 15) and semivariogram (Eq. 24) models based on the parameters from LOO can be compared with the models that fit the empirical values best (Fig. 4). The shape of empirical covariance function strongly depends on the sampling rate, especially for smaller distances, which impedes the assessment of $\sigma_{\text{LSC}}$/$\sigma_{K}$ this way. Therefore, we assume the determination of $\alpha_{\text{LSC}}$/$\alpha_{K}$ from the empirical covariances/variograms only. Figure 4 shows various coincidences of LOO and the empirical model fit. Worse fit of empirical variograms occurring especially in Fig. 4d, e can originate from the local detrending schemes in LOO, compared to empirical semivariograms determined from globally detrended data.

The estimated parameters $\alpha_{\text{LSC}}$/$\alpha_{K}$ in Fig. 5 and $\sigma_{{{\text{LSC}}}}$/$\sigma_{K}$ in Fig. 6 are indicated by the minima of the RMSLOO that are placed inside the contours visible on the RMSLOO surfaces drawn for the selected example epoch in Fig. 3. These parameters correspond to the best interpolation processes in the sense of LOO, and only these parameters are further applied in the calculation of the RMSLOO estimates of the modeling error in Fig. 7, their differences in Figs. 8 and 9, as well as in the example predictions in Figs. 10 and 11. The parametrization of LSC and OKR defines global $\alpha_{\text{LSC}}$ (Fig. 5a–c) and $\sigma_{\text{LSC}}$ (Fig. 6a–c) parameters or $\alpha_{K}$ (Fig. 5d) and $\sigma_{K}$ (Fig. 6d), respectively. This is because $C_{0}$ is determined for the whole dataset every time. It is different from UKR, where $\alpha_{K}$ and $\sigma_{K}$ should differ for different points. So the parameters indicated by the RMSLOO (Fig. 3e, f) in the single analyzed epoch are in fact a kind of average, which gives optimum fit of the prediction to the data when applied to all point predictions. It means that individual point predictions arrive at the same parameters even though they have various $C_{0}$ values calculated from the locally detrended residuals (Eq. 29). The $\alpha_{K}$ parameters for the whole day are shown in Fig. 5e, f in orange, to highlight their average character based on the variable local trend and the local $C_{0}$.

The $\sigma_{K}$ parameters determined by the smallest RMSLOO in UKR are also presented in orange (Fig. 6e, f), as they come from the same LOO validation with $C_{0}$ different at every point. Figure 6 shows the determination of $\sigma_{\text{LSC}}$/$\sigma_{K}$ for all the investigated methods, through the whole day at 2-h intervals. The drawback of the slightly inaccurate $C_{0}$, as $C_{0}$ is determined from the noisy data and consequently affected $\sigma_{\text{LSC}}$ and $\sigma_{K}$, has no practical influence on the modeling precision determined by the RMSLOO, which is explained in Pardo-Igúzquiza et al. 2009 and Jarmołowski and Bakuła (2014). They show there that $C_{0}$ and $\sigma_{\text{LSC}}$ (or $\sigma_{K}$) are dependent on each other, and the modeling results depend on the relation between these two parameters. Besides $\sigma_{{{\text{LSC}}}}$/$\sigma_{K}$, Fig. 6 also presents the minima and maxima of a posteriori error estimates of the individual prediction methods, denoted $\sigma ^{\prime}_{\text{LSC}}$, $\sigma ^{\prime}_{OKR}$ and $\sigma ^{\prime}_{{{\text{UKR}}}}$. The minima of $\sigma ^{\prime}_{\text{LSC}}$, $\sigma ^{\prime}_{OKR}$ and $\sigma ^{\prime}_{UKR}$ are very close to $\sigma_{{{\text{LSC}}}}$ or $\sigma_{K}$ for all methods, because at most of the points a posteriori estimates are close to a priori noise values, and only some individual values at the margins of the area obtain worse $\sigma ^{\prime}$ estimates. The estimates $\sigma ^{\prime}_{{{\text{LSC}}}}$, $\sigma ^{\prime}_{{{\text{OKR}}}}$ and $\sigma ^{\prime}_{{{\text{UKR}}}}$ are strongly dependent on $\sigma_{{{\text{LSC}}}}$ or $\sigma_{K}$, and therefore an overestimated $C_{0}$, which leads to an overestimated $\sigma_{{{\text{LSC}}}}$ or $\sigma_{K}$. In consequence, this provides overestimated a posteriori errors, which are smaller in practice. The especially large noise indicators (both a priori and a posteriori), in case of the detrending by the mean (Fig. 6a, d), are suspected to be related to the bias that comes from insufficient detrending and the influence of far zone correlation. The removal of the mean appears as not sufficient for the local areas, especially in case of TEC data, as its largest anomalies, extending over tens of degrees, need to be removed in order to obtain approximately Gaussian residuals.

The LOO validation process within the selected ranges of $\alpha_{\text{LSC}}$/$\alpha_{K}$ and $\sigma_{\text{LSC}}$/$\sigma_{K}$ parameters enables us to find the smallest values of the RMSLOO for each epoch, which identify the optimal covariance parameters. These RMSLOO minima are presented in Fig. 7a–f, where no apparent differences can be found between the methods, despite the differences in the parametrization (Figs. 5 and 6). Figure 7 describes the RMSLOO calculated for the points inside the red rectangle from Fig. 1 (white bars) and outside it (black bars). The differences between the estimates of $\alpha_{\text{LSC}}$/$\alpha_{K}$ and $\sigma_{{{\text{LSC}}}}$/$\sigma_{K}$ are often significant (Figs. 5, 6), whereas the differences of RMSLOO minima between the methods are smaller (Fig. 7). This was theoretically provided and justified in Sansó et al. (1999), who notice that the error estimates are more sensitive to parameters change than estimated values. It is evident at the same time that individual optimal parameters estimated for particular methods noticeably affect the minima of RMSLOO only at data margins (Fig. 7). This means that all the predictions are at a similar level of quality if we apply a precise LOO parametrization for homogeneous dense data interpolation. Referring to the noise estimates, it must be concluded that the RMSLOO is a better estimate of the noise than a priori noise estimates $\sigma_{{{\text{LSC}}}}$/$\sigma_{K} ,$ and a posteriori errors $\sigma ^{\prime}_{{{\text{LSC}}}}$/$\sigma ^{\prime}_{{{\text{OKR}}}}$/$\sigma ^{\prime}_{{{\text{UKR}}}} ,$ which are strongly related to a priori values, due to the above-mentioned error sensitivity.

In order to assess possible smaller-scale advantages of some methods, the values of RMSLOO minima from kriging are subtracted from the RMSLOO minima from LSC. Figure 8g–i shows increasing number of negative differences of the RMSLOO minima, which indicates small advantage of LSC with respect to UKR, in terms of a smaller average RMSLOO minimum. This indicates the problems with higher-order detrending inside UKR variogram matrix, for locally selected data, which rapidly increase at the margins of the data, i.e., outside the red zone from Fig. 1 (Fig. 9g–i).

Aside from analyzing the RMSLOO, which is an empirical measure of the accuracy in terms of cross-validation, the VTEC models are created using different six modeling schemes for large areas extended to sparse marginal data regions and extrapolation regions. These grids allow for the observation of the differences in the worsening conditions, when we interpolate at the data margins, where the data lose their homogeneous distribution. Two sets of models are calculated in 2-h intervals, as well as the covariance parameters above: one set without outliers visible in Fig. 2 and the other including these outliers in the estimation process. The parametrization used in both cases is based on the same LOO validation from Figs. 5 and 6. Figure 10 shows the models calculated without outliers, and Fig. 11 shows the models including outliers in the estimation. The range of data selection for the estimation is extended to 40° in order to enable the covering of the extrapolated areas. Figures 10a and 11a show the data used in the interpolation and extrapolation in order to track where the extrapolated regions are. In fact, these regions obtain most of the signal from the trend restoring process in LSC, whereas in OKR and UKR they are affected by inadequate trend modeling, as they are based on limited data. The differences between LSC and kriging for the respective detrending orders do not exceed 1 TECU inside the interpolation zone, for the models free of outliers (Fig. 10g, i). The extrapolations coincide even better for first-order trend (Fig. 10h) than for the mean removal option (Fig. 10g). The extrapolation fails completely in UKR with the second-order trend, as this polynomial obtains improperly exaggerated curvature from the local data, especially at longer distances from the data points.

The differences between the respective models created with the restored outliers reach or exceed 1 TECU in case of UKR (Fig. 11h, i). Of course, every modeling process is preceded by an effort of outliers elimination; however, there can appear a case of inefficient outliers detection/elimination or small data samples, which does not allow for the outliers removal. These can be the cases for which this extension of the study can indicate a safer method of the interpolation. Nevertheless, the differences between the models in Fig. 11h, i do not indicate which one fits the potentially good physical field better.

The only independent source of the information about the ‘true’ physical value of VTEC, aside from the data points free of outliers used for LOO and models, is data remaining after the selection process shown by black circles in Fig. 2. Therefore, the models from Fig. 10a–f and those from Fig. 11a–f are interpolated back using simple bilinear interpolation from 1° grids in the positions of previously unused data free of outliers. Then, the differences between unused data points and interpolated grids from Fig. 10 are compared to differences between the same data and grids from Fig. 11 in all epochs with a 2-h time interval. The results can be viewed in Fig. 12, which provide three interesting observations. The models without the outliers fit with the same accuracy for LSC and kriging across the day (Fig. 12a). The models estimated with outliers fit with similar accuracy for LSC and kriging only in time where the sun has left the investigated area (Fig. 12b). When the equatorial anomaly passes the China region, a predominant number of LSC solutions are better than UKR solutions based on first- and second-order local polynomial trends (Fig. 12b). The most suspected reason of LSC advantage is global detrending, which, based on a large dataset, becomes more robust to the individual outliers with respect to the local trend fitting.

Fig. 12

Standard deviations of comparison between values interpolated from models created by the six methods in the positions of free of outliers data points and data: a the models are interpolated from data without outliers, and b the models are interpolated from data including outliers

6 Conclusions

This work investigates LSC, OKR and UKR and proves their consistency under the conditions of precise parametrization, homogeneous spatial distribution, lack of outliers and equivalent detrending, which numerically confirms the comments provided by Dermanis (1984). This consistency is observed from the minima of RMSLOO, which are comparable for all six methods tested in this work with regard to dense data without significant outliers and far from data gaps. However, the margins of the data where the gaps start to occur, as well as the places where outliers remain among the correlated data, show a significantly better validation results when modeled with LSC/SKR. Additionally, the daylight hours and equatorial anomaly pass turn out to be challenging for UKR TEC modeling. The unbiasedness constraint applied in OKR and UKR is often hastily considered as a substantial advantage in comparison with LSC and SKR. The actual study shows a worse performance of the local detrending applied in UKR in comparison with the global trend removal applied in LSC/SKR. The superiority of global detrending in LSC is confirmed numerically for the sparse data regions and also in case of the outlier occurrences.

This study investigates the lowest orders of the trend, as they are most often used in practice, and the aim of this work was to assess LSC, OKR and UKR together. Extended data areas and specific properties of the signal in terms of its variance can, however, require higher-order trends so as to obtain homogeneous statistical distribution of the residuals. Otherwise, due to the imperfect distribution of the residuals, the estimation of the parameters can generate lower accuracy in some cases, as demonstrated in this paper.

Therefore, unbiased detrending has been proven to be crucial in stochastic modeling. The drawback of UKR is such that the polynomials fit worse when based on a limited subset of the data, especially if more noisy or distant data are applied. It is a common practice in gravity field modeling that detrending is performed in the so-called remove–restore method, with the use of lower-order trend from spherical harmonic expansion of geopotential functionals, i.e., using existing global geopotential models (GGM). In TEC modeling, the equatorial anomaly includes the predominant part of the TEC signal and, therefore, in times of the increasing number of GIMs, their applicability in VTEC data detrending can become especially valuable. This is of course associated with the application of LSC/SKR instead of OKR or UKR. The drawback of GIMs lies in their relatively low order of spherical harmonic expansion, which may still introduce some bias in detrending of local TEC observations.