Effect of reduced opportunities on bargaining outcomes: an experiment with status asymmetries

Abstract

Several allocation rules (such as the Kalai–Smorodinsky solution) allow for possible violations of the ‘independence of irrelevant alternatives’ (IIA) axiom in cooperative bargaining game theory. Nonetheless, there is no conclusive evidence on how contractions of feasible sets exactly affect bargaining outcomes. We have been able to identify a definite behavioral channel through which such contractions actually determine the outcomes of negotiated bargaining. We find that the direction and the extent of changes in bargaining outcomes, due to contraction of the feasible set, respond to the level of (given) agent asymmetry with a remarkable degree of regularity. Alongside, we conclude that the validity of the IIA axiom is only limited to symmetric games.

Appendices

Appendix 1: Thought experiment

Appendix 2: Test details

Appendix 3: Working of sample size for the control group

Let the ith pair of shares be ($x_{1}^{i}$,$x_{2}^{i}$), where $x_{1}^{i}$ + $x_{2}^{i}$ = 1. Since |$x_{1}^{i}$ – 0.5| =|$x_{2}^{i}$ – 0.5|, we can define, without loss of generality Z_i =|$x_{1}^{i}$ – 0.5|. Then let $\overline{Z}$ = $\frac{{Z_{1} + \cdots + Z_{n} }}{n}$ (where n is the number of observed pairs). $\overline{Z}$ measures the average deviation of the negotiated shares from the equal division solution (0.5, 0.5). Suppose that the population mean of this variable is μ. Now, consider the test of the null hypothesis that μ₀ = 0 (i.e. the equal division solution is the population mean). The question is: what would be the minimum sample that is required for such a test to have reasonable power against an alternative hypothesis that the population mean is μ₁ > 0? We consider the alternative hypothesis to be μ₁ = 0.02. It is clear that the sample size that has reasonable power for this alternative hypothesis would also have at least that much power for any μ₁ > 0.02. We do not make any assumption(s) on the distribution of Z_i (and therefore $\overline{Z}$) under the null or the alternate hypothesis (Maniadis et al. 2014).

Let α be the size of the type-I error. Let c be a non-negative constant such that P($\overline{Z}$ – μ₀ > c |μ = μ₀) ≤ α. In other words, the null is rejected whenever $\overline{Z}$ > μ₀ + c. To determine c as a function of α and n, we note the following inequalities (the first one of which is P($\overline{Z }$ ≤ μ₀ + c) ≥ P(μ₀ – c ≤ $\overline{Z}$ ≤ μ₀ + c) ≥ P(μ₀ – c < $\overline{Z }$ < μ₀ + c)).

$$P(\overline{Z } \le \mu_{0} + \, c) \ge \, P(\mu_{0} {-}c \, < \overline{Z } < \, \mu_{0} + \, c); \, \{ \because {\text{LHS spans more values}}\}$$

$$P(\mu_{0} {-}c \, < \overline{Z } < \, \mu_{0} + \, c) \, = \, P(|\overline{Z} {-}\mu_{0} | < \, c) \, \ge \, 1{-}\frac{{\sigma_{Z}^{2} }}{{nc^{2} }} ; \, \{ \because {\text{Chebyshev}}^{\prime}{\text{s inequality}}\}$$

We combine the two inequalities above as follows

$$\begin{gathered} P(\overline{Z } \le \, \mu_{0} + \, c) \ge \, 1{-}\frac{{\sigma_{Z}^{2} }}{{nc^{2} }} \hfill \\ \Rightarrow P(\overline{Z } {-}\mu_{0} > \, c|\mu \, = \, \mu_{0} ) \, \le \frac{{\sigma_{Z}^{2} }}{{nc^{2} }} \hfill \\ \Rightarrow P\left( {\text{Type I error}} \right) \le \frac{{\sigma_{Z}^{2} }}{{nc^{2} }} = \, \alpha \hfill \\ \Rightarrow c \, = \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} \hfill \\ \end{gathered}$$

(4)

Thus, the probability of a Type-I error does not exceed α when c = $\frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}$. Now we turn to Type II error (which should not exceed β).

$$P({\text{Type II error}}) \, = \, P(\overline{Z } < \, \mu_{0} + \, c|\mu \, = \, \mu_{1} )$$

Now μ₀ = 0, and we substitute for c from (4), we get

$$P\left( {\text{Type II error}} \right) = \, P(\overline{Z } < \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} |\mu = \mu_{1} )$$

Note that for any k, we know from Chebyshev’s inequality that

$$P(\mu_{1} {-}k \, < \overline{Z } < \, \mu + \, k|\mu \, = \, \mu_{1} ) \, \ge \, 1{-} \frac{{\sigma_{Z}^{2} }}{{nk^{2} }}$$

We now take k = μ₁ – $\frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}$ in the above inequality to get 

$$P\left( {\frac{{\sigma_{Z} }}{{\underbrace{\sqrt {\alpha n}}_{{\mu_{1} - k}} }} < \overline{Z } < {\underbrace {{2\mu_{1} {-} \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}}}_{{\mu_{1} + k}} }\;\; {|}}{{\mu = \mu_{1}} } \right) \ge \, 1{-}\frac{{\sigma_{Z}^{2} }}{{nk^{2} }}$$

(5)

But

$$P\left( {\overline{Z } \ge \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} |\mu \, = \, \mu_{1} } \right) \ge P\left( {\frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} < \overline{Z } < 2\mu_{1} {-}\frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}|\mu = \mu_{1} } \right); \, \{ \because {\text{LHS spans more values}}\} .$$

(6)

The LHS above spans more values since:

$$P\left( {\overline{Z } \ge \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} |\mu \, = \, \mu_{1} } \right) \ge P\left( {\overline{Z } > \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}|\mu = \mu_{1} } \right) \ge P\left( {\frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} < \overline{Z } < 2\mu_{1} - \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}|\mu = \mu_{1} } \right).$$

On combining the inequalities (5) and (6), we get

$$\begin{aligned} & P\left( {\overline{Z } \ge \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} |\mu = \mu_{1} } \right) \ge { }1 {-}{ }\frac{{\sigma_{Z}^{2} }}{{nk^{2} }} \\ & \quad \Rightarrow 1 {-} P\left( {\overline{Z } \ge \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} |\mu = \mu_{1} } \right) \le 1 {-} \left( {1 {-}{ }\frac{{\sigma_{Z}^{2} }}{{nk^{2} }}} \right) = { }\frac{{\sigma_{Z}^{2} }}{{nk^{2} }} \\ & \quad \Rightarrow P\left( {\overline{Z }< { \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }} } |\mu = \mu_{1} } \right) \le { }\frac{{\sigma_{Z}^{2} }}{{nk^{2} }} \\ & \quad \Rightarrow P\left( {\text{Type II error}} \right) \le { }\frac{{\sigma_{Z}^{2} }}{{nk^{2} }}{ } = { }\beta . \\ \end{aligned}$$

(7)

Thus, the probability of a Type II error does not exceed β when $\frac{{\sigma_{Z}^{2} }}{{nk^{2} }}$ = β. Substituting for k = μ₁ – $\frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}$, we get

$$\beta \, = \frac{{\sigma_{Z}^{2} }}{{n\left( {\mu_{1} {-} \frac{{\sigma_{Z} }}{{\sqrt {\alpha n} }}} \right)^{2} }} = \frac{{\alpha \sigma_{Z}^{2} }}{{\left( {\mu_{1} \sqrt {\alpha n} {-} \sigma_{Z} } \right)^{2} }}$$

(8)

$$\Rightarrow n \, = \frac{{\sigma_{Z}^{2} }}{{\left( {\mu_{1} {-} \mu_{0} } \right)^{2} }}\left( {\frac{1}{\sqrt \alpha } + \frac{1}{\sqrt \beta }} \right)^{2}$$

(9)

In this expression, we fix the probabilities of Type I error (α) and Type II error (β) to be 0.05 and 0.10 respectively. We take μ₁ = 0.02. The only limitation is that we do not know the value of $\sigma_{Z}$. To estimate $\sigma_{Z}$, we use a pilot study that had 14 subjects (7 pairs) in the control group. In this sample, $\widehat{{\sigma_{Z} }}$ = 0.0075592. Using this value gives us n* = 8.33 ≈ 9 pairs (18 subjects). Note that c equals 0.01 for this value of n. In other words, with just 18 subjects, we can be 95% confident that the average outcome is the 50–50% split (and not a 51–49% split).

Appendix 4: Derivations of the bargaining solutions

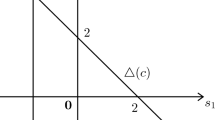
The axioms of symmetry and efficiency together, in the Nash and the KS bargaining framework, are sufficient to guarantee that X and Y get 50% each (of the pie). We verify this in our context where our agents X and Y receive payoffs x and y, with x + y = 1. I assume a zero disagreement–payoff vector. The feasible set of interest is shown in the shaded region of Fig. 1a.

The symmetric Nash solution: This solution can be formulated as follows (ignoring the non-negativity constraint)

$$\begin{array}{*{20}c} {{\text{Maximize}}:} \\ {{\text{Subject to}}:} \\ \end{array} \begin{array}{*{20}c} { xy} \\ { x + y = 1} \\ \end{array}$$

which is the same as the following problem

$${\text{Maximise}} :x\left( {1 - x} \right)$$

which involves feeding the constraint into the objective function. The solution to the above problem x = y = 1/2 is our unique (symmetric) Nash Bargaining solution.

The symmetric Kalai–Smorodinsky solution: The coordinates of the ideal point are given by (1, 1). The equation of the line joining the disagreement payoff (0, 0) and the ideal point is given by

$$\frac{x - 0}{{1 - 0}} = \frac{y - 0}{{1 - 0}} \Rightarrow x = y$$

feeding the constraint (y = 1 − x) into which gives us x = 1 − x, or x = y = 1/2 as our KS solution.

To summarize, for a symmetric game involving the division of a given pie size (say $1) in the absence of any (favorable) contraction, theory (Nash, KS and others) predicts an equal split i.e. both the individuals X and Y, get to keep 50 cents each.

The asymmetric Nash solution: For individual X with a higher bargaining power β, this allocation rule that puts more weight on agent X’s payoff, is formulated as follows.

$$\begin{array}{*{20}c} {{\text{Maximize}}:} \\ {{\text{Subject to}}:} \\ \end{array} \begin{array}{*{20}c} { x^{1 + \beta } y} \\ { x + y = 1} \\ \end{array}$$

The solution to the above problem is x = (1 + β)/(2 + β) > 1/2.²⁸ In other words, the agent with a higher bargaining power gets the higher share.

The asymmetric Kalai–Smorodinsky solution: Here, agent X’s higher bargaining power (β) can be captured in a different way. This solution concept is explained in Fig. 2. The equation of the line joining the disagreement payoff and the ideal point (1 + β, 1) is given by

$$\frac{x - 0}{{1 + \beta - 0}} = \frac{y - 0}{{1 - 0}} \Rightarrow x = \left( {1 + \beta } \right)y.$$

Feeding the constraint (y = 1 − x) into which again gives us x = (1 + β)/(2 + β) > 1/2 (the person with a higher bargaining power gets the higher share). Both the solutions predict the same asymmetric outcome in the presence of asymmetric bargaining power. Note that putting β = 0 above gives back the symmetric solution.

The symmetric Kalai–Smorodinsky solution with contraction: There is a cap on individual Y′s payoff equivalent to 1 − α. The coordinates of the ideal point now become (1, 1 − α). The equation of the line that intersects this point with the disagreement payoff is given by

$$\frac{x - 0}{{1 - 0}} = \frac{y - 0}{{1 - \alpha - 0}} \Rightarrow \frac{x}{y} = \frac{1}{{\left( {1 - \alpha } \right)}} > 1; \left\{ {\because 1 > 1 - \alpha } \right\}.$$

x > y. Finally, using the constraint y = 1 − x gives us x_KS = 1/(2 − α);∀ α ∈ [0,1], the Nash solution is given as

$${\text{Nash}}:x_{N} = \left\{ {\begin{array}{*{20}c} {0.5 ;\;{\text{for}} \;0 \le \alpha < 0.5} \\ {\alpha ;\;{\text{for }\;}0.5 \le \alpha \le 1 } \\ \end{array} } \right..$$

The KS solution (written below) is therefore, different from Nash when there is feasible set contraction.

Asymmetric bargaining in the presence of contraction: The Nash solution remains as above but the KS solution changes to x_KS = (1 + β)/(2 + β − α). Note again that in the absence of asymmetry (β = 0), the KS solution above is identical to the one involving only contraction.

Appendix 5: Instructions to candidates