Additive multi-effort contests

Abstract

This article analyzes rent seeking with multiple additive efforts for each of two players. Impact on rent seeking occurs even when a player exerts only one effort. This contrasts with models of multiplicative efforts with impact on rent seeking only when a player exerts all its available efforts. An analytical solution is developed when the contest intensities are below one, and equal to one for one effort. Then, additional efforts causing interior solutions give players higher expected utilities and lower rent dissipation, which contrasts with earlier findings for multiplicative efforts. Players cut back on the effort with contest intensity equal to one, and exert alternative efforts instead. Accounting for solutions which have to be determined numerically, a Nash equilibrium selection method is provided. For illustration, an example with maximum two efforts for each player is provided. Equilibria are shown where both players choose both efforts, or one player withdraws from its most costly effort. Both players may collectively prefer to exclude one of their efforts, though in equilibrium, they may prefer both efforts. When all contest intensities are equal to one or larger than one, only the one most cost-effective effort is exerted, due to the logic of linear or convex production. Rent dissipation increases in the contest intensity, and is maximum when the players are equally advantaged determined by unit effort cost divided by impact.

1 Introduction

1.1 Background

Earlier rent seeking research has mostly assumed one effort for each player, which is limiting given the plethora of possible efforts. The literature gradually expands to account for multiple efforts for each player. How multiple efforts interact to impact rent seeking is currently poorly understood. This article intends to improve this understanding. Examples of rents are R&D budgets, promotions, licenses, privileges, monopoly opportunities, election opportunities, struggles for government support between different industries, competition for budgets by interest groups, and government distribution of public goods. Examples of efforts to obtain rents are multifarious, e.g. lobbying, influence strategies, interference struggles, litigation, strikes and lockouts, political campaigns, commercial efforts to raise rivals’ costs (Salop and Scheffman 1983), economic and political maneuvers (Hirshleifer 1995), coaxing, prompting, inducing, urging, extorting, exacting, persuasion techniques, pressure methods, promotions, briberies, skirmishes, battle, combat, and fighting with or without violence.

1.2 Contribution

This article acknowledges that each player may have available arbitrarily many efforts which may or may not overlap with the contending player’s available efforts. Each effort may be of different nature and operate according to its own logic. Analyzing multiple additive efforts supplements the earlier literature which commonly assumes one effort, or usually assumes multiplicative efforts which all have to be exerted to ensure impact. Formally in this article, efforts may have three different characteristics, i.e. different unit costs, different impacts, and different contest intensities. Efforts operate additively in the contest success function, which has been insufficiently analyzed in the literature. The model is chosen to enable each player to incur a different cost of effort, and have a different impact with a different contest intensity for each effort.

In the rent seeking literature, the contest intensity or decisiveness parameter is generally a parameter at the contest level, and thus equivalent for both or all players. The authors are not aware of literature modeling different contest intensity parameters for different players. In this article, each effort operates according to its own logic with an intensity, scaling and impact independent of the other efforts. Hence, the contest intensity parameters generally differ across players. Specific efforts by one player are thus not matched against specific efforts by the other player. Instead, each player’s efforts are added up into an effort production function which competes against the other player’s effort production function.

In the contest success function, additive efforts are substitutable while multiplicative efforts are complementary. However, when accounting for both the contest success function and the cost of exerting efforts, a new function emerges. For this new function, multiple efforts with different production functions and unit effort costs can generally be of the same kind or nature, can be substitutes for each other, or can complement each other in various ways. All these kinds are possible with additive efforts in the contest success function (Proposition 3) since the subtraction of effort costs in the players’ expected utilities causes linkages between the players’ efforts.

To illustrate the prevalence of additive efforts and how they differ from single efforts, consider two examples. The first illustrates how a lobbying firm may hire different kinds of professionals to be able to exert multiple additive efforts, one effort for each professional. The lobbying firm evaluates hiring any combination of professionals with substitutable training causing different production functions operating additively, with different unit effort costs, e.g. professionals with any degree and experience in economics versus political science, a man versus a woman, human effort versus machine effort, etc. Since the efforts are not of the same kind, a close look at how the efforts substitute or complement each other is needed. For example, an office clerk can manually compile statistics to support a rent application, or advanced computers and software can be employed to do the same work.

Second, consider multiple players interpreted to interact statically. Each player hires multiple professionals with various kinds of expertise, to enable each player to exert multiple additive efforts. The players compete for an elected office position, e.g. US president. Each player hires professionals with various kinds of expertise, i.e. political analysts to develop views and positions on issues, media professionals for spin control, social media operatives, business people to recruit donors, telephone operators to convince voters, geographically dispersed ground troops knocking on people’s doors, speech writers to tune messages for big rallies and local meetings, gossip developers, and specialists in negative campaigning. These efforts may jointly and independently add up to a campaign’s effort production function which impacts the contest with the other player(s). It is quite possible for a player’s campaign to be successful even if some efforts are missing, e.g. due to strategic choice, oversight, lacking competence, or deficient funding. For example, a player may decide to eliminate negative campaigning and ground troops. Alternatively, a player may rely on big colorful rallies applying hitherto unknown influence techniques that the other players are unable or unwilling to apply. Combining the additive contest success function with the subtraction of efforts’ costs may cause independence, substitutability, or complementarity between efforts.

One alternative to additive efforts is multiplicative efforts of the Cobb–Douglas type analyzed by Arbatskaya and Mialon (2010), extended to a two-stage contest by Arbatskaya and Mialon (2012). One of their examples, also provided by Tullock (1980) and Krueger (1974), is that “firms may be able to obtain rents from the government not only by improving their efficiency, but also by lobbying or even bribing government officials” (Arbatskaya and Mialon 2010). Multiplicative efforts can be descriptive of this phenomenon when both improved efficiency and lobbying are mandatory for successful rent seeking. That is, improved efficiency without lobbying guarantees no success, and lobbying without improved efficiency guarantees no success. For some phenomena such as career promotions, requiring all efforts to be mandatory can be realistic even as the number of efforts increases. For other phenomena, as the number of efforts increases, Cobb–Douglas type multiplicative efforts may become increasingly unrealistic since each effort must be strictly positive to ensure success. The current article opens for the possibility that improved efficiency without lobbying, or lobbying without improved efficiency, may both constitute successful rent seeking, although both operating additively may be even more successful. The different assumptions of additive and multiplicative efforts cause different results regarding efforts, expected utilities, and rent dissipation. For example, for additional efforts, Arbatskaya and Mialon (2010) find increased rent dissipation when the contest becomes more balanced, whereas we find decreased rent dissipation caused by players optimizing more cost effectively across efforts.

1.3 Literature

The rent seeking literature has developed fruitfully for half a century (Congleton et al. 2008). Early developments are by Krueger (1974), Posner (1975) Tullock (1980), etc., reviewed by Nitzan (1994). Skaperdas (1996) considers symmetric contests, Clark and Riis (1998) analyze asymmetric contests, Cubel and Sanchez-Pages (2016) assess difference-form contest success functions, Bozbay and Vesperoni (2018) evaluate contest success functions for networks and Münster (2009) examines group contests. Rai and Sarin (2009) allow multiple types of investments.

Rai and Sarin (2009) exemplify multiple types of investments with a linear production function and the Cobb–Douglas production function. Their linear production function involves two additive efforts which contestants may substitute between. They treat one investment as fixed which causes the contest success function analyzed by e.g. Nti (2004) and Hausken and Zhuang (2012). Another example of efforts, but not of the Cobb–Douglas type, are by Epstein and Hefeker (2003). Assuming two efforts for each player, the first is conventional rent seeking. The second effort may be absent, or it may reinforce the first effort. They find that two efforts strengthen the player with the higher stake and decreases relative rent dissipation.

Influenced by Dixit’s (1987) analysis of precommitment in contests, Yildirim (2005) analyzes a two-period game where both players simultaneously choose one effort each in period 1, which becomes public knowledge, and both players simultaneously choose whether to add one effort in period 2, so that the probability of winning depends on the cumulative effort levels. Melkonyan (2013) considers hybrid contests where the players forfeit one resource each ex-ante, and commit one resource each ex-ante which is expended ex-post by the winning player. He finds no rent overdissipation, and that more players cause less ex-ante and more ex-post expenditures by individual players, and more ex-ante and ex-post expenditures across all players. Hausken (2020) analyzes additive efforts for arbitrarily many players assuming contest intensity one for each effort in the contest success function. That is, each effort has proportional impact since the exponent to each effort equals one. He finds that 50% of the rent is dissipated when the players have equal ratios of unit cost divided by impact, and that rent dissipation decreases as the players’ ratios become more unequal. Clark and Konrad (2007) evaluate contests in multiple dimensions. Winning a certain number of contests is required to win the prize.

Osorio (2018) analyzes a model with multiple efforts and two allocation systems. The I-system is a sum of independent contests where each player exerts one effort for each prize. The A-system resembles the approach in the current article where the players’ multi-issue efforts are aggregated additively into a single outcome. Assuming the same contest intensity for both players and across all efforts, he finds that the A-system tends to induce higher total efforts than the I-system. With decreasing returns to effort, the players distribute their efforts over all issues, while with increasing returns to effort, the players focus on only one issue.

Supplementing rent seeking with sabotage is another example of multiple efforts. Konrad (2000) assumes that one effort improves the player’s contest success, whereas a second effort decreases the rival players’ success, which may increase lobbying efforts and rent dissipation. Chen (2003) considers competition for promotion involving efforts to enhance one’s own performance and efforts to sabotage the opponents’ performance. He finds that abler competitors are subject to more attacks. Amegashie and Runkel (2007) study sabotage in a three-stage elimination contest between four players. They find one equilibrium where only the most able contestant engages in sabotage, and one equilibrium without sabotage. Krakel (2005) assumes that each player in the first stage chooses help, sabotage, or no action, and in the second stage chooses effort to win the tournament, which causes a variety of equilibria. See Chowdhury and Gürtler (2015) for a survey.

Multiple efforts, i.e. production and appropriation, are also present in the conflict models by Hirshleifer (1995), Skaperdas and Syropoulos (1997), and Hausken (2005), but contest success depends only on appropriation.

Chowdhury and Sheremeta (2015) propose a procedure to identify strategically equivalent contests which generate the same equilibrium efforts but different equilibrium payoffs. That procedure may potentially be used to compare the equilibrium efforts in this article with efforts in other contests to identify strategically equivalent contests.

Section 2 presents the model assuming multiple additive efforts. Section 3 solves the model generally and presents the structure of the solutions. Section 4 analyzes the model when all contest intensities except maximum one are less than one. Section 5 analyzes the model when all contest intensities are equal to or larger than one. Section 6 compares results of when rent dissipation, efforts and expected utilities increase or decrease. Section 7 concludes.

2 The model

The nomenclature is shown in “Appendix A”. This article analyzes the simultaneous interaction between players 1 and 2 in a one-period game. Define $\varvec{x}_{\varvec{i}} = \left({x_{i1}, \ldots, x_{{iK_{i}}}} \right)$ as the vector of player $i$’s $K_{i}$ efforts, $\varvec{x} = \left({\varvec{x}_{1},\varvec{x}_{2}} \right)$ as the vector of the two players’ $\mathop {\sum_{i = 1}^{2} {K_{i}}}$ efforts, $\varvec{x}_{{- \varvec{i}}}$ as the vector of player $j$’s $K_{j}$ efforts, $i,j = 1,2, i \ne j$, and $\varvec{x}_{- ik}$ as the vector of the two players’ $\left({\mathop \sum \limits_{i = 1}^{2} K_{i}} \right) - 1$ efforts aside from player $i$’s effort $k \in \left\{{1, \ldots,K_{i}} \right\}$. Player $i \in \left\{{1,2} \right\}$ exerts $K_{i}$ efforts $x_{ik}$, $k \in \left\{{1, \ldots,K_{i}} \right\}$ at unit cost $c_{ik} > 0$ to increase its probability $p_{i} = p_{i} \left({\varvec{x}_{1},\varvec{x}_{2}} \right)$ of winning a rent with value $S \ge 0$. A risk neutral player $i$’s winning probability $p_{i}$ can also be interpreted as the fraction of the rent earned by player $i$ if the rent is sharable. Player $i$’s Constant Elasticity of Substitution production (impact) function is

$$f_{i} \left({\varvec{x}_{\varvec{i}}} \right) = \mathop \sum \limits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}},$$

(1)

where $d_{ik} > 0$ is a proportional scaling parameter for impact, and $m_{ik} \ge 0$ is player $i$’s contest intensity or decisiveness which scales as an exponent the impact of each effort $x_{ik}$. This model is chosen since it is sufficiently flexible and encompassing to enable each player $i$ to incur a different cost $c_{ik}$ for each effort $x_{ik}$, where each effort $x_{ik}$ has a different impact $d_{ik}$, with a different contest intensity $m_{ik}$, on player $i$’s probability $p_{i}$ of winning the rent $S$, $k = 1,2, \ldots,K_{i}$. When $m_{ik} = 0$, the effort has no impact. When $0 < m_{ik} < 1$, the effort has less than proportional impact. When $m_{ik} = 1$, the effort has proportional impact. When $m_{ik} > 1$, the effort has more than proportional impact. Each type of effort $x_{ik}$ is characterized by the vector ($c_{ik}$, $d_{ik}$, $m_{ik}$), i.e. the unit effort cost $c_{ik}$, the proportional scaling parameter $d_{ik}$ for impact, and the contest intensity $m_{ik}$. Applying the ratio-form contest success function (Skaperdas 1996) $p_{i} = p_{i} \left({\varvec{x}_{1},\varvec{x}_{2}} \right)$ for player $i$’s winning probability, and inserting (1), player $i$’s expected utility is

$$\begin{aligned} u_{i} & = u_{i} \left({\varvec{x}_{1},\varvec{x}_{2}} \right) = p_{i} \left({\varvec{x}_{1},\varvec{x}_{2}} \right)S - \mathop \sum \limits_{k = 1}^{{K_{i}}} c_{ik} x_{ik} \hfill \\ & = \left\{{\begin{array}{l} {\frac{{S\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}}}{{\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}} + \mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}}} - \mathop \sum \limits_{k = 1}^{{K_{i}}} c_{ik} x_{ik}\; {\text{if }}x_{1k} \in {\mathbb{R}}_{+ +}^{1} {\text{or }}x_{2k} \in {\mathbb{R}}_{+ +}^{1}} \\ {\frac{S}{2}\;{\text{if }}\varvec{x} = \left({0,0} \right) } \\ \end{array}} \right. \hfill \\ \end{aligned}$$

(2)

Equation (2) states that if player $i$ exerts at least one strictly positive effort, then its winning probability is strictly positive regardless of its other efforts and the other player’s efforts. This contrasts with Arbatskaya and Mialon’s (2010) model of multiplicative efforts where $m_{ik} = d_{ik} = 1$. First, they require that all the $K_{i}$ efforts by at least one player have to be strictly positive in order for its winning probability to be strictly positive regardless of the other player’s efforts. Technically, they require all player $i$’s $K_{i}$ efforts to be strictly positive, giving $\varvec{x}_{\varvec{i}} \in {\mathbb{R}}_{+}^{{K_{i}}} \backslash {\mathbb{R}}_{+ +}^{{K_{i}}}$ which is a collection of coordinate hyperplanes (in the positive orthant), whereas we require at least one of player $i$’s $K_{i}$ efforts to be strictly positive, which gives the singleton $x_{ik} \in {\mathbb{R}}_{+}^{1} \backslash {\mathbb{R}}_{+ +}^{1} = \left\{0 \right\}$.

Second, Arbatskaya and Mialon (2010) do not require all winning probabilities to sum to one, whereas we do so that the entire prize $S$ gets allocated under all circumstances. Thus, (2) states that if player $i$ exerts at least one strictly positive effort, while all efforts by the other player equal zero, then player $i$’s winning probability is one, and the other player’s winning probability is zero. Accordingly, if player $i$ exerts no efforts, and the other player exerts at least one strictly positive effort, then player $i$’s winning probability is zero. If both players withdraw from exerting effort, then their winning probabilities are equal and sum to one. Rent dissipation is defined as

$$D = \frac{1}{S}\mathop \sum \limits_{i = 1}^{2} \mathop \sum \limits_{k = 1}^{{K_{i}}} c_{ik} x_{ik}.$$

(3)

3 Solving the model

3.1 The first-order conditions

This solution involves determining Nash equilibria (Nash 1951), from which no player has an incentive to deviate unilaterally.¹ A Nash equilibrium is a combination of strategies $\left({\varvec{x}_{1}^{*},\varvec{x}_{2}^{*}} \right)$ such that²

$$\begin{aligned} u_{1} \left({\varvec{x}_{1}^{*},\varvec{x}_{2}^{*}} \right) \ge u_{1} \left({\varvec{x}_{1},\varvec{x}_{2}^{*}} \right) \forall \; \varvec{x}_{1}, \hfill \\ u_{2} \left({\varvec{x}_{1}^{*},\varvec{x}_{2}^{*}} \right) \ge u_{2} \left({\varvec{x}_{1}^{*},\varvec{x}_{2}} \right) \forall \varvec{x}_{2}. \hfill \\ \end{aligned}$$

(4)

Differentiating (2), the first-order condition if $m_{ik} \ne 0$ and $d_{ik} \ne 0$ is

$$\begin{aligned} \frac{{\partial u_{i}}}{{\partial x_{ik}}} &= \frac{{Sm_{ik} d_{ik} x_{ik}^{{m_{ik} - 1}} \mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}}}{{\left({\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}} + \mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}} \right)^{2}}} - c_{ik} = 0 \hfill \\ & \Leftrightarrow \frac{{S\mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}}}{{\left({\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}} + \mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}} \right)^{2}}} = \frac{{c_{ik}}}{{m_{ik} d_{ik} x_{ik}^{{m_{ik} - 1}}}},\quad i,j = 1,2,i \ne j. \hfill \\ \end{aligned}$$

(5)

If $d_{ik} = 0$, effort $x_{ik}$ has no impact on $f_{i} \left({\varvec{x}_{\varvec{i}}} \right)$ in (1), causing the corner solution $x_{ik} = 0$. Inserting $m_{ik} = 0$ into (5) gives $\frac{{\partial u_{i}}}{{\partial x_{ik}}} = - c_{ik} < 0$, which also causes $x_{ik} = 0$.

3.2 The structure of the solutions

Section 4 determines the general solution when $0 \le m_{i1} \le 1$ and $0 \le m_{ik} < 1$$\forall \; k = 2, \ldots,K_{i}$, $i = 1,2$, where player $i$’s production $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}$ is concave in effort $x_{ik}$, or linear in $x_{i1}$ when $m_{i1} = 1$. Hence, player $i$ generally exerts more than one effort since the marginal benefit of effort decreases when effort $x_{ik}$ increases. Section 5 determines the general solution when $m_{ik} \ge 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$, where player $i$’s production $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}$ is convex or linear in effort $x_{ik}$. Convex production causes player $i$ to exert only one effort since the marginal benefit of effort increases when effort $x_{ik}$ increases. Linear production, $m_{ik} = 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$, also causes player $i$ to exert only one effort, as shown by Hausken (2020). When player $i$’s production $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}$ is concave in effort $x_{ik}$, while player $j$’s production $\mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}$ is convex in effort $x_{jk}$, then player $i$ generally exerts multiple efforts, while player $j$ exerts one effort. When $0 \le m_{ik} \le 1$ for $k = 1, \ldots,K_{iq} < K_{i}$, while $m_{ik} > 1$ for $k = K_{iq} + 1, \ldots,K_{i}$, for player $i$, more specialized analyses are required. “Appendix B” determines the solution when $K_{i} = K_{j} = 1$.

4 Solution when $0 \le \varvec{m}_{{\varvec{i}1}} \le 1$ and $\le \varvec{m}_{{\varvec{ik}}} < 1$ $\forall \varvec{k} = 2, \ldots,\varvec{K}_{\varvec{i}}$, $\varvec{i} = 1,2$

Section 4.1 provides the general solution. Section 4.5 assumes equal contest intensities across efforts, $m_{ik} = m_{i}$, $k = 1,2, \ldots,K_{i}$; and thereafter also across players, $m_{ik} = m$, $k = 1,2, \ldots,K_{i}$. Section 4.2 assumes $K_{i}$ efforts against $K_{j}$ efforts. Section 4.3 assumes one effort against $K_{j}$ efforts. Corner solutions are presented in Appendices. Section 4.4 considers an example.

4.1 General solution

When $0 \le m_{i1} \le 1$ and $0 \le m_{ik} < 1$$\forall \; k = 2, \ldots,K_{i}$, $i = 1,2$, player $i$’s production $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}$ across its $K_{i}$ efforts is concave in each effort $x_{ik}$, or linear in $x_{i1}$ when $m_{i1} = 1$. Hence, player $i$’s marginal benefit from increasing its effort $x_{ik}$ decreases. “Appendix C” shows that the stationary point is a global maximum. Equation (5) allows expressing all efforts for each player as functions of one effort for that player. Without loss of generality, we choose that one effort to be $x_{i1}$ for player $i$, and thus, we also assume $d_{i1} > 0$ so that $x_{i1}$ has impact, $i = 1,2$. Solving (5) gives

$$\frac{{c_{ik}/d_{ik}}}{{m_{ik} x_{ik}^{{m_{ik} - 1}}}} = \frac{{c_{i1}/d_{i1}}}{{m_{i1} x_{i1}^{{m_{i1} - 1}}}} \Leftrightarrow x_{ik} = x_{i1}^{{\frac{{1 - m_{i1}}}{{1 - m_{ik}}}}} \left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{m_{i1} c_{ik}/d_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}},\quad k = 2, \ldots,K_{i}$$

(6)

Inserting (6) into (5) and solving gives

$$x_{i1}^{{m_{i1}}} = \frac{{Sc_{j1} m_{i1}^{2} d_{i1} m_{j1} d_{j1} x_{j1}^{{1 - m_{j1}}}}}{{\left({m_{j1} c_{i1} d_{j1} x_{i1}^{{1 - m_{i1}}} + m_{i1} c_{j1} d_{i1} x_{j1}^{{1 - m_{j1}}}} \right)^{2}}} - \mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{d_{ik}}}{{d_{i1}}}x_{i1}^{{\frac{{m_{ik} (1 - m_{i1})}}{{1 - m_{ik}}}}} \left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{m_{i1} c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}},$$

(7)

which are two equations with two unknowns $x_{i1}$ and $x_{j1}$. Although (6) and (7) are numerically solvable, they are not analytically solvable for all $m_{ik}$.

Explanation 1

Assume that $0 \le m_{ik} \le 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$. When solving (6) and (7) gives $x_{ik} > 0$$\forall \; k = 1,\ldots,K_{i}$, an interior equilibrium solution is determined by (6) and (7). The players’ expected utility $u_{i}$, $i = 1,2$, and rent dissipation $D$ follow from inserting (6) and (7) into (2) and (3). The corner solution is presented in “Appendix D”.

Proof

Follows from (2), (3), (5)–(7), and “Appendix C”. $\square$

4.2 $K_{i}$ efforts against $K_{j}$ efforts when $m_{i1} = 1,i,j = 1,2$, $i \ne j$

Although (6) and (7) are numerically solvable, two simple assumptions enable analytical solution. First, we assume the common choice of contest intensity one for one of the efforts, without loss of generality effort $x_{i1}$, i.e. $m_{i1} = 1$. Second, to avoid division with zero, we exclude $m_{ik} = 0$ and $m_{ik} = 1$ for the other efforts. This still enables $m_{ik}$ to be arbitrarily close to 0 or 1. This gives

Assumption 1

$m_{i1} = 1$, $0 \le m_{ik} < 1,k = 2, \ldots,K_{i}$, $i = 1,2$.

Inserting $m_{i1} = 1$ into (6) and (7) gives the efforts

$$\begin{aligned} x_{i1} & = \frac{{S\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}}}{{c_{i1} \left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}} - \mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{d_{ik}}}{{d_{i1}}}\left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}}, \hfill \\ x_{ik} & = \left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}},\quad k = 2, \ldots,K_{i},i,j = 1,2, i \ne j, \hfill \\ \end{aligned}$$

(8)

which are inserted into (2) and (3) to yield player $i$’s expected utility

$$u_{i} = \frac{S}{{\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}} + \mathop \sum \limits_{k = 2}^{{K_{i}}} c_{ik} \left({\frac{1}{{m_{ik}}} - 1} \right)\left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}},$$

(9)

and rent dissipation

$$D = \frac{1}{S}\mathop \sum \limits_{i = 1}^{2} \left({\frac{{S\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}}}{{\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}} - \mathop \sum \limits_{k = 2}^{{K_{i}}} c_{ik} \left({\frac{1}{{m_{ik}}} - 1} \right)\left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}}} \right).$$

(10)

Equation (8) for $x_{i1}$ shows one positive term consisting of the characteristics $c_{i1}$, $c_{j1}$, $d_{i1}$, $d_{j1}$ of the first efforts in the contest between players $i$ and $j$, and one negative term consisting of the characteristics of all the other efforts of player $i$. This subtraction illustrates how player $i$ cuts back on effort $x_{i1}$ if it can more cost effectively utilize its other efforts. However, the subtraction cannot cause negative effort $x_{i1}$. This gives

Assumption 2

$x_{i1} > 0 \Leftrightarrow \frac{{S\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}}}{{c_{i1} \left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}} > \mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{d_{ik}}}{{d_{i1}}}\left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}},i,j = 1,2, i \ne j$.

Summing up, Assumption 1 assumes that player $i$’s effort $x_{i1}$, $i = 1,2$, has contest intensity $m_{i1} = 1$, and that player $i$’s $K_{i} - 1$ other efforts $x_{ik}$ have contest intensities $m_{ik}$ weakly above zero and strongly below one. Assumption 2 assumes that an interior solution exists, by requiring player $i$’s effort $x_{i1}$ to be positive, i.e. $x_{i1} > 0$. We next apply Assumptions 1 and 2 in Explanation 2 and in several propositions and lemmas.

Explanation 2

When Assumptions 1 and 2 are satisfied, an interior equilibrium solution is determined by (8). The players’ expected utility $u_{i}$, $i = 1,2$, and rent dissipation $D$ are determined by (9) and (10). The corner solution is presented in “Appendix E”.

Proof

Follows from (8)–(10), “Appendix C”. Assumption 2 ensures $x_{i1} > 0$. $\square$

Proposition 1

When Assumptions 1 and 2 are satisfied, then $\frac{{\partial x_{i1}}}{{\partial K_{i}}} < 0,\frac{{\partial x_{i1}}}{{\partial c_{i1}}} < 0, \frac{{\partial x_{i1}}}{{\partial c_{ik}}} > 0,\frac{{\partial x_{i1}}}{{\partial d_{ik}}} < 0, \frac{{\partial x_{i1}}}{\partial S} > 0,$$\frac{{\partial x_{i1}}}{{\partial d_{jk}}} = \frac{{\partial x_{i1}}}{{\partial c_{jk}}} = \frac{{\partial x_{i1}}}{{\partial m_{jk}}} = 0$, $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$.

Proof

Appendix F.

Proposition 1 states that player $i$’s effort $x_{i1}$ decreases as the number $K_{i}$ of efforts increases. Increasing the dimensionality of $K_{i}$ in Propositions 1, 2, 4, 5 means that the counting parameter $k$ in the summation increases. Thus, the conditions on the parameters involving $k$ are automatically preserved for successively higher $k$. Additional available efforts $x_{ik}$ enable player $i$ to optimally and thus, cost effectively choose among these additional efforts, and thus cut back on the extent to which the effort $x_{i1}$ is utilized. But limits exist. Equation (8) shows that $x_{i1}$ can decrease towards a corner solution $x_{i1} = 0$ as considered in “Appendix E”. Player $i$’s effort $x_{i1}$ decreases, eventually reaching $x_{i1} = 0$, when its unit cost $c_{i1}$ increases, or the impact $d_{ik}$ of player $i$’s other efforts $x_{ik}$ increases. Conversely, $x_{i1}$ increases when the rent S or the unit costs $c_{ik}$ of player $i$’s other efforts $x_{ik}$ increases. Furthermore, $x_{i1}$ is independent of $d_{jk}$, $c_{jk}$, and $m_{jk}$. “Appendix F” presents all the derivatives.

Proposition 2

When Assumptions 1 and 2 are satisfied, then $\frac{{\partial x_{ik}}}{{\partial K_{i}}} = 0,\frac{{\partial x_{ik}}}{{\partial c_{ik}}} < 0$,$\frac{{\partial x_{ik}}}{{\partial d_{ik}}} > 0$,$\frac{{\partial x_{ik}}}{{\partial c_{i1}}} > 0,\frac{{\partial x_{ik}}}{{\partial d_{i1}}} < 0$, $\frac{{\partial x_{ik}}}{{\partial d_{j1}}} = \frac{{\partial x_{ik}}}{{\partial d_{jk}}} = \frac{{\partial x_{ik}}}{{\partial c_{j1}}} = \frac{{\partial x_{ik}}}{{\partial c_{jk}}} = \frac{{\partial x_{ik}}}{{\partial m_{jk}}} = \frac{{\partial x_{ik}}}{\partial S} = 0$, $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$.

Proof

Appendix F.

Proposition 2 shows that player $i$’s effort $x_{ik}$ increases in its impact $d_{ik}$ and unit cost $c_{i1}$, and decreases in its unit cost $c_{ik}$ and impact $d_{i1}$. That $x_{i1}$ decreases in $K_{i}$ (Proposition 1) follows since the marginal return of additional efforts $x_{ik}$ is high at low effort levels. These additional efforts will be used until a constant return on $x_{i1}$ is reached. Any further effort exertion would require an increase in $x_{i1}$. Furthermore, $x_{ik}$ is independent of $d_{j1}$, $d_{jk}$, $c_{j1}$, $c_{jk}$, $m_{jk}$, and $S$. Whereas $x_{i1}$ decreases in $K_{i}$ and $x_{ik}$ is independent of $K_{i}$, Arbatskaya and Mialon (2010) find that adding additional efforts decreases the effort amounts for the efforts already in play if the added efforts unbalance the contest, i.e. makes one player sufficiently stronger or more advantaged. However, Epstein and Hefeker (2003) find that if both players use their second efforts, they will invest less in their first efforts, which is more in accordance with our finding.

Definition

Two efforts $x_{ik}$ and $x_{iq}$, $i = 1,2$, $k,q = 1, \ldots,K_{i}$, $k \ne q$, are substitutes for each other if exerting more (less) of effort $x_{ik}$ decreases (increases) the need for effort $x_{iq}$. The two efforts $x_{ik}$ and $x_{iq}$ are complements for each other if exerting more of effort $x_{ik}$ increases the need for effort $x_{iq}$.

Proposition 3

The efforts $x_{ik}$ and $x_{i1}$,$k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$, can be substitutes due to variation in the parameter $\alpha$ when $\frac{{\partial x_{ik}}}{\partial \alpha} > 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} < 0$, or $\frac{{\partial x_{ik}}}{\partial \alpha} < 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} > 0$; can be complements due to variation in the parameter $\alpha$ when $\frac{{\partial x_{ik}}}{\partial \alpha} > 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} > 0$, or $\frac{{\partial x_{ik}}}{\partial \alpha} < 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} < 0$; and otherwise can be neither substitutes nor complements, where $\alpha = c_{i1},c_{j1},d_{i1},d_{j1},c_{ik},c_{jk},d_{ik},d_{jk}$, $m_{ik},m_{jk}$, $K_{i},K_{j},S.$

Proof

Whether $x_{ik}$ and $x_{i1}$ in Proposition 3 are substitutes, complements, or neither substitutes nor complements, follows from the signs of the derivatives in “Appendix F”. The opposite signs $\frac{{\partial x_{ik}}}{{\partial c_{i1}}} > 0$ and $\frac{{\partial x_{i1}}}{{\partial c_{i1}}} < 0$, opposite signs $\frac{{\partial x_{ik}}}{{\partial d_{ik}}} > 0$ and $\frac{{\partial x_{i1}}}{{\partial d_{ik}}} < 0$, and opposite signs $\frac{{\partial x_{ik}}}{{\partial c_{ik}}} < 0$ and $\frac{{\partial x_{i1}}}{{\partial c_{ik}}} > 0$, imply that $x_{ik}$ and $x_{i1}$ can be substitutes for each other. Whereas $\frac{{\partial x_{ik}}}{{\partial c_{j1}}} = \frac{{\partial x_{ik}}}{{\partial d_{j1}}} = 0$, $\frac{{\partial x_{i1}}}{{\partial c_{j1}}} > 0$ and $\frac{{\partial x_{i1}}}{{\partial d_{j1}}} < 0$ if $\frac{{c_{i1}}}{{c_{j1}}} > \frac{{d_{i1}}}{{d_{j1}}}$. Hence, changing $c_{j1}$ and $d_{j1}$ may increase or decrease $x_{i1}$ while $x_{ik}$ remains unchanged. Hence, $x_{ik}$ and $x_{i1}$ may be neither complements nor substitutes for each other. Whereas $\frac{{\partial x_{ik}}}{{\partial d_{i1}}} < 0$, (45) in “Appendix F” specifies the parameter values when $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} < 0$ which causes $x_{ik}$ and $x_{i1}$ to be substitutes, and when $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} > 0$ which causes $x_{ik}$ and $x_{i1}$ to be complements. “Appendix G” exemplifies.□

Proposition 4

When Assumptions 1 and 2 are satisfied, then $\frac{{\partial u_{i}}}{{\partial K_{i}}} > 0$, $\frac{{\partial u_{i}}}{{\partial c_{ik}}} < 0,\frac{{\partial u_{i}}}{{\partial d_{ik}}} > 0, \frac{{\partial u_{i}}}{\partial S} > 0$, $\frac{{\partial u_{i}}}{{\partial d_{jk}}} = \frac{{\partial u_{i}}}{{\partial c_{jk}}} = \frac{{\partial u_{i}}}{{\partial m_{jk}}} = 0,$$k = 2, \ldots,K_{i},i = 1,2$.

Proof

Appendix F.

Proposition 4 shows that player $i$’s expected utility $u_{i}$ increases in the number $K_{i}$ of available efforts due to increased cost effectiveness. This useful result combined with Proposition 1 means that if a player’ rent seeking is moderately successful by focusing solely on improved efficiency as its single effort, increased success can be obtained by adding e.g. lobbying or bribing as a second effort, and cutting back on the first effort. Further, $u_{i}$ increases in the rent $S$ and the impact $d_{ik}$, and decreases in the unit cost $c_{ik}$.

Proposition 5

When Assumptions 1 and 2 are satisfied, then $\frac{\partial D}{{\partial K_{i}}} < 0$, $\frac{\partial D}{{\partial c_{ik}}} > 0,\frac{\partial D}{{\partial d_{ik}}}< {0, \frac{\partial D}{\partial S}} > 0$, $k = 2, \ldots,K_{i},i = 1,2$.

Proof

Appendix F.

Proposition 5 shows that rent dissipation $D$ decreases in the number $K_{i}$ of available efforts, and the impact $d_{ik}$, since players with more efforts optimize more cost effectively across efforts. Adding more efforts $x_{ik}$ with lower contest intensities $0 < m_{ik} < 1$ allows the effort $x_{i1}$, $m_{i1} = 1$, to decrease, which decreases rent dissipation. This result is reminiscent of the well-known result [e.g. Hausken (2005) and the references therein] for single-effort rent dissipation which decreases as the contest intensity decreases. Rent dissipation $D$ increases in the unit effort cost $c_{ik}$, and the rent $S$. Arbatskaya and Mialon (2010) also find that additional efforts decrease rent dissipation, but only when the contest becomes more unbalanced (asymmetric), so that one player is advantaged. However, when the contest becomes more balanced contests, additional efforts tend to increase rent dissipation since they increase the contest’s discriminatory power defined as the sum of the contest intensities (equal for both players) across all efforts (both players have equally many efforts). Their result follows from multiplication of efforts in the contest success function. They thus find that sufficiently symmetric players prefer to eliminate additional efforts, but in equilibrium, they utilize the additional efforts.

4.3 One effort $K_{i} = 1$ against $K_{j} \ge 1$ efforts when $0 \le m_{i1} \le 1$ and $m_{j1} = 1,i,j = 1,2$,$i \ne j$

Different efforts may require different technologies, kinds of competence, and training. Some efforts may be unavailable for judicial reasons, because certificates are lacking, or fees have not been paid. Even if several efforts are available, a player may prefer one effort to avoid cognitive overload, to ensure simplicty, or due to various individual preferences. This section assumes that one player has available or chooses only one effort. Assume $K_{i} = 1$ without loss of generality. Thus, player ${i}$ chooses one effort $x_{i1}$. We thus seek replacements for Assumptions 1 and 2 that enable analytical solution as an alternative to the numerical solutions based on (6) and (7). We do not require $m_{i1} = 1$ for player $i$’s one and only effort, i.e. $0 \le m_{i1} \le 1$, but we do require $m_{j1} = 1$ for player $j$’s first effort $x_{i1}$, and furthermore, $0 \le m_{jk} < 1$ for player $j$’s other efforts to avoid division with zero. This gives

Assumption 3

$K_{i} = m_{j1} = 1,0 \le m_{i1} \le 1,0 \le m_{jk} < 1,k = 2, \ldots,K_{j}$, $i,j = 1,2,i \ne j$.

Hence, Assumption 3 is equivalent to Assumption 1 for player $j$, whereas for player $i$, we simply require $0 \le m_{i1} \le 1$ for its $K_{i} = 1$ effort. Inserting $m_{j1} = 1$ and $K_{i} = 1$ into (6) and (7) gives

$$\begin{aligned} x_{i1}^{{m_{i1}}} & = \frac{{S\frac{{c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}}}}{{c_{i1} \left({\frac{{x_{i1}^{{1 - m_{i1}}} c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}} + 1} \right)^{2}}}, \hfill \\ x_{j1} & = \frac{{S\frac{{x_{i1}^{{1 - m_{i1}}} c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}}}}{{c_{j1} \left({\frac{{x_{i1}^{{1 - m_{i1}}} c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}} + 1} \right)^{2}}} - \mathop \sum \limits_{k = 2}^{{K_{j}}} \frac{{d_{jk}}}{{d_{j1}}}\left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{jk}}}{{1 - m_{jk}}}}}, \hfill \\ x_{jk} & = \left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{1}{{1 - m_{jk}}}}},\quad k = 2, \ldots,K_{j},\;i,j = 1,2, i \ne j, \hfill \\ \end{aligned}$$

(11)

which simplifies to (8) when $m_{i1} = 1$.³ Inserting (11) and $K_{i} = m_{i1} = m_{j1} = 1$ into (2) and (3) yield

$$\begin{aligned} u_{i} & = \frac{S}{{\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}},u_{j} = \frac{{S\left({\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}}{{\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}} + \mathop \sum \limits_{k = 2}^{{K_{j}}} c_{jk} \left({\frac{1}{{m_{jk}}} - 1} \right)\left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{1}{{1 - m_{jk}}}}}, \hfill \\ D & = \frac{{2\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}}}{{\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}} - \frac{1}{S}\mathop \sum \limits_{k = 2}^{{K_{j}}} c_{jk} \left({\frac{1}{{m_{jk}}} - 1} \right)\left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{1}{{1 - m_{jk}}}}}. \hfill \\ \end{aligned}$$

(12)

Just as for (8) causing Assumption 2, (11) for $x_{j1}$ shows one positive term consisting of characteristics of the first efforts in the contest between players $i$ and $j$, and one negative term consisting of the characteristics of player $j$’s other efforts. The subtraction analogously illustrates how player $j$ cuts back on effort $x_{j1}$ if it can more cost effectively utilize its other efforts. As in Assumption 2, the subtraction cannot cause negative $x_{j1}$. This gives

Assumption 4

$x_{j1} > 0 \Leftrightarrow \frac{{S\frac{{x_{i1}^{{1 - m_{i1}}} c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}}}}{{c_{j1} \left({\frac{{x_{i1}^{{1 - m_{i1}}} c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}} + 1} \right)^{2}}} > \mathop \sum \limits_{k = 2}^{{K_{j}}} \frac{{d_{jk}}}{{d_{j1}}}\left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{jk}}}{{1 - m_{jk}}}}},i,j = 1,2, i \ne j$.

Summing up, Assumption 3 assumes that player $i$ has only one effort $x_{i1}$ with a contest intensity $m_{i1}$ weakly above zero and weakly below one, that player $j$’s effort $x_{j1}$ has contest intensity $m_{j1} = 1$, that player $j$’s $K_{j} - 1$ other efforts $x_{jk}$ have contest intensities $m_{jk}$ weakly above zero and strongly below one. Assumption 4 assumes that an interior solution exists, by requiring player $j$’s effort $x_{j1}$ to be positive, i.e. $x_{j1} > 0$. We next apply Assumptions 3 and 4 in Explanation 3 and Proposition 6.

Explanation 3

When Assumptions 3 and 4 are satisfied, an interior equilibrium solution is determined by (11). When $m_{i1} = 1$, $i = 1,2$, the players’ expected utilities $u_{i}$ and $u_{j}$ and rent dissipation $D$ are determined by (12). The corner solution is presented in “Appendix H”.

Proof

Follows from (11), (12), “Appendix C”. □

Proposition 6

When Assumptions 3 and 4 are satisfied, then $\frac{{\partial x_{i1}}}{{\partial K_{j}}} = \frac{{\partial x_{i1}}}{{\partial c_{jk}}} = \frac{{\partial x_{i1}}}{{\partial d_{jk}}} = 0,\frac{{\partial x_{i1}}}{\partial S} > 0$, $k = 2, \ldots,K_{j},i,j = 1,2, i \ne j$.

Proof

Follows from (11).

Proposition 6 states that player $i$’s single effort $x_{i1}$ does not depend on the number $K_{j}$ of efforts exerted by player $j$. Economically, player $i$, exerting only one effort $x_{i1}$, is concerned about the summed up efforts of player j, not how player $j$ chooses between its various efforts. This follows since player $j$ optimizes cost effectively across efforts so that $K_{j}$ does not impact player $i$.

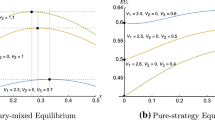
4.4 An example: maximum two efforts for each player

This section assumes $K_{i} \le 2,m_{i1} = 1,0 < m_{i2} < 1,i = 1,2.$ Maximum two efforts for each player can illustrate an interior solution and a corner solution. Inserting $K_{i} = 2$ and $x_{i1} = 0$ into (8) and solving with respect to $c_{i2}$ gives

$$c_{i2} = m_{i2} d_{i2} \frac{{c_{i1}}}{{d_{i1}}}\left({\frac{{d_{i2} \left({c_{i1}/d_{i1} + c_{j1}/d_{j1}} \right)^{2}}}{{Sc_{j1}/d_{j1}}}} \right)^{{\frac{{1 - m_{i2}}}{{m_{i2}}}}},\quad i,j = 1,2, i \ne j.$$

(13)

Figure 1 assumes $c_{i1} = c_{j1} = d_{i1} = d_{j1} = d_{i2} = d_{j2} = m_{i1} = m_{j1} = 1$ and $S = 10$ and plots $c_{i2} = c_{j2}$ as a function of $m_{i2} = m_{j2}$ when $x_{i1} = x_{j1} = 0$.

Fig. 1

Regions for the interior solution $x_{i1} = x_{j1} > 0$ and corner solution $x_{i1} = x_{j1} = 0$ separated by plotting $c_{i2} = c_{j2}$ as a function of $m_{i2} = m_{j2}$ according to (13)

Above and to the left of the convex curve the unit costs $c_{i2} = c_{j2}$ of efforts $x_{i2}$ and $x_{j2}$ are sufficiently high, and the contest intensities $m_{i2} = m_{j2}$ are sufficiently low, making it worthwhile for the players to exert the efforts $x_{i1}$ and $x_{j1}$ additionally in an interior solution. Conversely, below and to the right of the convex curve, the corner solution $x_{i1} = x_{j1} = 0$ applies.

Aside from $c_{i1}$ which varies, Fig. 2 makes the same assumptions as in Fig. 1, i.e. $c_{j1} = d_{i1} = d_{j1} = d_{i2} = d_{j2} = m_{i1} = m_{j1} = 1$ and $S = 10$. Additionally, Fig. 2 assumes $c_{i2} = c_{j2} = 1$ and $m_{i2} = m_{j2} = 0.5$. Figure 2 plots the players’ efforts $x_{i1},x_{i2},x_{j1},x_{j2},$ etc. and expected utilities $u_{i},u_{j}$, etc. as functions of player $i$’s unit cost $c_{i1}$ of effort $x_{i1}$.

Fig. 2

Efforts $x_{i1},x_{i2},x_{j1},x_{j2}$, etc. and expected utilities $u_{i},u_{j}$, etc. as functions of $c_{i1}$ when $c_{j1} = c_{i2} = c_{j2} = d_{i1} = d_{j1} = d_{i2} = d_{j2} = m_{i1} = m_{j1} = 1$, $m_{i2} = m_{j2} = 0.5$, $S = 10$

Player $i$’s effort $x_{i1}$ decreases as its unit effort cost $c_{i1}$ increases ($\frac{{\partial x_{i1}}}{{\partial c_{i1}}} < 0$ in Proposition 1) eventually reaching zero when $c_{i1} = 2.09$. Player $i$ cannot afford the high unit effort cost. This gives the corner solution $x_{i1} = 0$ when $c_{i1} > 2.09$. Conversely, player $i$’s effort $x_{i2}$ increases as $c_{i1}$ increases ($\frac{{\partial x_{i2}}}{{\partial c_{i1}}} > 0$ in Proposition 2). Player $i$’s expected utility $u_{i}$ decreases convexly to 2.14 as $c_{i1}$ increases to $2.09$, while player $j$’s expected utility $u_{j}$ increases to 4.83. When $c_{i1}$ is low, to the advantage of player $i$, the first term in the expression for player $j$’s effort $x_{j1}$ in (8) is low and cannot compensate for the negative second term. The given parameter values cause the corner solution $x_{j1} = 0$ when $c_{i1} < 0.06$.

Table 1 applies (4) to illustrate Nash equilibrium determination, by presenting a $3 \times 3$ matrix accounting for each player’s three possibilities. That is, player $i$ can choose two efforts $x_{i1}$ and $x_{i2}$ where $m_{i1} = 1$ and $m_{i2} = 1/2$, one effort $x_{i1}$ where $m_{i1} = 1$, or one effort $x_{i2}$ where $m_{i2} = 1/2$. Analogously, player $j$ can choose two efforts $x_{j1}$ and $x_{j2}$ where $m_{j1} = 1$ and $m_{j2} = 1/2$, one effort $x_{j1}$ where $m_{j1} = 1$, or one effort $x_{j2}$ where $m_{j2} = 1/2$.

Table 1 $3 \times 3$ matrix for the players’ efforts $x_{i1},x_{i2},x_{j1},x_{j2}, etc.$ and expected utilities $u_{i},u_{j}$, etc

$\frac{{\partial u_{i}}}{{\partial K_{i}}} > 0$ and $\frac{{\partial u_{j}}}{{\partial K_{j}}} > 0$ in Proposition 4 and (9) in Sect. 4.2 imply that each player prefers the second effort in addition to the first effort when the first effort has contest intensity $m_{i1} = m_{j1} = 1$. Thus, $u_{i}$ > $u_{i1s}$ and $u_{j}$ > $u_{j1s}$ in Fig. 2. Each player’s second effort as a single effort is not covered by Sect. 4.2 since $m_{i2} = 1/2$ or $m_{j2} = 1/2$. Player $i$’s second effort as a single effort against player $j$ exerting both efforts is expressed as $x_{i2sd}$ shown in the lower left cell in Table 1. The first subscript s means “single effort” by player $i$. The second subscript d means “double effort” by player $j$. Player $i$’s second effort as a single effort against player $j$ exerting only the first effort is expressed as $x_{i2ss}$ shown in the lower middle cell in Table 1. Proposition 5 implies $x_{i2sd} = x_{i2ss}$, and $x_{j2sd} = x_{j2ss}$ which is player $j$’s second effort as a single effort against player $i$ exerting both efforts or only the first effort.

An expected utility shown in bold in Table 1 means that this expected utility is highest for at least one value of $c_{i1}$. When both expected utilities are in bold within a given cell in Table 1 for the same value of $c_{i1}$, then the two expected utilities are Nash equilibrium expected utilities as defined in (4).

For the intermediate range $0.44 \le c_{i1} \le 1.55$ in Fig. 2, $\left({\varvec{u}_{\varvec{i}},\varvec{u}_{\varvec{j}}} \right)$ is the equilibrium which means that both players choose both efforts. For the upper range $1.55 \le c_{i1} \le 2.09$, the high unit effort cost $c_{i1}$ makes effort $x_{i1}$ too costly for player $i$ which prefers only the second single effort $x_{i2sd}$ with low contest intensity $m_{i2} = 1/2$. Player $j$ still prefers both efforts causing the equilibrium $\left({\varvec{u}_{{\varvec{isd}}},\varvec{u}_{{\varvec{jds}}}} \right)$. Conversely, for the lower range $0.06 \le c_{i1} \le 0.44$, the low unit effort cost $c_{i1}$ makes player $i$ advantaged. Player $j$ can no longer compete cost effectively with both efforts, and settles for the single second effort $x_{j2sd}$ with low contest intensity $m_{j2} = 1/2$. This causes the equilibrium $\left({\varvec{u}_{{\varvec{ids}}},\varvec{u}_{{\varvec{jsd}}}} \right)$.

Between the two dashed vertical lines in Fig. 2, $0.66 \le c_{i1} \le 1.45$, the players collectively prefer to exert only their second efforts $x_{i2s}$ and $x_{j2s}$ as single efforts causing $(u_{i2s},u_{j2s})$, in the lower right cell in Table 1, which is not an equilibrium. For it to arise, coordination is needed. Two examples are “burning one’s bridges in war” (Schelling 1960) or mutually agreeing on low intensity interaction with $m_{i2} = m_{j2} = 1/2$.

4.5 Equal contest intensities $m_{ik} = m_{i}$ and $m_{ik} = m$ across efforts and players

“Appendix I” shows that inserting equal contest intensities $0 \le m_{ik} = m_{i} < 1$ across efforts for player $i$, $i = 1,2$, $k = 1,2, \ldots,K_{i}$, into (7) causes one equation with one unknown $x_{j1}$ for player $j$ expressed on implicit form, from which $x_{i1}$ for player $i$ follows on explicit form. “Appendix I” further shows that inserting the same contest intensity $0 \le m_{ik} = m < 1$, $k = 1,2, \ldots,K_{i}$, for both players $i = 1,2$ across all their $K_{i}$ efforts into (6) and (7) causes the explicit form solution

$$\begin{aligned} x_{j1}& = \frac{Sm}{{Q_{i}^{m} \frac{{c_{j1}}}{{d_{j1}}}\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}Q_{i}^{1 - m}} \right)^{2} V_{i}}}, x_{i1} = Q_{i} x_{j1}, \hfill \\ Q_{i} & = \frac{{V_{j} c_{j1}/d_{j1}}}{{V_{i} c_{i1}/d_{i1}}},V_{i} \equiv \mathop \sum \limits_{k = 1}^{{K_{i}}} d_{ik} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{m}{1 - m}}}, \hfill \\ V_{j} & \equiv \mathop \sum \limits_{k = 1}^{{K_{j}}} d_{jk} \left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{m}{1 - m}}},x_{ik} = x_{i1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}},\quad k = 2, \ldots,K_{i}, \hfill \\ \end{aligned}$$

(14)

which is inserted into (2) and (3) to yield player $i$’s expected utility

$$u_{i} = \frac{{S\left({1 + \left({1 - m} \right)\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}Q_{i}^{1 - m}} \right)}}{{\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}Q_{i}^{1 - m}} \right)^{2}}},$$

(15)

and rent dissipation

$$D = m\mathop \sum \limits_{i = 1}^{2} \frac{{\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}Q_{i}^{1 - m}}}{{\left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}Q_{i}^{1 - m}} \right)^{2}}},\quad i,j = 1,2,i \ne j.$$

(16)

Differentiating (5), player $i$’s second-order condition if $m_{ik} \ne 0$ and $d_{ik} \ne 0$ is

$$\frac{{{\partial ^2}{u_i}}}{{\partial x_{ik}^2}} = \frac{{Sm{d_{ik}}x_{ik}^{m - 2}\left( {\left( {m - 1} \right)\left( {\mathop \sum \nolimits_{k = 1}^{{K_i}} {d_{ik}}x_{ik}^m + \mathop \sum \nolimits_{k = 1}^{{K_j}} {d_{jk}}x_{jk}^m} \right) - 2{d_{ik}}x_{ik}^m} \right)\mathop \sum \nolimits_{k = 1}^{{K_j}} {d_{jk}}x_{jk}^m}}{{{{\left( {\mathop \sum \nolimits_{k = 1}^{{K_i}} {d_{ik}}x_{ik}^m + \mathop \sum \nolimits_{k = 1}^{{K_j}} {d_{jk}}x_{jk}^m} \right)}^3}}},$$

(17)

which is satisfied as negative since m < 1.

Proposition 7

When $0 \le m_{ik} = m < 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$, then $\frac{{\partial x_{i1}}}{{\partial c_{i1}}} < 0, \frac{{\partial x_{i1}}}{{\partial c_{ik}}} > 0,\frac{{\partial x_{i1}}}{{\partial d_{ik}}} < 0, \frac{{\partial x_{i1}}}{\partial S} > 0$, $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$.

Proof

Appendix J.

The four inequalities in Proposition 7 confirm the same inequalities in Proposition 1, where the contest intensity $m_{ik}$ varies across players and efforts. This emphasizes the robustness of the results.

Proposition 8

When $0 \le m_{ik} = m < 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$, then $\frac{{\partial x_{ik}}}{{\partial c_{ik}}} < 0,\frac{{\partial x_{ik}}}{{\partial c_{i1}}} > 0,\frac{{\partial x_{ik}}}{{\partial d_{i1}}} < 0, \frac{{\partial x_{ik}}}{\partial S} > 0$, $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$.

Proof

Appendix J.

The first three inequalities in Proposition 8 confirm the same inequalities in Proposition 2. The inequality $\frac{{\partial x_{ik}}}{{\partial d_{ik}}} > 0$ holds when the condition in (61) in “Appendix J” holds. The inequality $\frac{{\partial x_{ik}}}{\partial S} > 0$ differs from $\frac{{\partial x_{ik}}}{\partial S} = 0$ in Proposition 2 since $m_{i1} = 1$ causes $x_{ik}$ to be independent of $x_{i1}$ in (6) and (8), but not in (14).

Proposition 9

The efforts $x_{ik}$ and $x_{i1}$,$k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$, can be substitutes due to variation in the parameter $\alpha$ when $\frac{{\partial x_{ik}}}{\partial \alpha} > 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} < 0$, or $\frac{{\partial x_{ik}}}{\partial \alpha} < 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} > 0$; and can be complements due to variation in the parameter $\alpha$ when $\frac{{\partial x_{ik}}}{\partial \alpha} > 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} > 0$, or $\frac{{\partial x_{ik}}}{\partial \alpha} < 0$ and $\frac{{\partial x_{i1}}}{\partial \alpha} < 0$; where $\alpha = c_{i1},c_{j1},d_{i1},d_{j1},c_{ik},c_{jk},d_{ik},d_{jk},S.$

Proof

Whether $x_{ik}$ and $x_{i1}$ in Proposition 9 are substitutes or complements, follows from the signs of the derivatives in “Appendix J”. The opposite signs $\frac{{\partial x_{ik}}}{{\partial c_{i1}}} > 0$ and $\frac{{\partial x_{i1}}}{{\partial c_{i1}}} < 0$, opposite signs $\frac{{\partial x_{ik}}}{{\partial d_{ik}}} > 0$ (when the condition in (61) in “Appendix J” holds) and $\frac{{\partial x_{i1}}}{{\partial d_{ik}}} < 0$, and opposite signs $\frac{{\partial x_{ik}}}{{\partial c_{ik}}} < 0$ and $\frac{{\partial x_{i1}}}{{\partial c_{ik}}} > 0$, imply that $x_{ik}$ and $x_{i1}$ can be substitutes for each other. Whereas $\frac{{\partial x_{ik}}}{{\partial d_{i1}}} < 0$, (60) in “Appendix J” specifies the parameter values when $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} < 0$ which causes $x_{ik}$ and $x_{i1}$ to be substitutes, and when $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} > 0$ which causes $x_{ik}$ and $x_{i1}$ to be complements. □

Proposition 9 confirms the finding in Proposition 3 that the efforts $x_{ik}$ and $x_{i1}$, $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j,$ can be substitutes or complements to each other.

Proposition 10

When $0 \le m_{ik} = m < 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$, then $\frac{{\partial u_{i}}}{{\partial c_{i1}}} < 0$, $\frac{{\partial u_{i}}}{{\partial c_{j1}}} > 0$, $\frac{{\partial u_{i}}}{{\partial c_{ik}}} < 0$, $\frac{{\partial u_{i}}}{{\partial c_{jk}}} > 0$, $\frac{{\partial u_{i}}}{{\partial d_{i1}}} > 0$, $\frac{{\partial u_{i}}}{{\partial d_{j1}}} < 0$, $\frac{{\partial u_{i}}}{{\partial d_{ik}}} > 0$, $\frac{{\partial u_{i}}}{{\partial d_{jk}}} < 0$, $\frac{{\partial u_{i}}}{\partial S} > 0,$$k = 2, \ldots,K_{i},i = 1,2$.

Proof

Appendix J.

Proposition 10 confirms the two inequalities $\frac{{\partial u_{i}}}{{\partial c_{ik}}} < 0$ and $\frac{{\partial u_{i}}}{{\partial d_{ik}}} > 0$ in Proposition 4, where player $i$’s expected utility $u_{i}$ increases in the impact $d_{ik}$, and decreases in the unit cost $c_{ik}$, of effort $x_{ik}$. More generally, in Proposition 10 $u_{i}$ also increases in the impact $d_{i1}$, and decreases in the unit cost $c_{i1}$, of effort $x_{i1}$. Furthermore, and conversely, player $i$’s $u_{i}$ decreases in the impacts $d_{jk}$ and $d_{j1}$, and increases in the unit costs $c_{jk}$ and $c_{j1}$, of efforts $x_{jk}$ and $x_{j1}$ for player $j$. These results follow since $u_{i}$ in (15), where $m_{ik} = m < 1 \; \forall \; k$, is analytically more straightforward than $u_{i}$ in (9).

4.6 Exemplifying the sensitivity of assuming $m_{i1} = 1$ in Sect. 4.2, $i,j = 1,2$,$i \ne j$

The benchmark contest intensity in the rent seeking literature is $m_{ik} = 1$$\forall \; k = 1, \ldots,K_{i}$, $i = 1,2$. Generally, players have different contest intensities, and player $i$ may have different contest intensities for its $K_{i}$ efforts. Given that player $i$ has different contest intensities for its $K_{i}$ efforts, it may be plausible that one of these efforts is close to one, or can be approximated to be close to one. Without loss of generality, we assume that $m_{i1} = 1$ for player $i$’s effort $x_{i1}$, $i = 1,2$. To the extent $m_{i1} = 1$ is not plausible, the analytical solution in the previous Sect. 4.5 for equal contest intensities $0 \le m_{ik} = m < 1$, which can be much lower than $m_{ik} = m$, can be used as an approximation. Alternatively, if the contest intensities are larger than one, i.e. $m_{ik} \ge 1,k = 1, \ldots,K_{i}$, $i = 1,2$, the analytical solution in the next Sect. 5 applies.

Since only $m_{i1} = 1$ in Sect. 4.2, while $0 \le m_{ik} < 1,\; \forall \; k = 2, \ldots,K_{i}$, $i = 1,2$, player $i$ exerts more than one effort, in contrast to $m_{ik} \ge 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$, where player $i$ exerts only one effort, as shown in the next section. To assess the sensitivity of assuming $m_{i1} = 1$ for effort $x_{i1}$, let us assume $m_{ik} = m$ for all the other efforts $x_{ik}$, $\forall \; k = 2, \ldots,K_{i}$, for both players $i = 1,2$. Furthermore, to focus solely on the sensitivity of $m$, assume that both players have equally many efforts $K_{i} = K$, and the same unit cost $c_{ik} = c$ and impact $d_{ik} = d$ for all their efforts, $\forall \; k = 1, \ldots,K_{i}$, $i = 1,2$. This is assumed since $\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}$ has straightforward impact on $x_{ik}$ in (8), and $\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}} = 1$ implies $x_{ik} = m^{{\frac{1}{1 - m}}}$ in (8). Inserting into (8), (9), (10) gives$x_{i1}$, $x_{ik}$, $u_{i}$ and $D$ in the middle column in Table 2. As comparison, replacing $m_{i1} = 1$ with $m_{i1} = m$, and otherwise inserting the same parameter values $m_{ik} = m$$\forall \; k = 2, \ldots,K_{i}$, $K_{i} = K$, $c_{ik} = c$, $d_{ik} = d$, $i = 1,2$, into (14), (15), (16) gives the right column in Table 2.

Table 2 Comparing $x_{i1}$, $x_{ik}$, $u_{i}$ and $D$ when $m_{i1} = 1$ (middle column) and $m_{i1} = m$ (right column), $m_{ik} = m$$\forall \; k = 2, \ldots,K_{i}$, $K_{i} = K$, $c_{ik} = c$, $d_{ik} = d$, $i = 1,2$

The right column in Table 2, assuming the same contest intensity $m$ for all the $K$ efforts for both players, shows how each effort $x_{i1} = x_{ik}$ increases in the contest intensity $m$ and rent $S$, and decreases in the number $K$ of efforts and the unit effort cost $c$. Furthermore, player $i$’s expected utility $u_{i}$ decreases in $m$ and increases in $S$, while the rent dissipation $D$ increases in $m$. In contrast, when $m_{i1} = 1$ in the middle column, player $i$’s effort $x_{i1}$ increases in the rent $S$ and decreases in the unit cost $c$ (due to the positive term $\frac{S}{4c})$, decreases in the number $K - 1$ of other efforts, and increases in the contest intensity $m$ for these other efforts (due to the negative term $\left({K - 1} \right)m^{{\frac{m}{1 - m}}} = \frac{{\left({K - 1} \right)}}{m}x_{ik}$). That is, higher $m$ causes not only higher effort $x_{ik}$ for the $K - 1$ other efforts, but also higher effort $x_{i1}$. This also follows from Lemma 2 in “Appendix F” where $\frac{{\partial x_{i1}}}{{\partial m_{ik}}} > 0 \text{ if }\ln \left({m_{ik}} \right) < m_{ik} - 1$. The right column and middle column in Table 2 are equivalent when $K = m_{i1} = 1$, i.e. $x_{i1} = \frac{S}{4c}$, $u_{i} = \frac{S}{4}$, $D = \frac{1}{2}$.

Figure 3 plots $x_{i1}$, $x_{ik}$, $u_{i}$ and $D$ as functions of the contest intensity $m$ when $m_{i1} = 1$ (filled symbols) and $m_{i1} = m$ (unfilled symbols), $m_{ik} = m$$\forall \; k = 2, \ldots,K_{i}$, $K_{i} = K$, $c_{ik} = c$, $d_{ik} = d$, $i = 1,2$. The rent is $S = 4$ and each player’s unit effort cost is $c = 1$. Division of the expected utility $u_{i}$ with 4, $u_{i}/4$, is for scaling purposes. Panel a assumes $K = 2$ efforts for each player. When $m_{i1} = 1$, as the contest intensity decreases from $m = 1$ to $m = 0$, player $i$’s first effort $x_{i1}$ decreases concavely from $x_{i1} = 0.63$ to $x_{i1} = 0$, while its second effort $x_{i2}$ decreases concavely from $x_{i2} = 0.37$ to $x_{i2} = 0$. These two efforts when $m = 1$ sum to $x_{i1,m = 1} + x_{i2,m = 1} = 1$, which also is player $i$’s effort when $K = 1$. As the contest intensity decreases from $m = 1$ to $m = 0$, player $i$’s expected utility increases convexly from $u_{i} = 1$ to $u_{i} = 2$, while the rent dissipation decreases concavely from $D = 0.5$ to $D = 0$. When $m_{i1} = m_{i2} = m$, applying the right column in Table 2, Fig. 3 panel a shows, as the contest intensity decreases from $m = 1$ to $m = 0$, that player $i$’s two efforts, and the rent dissipation, decrease linearly from $x_{i1} = x_{i2} = D = 0.5$ to $x_{i1} = x_{i2} = D = 0$, while its expected utility increases linearly from $u_{i} = 1$ to $u_{i} = 2$. These two efforts when $m = 1$ also sum to $x_{i1,m = 1} + x_{i2,m = 1} = 1$.

Fig. 3

$x_{i1}$, $x_{ik}$, $u_{i}$ and $D$ when $m_{i1} = 1$ (filled symbols) and $m_{i1} = m$ (unfilled symbols), $m_{ik} = m$$\forall \; k = 2, \ldots,K_{i}$, $K_{i} = K$, $c_{ik} = c$, $d_{ik} = d$, $i = 1,2$, $S = 4$, $c = 1$. Panel a $K = 2$. Panel b $K = 3$

Figure 3 panel b increases player $i$’s number of efforts to $K = 3$. When $m_{i1} = 1$, that causes the negative term impacting player $i$’s first effort $x_{i1}$ in (8) to be higher in absolute value, so that more is subtracted from $\frac{S}{4c}$. Hence, $x_{i1}$ is lower in panel b than in panel a. As the contest intensity decreases from $m = 1$ to $m = 0.5$, player $i$’s first effort $x_{i1}$ decreases concavely from $x_{i1} = 0.26$ to $x_{i1} = 0$, while its second and third efforts $x_{i2} = x_{i3}$ decrease concavely from $x_{i2} = x_{i3} = 0.37$ to $x_{i2} = x_{i3} = 0.25$, which $x_{i2}$ also does in panel a, in accordance with Table 2. These three efforts when $m = 1$ also sum to $x_{i1,m = 1} + x_{i2,m = 1} + x_{i3,m = 1} = 1$. As the contest intensity decreases from $m = 1$ to $m = 0.5$, player $i$’s expected utility increases convexly from $u_{i} = 1$ to $u_{i} = 1.5$, while the rent dissipation decreases concavely from $D = 0.5$ to $D = 0.25$. As $m$ decreases below $m = 0.5$, Assumption 2 is no longer satisfied, as $x_{i1}$ in (8) would be negative. Hence, a corner solution applies where $x_{i1} = 0$, and $x_{i2}$ and $x_{i3}$ are determined in a model with $K = 2$ efforts. Applying the right column in Table 2 for $K = 2$, these two efforts are $x_{i2} = x_{i3} = \frac{m}{2}$. Hence, as the contest intensity decreases from $m = 0.5$ to $m = 0$, player $i$’s second and third efforts $x_{i2} = x_{i3}$ decrease linearly from $x_{i2} = x_{i3} = 0.25$ to $x_{i2} = x_{i3} = 0$, while its expected utility increases linearly from $u_{i} = 1.5$ to $u_{i} = 2$, and the rent dissipation decreases linearly from $D = 0.25$ to $D = 0$. When $m_{i1} = m_{i2} = m$, Fig. 3b shows, as the contest intensity decreases from $m = 1$ to $m = 0$, that player $i$’s three efforts decrease linearly from $x_{i1} = x_{i2} = x_{i3} = 0.33$ to $x_{i1} = x_{i2} = x_{i3} = 0$. As in panel a, player $i$’s expected utility increases linearly from $u_{i} = 1$ to $u_{i} = 2$, and the rent dissipation decreases linearly from $D = 0.5$ to $D = 0$.

5 Solution when $\varvec{m}_{{\varvec{ik}}} \ge 1 \forall \varvec{k} = 1, \ldots,\varvec{K}_{\varvec{i}}$, $\varvec{i} = 1,2$

Section 5.1 provides the general solution. Section 5.2 assumes equal contest intensities for players $i$ and $j$.

5.1 General solution

When $m_{ik} > 1,k = 1, \ldots,K_{i}$, $i = 1,2$, player $i$’s production $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}$ across its $K_{i}$ efforts is convex in each effort $x_{ik}$. Since the marginal utility thus increases in each effort $x_{ik}$, higher effort $x_{ik}$ for each $k$ has higher impact on player $i$’s probability $p_{i}$ of winning the rent $S$. Hence, player $i$ will choose one positive effort $x_{i\kappa \left(i \right)} > 0$, $\kappa \left(i \right) = 1, \ldots,K_{i}$, where the impact on winning the rent $S$ is highest, and choose zero effort for all the other $K_{i}$ efforts, i.e. $x_{ik} = 0$ for $k \ne \kappa \left(i \right)$, $k = 1, \ldots,K_{i}$, which also can be written as $k = 1, \ldots,\kappa \left(i \right) - 1,\kappa \left(i \right) + 1, \ldots,K_{i}$ Define $\kappa \left(i \right)$, $\kappa \left(i \right) = 1, \ldots,K_{i}$, as the one effort player $i$ chooses to exert. The $\kappa \left(i \right)$ is chosen so that $\kappa (i) = \mathop{\text{argmax}}\nolimits_{{\kappa (i) = 1, \ldots,K_{i}}} \left({d_{i1} x_{i1}^{{m_{i1}}},d_{i2} x_{i2}^{{m_{i2}}}, \ldots,d_{{iK_{i}}} x_{{iK_{i}}}^{{m_{{iK_{i}}}}}} \right)$, which depends on $c_{ik}$, $d_{ik}$,$m_{ik}$, and the other parameters. Hence, $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}$ simplifies to $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}} = d_{i\kappa \left(i \right)} x_{i\kappa \left(i \right)}^{{m_{i\kappa \left(i \right)}}}$, which is inserted into (5) to yield the two first-order conditions

$$\begin{aligned} \frac{{Sd_{j\kappa \left(j \right)} x_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}}}{{\left({d_{i\kappa \left(i \right)} x_{i\kappa \left(i \right)}^{{m_{i\kappa \left(i \right)}}} + d_{j\kappa \left(j \right)} x_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}} \right)^{2}}} = \frac{{c_{i\kappa \left(i \right)}}}{{m_{i\kappa \left(i \right)} d_{i\kappa \left(i \right)} x_{i\kappa \left(i \right)}^{{m_{i\kappa \left(i \right)} - 1}}}}, \hfill \\ \frac{{Sd_{i\kappa \left(i \right)} x_{i\kappa \left(i \right)}^{{m_{i\kappa \left(i \right)}}}}}{{\left({d_{i\kappa \left(i \right)} x_{i\kappa \left(i \right)}^{{m_{i\kappa \left(i \right)}}} + d_{j\kappa \left(j \right)} x_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}} \right)^{2}}} = \frac{{c_{j\kappa \left(j \right)}}}{{m_{j\kappa \left(j \right)} d_{j\kappa \left(j \right)} x_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)} - 1}}}}, \hfill \\ \end{aligned}$$

(18)

for the two players $i$ and $j$. Solving (18) gives

$$\begin{aligned} x_{i\kappa \left(i \right)}& = \frac{{m_{i\kappa \left(i \right)} c_{j\kappa \left(j \right)}}}{{m_{j\kappa \left(j \right)} c_{i\kappa \left(i \right)}}}x_{j\kappa \left(j \right)}, \hfill \\ x_{j\kappa \left(j \right)}^{{1 + m_{j\kappa \left(j \right)} - m_{i\kappa \left(i \right)}}} & = \frac{{Sm_{i\kappa \left(i \right)} \left({\frac{{m_{j\kappa \left(j \right)} c_{i\kappa \left(i \right)}}}{{m_{i\kappa \left(i \right)} c_{j\kappa \left(j \right)}}}} \right)^{{m_{i\kappa \left(i \right)} + 1}} \frac{{d_{j\kappa \left(j \right)}}}{{d_{i\kappa \left(i \right)}}}}}{{c_{i\kappa \left(i \right)} \left({x_{j\kappa \left(j \right)}^{{m_{i\kappa \left(i \right)} - m_{j\kappa \left(j \right)}}} + \left({\frac{{m_{j\kappa \left(j \right)} c_{i\kappa \left(i \right)}}}{{m_{i\kappa \left(i \right)} c_{j\kappa \left(j \right)}}}} \right)^{{m_{i\kappa \left(i \right)}}} \frac{{d_{j\kappa \left(j \right)}}}{{d_{i\kappa \left(i \right)}}}} \right)^{2}}}, \hfill \\ x_{ik} & = 0\quad {\text{for }}k \ne \kappa \left(i \right), k = 1, \ldots,K_{i}; x_{jk} = 0\;\; \text{for }k \ne \kappa \left(j \right),k = 1, \ldots,K_{j}, \hfill \\ \end{aligned}$$

(19)

where $x_{i\kappa \left(i \right)}$ appears on explicit form as a function of $x_{j\kappa\left(j \right)}$, and $x_{j\kappa\left(j \right)}$ appears on implicit form. To identify the optimal effort $x_{j\kappa\left(j \right)}$, player $j$ determines its $x_{j\kappa\left(j \right)}$ numerically for all the $K_{j}$ efforts, and uses $\kappa \left(j \right) = \mathop {\text{argmax}}\nolimits_{{\kappa \left(j \right) = 1, \ldots,K_{j}}} \left({d_{j1} x_{j1}^{{m_{j1}}},d_{j2} x_{j2}^{{m_{j2}}}, \ldots,d_{{jK_{j}}} x_{{jK_{j}}}^{{m_{{jK_{j}}}}}} \right)$. Analogously, player $i$ uses (19) to determine its $x_{i\kappa \left(i \right)}$ numerically for all the $K_{i}$ efforts, and uses $\kappa \left(i \right) = \mathop {\text{argmax}}\nolimits_{{\kappa \left(i \right) = 1, \ldots,K_{i}}} \left({d_{i1} x_{i1}^{{m_{i1}}},d_{i2} x_{i2}^{{m_{i2}}}, \ldots,d_{{iK_{i}}} x_{{iK_{i}}}^{{m_{{iK_{i}}}}}} \right)$.

5.2 Equal contest intensities for players $i$ and $j$

Let us illustrate for equal contest intensities $m_{i\kappa \left(i \right)} = m_{j\kappa \left(j \right)}$ for players $i$ and $j$, which enables expressing $x_{j\kappa \left(j \right)}$ in (19) on explicit form, i.e.

$$\begin{aligned} x_{i\kappa \left(i \right)} & = \frac{{c_{j\kappa \left(j \right)}}}{{c_{i\kappa \left(i \right)}}}x_{j\kappa \left(j \right)},x_{j\kappa \left(j \right)} = \frac{{Sm_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}}}{{c_{j\kappa \left(j \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{2}}}, \hfill \\ x_{ik}& = 0\quad {\text{for }}k \ne \kappa \left(i \right), k = 1, \ldots,K_{i}; x_{jk} = 0 \,for \,k \ne \kappa \left(j \right),k = 1, \ldots,K_{j}. \hfill \\ \end{aligned}$$

(20)

Inserting (20) into (2) and (3), player $i$’s expected utility is

$$u_{i} = \frac{{S\left({1 + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{\left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{2}}},$$

(21)

and the rent dissipation is

$$D = \frac{{2m_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}}}{{\left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{2}}}.$$

(22)

Differentiating (5) and inserting (20), player $i$’s second-order condition if $m_{ik} \ne 0$ and $d_{ik} \ne 0$ is

$$\frac{{\partial^{2} u_{i}}}{{\partial x_{i\kappa \left(i \right)}^{2}}} = - \frac{{Sm_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)} + 2}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)} + 2}}/d_{j\kappa \left(j \right)}}}\left({1 + m_{j\kappa \left(j \right)} + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{x_{j\kappa \left(j \right)}^{2} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}.$$

(23)

Requiring that player $i$’s expected utility in (21) is positive, $u_{i} \ge 0$, and that player $i$’s second-order condition in (23) is negative, $\frac{{\partial^{2} u_{i}}}{{\partial x_{ik}^{2}}} \le 0$, imply that the solution in (20) is valid when Assumption 5 is satisfied.

Assumption 5

$$m_{i\kappa \left(i \right)} = m_{j\kappa \left(j \right)} \ge 1,$$

$$1 + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} \ge 0,$$

$$1 + m_{j\kappa \left(j \right)} + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} \ge 0,$$

$$\kappa \left(i \right) = \mathop {\text{argmax}}\limits_{{\kappa \left(i \right) = 1, \ldots,K_{i}}} \left({d_{i1} x_{i1}^{{m_{i1}}},d_{i2} x_{i2}^{{m_{i2}}}, \ldots,d_{{iK_{i}}} x_{{iK_{i}}}^{{m_{{iK_{i}}}}}} \right),$$

$$\kappa \left(j \right) = \mathop {\text{argmax}}\limits_{{\kappa \left(j \right) = 1, \ldots,K_{j}}} \left({d_{j1} x_{j1}^{{m_{j1}}},d_{j2} x_{j2}^{{m_{j2}}}, \ldots,d_{{jK_{j}}} x_{{jK_{j}}}^{{m_{{jK_{j}}}}}} \right),\quad i,j = 1,2, i \ne j.$$

The solution in (20), (21), (22), which applies when the three inequalities in Assumption 5 are satisfied, is equivalent to the solution in “Appendix B” for one effort $K_{i} = 1$ by player $i$ against one effort $K_{j} = 1$ by player $j$, $i,j = 1,2, i \ne j$. The two differences are that in “Appendix B”, each player $i$ has only one available effort, $K_{i} = 1$, $i = 1,2$, and $m_{i1} = m_{j1} \ge 1$ is not required.

When $m_{i\kappa \left(i \right)} = m_{j\kappa \left(j \right)} = 1$, Eqs. (20), (21), (22) are equivalent to Hausken’s (2020) Eqs. (6), (7), (10), respectively. Then the requirement $\kappa \left(i \right) = \mathop {\text{argmax}}\nolimits_{{\kappa \left(i \right) = 1, \ldots,K_{i}}} \left({d_{i1} x_{i1}^{{m_{i1}}},d_{i2} x_{i2}^{{m_{i2}}}, \ldots,d_{{iK_{i}}} x_{{iK_{i}}}^{{m_{{iK_{i}}}}}} \right)$ simplifies to $d_{i\kappa \left(i \right)}/c_{i\kappa \left(i \right)} = \mathop {\max}\nolimits_{{i = 1, \ldots,K_{i}}} \left({d_{i1}/c_{i1},d_{i2}/c_{i2}, \ldots,d_{{iK_{i}}}/c_{{iK_{i}}}} \right)$, which is equivalent to Hausken’s (2020) Eq. (9), which identifies the one optimal effort $x_{i\kappa \left(i \right)}$ player $i$ exerts when $m_{i\kappa \left(i \right)} = m_{j\kappa \left(j \right)} = 1$.

Proposition 11

Assume that Assumption 5 is satisfied. $\partial x_{i\kappa \left(i \right)}/\partial \left({c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}} \right) < 0$, $\partial u_{i}/\partial \left({c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}} \right) < 0$. If $c_{i\kappa \left(i \right)}/d_{i\kappa \left(i \right)} > c_{j\kappa \left(j \right)}/d_{j\kappa \left(j \right)}$, then $\partial x_{i\kappa \left(i \right)}/\partial \left({c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}} \right) > 0$ and $\partial u_{i}/\partial \left({c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}} \right) > 0$, and $\partial D/\partial \left({c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}} \right) < 0$, $i,j = 1,2, i \ne j$.

Proof

Hausken’s (2020) Appendix A.

Proposition 11 states that player $i$’s effort $x_{i\kappa \left(i \right)}$ and expected utility $u_{i}$ decrease as player $i$ becomes disadvantaged with a higher ratio $c_{i\kappa \left(i \right)}/d_{i\kappa \left(i \right)}$ of unit effort cost divided by the scaling parameter $d_{i\kappa \left(i \right)}$ for player $i$’s impact on the contest with player $j$. Player $i$’s effort $x_{i\kappa \left(i \right)}$ thus becomes less worthwhile, and it earns lower expected utility $u_{i}$. Furthermore, if player $i$ is disadvantaged with a higher unit cost to impact ratio $c_{i\kappa \left(i \right)}/d_{i\kappa \left(i \right)} > c_{j\kappa \left(j \right)}/d_{j\kappa \left(j \right)}$ than player $j$, then its effort $x_{i\kappa \left(i \right)}$ and expected utility $u_{i}$ increase in player $j$’s ratio $c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}$. Being disadvantaged induces player $i$ to exert higher effort $x_{i\kappa \left(i \right)}$, causing higher expected utility $u_{i}$. Finally, if player $i$ is disadvantaged with high ratio $c_{i\kappa \left(i \right)}/d_{i\kappa \left(i \right)} > c_{j\kappa \left(j \right)}/d_{j\kappa \left(j \right)}$, then the rent dissipation $D$ decreases in player $i$’s ratio $c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}$. That follows since the players then become more unequally matched, expressed with player $i$’s ratio $c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}$ becoming more different from player $j$’s ratio $c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}$. That insight is expanded upon in Proposition 12.

Proposition 12

Assume that Assumption 5 is satisfied. Rent dissipation is maximum, i.e. $D = \frac{{m_{j\kappa \left(j \right)}}}{2}$, when the players have equal ratios $c_{i\kappa \left(i \right)}/d_{i\kappa \left(i \right)} = c_{j\kappa \left(j \right)}/d_{j\kappa \left(j \right)}$ of unit cost $c_{i\kappa \left(i \right)}$ divided by impact $d_{i\kappa \left(i \right)}$, and minimum, i.e. $D = 0$, in two extreme circumstances. The first is that player $i$ is maximally advantaged expressed as $c_{i\kappa \left(i \right)} = 0$ causing $\mathop {\lim}\limits_{{c_{i\kappa \left(i \right)} \to 0}} x_{i\kappa \left(i \right)} = \frac{S}{{d_{i\kappa \left(i \right)} c_{j\kappa \left(j \right)}/d_{j\kappa \left(j \right)}}}$ when $m_{j\kappa \left(j \right)} = 1$ and $\mathop {\lim}\limits_{{c_{i\kappa \left(i \right)} \to 0}} x_{i\kappa \left(i \right)} = 0$ when $m_{j\kappa \left(j \right)} > 1$. The second is that player $i$ is maximally disadvantaged expressed as $c_{i\kappa \left(i \right)} = \infty$ causing $\mathop {\lim}\limits_{{c_{i\kappa \left(i \right)} \to \infty}} x_{i\kappa \left(i \right)} = 0$.

Proof

Straightforward generalization of Hausken’s (2020) Proposition 4 from $m_{j\kappa \left(j \right)} = 1$ to $m_{j\kappa \left(j \right)} \ge 1$. The positive limit value is determined using L’Hopital’s rule.

Proposition 12 specifies maximum rent dissipation $D = \frac{{m_{j\kappa \left(j \right)}}}{2}$ when the players are equally matched with equal unit cost to impact ratios $c_{i\kappa \left(i \right)}/d_{i\kappa \left(i \right)} = c_{j\kappa \left(j \right)}/d_{j\kappa \left(j \right)}$. Then they fight or compete especially fiercely, and even more fiercely as the contest intensity $m_{j\kappa \left(j \right)}$ increases. That insight is expanded upon in Proposition 13.

Proposition 13

Assume that Assumption 5 is satisfied. $\frac{\partial D}{{\partial m_{j\kappa \left(j \right)}}} > 0$ and $\frac{{\partial x_{i\kappa \left(i \right)}}}{{\partial m_{j\kappa \left(j \right)}}} > 0$ when $f\left({\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}} \right) = 1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} + \left({1 - \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)Ln\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}}}} \right) > 0$, and $\frac{{\partial u_{i}}}{{\partial m_{j\kappa \left(j \right)}}} < 0$ when $g\left({\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}} \right) = \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({Ln\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)} - 1}}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)} - 1}}}}} \right) - 1} \right) + Ln\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)} + 1}}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)} + 1}}}}} \right) - 1 < 0$, where $f\left(0 \right) = \mathop {\lim}\limits_{{c_{i\kappa \left(i \right)}/c_{j\kappa \left(j \right)} \to \infty}} f\left({\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}} \right) = g\left(0 \right) = - \infty$, $f\left(1 \right) = 1 + \frac{{d_{j\kappa \left(j \right)}}}{{d_{i\kappa \left(i \right)}}}$, $g\left(1 \right) = - 2$, and $g\left({\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}} \right) < 0 \Leftrightarrow m_{j\kappa \left(j \right)} > {\text{Max}}\left({1,\frac{1}{{Ln\left({\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}} \right)}} + \frac{{\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} - 1}}{{\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} + 1}}} \right).$

Proof

Appendix K.

Proposition 13 states that rent dissipation $D$ and player $i$’s effort $x_{i\kappa \left(i \right)}$ increase when the contest intensity $m_{j\kappa \left(j \right)}$ increases, provided that player $i$ is neither too advantaged expressed with low $\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}$, nor too disadvantaged expressed with high $\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}$. In particular, for equally matched players expressed as $c_{i\kappa \left(i \right)}/d_{i\kappa \left(i \right)} = c_{j\kappa \left(j \right)}/d_{j\kappa \left(j \right)}$ and $d_{i\kappa \left(i \right)} = d_{j\kappa \left(j \right)}$, both rent dissipation $D$ and player $i$’s effort $x_{i\kappa \left(i \right)}$ increase in $m_{j\kappa \left(j \right)}$. Mathematically, $f\left({\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}} \right)$ is inverse U shaped in $\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}$, and negative when $\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}$ is low or high.

Player $i$’s expected utility $u_{i}$ decreases when the contest intensity $m_{j\kappa \left(j \right)}$ increases, with one exception expressed in the last inequality in Proposition 13. First, player $i$ must be sufficiently disadvantaged expressed as $c_{i\kappa \left(i \right)} > c_{j\kappa \left(j \right)}$ so that $Ln\left({\frac{{c_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}}}} \right) > 0$. Second, $m_{j\kappa \left(j \right)}$ must be low (though $m_{j\kappa \left(j \right)} \ge 1$) so that the last inequality in Proposition 13 is not satisfied. As $m_{j\kappa \left(j \right)}$ increases above this low value, even a disadvantaged player $i$’s expected utility $u_{i}$ decreases in $m_{j\kappa \left(j \right)}$.

6 Comparing results of when rent dissipation, efforts and expected utilities increase or decrease

Conflicting results exist in the literature for when rent dissipation increases or decreases, which depends on how players exert efforts. Two influential factors are whether the contest is of the Cobb–Douglas type or not, and whether the contest is or becomes more balanced (symmetric) or unbalanced (asymmetric, i.e. one player is sufficiently stronger or more advantaged than the other player).

Arbatskaya and Mialon (2010) assume the Cobb–Douglas type contest. They find that when adding efforts (activities, arms) to a contest which makes the overall contest more (less) balanced, then rent dissipation increases (decreases), expected utilities decrease (increase), and the current efforts increase (decrease). These results differ from the current article where adding efforts, when $m_{i1} = 1$, $0 \le m_{ik} < 1,k = 2, \ldots,K_{i}$, $i = 1,2$, causes rent dissipation and current efforts to decrease, so that the players earn higher expected utilities, regardless of whether the added efforts cause the overall contest to be more or less balanced. The two articles give the same result only when adding efforts makes the overall contest less balanced, i.e. more asymmetric. But making a contest more asymmetric can be expected to cause similar results for a variety of different models since the advantaged player can be expected to withdraw effort due to superiority (i.e. strength), while the disadvantaged player can be expected to withdraw effort due to inferiority (i.e. weakness), thus intuitively causing less rent dissipation and higher expected utilities. The main reason for the different results when adding efforts makes the contest more balanced or symmetric is that Cobb–Douglas type multiplicative efforts require each effort to be strictly positive to ensure success. For example, for the multiplicative approach the products $0 \times 10 = 0$, $1 \times 9 = 9$, $5 \times 5 = 25$, $9 \times 1 = 9$, $10 \times 0 = 0$ illustrate that multiplying the equally large numbers $5$ and $5$ gives the highest product $25$. Thus, in symmetric contests, the players are more strongly induced to ensure that all their efforts are above a certain level. In contrast, with additive efforts analyzed in this article, adding efforts (regardless of whether the overall contest is or becomes more or less balanced) gives each player more opportunities to choose the preferred efforts cost effectively. For example, for the additive approach the sums $0 + 10 = 10$, $1 + 9 = 10$, $5 + 5 = 10$, $9 + 1 = 10$, $10 + 0 = 10$ give the same sum $10$, and hence, do not require the players to choose efforts above a certain level. Instead, the players strike balances optimally between their efforts, depending on each effort’s unit effort cost, impact, and contest intensity. If $m_{i\kappa \left(i \right)} = m_{j\kappa \left(j \right)} \ge 1$, as in Sect. 5.2, each player’s one current effort remains unchanged if it remains cost effective for both players, which causes unchanged rent dissipation and expected utilities, or is replaced with a more cost-effective effort, the impact of which has to be analyzed in each particular case.

Epstein and Hefeker (2003) consider a contest, not of the Cobb–Douglas type, assuming maximum two efforts for each player. The first effort is conventional rent seeking. The second effort may be absent, or may reinforce the first effort. They find that if both players use their second of two available efforts, they will invest less in their first efforts, regardless of whether the contest is or becomes more symmetric or asymmetric. This result is more compatible with the current article. The result is caused by the same reason that the second effort does not have to be above a certain level, as in the Cobb–Douglas type contest, but can be absent. Thus, each player has a choice whether or not to exert the second effort. Given this choice, each player chooses the second effort only when it is cost effective to do so, and then cuts back on its first effort. Epstein and Hefeker (2003) find that if at least one player exerts both efforts, compared with both players exerting only one effort, rent dissipation increases when the players’ stakes are sufficiently symmetric, and otherwise decreases. This result differs from the current article where rent dissipation inevitably decreases when more efforts become available. Summing up, Arbatskaya and Mialon (2010) find decreased rent dissipation when adding efforts causes a more asymmetric (unbalanced) contest, Epstein and Hefeker (2003) find decreased rent dissipation when adding at least one effort in asymmetric contests, and this article finds inevitably decreased rent dissipation when more efforts become available.

7 Conclusion

This article analyzes a static rent seeking model where two players exert multiple additive efforts simultaneously in a one-period game. The model assumes exerting one effort to be sufficient to win a rent, since efforts are substitutable in the contest success function. In contrast, the multiplicative Cobb–Douglas production function analyzed e.g. by Arbatskaya and Mialon (2010) requires that a player exerts all its efforts, since efforts are complementary in the contest success function.

Assuming arbitrarily many efforts for each player, the article distinguishes between contest intensities below one, equal to one, or larger than one. Analyzing contest intensities below one, and maximum one contest intensity equal to one, is challenging since when production is concave in effort (and linear for at most one effort), then more than one effort is exerted, since the marginal benefit of effort decreases when effort increases. An analytical solution is determined when the contest intensity for one effort for each player equals one, while the contest intensities for the other efforts are strictly below one. Additional efforts causing interior solutions enable each player to optimize cost effectively across efforts, cutting back on the effort with contest intensity equal to one. Adding new efforts eventually causes the new efforts to decrease towards zero. This result is due to a heavier reliance of each player on efforts with diminishing returns (contest intensity less than one) rather than constant return (contest intensity equal to one). Similarly, Epstein and Hefeker (2003) find that if both players use their second of two available efforts, they will invest less in their first efforts, assuming that their second efforts reinforce their first efforts. Interestingly, both Epstein and Hefeker (2003) and the current article generate this result, with different approaches. Additional efforts causing corner solutions have to be analyzed specifically, since they may not be used, and may thus not improve a player’s equilibrium expected utility.

We find that if one player exerts one effort, this effort does not depend on the number of efforts exerted by the other player which optimizes across efforts. Cost optimization across multiple additive efforts causes lower rent dissipation and higher expected utilities as the number of efforts increases. That is, a higher dimensionality of the contest results in less rent dissipation. This contrasts with Arbatskaya and Mialon’s (2010) finding that additional efforts that balances a contest (makes it more symmetric) increases rent dissipation when efforts are multiplicative of the Cobb–Douglas type. It also contrasts with Epstein and Hefeker’s (2003) finding of increased rent dissipation when the players’ stakes are sufficiently symmetric.

A Nash equilibrium selection method is provided for the event that it may not be optimal for both players to exert all their available efforts, accounting for solutions which have to be determined numerically. An example is provided with maximum two efforts for each player. Nash equilibria are determined where both players choose both efforts, or one player withdraws from its most costly effort to exert only the least costly effort. We also illustrate how both players may collectively prefer to exclude one of their efforts, though in equilibrium they prefer both efforts.

When all contest intensities are equal to one or larger than one, only the one most cost effective effort is exerted, since linear or convex production causes the marginal benefit of effort to be zero or increase when effort increases. Rent dissipation increases in the contest intensity, and is maximum when the players are equally matched in terms of their unit effort cost divided by impact of their effort. Furthermore, rent dissipation and a player’s effort increase when the contest intensity increases, provided that the player is neither too advantaged nor too disadvantaged compared with the other player. Being advantaged or disadvantaged causes decreased efforts due to superiority and inferiority, respectively.

Whereas Arbatskaya and Mialon (2010) as policy implications find that additional socially unproductive efforts may unbalance contests causing increased rent dissipation and decreased expected utilities, we find that both social and non-social additional efforts decrease rent seeking and increase expected utilities due to players’ optimization across efforts. For policy, careful analysis is required to determine whether multiple efforts are additive or multiplicative. Future research should analyze increasingly general functional forms for the contest success function and analyze empirically which forms are descriptive.

Future research may also proceed beyond multiple additive efforts analyzed in this article, and multiplicative efforts analyzed in the earlier literature, by assuming that a player’s production (impact) function depends in a less separable way on the multiple efforts exerted by multiple players. For example, if two teams play football, one team’s success may (in part) depend on how the strength of its attacking line is matched by the defense of the other team.

Appendices

Appendix A: Nomenclature

$x_{ik}$ player $i$’s effort, $i = 1,2$, $k = 1, \ldots,K_{i}$

$K_{i}$ number of efforts for player $i$

$S$ rent

$c_{ik}$ player $i$’s unit cost of effort $x_{ik}$

$d_{ik}$ scaling parameter for player $i$’s impact of effort $x_{ik}$

$m_{ik}$ contest intensity or decisiveness for player $i$’s effort $x_{ik}$

$p_{i}$ probability that player $i$ wins the rent

$u_{i}$ player $i$’s expected utility

Appendix B: One effort against one effort

Inserting $K_{i} = K_{j} = 1$ into (5) and solving gives $x_{i1} = \frac{{m_{i1} c_{j1}}}{{m_{j1} c_{i1}}}x_{j1}$ causing (5) to be analytically solvable when $m_{i1} = m_{j1}$, which gives

$$\begin{aligned} x_{i1} & = \frac{{c_{j1}}}{{c_{i1}}}x_{j1},x_{j1} = \frac{{Sm_{j1} \frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}}}}{{c_{j1} \left({1 + \frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}}} \right)^{2}}},D = \frac{{2c_{j1} x_{j1}}}{S}, \hfill \\ u_{i} & = \frac{{S\left({1 + \left({1 - m_{j1}} \right)\frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}}} \right)}}{{\left({1 + \frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}}} \right)^{2}}},\quad i,j = 1,2, i \ne j, \hfill \\ \end{aligned}$$

(24)

which is consistent with (8), (9), and (10) when $m_{i1} = m_{j1} = 1$. Differentiating (5) when $K_{i} = K_{j} = 1$, $m_{i1} = m_{j1}$, and $x_{i1} = \frac{{c_{j1}}}{{c_{i1}}}x_{j1}$, the second-order conditions are

$$\frac{{\partial^{2} u_{i}}}{{\partial x_{i1}^{2}}} = - \frac{{Sm_{j1} \frac{{c_{i1}^{{m_{j1} + 2}}/d_{i1}}}{{c_{j1}^{{m_{j1} + 2}}/d_{j1}}}\left({1 + m_{j1} + \left({1 - m_{j1}} \right)\frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}}} \right)}}{{x_{j1}^{2} \left({1 + \frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}}} \right)^{3}}} \le 0,$$

(25)

which is satisfied when the second inequality in Assumption B1 is satisfied. The first inequality in Assumption B1 requires that the expected utility $u_{i} \ge 0$ in (23) is positive.

Assumption B1

$K_{i} = K_{j} = 1$, $m_{i1} = m_{j1}$, $i,j = 1,2, i \ne j,$

$$1 + \left({1 - m_{j1}} \right)\frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}} \ge 0,$$

$$1 + m_{j1} + \left({1 - m_{j1}} \right)\frac{{c_{i1}^{{m_{j1}}}/d_{i1}}}{{c_{j1}^{{m_{j1}}}/d_{j1}}} \ge 0, i,j = 1,2, i \ne j.$$

Explanation B1

When Assumption B1 is satisfied, an interior equilibrium solution is determined by (24), which also specifies the players’ expected utilities $u_{i}$ and $u_{j}$ and rent dissipation $D$, $i,j = 1,2,i \ne j$.

Proof

Follows from (24) and (25). When the two inequalities in Assumption B1 are satisfied, $u_{i} > 0$ and $u_{j} > 0$, and hence, corner solutions are impossible. $\square$

Appendix C: Guaranteeing that the stationary point is a global maximum

Assume $0 \le m_{ik} \le 1,k = 1, \ldots,K_{i}$. The author has shown (available upon request) that the Hessian matrix is negative semi-definite when $1 \le K_{i} \le 5$. For $K_{i} \ge 6$ the analysis is increasingly labor intensive. Fortunately the following simpler approach is possible. Define player $i$’s output as

$$A_{i} \equiv \mathop \sum \limits_{k = 1}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}},$$

(26)

Player $i$’s output $A_{i}$ and aggregate cost $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} c_{ik} x_{ik}$ in (2) are additively separable in each dimension $k = 1, \ldots,K_{i}$, and respectively concave and linear in $x_{ik}$. For any given level of output $A_{i} > 0$, player i must exert efforts to minimize the aggregate cost, i.e. minimize

$${{\varLambda}} = c_{ik} x_{ik} - \lambda_{i} d_{ik} x_{ik}^{{m_{ik}}},$$

(27)

where $\lambda_{i} > 0$ takes the unique value such that $A_{i}^{*} \left({\lambda_{i}} \right) = A_{i}$, and superscript * expresses optimum. Differentiating (27), equating with zero, and solving, gives

$$\frac{{\partial {{\varLambda}}}}{{\partial x_{ik}}} = c_{ik} - \lambda_{i} d_{ik} m_{ik} x_{ik}^{{m_{ik} - 1}} = 0 \Leftrightarrow x_{ik}^{*} \left({\lambda_{i}} \right) \equiv x_{ik}^{*} \equiv \left({\frac{{\lambda_{i} m_{ik}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}},$$

(28)

which is inserted into (26) to yield

$$A_{i}^{*} \left({\lambda_{i}} \right) \equiv A_{i}^{*} \equiv \mathop \sum \limits_{k = 1}^{{K_{i}}} d_{ik} \left({\frac{{\lambda_{i} m_{ik}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}}.$$

(29)

Hence, player $i$’s expected utility maximization problem reduces to a single dimension by identifying the $\lambda_{i}$ that maximizes

$$u_{i}^{*} \left({\lambda_{i},\lambda_{j}} \right) = \frac{{SA_{i}^{*}}}{{A_{i}^{*} + A_{j}^{*}}} - \mathop \sum \limits_{k = 1}^{{K_{i}}} c_{ik} x_{ik}^{*}.$$

(30)

For $m_{ik} \le 1/2$ we straightforwardly see that the win probability $A_{i}^{*}$ is concave in $\lambda_{i}$. As the aggregate cost $\mathop \sum \nolimits_{k = 1}^{{K_{i}}} c_{ik} x_{ik}^{*}$ is convex in $\lambda_{i}$, $u_{i}^{*} \left({\lambda_{i},\lambda_{j}} \right)$ is concave in $\lambda_{i}$. Hence, a first-order condition identifies the unique maximizer of $u_{i}^{*} \left({\lambda_{i},\lambda_{j}} \right)$ and implicitly defines a best-response function $\lambda_{i}^{*} \left({\lambda_{j}} \right)$. More generally for $0 \le m_{ik} \le 1$, differentiating (30) twice gives

$$\frac{{\partial u_{i}^{*} \left({\lambda_{i},\lambda_{j}} \right)}}{{\partial \lambda_{i}}} = \left({\frac{{SA_{j}^{*}}}{{\lambda_{i} \left({A_{i}^{*} + A_{j}^{*}} \right)^{2}}} - 1} \right)\mathop \sum \limits_{k = 1}^{{K_{i}}} B_{ik} = 0,B_{ik} \equiv \frac{{d_{ik} m_{ik}}}{{1 - m_{ik}}}\left({\frac{{\lambda_{i} m_{ik}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}},$$

(31)

and (after some tedious calculations)

$$\frac{{\partial^{2} u_{i}^{*} \left({\lambda_{i},\lambda_{j}} \right)}}{{\partial \lambda_{i}^{2}}} = \frac{{SA_{j}^{*} \mathop \sum \nolimits_{k = 1}^{{K_{i}}} \frac{{2m_{ik} - 1}}{{1 - m_{ik}}}B_{ik}}}{{\lambda_{i}^{2} \left({A_{i}^{*} + A_{j}^{*}} \right)^{2}}} - \frac{{2SA_{j}^{*} \left({\mathop \sum \nolimits_{k = 1}^{{K_{i}}} B_{ik}} \right)^{2}}}{{\lambda_{i}^{2} \left({A_{i}^{*} + A_{j}^{*}} \right)^{3}}} - \frac{1}{{\lambda_{i}}}\mathop \sum \limits_{k = 1}^{{K_{i}}} \frac{{m_{ik}}}{{1 - m_{ik}}}B_{ik}.$$

(32)

The first-order equation in (31) is solved to yield

$$\left({A_{i}^{*} + A_{j}^{*}} \right)^{2} = \frac{{SA_{j}^{*}}}{{\lambda_{i}}},$$

(33)

which is inserted into (32) to yield

$$\frac{{\partial^{2} u_{i}^{*} \left({\lambda_{i},\lambda_{j}} \right)}}{{\partial \lambda_{i}^{2}}} = \frac{1}{{\lambda_{i}}}\mathop \sum \limits_{k = 1}^{{K_{i}}} \left({\frac{{2m_{ik} - 1}}{{1 - m_{ik}}} - \frac{{m_{ik}}}{{1 - m_{ik}}}} \right)B_{ik} - \frac{{2SA_{j}^{*} \left({\mathop \sum \nolimits_{k = 1}^{{K_{i}}} B_{ik}} \right)^{2}}}{{\lambda_{i}^{2} \left({A_{i}^{*} + A_{j}^{*}} \right)^{3}}}.$$

(34)

A sufficient but not necessary requirement for (34) to be negative is $0 \le m_{ik} \le 1$. To show that the best-response functions of the two players intersect each other, supplementing (33) with the first-order equation for player $j$ and solving gives

$$\left({A_{i}^{*} + A_{j}^{*}} \right)^{2} = \frac{{SA_{j}^{*}}}{{\lambda_{i}}} = \frac{{SA_{i}^{*}}}{{\lambda_{j}}} \Rightarrow \lambda_{i} = \frac{{A_{j}^{*}}}{{A_{i}^{*}}}\lambda_{j}.$$

(35)

Hence, the players’ best-response functions are

$$\lambda_{i}^{*} \left({\lambda_{j}} \right) = \frac{{A_{j}^{*} \left({\lambda_{j}} \right)}}{{A_{i}^{*} \left({\lambda_{i}^{*} \left({\lambda_{j}} \right)} \right)}}\lambda_{j}, \quad \lambda_{j}^{*} \left({\lambda_{i}} \right) = \frac{{A_{i}^{*} \left({\lambda_{i}} \right)}}{{A_{j}^{*} \left({\lambda_{j}^{*} \left({\lambda_{i}} \right)} \right)}}\lambda_{i},$$

(36)

which intersect each other. As an example, inserting $K_{i} = K_{j} = 1$ and $m_{ik} = 1/2$ into (29) gives

$$A_{i}^{*} \left({\lambda_{i}} \right) = \frac{{\lambda_{i}}}{{2c_{i1}}}, \quad A_{j}^{*} \left({\lambda_{j}} \right) = \frac{{\lambda_{j}}}{{2c_{j1}}},$$

(37)

which is inserted into (36) to yield

$$\lambda_{i}^{*} \left({\lambda_{j}} \right) = \sqrt {\frac{{c_{i1}}}{{c_{j1}}}} \lambda_{j}, \quad \lambda_{j}^{*} \left({\lambda_{i}} \right) = \sqrt {\frac{{c_{j1}}}{{c_{i1}}}} \lambda_{i}$$

(38)

which intersect each other. As an example, inserting $K_{i} = K_{j} = 1$ and $m_{ik} = 2/3$ into (28) gives

$$A_{i}^{*} \left({\lambda_{i}} \right) = d_{ik} \left({\frac{{2\lambda_{i} d_{ik}}}{{3c_{ik}}}} \right)^{2},\quad A_{j}^{*} \left({\lambda_{j}} \right) = d_{jk} \left({\frac{{2\lambda_{j}}}{{3c_{jk}/d_{jk}}}} \right)^{2},$$

(39)

which is inserted into (36) to yield

$$\lambda_{i}^{*} \left({\lambda_{j}} \right) = \frac{{c_{ik}^{2/3}/d_{ik}}}{{c_{jk}^{2/3}/d_{jk}}}\lambda_{j}, \quad \lambda_{j}^{*} \left({\lambda_{i}} \right) = \frac{{c_{jk}^{2/3}/d_{jk}}}{{c_{ik}^{2/3}/d_{ik}}}\lambda_{i},$$

(40)

which intersect each other. □

Appendix D: Corner solution for the general solution in Sect. 4.1

Procedure When the conditions for Explanation 1 are not satisfied, $K_{i}$ corner solutions are possible where exactly one effort $x_{ik}$, $k = 1, \ldots,K_{i}$, by player $i$ equals zero, and all other efforts by both players are strictly positive. Define $\left({\begin{array}{*{20}c} {K_{i}} \\ {Z_{i}} \\ \end{array}} \right)$ as the binomial coefficient for the number of ways in which an integer $Z_{i}$ can be selected among an integer $K_{i}$. Generally, $\left({\begin{array}{*{20}c} {K_{i}} \\ {Z_{i}} \\ \end{array}} \right)$ corner solutions are possible where exactly $Z_{i}$ efforts by player $i$ equal zero, and all other efforts by both players are strictly positive. Generally, $\left({\begin{array}{*{20}c} {K_{1} + K_{2}} \\ {Z_{1} + Z_{2}} \\ \end{array}} \right)$ corner solutions are possible where exactly $Z_{1}$ efforts by player 1 equal zero and exactly $Z_{2}$ efforts by player 2 equal zero, and all other efforts by both players are strictly positive. We exclude $Z_{i} = K_{i}$ since both players must have at least one strictly positive effort to enable a game. We also exclude $Z_{1} = Z_{2} = 0$ which is the interior solution in the previous Sect. 4.1 where all $K_{1} + K_{2}$ efforts are strictly positive. Hence, $Z_{i} = 0, \ldots,K_{i} - 1$, $1 \le Z_{1} + Z_{2} \le K_{1} + K_{2} - 2$. This gives $\mathop \sum \limits_{i = 1}^{2} \mathop \sum \limits_{{\begin{array}{*{20}c} {Z_{i} = 0, \ldots,K_{i} - 1,} \\ {1 \le Z_{1} + Z_{2} \le K_{1} + K_{2} - 2} \\ \end{array}}} \left({\begin{array}{*{20}c} {K_{1} + K_{2}} \\ {Z_{1} + Z_{2}} \\ \end{array}} \right)$ possible corner solutions which we identify with the three digits $Z_{1} Z_{2} k$, separated by commas when needed, where $k$ is a counting parameter.

The corner solutions are straightforward but tedious and extremely space consuming to set up. We thus sketch the procedure. One convenient approach is to relabel the subscripts of the variables to use (6) and (7) as combinations of strategic choice variables are systematically set to zero for each corner solution. We illustrate this for the $K_{i}$ possible corner solutions where exactly one $x_{ik}$, $k = 1, \ldots,K_{i}$, equals zero. We start with $x_{i1} = 0$. To determine $x_{i2}, \ldots,x_{{iK_{i}}}$ using (6) and (7), we replace all subscripts $k = 2, \ldots,K_{i}$ with subscripts $k = 1, \ldots,K_{i} - 1$, thus determining $x_{i1}, \ldots,x_{{i,K_{i} - 1}}$ using (6) and (7). If, analogously to Explanation 1, $x_{ik} > 0$$\forall \; k = 1, \ldots,K_{i} - 1$ and $x_{jk} > 0$$\forall \; k = 1, \ldots,K_{j}$, $i,j = 1,2,i \ne j$, all subscripts $k = 1, \ldots,K_{i} - 1$ for player $i$ are changed back to subscripts $k = 2, \ldots,K_{i}$, thus shifting $x_{i1}, \ldots,x_{{i,K_{i} - 1}}$ back to $x_{i2}, \ldots,x_{{iK_{i}}}$ so that $x_{i1} = 0$ is part of the corner solution.

We next set $x_{i2} = 0$. To determine $x_{i1},x_{i3}, \ldots,x_{{iK_{i}}}$ using (6) and (7), we replace all subscripts $k = 1,3, \ldots,K_{i}$ with subscripts $k = 1, \ldots,K_{i} - 1$, thus determining $x_{i1}, \ldots,x_{{i,K_{i} - 1}}$ using (6) and (7). If $x_{ik} > 0$$\forall \; k = 1, \ldots,K_{i} - 1$ and $x_{jk} > 0$$\forall \; k = 1, \ldots,K_{j}$, $i,j = 1,2,i \ne j$, all subscripts $k = 1, \ldots,K_{i} - 1$ for player $i$ are changed back to subscripts $k = 1,3, \ldots,K_{i}$, thus shifting $x_{i1}, \ldots,x_{{i,K_{i} - 1}}$ back to $x_{i1},x_{i3}, \ldots,x_{{iK_{i}}}$ so that $x_{i2} = 0$ is part of the corner solution. We continue the procedure for $x_{i3} = 0$,…, $x_{{K_{i}}} = 0$. This causes maximum $K_{1} + K_{2}$ corner solutions.

We next set two efforts to zero, either one effort by each player or two efforts by one of the players. We start with $x_{i1} = x_{i2} = 0$. To determine $x_{i3}, \ldots,x_{{iK_{i}}}$ using (6) and (7), we replace all subscripts $k = 3, \ldots,K_{i}$ with subscripts $k = 1, \ldots,K_{i} - 2$, thus determining $x_{i1}, \ldots,x_{{i,K_{i} - 2}}$ using (6) and (7). Continuing as above gives the various solutions, etc.

Explanation D1

Assume that $0 \le m_{ik} \le 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$. When solving (6) and (7), and using the Procedure described above, gives $x_{ik} = 0$ for at least one $k = 1,\ldots,K_{i}$, $i = 1,2$, and all other efforts are strictly positive, $x_{iq} > 0$$\forall q = 1,\ldots,K_{i}$, $q \ne k$, a corner equilibrium solution is determined by (6) and (7). The players’ expected utility $u_{i}$, $i = 1,2$, and rent dissipation $D$ follow from inserting (6) and (7) into (2) and (3).

Proof

Follows from (2), (3), (5)–(7), “Appendix C”, and the Procedure in “Appendix D”.□

Appendix E: Corner solution for Sect. 4.2

Assuming that Assumption 2 is not satisfied for one of the players, i.e. $x_{i1} \le 0$ for player $i$ without loss of generality, but is satisfied for the other player, $x_{j1} > 0$ for player $j$, is written as follows:

Assumption E1

$\begin{aligned} &x_{i1} \le 0 \Leftrightarrow \frac{{S\frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}}}{{c_{i1} \left({1 + \frac{{c_{i1}/d_{i1}}}{{c_{j1}/d_{j1}}}} \right)^{2}}} \le \mathop \sum \nolimits_{k = 2}^{{K_{i}}} \frac{{d_{ik}}}{{d_{i1}}}\left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}}, \\ & x_{j1} > 0 \Leftrightarrow \frac{{S\frac{{c_{j1}/d_{j1}}}{{c_{i1}/d_{i1}}}}}{{c_{j1} \left({1 + \frac{{c_{j1}/d_{j1}}}{{c_{i1}/d_{i1}}}} \right)^{2}}} > \mathop \sum \nolimits_{k = 2}^{{K_{j}}} \frac{{d_{jk}}}{{d_{j1}}}\left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{jk}}}{{1 - m_{jk}}}}},\quad i,j = 1,2, i \ne j. \hfill \\ \end{aligned}$

When Assumption E1 is satisfied, we set $x_{i1} = 0$ for player $i$ according to (8) to cause a corner solution. Assuming $x_{i1} = 0$ and inserting $m_{i1} = m_{j1} = 1$ into (5) for player $i$ for $k = 2$ gives

$$x_{i1} = 0,\frac{{d_{j1} x_{j1} + \mathop \sum \limits_{k = 2}^{{K_{j}}} d_{jk} \left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{jk}}}{{1 - m_{jk}}}}}}}{{\left({d_{i2} x_{i2} + \mathop \sum \limits_{k = 3}^{{K_{i}}} d_{ik} x_{i2}^{{\frac{{m_{ik} (1 - m_{2k})}}{{1 - m_{ik}}}}} \left({\frac{{m_{ik} c_{i2}/d_{i2}}}{{m_{i2} c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}} + d_{j1} x_{j1} + \mathop \sum \limits_{k = 2}^{{K_{j}}} d_{jk} \left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{jk}}}{{1 - m_{jk}}}}}} \right)^{2}}} = \frac{{c_{i2} x_{i2}^{{1 - m_{i2}}}}}{{Sm_{i2} d_{i2}}}.$$

(41)

The solution for player $i$ for $k = 3, \ldots,K_{i}$ is determined by (6), i.e.

$$x_{ik} = x_{i2}^{{\frac{{1 - m_{2k}}}{{1 - m_{ik}}}}} \left({\frac{{m_{ik} c_{i2}/d_{i2}}}{{m_{i2} c_{ik}/d_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}},\quad k = 3, \ldots,K_{i}.$$

(42)

The solution for player $j$ for $k = 1$ is determined by (5) by relabeling subscripts and superscripts, i.e.

$$\frac{{S\mathop \sum \nolimits_{k = 2}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}}}}{{\left({\mathop \sum \nolimits_{k = 2}^{{K_{i}}} d_{ik} x_{ik}^{{m_{ik}}} + \mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}} \right)^{2}}} = \frac{{c_{j1}}}{{d_{j1}}}.$$

(43)

The solution for player $j$ for $k = 2, \ldots,K_{j}$ is determined by (6) by relabeling subscripts and superscripts, i.e.

$$x_{jk} = \left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{1}{{1 - m_{jk}}}}},k = 2, \ldots,K_{j}$$

(44)

Solving (42) with respect to $x_{j1}$ and inserting (43) gives

$$x_{{j1}} = \left\{ {\begin{array}{l} {\frac{1}{{d_{{j1}} }}\left( {\sqrt {\frac{{d_{{j1}} S}}{{c_{{j1}} }}} - \sqrt {\mathop \sum \limits_{{k = 2}}^{{K_{i} }} d_{{ik}} x_{{i2}}^{{\frac{{m_{{ik}} (1 - m_{{2k}} )}}{{1 - m_{{ik}} }}}} \left( {\frac{{m_{{ik}} c_{{i2}} /d_{{i2}} }}{{m_{{i2}} c_{{ik}} /d_{{ik}} }}} \right)^{{\frac{{m_{{ik}} }}{{1 - m_{{ik}} }}}} } } \right)\sqrt {\mathop \sum \limits_{{k = 2}}^{{K_{i} }} d_{{ik}} x_{{i2}}^{{\frac{{m_{{ik}} (1 - m_{{2k}} )}}{{1 - m_{{ik}} }}}} \left( {\frac{{m_{{ik}} c_{{i2}} /d_{{i2}} }}{{m_{{i2}} c_{{ik}} /d_{{ik}} }}} \right)^{{\frac{{m_{{ik}} }}{{1 - m_{{ik}} }}}} } } \\ {\quad \quad - \frac{1}{{d_{{j1}} }}\mathop \sum \limits_{{k = 2}}^{{K_{j} }} d_{{jk}} \left( {\frac{{m_{{jk}} c_{{j1}} /d_{{j1}} }}{{c_{{jk}} /d_{{jk}} }}} \right)^{{\frac{{m_{{jk}} }}{{1 - m_{{jk}} }}}} = x_{{j1c}} {\text{ when }} x_{{j1c}} > 0} \\ {0 \quad \quad \quad {\text{otherwise}}} \\ \end{array} .} \right.$$

(45)

Although (45) expresses $x_{j1}$ analytically as a function of $x_{i2}$, $x_{i2}$ is not analytically solvable since $m_{j2} < 1$ (Assumption 1). If we change Assumption 1 by setting $m_{j2} = 1$, (41)–(45) are analytically solvable, after which the procedure in “Appendix D” is applicable. Reversing both inequalities in Assumption E1 implies $x_{j1} = 0$ which, together with $m_{i1} = m_{j1} = 1$, imply equations analogous to (41)–(45). Reversing both inequalities in Assumption 2 implies that also $x_{i1} = x_{j1} = 0$ has to be checked. Since analytical solution is impossible, numerical solution and the general procedure in “Appendix D” are appropriate.

Appendix F: First-order derivatives and lemmas for Sect. 4.2

Differentiating (8) when $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$, gives

$$\begin{aligned} \frac{{\partial x_{i1}}}{{\partial K_{i}}} < 0,\,\frac{{\partial x_{i1}}}{{\partial d_{i1}}} & = \frac{{c_{j1} d_{j1} (c_{i1} d_{j1} - c_{j1} d_{i1})S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} + \frac{1}{{d_{i1}^{2}}}\mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{d_{ik}}}{{(1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}}, \hfill \\ \frac{{\partial x_{i1}}}{{\partial d_{j1}}} & = \frac{{c_{j1} d_{i1} (c_{j1} d_{i1} - c_{i1} d_{j1})S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}}, \frac{{\partial x_{i1}}}{{\partial d_{ik}}} = \frac{- 1}{{d_{i1} (1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}} < 0, \hfill \\ \frac{{\partial x_{i1}}}{{\partial d_{jk}}} = 0, \frac{{\partial x_{i1}}}{{\partial c_{i1}}} & = \frac{{- 2c_{j1} d_{i1} d_{j1}^{2} S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} - \frac{1}{{c_{i1}^{2}}}\mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{c_{ik}}}{{\left({1 - m_{ik}} \right)}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} < 0, \hfill \\ \frac{{\partial x_{i1}}}{{\partial c_{j1}}}& = \frac{{d_{i1} d_{j1} (c_{i1} d_{j1} - c_{j1} d_{i1})S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i1}}}{{\partial c_{ik}}} & = \frac{1}{{c_{i1} (1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} > 0, \hfill \\ \frac{{\partial x_{i1}}}{{\partial c_{jk}}} = 0, \frac{{\partial x_{i1}}}{{\partial m_{ik}}} & = \frac{{- d_{ik} \left({1 - m_{ik} + \ln \left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)} \right)}}{{d_{i1} (1 - m_{ik})^{2}}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}}, \hfill \\ \frac{{\partial x_{i1}}}{{\partial m_{jk}}} & = 0, \frac{{\partial x_{i1}}}{\partial S} = \frac{{c_{j1} d_{i1} d_{j1}}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{2}}} > 0, \hfill \\ \end{aligned}$$

(46)

and

$$\begin{aligned} \frac{{\partial x_{ik}}}{{\partial K_{i}}} & = 0,\frac{{\partial x_{ik}}}{{\partial d_{i1}}} = \frac{- 1}{{d_{i1} (1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} < 0, \hfill \\ \frac{{\partial x_{ik}}}{{\partial d_{j1}}} & = 0, \frac{{\partial x_{ik}}}{{\partial d_{ik}}} = \frac{1}{{d_{ik} (1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} > 0, \hfill \\ \frac{{\partial x_{ik}}}{{\partial d_{jk}}} & = 0, \frac{{\partial x_{ik}}}{{\partial c_{i1}}} = \frac{1}{{c_{i1} (1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} > 0, \hfill \\ \frac{{\partial x_{ik}}}{{\partial c_{j1}}} & = 0, \frac{{\partial x_{ik}}}{{\partial c_{ik}}} = \frac{- 1}{{c_{ik} (1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} < 0, \hfill \\ \frac{{\partial x_{ik}}}{{\partial c_{jk}}} &= 0, \frac{{\partial x_{ik}}}{{\partial m_{ik}}} = \frac{{\left({1 - m_{ik} + m_{ik} \ln \left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)} \right)}}{{m_{ik} (1 - m_{ik})^{2}}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}},\hfill \\ \frac{{\partial x_{ik}}}{{\partial m_{jk}}} & = 0,\frac{{\partial x_{ik}}}{\partial S} = 0. \end{aligned}$$

(47)

The inequality $\frac{{\partial x_{i1}}}{{\partial K_{i}}} < 0$ occurs since a minus sign appears before the summation sign with $K_{i}$ as the upper bound. Since the expression within the summation is positive, increasing the upper bound $K_{i}$ causes lower $x_{i1}$. Differentiating (9) gives

$$\begin{aligned} \frac{{\partial u_{i}}}{{\partial K_{i}}} > 0,\frac{{\partial u_{i}}}{{\partial d_{i1}}} & = \frac{{2c_{i1} c_{j1}^{2} d_{i1} d_{j1} S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} - \mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{c_{ik}}}{{m_{ik} d_{i1}}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}}, \hfill \\ \frac{{\partial u_{i}}}{{\partial d_{j1}}} & = \frac{{- 2c_{i1} c_{j1}^{2} d_{i1}^{2} S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} < 0,\frac{{\partial u_{i}}}{{\partial d_{ik}}} = \frac{{c_{i1}}}{{d_{i1}}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}} > 0, \hfill \\ \frac{{\partial u_{i}}}{{\partial d_{jk}}} = 0,\frac{{\partial u_{i}}}{{\partial c_{i1}}} & = \frac{{- 2c_{j1}^{2} d_{i1}^{2} d_{j1} S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} + \mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{d_{ik}}}{{d_{i1}}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}}, \hfill \\ \frac{{\partial u_{i}}}{{\partial c_{j1}}} & = \frac{{2c_{i1} c_{j1} d_{i1}^{2} d_{j1} S}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} > 0,\frac{{\partial u_{i}}}{{\partial c_{ik}}} = - \left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} < 0,\frac{{\partial u_{i}}}{{\partial c_{jk}}} = 0, \hfill \\ \frac{{\partial u_{i}}}{{\partial m_{ik}}} & = \frac{{c_{ik} \ln \left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)}}{{m_{ik} (1 - m_{ik})}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}},\frac{\partial u}{{\partial m_{jk}}} = 0, \hfill \\ \frac{\partial u}{\partial S} & = \frac{{c_{j1}^{2} d_{i1}^{2}}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{2}}} > 0. \hfill \\ \end{aligned}$$

(48)

The inequality $\frac{{\partial u_{i}}}{{\partial K_{i}}} > 0$ occurs since a plus sign appears before the summation sign with $K_{i}$ as the upper bound. Since the expression within the summation is positive, increasing the upper bound $K_{i}$ causes higher $u_{i}$. Differentiating (10) gives

$$\begin{aligned} \frac{\partial D}{{\partial K_{i}}} & < 0,\frac{\partial D}{{\partial d_{i1}}} = \frac{{c_{i1} c_{j1} d_{j1} \left({c_{i1} d_{j1} - c_{j1} d_{i1}} \right)}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} + \mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{c_{ik}}}{{d_{i1} m_{ik} S}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}}, \hfill \\ \frac{\partial D}{{\partial d_{ik}}}& = - \frac{{c_{i1}}}{{d_{i1} S}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}} < 0, \frac{\partial D}{{\partial c_{i1}}} = \frac{{c_{j1} d_{i1} d_{j1} \left({c_{j1} d_{i1} - c_{i1} d_{j1}} \right)}}{{\left({c_{j1} d_{i1} + c_{i1} d_{j1}} \right)^{3}}} - \mathop \sum \limits_{k = 2}^{{K_{i}}} \frac{{d_{ik}}}{{d_{i1} S}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{{m_{ik}}}{{1 - m_{ik}}}}}, \hfill \\ \frac{\partial D}{{\partial c_{ik}}} & = \frac{1}{S}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} > 0,\frac{\partial D}{{\partial m_{ik}}} = - \frac{{c_{ik} \ln \left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)}}{{m_{ik} (1 - m_{ik})S}}\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}}, \hfill \\ \frac{\partial D}{\partial S} & = \frac{1}{{S^{2}}}\mathop \sum \limits_{k = 2}^{{K_{i}}} c_{ik} \left({\frac{1}{{m_{ik}}} - 1} \right)\left({\frac{{m_{ik} d_{ik} c_{i1}}}{{d_{i1} c_{ik}}}} \right)^{{\frac{1}{{1 - m_{ik}}}}} > 0. \hfill \\ \end{aligned}$$

(49)

The inequality $\frac{\partial D}{{\partial K_{i}}} < 0$ occurs since a minus sign appears before the summation sign with $K_{i}$ as the upper bound. Since the expression within the summation is positive, increasing the upper bound $K_{i}$ causes lower $D$.

Lemma 1

When Assumptions 1 and 2 are satisfied and $\frac{{c_{i1}}}{{d_{i1}}} > \frac{{c_{j1}}}{{d_{j1}}}$, then $\frac{{\partial x_{i1}}}{{\partial c_{j1}}} > 0$ and $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} > 0$.

Proof

Appendix F.

Lemma 1 assumes that player $i$ is disadvantaged in terms of $c_{i1}/d_{i1}$ being high compared with $c_{j1}/d_{j1}$ for player $j$. Then player $i$ benefits from player $j$’s unit effort cost $c_{j1}$ increasing, and benefits from its own scaling parameter $d_{i1}$ for impact increasing.

Lemma 2

When Assumptions 1 and 2 are satisfied, then $\frac{{\partial x_{i1}}}{{\partial m_{ik}}} > 0\, \text{if }\ln \left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right) < m_{ik} - 1$, $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$.

Proof

Appendix F.

The if-condition in Lemma 2 follows since the dependence of player $i$’s effort $x_{i1}$ on the contest intensity $m_{ik}$ depends on both the characteristics $c_{i1}$ and $d_{i1}$, and on the characteristics $m_{ik}$, $c_{ik}$, and $d_{ik}$ when $k = 2, \ldots,K_{i}$.

Lemma 3

When Assumptions 1 and 2 are satisfied, then $\frac{{\partial x_{ik}}}{{\partial m_{ik}}} > 0 \,\text{if }\ln \left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right) > 1 - \frac{1}{{m_{ik}}}$, $k = 2, \ldots,K_{i},i = 1,2$.

Proof

Appendix F.

The if-condition in Lemma 3 follows since the dependence of player $i$’s effort $x_{ik}$ on the contest intensity $m_{ik}$ depends on the characteristics of these contests.

Lemma 4

When Assumptions 1 and 2 are satisfied, then $\frac{{\partial u_{i}}}{{\partial m_{ik}}} > 0 \, if\ln \left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right) > 0$, $k = 2, \ldots,K_{i},i = 1,2$.

Proof

Appendix F.

The if-condition in Lemma 4 follows since the dependence of player $i$’s expected utility $u_{i}$ on the contest intensity $m_{ik}$ depends on the characteristics of the contests. For example when $\frac{{d_{ik} c_{i1}}}{{d_{i1} c_{ik}}} = 1$ which causes negative logarithm, $u_{i}$ decreases in the contest intensity $m_{ik}$.

Lemma 5

When Assumptions 1 and 2 are satisfied, then $\frac{\partial D}{{\partial m_{ik}}}< {0 \,\text{if }\ln \left({\frac{{m_{ik} c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)} > 0$, $k = 2, \ldots,K_{i},i = 1,2$.

Proof

Appendix F.

The if-condition in Lemma 5 follows since the dependence of rent dissipation $D$ on the contest intensity $m_{ik}$ depends on the characteristics of the contests. For example when $\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}} = 1$ which causes negative logarithm, $D$ increases in the contest intensity $m_{ik}$.

Lemma 6

When Assumptions 1 and 2 are satisfied, and $c_{i1}/d_{i1} = c_{j1}/d_{j1}$, then $\frac{\partial D}{{\partial c_{i1}}} < 0$ and $\frac{\partial D}{{\partial d_{i1}}} > 0$, $i,j = 1,2, i \ne j$.

Proof

Appendix F.

The if-condition $c_{i1} d_{j1} = c_{j1} d_{i1}$ in Lemma 6 follows since the dependence of rent dissipation $D$ on $d_{i1}$ and $c_{i1}$ is complicated.

Appendic G: Examples of $\varvec{x}_{{\varvec{ik}}}$ and $\varvec{x}_{{\varvec{i}1}}$ being substitutes and complements for each other, $\varvec{k} = 2, \ldots,\varvec{K}_{\varvec{i}},\varvec{i} = 1,2$

Inserting $m_{ik} = m_{jk} = \frac{1}{2},c_{i1} = c_{j1} = d_{j1} = c_{ik} = c_{jk} = d_{ik} = d_{jk} = 1$, and $S = 4$, $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$, into $\frac{{\partial x_{i1}}}{{\partial d_{i1}}}$ in (46) in “Appendix F”, (8)–(10) gives

$$\begin{aligned} \frac{{\partial x_{i1}}}{{\partial d_{i1}}} & = \frac{{4(1 - d_{i1})}}{{\left({1 + d_{i1}} \right)^{3}}} + \frac{1}{{d_{i1}^{3}}},x_{i1} = \frac{{4d_{i1}}}{{\left({1 + d_{i1}} \right)^{2}}} - \frac{1}{{2d_{i1}^{2}}},x_{ik} = \frac{1}{{4d_{i1}^{2}}}, \hfill \\ u_{i} & = \frac{{4d_{i1}^{2}}}{{\left({1 + d_{i1}} \right)^{2}}} + \frac{{K_{i} - 1}}{{4d_{i1}^{2}}},D = \frac{1}{4}\mathop \sum \limits_{i = 1}^{2} \left({\frac{{4d_{i1}}}{{\left({1 + d_{i1}} \right)^{2}}} - \frac{{K_{i} - 1}}{{4d_{i1}^{2}}}} \right),\quad k = 2, \ldots,K_{i},i,j = 1,2, i \ne j. \hfill \\ \end{aligned}$$

(50)

Figure 4 panel a plots $x_{i1}$, $x_{ik}$, $u_{i}$, and $D$ as functions of $d_{i1}$ when $K_{i} = 2$, and thus $k = 2$. Division of $u_{i}$ with 4 is for scaling purposes. The efforts $x_{ik}$ and $x_{i1}$ are substitutes due to $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} > 0$ in (50) when $0.72 < d_{i1} < 1.89$. In contrast, $x_{ik}$ and $x_{i1}$ are complements due to $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} < 0$ in (50) when $d_{i1} > 1.89$. Thus $\frac{{\partial x_{i1}}}{{\partial d_{i1}}} = 0$ when $d_{i1} = 1.89$ shown with the rightmost vertical dashed line. The inverse U shape for $x_{i1}$ follows since player $i$ exerts low effort $x_{i1}$ when impact $d_{i1}$ is low. That’s also when player $i$ substitutes from $x_{i1}$ to $x_{ik}$. No need exists to exert high effort when impact $d_{i1}$ is high. The need to exert high effort $x_{i1}$ is when impact $d_{i1}$ is intermediate. Solving the two equations for $x_{ik}$ and $x_{i1}$ in (50) to eliminate $d_{i1}$ gives

$$x_{i1} = \frac{{8\sqrt {x_{ik}}}}{{\left({1 + 2\sqrt {x_{ik}}} \right)^{2}}} - 2x_{ik}$$

(51)

which is plotted in Fig. 4b. $x_{ik}$ and $x_{i1}$ are substitutes when $x_{ik} > 0.0698$, and otherwise complements.

Fig. 4

Parameter values $m_{ik} = m_{jk} = \frac{1}{2},c_{i1} = c_{j1} = d_{j1} = c_{ik} = c_{jk} = d_{ik} = d_{jk} = 1$, $S = 4, K_{i} = 2$. Panel a $x_{i1}$, $x_{ik}$, $u_{i}$, and $D$ as functions of $d_{i1}$. Division of $u_{i}$ with 4 is for scaling purposes. Panel b $x_{i1}$ as a function of $x_{ik}$

Inserting $c_{i1} = c_{ik} = d_{ik} = 1$ into $\frac{{\partial x_{i1}}}{{\partial m_{ik}}}$ in (46) and $\frac{{\partial x_{ik}}}{{\partial m_{ik}}}$ in (47) gives

$$\begin{aligned} \frac{{\partial x_{i1}}}{{\partial m_{ik}}} & > 0\;{\text{and}}\;\frac{{\partial x_{ik}}}{{\partial m_{ik}}} > 0\;\quad {\text{when}}\;d_{i1} = 1\;{\text{and}}\;0 < m_{ik} < 1, \hfill \\ \frac{{\partial x_{i1}}}{{\partial m_{ik}}} & > 0\;{\text{and}}\;\frac{{\partial x_{ik}}}{{\partial m_{ik}}} > 0\;\quad{\text{when}}\;d_{i1} = 2\;{\text{and}}\;0 < m_{ik} < 0.37, \hfill \\ \frac{{\partial x_{i1}}}{{\partial m_{ik}}} & > 0\;{\text{and}}\;\frac{{\partial x_{ik}}}{{\partial m_{ik}}} < 0\;\quad{\text{when}}\;d_{i1} = 2\;{\text{and}}\;0.37 < m_{ik} < 1. \hfill \\ \end{aligned}$$

(52)

Hence, $m_{ik}$ variation causes $x_{ik}$ and $x_{i1}$ to be substitutes in the third instance, and complements in the first two instances.

Appendix H: Corner solution for Sect. 4.3

Assuming that Assumption 4 is not satisfied for player $j$’s first effort, i.e. $x_{j1} \le 0$ according to (11), is written as follows:

Assumption H1

$x_{j1} \le 0 \Leftrightarrow \frac{{S\frac{{x_{i1}^{{1 - m_{i1}}} c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}}}}{{c_{j1} \left({\frac{{x_{i1}^{{1 - m_{i1}}} c_{i1}/d_{i1}}}{{m_{i1} c_{j1}/d_{j1}}} + 1} \right)^{2}}} \le \mathop \sum \limits_{k = 2}^{{K_{j}}} \frac{{d_{jk}}}{{d_{j1}}}\left({\frac{{m_{jk} c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{jk}}}{{1 - m_{jk}}}}},i,j = 1,2, i \ne j$.

When Assumption H1 is satisfied, we set $x_{j1} = 0$. Inserting $x_{j1} = 0$ and $K_{i} = m_{i1} = m_{j1} = 1$ into (5) gives

$$\begin{aligned} x_{j1} & = 0,\frac{{d_{i1} x_{i1}}}{{\left({d_{j2} x_{j2} + \mathop \sum \nolimits_{k = 3}^{{K_{j}}} d_{jk} x_{j2}^{{\frac{{m_{jk} \left({1 - m_{j2}} \right)}}{{1 - m_{jk}}}}} \left({\frac{{m_{jk} c_{j2}/d_{j2}}}{{m_{j2} c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{jk}}}{{1 - m_{jk}}}}} + d_{i1} x_{i1}} \right)^{2}}} = \frac{{c_{j2} x_{j2}^{{1 - m_{j2}}}}}{{Sm_{j2} d_{j2}}}, \hfill \\ x_{jk} & = x_{j2}^{{\frac{{1 - m_{j2}}}{{1 - m_{jk}}}}} \left({\frac{{m_{jk} c_{j2}/d_{j2}}}{{m_{j2} c_{jk}/d_{jk}}}} \right)^{{\frac{1}{{1 - m_{jk}}}}},\quad k = 3, \ldots,K_{j},\frac{{\mathop \sum \nolimits_{k = 2}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}}}{{\left({d_{i1} x_{i1} + \mathop \sum \nolimits_{k = 2}^{{K_{j}}} d_{jk} x_{jk}^{{m_{jk}}}} \right)^{2}}} = \frac{{c_{i1}}}{{Sd_{i1}}}. \hfill \\ \end{aligned}$$

(53)

Solving the last equation in (53) with respect to $x_{i1}$ and inserting the third equation gives

$$x_{{i1}} = \left\{ {\begin{array}{l} {\frac{1}{{d_{{i1}} }}\left( {\sqrt {\frac{{d_{{i1}} S}}{{c_{{i1}} }}} - \sqrt {\mathop \sum \limits_{{k = 2}}^{{K_{j} }} d_{{jk}} x_{{j2}}^{{\frac{{m_{{jk}} \left( {1 - m_{{j2}} } \right)}}{{1 - m_{{jk}} }}}} \left( {\frac{{m_{{jk}} c_{{j2}} /d_{{j2}} }}{{m_{{j2}} c_{{jk}} /d_{{jk}} }}} \right)^{{\frac{{m_{{jk}} }}{{1 - m_{{jk}} }}}} } } \right)} \\ {\quad \times\sqrt {\mathop \sum \limits_{{k = 2}}^{{K_{j} }} d_{{jk}} x_{{j2}}^{{\frac{{m_{{jk}} \left( {1 - m_{{j2}} } \right)}}{{1 - m_{{jk}} }}}} \left( {\frac{{m_{{jk}} c_{{j2}} /d_{{j2}} }}{{m_{{j2}} c_{{jk}} /d_{{jk}} }}} \right)^{{\frac{{m_{{jk}} }}{{1 - m_{{jk}} }}}} } = x_{{i1c}} \quad {\text{when}}\;x_{{jkc}} > 0 } \\ {0\quad \quad \quad {\text{otherwise}}} \\ \end{array} } \right..$$

(54)

Analogously to (45), (54) expresses $x_{i1}$ analytically as a function of $x_{j2}$, but $x_{j2}$ is not analytically solvable since $m_{jk} < 1$ (Assumption 3). Thus numerical solution and the procedure in “Appendix D” are appropriate.

Appendix I: Special cases $\varvec{m}_{{\varvec{ik}}} = \varvec{m}_{\varvec{i}}$ and $\varvec{m}_{{\varvec{ik}}} = \varvec{m}$ of the general solution in Sect. 4.1

Inserting $m_{ik} = m_{i}$, $k = 1,2, \ldots,K_{i}$, into (6) and (7) gives

$$x_{ik} = x_{i1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{{1 - m_{i}}}}},\quad k = 2, \ldots,K_{i},$$

(55)

and

$$x_{i1}^{{m_{i}}} \mathop \sum \limits_{k = 1}^{{K_{i}}} d_{ik} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{i}}}{{1 - m_{i}}}}} = \frac{{Sc_{j1} m_{i}^{2} d_{i1}^{2} m_{j} d_{j1} x_{j1}^{{1 - m_{j}}}}}{{\left({m_{j} d_{j1} c_{i1} x_{i1}^{{1 - m_{i}}} + m_{i} d_{i1} c_{j1} x_{j1}^{{1 - m_{j}}}} \right)^{2}}},$$

(56)

Expressing (56) for both players $i$ and $j$ gives

$$\begin{aligned} \frac{{\left({m_{j} d_{j1} c_{i1} x_{i1}^{{1 - m_{i}}} + m_{i} d_{i1} c_{j1} x_{j1}^{{1 - m_{j}}}} \right)^{2}}}{{Sm_{i} m_{j} d_{i1} d_{j1}}} = \frac{{c_{j1} m_{i} d_{i1} x_{j1}^{{1 - m_{j}}}}}{{x_{i1}^{{m_{i}}} \mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{i}}}{{1 - m_{i}}}}}}}, \hfill \\ \frac{{\left({m_{j} d_{j1} c_{i1} x_{i1}^{{1 - m_{i}}} + m_{i} d_{i1} c_{j1} x_{j1}^{{1 - m_{j}}}} \right)^{2}}}{{Sm_{i} m_{j} d_{i1} d_{j1}}} = \frac{{c_{i1} m_{j} d_{j1} x_{i1}^{{1 - m_{i}}}}}{{x_{j1}^{{m_{j}}} \mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} \left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{j}}}{{1 - m_{j}}}}}}}, \hfill \\ \end{aligned}$$

(57)

which is solved to yield

$$x_{i1} = Q_{i} x_{j1},Q_{i} \equiv \frac{{m_{i} c_{j1}/d_{j1}}}{{m_{j} c_{i1}/d_{i1}}}\frac{{\mathop \sum \nolimits_{k = 1}^{{K_{j}}} d_{jk} \left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{{m_{j}}}{{1 - m_{j}}}}}}}{{\mathop \sum \nolimits_{k = 1}^{{K_{i}}} d_{ik} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{i}}}{{1 - m_{i}}}}}}},i,j = 1,2,i \ne j$$

(58)

which is inserted into (56) and solved to yield

$$Q_{i}^{{m_{i}}} x_{j1}^{{m_{i}}} \mathop \sum \limits_{k = 1}^{{K_{i}}} d_{ik} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{{m_{i}}}{{1 - m_{i}}}}} = \frac{{Sc_{j1} m_{i}^{2} d_{i1}^{2} m_{j} d_{j1} x_{j1}^{{1 - m_{j}}}}}{{\left({m_{j} d_{j1} c_{i1} Q_{i}^{{1 - m_{i}}} x_{j1}^{{1 - m_{i}}} + m_{i} d_{i1} c_{j1} x_{j1}^{{1 - m_{j}}}} \right)^{2}}}.$$

(59)

Equation (59) is one equation with one unknown $x_{j1}$ expressed on implicit form. Once $x_{j1}$ is determined (numerically or otherwise), $x_{i1}$ follows from (58) and $x_{ik}$ follows from (55), $k = 2, \ldots,K_{i}$, $i = 1,2$. The most plausible approach to express $x_{j1}$ in (59) on explicit form is to assume $m_{i} = m_{j} = m$, which is inserted into (59) to yield (14), where (58) and (55) have been inserted. Osorio (2018) considers a special case of (14) where $c_{ik} = c_{i} = c_{j} = c$, $k = 1,2$, $K_{i} = 2$, which is inserted into (14) to yield

$$\begin{aligned} x_{j1}& = \frac{{Smd_{j1}^{{\frac{1}{1 - m}}}}}{{c\left({d_{j1}^{{\frac{1}{1 - m}}} + d_{j2}^{{\frac{1}{1 - m}}}} \right)}}\frac{{\left({d_{i1}^{{\frac{1}{1 - m}}} + d_{i2}^{{\frac{1}{1 - m}}}} \right)^{m - 1} \left({d_{j1}^{{\frac{1}{1 - m}}} + d_{j2}^{{\frac{1}{1 - m}}}} \right)^{m - 1}}}{{\left({\left({d_{i1}^{{\frac{1}{1 - m}}} + d_{i2}^{{\frac{1}{1 - m}}}} \right)^{m - 1} + \left({d_{j1}^{{\frac{1}{1 - m}}} + d_{j2}^{{\frac{1}{1 - m}}}} \right)^{m - 1}} \right)^{2}}}, x_{i1} = Q_{i} x_{j1}, \hfill \\ Q_{i} & = \frac{{d_{i1}^{{\frac{1}{1 - m}}} \left({d_{j1}^{{\frac{1}{1 - m}}} + d_{j2}^{{\frac{1}{1 - m}}}} \right)}}{{d_{j1}^{{\frac{1}{1 - m}}} \left({d_{i1}^{{\frac{1}{1 - m}}} + d_{i2}^{{\frac{1}{1 - m}}}} \right)}}, x_{i2} = x_{i1} \frac{{d_{i2}^{{\frac{1}{1 - m}}}}}{{d_{i1}^{{\frac{1}{1 - m}}}}}, \hfill \\ \end{aligned}$$

(60)

which is equivalent to Osorio’s (2018) Eq. (8) Proposition 3 when $x_{j1} = x_{j} \left(A \right)$, $d_{i1} = \lambda_{1}$, $d_{i2} = \lambda_{2}$, $d_{j1} = 1 - \lambda_{1}$, $d_{j2} = 1 - \lambda_{2}$, $m = {{\alpha}}$, $S = v$, $c = 1$.

Appendix J: First-order derivatives and lemma for Sect. 4.5

Differentiating (14) when $k = 2, \ldots,K_{i},i,j = 1,2, i \ne j$, gives

$$\begin{aligned} V_{i2} & \equiv \mathop \sum \limits_{k = 2}^{{K_{i}}} d_{ik} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{m}{1 - m}}},\frac{{\partial x_{i1}}}{{\partial d_{i1}}} = \frac{{d_{j1} Q_{i}^{m + 1} m\left({V_{i2} \left({V_{j} + V_{i2} Q_{i}^{m}} \right) + d_{i1} \left({\left({V_{j} - d_{i1} Q_{i}^{m}} \right)\left({1 - m} \right) + V_{i2} Q_{i}^{m} m} \right)} \right)S}}{{c_{j1} d_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}}, \hfill \\ \frac{{\partial x_{i1}}}{{\partial d_{j1}}} & = \frac{{d_{i1} Q_{i}^{m} m\left({- V_{j} + V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i1}}}{{\partial d_{ik}}}& = - \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{m}{1 - m}}} d_{j1} Q_{i}^{m + 1} m\left({V_{i} Q_{i}^{m} \left({2 - m} \right) + V_{j} m} \right)S}}{{c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}} < 0, \hfill \\ \frac{{\partial x_{i1}}}{{\partial d_{jk}}} & = \frac{{\left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{m}{1 - m}}} d_{i1} Q_{i}^{m} m\left({- V_{j} + V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i1}}}{{\partial c_{i1}}} & = - \frac{{d_{j1} Q_{i}^{m + 1} m\left({V_{i2} \left({V_{j} + V_{i2} Q_{i}^{m}} \right) + d_{i1} \left({\left({d_{i1} Q_{i}^{m} + V_{i2} Q_{i}^{m}} \right)\left({1 - m} \right)^{2} + V_{i2} Q_{i}^{m} + V_{j} \left({1 - m^{2}} \right)} \right)} \right)S}}{{c_{i1} c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}} < 0, \hfill \\ \frac{{\partial x_{i1}}}{{\partial c_{j1}}} & = \frac{{d_{i1} d_{j1} Q_{i}^{m} m^{2} \left({V_{j} - V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i1}}}{{\partial c_{ik}}} &= \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{m}{1 - m}}} d_{ik} d_{j1} Q_{i}^{m + 1} m^{2} \left({V_{j} m + V_{i} Q_{i}^{m} \left({2 - m} \right)} \right)S}}{{c_{ik} c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}} > 0, \hfill \\ \frac{{\partial x_{i1}}}{{\partial c_{jk}}} & = \frac{{\left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{m}{1 - m}}} d_{i1} d_{jk} Q_{i}^{m} m^{2} \left({V_{j} - V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} c_{jk} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \frac{{\partial x_{i1}}}{\partial S} > 0, \hfill \\ \end{aligned}$$

(61)

and

$$\begin{aligned} \frac{{\partial x_{ik}}}{{\partial d_{i1}}} & = - \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} d_{j1} Q_{i}^{m + 1} m\left({V_{j} m + V_{i} Q_{i}^{m} \left({2 - m} \right)} \right)S}}{{c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}} < 0, \hfill \\ \frac{{\partial x_{ik}}}{{\partial d_{j1}}} & = \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} d_{i1} Q_{i}^{m} m\left({- V_{j} + V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{ik}}}{{\partial d_{ik}}} & = \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} d_{j1} Q_{i}^{m + 1} m\left({c_{i1} V_{i} \left({V_{j} + V_{i} Q_{i}^{m}} \right) - c_{ik} d_{i1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} \left({V_{i} Q_{i}^{m} \left({2 - m} \right) + V_{j} m} \right)} \right)S}}{{c_{j1} c_{i1} d_{ik} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}}, \hfill \\ \frac{{\partial x_{ik}}}{{\partial d_{jk}}} & = \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} \left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{m}{1 - m}}} d_{i1} Q_{i}^{m} m\left({- V_{j} + V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{ik}}}{{\partial c_{i1}}} & = \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} d_{i1} d_{j1} Q_{i}^{m + 1} m^{2} \left({V_{j} m + V_{i} Q_{i}^{m} \left({2 - m} \right)} \right)S}}{{c_{i1} c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}} > 0, \hfill \\ \frac{{\partial x_{ik}}}{{\partial c_{j1}}} & = \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} d_{i1} d_{j1} Q_{i}^{m} m^{2} \left({V_{j} - V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ W_{ij} & \equiv d_{ik} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{m}{1 - m}}} \left({1 - m} \right)^{2} + \mathop \sum \limits_{{\begin{array}{*{20}c} {q = 1,} \\ {q \ne k} \\ \end{array}}}^{{K_{i}}} d_{iq} \left({\frac{{c_{i1}/d_{i1}}}{{c_{iq}/d_{iq}}}} \right)^{{\frac{m}{1 - m}}}, \hfill \\ \frac{{\partial x_{ik}}}{{\partial c_{ik}}} & = - \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} d_{j1} Q_{i}^{m + 1} m\left({c_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)W_{ij} + 2c_{ik} d_{i1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} V_{j} \left({1 - m} \right)m} \right)S}}{{c_{j1} c_{i1} c_{ik} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3} \left({1 - m} \right)}} < 0, \hfill \\ \frac{{\partial x_{ik}}}{{\partial c_{jk}}} & = \frac{{\left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} \left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{1}{1 - m}}} d_{i1} d_{j1} Q_{i}^{m} m^{2} \left({V_{j} - V_{i} Q_{i}^{m}} \right)S}}{{c_{i1} c_{j1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{ik}}}{\partial S} & > 0. \hfill \\ \end{aligned}$$

(62)

Differentiating (15) gives

$$\begin{aligned} X_{ij} & \equiv \frac{{\left({c_{i1} d_{j1} \left({1 - m} \right) + c_{j1} d_{i1} \left({1 + m} \right)Q_{i}^{m - 1}} \right)S}}{{V_{i} \left({c_{i1} d_{j1} + c_{j1} d_{i1} Q_{i}^{m - 1}} \right)^{3}}},\frac{{\partial u_{i}}}{{\partial d_{i1}}} = c_{i1} c_{j1} d_{i1} d_{j1} Q_{i}^{m - 1} X_{ij} > 0, \hfill \\ \frac{{\partial u_{i}}}{{\partial d_{j1}}} & = - c_{j1}^{2} d_{i1}^{2} Q_{i}^{m - 2} X_{ij} < 0,\frac{{\partial u_{i}}}{{\partial d_{ik}}} = c_{i1} c_{j1} d_{i1} d_{j1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{m}{1 - m}}} Q_{i}^{m - 1} X_{ij} > 0, \hfill \\ \frac{{\partial u_{i}}}{{\partial d_{jk}}} & = - c_{j1}^{2} d_{i1}^{2} \left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{m}{1 - m}}} Q_{i}^{m - 2} X_{ij} < 0,\frac{{\partial u_{i}}}{{\partial c_{i1}}} = - c_{j1} d_{i1}^{2} d_{j1} mQ_{i}^{m - 1} X_{ij} < 0, \hfill \\ \frac{{\partial u_{i}}}{{\partial c_{j1}}} & = c_{j1} d_{i1}^{2} d_{j1} mQ_{i}^{m - 2} X_{ij} > 0,\frac{{\partial u_{i}}}{{\partial c_{ik}}} = - c_{j1} d_{i1}^{2} d_{j1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} mQ_{i}^{m - 1} X_{ij} < 0, \hfill \\ \frac{{\partial u_{i}}}{{\partial c_{jk}}} & = c_{j1} d_{i1}^{2} d_{j1} \left({\frac{{c_{j1}/d_{j1}}}{{c_{jk}/d_{jk}}}} \right)^{{\frac{1}{1 - m}}} mQ_{i}^{m - 2} X_{ij} > 0,\frac{{\partial u_{i}}}{\partial S} > 0. \hfill \\ \end{aligned}$$

(63)

Differentiating (16) gives

$$\begin{aligned} \frac{\partial D}{{\partial d_{i1}}} & = \frac{{2V_{j} Q_{i}^{m} m\left({V_{j} - V_{i} Q_{i}^{m}} \right)}}{{\left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \frac{\partial D}{{\partial d_{ik}}} = \frac{{2V_{i} c_{i1} d_{j1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{m}{1 - m}}} mQ_{i}^{m} Q_{i} \left({V_{j} - V_{i} Q_{i}^{m}} \right)}}{{c_{j1} d_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{\partial D}{{\partial c_{i1}}} & = \frac{{2d_{i1} V_{j} Q_{i}^{m} m^{2} \left({- V_{j} + V_{i} Q_{i}^{m}} \right)}}{{c_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}},\frac{\partial D}{{\partial c_{ik}}} = \frac{{2V_{i} d_{i1} d_{j1} \left({\frac{{c_{i1}/d_{i1}}}{{c_{ik}/d_{ik}}}} \right)^{{\frac{1}{1 - m}}} m^{2} Q_{i}^{m} Q_{i} \left({- V_{j} + V_{i} Q_{i}^{m}} \right)}}{{c_{j1} d_{i1} \left({V_{j} + V_{i} Q_{i}^{m}} \right)^{3}}}, \hfill \\ \frac{\partial D}{\partial S} &= 0. \end{aligned}$$

(64)

$\frac{{\partial Q_{i}}}{{\partial K_{i}}} < 0$ since $K_{i}$ appears in (14) as the upper bound of a summation in the denominator. $\frac{{\partial V_{i}}}{{\partial K_{i}}} > 0$. The derivatives $\frac{{\partial x_{i1}}}{{\partial K_{i}}}$, $\frac{{\partial x_{ik}}}{{\partial K_{i}}}$, $\frac{{\partial u_{i}}}{{\partial K_{i}}}$, $\frac{\partial D}{{\partial K_{i}}}$ have no clear signs. $\frac{{\partial x_{i1}}}{\partial m}$, $\frac{{\partial x_{ik}}}{\partial m}$, $\frac{{\partial u_{i}}}{\partial m}$, $\frac{\partial D}{\partial m}$ are too voluminous to analyze analytically.

Lemma 7

When $0 \le m_{ik} = m < 1 \; \forall \; k = 1, \ldots,K_{i}$, $i = 1,2$ and $V_{j} < V_{i} Q_{i}^{m}$, then $\frac{\partial D}{{\partial c_{ik}}} > 0,\frac{\partial D}{{\partial c_{i1}}} > 0,\frac{\partial D}{{\partial d_{ik}}} < 0$, $\frac{\partial D}{{\partial d_{i1}}} < 0$, $k = 2, \ldots,K_{i},i = 1,2$.

Proof

Appendix J.

Lemma 7 confirms the two inequalities $\frac{\partial D}{{\partial c_{ik}}} > 0$ and $\frac{\partial D}{{\partial d_{ik}}} < 0$ in Proposition 5 when$V_{j} < V_{i} Q_{i}^{m}$ is satisfied.

Appendix K: First-order derivatives for Sect. 5.2

Differentiating (20) gives

$$\begin{aligned} \frac{{\partial x_{i\kappa \left(i \right)}}}{\partial S} & > 0,\,\frac{{\partial x_{i\kappa \left(i \right)}}}{{\partial c_{i\kappa \left(i \right)}}} = \frac{{Sm_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({- 1 + m_{j\kappa \left(j \right)} - \left({1 + m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{c_{i\kappa \left(i \right)}^{2} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i\kappa \left(i \right)}}}{{\partial c_{j\kappa \left(j \right)}}} & = \frac{{Sm_{j\kappa \left(j \right)}^{2} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} - 1} \right)}}{{c_{i\kappa \left(i \right)} c_{j\kappa \left(j \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i\kappa \left(i \right)}}}{{\partial d_{i\kappa \left(i \right)}}} &= \frac{{Sm_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} - 1} \right)}}{{c_{i\kappa \left(i \right)} d_{i\kappa \left(i \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i\kappa \left(i \right)}}}{{\partial d_{j\kappa \left(j \right)}}} & = \frac{{Sm_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 - \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{c_{i\kappa \left(i \right)} d_{j\kappa \left(j \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial x_{i\kappa \left(i \right)}}}{{\partial m_{j\kappa \left(j \right)}}} &= \frac{{S\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} + \left({1 - \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)Ln\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}}}} \right)} \right)}}{{c_{i\kappa \left(i \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \end{aligned}$$

(65)

Differentiating (21) gives

$$\begin{aligned} \frac{{\partial u_{i}}}{\partial S}& > 0,\;\frac{{\partial u_{i}}}{{\partial c_{i\kappa \left(i \right)}}} = - \frac{{Sm_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 + m_{j\kappa \left(j \right)} + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{c_{i\kappa \left(i \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial u_{i}}}{{\partial c_{j\kappa \left(j \right)}}} & = \frac{{Sm_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 + m_{j\kappa \left(j \right)} + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{c_{j\kappa \left(j \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial u_{i}}}{{\partial d_{i\kappa \left(i \right)}}} & = \frac{{S\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 + m_{j\kappa \left(j \right)} + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{d_{i\kappa \left(i \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial u_{i}}}{{\partial d_{j\kappa \left(j \right)}}} & = - \frac{{S\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 + m_{j\kappa \left(j \right)} + \left({1 - m_{j\kappa \left(j \right)}} \right)\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{d_{j\kappa \left(j \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{{\partial u_{i}}}{{\partial m_{j\kappa \left(j \right)}}} & = \frac{{S\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({Ln\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)} - 1}}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)} - 1}}}}} \right) - 1} \right) + Ln\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)} + 1}}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)} + 1}}}}} \right) - 1} \right)}}{{\left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}. \hfill \\ \end{aligned}$$

(66)

Differentiating (21) gives

$$\begin{aligned} \frac{\partial D}{\partial S} & = 0,\frac{\partial D}{{\partial c_{i\kappa \left(i \right)}}} = \frac{{2m_{j\kappa \left(j \right)}^{2} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 - \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{c_{i\kappa \left(i \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{\partial D}{{\partial c_{j\kappa \left(j \right)}}} & = \frac{{2m_{j\kappa \left(j \right)}^{2} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} - 1} \right)}}{{c_{j\kappa \left(j \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{\partial D}{{\partial d_{i\kappa \left(i \right)}}} & = \frac{{2m_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} - 1} \right)}}{{d_{i\kappa \left(i \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{\partial D}{{\partial d_{j\kappa \left(j \right)}}} & = \frac{{2m_{j\kappa \left(j \right)} \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 - \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)}}{{d_{j\kappa \left(j \right)} \left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}, \hfill \\ \frac{\partial D}{{\partial m_{j\kappa \left(j \right)}}} & = \frac{{2\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}\left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}} + \left({1 - \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)Ln\left({\frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}}}} \right)} \right)}}{{\left({1 + \frac{{c_{i\kappa \left(i \right)}^{{m_{j\kappa \left(j \right)}}}/d_{i\kappa \left(i \right)}}}{{c_{j\kappa \left(j \right)}^{{m_{j\kappa \left(j \right)}}}/d_{j\kappa \left(j \right)}}}} \right)^{3}}}. \hfill \\ \end{aligned}$$

(67)