Minimum quality standards and benchmarking in differentiated duopoly

Abstract

We study a two-period model of a duopoly with goods differentiated by quality. The periods’ length corresponds to the goods’ useful lifespan, and consumers are heterogeneous in their valuation of quality. In the second period, the regulator fixes a minimum quality standard based either on the quality supplied by the high-quality firm in the first period (strict regulation) or on the average quality supplied in the first period (average regulation). Assuming a covered market, we show that such an approach leads to decreasing qualities in the first period, and increasing qualities in the second one. In both periods, net utility aggregated over consumers is increasing and profits aggregated over firms are decreasing. Taken together, average regulation always leads to an increase in the present value of welfare, whereas strict regulation can cause a decline. If the discount factor exceeds a certain threshold, a policy based on average regulation is even superior to implementing the optimal minimum quality standard already in the first period.

1 Introduction

We study the welfare effects of introducing a minimum quality standard (MQS) based on a benchmarking mechanism into a two-period model of duopoly where products are differentiated by quality. The related literature traces back to the seminal contributions of Ronnen (1991) and Crampes and Hollander (1995) who assume that the demand side is described by a continuum of consumers differing by the value that they assign to quality, and the supply side is given by two firms each offering one single quality. Both firms share the same technology where costs depend on quality. Under the assumption of quality competition in the first stage and price competition in the second stage, the authors show that an appropriately fixed MQS can increase welfare since it intensifies price competition by limiting product differentiation. Subsequently, this model has been modified and extended in several ways. For a detailed overview see Michaelis and Ziesemer (2017, pp. 620).

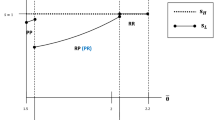
In contrast to the advanced theoretical topics dealt with in the recent MQS-literature,¹ we are concerned with the more basic question of how to fix an appropriate MQS in practical policies. Of course, in a first-best world, it should be fixed in such a way that it maximizes welfare. In practice, however, any such attempt would be hardly feasible due to the regulator’s limited information about preferences and technologies. Therefore, we will analyze an alternative approach that relies on a simple benchmarking procedure. We borrowed this idea from the Japanese Top Runner Program (JTRP) which aims at enhancing the energy-efficiency of energy-consuming goods. The JTRP covers 31 products and obliges their producers to establish the currently highest efficiency level for the respective good by a certain target year (see, e.g., Kimura 2014, METI 2015). Applied to the topic of our paper, this mechanism can be described by a two-period model where the regulator introduces an MQS in period $t = 2$ which is based on the qualities offered in period $t = 1$. We consider two different cases: Under strict regulation, which is perfectly in line with the JTRP, the MQS is fixed according to the quality chosen by the high-quality firm in $t = 1$. Under average regulation, which is a softened variant of the JTRP, the MQS is fixed according to the average quality offered in $t = 1$. The complete time sequence of our model is shown in Fig. 1.

Fig. 1

Time sequence of the model

If we consider only the first period in Fig. 1, the MQS to be introduced in the second period is irrelevant. In this case, our approach corresponds to the standard set-up of a differentiated duopoly with Bertrand competition (e.g., Shaked and Sutton 1982). If we consider only the second period, the MQS is exogenously fixed and our approach resembles the standard set-up used for analyzing the impacts of an MQS in a differentiated duopoly with Bertrand competition (e.g., Crampes and Hollander, 1995). With both periods taken together, however, the MQS becomes endogenous and depends on the firms’ decisions in the first period. In contrast to this, the models employed in the literature usually assume that the MQS either is completely exogenous or results from welfare maximization by a social planner. In virtually none of these models are the firms able to influence the MQS by their choice of quality since the regulator is the first mover and the firms only react to the standard imposed. The only exception is a paper by Lutz et al. (2000) where the high-quality firm moves first and makes a sunk investment in quality which influences the standard resulting from welfare maximization by the regulator. Hence, our model is related to Lutz et al. (2000) but we replace the demanding procedure of welfare maximization by a simple benchmarking approach which can be implemented in practice more easily.²

The economic rationale behind the timing of regulation in our model results from the observation that practical policies often involve a considerable delay between the legal adoption and the actual implementation of a new standard (for empirical evidence see Lutz et al. 2000). Normally, in this transition period the firms are no longer able to influence the forthcoming regulation. In contrast, within a benchmarking approach according to the JTRP, the firms have ample time to shape the impending standard by altering the qualities supplied. This, of course, gives rise to strategic decision-making. In particular, there is an incentive to lower quality in $t = 1$ to dampen the standard to be introduced in $t = 2$. Nevertheless, the following analysis shows that a benchmarking approach based on average regulation can increase welfare in both periods. The underlying effects are an increase in consumers’ utility that always outweighs the decrease in firms’ profits. In contrast, under strict regulation the forthcoming standard is too severe such that the gains in welfare are smaller or even negative depending on the discount factor applied by the firms. For the case of more than two firms, we find in line with the basic literature on the effects of an MQS in oligopoly (Scarpa 1998; Pezzino 2010) that welfare will decrease under both regulatory schemes.

The remainder of our paper is organized as follows. In Sect. 2, we introduce the model and in Sect. 3, we calculate the unregulated equilibrium. In Sect. 4, we derive the regulated equilibria for two different benchmarking approaches. In Sect. 5, we analyze the resulting welfare effects and compare them to the outcome obtained from applying the optimal MQS. In Sect. 6, we briefly consider the case of more than two firms, and finally in Sect. 7 we discuss our main conclusions.

2 The model

Due to the complexity added by the dynamics to be considered below, we keep our model as simple as possible.³ The time horizon covers two periods $t = 1,2$ where the length of each period corresponds to the useful lifespan of the considered goods. There exist two firms $j = H, L$ each producing a single variant differentiated by quality $q_{jt} \ge 0$. Without loss in generality, we assume $q_{Ht} \ge q_{Lt}$, i.e., firm $H$ is the high- and firm $L$ is the low-quality producer. The price of variant $j$ in period $t$ is denoted by $p_{jt}$. Both firms share the same technology where costs per unit are independent of quantity but increasing in quality. In line with several other studies on MQS,⁴ we assume quadratic unit costs $c\left( {q_{jt} } \right) = \gamma q_{jt}^{2}$ with $\gamma > 0$.

The demand side consists of a unit mass of consumers indexed by $i$, each buying one unit per period. The net utility of consumer $i$ buying variant $j$ in period $t$ is given by $\overline{u} + \alpha_{i} q_{jt} - p_{jt}$. The term $\overline{u}$ indicates a baseline utility independent of quality which is assumed to be sufficiently large to ensure that the market is always completely covered (see, e.g., Kuhn 2007).⁵ Moreover, $\alpha_{i}$ which is distributed uniformly on the interval $\alpha_{i} \in \left[ {a,a + z} \right]$ with $a \ge 0$ and $z > 0$ represents the individual valuation of quality by the consumer $i$. Solving the equation $\overline{u} + \alpha_{i} q_{Ht} - p_{Ht} = \overline{u} + \alpha_{i} q_{Lt} - p_{Lt}$ for $\alpha_{i}$ yields the indifferent consumer’s position in period $t$: $\hat{\alpha }_{t} = \left( {p_{Ht} - p_{Lt} } \right)/\left( {q_{Ht} - q_{Lt} } \right)$. The accompanying market shares are given by $s_{Lt} = \left( {\hat{\alpha }_{t} - a} \right)/z$ for firm $L$ and $s_{Ht} = 1 - s_{Lt} = \left( {a + z - \hat{\alpha }_{t} } \right)/z$ for firm $H$.

In each period, firms compete in two stages: In the quality game in stage one, they simultaneously choose qualities $q_{jt}$, and in the price game in stage two they simultaneously choose prices $p_{jt}$. In period $t = 1$ there is no regulation of quality, whereas in period $t = 2$ an MQS denoted by $\overline{q}$ is introduced. Strict regulation implies $\overline{q} = q_{H1}$ and average regulation implies $\overline{q} = \left( {q_{L1} + q_{H1} } \right)/2$. The solution concept is subgame perfect equilibrium, i.e., we solve the model backwards.

3 Unregulated equilibrium

Without regulation, there are no dynamic effects and the equilibria in both periods will be identical. Hence, it suffices to calculate the equilibrium for a representative period $t$. As can easily be checked for the price game in the second stage, maximizing the firms’ profits $\pi_{jt} = s_{jt} \left( {p_{jt} - \gamma q_{jt}^{2} } \right)$ and solving the resulting reaction functions for the prices $p_{jt}$ yields:

$$p_{{{\text{Lt}}}} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) = {{\left[ {\left( {z - a} \right)\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right) + \gamma \left( {q_{{{\text{Ht}}}}^{2} + 2q_{{{\text{Lt}}}}^{2} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {z - a} \right)\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right) + \gamma \left( {q_{{{\text{Ht}}}}^{2} + 2q_{{{\text{Lt}}}}^{2} } \right)} \right]} 3}} \right. \kern-\nulldelimiterspace} 3}$$

(1)

$$p_{{{\text{Ht}}}} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) = {{\left[ {\left( {a + 2z} \right)\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right) + \gamma \left( {2q_{{{\text{Ht}}}}^{2} + q_{{{\text{Lt}}}}^{2} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {a + 2z} \right)\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right) + \gamma \left( {2q_{{{\text{Ht}}}}^{2} + q_{{{\text{Lt}}}}^{2} } \right)} \right]} 3}} \right. \kern-\nulldelimiterspace} 3}$$

(2)

Inserting (1) and (2) into $\hat{\alpha }_{t}$ as calculated in Sect. 2 yields the indifferent consumer’s position solely in terms of qualities: $\hat{\alpha }_{t} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) = \left[ {2a + z + \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]/3$. The corresponding market shares are:

$$s_{{{\text{Lt}}}} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) = {{\left[ {z - a + \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {z - a + \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]} {3z}}} \right. \kern-\nulldelimiterspace} {3z}}$$

(3)

$$s_{{{\text{Ht}}}} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) = {{\left[ {2z + a - \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {2z + a - \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]} {3z}}} \right. \kern-\nulldelimiterspace} {3z}}$$

(4)

Hence, a duopoly equilibrium with both firms active in the market (which is the one of interest in this paper) requires $a - z < \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right) < a + 2z$ such that $s_{jt} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) > 0$ for $j = H, L$. In the next step, the reduced profit functions that we need for the quality game in the first stage can be calculated by inserting (1) to (4) into $\pi_{jt} = s_{jt} \left( {p_{jt} - \gamma q_{jt}^{2} } \right)$:

$$\pi_{{{\text{Lt}}}} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) = {{\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right)\left[ {a - z - \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]^{2} } \mathord{\left/ {\vphantom {{\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right)\left[ {a - z - \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]^{2} } {9z}}} \right. \kern-\nulldelimiterspace} {9z}},$$

(5)

$$\pi_{{{\text{Ht}}}} \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right) = {{\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right)\left[ {a + 2z - \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]^{2} } \mathord{\left/ {\vphantom {{\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right)\left[ {a + 2z - \gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)} \right]^{2} } {9z}}} \right. \kern-\nulldelimiterspace} {9z}}.$$

(6)

The first-order conditions $\partial \pi_{jt } \left( {q_{{{\text{Ht}}}} ,q_{{{\text{Lt}}}} } \right)/\partial q_{jt} = 0$ lead to the following reaction functions:

$$q_{{{\text{Lt}}}} \left( {q_{{{\text{Ht}}}} } \right) = {{\left( {a - z + \gamma q_{{{\text{Ht}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {a - z + \gamma q_{{{\text{Ht}}}} } \right)} {3\gamma }}} \right. \kern-\nulldelimiterspace} {3\gamma }}$$

(7)

$$q_{{{\text{Ht}}}} \left( {q_{{{\text{Lt}}}} } \right) = {{\left( {a + 2z + \gamma q_{{{\text{Lt}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {a + 2z + \gamma q_{{{\text{Lt}}}} } \right)} {3\gamma }}} \right. \kern-\nulldelimiterspace} {3\gamma }}.$$

(8)

Due to $\partial q_{{{\text{Lt}} }} \left( {q_{{{\text{Ht}}}} } \right)/\partial q_{{{\text{Ht}}}} > 0$ and $\partial q_{{{\text{Ht}} }} \left( {q_{{{\text{Lt}}}} } \right)/\partial q_{{{\text{Lt}}}} > 0$ qualities are strategic complements. Solving (7) and (8) for $q_{jt}$ yields $q_{{{\text{Lt}}}}^{o} = \left( {4a - z} \right)/8\gamma$ and $q_{{{\text{Ht}}}}^{o} = \left( {4a + 5z} \right)/8\gamma$.⁶⁷ However, since negative values for quality are ruled out, $q_{{{\text{Lt}}}}^{o}$ and $q_{{{\text{Ht}}}}^{o}$ represent the equilibrium only if $z \le 4a$. In contrast, for $z > 4a$ the consumers’ preferences are too heterogeneous and our model leads to a corner solution where the firm $L$ always chooses $\tilde{q}_{{{\text{Lt}}}}^{o} = 0$ and firm $H$ chooses $\tilde{q}_{{{\text{Ht}}}}^{o} = \left( {a + 2z} \right)/3\gamma$ according to (8).

In the following, we concentrate on the more interesting case of an interior solution with $z \le 4a$. In the next step, inserting $q_{{{\text{Lt}}}}^{o}$ and $q_{{{\text{Ht}}}}^{o}$ into (1) and (2) yields the accompanying prices $p_{{{\text{Lt}}}}^{o} = \left[ {8a\left( {2a - z} \right) + 25z^{2} } \right]/64\gamma$ and $p_{{{\text{Ht}}}}^{o} = \left[ {8a\left( {2a + 5z} \right) + 49z^{2} } \right]/64\gamma$. Moreover, it can easily be calculated that the indifferent consumer is located at the center of the market, i.e. $\hat{\alpha }_{t}^{o} = a + \left( {z/2} \right)$, and the market shares are $s_{jt}^{o} = 1/2$ with profits of $\pi_{jt}^{o} = 3z^{2} /16\gamma$ for $j = H,L$. Hence, everything else equal, the higher the degree of heterogeneity in consumers’ preferences (given by the parameter $z$), the higher the firms’ profits are. The economic explanation is straightforward: Preferences that are more heterogeneous increase the importance of differences in quality from the viewpoint of consumers. This, in turn, relaxes price competition and increases profits (see, e.g., Shaked and Sutton 1982).

4 Regulated equilibria

Before analyzing the equilibria for strict regulation with $\overline{q}^{s} = q_{H1}$ and average regulation with $\overline{q}^{a} = \left( {q_{L1} + q_{H1} } \right)/2$, it is useful to consider the general effects of introducing a binding standard $\overline{q} > q_{{{\text{Lt}}}}^{o}$ in period $t$. Concerning the price game in the second stage, there is no difference from the unregulated case analyzed above. However, in the quality game in the first stage, the standard forces firm $L$ to increase its quality up to $q_{{{\text{Lt}}}} \left( {\overline{q}} \right) = \overline{q}$ and firm $H$ will decide for $q_{{{\text{Ht}}}} \left( {\overline{q}} \right) = \left( {a + 2z + \gamma \overline{q}} \right)/3\gamma$ according to its reaction function (8). Inserting $q_{{{\text{Lt}}}} \left( {\overline{q}} \right)$ and $q_{{{\text{Ht}}}} \left( {\overline{q}} \right)$ into the reduced profit functions (5) and (6) yields the profits solely in terms of $\overline{q}$:

$$\pi_{{{\text{Lt}}}} \left( {\overline{q}} \right) = {{\left( {a + 2z - 2\gamma \overline{q}} \right)\left( {2a - 5z - 4\gamma \overline{q}} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a + 2z - 2\gamma \overline{q}} \right)\left( {2a - 5z - 4\gamma \overline{q}} \right)^{2} } {243z\gamma }}} \right. \kern-\nulldelimiterspace} {243z\gamma }},$$

(9)

$$\pi_{{{\text{Ht}}}} \left( {\overline{q}} \right) = {{4\left( {a + 2z - 2\gamma \overline{q}} \right)^{3} } \mathord{\left/ {\vphantom {{4\left( {a + 2z - 2\gamma \overline{q}} \right)^{3} } {243z\gamma }}} \right. \kern-\nulldelimiterspace} {243z\gamma }}.$$

(10)

Comparing $\pi_{{{\text{Ht}}}} \left( {\overline{q}} \right)$ with the unregulated profit $\pi_{Ht}^{o}$ and taking into account $\overline{q} > q_{{{\text{Lt}}}}^{o}$ reveals $\pi_{{{\text{Ht}}}} \left( {\overline{q}} \right) < \pi_{{{\text{Ht}}}}^{o}$ such that firm $H$ is worse off under the standard. In contrast, for firm $L$ we obtain $\pi_{{{\text{Lt}}}} \left( {\overline{q}} \right) > \pi_{{{\text{Lt}}}}^{{\text{o}}}$ if $\overline{q} < \hat{q}$ with $\hat{q}: = \left[ {8a - z\left( {11 - 9\sqrt 5 } \right)} \right]/16\gamma > q_{Lt}^{o}$. Hence, firm $L$ gains from the standard as long as it is not too severe and satisfies the condition $\overline{q} < \hat{q}$. The economic intuition is based on two effects: First, both firms suffer since the standard limits the scope for product differentiation and tightens price competition. Second, as already emphasized by Ronnen (1991, p.500) and Crampes and Hollander (1995, p.76), the standard applied enables firm $L$ to commit to quality which has the same effect as granting a first-mover advantage to it. If the standard satisfies $\overline{q} < \hat{q}$, firm $L^{\prime}s$ advantage from the commitment effect outweighs its disadvantage from the tightened price competition and its profit increases.

4.1 Strict regulation

Replacing $\overline{q}$ in (9) and (10) for $t = 2$ by the strict standard $\overline{q}^{s} = q_{H1}$ yields the firms’ second-period profits solely as a function of firm $H^{\prime}s$ decision on quality in period $t = 1$:

$$\pi_{L2}^{s} \left( {q_{H1} } \right) = {{\left( {a + 2z - 2\gamma q_{H1} } \right)\left( {2a - 5z - 4\gamma q_{H1} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a + 2z - 2\gamma q_{H1} } \right)\left( {2a - 5z - 4\gamma q_{H1} } \right)^{2} } {243z\gamma }}} \right. \kern-\nulldelimiterspace} {243z\gamma }},$$

(11)

$$\pi_{H2}^{s} \left( {q_{H1} } \right) = {{4\left( {a + 2z - 2\gamma q_{H1} } \right)^{3} } \mathord{\left/ {\vphantom {{4\left( {a + 2z - 2\gamma q_{H1} } \right)^{3} } {243z\gamma }}} \right. \kern-\nulldelimiterspace} {243z\gamma }}.$$

(12)

With their decisions in $t = 1$, both firms $j = H, L$ aim at maximizing the present value of total profits $\Pi_{j}^{s} \left( {q_{H1} ,q_{L1} } \right): = \pi_{j1} \left( {q_{H1} ,q_{L1} } \right) + \delta \cdot \pi_{j2}^{s} \left( {q_{H1} } \right)$.⁸ The parameter $\delta \in \left( {0,1} \right]$ indicates the discount factor. In the following, we use the abbreviation $\lambda : = \sqrt {9 - 8\delta }$ for simplifying terms. It should carefully be noted that $\lambda$ is a strictly decreasing function of $\delta$ with $\lambda \in \left[ {1,3} \right)$.

From the first-order conditions, $\partial \Pi_{j}^{s} \left( {q_{H1} ,q_{L1} } \right)/\partial q_{j1} = 0$ we derive the reaction functions $q_{L1}^{s} \left( {q_{H1} } \right) = \left( {a - z + \gamma q_{H1} } \right)/3\gamma$ and $q_{H1}^{s} \left( {q_{L1} } \right) = \left[ {\lambda \left( {a + 2z} \right) + 3\gamma q_{L1} } \right]/\gamma \left( {3 + 2\lambda } \right)$. For firm $L$ we obtain the same reaction function as in the unregulated case because $L$ is not able to influence the second-period outcome via the choice of $q_{L1}$. In contrast, the new reaction function of firm $H$ implies that for any given $q_{L1}$ firm $H$ will choose a lower level of quality than in the unregulated case: $q_{H1}^{s} \left( {q_{L1} } \right) < q_{H1}^{o} \left( {q_{L1} } \right)$. The economic rationale is obvious since everything else equal the profits of firm $H$ in period $t = 2$ are the lower, the higher is $\overline{q}^{s}$.

Next, solving $q_{L1}^{s} \left( {q_{H1} } \right)$ and $q_{H1}^{s} \left( {q_{L1} } \right)$ for $q_{j1}$ yields the qualities resulting in period ${ }t = 1$ under strict regulation⁹:

$$q_{L1}^{s} = {{\left[ {a\left( {1 + \lambda } \right) - z} \right]} \mathord{\left/ {\vphantom {{\left[ {a\left( {1 + \lambda } \right) - z} \right]} {2\gamma \left( {1 + \lambda } \right)}}} \right. \kern-\nulldelimiterspace} {2\gamma \left( {1 + \lambda } \right)}},$$

(13)

$$q_{H1}^{s} = {{\left[ {a\left( {1 + \lambda } \right) + z\left( {2\lambda - 1} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {a\left( {1 + \lambda } \right) + z\left( {2\lambda - 1} \right)} \right]} {2\gamma \left( {1 + \lambda } \right)}}} \right. \kern-\nulldelimiterspace} {2\gamma \left( {1 + \lambda } \right)}}.$$

(14)

In the following, we again concentrate on the more interesting case of an interior solution.¹⁰ Comparing $q_{j1}^{s}$ with the outcome of the unregulated case reveals that both firms will lower their quality: $q_{j1}^{s} < q_{j1}^{o}$. The economic reasoning is that firm $H$ reduces its quality because of the standard’s detrimental effect on its second-period profits, and this decrease in $q_{H1}$ induces firm $L$ also to reduce its quality since qualities are strategic complements.

Moreover, due to $q_{H1}^{s} \left( {q_{L1} } \right) < q_{H1}^{o} \left( {q_{L1} } \right)$ we observe a decreasing degree of product differentiation: $q_{H1}^{s} - q_{L1}^{s} < q_{H1}^{o} - q_{L1}^{o}$. The economic rationale for this result is the assumption $\partial^{2} c(q)/\partial q^{2} > 0$ which implies for any $q_{H} > q_{L}$ that improving quality is more costly for firm $H$ than for firm $L$ (see also Ronnen 1991, p.498).

In the next step, from inserting $q_{L1}^{s}$ and $q_{H1}^{s}$ into (1) and (2) for $t = 1$ we obtain the equilibrium prices:

$$p_{L1}^{s} = {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} - 6az\left( {1 + \lambda } \right) + \left( {3 + 8\lambda^{2} } \right)z^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} - 6az\left( {1 + \lambda } \right) + \left( {3 + 8\lambda^{2} } \right)z^{2} } \right]} {12\gamma \left( {1 + \lambda } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {12\gamma \left( {1 + \lambda } \right)^{2} }},$$

(15)

$$p_{H1}^{s} = {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} + 6az\left( {1 + \lambda } \right)\left( {2\lambda - 1} \right) + \left( {3 + 16\lambda^{2} } \right)z^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} + 6az\left( {1 + \lambda } \right)\left( {2\lambda - 1} \right) + \left( {3 + 16\lambda^{2} } \right)z^{2} } \right]} {12\gamma \left( {1 + \lambda } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {12\gamma \left( {1 + \lambda } \right)^{2} }}.$$

(16)

Compared to the unregulated case, both prices are decreasing: $p_{j1}^{s} < p_{j1}^{o}$. From an economic point of view, this result does not come as a surprise since production costs decrease due to $q_{j1}^{s} < q_{j1}^{o}$ and price competition intensifies due to $q_{H1}^{s} - q_{L1}^{s} < q_{H1}^{o} - q_{L1}^{o}$.

Finally, inserting $q_{L1}^{s}$ and $q_{H1}^{s}$ into (3)–(6) yields market shares of $s_{L1}^{s} = 2\lambda /3\left( {1 + \lambda } \right) < s_{L1}^{o}$ and $s_{H1}^{s} { = }\left( {3 + \lambda } \right)/{3}\left( {1 + \lambda } \right){ > }s_{H1}^{o}$ with accompanying profits of $\pi_{L1}^{s} = 4z^{2} \lambda^{3} /9\gamma \left( {1 + \lambda } \right)^{3} < \pi_{L1}^{o}$ and $\pi_{H1}^{s} = z^{2} \lambda \left( {3 + \lambda } \right)^{2} /9\gamma \left( {1 + \lambda } \right)^{3} > \pi_{H1}^{o}$. Hence, despite the intensified price competition, in $t = 1$ the high-quality firm gains from the regulation. The economic reason is obvious: Analogous to the findings of Ronnen (1991, p. 500) and Crampes and Hollander (1995, p.76), firm $H^{\prime}s$ influence on the forthcoming standard enables it to commit to quality and this advantage outweighs its disadvantage caused by the more intense price competition.

We now turn to period $t = 2$. The results above imply $q_{H1}^{s} > q_{L2}^{o}$ such that the standard $\overline{q}^{s}$ is binding for firm $L$.¹¹ Consequently, we obtain from $q_{L2}^{s} = q_{H1}^{s}$:

$$q_{L2}^{s} = {{\left[ {a\left( {1 + \lambda } \right) + z\left( {2\lambda - 1} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {a\left( {1 + \lambda } \right) + z\left( {2\lambda - 1} \right)} \right]} {2\gamma \left( {1 + \lambda } \right)}}} \right. \kern-\nulldelimiterspace} {2\gamma \left( {1 + \lambda } \right)}}.$$

(17)

Next, inserting $q_{L2}^{s}$ into firm $H^{\prime}s$ reaction function (8) for $t = 2$ yields:

$$q_{H2}^{s} = {{\left[ {a\left( {1 + \lambda } \right) + z\left( {2\lambda + 1} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {a\left( {1 + \lambda } \right) + z\left( {2\lambda + 1} \right)} \right]} {2\gamma \left( {1 + \lambda } \right)}}} \right. \kern-\nulldelimiterspace} {2\gamma \left( {1 + \lambda } \right)}}.$$

(18)

Compared to the unregulated case we obtain $q_{j2}^{s} > q_{j2}^{o}$ and $q_{H2}^{s} - q_{L2}^{s} < q_{H2}^{o} - q_{L2}^{o}$. Hence, qualities increase and the degree of product differentiation decreases again. Moreover, inserting the qualities $q_{L2}^{s}$ and $q_{H2}^{s}$ into (1) and (2) for $t = 2$ yields the equilibrium prices:

$$p_{L2}^{s} = {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} + 6az\left( {1 + \lambda } \right)\left( {2\lambda - 1} \right) + \left( {7 + 12\lambda^{2} } \right)z^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} + 6az\left( {1 + \lambda } \right)\left( {2\lambda - 1} \right) + \left( {7 + 12\lambda^{2} } \right)z^{2} } \right]} {12\gamma \left( {1 + \lambda } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {12\gamma \left( {1 + \lambda } \right)^{2} }},$$

(19)

$$p_{H2}^{s} = {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} + 6az\left( {1 + \lambda } \right)\left( {2\lambda + 1} \right) + \left[ {11 + 12\lambda \left( {1 + \lambda } \right)} \right]z^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {3a^{2} \left( {1 + \lambda } \right)^{2} + 6az\left( {1 + \lambda } \right)\left( {2\lambda + 1} \right) + \left[ {11 + 12\lambda \left( {1 + \lambda } \right)} \right]z^{2} } \right]} {12\gamma \left( {1 + \lambda } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {12\gamma \left( {1 + \lambda } \right)^{2} }}.$$

(20)

At first glance, the standard’s impact on prices in $t = 2$ is ambiguous because qualities and production costs increase but product differentiation decreases. However, as shown in Appendix A.2, for the case of an interior solution the effect of a smaller product differentiation dominates such that prices will increase in total.

Next, inserting $q_{j2}^{s}$ into (3)–(6) yields market shares of $s_{L2}^{s} { = }\left( {1 + 3\lambda } \right)/{3}\left( {1 + \lambda } \right){ > }s_{L2}^{o}$ and $s_{H2}^{s} { = 2}/{3}\left( {1 + \lambda } \right){ < }s_{H2}^{o}$ with profits of $\pi_{L2}^{s} { = }z^{2} \left( {1 + 3\lambda } \right)^{2} /9\gamma \left( {1 + \lambda } \right)^{3}$ and $\pi_{H2}^{s} { = }4z^{2} /9\gamma \left( {1 + \lambda } \right)^{3}$. Comparing firm $H^{\prime}s$ profit to the unregulated case shows $\pi_{H2}^{s} { < }\pi_{H2}^{o}$. For firm $L$, however, the relation between $\pi_{L2}^{s}$ and $\pi_{L2}^{o}$ depends on the magnitude of the discount factor $\delta$: we obtain $\pi_{L2}^{s} { < }\pi_{L2}^{o}$ if $\delta < \hat{\delta }$ and $\pi_{L2}^{s} { > }\pi_{L2}^{o}$ if $\delta > \hat{\delta }$ with $\hat{\delta }: = \left( {13 - 3\sqrt 5 } \right)/18 \approx 0.350$. The economic explanation of this result is straightforward: From the discussion at the beginning of Sect. 4, we already know that firm $L$ is better off under a minimum quality standard that is not too severe. However, if the discount factor falls short of the threshold $\hat{\delta }$, the adaption of quality by firm $H$ in period $t = 1$ will be too weak. Therefore, the standard introduced in $t = 2$ will be too high and the profit of firm $L$ will decrease because its disadvantage from an intensified price competition outweighs its advantage from being able to commit to quality.

The analysis presented so far, however, entails a possible caveat that should carefully be recognized¹²: To ensure that $\left\{ {q_{H1}^{s} ,q_{L1}^{s} } \right\}$ is indeed a Nash-equilibrium it must hold that none of the two firms has an incentive to change its quality as long as the other firm sticks to $q_{j1}^{s}$. Concerning firm $L$ this condition is obviously satisfied since $L$ is not able to influence the forthcoming standard. In contrast, firm $H$ could choose a quality $q_{H1} \le q_{Lt}^{o}$ such that the standard in the second period is non-binding. Compared to $q_{H1}^{s}$ this would lead to a smaller degree of product differentiation and $\pi_{H1}$ would decrease whereas $\pi_{H2}$ would increase up to the unregulated level $\pi_{H2}^{o}$. In Appendix 2 we show that such a strategy does not pay for $H$ and our solution $\left\{ {q_{H1}^{s} ,q_{L1}^{s} } \right\}$ is indeed a Nash-equilibrium.

Before proceeding to summarize our key findings in Proposition 1, we note that for the sake of clarity we display all thresholds regarding the discount factor $\delta$ in our Propositions as numerical figures rounded to three digits. We chose this approach because the formulas describing the exact magnitudes of the thresholds are extremely complex since they result from solving power equations of a higher order.

Proposition 1

Introducing a standard $\overline{q}^{s} = q_{H1}$ in $t = 2$ induces a unique subgame perfect equilibrium with qualities $q_{jt}^{s}$ according to (13), (14), (17) and (18). A comparison with the unregulated case reveals the following effects (see Appendix A.2):

 − Qualities: $q_{j1}^{s} < q_{j1}^{o}$ and $q_{j2}^{s} > q_{j2}^{o}$ for $j = H, L$ ; $q_{Ht}^{s} - q_{Lt}^{s} < q_{Ht}^{o} - q_{Lt}^{o}$ for $t = 1,2$ .

 − Prices: $p_{j1}^{s} < p_{j1}^{o}$ and $p_{j2}^{s} > p_{j2}^{o}$ for $j = H, L$ .

 − Profits: $\pi_{H1}^{s} > \pi_{H1}^{o}$, $\pi_{L1}^{s} < \pi_{L1}^{o}$, $\pi_{H2}^{s} < \pi_{H2}^{o}$  and  $\pi_{L2}^{s} \left\{ {\begin{array}{*{20}c} { > \pi_{L2}^{o} \, {\text{if}}\, \delta > 0.350} \\ { < \pi_{L2}^{o} \, {\text{if}}\, \delta < 0.350} \\ \end{array} } \right.$.

Finally, we note that everything else equal, the effects described in Proposition 1 are in period $t = 1$ the weaker and in period $t = 2$ the stronger, the lower is the discount factor $\delta$. The economic intuition behind this result is clear: Lowering the discount factor reduces the weight attached to the outcome in the second period. This, in turn, diminishes the incentive for a pre-emptive lowering of qualities in the first period and strengthens the standard imposed in the second period.

4.2 Average regulation

We now turn to the case of average regulation. The main difference to strict regulation relates to the additional strategic incentive stemming from firm $L^{\prime}s$ ability to influence the standard directly. Replacing $\overline{q}$ in (9) and (10) for $t = 2$ by $\overline{q}^{a} = \left( {q_{L1} + q_{H1} } \right)/2$ yields the firms’ second-period profits as a function of their decisions on quality in period $t = 1$:

$$\pi_{L2}^{a} \left( {q_{H1} ,q_{L1} } \right) = {{\left[ {a + 2z - \gamma \left( {q_{H1} + q_{L1} } \right)} \right]\left[ {2a - 5z - 2\gamma \left( {q_{H1} + q_{H1} } \right)} \right]^{2} } \mathord{\left/ {\vphantom {{\left[ {a + 2z - \gamma \left( {q_{H1} + q_{L1} } \right)} \right]\left[ {2a - 5z - 2\gamma \left( {q_{H1} + q_{H1} } \right)} \right]^{2} } {243z\gamma }}} \right. \kern-\nulldelimiterspace} {243z\gamma }},$$

(21)

$$\pi_{H2}^{a} \left( {q_{H1,} q_{L1} } \right) = {{4\left[ {a + 2z - \gamma \left( {q_{H1} + q_{L1} } \right)} \right]^{3} } \mathord{\left/ {\vphantom {{4\left[ {a + 2z - \gamma \left( {q_{H1} + q_{L1} } \right)} \right]^{3} } {243z\gamma }}} \right. \kern-\nulldelimiterspace} {243z\gamma }}.$$

(22)

The profits in the first period, $\pi_{j1} \left( {q_{H1} ,q_{L1} } \right)$, still follow from inserting $t = 1$ into (5) and (6), and the present value of profits is $\Pi_{j}^{a} \left( {q_{H1} ,q_{L1} } \right): = \pi_{j1} \left( {q_{H1} ,q_{L1} } \right) + \delta \cdot \pi_{j2}^{a} \left( {q_{H1} ,q_{L1} } \right)$. From the first-order conditions $\partial \Pi_{j}^{a} \left( {q_{H1} ,q_{L1} } \right)/\partial q_{j1} = 0$ we obtain the following reaction functions with $\Theta : = 144a\left( {a - 2z} \right) + z^{2} \left[ {711 - \left( {72 - \lambda^{2} } \right)\lambda^{2} } \right]$¹³:

$$q_{L1}^{a} \left( {q_{H1} } \right) = {{\left[ {\left( {a - z} \right)\left( {90 - 2\lambda^{2} } \right) - 2\gamma \left( {27 - \lambda^{2} } \right)q_{H1} + 3\sqrt {\Theta + 576\gamma \left( {z - a + \gamma q_{H1} } \right)q_{H1} } } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {a - z} \right)\left( {90 - 2\lambda^{2} } \right) - 2\gamma \left( {27 - \lambda^{2} } \right)q_{H1} + 3\sqrt {\Theta + 576\gamma \left( {z - a + \gamma q_{H1} } \right)q_{H1} } } \right]} {2\gamma \left( {63 - \lambda^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {2\gamma \left( {63 - \lambda^{2} } \right)}},$$

(23)

$$q_{H1}^{a} \left( {q_{L1} } \right) = {{\left[ {\left( {a + 2z} \right)\left( {9 + \lambda^{2} } \right) + \gamma \left( {27 - \lambda^{2} } \right)q_{L1} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {a + 2z} \right)\left( {9 + \lambda^{2} } \right) + \gamma \left( {27 - \lambda^{2} } \right)q_{L1} } \right]} {\gamma \left( {45 + \lambda^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\gamma \left( {45 + \lambda^{2} } \right)}} .$$

(24)

As indicated by (24), the reaction function of firm $H$ is still linearly increasing in $q_{L1}$ but its slope has changed. Compared to the reaction function under strict regulation we obtain $\partial q_{H1}^{a} \left( {q_{L1} } \right)/\partial q_{L1} > \partial q_{H1}^{s} \left( {q_{L1} } \right)/\partial q_{L1}$ if $\delta < 9\left( {\sqrt 2 - 1} \right)/4 \approx 0.932$. Hence, for a wide range of possible discount factors firm $H$ reacts stronger to a change in $q_{L1}$ to compensate for its partial loss of control over the forthcoming standard.

With $q_{L1}$ drawn at the vertical axis, the reaction function of firm $L$ as given by (23) is now U-shaped with a minimum at $\tilde{q}_{H1} = \left[ {12\left( {a - z} \right) + z\left( {27 - \lambda^{2} } \right)\sqrt {\left( {9 - \lambda^{2} } \right)/\left( {9 + \lambda^{2} } \right)} } \right]/24\gamma .$ The economic rationale behind this shape is that a decrease in $q_{H1}$ induces two opposite effects on the optimal decision of firm $L$. On the one hand, a decrease in $q_{H1}$ leads to an incentive to reduce $q_{L1}$ to maintain a certain level of product differentiation. This is the same mechanism as under strict regulation. On the other hand, however, there is now also an incentive to increase $q_{L1}$ because within a certain range a higher standard intensifies firm $L^{\prime}s$ advantage from being able to commit to quality in $t = 2$.¹⁴ Hence, for $q_{H1} > \tilde{q}_{H1}$ the former incentive dominates over the latter one, whereas for $q_{H1} < \tilde{q}_{H1}$ the opposite holds.¹⁵

Solving the above reaction functions (23) and (24) for $q_{j1}$ leads to the qualities supplied in period $t = 1$ under average regulation¹⁶:

$$q_{L1}^{a} = {{\left[ {864a - z\left[ {1107 + \left( {18 - \lambda^{2} } \right)\lambda^{2} - \left( {45 + \lambda^{2} } \right)\sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right]} \right]} \mathord{\left/ {\vphantom {{\left[ {864a - z\left[ {1107 + \left( {18 - \lambda^{2} } \right)\lambda^{2} - \left( {45 + \lambda^{2} } \right)\sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right]} \right]} {1728\gamma }}} \right. \kern-\nulldelimiterspace} {1728\gamma }} ,$$

(25)

$$q_{H1}^{a} = {{\left[ {864a + z\left[ {27 + \left( {90 - \lambda^{2} } \right)\lambda^{2} + \left( {27 - \lambda^{2} } \right)\sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right]} \right]} \mathord{\left/ {\vphantom {{\left[ {864a + z\left[ {27 + \left( {90 - \lambda^{2} } \right)\lambda^{2} + \left( {27 - \lambda^{2} } \right)\sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right]} \right]} {1728\gamma }}} \right. \kern-\nulldelimiterspace} {1728\gamma }} .$$

(26)

Inserting $q_{L1}^{a}$ and $q_{H1}^{a}$ into $\overline{q}^{a} = \left( {q_{L1} + q_{H1} } \right)/2$ yields the standard to be introduced in the second period: $\overline{q}^{a} = \left[ {24a + z\left( {\lambda^{2} - 15 + \eta } \right)} \right]/48\gamma$ with $\eta : = \left[ {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } \right]^{1/2}$. Due to $\overline{q}^{a} > q_{L2}^{o}$ for $\lambda \in \left[ {1,3} \right)$ this standard is binding for firm $L$. Consequently, we obtain:

$$q_{L2}^{a} = {{\left[ {24a + z\left( {\lambda^{2} - 15 + \sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {24a + z\left( {\lambda^{2} - 15 + \sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right)} \right]} {48\gamma }}} \right. \kern-\nulldelimiterspace} {48\gamma }} .$$

(27)

Moreover, inserting $q_{L2}^{a}$ into firm $H^{\prime}s$ reaction function (8) for ${\text{t } = \text{ 2}}$ yields:

$$q_{H2}^{a} = {{\left[ {72a + z\left( {\lambda^{2} + 81 + \sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {72a + z\left( {\lambda^{2} + 81 + \sqrt {405 - \left( {18 - \lambda^{2} } \right)\lambda^{2} } } \right)} \right]} {144\gamma }}} \right. \kern-\nulldelimiterspace} {144\gamma }} .$$

(28)

The remaining lines of calculation concerning prices, market shares and profits are the same as in Sect. 4.1. We, therefore, confine ourselves to summarize the corresponding results as compactly as possible using the abbreviations $\eta : = \left[ {405 - \lambda^{2} \left( {18 - \lambda^{2} } \right)} \right]^{1/2}$ and $\varphi : = 63 - \eta - \lambda^{2}$ for simplifying terms. In $t = 1$, the resulting prices are:

$$p_{L1}^{a} = {{\left[ {48z^{2} \varphi \left( {9 + \lambda^{2} } \right)\left( {9 + \eta + \lambda^{2} } \right) + \left[ {z\left[ {\left( {\eta - 18} \right)\lambda^{2} + 45\eta - 1107 + \lambda^{4} } \right] + 864a} \right]^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {48z^{2} \varphi \left( {9 + \lambda^{2} } \right)\left( {9 + \eta + \lambda^{2} } \right) + \left[ {z\left[ {\left( {\eta - 18} \right)\lambda^{2} + 45\eta - 1107 + \lambda^{4} } \right] + 864a} \right]^{2} } \right]} {2985984\gamma }}} \right. \kern-\nulldelimiterspace} {2985984\gamma }},$$

(29)

$$p_{H1}^{a} = {{\left[ {48z^{2} \varphi^{2} \left( {9 + \lambda^{2} } \right) + \left[ {z\left[ {\left( {\eta - 90} \right)\lambda^{2} - 27\left( {\eta + 1} \right) + \lambda^{4} } \right] - 864a} \right]^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {48z^{2} \varphi^{2} \left( {9 + \lambda^{2} } \right) + \left[ {z\left[ {\left( {\eta - 90} \right)\lambda^{2} - 27\left( {\eta + 1} \right) + \lambda^{4} } \right] - 864a} \right]^{2} } \right]} {2985984\gamma }}} \right. \kern-\nulldelimiterspace} {2985984\gamma }}.$$

(30)

The market share of firm $L$ in $t = 1$ is $s_{L1}^{a} = \left( {9 + \lambda^{2} + \eta } \right)/72$,¹⁷ and the accompanying profits are $\pi_{L1}^{a} = z^{2} \varphi \left( {9 + \lambda^{2} } \right)\left( {9 + \lambda^{2} + \eta } \right)^{2} /4478976\gamma$ and $\pi_{H1}^{a} = z^{2} \varphi^{3} \left( {9 + \lambda^{2} } \right)/4478976\gamma$. For $t = 2$, we obtain prices of:

$$p_{L2}^{a} = {{\left[ {8z^{2} \varphi \left( {45 + \eta + \lambda^{2} } \right) + 27\left[ {24a + z\left( {\eta + \lambda^{2} - 15} \right)} \right]^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {8z^{2} \varphi \left( {45 + \eta + \lambda^{2} } \right) + 27\left[ {24a + z\left( {\eta + \lambda^{2} - 15} \right)} \right]^{2} } \right]} {62208\gamma }}} \right. \kern-\nulldelimiterspace} {62208\gamma }},$$

(31)

$$p_{H2}^{a} = {{\left[ {8z^{2} \varphi^{2} + 3\left[ {72a + z\left( {\eta + \lambda^{2} + 81} \right)} \right]^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {8z^{2} \varphi^{2} + 3\left[ {72a + z\left( {\eta + \lambda^{2} + 81} \right)} \right]^{2} } \right]} {62208\gamma }}} \right. \kern-\nulldelimiterspace} {62208\gamma }}.$$

(32)

The market share of firm $L$ in $t = 2$ is $s_{L2}^{a} = \left( {45 + \lambda^{2} + \eta } \right)/108$, and the accompanying profits are $\pi_{L2}^{a} = z^{2} \varphi \left( {45 + \lambda^{2} + \eta } \right)^{2} /839808\gamma$ and $\pi_{H2}^{a} = z^{2} \varphi^{3} /839808\gamma$.

Finally, in Appendix A.3 we proof analogously to the case of strict regulation that none of the two firms has an incentive to strive or a non-binding standard. Proposition 2 summarizes our key findings from comparing average regulation with the unregulated case:

Proposition 2

Introducing a standard $\overline{q}^{a} = \left( {q_{L1} + q_{H1} } \right)/2$ in $t = 2$ induces a unique subgame perfect equilibrium with qualities according to (25)–(28). A comparison with the unregulated case reveals the following effects (see Appendix A.3):

 − Qualities: $q_{j1}^{a} < q_{j1}^{o}$ and $q_{j2}^{a} > q_{j2}^{o}$ for $j = H, L$ ; $q_{Ht}^{a} - q_{Lt}^{a} < q_{Ht}^{o} - q_{Lt}^{o}$ for $t = 1,2$ .

 − Prices: $p_{j1}^{a} < p_{j1}^{o}$ and $p_{j2}^{a} > p_{j2}^{o}$ for $j = H, L$ .

 − Profits: $\pi_{H1}^{a}$ $\left\{ {\begin{array}{*{20}c} { < \pi_{H1}^{o} \,\,{\text{if}}\,\,\delta > 0.696} \\ { > \pi_{H1}^{o} \,{\text{if}} \,\delta < 0.696} \\ \end{array} } \right.$ , $\pi_{L1}^{a} < \pi_{L1}^{o}$ , $\pi_{H2}^{a} < \pi_{H2}^{o}$ and $\pi_{L2}^{a} > \pi_{L2}^{o}$ .

As expected, a comparison of Propositions 1 and 2 shows that the general impacts of both regulations are quite similar: qualities decrease in the first period and increase in the second period, whereas product differentiation decreases in both periods. The only differences relate to the change in the firms’ profits compared to the unregulated equilibrium. In contrast to strict regulation, firm $H^{\prime}s$ profit in $t = 1$ will now decrease if the discount factor is sufficiently high, and firm $L^{\prime}s$ profit in $t = 2$ will now always increase. The economic reason is that switching from strict to average regulation advantages firm $L$ and disadvantages firm $H$ which is no longer able to decide on the standard alone.

Moreover, due to $q_{L2}^{a} < q_{L2}^{s}$ (see Proposition 3 below) the standard under average regulation is always lower compared to its counterpart under strict regulation: $\overline{q}^{a} < \overline{q}^{s}$.

5 Welfare analysis

We denote welfare in period $t$ by $W_{t} \left( {q_{{{\text{Lt}}}} ,q_{{{\text{Ht}}}} } \right): = \Pi_{t} \left( {q_{{{\text{Lt}}}} ,q_{{{\text{Ht}}}} } \right) + U_{t} \left( {q_{{{\text{Lt}}}} ,q_{{{\text{Ht}}}} } \right)$. The first summand indicates profits aggregated over both firms and the second summand indicates net utility aggregated over consumers. Aggregated profits can easily be calculated by adding up the reduced profit functions [5] and [6]:

$$\Pi_{t} \left( {q_{{{\text{Lt}}}} ,q_{{{\text{Ht}}}} } \right) = {{\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right)\left[ {5z^{2} + 2a\left( {a + z} \right) + 2\gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)\left[ {\gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right) - 2a - z} \right]} \right]} \mathord{\left/ {\vphantom {{\left( {q_{{{\text{Ht}}}} - q_{{{\text{Lt}}}} } \right)\left[ {5z^{2} + 2a\left( {a + z} \right) + 2\gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right)\left[ {\gamma \left( {q_{{{\text{Ht}}}} + q_{{{\text{Lt}}}} } \right) - 2a - z} \right]} \right]} {9z}}} \right. \kern-\nulldelimiterspace} {9z}}.$$

(33)

To derive aggregated net utility, we start with the observation that consumers characterized by $\alpha_{i} < \hat{\alpha }_{t} \left( {q_{{{\text{Lt}}}} ,q_{{{\text{Ht}}}} } \right)$ buy variant $L$, whereas consumers characterized by $\alpha_{i} > \hat{\alpha }_{t} \left( {q_{{{\text{Lt}}}} ,q_{{{\text{Ht}}}} } \right)$ buy variant $H$. Since $\alpha_{i}$ is distributed uniformly on $\alpha_{i} \in \left[ {a,a + z} \right]$, the position of the average consumer buying variant $L$ is $\tilde{\alpha }_{Lt} \left( {q_{Lt} ,q_{Ht} } \right) = 0.5\left[ {a + \hat{\alpha }_{t} \left( {q_{Lt} ,q_{Ht} } \right)} \right]$, and the position of the average consumer buying $H$ is $\tilde{\alpha }_{Ht} \left( {q_{Lt} ,q_{Ht} } \right) = 0.5\left[ {a + z + \hat{\alpha }_{t} (q_{Lt} ,q_{Ht} )} \right]$. Consequently, the net utility of the average consumer buying variant $j$ in period $t$ can be calculated as $\tilde{u}_{jt} \left( {q_{Lt} ,q_{Ht} } \right) = \overline{u} + \tilde{\alpha }_{jt} \left( {q_{Lt} ,q_{Ht} } \right) \cdot q_{jt} - p_{jt} \left( {q_{Lt} ,q_{Ht} } \right)$. Finally, weighting $\tilde{u}_{jt} \left( {q_{Lt} ,q_{Ht} } \right)$ by market shares $s_{jt} \left( {q_{Lt} ,q_{Ht} } \right)$ and adding up over both variants $j = L,H$ yields the consumers’ aggregated net utility:

$$U_{t} \left( {q_{Lt} ,q_{Ht} } \right)\sum\nolimits_{j = L,H} {s_{jt} \left( {q_{Lt} ,q_{Ht} } \right)\left[ {\overline{u} + \tilde{\alpha }_{jt} \left( {q_{Lt} ,q_{Ht} } \right) \cdot q_{jt} - p_{jt} \left( {q_{Lt} ,q_{Ht} } \right)} \right]}.$$

(34)

As point of reference, we first calculate the optimal standard, denoted by $\overline{q}^{ * }$. Inserting $q_{Lt} \left( {\overline{q}} \right) = \overline{q}$ as well as $q_{Ht} \left( {\overline{q}} \right) = \left( {a + 2z + \gamma \overline{q}} \right)/3\gamma$ into (33), (34) and adding up both expressions, we obtain welfare in period $t$ directly as a function of the standard, i.e. $W_{t} \left( {\overline{q}} \right)$. Solving $\partial W_{t} \left( {\overline{q}} \right)/\partial \overline{q} = 0$ for $\overline{q}$ and verifying the second-order condition yields:

$$\overline{q}^{ * } = {{\left[ {40a + z\left( {3\sqrt {145} - 25} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {40a + z\left( {3\sqrt {145} - 25} \right)} \right]} {80\gamma }}} \right. \kern-\nulldelimiterspace} {80\gamma }}.$$

(35)

Due to $\overline{q}^{ * } > q_{Lt}^{o}$ the standard is binding for firm $L$. Hence, the resulting qualities are $q_{Lt}^{ * } = \overline{q}^{ * }$ and $q_{Ht}^{ * } = \left[ {40a + z\left( {\sqrt {145} + 45} \right)} \right]/80\gamma .$ However, before proceeding, it is important to note that applying $\overline{q}^{ * }$ will increase welfare but it will not lead to the optimal combination of qualities that maximizes $W_{t} \left( {q_{Lt} ,q_{Ht} } \right)$.¹⁸ The economic reason is that the introduction of an MQS only allows the regulator to directly control the decision of firm $L$. In contrast, firm $H$ continues to follow its reaction function (8) such that for any quality $q_{Lt}$ enforced by an MQS the corresponding quality $q_{Ht}$ is predetermined. Hence, like strict or average regulation, even an optimized MQS is also only a second best solution.

Comparing $\overline{q}^{ * }$ with $\overline{q}^{s}$ reveals $\overline{q}^{s} > \overline{q}^{ * }$ for $\delta \in (0,1]$. Hence, under strict regulation the standard is always too severe compared to the optimal one. In contrast, for average regulation we obtain $\overline{q}^{a} < \overline{q}^{ * }$ if $\delta > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }$ and $\overline{q}^{a} > \overline{q}^{ * }$ if $\delta < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }$ with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } : = 3\left( {55 - \sqrt {145} } \right)/160 \approx 0.806$ (see Appendix A.4 for both results).

In the following welfare analysis, we compare strict and average regulation not only with each other but also with the (hypothetical) case that the regulator has complete information about the firms’ cost functions and the consumers’ preferences and introduces the optimal standard $\overline{q}^{ * }$ already in period $t = 1$. As a pre-requisite, Proposition 3 summarizes our results from comparing qualities and product differentiation:

Proposition 3

Comparing the regulatory schemes’ impacts on the qualities supplied in equilibrium reveals $q_{j1}^{ * } > \max \,\{ q_{j1}^{s} ,q_{j1}^{a} \}$ and $q_{j2}^{s} > q_{j2}^{a}$ for $j = H,L$ as well as (see Appendix A.4 ):

$$q_{L1}^{a} < q_{L1}^{s} \,\,if\,\,\delta < 0.349,q_{H1}^{a} < q_{H1}^{s} \,\,if\,\,\delta < 0.829,\,q_{L2}^{a} > q_{L2}^{ * } \,\,if\,\,\delta < 0.806,\,q_{H2}^{a} > q_{H2}^{ * } \,\,if\,\,\delta < 0.806.$$

$$q_{L1}^{a} > q_{L1}^{s} \,\,if\,\,\delta > 0.349,\,q_{H1}^{a} > q_{H1}^{s} \,\,if\,\,\delta > 0.829,\,q_{L2}^{a} < q_{L2}^{ * } \,\,if\,\,\delta > 0.806,q_{H2}^{a} < q_{H2}^{ * } \,\,if\,\,\delta > 0.806.$$

Moreover, concerning the degree of product differentiation, denoted by $\Delta q_{t} : = q_{Ht} - q_{Lt}$, we obtain $\Delta q_{1}^{s} > \Delta q_{1}^{a}$, $\Delta q_{2}^{a} > \Delta q_{2}^{s}$, $\Delta q_{2}^{ * } > \Delta q_{2}^{s}$ and:

$$\Delta q_{1}^{s} > \Delta q_{1}^{ * } \,\,\,if\,\,\,\delta < 0.898,\,\Delta q_{1}^{a} > \Delta q_{1}^{ * } \,\,\,if\,\,\,\delta < 0.736,\,\Delta q_{2}^{a} < \Delta q_{2}^{ * } \,\,\,{\text{if}}\,\,\,\delta < 0.806.$$

$$\Delta q_{1}^{s} < \Delta q_{1}^{ * } \,\,\,if\,\,\,\delta > 0.898,\,\Delta q_{1}^{a} < \Delta q_{1}^{ * } \,\,\,if\,\,\,\delta > 0.736,\,\Delta q_{2}^{a} > \Delta q_{2}^{ * } \,\,\,{\text{if}}\,\,\,\delta > 0.806.$$

Based on our previous analysis, most of the results stated in Proposition 3 are not surprising. Concerning the first period, however, we find for a sufficiently small discount factor that the pre-emptive reduction in quality is under average regulation stronger than under strict regulation (i.e., $q_{j1}^{a} < q_{j1}^{s}$). In this case, the less stringent regulation leads to the stronger adaption in $t = 1$. The economic reason for this somewhat unexpected result is the joint-effect caused by the impact of discounting on the firms’ reaction functions as discussed above. In particular, lowering the discount factor increases firm $L^{\prime}s$ incentive to lower quality and at the same time firm $H^{\prime}s$ reaction to a decrease in $q_{L1}$ becomes stronger compared to the case of strict regulation. Both effects reinforce each other in diminishing qualities.

Next, inserting the equilibrium-qualities calculated above for the unregulated case as well as for the different standards into (33) yields the firms’ aggregated profits. Comparing the resulting expressions leads to Proposition 4:

Proposition 4

Denoting profits aggregated over firms in period t by $\Pi_{t}$ and comparing the different standards with each other as well as with the unregulated case reveals $\Pi_{t}^{o} > \max \,\{ \Pi_{t}^{s} ,\Pi_{t}^{a} ,\Pi_{t}^{ * } \}$ for $t = 1,2$ and (see Appendix A.5):

$$\begin{array}{*{20}l} {\Pi_{1}^{s} > \Pi_{1}^{a} > \Pi_{1}^{ * } \,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta < 0.662} \hfill \\ {\Pi_{1}^{s} > \Pi_{1}^{ * } > \Pi_{1}^{a} \,\,\,{\text{if}}\,\,\,0.662 < \delta < 0.898} \hfill \\ {\Pi_{1}^{ * } > \Pi_{1}^{s} > \Pi_{1}^{a} \,\,\,i{\text{f}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta > 0.898} \hfill \\ \end{array} \,{\text{and}}\;\begin{array}{*{20}l} {\Pi_{2}^{ * } > \Pi_{2}^{a} > \Pi_{2}^{s} \,\,\,{\text{if}}\,\,\,\delta < 0.806} \hfill \\ {\Pi_{2}^{a} > \Pi_{2}^{ * } > \Pi_{2}^{s} \,\,\,i{\text{f}}\,\,\,\delta > 0.806.} \hfill \\ \end{array}$$

Compared to the unregulated case, firms’ aggregated profits are decreasing in both periods and under each of the standards considered. Moreover, a direct comparison between strict and average regulation reveals that the decrease in aggregated profits under average regulation is in the first period stronger than under strict regulation whereas in the second period the opposite holds. The economic explanation are the standards’ different impacts on the degree of product differentiation and the intensity of price competition as stated in Proposition 3: In $t = 1$, average regulation leads to a lower degree of product differentiation (implying a more intense price competition) than strict regulation, and in $t = 2$ the reverse is true.

Finally, the ranking between strict or average regulation on the one hand and the optimal standard, on the other hand, depends on the discount factor $\delta$. In general, the higher the discount factor, the more likely is the optimal standard superior in the first period, and the opposite holds in the second period.

We now turn to the demand side. Inserting the equilibrium-qualities calculated above into (34) yields the consumers’ aggregated net utility. By comparing the resulting expressions, we derive Proposition 5:

Proposition 5

Denoting net utility aggregated over consumers in period t by $U_{t}$ and comparing the different standards with each other as well as with the unregulated case reveals $U_{t}^{o} < \min \,\{ U_{t}^{s} ,U_{t}^{a} ,U_{t}^{ * } \}$ for $t = 1,2$ and (see Appendix A.6 ):

$$\begin{array}{*{20}l} {U_{1}^{ * } > U_{1}^{a} > U_{1}^{s} \,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta < 0.636} \hfill \\ {U_{1}^{a} > U_{1}^{ * } > U_{1}^{s} \,\,\,{\text{if}}\,\,\,0.636 < \delta < 0.898} \hfill \\ {U_{1}^{a} > U_{1}^{s} > U_{1}^{ * } \,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta > 0.898} \hfill \\ \end{array} \,\,\,{\text{and}}\,\,\begin{array}{*{20}l} {U_{2}^{a} > U_{2}^{ * } > U_{2}^{s} \,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta < 0.433} \hfill \\ {U_{2}^{a} > U_{2}^{s} > U_{2}^{ * } \,\,\,i{\text{f}}\,\,\,0.433 < \delta < 0.549} \hfill \\ {U_{2}^{s} > U_{2}^{a} > U_{2}^{ * } \,\,\,{\text{if}}\,\,\,0.549 < \delta < 0.806} \hfill \\ {U_{2}^{s} > U_{2}^{ * } > U_{2}^{a} \,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta > 0.806.} \hfill \\ \end{array}$$

Compared to the unregulated case, consumers ‘aggregated net utility is increasing in both periods and under each of the standards considered. The economic reason is obvious: In the first period, under strict or average regulation the positive effects of decreasing prices dominate the negative effects of decreasing qualities, whereas under the optimal standard the positive effects of increasing qualities dominate the negative effects of increasing prices. In the second period, the latter relation between positive and negative effects holds under the optimal standard as well as under strict or average regulation.

Moreover, a direct comparison between strict and average regulation shows that in the first period average regulation is always superior. In contrast, in the second period the relation depends on the discount factor: The higher $\delta$, the more likely is strict regulation superior compared to average regulation. Likewise, the ranking between strict or average regulation on the one hand and the optimal standard, on the other hand, depends on the discount factor: In the first period, increasing $\delta$ diminishes the relative attractiveness of the optimal standard, whereas in the second period there is no uniform pattern.

Next, we consider welfare in period t. Inserting the equilibrium-qualities calculated above into $W_{t} \left( {q_{Lt} ,q_{Ht} } \right)$ and comparing the expressions obtained leads to Proposition 6:

Proposition 6

Denoting welfare in period t by $W_{t}$ and comparing the effects of the different standards with each other as well as with the unregulated case reveals (see Appendix A.7 ):

$$\begin{array}{*{20}l} {W_{1}^{ * } > W_{1}^{a} > W_{1}^{s} > W_{1}^{o} \,\,\,{\text{if}}\,\,\,\delta < 0.520} \hfill \\ {W_{1}^{a} > W_{1}^{ * } > W_{1}^{s} > W_{1}^{o} \,\,\,{\text{if}}\,\,\,\delta > 0.520} \hfill \\ \end{array} \,\,{\text{and}}\,\,\begin{array}{*{20}l} {W_{2}^{ * } > W_{2}^{a} > W_{2}^{o} > W_{2}^{s} \,\,\,{\text{if}}\,\,\,\delta < 0.901} \hfill \\ {W_{2}^{ * } > W_{2}^{a} > W_{2}^{s} > W_{2}^{o} \,\,\,{\text{if}}\,\,\,\delta > 0.901.} \hfill \\ \end{array}$$

However, there exist two exceptions from the above relations: For $\delta = 0.898$ we obtain $W_{1}^{ * } = W_{1}^{s}$ and for $\delta = 0.806$ we obtain $W_{2}^{ * } = W_{2}^{a}$.¹⁹

Hence, compared to the unregulated situation, average regulation is beneficial in both periods since the consumers’ increase in net utility dominates the firms’ losses in profits. In contrast, the increase in welfare caused by strict regulation is always smaller compared to average regulation and can even become negative in the second period. The latter occurs if the discount factor falls short of the threshold $\delta \approx 0.901$. In this case, the reduction of quality by firm $H$ in period $t = 1$ is not strong enough such that the standard introduced in period $t = 2$ will be too severe. The economic rationale behind this result is in line with Crampes and Hollander (1995, p. 77) who conclude that an MQS “sufficiently close to the quality chosen by the low-quality producer in the unregulated equilibrium” can improve welfare.

Moreover, a comparison with the welfare effects of the optimal standard $\overline{q}^{ * }$ leads for $t = 1$ to the (possibly surprising) result that average regulation is superior to applying $\overline{q}^{ * }$ if the discount factor exceeds the threshold $\delta \approx 0.520$. In this case, the reduction in qualities (accompanied by lower prices) induced under average regulation is more beneficial than the increase in qualities (accompanied by higher prices) enforced by the optimal standard. The economic background of this result is the above-mentioned observation that average regulation as well as applying the optimal standard are both only second-best solutions. Hence, there is no a priori reason to suppose that one of these solutions is always superior to the other.

In the last step, we consider the standards, impact on the present value of total welfare denoted by $W(q_{Lt,} q_{Ht} ): = W_{1} (q_{L1,} q_{H1} ) + \delta \cdot W_{2} (q_{L2,} q_{H2} )$.²⁰ Inserting the equilibrium-qualities calculated above and analyzing the resulting expressions leads to our final proposition:

Proposition 7:

Denoting the present value of total welfare by $W$ and comparing the effects of the different standards with each other as well as with the unregulated case reveals (see Appendix A.8 ):

$$\begin{array}{*{20}l} {W^{ * } > W^{a} > W^{o} > W^{s} \,\,\,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta < 0.558} \hfill \\ {W^{a} > W^{ * } > W^{o} > W^{s} \,\,\,\,\,{\text{if}}\,\,\,\,\,0.558 < \delta < 0.747} \hfill \\ {W^{a} > W^{ * } > W^{s} > W^{o} \,\,\,\,\,{\text{if}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\delta > 0.747.} \hfill \\ \end{array}$$

Under average regulation, the gains in welfare compared to the unregulated case are a strictly increasing function of the discount factor $\delta$.

Hence, despite of the firms’ strategic incentive to dampen the forthcoming standard, the introduction of an MQS based on the average quality initially supplied always leads to an increase in the present value of welfare. If the discount factor exceeds the threshold $\delta \approx 0.558$, the gains in welfare under average regulation are even higher than those obtained from applying the optimal MQS. In contrast, an MQS based on the high quality initially supplied leads only to a smaller increase in welfare that becomes even negative if the discount factor falls short of the threshold $\delta \approx 0.747$.

Moreover, everything else equal, the gains in welfare under average regulation are the higher, the higher is the discount factor applied. Of course, one might suspect that this result is trivial since it might be solely driven by the diminishing effect of discounting on the present value of welfare enjoyed in the second period. To dispel this suspicion we also calculated normalized welfare $\tilde{W}(q_{Lt} ,q_{Ht} ): = [1/(1 + \delta )] \cdot W_{1} (q_{L1} ,q_{H1} ) + [\delta /(1 + \delta )] \cdot W_{2} (q_{L2} ,q_{H2} )$. This transformation eliminates the direct effect of $\delta$ on the weight attached to the second period and leaves only the strategic effects on the firms’ decisions. In Appendix A.8, we show that the difference $\tilde{W}(q_{Lt}^{a} ,q_{Ht}^{a} ) - \tilde{W}(q_{Lt}^{o} ,q_{Ht}^{o} )$, which indicates the gains in welfare compared to the unregulated situation, is strictly increasing in $\delta$.

Finally, we note that all results derived above rely on the assumption of a covered market. This requires that even the consumer with the lowest valuation of quality (i.e., $\alpha_{i} = a$) decides to buy the good. Since this consumer chooses variant L, the general condition for market-coverage in period t is $\overline{u} + aq_{Lt} - p_{Lt} > 0$. This implies that the baseline utility $\overline{u}$ has to exceed the threshold $\hat{u}_{t} : = p_{Lt} - aq_{Lt}$. Inserting $p_{Lt}^{o}$ and $q_{Lt}^{o}$ yields the threshold for the unregulated case: $\hat{u}_{t}^{o} = \left( {25z^{2} - 16a^{2} } \right)/64\gamma$. This threshold is the lower, the higher is the minimum valuation of quality given by the parameter $a$. Hence, assuming a covered market in the unregulated case is justified if either the baseline utility or the minimum valuation of quality (or a suitable combination of both) is sufficiently high such that $\overline{u} > \hat{u}_{t}^{o}$.

Concerning market-coverage under quality regulation, we concentrate on the more beneficial case of average regulation. Calculating along the same lines as above we arrive at the respective thresholds $\hat{u}_{1}^{a}$ and $\hat{u}_{2}^{a}$. As shown in Appendix A.9, both thresholds are strictly increasing in $\lambda$. Hence, to derive a sufficient condition for market coverage, it suffices to examine $\hat{u}_{t}^{a}$ for the case of $\lambda = 3$. In doing so, we obtain $\hat{u}_{1}^{a} = \hat{u}_{t}^{o}$ for $t = 1$. Consequently, if the market is covered without regulation it will also be covered under average regulation in $t = 1$.²¹ For $t = 2$, however, we obtain $\hat{u}_{2}^{a} = \left( {19z^{2} - 12a^{2} } \right)/48\gamma > \hat{u}_{t}^{o}$. I.e., even if the market is covered in the first period, it might switch to an uncovered one in the second period.

6 The case of more than two firms

Our analysis above concentrated on the case of duopoly although this might lead to results that are not robust if the number of firms becomes larger. To our best knowledge, Scarpa (1998) and Pezzino (2010) are the only two studies yielding a comprehensive analysis of this issue.²² Both authors concentrate on a constellation with three firms. In contrast to our approach, they assume that (1) the MQS is exogenously given such that it does not depend on the firms’ decisions, (2) the market is always uncovered and (3) there are only quality-dependent fixed cost. Contrary to the common findings for the case of duopoly, both authors show that introducing a binding MQS always reduces welfare.

Since our approach partly differs from Scarpa (1998) und Pezzino (2010), it is a priori unclear whether their result can be transferred to an MQS based on benchmarking as studied in the present paper. We, therefore, analyzed an extended numerical version of our model assuming that there is a third firm $M$ that offers a quality between $q_{Lt}$ and $q_{Ht}$. In line with the studies cited above, our results suggest that strict as well as average regulation will reduce welfare if there are three firms.²³ The main economic reason is that with more than two firms the differences between the optimal and the unregulated qualities become almost negligible (see also Schmidt 2009). Hence, introducing an MQS in such a situation implies harmful overregulation even if the standard is based on benchmarking.

7 Conclusions

We analyzed a two-period model of an MQS based on benchmarking in a differentiated duopoly. Although we are aware that our model is by far too simple to derive definite policy conclusions, we identified at least two interesting implications:

• −First, in principle, a standard based on benchmarking can increase welfare but this approach should be handled with care since it entails the risk that the resulting standard is too severe and might even reduce welfare. Therefore, the average quality supplied in the market seems to be a more suitable benchmark than the high quality.

• −Second, everything else equal, the gains in welfare resulting from a benchmark based on the average quality are the higher, the higher is the discount factor applied by the firms. For a given annual discount rate, however, the discount factor will be the higher the shorter is the considered good’s useful lifespan that determines the length of each period in our model. Consequently, our benchmarking approach seems to be particularly beneficial for goods that are not too long-lived.

However, the significance of our results is limited by several restrictive assumptions. Examples are the use of a quadratic cost function and the assumption that the valuation of quality is uniformly distributed across consumers. The most serious limitation of our model presumably stems from the assumption of a covered market. In particular, our analysis has shown that a market, which is covered without regulation, might switch to an uncovered market after the MQS has been introduced in the second period.

Within the framework of our model, the assumption of full market-coverage is justified if either the baseline utility or the minimum valuation of quality (or a suitable combination of both) is sufficiently high. Whether this condition will be satisfied in practice, mainly depends on the specific good under consideration and on the question which particular feature of this good is regulated by the MQS. Suitable examples where the above condition is likely to be satisfied are safety regulations of cars and pharmaceuticals as well as regulations concerning the quality of medical services and devices. Moreover, there exists a wide range of quality-regulated goods and services whose consumption is mandatory due to legal requirements. In this case, the market will automatically be covered irrespective of the magnitude of baseline utility or the minimum valuation of quality. Prominent examples are several kinds of mandatory safety products like cyclists’ helmets, smoke detectors or child safety seats for cars. Further examples relate to mandatory insurances for, e.g., health care or vehicle third-party liability.

Of course, in practice there also exist numerous cases of quality-regulated goods, where the assumption of full market-coverage is at least questionable. For instance, the regulated feature of goods sometimes relates to ecological characteristics. Although environmental awareness seems to increase steadily, there are still a lot of consumers who do not care much about the environment. With respect to our model, this implies a rather small minimum valuation of quality. Hence, as far as the baseline utility of the regulated good is also small, market-coverage is unlikely. In this case, it cannot be ruled out that after introducing an MQS overall welfare will decrease since the net utility of consumers at the lower-quality end of the market who decide not to buy at all will drop to zero. However, the analytical difficulties associated with considering an uncovered market are left to future research.

Appendix

Note: In this truncated version of the Appendix, we only provide the main ideas of our calculations and proofs. The complete Appendix is available in Online Resource 2.

1.1 A.1 Check for leapfrogging

The equilibria calculated above require that leapfrogging can be ruled out. I.e., firm $H$ has no incentive to choose a position $q_{Ht} < q_{Lt}$ when firm $L$ sticks to its equilibrium position, and firm $L$ has no incentive to choose a position $q_{Lt} > q_{Ht}$ when firm $H$ sticks to its equilibrium position. As a pre-requisite, we note that under both regulations leapfrogging by firm $H$ in the second period can be excluded a priori since it would violate the minimum quality standard. Moreover, for the special case of $\lambda { = 3}$ (i.e., due to $\delta { = 0}$ the firms completely ignore the effect of their decisions on the forthcoming standard), the unregulated equilibrium coincides with the regulated equilibria obtained for period $t = 1$. Hence, the proof only needs to cover the cases of strict and average regulation.

The remaining proof proceeds as follows: First, we calculate the firms’ maximum possible profits in case of leapfrogging, denoted by $\hat{\pi }_{jt}^{s}$ for strict regulation and $\hat{\pi }_{jt}^{a}$ for average regulation. In the second step, we compare $\hat{\pi }_{jt}^{s}$ and $\hat{\pi }_{jt}^{a}$ with the respective equilibrium profits calculated in Sect. 4, $\pi_{jt}^{s}$ and $\pi_{jt}^{a}$. Concerning firm $H$ this comparison reveals $\pi_{H1}^{s} > \hat{\pi }_{H1}^{s}$ and $\pi_{H1}^{a} > \hat{\pi }_{H1}^{a}$ for $\lambda \in [1,3)$ such that leapfrogging can be ruled out. With respect to firm $L$, the same holds in both periods. The only exception is the special case $\lambda = 1$ (i.e., no discounting at all) which leads to $\pi_{L1}^{s} = \hat{\pi }_{L1}^{s}$. However, if a cheap low-quality producer like firm $L$ tries to penetrate the high-quality segment of the market, it will most likely be forced to change marketing strategies or distribution channels. Although the associated costs are not quantifiable, it is obvious that even arbitrary small costs will suffice to prevent leapfrogging.

1.2 A.2 Proof of Proposition 1

To show that firm $H$ will not try to achieve a non-binding standard under strict regulation, we denote the quality that maximizes $H^{\prime}s$ profit for given $q_{L1}^{s}$ and under the restriction that the standard in $t = 2$ is non-binding by $q_{H1}^{n}$. In the first step, we show that $q_{H1}^{n} = q_{Lt}^{o}$ holds. The reason is that a further reduction of quality would lead to an unnecessarily strong decrease in product differentiation. This, in turn, would reduce $H^{\prime}s$ profit in $t = 1$ without changing the outcome in $t = 2$. In the second step, we show that the presents value of $H^{\prime}s$ profit with the strategy $\left\{ {q_{H1}^{n} ,q_{L1}^{s} } \right\}$ is always smaller compared to the strategy $\left\{ {q_{H1}^{s} ,q_{L1}^{s} } \right\}$.

To derive the results from comparing strict regulation with the unregulated case as stated in Proposition 1, we first calculate the respective differences for the considered variables (e.g., $\Delta q_{L1}^{s} : = q_{L1}^{s} - q_{L1}^{o}$ for the qualities offered by firm $L$ in $t = 1$). The signs of the resulting differences depend only on the magnitude of $\lambda$. Due to $\lambda = \sqrt {9 - 8\delta }$ and $\delta \in (0,1]$, this magnitude is restricted to the domain $\lambda \in [1,3)$. Hence, the results stated in Proposition 1 can easily be obtained by plotting the graphs of the respective differences for $\lambda \in [1,3)$ and by calculating zeros if necessary. In the latter case, to derive the accompanying thresholds in terms of the discount factor $\delta$ the resulting zeros are transformed using $\delta = (9 - \lambda^{2} )/8$.

1.3 A.3 Proof of Proposition 2

In case of average regulation, a non-binding standard $\overline{q}^{a} \le q_{Lt}^{o}$ requires $(q_{L1} + q_{H1} )/2 \le q_{Lt}^{o}$. The main difference compared to strict regulation is that now both firms are able to achieve $\overline{q}^{a} \le q_{Lt}^{o}$ with their decision on quality in period $t = 1$. The proof that such a strategy does not pay for firm $H$ proceeds analogously to the corresponding proof for strict regulation outlined in Appendix A.2. With respect to firm $L$, however, an additional complication occurs: The argument used in Appendix A.2, that due to the impact on product differentiation firm $H$ will lower its quality only so far that the standard just does not bind, cannot directly be transferred to firm $L$. The reason is that for any given $q_{H1}$ a reduction in $q_{L1}$ would actually increase product differentiation. Nevertheless, the complete Appendix provided in Online Resource 2 shows that also firm $L$ will not lower its quality any further than necessary to guarantee $\overline{q}^{a} \le q_{Lt}^{o}$. After this step, it is easy to show that the present value of $L^{\prime}s$ profit in case of a non-binding standard is always smaller than in the equilibrium calculated in Sect. 4.2.

To derive the results from comparing average regulation with the unregulated case as stated in Proposition 2, we analyze the corresponding differences between variables following follow the same steps as already outlined in Appendix A.2.

1.4 A.4–A.8 Proof of Propositions 3–7

To derive the results stated in Propositions 3–7, we analyze the corresponding differences between variables following the same steps as already outlined in Appendix A.2.

1.5 A.9 Market coverage under average regulation

To prove that the thresholds $\hat{u}_{1}^{a}$ and $\hat{u}_{1}^{a}$ are strictly increasing in $\lambda$ we calculate the expressions $\hat{u}_{t}^{a} : = p_{Lt} (q_{Lt}^{a} ,q_{Ht}^{a} ) - aq_{Lt} (q_{Lt}^{a} ,q_{Ht}^{a} )$ for $t = 1,2$ and show that the sign of the first derivatives with respect to $\lambda$ satisfy the condition $\partial \hat{u}_{t}^{a} /\partial \lambda > 0$ for $\lambda \in [1,3)$.