Knowledge Transfer, Transitional Dynamics and Optimal Research & Development Policy in a Dynamic Monopoly Setting

Abstract

This paper focuses on the question of whether or not a reduction of the knowledge barrier is good for welfare. Based on a dynamic monopoly setting with simultaneous investment decisions in process as well as in product Research & Development (R&D), we show that a reduction of the knowledge barrier has ambiguous welfare consequences: due to a lower knowledge barrier, product quality and welfare increase in the short-run. However, this may not necessarily be the case in the long-run. One reason is that a positive long-lasting knowledge barrier shock triggers the monopolist sub-optimally to reduce its product R&D investments today and in the future at the cost of future product quality. This in turn may reduce welfare. Accordingly, to realize the first-best level of product quality, the long-run optimal R&D subsidy rate for product innovations increases with a reduction of the knowledge barrier.

1 Introduction

Knowledge and its management are of crucial importance for a firm’s inventiveness and, hence, is essential for its sustainable competitive advantage. In general, knowledge itself has an internal as well as an external dimension. For instance, firms can increase their own knowledge stock by either investing in product R&D or process R&D, or both. However, theoretically, a firm can also exploit external knowledge that is produced by its competitors. Ironically, new knowledge—accessed externally or internally—also generates types of knowledge barriers, which may hinder the firm’s ability to exploit the accumulated and existing stock of knowledge (Caldwell 1967).

The knowledge barrier is also a subject of research in knowledge management.¹ In general and applied to an economic setting, the knowledge barrier refers to any impediment that prevents existing knowledge from being used elsewhere. This interpretation is consistent with Attewell’s (1992) view of knowledge barriers as the absence of ability to access existing knowledge. Knowledge barriers are relevant within the firm as well as with respect to knowledge that is external to the firm. The former is also known as internal stickiness (Szulanski 1996, 2003).² Consistent with this somewhat vague concept of knowledge barriers, we consider anything that prevents existing knowledge from being applied, transferred, shared or diffused. We take account of these barriers in our theoretical approach at several instances whenever existing knowledge affects the economic environment of the firm. We distinguish explicitly between barriers to accessing internal knowledge and to accessing external existing knowledge.

Following the knowledge management literature, the reduction of knowledge barriers goes hand in hand with improving knowledge transfer and knowledge sharing. While the latter is usually focused on what is happening inside the firm, the former is often applied to knowledge at a higher aggregated level that includes also inter-business relations (Choo and Alvarenga Neto 2010). To reduce knowledge barriers, the relevant economic literature suggests fostering the firm-specific, underlying learning process and, thereby to increase the firms’ absorption capacities (Cohen and Levinthal 1990). Lichtenthaler (2009) considers a firm’s absorption capacity as important to transform knowledge into innovations for improved products and production processes. Consistent with the concept of “a learning economy” that was proposed by Lundvall and Johnson (1994), we argue that a conditio sine qua non to reduce the firm’s knowledge barriers is learning. As a link to the knowledge management literature, learning includes sharing and transferring knowledge from where it originates towards where it can contribute to productivity. This interpretation is consistent with Demircioglu and Audretsch (2017), who point out that learning can be seen as a critical dimension reducing the knowledge barrier. However, the authors also highlight that more research is needed to explore the link between knowledge barriers and innovation. Our paper not only addresses this issue specifically, but goes a step further by asking whether or not a reduction of the knowledge barrier is beneficial for welfare.

In our setting, we focus on an abstract form of learning without specifying the learning process itself. For instance, a direct effect of learning is reflected in a reduction of innovation costs. This might happen if a firm successfully makes use of its own accumulated knowledge through sharing it within the firm. As a second effect, learning also increases the accumulation of knowledge within the firm which is again related to knowledge sharing. Further, learning makes it easier to benefit from external knowledge spillovers which would typically be seen as a knowledge transfer.

Strategic investment decisions (in knowledge) always have a dynamic dimension as today’s decisions in most cases affect the conditions for future investments.³ In recent years, some efforts have been made to discuss the inherently dynamic nature of product and process improvement, ranging from the specific patterns of R&D races, to the timing of innovative ventures, to spillover effects. For example, Lambertini and Mantovani (2009) focused on the dynamic behavior of a multiproduct monopolist that invests in process and product innovation, whereas Lambertini and Orsini (2015), Li and Ni (2016), or more recently, Zhong and Zhang (2018) consider a monopolist that invests in cost-reducing and quality-enhancing endeavors. Common to this last mentioned strand of literature is the result that due to the monopoly power with respect to product quality, the firm distorts product quality downwards compared to what is optimal from a social point of view. However, none of these articles has analyzed the dynamic adjustment of welfare that is due to a potential unforeseen shock in the knowledge barrier sphere: unforeseen changes where knowledge is shared or transferred. Consequently, none of the articles have discussed the optimal policy design when external and internal knowledge transfers and sharing are present.

Process and product innovations differ. We distinguish them by introducing a product innovation with a specific cost component to the monopolist. Additionally, a product innovation represents an increase in the consumer’s marginal utility. Consistent with the literature, we refer to this as an improvement in the monopolist’s product quality. Such innovations are subject to a scale-independent production cost component. This will give rise to a scale effect in product quality that is exploited by the monopolists market power. Since the existing literature almost entirely focuses on the role of scale in process innovations (see, e.g., Cohen and Klepper 1996a, b), little attention has been paid to the role of scale in product innovations.

This paper fills these gaps. First, we combine the dynamic models that were introduced by Lambertini and Orsini (2015), Li and Ni (2016), and Zhong and Zhang (2018) and, inter alia, solve the control problem for the monopolist’s equilibrium product quality. We show that this hyperbolic equilibrium is a degenerate saddle, which implies that there exists a path to which the economy converges in the long-run. We find that product quality increases with a decreasing knowledge barrier. Next, we compute the socially optimal solution. We find that the socially optimal level of product quality is higher due to under-investments in product quality in the decentralized setting. However, the level of process R&D is socially optimal, which is consistent with the literature.⁴ Hence, in order to establish the first-best solution, we propose a policy that imposes a product R&D subsidy scheme that is completely lump-sum financed by consumers.

The paper makes the following important points: (1) we find that the higher is the optimal, long-run subsidy-rate, the lower is the knowledge barrier. For instance, a lower knowledge barrier allows for better accessing existing knowledge. This increases product quality today but—and this is important—for a given depreciation rate, product quality decreases in the future since private R&D efforts decrease. A higher subsidy then counteracts the lower private incentive to invest in own product R&D due to a low knowledge barrier. Further, only in the long-run where product quality is constant, the optimal subsidy-rate is constant as well. During the transitional phase towards the steady-state, the optimal subsidy is time-varying.

(2) Performing a numerical simulation study, we show that welfare may considerably differ in the short-run from its long-run level. This finding has important policy implications: if policy makers focus on the short-run welfare effects of reducing the knowledge barrier, the policy recommendation that may be optimal in the long-run can be biased in the short-run. Hence, welfare effects in the short-run may differ considerably from those in the long-run as speculated by Audretsch (1995).

To clarify this last issue, we run several numerical simulations of our model over its transition towards the long-run equilibrium. We find heterogeneity with respect to the effects of knowledge barrier reductions across different types of barriers as well as during the short- and long-run. Additionally, we find R&D policy to generate different welfare outcomes in the short- and long-run as well. As will be seen, market size plays an important role in all of the mentioned effects.

The plan of the paper is as follows: Sect. 2 introduces the model and solves for the monopolist’s long-run equilibrium. The stability properties of this equilibrium are developed in Sect. 3. Section 4 provides our welfare analysis, and Sect. 5 establishes the welfare optimal R&D policy. Section 6 focuses on the transitional dynamics of welfare effects that are due to knowledge barrier shocks and R&D subsidies. Section 7 concludes.

2 The Model

2.1 Consumers

In what follows, we derive a dynamic extension of the static Mussa and Rosen (1978) framework. Let us consider a single-product monopoly which sells a non-durable good of quality q(t) at a price p(t) over a continuous time span $t\in [0,\infty ^{+}]$. Similar to Lambertini (2018), Lambertini and Orsini (2015), or Zhong and Zhang (2018), the marginal willingness to pay $\theta \in [\Theta -1,\Theta ]$ with $\Theta >1$ is uniformly distributed with a density function $d, d\ge 1$. Hence, the total mass of consumers is $d\ge 1$ which is at the same time also representing market size. Assuming further that the market is fully covered at any time $t\in [0,\infty ^{+}]$,⁵ the net-utility of a representative consumer purchasing a single unit of the good at quality q(t) is given by:

$$\begin{aligned} {{\mathscr {U}}}=\theta q(t)-p(t)\ge 0. \end{aligned}$$

(1)

Under full market coverage, we have that $x(t)=d$ and the profit-maximizing price $p^{m}{(t)}$ completely extracts the surplus from the poorest consumer: $p^{m}{(t)}=(\Theta -1)q(t).$

2.2 In-House Product and Process Innovation

We assume that the monopoly conducts all of its R&D activities in-house. At any $t\in [0,\infty ^{+}]$, the monopoly has to set the levels of product and process innovations simultaneously. Following Chenavaz (2012), product innovations increase the cumulative level of product quality q(t), while investments in the production process decrease the cumulative production costs c(t) accordingly. Hence, the dynamics of q(t) and c(t) can be fully described by the following system of differential equations:

$$\begin{aligned} {\dot{q}}(t)\equiv \frac{\partial q(t)}{\partial t}=\left[ k(t)-\delta \right] q(t), \end{aligned}$$

(2)

$$\begin{aligned} {\dot{c}}(t)\equiv \frac{\partial c(t)}{\partial t}=-\left[ h(t)-\eta \right] c(t), \end{aligned}$$

(3)

with k(t) and h(t) as the R&D efforts in product and process improvements, respectively. $\delta \in (0,1)$ is the constant depreciation rate on product quality, while $\eta \in (0,1)$ represents the production technology’s obsolescence rate.

Both, q(t) and c(t), are state variables in our problem. Increasing product quality at one particular instance in time also has influence on quality’s entire future path. An increment in quality is therefore an investment with instantaneous as well as future returns. If $k(t)=0$ for $t\in [0,\infty ^{+}]$ would be chosen, quality would decay down to zero in the very long run. The same property applies in general to the costs c(t). Of course, the sign of the effects requires a different interpretation. Without steady investments into cost reductions beyond the obsolescence rate, costs c(t) would diverge to infinity. Hence, production costs as well as the level of product quality require maintenance in the long run.

We assume the monopoly’s total cost function C(t) at any $t\in [0,\infty ^{+}]$:

$$\begin{aligned} C(t)=c(t)x(t)+\alpha k^{2}(t)+\beta h^{2}(t)+\gamma q(t)^{2}, \end{aligned}$$

(4)

with x(t) as the firm’s output. The second, third and fourth term of Eq. (4) show the R&D costs in product and process R&D as well as the costs implied by the chosen product quality, respectively. We assume that these costs to follow a quadratic representation to reflect their distinctive character when compared with ordinary marginal costs in production. The choice of a quadratic representation is consistent with the related literature. While marginal costs c(t) are independent of scale in general, the other terms reflect increasing marginal cost contributions in the respective dimensions. Costs increase more than proportionally in the chosen gross investments into quality improvement and cost reductions as well as the level of quality at which production takes place. These three components give rise to a technology with quasi-fixed costs. This also justifies the monopolistic market environment that we have chosen.

As costs depend on the level of quality q(t) in a quadratic way, product innovations have a distinguishing feature in our set-up as compared with process innovations. This term will introduce a scale effect as will be seen below. The larger is the market for the monopolist’s product, the higher will be the chosen level of quality.

2.3 Knowledge Accumulation

We follow Li and Ni (2016) or Zhong and Zhang (2018) and stipulate that knowledge is created by process and product innovations and accumulates according to the following rules:

$$\begin{aligned} A_{k}(t)={\bar{A}}_{k}+\sigma _{k}\int _{0}^{t}k(s)ds-\omega _{k}\int _{0}^{t}A_{k}(s)ds, \end{aligned}$$

(5)

$$\begin{aligned} A_{h}(t)={\bar{A}}_{h}+\sigma _{h}\int _{0}^{t}h(s)ds-\omega _{h}\int _{0}^{t}A_{h}(s)ds. \end{aligned}$$

(6)

${\bar{A}}_{i}>0$ for $i=\{h,k\}$ represent an externally given knowledge stock. $\omega _{i}\in (0,1)$ denote the depreciation rates on accumulated knowledge. This mirrors the view of Jorgenson (1974), Griliches (1998) and others that new ideas replace older ones as they become obsolete. $\sigma _{i}\in (0,1)$ denote the knowledge accumulation rates that arise from investments in product and process innovations.

$\sigma _{i}$ are part of our approach to modeling the knowledge barrier: larger values for $\sigma _{i}$ reduce the knowledge barrier. At this particular instance, we try to reflect the within-firm dimension of the knowledge barrier. This specific barrier limits the amount of the firm’s knowledge stock that can be gained from the innovative actions that represent pieces of knowledge that are required to raise quality or reduce costs. This additionally refers to knowledge-sharing within the firm, which is familiar from the literature on knowledge management. We also link learning abilities with knowledge barriers, as was mentioned in the introduction. Increasing $\sigma _{i}$ may represent an increase in learning efforts.⁶ As such, learning effort is helpful in reducing the knowledge barrier at this particular point in the firm’s knowledge creation process.

2.4 External Knowledge Spillover

There is by now a voluminous literature that points to the importance of knowledge spillovers for R&D endeavors: at the firm level as well as at the macroeconomic level (among others, see Audretsch 1995; Audretsch and Feldman 1996; Acs et al. 2013). It is straightforward to incorporate knowledge spillovers in our dynamic setting which, at the same time, also represent knowledge transfers from external sources as discussed in the knowledge management literature. We assume that the external, and hence, exogenous sources of knowledge and their internal counterparts are perfect substitutes. Unlike in Klarl (2014), there is no knowledge spillover across product and process innovations which implies that the monopolists cannot exploit the process R&D knowledge stock to increase product quality and vice-versa.⁷ We follow Cellini and Lambertini (2009) and re-express the state dynamics of q(t) and c(t) in the following way:

$$\begin{aligned} {\dot{q}}(t)\equiv \frac{\partial q(t)}{\partial t}=[k(t)-\delta +\kappa _{k}{\tilde{k}}(t)]q(t), \end{aligned}$$

(7)

$$\begin{aligned} {\dot{c}}(t)\equiv \frac{\partial c(t)}{\partial t}=-[h(t)-\eta +\kappa _{h}{\tilde{h}}(t)]c(t), \end{aligned}$$

(8)

where the parameter $\kappa _{i},\, i=\{h,k\}$ measures the positive knowledge transfers that the monopolist receives from external knowledge sources. For simplicity, we assume that external investments ${\tilde{k}}(t)$ and ${\tilde{h}}(t)$ grow at an exogenous, constant net rate $g_{i}-\varsigma _{i},\, i=h,k$, where $g_{i}\in (0,1)$ ($\varsigma _{i}\in (0,1)$) represent the external knowledge accumulation (depreciation) rate. This is the second instance where we introduce the knowledge barrier to our problem. Obviously, a larger value of $\kappa _{i}$ can be interpreted as a reduction in this dimension of the knowledge barrier, which leads to a better transfer of knowledge from external sources towards the firm.

2.5 Internal Learning by Doing

We already take account of knowledge sharing within the monopolist’s firm at the stage of accumulating knowledge [see Eqs. (5) and (6)]. This, however, represents knowledge-sharing in an incomplete way, as the monopolist might also draw on the level of accumulated knowledge. This will happen whenever something can be learned from the accumulated experiences that is represented in the model by $A_{h}(t)$ and $A_{k}(t)$. As we believe that this is reasonably the case, we follow Thompson (2010) and Clarke et al. (1982), among others, in assuming that learning from in-house knowledge stocks immediately reduces R&D costs. Hence at any $t\in [0,\infty ^{+}]$, the monopolist’s total cost function has to be adjusted in the following manner (see Li and Ni 2016):

$$\begin{aligned} C(t)=c(t)x(t)+\alpha k^{2}(t)-\tau _{k}\Gamma _{k}(t)+\beta h^{2}(t)-\tau _{h}\Gamma _{h}+\gamma q(t)^{2}, \end{aligned}$$

(9)

where $\tau _{i}\in (0,1),\, i=\{h,k\}$ denote the cost reducing impact of the monopolist’s accumulated knowledge in excess of the externally available knowledge stock. This excess knowledge is given by the knowledge-gaps

$$\begin{aligned} \Gamma _{k}(t) \equiv A_{k}(t)-{\bar{A}}_{k}, \end{aligned}$$

(10)

$$\begin{aligned} \Gamma _{h}(t) \equiv A_{h}(t)-{\bar{A}}_{h}. \end{aligned}$$

(11)

The impact of the knowledge gaps on total production costs is limited again by the knowledge barrier. As both internally accumulated and external knowledge stocks affect production costs, $\tau _{i}$ refers to the ability of knowledge sharing and transfer. We interpret this as a learning rate from firm-specific knowledge that is acquired by product and process innovations translating into lower firm specific production costs. Ceteris paribus, larger knowledge gaps lead to larger cost-saving potentials. Thus, besides $\kappa _{i}$ and $\sigma _{i}$, $\tau _{i}$ are the last elements that represent the various aspects of the knowledge barrier in our set-up.

2.6 The Monopolist’s Problem

The objective of the monopolist is to set the optimal level of investments in product and process R&D which in turn maximizes the discounted profit flow, $\Pi (t)$. Thus, the monopolist’s problem can be expressed as:

$$\begin{aligned} \text {max}_{\{k(t),h(t)\}}\Pi (t)\equiv \int _{0}^{\infty ^{+}}\pi (t)\exp [-\rho t]dt \end{aligned}$$

(12)

$$\begin{aligned} &\text {s.t.}\nonumber \\ \pi (t)&= [(\Theta -1)q(t)-c(t)]d-[\alpha k^{2}(t)-\tau _{k}\Gamma _{k}]-[\beta h^{2}(t)-\tau _{h}\Gamma _{h}]-\gamma q(t)^{2},\nonumber \\ {\dot{q}}(t)&= [k(t)-\delta +\kappa _{k}{\tilde{k}}(t)] q(t),\quad {\dot{c}}(t)=-[h(t)-\eta +\kappa _{h}{\tilde{h}}(t)]c(t),\nonumber \\ {\dot{A}}_{k}(t)&= \sigma _{k}k(t)-\omega _{k}A_{k}(t),\quad {\dot{A}}_{h}(t)=\sigma _{h}h(t)-\omega _{h}A_{h}(t),\nonumber \\ {\Gamma _{k}(t)}&= {A_{k}(t)-{\bar{A}}_{k},\quad \Gamma _{h}(t)=A_{h}(t)-{\bar{A}}_{h},}\nonumber \\ \dot{{\tilde{k}}}(t)&= [g_{k}-\varsigma _{k}]{\tilde{k}}(t), \quad \dot{{\tilde{h}}}(t)=[g_{h}-\varsigma _{h}]{\tilde{h}}(t),\nonumber \\ {\tilde{k}}(0)&= {\tilde{k}}_{0}>0,\quad {\tilde{h}}(0)={\tilde{h}}_{0}>0,\nonumber \\ q(0)&= q_{0}>0, \quad c(0)=c_{0}\in (0,(\Theta -1)q(0)),\nonumber \\ A_{k}(0)&= {\bar{A}}_{k}>0,\quad A_{h}(0)={\bar{A}}_{h}>0, \end{aligned}$$

(13)

and the appropriate transversality conditions that are specified below. In order to guarantee that the market is fully covered even at $t=0$, we have to impose an initial condition on the marginal costs: c(0). This imposition guarantees that the marginal costs are strictly lower than the spending of the poorest consumer that exists in the market.

2.7 Equilibrium

The firm’s current value Hamiltonian ${{\mathscr {H}}}$ is given by:

$$\begin{aligned} {{\mathscr {H}}}\,&=\, \left\{(\Theta -1)[q(t)-c(t)]d-[\alpha k^{2}(t)-\tau _{k}\Gamma _{k}]-[\beta h^{2}(t)-\tau _{h}\Gamma _{h}]-\gamma q(t)^{2} \right.\\& \left.\quad +\,\lambda _{1}(t)[(k(t)-\delta +\kappa _{k}{\tilde{k}}(t)) q(t)]\right.\\&\left.\quad +\,\lambda _{2}(t)[-(h(t)-\eta +\kappa _{h}{\tilde{h}}(t))c(t)]\right.\\&\left.\quad +\,\lambda _{3}(t)[\sigma _{k}k(t)-\omega _{k}A_{k}(t)]\right.\\&\left.\quad +\,\lambda _{4}(t)[\sigma _{h}h(t)-\omega _{h}A_{h}(t)]\right.\\&\left.\quad +\,\lambda_{5}(t)(g_{k}-\varsigma _{k}){\tilde{k}}(t)\right.\\&\left.\quad +\,\lambda _{6}(t)(g_{h}-\varsigma _{h}){\tilde{h}}(t)\right\}, \end{aligned}$$

where $\lambda _{i}$ for $i=\{1,\ldots ,6\}$ are the costate variables that are associated with $q,c,A_{k},A_{h},{\tilde{k}}$ and ${\tilde{h}}$. Henceforth, we shall omit the indication of the time argument t for the sake of brevity whenever no confusion can arise. Here, we assume that the initial condition for c(0) is fulfilled right from the beginning. The first order conditions (FOCs) for the controls k, h and the costate equations are:

$$\begin{aligned} k{:}\,-2\alpha k+\lambda _{1}q+\lambda _{3}\sigma _{k}=0, \end{aligned}$$

(14)

$$\begin{aligned} h{:}\,-2\beta h-\lambda _{2}c+\lambda _{4}\sigma _{h}=0, \end{aligned}$$

(15)

$$\begin{aligned} \lambda _{1}{:}\,{\dot{\lambda }}_{1}=(\rho {-k}+\delta -\kappa _{k}{\tilde{k}})\lambda _{1}-({\Theta }-1)d+2q\gamma , \end{aligned}$$

(16)

$$\begin{aligned} \lambda _{2}{:}\,{\dot{\lambda }}_{2}=(\rho +h+\kappa _{h}{\tilde{h}}-\eta )\lambda _{2}+d, \end{aligned}$$

(17)

$$\begin{aligned} \lambda _{3}{:}\,{\dot{\lambda }}_{3}=(\rho +\omega _{k})\lambda _{3}-\tau _{k}, \end{aligned}$$

(18)

$$\begin{aligned} \lambda _{4}{:}\,{\dot{\lambda }}_{4}=(\rho +\omega _{h})\lambda _{4}-\tau _{h}, \end{aligned}$$

(19)

$$\begin{aligned} \lambda _{5}{:}\,{\dot{\lambda }}_{5}=-\kappa _{k}q\lambda _{1}-{(g_k-\varsigma _{k}-\rho )}\lambda _{5}, \end{aligned}$$

(20)

$$\begin{aligned} \lambda _{6}{:}\,{\dot{\lambda }}_{6}=+\kappa _{h}c\lambda _{2}-{(g_h-\varsigma _{h}-\rho )}\lambda _{6}. \end{aligned}$$

(21)

The corresponding transversality conditions are given by: $\lim _{t\rightarrow \infty }\lambda _{1}(t)q(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{2}(t)c(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{3}(t)A_{k}(t)$ $\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{4}(t)A_{h}(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{5}(t){\tilde{k}}(t)\exp {(-\rho t)}=0$, and $\lim _{t\rightarrow \infty }\lambda _{6}(t){\tilde{h}}(t)\exp {(-\rho t)}=0$.

The transversality conditions make sure that neither knowledge nor product and process innovations are accumulated to an inefficiently high or low extent as time goes by.

From Eq. (14)–(15) we obtain for the optimal controls⁸:

$$\begin{aligned} k^{*}=\max \left\{ 0,\frac{\lambda _{1}q+\left( \frac{\tau _{k}}{\rho +\omega _{k}}\right) \sigma _{k}}{2\alpha }\right\} , \end{aligned}$$

(22)

$$\begin{aligned} h^{*}=\max \left\{ 0,\frac{-\lambda _{2}c+\left( \frac{\tau _{h}}{\rho +\omega _{h}}\right) \sigma _{h}}{2\beta }\right\} , \end{aligned}$$

(23)

as well as the control equations by differentiating (22) and (23) with respect to time:

$$\begin{aligned} {\dot{k}}=\frac{{\dot{q}}\lambda _{1}+q{\dot{\lambda }}_{1}}{2\alpha }, \end{aligned}$$

(24)

$$\begin{aligned} {\dot{h}}=-\frac{{\dot{c}}\lambda _{2}+c{\dot{\lambda }}_{2}}{2\beta }. \end{aligned}$$

(25)

Using (7), (18) and (14) in (24) and (8), (19) and (15) in (25) gives:

$$\begin{aligned} {\dot{k}}=\rho \left( k -\frac{\tau _{k}\sigma _{k}}{2\alpha (\rho +\omega _{k})}\right) -\frac{(\Theta -1)dq}{2\alpha }+\frac{2q^{2}\gamma }{2\alpha }, \end{aligned}$$

(26)

$$\begin{aligned} {\dot{h}}=\rho \left( h -\frac{\tau _{h}\sigma _{h}}{2\beta (\rho +\omega _{h})}\right) -\frac{cd}{2\beta }. \end{aligned}$$

(27)

The system consisting of Eqs. (26)–(27) and (7)–(8) establishes a system of differential equations that allows us to study the dynamic relationship between R&D investments in product and process innovations, product quality, and production costs when external knowledge spillovers and in-house learning-by-doing are present. This system ([S1]) can be formally stated as:

$$\begin{aligned} \text {[S1]} {\left\{ \begin{array}{ll} {\dot{k}}=\rho \left( k -\frac{\tau _{k}\sigma _{k}}{2\alpha (\rho +\omega _{k})}\right) -\frac{(\Theta -1)dq}{2\alpha }+\frac{2q^{2}\gamma }{2\alpha },\\ {\dot{h}}=\rho \left( h -\frac{\tau _{h}\sigma _{h}}{2\beta (\rho +\omega _{h})}\right) -\frac{cd}{2\beta },\\ {\dot{q}}=(k-\delta +\kappa _{k}{\tilde{k}})q,\\ {\dot{c}}=-(h-\eta +\kappa _{h}{\tilde{h}})c. \end{array}\right. } \end{aligned}$$

(28)

For the sake of simplicity and to keep analytical complexity at a reasonable minimum, we assume that ${\tilde{k}}$ and ${\tilde{h}}$ are constant over time. This requires either $g_{i}-\zeta _{i}=0$ or $g_{i}=0$ and $\zeta _{i}=0$ for $i=\{k,h\}$ and does not affect the overall findings of this paper. With the requirement that the steady state is time-invariant—${\dot{c}}={\dot{q}}={\dot{k}}={\dot{h}}=0$, solving system [S1] together with ${\dot{A}}_{k}={\dot{A}}_{h}=0$ delivers six possible sets of solutions—of which only one is economically sensible. We exclude corner solutions, such as zero product quality in the steady state.⁹ This solution ([Sol1]) is:

$$\begin{aligned} \text {[Sol1]} {\left\{ \begin{array}{ll} q^{sts}=\frac{\frac{\sqrt{\left( \rho +\omega _k\right) \left( 8 \gamma \rho \sigma _k \tau _k+\left( \rho +\omega _k\right) \left( d^2 (\Theta -1)^2-16 \alpha \gamma \delta \rho +16 \alpha \gamma \kappa _k {\tilde{k}} \rho \right) \right) }}{\rho +\omega _k}+d (\Theta -1)}{4 \gamma }{,}\\ c^{sts}=\frac{\rho }{d} \left[ 2 \beta ( \eta -{\tilde{h}}\kappa _{h})-\frac{\sigma _h \tau _h}{\rho +\omega _h}\right] {,}\\ k^{sts}=\delta -{\tilde{k}}\kappa _{k}{,}\\ h^{sts}=\eta -{\tilde{h}}\kappa _{h}{,}\\ A_{{k}}^{sts}=\frac{\sigma _k \left( \delta -{\tilde{k}}\kappa _k\right) }{\omega _{{k}}}{,}\\ A_{{h}}^{sts}=\frac{\sigma _h \left( \eta -{\tilde{h}}\kappa _h\right) }{\omega _{{h}}}{,} \end{array}\right. } \end{aligned}$$

(29)

and non-zero given steady state values ${\tilde{h}}^{sts}$ and ${\tilde{k}}^{sts}$. Reflecting [Sol1], the constraints

$$\begin{aligned} \tau _h< {\bar{\tau }}_h\equiv \frac{2 \beta \left( \eta -{\tilde{h}}\kappa _h\right) \left( \rho +\omega _h\right) }{\sigma _h}, \end{aligned}$$

(30)

$$\begin{aligned} \tau _k>{\bar{\tau }}_k\equiv \frac{2 \alpha \left( \delta -{\tilde{k}}\kappa _k\right) \left( \rho +\omega _k\right) }{\sigma _k} \end{aligned}$$

(31)

need to be satisfied simultaneously in order to obtain positive and real-valued levels for process as well as for product R&D investments.¹⁰

To understand the conditions, it is helpful to rewrite the critical values ${{\bar{\tau }}}_h$ and ${{\bar{\tau }}}_k$ by using [Sol1] for the steady-state investments as

$$\begin{aligned} {\bar{\tau }}_h\frac{\sigma _h}{\rho +\omega _h}&= 2\alpha k^{sts},\\ {\bar{\tau }}_k\frac{\sigma _h}{\rho +\omega _h}&= 2\beta h^{sts}. \end{aligned}$$

The critical values are the values for $\tau _h$ and $\tau _k$ that would exactly balance the long-run marginal benefits and marginal investment costs for process and product innovations. The left-hand side of each of the equations represents, respectively, the quality contribution or cost reduction through the long-run knowledge contribution of a marginal unit of investment $\frac{\sigma _i}{\rho +\omega _i}, i=\{h,k\}$ and its knowledge transfer/sharing effect via ${{\bar{\tau }}}_i$. The right-hand side of the equations clearly represent the costs of a marginal unit of investments into process and product innovation. At the critical values for $\tau _h$ and $\tau _k$, marginal long-run benefits and marginal investment costs need to equal each other. However, (31) implies that $\tau _k$ is larger than its critical value: Marginal long-run benefits outweigh marginal investment costs. This is due to the additional negative contribution of the quality level on overall costs C and the additional positive effect, since a higher quality level increases the monopolist’s revenues at the total scale of production. At the profit maximizing level, the former contribution outweighs the latter. $\tau _k>{{\bar{\tau }}}_k$ balances the net additional contributions of investments into product innovations. If the condition is violated, the monopolist wouldn’t have an incentive to invest into product innovations in steady-state.

$\tau _h$ needs to be smaller than ${{\bar{\tau }}}_h$. This inequality applies since there is an additional positive contribution of process innovations. They reduce the monopolist’s marginal production costs, and hence, contribute to profits at the total scale of production. This causes the profit maximizing allocation to tolerate a knowledge sharing/transfer effect below its critical value ${{\bar{\tau }}}_h$. If the condition is violated, the monopolist could drive marginal costs in production down to or even below zero.

As the obtained steady-state results are similar to Lambertini and Orsini (2015) or Zhong and Zhang (2018), we refrain from discussing the properties of the steady-state but refer to this relevant literature. However, for what follows, it is worth noting that the constant steady-state product quality $q^{sts}$ given by [Sol1] increases with a reduction of the knowledge barrier and the size of the market d.

3 Stability Analysis

In this section we show that our equilibrium point is a degenerate saddle-point. This implies that starting from a historical point, there exists a path on which the economy converges to a steady-state. To show this, we first linearize our model around [Sol1]. Let x be the $(6\times 1)$ vector $x'=[q,c,k,h,A_{k},A_{h}]$ and let us define ${{\mathscr {J}}}_{6\times 6}=Df(x^{Sol1})$ as the Jacobian matrix of the system that is evaluated at the equilibrium point [Sol1]. Hence, the linearized counterpart of [S1] is ${\dot{x}}={{\mathscr {J}}}x$ with $x\in {\mathbb {R}}^{6}$.

$$\begin{aligned}&{{\mathscr {J}}}\equiv \left[ \begin{array}{llllll}\frac{\partial {\dot{c}}}{\partial c}&{}\quad \frac{\partial {\dot{c}}}{\partial q}&{}\quad \frac{\partial {\dot{c}}}{\partial A_{k}}&{}\quad \frac{\partial {\dot{c}}}{\partial A_{h}}&{}\quad \frac{\partial {\dot{c}}}{\partial k}&{}\quad \frac{\partial {\dot{c}}}{\partial h}\\ \frac{\partial {\dot{q}}}{\partial c}&{}\quad \frac{\partial {\dot{q}}}{\partial q}&{}\quad \frac{\partial {\dot{q}}}{\partial A_{k}}&{}\quad \frac{\partial {\dot{q}}}{\partial A_{h}}&{}\quad \frac{\partial {\dot{q}}}{\partial k}&{}\quad \frac{\partial {\dot{q}}}{\partial h}\\ \frac{\partial {\dot{A}}_{k}}{\partial c}&{}\quad \frac{\partial {\dot{A}}_{k}}{\partial q}&{}\quad \frac{\partial {\dot{A}}_{k}}{\partial A_{k}}&{}\quad \frac{\partial {\dot{A}}_{k}}{\partial A_{h}}&{}\quad \frac{\partial {\dot{A}}_{k}}{\partial k}&{}\quad \frac{\partial {\dot{A}}_{k}}{\partial h}\\ \frac{\partial {\dot{A}}_{h}}{\partial c}&{}\quad \frac{\partial {\dot{A}}_{h}}{\partial q}&{}\quad \frac{\partial {\dot{A}}_{h}}{\partial A_{k}}&{}\quad \frac{\partial {\dot{A}}_{h}}{\partial A_{h}}&{}\quad \frac{\partial {\dot{A}}_{h}}{\partial k}&{}\quad \frac{\partial {\dot{A}}_{h}}{\partial h}\\ \frac{\partial {\dot{k}}}{\partial c}&{}\quad \frac{\partial {\dot{k}}}{\partial q}&{}\quad \frac{\partial {\dot{k}}}{\partial A_{k}}&{}\quad \frac{\partial {\dot{k}}}{\partial A_{h}}&{}\quad \frac{\partial {\dot{k}}}{\partial k}&{}\quad \frac{\partial {\dot{k}}}{\partial h}\\ \frac{\partial {\dot{h}}}{\partial c}&{}\quad \frac{\partial {\dot{h}}}{\partial q}&{}\quad \frac{\partial {\dot{h}}}{\partial A_{k}}&{}\quad \frac{\partial {\dot{h}}}{\partial A_{h}}&{}\quad \frac{\partial {\dot{h}}}{\partial k}&{}\quad \frac{\partial {\dot{h}}}{\partial h} \end{array}\right] \nonumber \\&\quad =\left[ \begin{array}{llllll} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -c\\ 0&{}\quad {0}&{}\quad 0&{}\quad 0&{}\quad q&{}\quad 0\\ 0&{}\quad 0&{}\quad -\omega _{k}&{}\quad 0&{}\quad \sigma _{k}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -\omega _{h}&{}\quad 0&{}\quad \sigma _{h}\\ 0&{}\quad \frac{4q\gamma -(\Theta -1)d}{2\alpha }&{}\quad 0&{}\quad 0&{}\quad \rho &{}\quad 0\\ -\frac{d}{2\beta }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \rho \end{array}\right] . \end{aligned}$$

(32)

For positive values of [Sol1], the six Eigenvalues of ${{\mathscr {J}}}$ that are associated with [Sol1] are real-valued.¹¹ It can be shown that four of them are negative-valued, whereas two of them are positive. We can show that [Sol1] fulfills the properties of a hyperbolic equilibrium point. In general, a hyperbolic equilibrium point is a fixed point that does not have any center manifolds.¹² For this fixed point, it can be shown that there exists a locally stable and unstable manifold. Further, according to the Hartman–Grobman theorem (see Teschl 2012, chapter 9.2. and 9.3), the behavior of a dynamic system in the domain near a hyperbolic equilibrium point is qualitatively the same as the behavior of its linearization near this equilibrium point due to its topological equivalence.

Hence, from the Hartman–Grobman theorem and the stable manifold theorem we can deduce that [Sol1] is a hyperbolic equilibrium point that is a (degenerate) saddle (see also Buiter 1984).

4 Welfare

In this section we focus on the welfare consequences of an unanticipated shock to the knowledge barrier. We assume a benevolent social planner is running the firm and, hence, is being in charge of choosing the R&D investment paths for product and process innovation that maximize the discounted, intertemporal social welfare. Social welfare (sw(t)) is defined as the sum of consumer surplus (cs(t)) and the profit stream ($\pi (t)$). For cs(t), we obtain:

$$\begin{aligned} cs(t):=\int _{\Theta -1}^{\Theta }(\theta q(t)-p(t))d\theta =\frac{q(t)}{2}. \end{aligned}$$

(33)

Thus, sw(t) can be re-expressed as:

$$\begin{aligned} sw(t):=\frac{q(t){[}1+2d(\Theta -1)-2\gamma q(t){]}}{2}-c(t)d-[\alpha k^{2}(t)-\tau _{k}\Gamma _{k}(t)]-[\beta h^{2}(t)-\tau _{h}\Gamma _{h}(t)]. \end{aligned}$$

(34)

Therefore, the planner’s current value Hamiltonian is given by:

$$\begin{aligned} {{\mathscr {H}}}&= \left\{ \frac{q(t){[}1+2d(\Theta -1)-2\gamma q(t){]}}{2}-c(t)d-[\alpha k^{2}(t)-\tau _{k}\Gamma _{k}(t)]-[\beta h^{2}(t)-\tau _{h}\Gamma _{h}(t)]\right. \nonumber \\&\quad \left. +\,\lambda _{1}(t)[(k(t)-\delta +\kappa _{k}{\tilde{k}}(t)) q(t)]\right. \nonumber \\&\quad \left. +\,\lambda _{2}(t)[-(h(t)-\eta +\kappa _{h}{\tilde{h}}(t))c(t)]\right. \nonumber \\&\quad \left. +\,\lambda _{3}(t)[\sigma _{k}k(t)-\omega _{1}A_{k}(t)]\right. \nonumber \\&\quad \left. +\,\lambda _{4}(t)[\sigma _{h}h(t)-\omega _{2}A_{h}(t)]\right. \nonumber \\&\quad \left. +\,\lambda _{5}(t)(g_{k}-\varsigma _{k}){\tilde{k}}(t)\right. \nonumber \\&\quad \left. +\,\lambda _{6}(t)(g_{h}-\varsigma _{h}){\tilde{h}}(t)\right\} , \end{aligned}$$

(35)

where $\lambda _{i}(t)$ for $i=\{1,\ldots ,6\}$ are the costate variables that are associated with $q,c,A_{k},A_{h},{\tilde{k}}$ and ${\tilde{h}}$. Applying the same apparatus as during the derivation of the decentralized solution, we can establish a system of differential equations that allows us to study the dynamics between R&D investments in product and process innovations, product quality, and production costs.¹³ This system ([S2]) can be formally written as:

$$\begin{aligned} \text {[S2]} {\left\{ \begin{array}{ll} {\dot{k}}=\rho \left( k -\frac{\tau _{k}\sigma _{k}}{2\alpha (\rho +\omega _{k})}\right) -\frac{(\Theta -1)dq}{2\alpha }+\frac{q}{2\alpha }\left( 2q\gamma -\frac{1}{2}\right) ,\\ {\dot{h}}=\rho \left( h -\frac{\tau _{h}\sigma _{h}}{2\beta (\rho +\omega _{h})}\right) -\frac{cd}{2\beta },\\ {\dot{q}}=(k-\delta +\kappa _{k}{\tilde{k}})q,\\ {\dot{c}}=-(h-\eta +\kappa _{h}{\tilde{h}})c. \end{array}\right. } \end{aligned}$$

(36)

Again requiring that the steady-state is time-invariant, we obtain six possible sets of solutions—of which only one is economically sensible. Further, this solution is a degenerate saddle-point, where the same rational applies as in the case that was analyzed in Sect. 3. When we compare the socially optimal outcome with the decentralized one, with the exception of the product quality—q—and investments in product quality—k—this solution coincides with [Sol1]. The optimal quality level—$q^{m}$—is:

$$\begin{aligned} q^{m}=\frac{1+2 d (\Theta -1)+\frac{\sqrt{\left( \rho +\omega _k\right) \left( 32 \gamma \rho \sigma _k \tau _k+\left( \rho +\omega _k\right) \left( (2 d (\Theta -1)+1)^2-64 \alpha \gamma \delta \rho +64 \alpha \gamma \kappa _k {{\tilde{k}}}\rho \right) \right) }}{\rho +\omega _k}}{8 \gamma }. \end{aligned}$$

(37)

Inspecting the expressions for $q^{m}$ and $q^{sts}$ in [Sol1] and (37) reveals that $q^m$ always exceeds $q^{sts}$ as long the latter is positive-valued [condition (31)]. Thus, we observe a general under-supply of product quality in the decentralized economy. Compared to the benevolent social planner, the monopolist chooses a non-optimal level of product R&D investments.

This can be easily seen by solving each of the ${\dot{k}}$ equations in [S1] and [S2] for the stationary solution of k given one particular level of quality q. Denoting the solutions by $k^{sts}(q)$ and $k^{m}(q)$, we find the difference $\Delta k(q):=k^{m}(q)-k^{sts}(q)=\frac{q}{4\alpha \rho }>0$. This is identical to the result in Lambertini and Orsini (2015).

The driving force that underlies the under-supply of quality in the decentralized setting is the absence of the consumer surplus in the monopolist’s objective function. On the contrary, the level of process innovations is socially efficient as the monopoly price p is not a function of the marginal costs and the market demand is invariant to changes in the latter.

5 Optimal R&D Policy

In the last section, we showed that from a welfare perspective, the monopolist’s profit incentives cause a downward distortion of product quality. Hence, the immediate question arises: What policy can establish the optimal level of product R&D that (in turn) would establish the optimal product quality level in the decentralized setting. We assume that the policy maker introduces a lump-sum financed R&D subsidy tax scheme with a subsidy rate $\xi (t)\in (0,1)$. Hence, the costs for setting up a R&D lab reduce to $\alpha k^{2}(1-\xi )$. We would like to emphasize here that the subsidy rate might well vary with t. It is straightforward that this finding implies that short-run welfare effects (during transition) of a public financed R&D subsidy significantly differs from its long-run counterpart. We will return to this point below.

Solving the monopolists profit maximization problem, we can show that the (second-best) subsidy-adjusted equilibrium level of R&D investment in product quality, $k^{sub}$, is given in steady-state as¹⁴:

$$\begin{aligned} k^{sub}=\frac{q \left( \rho +\omega _k\right) (d (\Theta -1)-2 \gamma q)+\rho \sigma _k \tau _k}{2 \alpha \rho (1-\xi ) \left( \rho +\omega _k\right) }. \end{aligned}$$

(38)

Hence, comparing Eq. (38) with the optimal level of product R&D, $k^{m}$, and solving for the subsidy rate $\xi$ by using the optimal solution for $q^{m}$, we arrive at the optimal product R&D subsidy rate, $\xi ^{opt}$:

$$\begin{aligned} \xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )=\frac{q^{m} \left( \rho +\omega _k\right) }{q^{m} \left( \rho +\omega _k\right) (2 d (\Theta -1)-4 \gamma q^{m}+1)+2 \rho \sigma _k \tau _k}\end{aligned}$$

(39)

$$\begin{aligned} =\frac{2 d (\Theta -1) \rho +\omega _k (2 d (\Theta -1)+1)+\rho +\sqrt{\Psi }}{32 \alpha \gamma \rho \left( \rho +\omega _k\right) \left( \delta -\kappa _k{\tilde{k}}\right) }, \end{aligned}$$

(40)

with $\Psi \equiv \left( \rho +\omega _k\right) \left( 32 \gamma \rho \sigma _k \tau _k+\left( \rho +\omega _k\right) \left( (2 d (\Theta -1)+1)^2-64 \alpha \gamma \rho \left( \delta - \kappa _k {\tilde{k}} \right) \right) \right) .$ Note that for ${\bar{\tau }}_{k}<\tau <\bar{{\bar{\tau }}}_{k}$ with $\bar{{\bar{\tau }}}_{k}\equiv \frac{4 \alpha \left( \rho +\omega _k\right) \left( \delta -\kappa _1 {\tilde{k}}\right) \left( 8 \alpha \gamma \rho (\delta -\kappa _{k} {\tilde{k}})+d (1-\Theta )\right) }{\sigma _k}$ [see Eq. (31)], it always holds that $\xi ^{opt}\in (0,1)$. Furthermore, $\Psi$ is increasing in d and therefore $\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )$ is increasing in market size. The optimal subsidy policy is, thus, more pronounced if the monopolist is active in smaller markets with less demand. Policy should target its subsidy policy on R&D in product innovations towards those firms that contribute to consumers’ surplus but that suffer at the same time from low market volumes.

Taken together, these findings guide the following proposition:

Proposition

• 1 The subsidy rate $\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )$ positively depends on the rate of knowledge accumulation, $\sigma _k$; the product innovations’ learning rate, $\tau _k$; and the knowledge spillover rate, $\kappa _{k}$.

• 2 The subsidy rate never turns into a tax—$\xi <0$—as long as $k\ge 0\Leftrightarrow \delta \ge {\tilde{k}}\kappa _{k}$ provided that $\Theta >1$.

• 3 Only along the steady-state, the subsidy rate is constant over time as the steady-state level of product quality is constant as well. However, during transition, the optimal subsidy rate is time-varying in a non-linear fashion with the level of product quality.

Proof

See “Appendix 4”.

Hence, the last proposition tells us that a reduction of the knowledge barrier implies a higher R&D subsidy given that the product quality is below the social optimal. A reduction in the knowledge barrier that is related to knowledge spillovers $\kappa _k$ reduces, ceteris paribus, steady-state investments in product innovations. This happens as the monopolist reduces its own (costly) investments and partially replaces them by (less costly ) external knowledge. As external knowledge carries a zero price, the reduction outweighs the additional external knowledge that is available due to the decreased knowledge barrier.

This has an additional effect on the impact of a subsidy on the quality level that is chosen by the monopolist. As investments in product innovations are reduced when there is a lower knowledge barrier, the implied cost reduction for the monopolist is more than proportionate as marginal investments cost are increasing. The discussed subsidy scheme targets exactly these costs and hence becomes less effective as its marginal impact is reduced by the non-linearity in investment costs (quadratic in our case).

A reduction in the knowledge barrier that is related to $\sigma _k$ and $\tau _k$ has similar effects on the effectiveness of the subsidy scheme. The lower knowledge barrier increases the social optimum quality level [see (37)], which—due to quadratic investment cost—causes more than proportionate higher costs in production. Consequently, the optimal subsidy rate has to increase to provide an appropriate incentive for the monopolist.

6 Transitional Dynamics

The main purpose of this paper is to persuade the reader that unexpected, knowledge-barrier related shocks—such as shocks to the learning rate or to knowledge spillover—have not only long-run, but also short-run welfare consequences. Hence, a policy maker with a pure long-run focus arrives at a misleading policy design for the short-run when it comes to a mitigation of such shocks only in the long-run.

To make this last point clear, we shock the decentralized economy and investigate the short and long-run welfare consequences. We do so by following the transitional dynamics and consider different assumptions with respect to the market size d. As argued above, market size is an important factor that influences the optimal R&D policy. To simulate the entire welfare transition path, we employ the relaxation algorithm that was suggested by Trimborn et al. (2008). Whether or not welfare increases or decreases depends on the (competing) forces of the consumer and producer surplus, respectively. Hence, the impetus of this simulation study is not to calibrate the model to real-world data, which is clearly beyond the scope of this contribution, but to persuade the reader that a welfare analysis that focuses exclusively on the long-run would be incomplete.¹⁵ Due to the fact that process R&D investment incentives are optimally chosen in the decentralized economy, we focus only on those parts of the knowledge barrier related to product R&D investments and the subsidy policy that targets product quality.¹⁶

6.1 Parameter Values

The chosen parameter space has to meet the parameter restrictions that were worked out above that ensure an economically meaningful equilibrium for our economy. Table 1 shows the parameter choice as well as the shock size expressed as percentage changes, respectively.

In total, we run four simulations: Each considers three different values for d. They show the welfare consequences of: an unanticipated positive knowledge spillover shock ($\Delta \kappa _{k}>0$); an unanticipated positive knowledge accumulation rate shock ($\Delta \sigma _{k}>0$); an unanticipated positive learning rate shock ($\Delta \tau _{k}>0$); as well as the welfare response to an unanticipated positive R&D subsidy shock ($\Delta \xi >0$). Without loss of generality we assume that ${\tilde{h}}$ and ${\tilde{k}}$ are constant over time as in the theoretical analysis above. It is important to note that we also assume that the shocks last forever: a shocked parameter does not return to its original value. For all simulation runs, we report the relative difference as compared with the benchmark economy (Table 1). Our stability analysis shows that, after the shock, the economy converges towards its new steady-state. Finally, for all scenarios, the calibration guarantees that product quality is below the optimal level.

Table 1 Parameter calibration for the benchmark economy

6.2 Results from Simulation

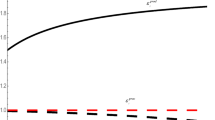
Figure 1 shows the welfare change during transition. For every shock scenario, Table 2 shows the welfare change in the short- and the long-run. Throughout transition, shocks to $\tau _k$ and $\sigma _k$ have positive effects on welfare [see panels (b) and (c)]. Increasing $\sigma _k$ enhances the accumulation of knowledge while increasing $\tau _k$ improves internal learning. Both imply cost reducing effects in the simulated scenarios which have positive effects on welfare. The effects are stronger when the market size is smaller.

Adjustment after an unanticipated knowledge spillovers shock follows a different pattern (panel (d) in Fig. 1): as $\kappa _k$ increases, the monopolists enjoys a higher rate of knowledge spillovers or external knowledge transfers. The subsequent reaction will be to reduce investments in product innovation which then leads to lower knowledge accumulation. Therefore, the knowledge gap will decline and, hence, production cost will increase. In the short-run, we see a positive effect on welfare. This happens because the reduction in investments have an instantaneous effect of reducing costs. R&D costs are quadratic in k; lower investment, thus, initially reduce the total costs of the monopolist. After a while, however, the negative consequences of lower investments become visible. The negative effect on accumulated knowledge now outweighs the instantaneous cost reduction, and overall production costs increase. The total welfare effect now becomes negative. Again, we find effects to be more pronounced in smaller markets.

The welfare effects of the subsidy are negative in the very short-run and positive afterwards (as expected) as can be seen from [panel (a) in Fig. 1]. The reason is again to be found in the time lag between an investment in product-quality R&D and its effect on production costs. Investment implies instantaneous (quadratic) cost, while cost reductions will be significant only after corresponding knowledge accumulation takes place. Once this has happened, welfare improves. Again smaller markets imply stronger effects.

To sum up, the purpose of this simulation study is to show that, first, shocks to the knowledge barrier might have heterogeneous effects; and, second, that the introduction of product innovation R&D subsidies potentially have distinct effects in the short- and the log-run. Besides this, market size is a crucial factor that influences the results. If market size d is small, the quasi fixed cost that is implied by R&D influences the behavior of the monopolist to a great extent because the R&D costs are large relative to total turnover. This needs to be kept in mind for policy, together with the finding that initial short-run effects of policy might be considerably different from their long-run counterparts. Although our analysis considers a stationary d, this might be of special importance for policy with respect to innovative ideas that suffer initially from a small market size.

Fig. 1

Welfare change at time t defined as the change of welfare relative to the new steady-state welfare level

Table 2 Short versus long-run absolute welfare changes relative to the new steady-state

7 Conclusion

Based on a dynamic monopoly setting with simultaneous investment decisions in process as well as in product R&D, the main impetus of the paper is to show that a reduction of the knowledge barrier due to long-lasting shocks has ambiguous welfare consequences: With the “standard” focus solely on the long-run, welfare effects are ambiguous as welfare directly depends on the calibrated parameter space. If the focus is on both the short- and the long-run, a simulation study highlights that short-run welfare effects may completely differ from their long-run counterparts. This is due to the fact that a knowledge barrier shock triggers the monopolist to sub-optimally reduce its product R&D investments today at the cost of lower future levels of knowledge. Hence, this finding has an important policy-implication: if a policy maker focuses on the short-run welfare effects of a decrease of the knowledge barrier, the policy recommendation that might be optimal in the long-run could be non-optimal in the short-run.

In this contribution we focus on the product R&D sphere as, in contrast to the process R&D investment sphere, the optimal solution for the product quality differs from the socially optimal one. Hence, we discuss the implementation of a consumer financed R&D subsidy that aims to realize the socially optimal product quality level. We find that in the short-run, this R&D subsidy rate is time-varying with the level of product quality and is constant only in the long-run. We also find that the R&D subsidy rate is higher, the lower is the knowledge barrier. Market size is a crucial factor for policy making as well. Smaller markets benefit relatively more from subsidy policies. At the same time, innovative monopolies are also in general more affected by knowledge barriers. This stresses our argument from the introductory section that product innovations should be discussed along with process innovations in the context of market size and should not be excluded from this discussion.

Appendices

Appendix 1: Monopolist’s Problem

The FOCs (18) and (19) allow for a closed form solution for $\lambda _3(t)$ and $\lambda _4(t)$. Rewrite these conditions as

$$\begin{aligned} {\dot{\lambda }}_j(t)+f_j(t)&= g_j(t), j=\{3,4\},\\ \text {with}\\ f_j(t)&= -(\rho +\omega _i),\quad g_j(t)=-\tau _i, i=\{k,h\}, \end{aligned}$$

we find

$$\begin{aligned} \lambda _j(t)&= \lambda _j(0)\exp \left[ -\int _0^tf_j(s)ds\right] +\int _0^tg_j(z)\exp \left[ -\int _z^t f_j(s)ds\right] dz. \end{aligned}$$

This delivers

$$\begin{aligned} \lambda _3(t)=\frac{\tau _k}{\rho +\omega _k}+\exp [(\rho +\omega _k)t]\left( \lambda _3(0)-\frac{\tau _k}{\rho +\omega _k}\right) , \end{aligned}$$

(41)

$$\begin{aligned} \lambda _4(t)=\frac{\tau _h}{\rho +\omega _h}+\exp [(\rho +\omega _h)t]\left( \lambda _4(0)-\frac{\tau _h}{\rho +\omega _h}\right) . \end{aligned}$$

(42)

With ${\tilde{k}}(t)$ and ${\tilde{h}}(t)$ constant, the steady-state fulfills ${\dot{c}}(t)={\dot{q}}(t)={\dot{k}}(t)={\dot{h}}(t)={\dot{A}}_{k}(t)={\dot{A}}_{h}(t)=0$. In a non-degenerate equilibrium, we need to have $\lim _{t\rightarrow \infty }{A}_{i}(t)=A_i^{sts}$ with $A_i^{sts}>0$ and finite.

The transversality conditions for ${A}_{i}(t)$ therefore imply $\lim _{t\rightarrow \infty }\exp [-\rho t]\lambda _j(t)A_{i}(t)=$ $A_{i}^{sts}\lim _{t\rightarrow \infty }\exp [-\rho t]\lambda _j(t)=0$. Using (41) and (42) then gives

$$\begin{aligned} \exp [-\rho t]\lambda _3(t)&= \exp [-\rho t]\frac{\tau _k}{\rho +\omega _k}+\exp [\omega _kt]\left( \lambda _3(0)-\frac{\tau _k}{\rho +\omega _k}\right) ,\\ \exp [-\rho t]\lambda _4(t)&= \exp [-\rho t]\frac{\tau _h}{\rho +\omega _h}+\exp [\omega _ht]\left( \lambda _4(0)-\frac{\tau _h}{\rho +\omega _h}\right) . \end{aligned}$$

Hence, the transversality conditions for ${A}_{k}(t)$ and ${A}_{h}(t)$ require $\lambda _3(t)=\frac{\tau _k}{\rho +\omega _k}$ and $\lambda _4(t)=\frac{\tau _h}{\rho +\omega _h}$ for all t as $\lambda _3(t)$ and $\lambda _4(t)$ otherwise explode or degenerate towards zero. Inserting these results into (16) and (17) respectively, gives the optimal controls in (22) and (23).

The Eigenvalues $\mu _i, i\in {1,\ldots ,6}$ of the Jacobian ${{\mathscr {J}}}$ are given by

$$\begin{aligned} \begin{array}{ll}\mu _1=-\omega _{k},&{}\quad \mu _2=-\omega _{h},\\ \mu _3=\frac{1}{2} \left( \rho -\frac{\sqrt{\alpha ^2 \beta \left( \beta \rho ^2+2 c^{sts} d\right) }}{\alpha \beta }\right) ,&{}\quad \mu _4=\frac{1}{2} \left( \rho -\frac{\sqrt{\alpha \beta ^2 \left( \alpha \rho ^2+2 q^{sts} (d(1-\theta )+4 \gamma q^{sts})\right) }}{\alpha \beta }\right) ,\\ \mu _5=\frac{1}{2} \left( \rho +\frac{\sqrt{\alpha ^2 \beta \left( \beta \rho ^2+2 c^{sts} d\right) }}{\alpha \beta }\right) ,&{}\quad \mu _6=\frac{1}{2} \left( \rho +\frac{\sqrt{\alpha \beta ^2 \left( \alpha \rho ^2+2 q^{sts} (d(1-\theta )+4 \gamma q^{sts})\right) }}{\alpha \beta }\right) .\end{array} \end{aligned}$$

Note that $\mu _{1}<0$, $\mu _2<0$, $\mu _3<0$ for $\tau _{h}<{\bar{\tau }}_{h}$, $\mu _4<0$ for $\tau _{k}>{\bar{\tau }}_{k}$, $\mu _5>0$ for $\tau _{h}>{\bar{\tau }}_{h}$ and $\mu _6>0$ for $\tau _{h}>{\bar{\tau }}_{h}$ where ${\bar{\tau }}_{h}$, ${\bar{\tau }}_{k}$ are given by (30) and (31).

Appendix 2: Centralized Solution

Given the Hamiltonian (35), the FOCs are

$$\begin{aligned} k{:}\,-2\alpha k+\lambda _{1}q+\lambda _{3}\sigma _{k}=0, \end{aligned}$$

(43)

$$\begin{aligned} h{:}\,-2\beta h-\lambda _{2}c+\lambda _{4}\sigma _{h}=0, \end{aligned}$$

(44)

$$\begin{aligned} \lambda _{1}{:}\,{\dot{\lambda }}_{1}=(\rho -k+\delta -\kappa _{k}{\tilde{k}})\lambda _{1}-(\Theta -1)d+2q\gamma -\frac{1}{2}, \end{aligned}$$

(45)

$$\begin{aligned} \lambda _{2}{:}\,{\dot{\lambda }}_{2}=(\rho +h+\kappa _{h}{\tilde{h}}-\eta )\lambda _{2}+d, \end{aligned}$$

(46)

$$\begin{aligned} \lambda _{3}{:}\,{\dot{\lambda }}_{3}=(\rho +\omega _{k})\lambda _{3}-\tau _{k}, \end{aligned}$$

(47)

$$\begin{aligned} \lambda _{4}{:}\,{\dot{\lambda }}_{4}=(\rho +\omega _{h})\lambda _{4}-\tau _{h}, \end{aligned}$$

(48)

$$\begin{aligned} \lambda _{5}{:}\,{\dot{\lambda }}_{5}=-\kappa _{k}q\lambda _{1}-{(g_k-\varsigma _{k}-\rho )}\lambda _{5}, \end{aligned}$$

(49)

$$\begin{aligned} \lambda _{6}{:}\,{\dot{\lambda }}_{6}=+\kappa _{h}c\lambda _{2}-{(g_h-\varsigma _{h}-\rho )}\lambda _{6}. \end{aligned}$$

(50)

The corresponding transversality conditions are given by: $\lim _{t\rightarrow \infty }\lambda _{1}(t)q(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{2}(t)c(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{3}(t)A_{k}(t)$ $\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{4}(t)A_{h}(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{5}(t){\tilde{k}}(t)\exp {(-\rho t)}=0$, and $\lim _{t\rightarrow \infty }\lambda _{6}(t){\tilde{h}}(t)\exp {(-\rho t)}=0$.

We note that the FOCs in this case differ only by condition (45) from the FOCs in the decentralized solution, as only the term $\frac{q(t)}{2}$ (which reflects consumers’ surplus) adds to the Hamiltonian.

Therefore, as in “Appendix 1”, the co-states associated with ${A}_{k}(t)$ and ${A}_{h}(t)$ need to be constant at $\lambda _3(t)=\frac{\tau _k}{\rho +\omega _k}$ and $\lambda _4(t)=\frac{\tau _h}{\rho +\omega _h}$. Using these expressions for $\lambda _3(t)$ and $\lambda _4(t)$ in (43) and (44) gives the same optimal controls as before [(22), (23)]

$$\begin{aligned} k^{*}=\max \left\{ 0,\frac{\lambda _{1}q+\left( \frac{\tau _{k}}{\rho +\omega _{k}}\right) \sigma _{k}}{2\alpha }\right\} ,\nonumber \\ h^{*}=\max \left\{ 0,\frac{-\lambda _{2}c+\left( \frac{\tau _{h}}{\rho +\omega _{h}}\right) \sigma _{h}}{2\beta }\right\} , \end{aligned}$$

(51)

which implies

$$\begin{aligned} {\dot{k}}=\frac{{\dot{q}}\lambda _{1}+q{\dot{\lambda }}_{1}}{2\alpha }, \end{aligned}$$

(52)

$$\begin{aligned} {\dot{h}}=-\frac{{\dot{c}}\lambda _{2}+c{\dot{\lambda }}_{2}}{2\beta }. \end{aligned}$$

(53)

Using (7), (47) and (43) in (52) and (8), (48) and (44) in (53) gives the dynamic system [S2]:

where we note that the only difference between [S2] and [S1] is the additional far right term in the first equation. The steady-state solution for the case ${\dot{c}}(t)={\dot{q}}(t)={\dot{k}}(t)={\dot{h}}(t)={\dot{A}}_{k}(t)={\dot{A}}_{h}(t)=0$ is then straightforward. Except for q, we find the same results as in case of the decentralized equation. In particular, the steady-state quality level in the centralized equilibrium, $q^{m}$ is found by solving for k in steady-state as in “Appendix 1” by using (55) and inserting the result into (54) in steady-state.

Appendix 3: R&D Policy

The Hamiltonian in this case is

$$\begin{aligned} {{\mathscr {H}}}&= \left\{(\Theta -1){[}q(t)-c(t)]d-[(1-\xi (t))\alpha k^{2}(t)-\tau _{k}\Gamma _{k}]-[\beta h^{2}(t)-\tau _{h}\Gamma _{h}]-\gamma q(t)^{2}\right.\\&\quad \left.+\,\lambda _{1}(t)[(k(t)-\delta +\kappa _{k}{\tilde{k}}(t)) q(t)]\right.\\&\left.\quad +\,\lambda _{2}(t)[-(h(t)-\eta +\kappa _{h}{\tilde{h}}(t))c(t)]\right.\\&\left.\quad +\,\lambda _{3}(t)[\sigma _{k}k(t)-\omega _{k}A_{k}(t)]\right.\\&\left.\quad +\,\lambda _{4}(t)[\sigma _{h}h(t)-\omega _{h}A_{h}(t)]\right.\\&\left.\quad +\,\lambda _{5}(t)(g_{k}-\varsigma _{k}){\tilde{k}}(t)\right.\\&\left.\quad +\,\lambda _{6}(t)(g_{h}-\varsigma _{h}){\tilde{h}}(t)\right\}, \end{aligned}$$

where $\lambda _{i}$ for $i=\{1,\ldots ,6\}$ are the costate variables associated with $q,c,A_{k},A_{h},{\tilde{k}}$ and ${\tilde{h}}$. Suppressing time arguments whenever possible, the first order conditions (FOCs) for the controls k, h and costate equations are:

$$\begin{aligned} k{:}\,-2(1-\xi )\alpha k+\lambda _{1}q+\lambda _{3}\sigma _{k}=0, \end{aligned}$$

(56)

$$\begin{aligned} h{:}\,-2\beta h-\lambda _{2}c+\lambda _{4}\sigma _{h}=0, \end{aligned}$$

(57)

$$\begin{aligned} \lambda _{1}{:}\,{\dot{\lambda }}_{1}=(\rho {-k}+\delta -\kappa _{k}{\tilde{k}})\lambda _{1}-({\Theta }-1)d+2q\gamma , \end{aligned}$$

(58)

$$\begin{aligned} \lambda _{2}{:}\,{\dot{\lambda }}_{2}=(\rho +h+\kappa _{h}{\tilde{h}}-\eta )\lambda _{2}+d, \end{aligned}$$

(59)

$$\begin{aligned} \lambda _{3}{:}\,{\dot{\lambda }}_{3}=(\rho +\omega _{k})\lambda _{3}-\tau _{k}, \end{aligned}$$

(60)

$$\begin{aligned} \lambda _{4}{:}\,{\dot{\lambda }}_{4}=(\rho +\omega _{h})\lambda _{4}-\tau _{h}, \end{aligned}$$

(61)

$$\begin{aligned} \lambda _{5}{:}\,{\dot{\lambda }}_{5}=-\kappa _{k}q\lambda _{1}-{(g_k-\varsigma _{k}-\rho )}\lambda _{5}, \end{aligned}$$

(62)

$$\begin{aligned} \lambda _{6}{:}\,{\dot{\lambda }}_{6}=+\kappa _{h}c\lambda _{2}-{(g_h-\varsigma _{h}-\rho )}\lambda _{6}. \end{aligned}$$

(63)

The corresponding transversality conditions are given by: $\lim _{t\rightarrow \infty }\lambda _{1}(t)q(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{2}(t)c(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{3}(t)A_{k}(t)$ $\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{4}(t)A_{h}(t)\exp {(-\rho t)}=0$, $\lim _{t\rightarrow \infty }\lambda _{5}(t){\tilde{k}}(t)\exp {(-\rho t)}=0$, and $\lim _{t\rightarrow \infty }\lambda _{6}(t){\tilde{h}}(t)\exp {(-\rho t)}=0$.

As in “Appendices 1 and 2”, (60) and (61) together with the transversality conditions involving $A_{k}$ and $A_{h}$ demand $\lambda _3$ and $\lambda _4$ to be constant for all t. Their values equal those in the preceding cases.

The optimal control $k^{{sub}}$ can be found by solving (56) for k and inserting $\lambda _3=\frac{\tau _k}{\rho +\omega _k}$ as

$$\begin{aligned} k^{{sub}}=\frac{\lambda _1 q^{sub}+\frac{\sigma _k \tau _k}{\omega _k+\rho }}{2\alpha (1-\xi )}, \end{aligned}$$

(64)

with $q^{{sub}}$ as the quality level resulting from the subsidy policy. Evaluating (58) in steady-state with ${\dot{\lambda }}_1=0$ gives

$$\begin{aligned} \lambda _1=\frac{(\Theta -1)d}{\rho }-\frac{2\gamma q^{{sub}}}{\rho }. \end{aligned}$$

Inserting this into (64) gives $k^{{sub}}$ as in the main text as

$$\begin{aligned} k^{sub}=\frac{q^{sub} \left( \rho +\omega _k\right) (d (\Theta -1)-2 \gamma q^{sub})+\rho \sigma _k \tau _k}{2 \alpha \rho (1-\xi ) \left( \rho +\omega _k\right) }. \end{aligned}$$

Returning to the case of the welfare optimum discussed in “Appendix 2”, we find the optimal investments into quality, $k^{m}$ by solving, first, (46) for $\lambda _1$ in steady-state with a constant level of quality and constant corresponding investments. Inserting this result into (43) and solving for (an interior) $k^m$ gives

$$\begin{aligned} k^m=\frac{q^m(\rho +\omega _k)\left( d(\Theta -1)-2\gamma q^m-\frac{1}{2}\right) +\rho \sigma _k \tau _k}{2\alpha \rho (\rho +\omega _k)}. \end{aligned}$$

Equalizing this expression with $k^{sub}$ above (and demanding that the level of quality is identical to $q^m$) leads to the optimal tax rate $\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )$ as in the main text in equation (39). Inserting $q^m$ given by (37) into (39) finally delivers (40).

Appendix 4: Proof of Propositions

• 1 $\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )$ increases in $\sigma _k$, $\tau _k$ and $\kappa _k$: This follows directly as $\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )$ positively depends on $\Psi$ which in turn depends positively on $\sigma _k$, $\tau _k$ and $\kappa _k$ $\square$

• 2 $\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )>0$: From (40), this follows whenever $\delta -\kappa _k>0$ holds. Inspecting (39) reveals that we find a positive $\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )$ if $2 d (\Theta -1)-4 \gamma q^{m}+1\ge 0$. This, however, is equal to the marginal increase in welfare that is due to quality changes in the social optimum and, hence, cannot be negative $\square$

• 3 Subsidy time varying off the steady-state Under the optimal subsidy scheme, the level of quality q and investments into product innovations k need to replicate its welfare maximizing counterparts. Equating the investments k that fulfill (64) and (51) respectively, and solving for the subsidy rate gives

  $$\begin{aligned} \xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )=q\frac{\lambda _1^m-\lambda _1^{sub}}{\lambda _1^mq+\frac{\sigma _k}{\rho +\omega _k}}, \end{aligned}$$

  where $\lambda _1^m$ and $\lambda _1^{sub}$ denote the shadow values of the quality level in the welfare optimum and under the subsidy scheme. Note that they are not equal as the subsidy affects this implicit price for quality. Differentiating this with respect to time leads to

  $$\begin{aligned} \frac{{{\dot{\xi }}}^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )}{\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )}=\frac{\dot{q}}{q}+\frac{{\dot{\lambda }}_1^m-{\dot{\lambda }}_1^{sub}}{{\lambda }_1^m-{\lambda }_1^{sub}}-\frac{{\dot{\lambda }}_1^mq+\lambda _1^{m}{\dot{q}}}{\lambda _1^mq+\frac{\sigma _k}{\rho +\omega _k}}, \end{aligned}$$

  where $\dot{q}$ fulfills (55). Making use of (52) gives

  $$\begin{aligned} \frac{{{\dot{\xi }}}^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )}{\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )}=\frac{\dot{q}}{q}+\frac{{\dot{\lambda }}_1^m-{\dot{\lambda }}_1^{sub}}{{\lambda }_1^m-{\lambda }_1^{sub}}-\frac{\dot{k}}{k}, \end{aligned}$$

  where $\dot{k}$ fulfills (52). Using the FOCs (45) and (58) together with (55), the middle term on the right-hand side is:

  $$\begin{aligned} \frac{{\dot{\lambda }}_1^m-{\dot{\lambda }}_1^{sub}}{{\lambda }_1^m-{\lambda }_1^{sub}}=\rho -\frac{1}{2(\lambda _1^m-\lambda _1^{sub})}. \end{aligned}$$

Hence,

$$\begin{aligned} \frac{{{\dot{\xi }}}^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )}{\xi ^{opt}(\sigma _k,\tau _k,\kappa _k,\cdot )}=\frac{\dot{q}}{q}+\rho -\frac{1}{2(\lambda _1^m-\lambda _1^{sub})}-\frac{\dot{k}}{k}. \end{aligned}$$

As the dynamics of the model imply transitional dynamics (see Sect. 3), all the terms in this result are time varying. Consequently, the optimal subsidy rate shares this property $\square$