Does vertical integration enhance non-price efficiency? Evidence from the movie theater industry

Abstract

This paper examines how vertical integration affects non-price efficiency in the movie theater industry. Adopting a discrete choice framework, we derive consumer welfare under capacity constraints and fixed prices, and show that allocating capacity proportionally to demand is efficient. Applying our approach to estimating the efficiency of movie theaters’ seat allocations, we show that integrated theaters may be more efficient than non-integrated ones at picking movies to screen and allocating seats across them. We propose a theoretical mechanism behind these results. Specifically, we show that integrated theaters have higher incentives to acquire demand information and hence can be more efficient in allocating the seats.

Appendix

Proof of Proposition 1

We solve

$$\begin{aligned} \max _{\left( s_{1},\dots ,s_{n}\right) \ge 0}\sum q_{j}\left[ \int _{z_{j}(s_{j})}^{\infty }u_{j}g_{j}(u)du+\int _{-\infty }^{z_{j}(s_{j})}{\bar{\varepsilon }}_{0}(u)g_{j}(u)du\right] \end{aligned}$$

subject to

$$\begin{aligned} q_{j}\int _{z_{j}(s_{j})}^{\infty }g_{j}(u)du-s_{j}\le & {} 0 \text{ for } \text{ each } j,\\ \sum s_{j}-C= & {} 0. \end{aligned}$$

If $\sum q_{j}\le C$, then $s_{j}^{*}=\frac{q_{j}}{\sum _{j\ne 0}q_{j}}C$ for each j is optimal. Suppose $\sum q_{j}>C$. Clearly, the inequality binds. Then the first-order conditions are:

$$\begin{aligned}&q_{j}g_{j}(z_{j}(s_{j}))z'_{j}(s_{j})\left[ \varepsilon _{0}(z_{j}(s_{j}))-z_{j}(s_{j})-\lambda _{j}\right] -\lambda _{j}+\mu = 0{ \text{ for } \text{ each } j,} \end{aligned}$$

(15)

$$\begin{aligned}&q_{j}\int _{z_{j}(s_{j})}^{\infty }g_{j}(u)du-s_{j} = 0 \text{ for } \text{ each } j, \end{aligned}$$

(16)

$$\begin{aligned}&\text{ and } \sum s_{j}-C = 0, \end{aligned}$$

(17)

where $\lambda _j$ for each j and $\mu$ are the corresponding Lagrange multipliers. Differentiating (16) with respect to $s_{j}$ yields $z'_{j}(s_{j})=-\frac{1}{g_{j}(z_{j}(s_{j}))q_{j}}$ for each j. Combining it with (15) for each j and k we get $z_{j}(s_{j})-\varepsilon _{0}(z_{j}(s_{j}))=z_{k}(s_{k})-\varepsilon _{0}(z_{k}(s_{k})),$ which holds if

$$\begin{aligned} z_{j}(s_{j})=z_{k}(s_{k}). \end{aligned}$$

(18)

When each $\varepsilon _{ij}$ is i.i.d. extreme value, one can show that for each j we have

$$\begin{aligned} g_{j}(x)=Ae^{-x}e^{-e^{-x}A}, \end{aligned}$$

(19)

where $A=1+\sum _{i\ne 0}\exp \alpha _{i}.$ From (16), (18), and (19) for each j and k we get $s_{j}q_{k}=s_{k}q_{j},$ and hence for each j we have $s_{j}=\frac{q_{j}}{\sum _{j\ne 0}q_{j}}C.$ $\square$

Proof of Proposition 1

(Proof of Proposition 2) The theater solves

$$\begin{aligned} \max _{s_{1,}s_{2}\ge 0}\sum _{j=1,2}\delta _{j}\left[ \int _{0}^{s_{j}}q_{j}dP^{\eta }(q_{j}|{\hat{q}}_{j})+s_{j}\int _{s_{j}}^{\infty }dP^{\eta }(q_{j}|{\hat{q}}_{j})\right] \end{aligned}$$

subject to

$$\begin{aligned} s_{1}+s_{2}=C. \end{aligned}$$

(20)

Clearly, the second order condition holds. From the first-order condition (13) using (11) we get

$$\begin{aligned} \delta _{j}\left[ 1-G^{\eta }\left( \frac{s_{1}-{\hat{q}}_{1}}{{\hat{q}}_{1}}\right) \right] =\delta _{i}\left[ 1-G^{\eta }\left( \frac{C-s_{1}-{\hat{q}}_{2}}{{\hat{q}}_{2}}\right) \right] . \end{aligned}$$

If $\delta _{j}=\delta _{i}=\lambda$, then $s_{j}=\frac{{\hat{q}}_{j}}{{\hat{q}}_{j}+{\hat{q}}_{i}}C$ for $j=1,2$. If $\delta _{j}=1$ and $\delta _{i}=\lambda$, then the result follows from LHS being decreasing and RHS increasing in $s_{1}$. $\square$

Before we provide the proof of Proposition 2 we need to introduce the following definition and lemma that can also be found in Persico (2000).

Definition 1

A function H(v) is quasi-monotone if $v'>v$ and $H(v)>0$ imply $H(v')\ge 0$.

Lemma 1

Let (c, d) be an interval of the real line, $J(\cdot )$ a nondecreasing function, $H(\cdot )$ a quasi-monotone function. Assume that for some measure $\mu$ on ${\mathbb {R}}$ we have $\int _{c}^{d}H(v)d\mu (v)=0.$ Then $\int _{c}^{d}H(v)J(v)d\mu \ge 0$.

Proof of Proposition 3

We shall show that the marginal value of information is higher for integrated theaters. Denote the type of a theater, independent or integrated, by subscript $\tau \in \left\{ Ind,Int\right\}$. For each $\tau$ let $s_{\tau }^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}$ be the optimal allocation for movie 1, and $\pi ^{\tau }(s_{\tau }^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2})$ the maximal profit given accuracy $\eta$, signals ${\hat{q}}_{1}$ and ${\hat{q}}_{2}$, and movie demands $q_{1}$ and $q_{2}$. Define

$$\begin{aligned} u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2}):=\pi ^{Int}(s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2})-\pi ^{Ind}(s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2}). \end{aligned}$$

We want to show that

$$\begin{aligned} \left. \frac{d}{d\theta }\iiiint _{{\mathbb {R}}_{+}}u(\theta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})dF^{\theta }({\hat{q}}_{1}|q_{1})dF^{\theta }({\hat{q}}_{2}|q_{2})dP(q_{1})dP(q_{2})\right| _{\theta =\eta }\ge 0. \end{aligned}$$

(21)

Note that from (10) it follows that $T_{\eta ,\theta ,q}({\hat{Q}}_{j}^{\eta }|q_{j})$ is distributed as ${\hat{Q}}_{j}^{\theta }$ . Hence applying the change of variable in (21) we have

$$\begin{aligned} & \iiiint _{{\mathbb {R}}_{+}}\left. \frac{du(\theta ,T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1}),T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2}),q_{1},q_{2})}{d\theta }\right| _{\theta =\eta }dF^{\eta }({\hat{q}}_{1}|q_{1})dF^{\eta }({\hat{q}}_{2}|q_{2})dP(q_{1})dP(q_{2})\\ &\quad =\left. \iiiint _{{\mathbb {R}}_{+}}\frac{du(\theta ,T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1}),T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2}),q_{1},q_{2})}{d\theta }\right| _{\theta =\eta }dP^{\eta }(q_{1}|{\hat{q}}_{1})dP^{\eta }(q_{2}|{\hat{q}}_{2})dF^{\eta }({\hat{q}}_{1})dF^{\eta }({\hat{q}}_{2}). \end{aligned}$$

We now show that the inner double integral above is nonnegative. Evaluating it we get:

$$\begin{aligned}&\iint _{{\mathbb {R}}_{+}}\frac{\partial \pi ^{Int}(s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2})}{\partial s_{Int}}\nonumber \\&\quad \left[ \left. \frac{\partial s_{Int}^{\theta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial \theta }\right| _{\theta =\eta }+\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left. \frac{\partial T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1})}{\partial \theta }\right| _{\theta =\eta }\right. \nonumber \\&\quad \left. +\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{2}}\left. \frac{\partial T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2})}{\partial \theta }\right| _{\theta =\eta }\right] \nonumber \\&\quad -\frac{\partial \pi ^{Ind}(s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2})}{\partial s_{Ind}}\left[ \left. \frac{\partial s_{Ind}^{\theta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial \theta }\right| _{\theta =\eta }\right. \nonumber \\&\quad \left. +\frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left. \frac{\partial T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1})}{\partial \theta }\right| _{\theta =\eta }+\frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{2}}\left. \frac{\partial T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2})}{\partial \theta }\right| _{\theta =\eta }\right] \nonumber \\&\qquad \times dP^{\eta }(q_{1}|{\hat{q}}_{1})dP^{\eta }(q_{2}|{\hat{q}}_{2}). \end{aligned}$$

(22)

For each $\tau$ we have $\left. \frac{\partial s_{\tau }^{\theta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial \theta }\right| _{\theta =\eta }$ is independent of $q_{1}$ and $q_{2}$, and

$$\begin{aligned} \iint _{{\mathbb {R}}_{+}}\frac{\partial \pi ^{\tau }(s_{\tau }^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2})}{\partial s_{\tau }}dP^{\eta }(q_{1}|{\hat{q}}_{1})dP^{\eta }(q_{2}|{\hat{q}}_{2})=0 \end{aligned}$$

by the first-order condition. So, we can rewrite (22) as

$$\begin{aligned}&\iint _{{\mathbb {R}}_{+}}\frac{\partial \pi ^{Int}(s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2})}{\partial s_{Int}}\left[ \frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left. \frac{\partial T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1})}{\partial \theta }\right| _{\theta =\eta }\right. \\&\quad \left. +\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{2}}\left. \frac{\partial T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2})}{\partial \theta }\right| _{\theta =\eta }\right] dP^{\eta }(q_{1}|{\hat{q}}_{1})dP^{\eta }(q_{2}|{\hat{q}}_{2})\\&\quad -\iint _{{\mathbb {R}}_{+}}\frac{\partial \pi ^{Ind}(s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}},q_{1},q_{2})}{\partial s_{Ind}}\left[ \frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left. \frac{\partial T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1})}{\partial \theta }\right| _{\theta =\eta }\right. \\&\quad \left. +\frac{\partial s_{Ind}^{\theta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{2}}\left. \frac{\partial T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2})}{\partial \theta }\right| _{\theta =\eta }\right] dP^{\eta }(q_{1}|{\hat{q}}_{1})dP^{\eta }(q_{2}|{\hat{q}}_{2}). \end{aligned}$$

Rearranging we get

$$\begin{aligned}&\iint _{{\mathbb {R}}_{+}}\frac{\partial u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})}{\partial {\hat{q}}_{1}}\left. \frac{\partial T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1})}{\partial \theta }\right| _{\theta =\eta }\\&\quad +\frac{\partial u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})}{\partial {\hat{q}}_{2}}\left. \frac{\partial T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2})}{\partial \theta }\right| _{\theta =\eta }dP^{\eta }(q_{1}|{\hat{q}}_{1})dP^{\eta }(q_{2}|{\hat{q}}_{2}). \end{aligned}$$

Integrating out $q_{2}$ in the first term and $q_{1}$ in the second term we have

$$\begin{aligned}&\int _{{\mathbb {R}}_{+}}\left[ \int _{{\mathbb {R}}_{+}}\frac{\partial u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})}{\partial {\hat{q}}_{1}}dP^{\eta }(q_{2}|{\hat{q}}_{2})\right] \left. \frac{\partial T_{\eta ,\theta ,q_{1}}({\hat{q}}_{1})}{\partial \theta }\right| _{\theta =\eta }dP^{\eta }(q_{1}|{\hat{q}}_{1})\\&\quad +\int _{{\mathbb {R}}_{+}}\left[ \int _{{\mathbb {R}}_{+}}\frac{\partial u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})}{\partial {\hat{q}}_{2}}dP^{\eta }(q_{1}|{\hat{q}}_{1})\right] \left. \frac{\partial T_{\eta ,\theta ,q_{2}}({\hat{q}}_{2})}{\partial \theta }\right| _{\theta =\eta }dP^{\eta }(q_{2}|{\hat{q}}_{2}). \end{aligned}$$

Now we use the Lemma to show that the two terms above are nonnegative. First, note that

$$\begin{aligned} \frac{\partial T_{\eta ,\theta ,q_{j}}({\hat{q}}_{j})}{\partial \theta }= & {} \lim _{\theta \downarrow \eta }\frac{T_{\eta ,\theta ,q_{j}}({\hat{q}}_{j})-T_{\eta ,\eta ,q_{j}}({\hat{q}}_{j})}{\theta -\eta }= \lim _{\theta \downarrow \eta }\frac{T_{\eta ,\theta ,q_{j}}({\hat{q}}_{j})-{\hat{q}}_{j}}{\theta -\eta } \end{aligned}$$

is increasing in $q_{j}$ because $T_{\eta ,\theta ,q_{j}}({\hat{q}}_{j})$ is increasing by assumption. By the first-order conditions

$$\begin{aligned} \iint _{{\mathbb {R}}_{+}}\frac{\partial u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})}{\partial {\hat{q}}_{j}}dP^{\eta }(q_{1}|{\hat{q}}_{1})dP^{\eta }(q_{2}|{\hat{q}}_{2})=0 \end{aligned}$$

(23)

for each j. So, to apply the Lemma it remains to show that

$$\begin{aligned} \int _{{\mathbb {R}}_{+}}\frac{\partial u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})}{\partial {\hat{q}}_{1}}dP^{\eta }(q_{2}|{\hat{q}}_{2}) \end{aligned}$$

(24)

is quasi-monotone in $q_{1}$, and

$$\begin{aligned} \int _{{\mathbb {R}}_{+}}\frac{\partial u(\eta ,{\hat{q}}_{1},{\hat{q}}_{2},q_{1},q_{2})}{\partial {\hat{q}}_{2}}dP^{\eta }(q_{1}|{\hat{q}}_{1}) \end{aligned}$$

(25)

is quasi-monotone in $q_{2}$. Using the definition of payoff rewrite (24) as:

$$\begin{aligned}&\int _{{\mathbb {R}}_{+}}\left[ \frac{\partial \min \left\{ q_{1},s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}\right\} }{\partial s_{Int}}+\lambda \frac{\partial \min \left\{ q_{2},C-s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}\right\} }{\partial s_{Int}}\right] \frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\\&\quad -\lambda \left[ \frac{\partial \min \left\{ q_{1},s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}\right\} }{\partial s_{Ind}}+\frac{\partial \min \left\{ q_{2},C-s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}\right\} }{\partial s_{Ind}}\right] \frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}dP^{\eta }(q_{2}|{\hat{q}}_{2}). \end{aligned}$$

Integrating the above we get

$$\begin{aligned}&\frac{\partial \min \left\{ q_{1},s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}\right\} }{\partial s_{Int}}\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}-\lambda \frac{\partial \min \left\{ q_{1},s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}\right\} }{\partial s_{Ind}}\frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\\&\quad +\lambda \left[ \frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left[ 1-P^{\eta }(C-s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}|{\hat{q}}_{2})\right] -\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left[ 1-P^{\eta }(C-s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}|{\hat{q}}_{2})\right] \right] . \end{aligned}$$

From Proposition 1 we know that $s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}>s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}$. Hence if

$$\begin{aligned} \frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left[ 1-P^{\eta }(C-s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}|{\hat{q}}_{2})\right] -\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}\left[ 1-P^{\eta }(C-s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}|{\hat{q}}_{2})\right] <0, \end{aligned}$$

(26)

then (24) is negative for $q_{1}\le s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}$, and positive for $q_{1}>s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}$, and hence is quasi-monotone in $q_{1}$. So, it remains to show (26). Because $s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}>s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}$, we get

$$\begin{aligned} 1-P^{\eta }(C-s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}|{\hat{q}}_{2})<1-P^{\eta }(C-s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}|{\hat{q}}_{2}). \end{aligned}$$

Therefore it is sufficient to prove that $\frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}<\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}.$ Implicitly differentiating the first-order conditions and using (11) we obtain

$$\begin{aligned} \frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}=\frac{s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{{\hat{q}}_{1}}\frac{\frac{1}{{\hat{q}}_{1}}g^{\eta }(z_{1}^{Ind})}{\frac{1}{{\hat{q}}_{1}}g^{\eta }(z_{1}^{Ind})+\frac{1}{{\hat{q}}_{2}}g^{\eta }(z_{2}^{Ind})}=\frac{s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{{\hat{q}}_{1}}\frac{\frac{1}{{\hat{q}}_{1}}h^{\eta }(z_{1}^{Ind})}{\frac{1}{{\hat{q}}_{1}}h^{\eta }(z_{1}^{Ind})+\frac{1}{{\hat{q}}_{2}}h^{\eta }(z_{2}^{Ind})}, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}=\frac{s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{{\hat{q}}_{1}}\frac{\frac{1}{{\hat{q}}_{1}}g^{\eta }(z_{1}^{Int})}{\frac{1}{{\hat{q}}_{1}}g^{\eta }(z_{1}^{Int})+\lambda \frac{1}{{\hat{q}}_{2}}g^{\eta }(z_{2}^{Int})}=\frac{s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{{\hat{q}}_{1}}\frac{\frac{1}{{\hat{q}}_{1}}h^{\eta }(z_{1}^{Int})}{\frac{1}{{\hat{q}}_{1}}h^{\eta }(z_{1}^{Int})+\frac{1}{{\hat{q}}_{2}}h^{\eta }(z_{2}^{Int})}, \end{aligned}$$

where $z_{1}^{\tau }=\frac{s_{\tau }^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}-{\hat{q}}_{1}}{{\hat{q}}_{1}}$ and $z_{2}^{\tau }=\frac{C-s_{\tau }^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}-{\hat{q}}_{1}}{{\hat{q}}_{1}}$, and $h^{\eta }(x)=\frac{g^{\eta }(x)}{1-G^{\eta }(x)}$ is the hazard function of $G^{\eta }(x)$. Finally, we get

$$\begin{aligned} \frac{\frac{\partial s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}}{\frac{\partial s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{\partial {\hat{q}}_{1}}}= & {} \frac{s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}\frac{1+\frac{{\hat{q}}_{1}}{{\hat{q}}_{2}}\frac{h^{\eta }(z_{2}^{Int})}{h^{\eta }(z_{1}^{Int})}}{1+\frac{{\hat{q}}_{1}}{{\hat{q}}_{2}}\frac{h^{\eta }(z_{2}^{Ind})}{h^{\eta }(z_{1}^{Ind})}}\\< & {} 1, \end{aligned}$$

where the inequality is due to $s_{Int}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}>s_{Ind}^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}$ by Proposition 1, $z_{2}^{Ind}=z_{1}^{Ind}$ and $z_{2}^{Int}<z_{1}^{Int}$ from the first-order condition, and $h^{\eta }(\cdot )$ is increasing by log-concavity of $g^{\eta }(x)$. Therefore (26) holds, and (23) is quasi-monotone. The proof that (25) is quasi-monotone in $q_{2}$ follows the similar steps using the fact that $\frac{s_{\tau }^{\eta ,{\hat{q}}_{1},{\hat{q}}_{2}}}{{\hat{q}}_{2}}<0$. Hence, the marginal value of information is higher for integrated theaters and the standard comparative statics argument yields the result. $\square$

1.1 Vertical integration and foreclosure

In this subsection, we quantify the foreclosure effect of vertical integration. First, we examine the prediction that non-integrated theaters do not discriminate movies based on the type of a distributor. Using the data on the seat allocation of non-integrated theaters we estimate the following model:

$$\begin{aligned} \ln (Seat\,Share)_{jhmt}^{Ind} = \beta _{VI}\,Integrated_{j}+\beta _{DS}\,\ln (Demand\,Share)_{jmt} + \psi _t + \psi _h + \varepsilon _{jhmt}, \end{aligned}$$

(27)

where $Seat\,Share_{jhmt}^{Ind}$ is movie j’s share of seats in non-integrated theater h operating in market m during weekends of week t. The variable of interest is dummy $Integrated_{j}$ equal to one if movie j is released by an integrated distributor and zero otherwise. We control for the relative movie demand by including $Demand\,Share_{jmt}$ which is movie j’s share in the total audience of all movies in market m during weekdays of week t. The higher the relative movie demand, the higher should be this movie’s seat share. Week and theater fixed effects, $\psi _t$ and $\psi _h$, are also included in the model.

Next, we investigate whether integrated theaters foreclose movies of rival distributors. Using the data on the seat allocation of integrated theaters we estimate

$$\begin{aligned} \ln (Seat\,Share)_{jhmt}^{VI} = \beta _{Own}\,Own_{jh}+\beta _{DS}\,\ln (Demand\,Share)_{jmt} + \psi _t + \psi _h +\varepsilon _{jhmt}. \end{aligned}$$

(28)

The model is similar to (27) except that dummy $Integrated_{j}$ is replaced with $Own_{jh}$ which is equal to one if movie j is released by the distributor affiliated with theater h and zero otherwise. Coefficient $\beta _{Own}$ measures the foreclosure effect of vertical integration.

The first two columns of Table 6 present estimates of model (27). As expected, there is no strong evidence that the seat share of independent movies is different from the seat share of movies of integrated distributors. Also, consistent with our prediction we observe a significant foreclosure effect in the last two columns of the table: the seat share is higher by 18% in an integrated theater for its own movies compared to other movies, controlling for the relative demand.

Table 6 Foreclosure

1.2 Additional Tables and Figures

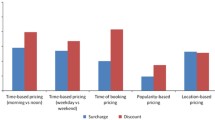
See Tables 7 and 8; Figs. 4, 5 and 6.

Table 7 Box office and per capita attendance

Table 8 Demand estimation with sub-samples

Fig. 4

Demand model fit. Notes: Each panel of the figure shows the observed and predicted movie demand on weekdays and weekends separately in each of the eight markets in the data. Predicted movie demand in a given week is the sum of estimated market shares of all movies in that week, averaged over the 5 years

Fig. 5

Demand model fit at the movie-level. Notes: Each panel of the figure presents a scatter plot for each region where the weekend within-industry share determines the position on the vertical axis and the predicted within-industry share determines the position on the horizontal axis

Fig. 6

Change in welfare loss after the organizational form change. The two panels of the figure show estimated welfare loss relative to 1 month prior to vertical integration or disintegration along with 95% confidence bands