Corruption, mortality rates, and development: policies for escaping from the poverty trap

Abstract

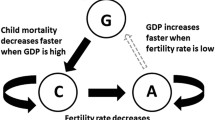
We construct a three-period overlapping generations model in which corruption, mortality and fertility rates, and economic development are determined endogenously. We consider a less developed economy suffering from a high degree of corruption and high mortality and fertility rates in a poverty trap. We focus on two policies: raising public sector wages as a means of reducing corruption and increasing public health spending as a means of improving the mortality rate. Our aim is to examine what effects each policy has on an economy and how governments can achieve economic development using one, or both, of these policies. Our theoretical analysis shows that implementing both policies simultaneously is essential for less developed economies to escape from the poverty trap and achieve economic development.

Appendices

The case of bureaucrats who also give birth and face a mortality rate

To ensure concreteness, we confirm that our results about the relationships between corruption, mortality and fertility rates, and development as well as the dynamics of an economy and multiple steady states hold in a scenario in which both households and bureaucrats give birth and face the mortality rate.

The utility of bureaucrats is

$$\begin{aligned} a \ln n_t^i+(1-a) \ln [\ln c_{a, t}^i+\beta \pi _t \ln c_{o, t+1}^i], \qquad i \in \{ CB, NB \}. \end{aligned}$$

(32)

First, we derive the optimal choices of non-corruptible bureaucrats ($i=NB$). Non-corruptible bureaucrats maximize (32) subject to $c_{a, t}^{NB}+s_t^{NB}=\omega _t-en_t^{NB}\omega _t$ and $c_{o, t+1}^{NB}=R_{t+1}s_t^{NB}/\pi _t$. Then, we obtain

$$\begin{aligned} c_{a,t}^{NB} = \frac{1-a}{1+(1-a)\beta \pi _{t}} \omega _t, \qquad&c_{o,t+1}^{NB} = \frac{(1-a)\beta R_{t+1} }{1+(1-a)\beta \pi _{t}} \omega _t, \\ s_t^{NB} = \frac{(1-a)\beta \pi _{t}}{1+(1-a)\beta \pi _{t}} \omega _t, \qquad&n_t^{NB} =\frac{a}{e[1+(1-a)\beta \pi _{t}]}. \end{aligned}$$

Second, we derive the optimal choices of corruptible bureaucrats ($i=CB$). The choices of corruptible bureaucrats who do not engage in corruption (i.e., honest bureaucrats) are the same as those of non-corruptible bureaucrats. In addition, corruptible bureaucrats who engage in corruption (i.e., dishonest bureaucrats) behave in a similar way as honest bureaucrats. If the government finds a bureaucrat behaving differently, such as larger savings, it can detect his/her corruption. Thus, to avoid being caught, dishonest bureaucrats must match their decisions regarding consumption in adulthood, savings, and number of children to those of honest bureaucrats. Furthermore, they invest illegal income in a foreign market (e.g., an offshore bank) where it is difficult for the government to observe their investment¹⁶. The return of the foreign market is $\mu R_{t+1}$. $\mu \in (0, 1)$ represents the costs and risk of investing illegal income in the foreign market. The optimal choices of honest and dishonest bureaucrats are summarized as follows.

$$\begin{aligned} c_{a,t}^{CB(honest)}&=c_{a,t}^{CB(dishonest)}=c_{a,t}^{NB}, \\ s_{a,t}^{CB(honest)}&=s_{a,t}^{CB(dishonest)}=s_{a,t}^{NB}, \\ n_{a,t}^{CB(honest)}&=n_{a,t}^{CB(dishonest)}=n_{a,t}^{NB}, \end{aligned}$$

and

$$\begin{aligned} c_{o,t+1}^{i}= {\left\{ \begin{array}{ll} \frac{(1-a)\beta R_{t+1}}{1+(1-a)\beta \pi _{t}} \omega _t =c_{o,t+1}^{NB} &\quad \text {if} \quad i=CB(honest), \\ \frac{(1-a)\beta R_{t+1}}{1+(1-a)\beta \pi _{t}} \omega _t +\frac{\mu (1-\delta )R_{t+1}G_t}{N_t^B} &\quad \text {if} \quad i=CB(dishonest). \end{array}\right. } \end{aligned}$$

This leads to the following indirect utility for each type of corruptible bureaucrat:

$$\begin{aligned} U_t^{CB(honest)}&= a \ln n_{a,t}^{CB(honest)}+(1-a) \left[ \ln c_{a,t}^{CB(honest)}+\beta \pi _t \ln c_{o,t+1}^{CB(honest)} \right] , \end{aligned}$$

(33)

$$\begin{aligned} U_t^{CB(dishonest)}&= a \ln n_{a,t}^{CB(dishonest)}+(1-a) \left[ (1-\chi )\ln c_{a,t}^{CB(dishonest)}\right. \nonumber \\&\quad \left. +\,\beta \pi _t \ln c_{o,t+1}^{CB(dishonest)} \right] . \end{aligned}$$

(34)

As in the basic model, dishonest bureaucrats face the cost of engaging in corruption, and this cost is proportional to their utility from consumption in adulthood. Since corruption occurs in adulthood, they lose a part of the utility from consumption in adulthood. We note that $U_t^{CB(honest)}$ and $U_t^{CB(dishonest)}$ depend on the stock of per capita capital, $k_t$, and the share of dishonest bureaucrats among the corruptible bureaucrats, $\sigma _t$, since $\omega _t$, $R_{t+1}$, and $G_t$ are a function of $k_t$, and $\pi _t$ is a function of $\sigma _t$.

A corruptible bureaucrat j chooses the probability of engaging in corruption, $\sigma _{jt} \in [0, 1]$, to maximize $U(\sigma _{jt}, \sigma _t, k_t)=\sigma _{jt} U^{CB(dishonest)}_t+(1-\sigma _{jt})U^{CB(honest)}_t$ given $k_t$ and $\sigma _t$. Since $U(\sigma _{jt}, \sigma _t, k_t)$ is affected by the strategies of other corruptible bureaucrats, we consider a Nash equilibrium.

Definition 1

$\sigma _{jt}^*$ is a Nash equilibrium if $\sigma _{jt}^*$ is the best response to $\sigma _{t}^*$ under the given $k_t$, for all corruptible bureaucrats. That is, $U(\sigma _{jt}^*, \sigma _t^*, k_t) \ge U(\sigma '_{jt}, \sigma _t^*, k_t)$ for all $\sigma '_{jt} \in [0,1]$ and all corruptible bureaucrats.

In the Nash equilibrium, $\sigma _{jt}^*=\sigma _{-jt}^*$ so that $\sigma _{jt}^*=\sigma _t^*$.

When $\partial U(\sigma _{jt}, \sigma _t, k_t)/\partial \sigma _{jt}>0$, $\sigma _{jt}=1$ becomes optimal, from (33) and (34), $\partial U(\sigma _{jt}, \sigma _t, k_t)/\partial \sigma _{jt}>0$ is rewritten as $k_t < {\tilde{k}}(\sigma _t)$, where

$$\begin{aligned} {\tilde{k}}(\sigma _t) \equiv \left\{ \frac{\kappa (\sigma _t) l^\alpha }{A} \left[ 1+\frac{\kappa (\sigma _t) \mu \theta l (1-\delta ) }{\beta \lambda } \right] ^\frac{\beta \pi (\sigma _t)}{\chi } \right\} ^\frac{1}{\alpha }. \end{aligned}$$

We note $\kappa (\sigma _t) \equiv [1+(1-a)\beta \pi (\sigma _t)]/[\rho (1-a)(1-\tau )(1-\alpha )]$. If $k_t<{\tilde{k}}(\sigma _t)$, a corruptible bureaucrat j takes $\sigma _{jt}=1$. Thus, $\sigma _t=1$ is realized since all the other corruptible bureaucrats choose the same strategy. This leads to $k_t<{\tilde{k}}(1)$. Then, the strategy $\sigma _{jt}=1$ if $k_t<{\tilde{k}}(1)$ is the Nash equilibrium. When $\partial U(\sigma _{jt}, \sigma _t, k_t)/\partial \sigma _{jt}<0$, we obtain $k_t>{\tilde{k}}(\sigma _t)$. $\sigma _{jt}=0$ is optimal if $k_t>{\tilde{k}}(\sigma _t)$ holds; then, $\sigma _t=0$ is realized. Thus, the strategy $\sigma _{jt}=0$ if $k_t>{\tilde{k}}(0)$ is the Nash equilibrium. We note that $d\pi (\sigma _t)/d\sigma _t<0$; the degree of corruption, $\sigma _t$, affects the survival rate, $\pi _t$, through which it determines the amount of public services. Then, we can prove that ${\tilde{k}}(1)<{\tilde{k}}(0)$ holds by using $d{\tilde{k}}(\sigma _t)/d\pi (\sigma _t)>0$. A similar discussion can be applied to the case of $\partial U(\sigma _{jt}, \sigma _t, k_t)/\partial \sigma _{jt}=0$. $\partial U(\sigma _{jt}, \sigma _t, k_t)/\partial \sigma _{jt}=0$ yields $k_t={\tilde{k}}(\sigma _t)$. In this case, $\sigma _{jt} \in [0,1]$ becomes optimal. However, there is a unique $\sigma _{jt}$ that satisfies $\sigma _{jt}={\tilde{\sigma }}_t$ and $k_t={\tilde{k}}({\tilde{\sigma }}_t)$ in the interval ${\tilde{k}}(1) \le k_t \le {\tilde{k}}(0)$ since ${\tilde{k}}(\sigma _t)$ is a decreasing function of its argument. Its inverse function, ${\tilde{\sigma }}_j(k_t)$, becomes the unique strategy. In addition, since ${\tilde{k}}(\sigma _t)$ is a decreasing function, ${\tilde{\sigma }}_j(k_t)$ must decrease with $k_t$; that is, $d{\tilde{\sigma }}_j(k_t)/dk_t<0$. Thus, the strategy ${\tilde{\sigma }}_j(k_t)$ if ${\tilde{k}}(1) \le k_t \le {\tilde{k}}(0)$ is the Nash equilibrium.

By summarizing the above discussion, we obtain a strategy of a corruptible bureaucrat:

$$\begin{aligned} \sigma (k_t)= {\left\{ \begin{array}{ll} 1 &\quad \text {for} \quad k_t< {\tilde{k}}(1), \\ {\tilde{\sigma }}(k_t) &\quad \text {for} \quad {\tilde{k}}(1) \le k_t \le {\tilde{k}}(0), \\ 0 &\quad \text {for} \quad {\tilde{k}}(0)<k_t. \end{array}\right. } \end{aligned}$$

(35)

This correspond to Eq. (22) in the basic model. The difference between the two equations is whether corruptible bureaucrats take a mixed strategy in the middle stages of development. In the extended model, some corruptible bureaucrats engage in corruption, while the others do not. The mixed strategy becomes optimal since a corruptible bureaucrat faces a mortality rate that is affected by strategies of other corruptible bureaucrats. The difference slightly changes the per capita public services, $f_t$; the quality of public health, $h_t$; the survival rate, $\pi _t$; and fertility rates, $n_t$, $n_t^{NB}$, $n_t^{CB(honest)}$, and $n_t^{CB(dishonest)}$. However, the intuition and mechanism behind the relationships between corruption, mortality and fertility rates, and economic development hold. That is, as economic development proceeds, the degree of corruption decreases, amount of public services increases, quality of public health improves, and mortality and fertility rates decrease.

Next, we consider the dynamics of per capita capital. The capital market clearing condition is $K_{t+1}=s_tN_t^H+s_t^{NB}(1-b)N_t^B+s_t^{CB(honest)}[1-\sigma (k_t)]bN_t^B+s_t^{CB(dishonest)}\sigma (k_t)bN_t^B$. From $N_{t+1}=n_tN_t^H+n_t^{NB}(1-b)N_t^B+n_t^{CB(honest)}[1-\sigma (k_t)]bN_t^B+n_t^{CB(dishonest)}\sigma (k_t)bN_t^B$, the condition is rewritten as follows:

$$\begin{aligned} k_{t+1}=\frac{1-a}{a}e\beta (1-\tau )(1-\alpha )Al^{-\alpha }[(1-\lambda )+\rho \lambda ] \pi (\sigma (k_t)) k_t^\alpha . \end{aligned}$$

(36)

Subsequently, taking into account (35), we obtain the following three dynamic equations:

$$\begin{aligned} k_{t+1}^C&= \frac{1-a}{a}e\beta (1-\tau )(1-\alpha )Al^{-\alpha }[(1-\lambda )+\rho \lambda ]{\underline{\pi }} k_t^\alpha&\quad \text {for} \quad k_t< {\tilde{k}}(1) \\ k_{t+1}^M&= \frac{1-a}{a}e\beta (1-\tau )(1-\alpha )Al^{-\alpha }[(1-\lambda )+\rho \lambda ]\pi ({\tilde{\sigma }}(k_t)) k_t^\alpha&\quad \text {for} \quad {\tilde{k}}(1) \le k_t \le {\tilde{k}}(0) \\ k_{t+1}^{NC}&= \frac{1-a}{a}e\beta (1-\tau )(1-\alpha )Al^{-\alpha }[(1-\lambda )+\rho \lambda ]{\bar{\pi }} k_t^\alpha&\quad \text {for} \quad {\tilde{k}}(0) < k_t \end{aligned}$$

where ${\underline{\pi }}=\varPi \left( [1-b(1-\gamma )]\theta \right)$, $\pi ({\tilde{\sigma }}(k_t))=\varPi \left( [1-{\tilde{\sigma }}(k_t)b(1-\gamma )]\theta \right)$, ${\bar{\pi }}=\varPi \left( \theta \right)$, and ${\underline{\pi }} \le \pi ({\tilde{\sigma }}(k_t)) \le {\bar{\pi }}$. As in the basic model, two stable steady states can exist¹⁷: $E_C$ and $E_{NC}$. $E_C$ is characterized by severe corruption, high mortality and fertility rates, and low development, while $E_{NC}$ is characterized by no corruption, low mortality and fertility rates, and high development. This result is the same as that in the basic model. However, we should note that it would be complicated in the extended model to consider the effective policy for a less developed country caught in a poverty trap since there are three dynamic equations ($k_{t+1}^C$, $k_{t+1}^M$, and $k_{t+1}^{NC}$) and two thresholds (${\tilde{k}}(1)$ and ${\tilde{k}}(0)$).

Proof of Lemma 1

By taking the partial derivatives of ${\hat{k}}(\rho , \theta )$, represented by (30) with respect to $\rho$ and $\theta$, respectively, we obtain

$$\begin{aligned} \frac{\partial {\hat{k}}(\rho , \theta )}{\partial \rho } = - \frac{{\hat{k}}(\rho , \theta )}{\alpha \rho } \frac{1-\lambda }{1-\lambda +\rho \lambda (1-\alpha )} \left\{ 1+\frac{1-\chi }{\chi }\frac{1}{1+\frac{\rho \lambda (1-\theta )(1-\alpha )}{\theta (1-\delta )[(1-\lambda )+\rho \lambda (1-\alpha )]}} \right\} <0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial {\hat{k}}(\rho , \theta )}{\partial \theta } = \frac{{\hat{k}}(\rho , \theta )}{\alpha (1-\theta )} \left\{ 1+\frac{1-\chi }{\chi }\frac{1}{\theta +\frac{\rho \lambda (1-\theta )(1-\alpha )}{(1-\delta )[(1-\lambda )+\rho \lambda (1-\alpha )]}} \right\} >0. \end{aligned}$$

In addition, we obtain

$$\begin{aligned} \lim _{\rho \rightarrow \infty } {\hat{k}}(\rho , \theta )= \left\{ \frac{\lambda }{(1-\theta )(1-\lambda )^{1-\alpha }A} \left[ 1+\frac{\theta (1-\delta )}{1-\theta } \right] ^\frac{1-\chi }{\chi } \right\} ^\frac{1}{\alpha } < \infty . \end{aligned}$$

Thus, ${\hat{k}}(\rho , \theta )$ decreases with $\rho$ and increases with $\theta$. As $\rho$ approaches infinity, ${\hat{k}}(\rho , \theta )$ converges to a finite value.

Proof of Lemma 2

By taking the partial derivative of $k^*(\rho , \theta )$, represented by (29) with respect to $\rho$, we obtain

$$\begin{aligned} \frac{\partial k^*(\rho , \theta )}{\partial \rho }= - \frac{k^*(\rho , \theta )\lambda }{(1-\lambda )+\rho \lambda (1-\alpha )} < 0. \end{aligned}$$

That is, $k^*(\rho , \theta )$ decreases with $\rho$. Similarly, by taking the partial derivative of $k^*(\rho , \theta )$ with respect to $\theta$, we obtain

$$\begin{aligned} \frac{\partial k^*(\rho , \theta )}{\partial \theta }=\frac{k^*(\rho , \theta )}{\theta (1-\alpha )} \left( \frac{d{\underline{\pi }}}{d\theta } \frac{\theta }{{\underline{\pi }}}-\frac{\theta }{1-\theta } \right) . \end{aligned}$$

$(d{\underline{\pi }}/{\underline{\pi }})/(d\theta /\theta )$ represents the degree to which a change in $\theta$ leads to a change in the survival rate, ${\underline{\pi }}$. Since the survival rate is given by (31), it has the following characteristics:

$$\begin{aligned} \frac{d}{d\theta } \left( \frac{d{\underline{\pi }}}{d\theta }\frac{\theta }{{\underline{\pi }}} \right) <0, \qquad \frac{d^2}{d\theta ^2} \left( \frac{d{\underline{\pi }}}{d\theta }\frac{\theta }{{\underline{\pi }}} \right) >0, \qquad \left. \frac{d{\underline{\pi }}}{d\theta } \frac{\theta }{{\underline{\pi }}} \right| _{\theta =0}=1, \qquad \left. \frac{d{\underline{\pi }}}{d\theta } \frac{\theta }{{\underline{\pi }}} \right| _{\theta =1}=\frac{1}{1+\phi }. \end{aligned}$$

On the other hand, we can show that

$$\begin{aligned} \frac{d}{d\theta } \left( \frac{\theta }{1-\theta } \right)>0, \qquad \frac{d^2}{d\theta ^2}\left( \frac{\theta }{1-\theta } \right) >0, \qquad \lim _{\theta \rightarrow 0} \frac{\theta }{1-\theta } =0, \qquad \lim _{\theta \rightarrow 1} \frac{\theta }{1-\theta } =\infty . \end{aligned}$$

Thus, there is a threshold, ${\hat{\theta }}=[-1+(1+\phi )^\frac{1}{2}]/\phi$, that satisfies $(d{\underline{\pi }}/{\underline{\pi }})/(d\theta /\theta )|_{\theta ={\hat{\theta }}}={\hat{\theta }}/(1-{\hat{\theta }})$. We also confirm ${\hat{\theta }}$ in Fig. 8. If $\theta \in (0, {\hat{\theta }})$, $(d{\underline{\pi }}/{\underline{\pi }})/(d\theta /\theta )>\theta /(1-\theta )$ holds. On the contrary, if $\theta \in [{\hat{\theta }}, 1)$, $(d{\underline{\pi }}/{\underline{\pi }})/(d\theta /\theta ) \le \theta /(1-\theta )$ holds. Thus, we obtain

$$\begin{aligned} \frac{\partial k^*(\rho , \theta )}{\partial \theta } {\left\{ \begin{array}{ll} >0 \quad \text {if} \quad \theta \in (0, {\hat{\theta }}), \\ \le 0 \quad \text {if} \quad \theta \in [{\hat{\theta }}, 1). \end{array}\right. } \end{aligned}$$

That is, $k^*(\rho , \theta )$ is hump-shaped in $\theta$.

Fig. 8

$(d{\underline{\pi }}/{\underline{\pi }})/(d\theta /\theta )$ and $\theta /(1-\theta )$