1 Introduction

Economic inequality is a major topic in economic research. Inequalities in economic resources and factors are useful to understand economic processes. Income inequality is central to issues related to economic inequality. Since Lorenz (1905) introduced the Lorenz curve, various income inequality indexes have been developed to quantitatively measure the degree of income inequality. Such indexes are used to examine whether income inequality is decreasing, whether a redistribution policy is effective at reducing economic inequality, whether a country is more or less unequal than other countries, and so on. The conventional approach is to compute a single index from the income distribution and the corresponding Lorenz curve. The Gini coefficient, defined statistically as the mean absolute difference of all pairs of incomes divided by twice the mean income, was introduced by Gini (1914). The Gini coefficient was further generalized by Donaldson and Weymark (1980) and Yitzhaki (1983). Gastwirth (2014) showed that the Gini coefficient underestimates the rate increase in inequality and modified the Gini coefficient by dividing the mean absolute difference of all pairs of incomes by the median income. Other measures include the coefficient of variation (CV) and the Pietra index. The Pietra index suggested by Schutz (1951) is the portion of the total income that would have to be redistributed. The Pietra index is also known as the Hoover index, the Robin Hood index, and the Ricci-Schutz index. Zanardi (1964) developed an index to measure the asymmetry of the Lorenz curve. In recent contributions, Gallegati et al. (2016) and Clementi et al. (2019) propose the Zanardi index as an appropriate measure of income inequality. There is a class of indexes based on information theory, members of which include the Atkinson index, the generalized entropy index, and the Theil index (Atkinson 1970; Shorrocks 1980; Theil 1967). Such indexes measure diversity in incomes. For a general overview of income inequality measurement, refer to Hao and Naiman (2010), Jenkins and Kerm (2011) and Cowell (2011).

As mentioned above, most of the currently available income inequality indexes are derived from the income distribution and the corresponding Lorenz curve. This approach suffers from the negative income problem. Negative incomes are frequently observed in reality. Self-employed individuals will have negative incomes when their firms and organizations experience losses. Negative incomes are also observed when employees repay an amount of debt that exceeds their earnings. Since most income inequality indexes assume that incomes are nonnegative, the negative incomes observed in the reality create problems in inequality measurement. The Atkinson index, the generalized entropy index, and the Theil index are not computable. The Gini coefficient requires the normalization proposed by Chen et al. (1982) and Raffinetti et al. (2015). It is well known that the CV and Pietra index are appropriate only for nonnegative variables at a ratio scale. Since the income shares for negative incomes cannot be interpreted as proportions, all income inequality indexes involving income shares are neither computable nor interpretable. Therefore, various remedial adjustments of negative incomes have been devised. For example, Cowell (2011) and Hao and Naiman (2010) suggest the deletion of non-positive incomes. OECD (2016) recommends replacing negative incomes with zero incomes. Bellù and Liberati (2006) advise replacing zero incomes with arbitrarily small positive incomes. Raffinetti et al. (2016) study the effects of these remedial adjustments on the Gini coefficient.

These remedial adjustments indicate that the nonnegative income assumption does not correspond to reality. The conventional approach attempts to resolve the inconsistency between this assumption and reality by adjusting the data, not the assumption. Therefore, we need a realistic approach based on something other than the income distribution.

In a recent work, Park et al. (2018) suggest that income inequality should be measured from unequally distributed (UD) incomes, not incomes. UD incomes are obtained from the income distribution by removing the parts of incomes associated with equality. The UD income approach neither requires the nonnegative income assumption nor suffers from the negative income problem. Park et al. (2018) also propose that income inequality should be represented by two indexes reflecting the location and dispersion of UD incomes. However, they do not present a general framework for measuring income inequality based on UD incomes. The aims of the present paper are (i) to propose a framework using the cumulative distribution function (CDF) and the unscaled Lorenz curve of UD incomes; (ii) to show that income inequality has two dimensions, horizontal and vertical, under the proposed framework; (iii) to develop new indexes for the two dimensions; and (iv) to present the relation between the new indexes and the popular Gini coefficient and CV.

This paper is organized as follows. Section 2 briefly reviews UD income. Section 3 adopts the CDF of UD income and represents income inequality as two types of departure from perfect equality. Normalized norms of the departures are proposed as new income inequality indexes. It is also shown that the normalized norm indexes are decomposed into three constituents, the Rawlsian index, the Gini coefficient, and the CV. Section 4 adopts the unscaled Lorenz curve of UD income and develops an income inequality index. It is shown that the index is equivalent to one of the normalized norm indexes derived in Sect. 3. The normalized norm indexes are illustrated using example income distributions and the Luxembourg Income Study (LIS) datasets in Sect. 5. Section 6 presents concluding remarks.

2 Unequally distributed income

We denote the income distribution of a population of n individuals by \({\mathbf {y}} = \left( y_1, y_2, \cdots , y_n \right) \), where \(y_i\) is the income of i-th individual. Without loss of generality, we assume that the incomes are ordered, that is, \(y_1 \le y_2 \le \dots \le y_n\). The total income and mean income are denoted by \(S_y =\sum _{i=1}^n y_i \) and \(\mu _y = S_y / n\), respectively.

We begin by noting that \(y_i = y_1 + \left( y_i - y_1 \right) \), \(i=1, 2, \dots n\). This expression indicates that all income values include \(y_1\), \(n y_1\) of \(S_y\) is equally distributed among the n individuals, and the remaining \(\left( S_y - n y_1 \right) \) is unequally distributed among the n individuals. The unequally distributed portions of the incomes, \(x_i = \left( y_i - y_1 \right) \), \(i = 1, 2, \dots , n\), are referred to as the UD incomes. The total and mean of the UD incomes are written as

$$\begin{aligned} S_x = \left( S_y - n y_1 \right) = n \left( \mu _y - y_1 \right) \text{ and } \mu _x = \left( \mu _y - y_1 \right) . \end{aligned}$$

We denote the UD income distribution by \({\mathbf {x}} = \left( x_1, x_2, \dots , x_n \right) \).

The income distribution encompasses the UD income distribution, and contains information about both equality and inequality. The UD income distribution is obtained by removing the parts of the incomes associated with equality from the income distribution. The amount of income associated with equality is \(ny_1\). The amount of income associated with inequality is \(\left( S_y - ny_1 \right) \), which is distributed as \({\mathbf {x}}\). Income inequality definitely exists in the UD income distribution. It is therefore reasonable to measure income inequality from the UD income distribution.

As defined in Cowell (2011), inequality is a departure from some idea of equality. In the field of income inequality, equality is represented by a perfectly equal income distribution \({\mathbf {y}}_{\mathrm{pe}} = \left( \mu _y, \dots , \mu _y \right) \), usually referred to as perfect equality. We should note that the most significant change from using the UD income approach occurs in the representation of perfect equality. The UD income distribution corresponding to perfect equality is obtained as \({\mathbf {x}}_{\mathrm{pe}} = \left( 0, 0, \cdots , 0 \right) \), the origin of the UD income space.

The income inequality of an income distribution is usually evaluated by the discrepancy from its corresponding \({\mathbf {y}}_{\mathrm{pe}}\). Two income distributions with the same n and different \(S_y\) correspond to different \({\mathbf {y}}_{\mathrm{pe}}\)s. Theoretically, there are infinitely many \({\mathbf {y}}_{\mathrm{pe}}\)s in the income space. Each of the two income distributions is compared to its corresponding \({\mathbf {y}}_{\mathrm{pe}}\). Two income distributions with the same n and \(S_y\) in general have different \(ny_1\)s. In this case, the two income distributions are compared to the same \({\mathbf {y}}_{\mathrm{pe}}\). However, regardless of \(S_y\) and \(\mu _y\), perfect equality in the UD income approach is uniquely represented by \({\mathbf {x}}_{\mathrm{pe}}\), the origin of the UD income space. The following two sections address how to measure the discrepancy of \({\mathbf {x}}\) from \({\mathbf {x}}_{\mathrm{pe}}\).

3 Normalized norm indexes from CDF

A general way to describe a distribution is the CDF. The CDFs for \({\mathbf {x}}\) and \({\mathbf {x}}_{\mathrm{pe}}\) are

$$\begin{aligned} F \left( x \right) = \left\{ \begin{array}{ll} 0 &{} \quad \text{ for } x< x_1, \\ \frac{i}{n} &{} \quad \text{ for } x_i \le x < x_{i+1}, i=1, 2, \cdots , n-1,\\ 1 &{} \quad \text{ for } x \ge x_n, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} F_{\mathrm{pe}} \left( x \right) = \left\{ \begin{array}{ll} 0 &{} \quad \text{ for } x < 0 \\ 1 &{} \quad \text{ for } x \ge 0 \end{array} \right. , \end{aligned}$$

respectively. Figure 1 depicts \(F \left( x \right) \) and \(F_{\mathrm{pe}} \left( x \right) \). Income inequality is then represented by the departure of \(F \left( x \right) \) from \(F_{\mathrm{pe}} \left( x \right) \). There are two types of departure, the vertical departure and the horizontal departure. The vertical departure is the difference between \(F \left( x \right) \) and \(F_{\mathrm{pe}} \left( x \right) \). Let \(Q \left( p \right) \) denote the quantile function of the UD income distribution \({\mathbf {x}}\), which is defined as

$$\begin{aligned} Q \left( p \right) = \inf \left\{ x : F \left( x \right) \ge p\right\} = \left\{ \begin{array}{ll} 0 &{} \quad \text{ for } p = 0 \\ x_i &{} \quad \text{ for } \frac{i-1}{n} < p \le \frac{i}{n}, i = 1, 2, \dots , n. \end{array} \right. \end{aligned}$$

The quantile function for \({\mathbf {x}}_{\mathrm{pe}}\) is obtained as \(Q_{\mathrm{pe}} (p) = 0\) for \(0 \le p \le 1\). The horizontal departure is the difference between \(Q \left( p \right) \) and \(Q_{\mathrm{pe}} \left( p \right) \). The size of the difference between two functions is usually assessed by norms. Thus, we compute the \(\ell _1\) and \(\ell _2\) norms of the vertical and horizontal departures.

Fig. 1
figure 1

Two types of departures of \(F \left( x \right) \) from \(F_{\mathrm{pe}} \left( x \right) \)

Full size image

Let us first consider the vertical departure. The \(\ell _1\) and \(\ell _2\) norms of the vertical departure, denoted by \(\ell _1^v\) and \(\ell _2^v\), are defined as

$$\begin{aligned} \ell _1^v = \int \left( 1 - F \left( x \right) \right) \mathrm{d}x \text{ and } \ell _2^v = \left[ \int \left( 1 - F \left( x \right) \right) ^2 \mathrm{d}x \right] ^{\frac{1}{2}}. \end{aligned}$$

Applying the results of Dorfman (1979) and Yitzhaki (1998), we have

$$\begin{aligned} \ell _1^v = \mu _x \text{ and } \ell _2^v = \left( \mu _x - \frac{\varGamma _x}{2} \right) ^{\frac{1}{2}}, \end{aligned}$$
(1)

where \(\varGamma _x\) is the Gini mean difference (GMD) of the UD income. To convert the norms to indexes, we normalize \(\ell _1^v\) and \(\ell _2^v\). Since \(\ell _1^v\) is in monetary units and \(\ell _2^v\) is in the square root of monetary units, \(\ell _1^v\) is normalized by \(\mu _y\), while \(\ell _2^v\) is normalized by \(\sqrt{\mu _y}\). The normalized vertical norm indexes, denoted by \(\widetilde{\ell _1^v}\) and \(\widetilde{\ell _2^v}\), are obtained as

$$\begin{aligned} \widetilde{\ell _1^v} = \frac{\mu _x}{\mu _y} \text{ and } \widetilde{\ell _2^v} = \left( \frac{\mu _x}{\mu _y} - \frac{\varGamma _x}{2 \mu _y} \right) ^{\frac{1}{2}}. \end{aligned}$$
(2)

Since \(\varGamma _x = \varGamma _y\) and the Gini coefficient is the GMD divided by twice the mean, we have

$$\begin{aligned} \widetilde{\ell _2^v} = \left[ \frac{\mu _x}{\mu _y} \left( 1 - G_x \right) \right] ^{\frac{1}{2}}= \left( \frac{\mu _x}{\mu _y} - G_y \right) ^{\frac{1}{2}}, \end{aligned}$$
(3)

where \(G_y\) and \(G_x\) are the Gini coefficients of income and UD income.

The normalized average vertical distance from perfect equality, \(\widetilde{\ell _1^v}\), is equal to the Rawlsian index introduced by Park et al. (2018). Since the Rawlsian index is the ratio of total UD income to total income, it can be interpreted as the magnitude of income inequality. There is another justification for the Rawlsian index. Since the \(y_i\)s are ordered, the simplest expression for perfect equality is \(y_1 = \mu _y\). Therefore, the discrepancy \(\mu _x = \left( \mu _y - y_1 \right) \) and the normalized \(\mu _x\) are sensible measures for the departure from perfect equality.

\(\widetilde{\ell _2^v}\) is obtained as a combination of the Rawlsian index and the Gini coefficient. It should be noted that the Gini coefficient is associated with the vertical departure and does not alone describe income inequality. Equation (3) contradicts the conventional notion that the greater income inequality is, the greater the Gini coefficient is. If a progressive transfer is not directed to the poorest, the mean UD income and the Rawlsian index are preserved while the Gini coefficient is reduced. Equation (3) states that progressive transfers preserving the mean UD income do not decrease the vertical departure. Income inequality can be improved through the progressive transfers reducing the mean UD income.

Next we consider the horizontal departure. As shown in Fig. 1, the horizontal departure is \(x_i\) for \(\left( i - 1 \right) /n < F \left( x \right) \le i/n\). The \(\ell _1\) and \(\ell _2\) norms of the horizontal departure, denoted by \(\ell _1^h\) and \(\ell _2^h\), are obtained as

$$\begin{aligned} \ell _1^h = \frac{\sum _{i=1}^n x_i}{n} = \mu _x \text{ and } \ell _2^h = \left( \frac{\sum ^n_{i=1} x_i^2}{n} \right) ^{\frac{1}{2}} = \left( \mu _x^2 + V_x \right) ^{\frac{1}{2}}, \end{aligned}$$
(4)

where \(V_x\) is the variance of UD income. Since both \(\ell _1^h\) and \(\ell _2^h\) are in monetary units, we normalize \(\ell _1^h\) and \(\ell _2^h\) by \(\mu _y\). The normalized \(\ell _1^h\) and \(\ell _2^h\) are obtained as

$$\begin{aligned} \widetilde{\ell _1^h} = \widetilde{\ell _1^v} \text{ and } \widetilde{\ell _2^h} = \frac{\mu _x}{\mu _y} \left( 1 + \mathrm{CV}_x^2 \right) ^{\frac{1}{2}} = \left[ \left( \frac{\mu _x}{\mu _y} \right) ^2 + \mathrm{CV}_y^2 \right] ^{\frac{1}{2}}, \end{aligned}$$
(5)

where \(\mathrm{CV}_y\) and \(\mathrm{CV}_x\) are the CVs of income and UD income. It is easily verified that \(\widetilde{\ell _2^h}\) is equal to the normalized Euclidean distance of \({\mathbf {x}}\) from perfect equality in the UD income space. Henceforth, we denote \(\widetilde{\ell _1^v}\) and \(\widetilde{\ell _1^h}\) simply by \(\widetilde{\ell _1}\) and call it the Rawlsian index.

We should note that the CV is associated with the horizontal departure. The Gini coefficient and CV are associated with different types of departure. Therefore, they are not substitutes for one another. Progressive transfers preserving the mean UD income reduce the horizontal departure but increase the vertical departure. Such progressive transfers affect the vertical and horizontal departures in opposite directions.

Most conventional income inequality indexes such as \(G_y\) and \(\mathrm{CV}_y\) describe the dispersion of the income distribution. The Rawlsian index measures the location of the UD income distribution, while \(G_x\) and \(\mathrm{CV}_x\) measure the dispersion of the UD income distribution. \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) are expressed as the combinations of the Rawlsian index and a dispersion measure.

The normalized norm indexes \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) suggest the following:

  1. (i)

    Income inequality has multiple dimensions. The normalized norm indexes \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) consider two dimensions of income inequality.

  2. (ii)

    The normalized norm indexes \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) involve both the location and dispersion of the UD income distribution. The location of the UD income distribution, described by the Rawlsian index \(\widetilde{\ell _1}\), is the primary constituent of income inequality.

  3. (iii)

    The dispersion of the income distribution should be distinguished from income inequality. The popular Gini coefficient and CV are associated with this dispersion. According to Equations (3) and (5), the Gini coefficient and CV represent only parts of income inequality.

  4. (iv)

    Progressive transfers preserving the mean UD income reduce dispersion of the UD income distribution. Such a reduction in dispersion decreases the horizontal departure but increases the vertical departure. An effective way to reduce both types of departures is to decrease the Rawlsian index. The Rawlsian index can be decreased by progressive transfers to the poorest.

4 A normalized norm index from the unscaled Lorenz curve

One of the most popular graphical representations of an income distribution is the Lorenz curve. Income inequality is usually measured by the area enclosed by the Lorenz curves for the income distribution and perfect equality. The area results in the Gini coefficient. This section attempts to derive an income inequality index from the Lorenz curve for the UD income distribution. Similar to the Lorenz curve for income, the Lorenz curve for the UD income is defined as

$$\begin{aligned} L(p) = \frac{\int _0^p Q (t) dt}{\mu _x}. \end{aligned}$$

However, the Lorenz curve for UD income is not applicable, because the Lorenz curve for \({\mathbf {x}}_{\mathrm{pe}}\) is not defined due to \(\mu _x = 0\). Thus, we use \(\int _0^p Q (t) dt\), which is referred to as the unscaled Lorenz curve and denoted by \(L^{u} (p)\).

Figure 2 depicts the unscaled Lorenz curves \(L^{u} (p)\) and \(L^{u}_{\mathrm{pe}} (p)\) for \({\mathbf {x}}\) and \({\mathbf {x}}_{\mathrm{pe}}\). Note that \(L^{u}_{\mathrm{pe}} (p)\) lies on the horizontal axis. The departure of \(L^{u} (p)\) from \(L^{u}_{\mathrm{pe}} (p)\) can be assessed by area \({\mathbf {B}}\), which is the \(\ell _1\) norm of the departure. The dotted diagonal line is not an unscaled Lorenz curve and does not represent perfect equality. The dotted diagonal line is a reference line for computing area \({\mathbf {A}}\) enclosed by \(L^{u} (p)\) and the dotted line. Since area \({\mathbf {A}}\) is \(\mu _x G_x / 2\), area \({\mathbf {B}}\) is obtained as

$$\begin{aligned} {\mathbf {B}} = \frac{1}{2} \mu _x \left( 1 - G_x \right) . \end{aligned}$$

Normalizing \({\mathbf {B}}\) by \(\mu _y\), we have

$$\begin{aligned} \frac{{\mathbf {B}}}{\mu _y} = \frac{1}{2} \frac{\mu _x}{\mu _y} \left( 1 - G_x \right) = \frac{1}{2} \left( \widetilde{\ell _2^v} \right) ^2. \end{aligned}$$
(6)

The normalized \(\ell _1\) norm of the difference between \(L^{u} (p)\) and \(L^{u}_{\mathrm{pe}} (p)\) is equivalent to \(\widetilde{\ell _2^v}\) obtained in the previous section. That is, the CDF and the unscaled Lorenz curve for UD income result in equivalent indexes.

Fig. 2
figure 2

Unscaled Lorenz curves \(L^{u} (p)\) and \(L^{u}_{\mathrm{pe}} (p)\) for \({\mathbf {x}}\) and \({\mathbf {x}}_{\mathrm{pe}}\)

Full size image

5 Application of normalized norm indexes

In this section, we apply the normalized norm indexes to example income distributions and real income datasets. First, consider the eight example income distributions in Table 1. The first seven income distributions \({\mathbf {y}}_i\), \(i=1, 2, \dots , 7\) have the same \(n=5\), \(S_y=15\), and \(\mu _y = 3\). Each of them is obtained from others by a series of transfers. So we can investigate the effect of transfers on income inequality. There are two couples of income distributions that \(G_y\) and \(\mathrm{CV}_y\) fail to distinguish with respect to income inequality, but the normalized norm indexes succeed. In order to examine the negative income problem, we also included an income distribution with a negative income.

\(G_y\) and \(\mathrm{CV}_y\) assess the income inequality of \({\mathbf {y}}_1\) and \({\mathbf {y}}_2\) as being the same. However, there is a difference between \({\mathbf {y}}_1\) and \({\mathbf {y}}_2\); 5 of \(S_y\) is evenly distributed among the individuals in \({\mathbf {y}}_1\), while none of \(S_y\) is evenly distributed among the individuals in \({\mathbf {y}}_2\). This difference is revealed by the Rawlsian index \(\widetilde{\ell _1}\). \({\mathbf {y}}_1\) has less \(\widetilde{\ell _1}\) than does \({\mathbf {y}}_2\). Although \({\mathbf {y}}_2\) has less \(G_x\) and \(\mathrm{CV}_x\) than \({\mathbf {y}}_1\), \({\mathbf {y}}_1\) has less \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) than \({\mathbf {y}}_2\) because it has less \(\widetilde{\ell _1}\). Unlike \(G_y\) and \(\mathrm{CV}_y\), the normalized norm indexes indicate that \({\mathbf {y}}_1\) is more equal than \({\mathbf {y}}_2\). A similar result is obtained from a comparison of \({\mathbf {y}}_3\) and \({\mathbf {y}}_4\). We can consider a series of progressive transfers preserving the mean UD income that transform \({\mathbf {y}}_1\) into \({\mathbf {y}}_4\). According to \(G_y\) and \(\mathrm{CV}_y\), \({\mathbf {y}}_1\) is more equal than \({\mathbf {y}}_4\). While \({\mathbf {y}}_1\) and \({\mathbf {y}}_4\) have the same Rawlsian index, \({\mathbf {y}}_4\) has less \(G_x\) and \(\mathrm{CV}_x\) than \({\mathbf {y}}_1\). However, according to \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\), \({\mathbf {y}}_4\) is more vertically unequal and horizontally equal than \({\mathbf {y}}_1\). A progressive transfer preserving the mean UD income decreases horizontal inequality but increases the vertical inequality. That is, a progressive transfer preserving the mean UD income does not reduce income inequality. We can observe this phenomenon when we compare \({\mathbf {y}}_4\) and \({\mathbf {y}}_5\). \({\mathbf {y}}_6\) is obtained from \({\mathbf {y}}_5\) by a progressive transfer reducing the mean UD income, i.e., the transfer reducing the Rawlsian index. Such progressive transfers decrease both horizontal income inequality and vertical income inequality and consequently decrease income inequality.

Table 1 Example income distributions
Full size table

Let us consider \({\mathbf {y}}_7\) in which a negative income value is observed. \(G_y\) and \(\mathrm{CV}_y\) for \({\mathbf {y}}_7\) in Table 1 are computed without any manipulation of the negative income value. If the negative income value is removed from \({\mathbf {y}}_7\), \({\mathbf {y}}_7\) will exhibit perfect equality. If the negative income value is replaced with zero, \({\mathbf {y}}_7\) will become \({\mathbf {y}}_8\). Replacement with zero primarily reduces UD income and the Rawlsian index. Consequently, income inequality is underestimated as seen from \(\widetilde{\ell _1}\)s, \(\widetilde{\ell _2^v}\)s and \(\widetilde{\ell _2^h}\)s for \({\mathbf {y}}_7\) and \({\mathbf {y}}_8\). According to \(G_y\), \({\mathbf {y}}_7\) is more unequal than \({\mathbf {y}}_1\) and \({\mathbf {y}}_2\). However, the normalized norm indexes assume that \({\mathbf {y}}_7\) is the most unequal income distribution among the income distributions in Table 1.

Next, we apply the normalized norm indexes to the latest LIS datasets for household disposable income after the year 2010 (LIS 2019). Because the years included in the datasets are not the same, this analysis is not intended to be a thorough cross-national comparison but is instead intended to test the applicability of the normalized norm indexes to cross-national comparison. The normalized norm indexes and the popular Gini coefficients and CVs for forty-two countries were computed and are presented in Table 2. The countries were arranged in increasing order of \(G_y\). The numbers in parentheses are ranks for each index. \(G_y\)’s in Table 2 are slightly different from the Gini coefficients published by the LIS Data Center. This is because the LIS Data Center computes the Gini coefficient after removing negative and zero income values.

Table 2 Analysis of the latest LIS datasets after the year 2010
Full size table

We first note that negative incomes are frequently observed. The Rawlsian index is greater than one when there are negative incomes. Twenty-seven countries have negative incomes. The normalized norm indexes provide considerably different information on income inequality than \(G_y\) and \(\mathrm{CV}_y\). The Gini coefficient indicates that Denmark and Norway belong to five most equal countries. However, all the normalized norm indexes indicate that Denmark and Norway are among the five most unequal countries. According to \(G_y\) and \(\mathrm{CV}_y\), Paraguay and South Africa are among the six most unequal countries. However, Paraguay and South Africa are two most equal countries from the perspective of \(\widetilde{\ell _2^h}\).

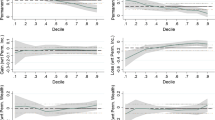
Less vertical departure does not mean less horizontal departure. That is, less \(\widetilde{\ell _2^v}\) is not always accompanied by less \(\widetilde{\ell _2^h}\). The ranks for \(\widetilde{\ell _2^v}\) are not the same as the ranks for \(\widetilde{\ell _2^h}\). \(\widetilde{\ell _2^v}\) is plotted against \(\widetilde{\ell _2^h}\) in Fig. 3. Figure 3 shows that less \(\widetilde{\ell _2^v}\) can be accompanied by greater \(\widetilde{\ell _2^h}\), especially when both \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) are small.

Fig. 3
figure 3

Plot of \(\widetilde{\ell ^v_2}\) against \(\widetilde{\ell ^h_2}\)

Full size image

The countries with the eleven largest Rawlsian indexes are Norway, Peru, Poland, Denmark, the UK, India, Serbia, Mexico, Germany, Israel, and Luxembourg. These countries correspond to the countries with the eleven largest \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\). The ranks of these countries on the Rawlsian index, \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) are the same. The countries with the five smallest Rawlsian indexes are the Czech Republic, Hungary, Slovenia, Brazil, and Russia. Their ranks for \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) are low but somewhat different from one another. This indicates that the Rawlsian index dominates \(\widetilde{\ell _2^v}\) and \(\widetilde{\ell _2^h}\) when the Rawlsian index is large. The \(\widetilde{\ell _2^v}\)’s and \(\widetilde{\ell _2^h}\)’s are plotted against \(\widetilde{\ell _1}\) in Figs. 4 and 5. Figures 4 and 5 show that there is a strong linear tendency between the Rawlsian index and the normalized \(\ell _2\) norm indexes. Exceptional cases from this linear tendency are observed when the Rawlsian index is small. When the Rawlsian index is small, the influences of \(G_x\) and \(\mathrm{CV}_x\), can surpass that of the Rawlsian index.

Fig. 4
figure 4

Plot of \(\widetilde{\ell ^v_2}\) against \(\widetilde{\ell _1}\)

Full size image
Fig. 5
figure 5

Plot of \(\widetilde{\ell ^h_2}\) against \(\widetilde{\ell _1}\)

Full size image

For a given income distribution, a progressive transfer maintaining the Rawlsian index decreases \(\widetilde{\ell _2^h}\) but increases \(\widetilde{\ell _2^v}\). Although the income distributions in Table 2 are different, we can observe similar negative correlations between \(\widetilde{\ell _2^h}\) and \(\widetilde{\ell _2^v}\) when the Rawlsian index is fixed. Figure 6 is a plot of \(\widetilde{\ell _2^v}\) against \(\widetilde{\ell _2^h}\) for seven countries with \(\widetilde{\ell _1} = 1\). The plot shows that \(\widetilde{\ell _2^h}\) and \(\widetilde{\ell _2^v}\) are negatively correlated.

Fig. 6
figure 6

Plot of \(\widetilde{\ell ^v_2}\) against \(\widetilde{\ell ^h_2}\) for the countries with \(\widetilde{\ell _1} = 1\)

Full size image

6 Conclusions

Measurement is the foundation of quantitative research. The proper measurement of income inequality is important for studying economic inequality. In this paper, we proposed a new framework for measuring income inequality. The framework is based on the UD income distribution, which is obtained from the income distribution by removing the equally distributed parts of incomes. We then derived the normalized norm indexes from the CDF and the unscaled Lorenz curve for the UD income distribution. The normalized norm indexes represent the location and the dispersion of the UD income distribution, while most conventional income inequality indexes reflect only the dispersion of the income distribution. By analyzing example income distributions and the LIS datasets, we showed that the normalized norm indexes are appropriate measures of income inequality and solve the negative income problem. However, it should be noted that the proposed indexes represent only one-dimensional views of income inequality. They describe the horizontal and vertical dimensions of the two-dimensional UD income distribution. Therefore, the horizontal and vertical normalized norm indexes are not alternatives to one another. Both the horizontal and vertical normalized norm indexes should be taken into consideration to comprehensively understand income inequality. For the sake of simplicity without sacrificing comprehensiveness, it would be desirable to devise a new index that reflects a two-dimensional view of income inequality. Our future research will be directed toward the development of such an index.