Introduction

Imagine secondary education students attempting to solve a problem in school. They may generate one or several solution attempts. Likely, they would only generate more and, ideally, better solution attempts to the problem, if they realized that their previous solution attempt was incorrect or incomplete. Designing the problem-solving material in the form of cases that differ in one feature at a time, and thereby allowing students to contrast these cases, could provide feedback to students about the correctness of their solution attempt when applying the solution attempt to these cases (Roll et al. 2014). Contrasting cases are small examples that each differ concerning one deep feature of a concept while keeping other features constant between cases (Loibl et al. 2017; Schwartz and Bransford 1998; Schwartz and Martin 2004), allowing for intuitive comparisons between cases. Students can use their intuitive comparisons of the cases to extract grounded feedback when they apply their solution attempts to these contrasting cases (Nathan 1998; Roll et al. 2014). This grounded feedback may help students to detect flaws in their solution attempts (i.e., that they did not consider the deep feature highlighted by the contrasting cases; Loibl et al. 2017). Thus, contrasting cases support students to detect the deep features and corresponding flaws in their solution attempts, and to improve their attempts accordingly. Students can only detect flaws in their own solution attempts (with the help of contrasting cases) if their own attempts indeed have flaws (i.e., incorrect or incomplete solutions attempts), which is more likely to occur during problem solving prior to instruction than during problem solving after instruction on how to solve such problems. In this paper, we study the effects of including the opportunity for students to contrast cases that differ in one feature at a time in the problem-solving material before or after instruction. By doing so, we also address the confound of previous studies that compared problem solving before or after instruction, but only included contrasting cases in the study materials of the problem solving first condition (e.g., Schwarz and Martin 2004).

Mathematical problem solving prior to and after instruction

In mathematics education, the teacher usually gives students clear instruction that fully explains the concepts and procedures, before letting them practice with applying the learned procedure on novel problems themselves (Schoenfeld 1992). Such instructional designs are often called direct instruction approaches (Kapur 2012; Kirschner et al. 2006). It has been argued that direct instruction is better for learning than instructional designs that rely on students’ own ability to discover the solution to a problem without guidance (Kirschner et al. 2006; Mayer 2004). Indeed, giving instruction prior to problem solving has been shown to improve students’ procedural fluency, that is, the ability to execute the right action sequences to solve a problem (Rittle-Johnson et al. 2001), compared to students who did not receive instruction prior to problem solving (Klahr and Nigam 2004). However, Schoenfeld (1992) argued that direct instruction often does not increase understanding of the functionality of each separate component in the procedure (e.g., dividing by N accounts for sample size when calculating the mean) and, thus, often does not improve students’ conceptual understanding of the target concept (Schoenfeld 1992). Conceptual understanding is defined as someone’s comprehension of the underlying components of a (mathematical) concept and the interrelations between these components (Rittle-Johnson et al. 2001). To improve conceptual understanding, students need to actively make sense of the underlying principles of the concept and try to relate these principles not only in mathematics, but also in other domains (Koedinger et al. 2012). Prominent examples are the claim-evidence-reasoning framework (McNeill and Krajcik 2012) often applied in science education (e.g., Shemwell et al. 2015) or the attempt to facilitate schema acquisition by analogical reasoning (e.g., Gentner et al. 2003; Gick and Paterson 1992). With regard to mathematics education, Rittle-Johnson and Star (2009) reviewed the beneficial effects of comparisons, including the comparison of different solution methods to one problem. Schoenfeld (1992) argued that teachers could elicit sense-making activities by engaging students in the exploration of a mathematical problem and its patterns by first letting them generate solution attempts and only afterwards provide instruction on the correct solution.

In recent years, multiple studies investigated the effect of delaying instruction until students have completed an unguided problem-solving phase on the acquisition of both, conceptual understanding and procedural fluency (see Darabi et al. 2018; Loibl et al. 2017 for a meta-analysis and a review). In these studies, students engage in a problem-solving phase before receiving instruction (PS-I). During the problem-solving phase, students generate solutions to a problem that requires the application of a yet unlearned concept (Kapur and Bielaczyc 2012). Instruction on the concept and the correct solution follows in the subsequent instruction phase. For example, Kapur (2012) asked students to generate as many mathematical methods as possible to compare three soccer players on consistency, using fictive data about the number of goals per player per season. After the problem-solving phase, students received instruction on the correct method to calculate consistency (i.e., by calculating the standard deviation). This study and similar studies have shown beneficial effects of PS-I (d = 0.6 to 2.3) compared to direct instruction, in which instruction is provided before students engage in problem solving (I-PS) on conceptual understanding (DeCaro and Rittle-Johnson 2012; Kapur 2010, 2011, 2012, 2014; Kapur and Bielaczyc 2012; Loibl and Rummel 2014a, b). However, the results on procedural fluency are less clear (see Loibl et al. 2017; we will return to procedural fluency in the section “Effects of the order of the learning phases on procedural fluency”).

Learning mechanisms underlying the beneficial effects of PS-I on conceptual understanding

In their review, Loibl et al. (2017) identified three mechanisms that might explain why PS-I facilitates learning: by activating prior knowledge, becoming aware of knowledge gaps, and recognizing deep features of the target concept. PS-I activates prior knowledge by engaging students in unguided problem solving (Kapur 2016; Kapur and Bielaczyc 2012; Loibl et al. 2017). Activating relevant prior knowledge (i.e., existing cognitive schemas) facilitates the organization and integration of new information (Mayer 2002), and has been shown to make students more susceptible to subsequent instruction (Schmidt et al. 1989).

In addition to activating correct prior knowledge, students in PS-I studies might also activate prior knowledge that contains incorrect or incomplete ideas, as they are not yet familiar with the target concept (Loibl et al. 2017; Schwartz and Martin 2004). Indeed, students usually generate incorrect or incomplete solution attempts during this phase (Kapur 2012; Roll et al. 2011). However, while incorrect prior knowledge could hinder learning when this is inconsistent with subsequent instruction (Duit and Treagust 2012), it could make students aware of their knowledge gaps, when their attention is drawn to the mistakes in their generated solution attempts (Kapur 2016; Loibl et al. 2017). Once students recognize a mistake or gap in their knowledge, they may undertake actions to solve this (Chi 2000; VanLehn 1999), such as focusing the attention on the yet-to-be-learnt knowledge components during the subsequent instruction (Loibl et al. 2017; VanLehn et al. 2003).

Moreover, PS-I facilitates students in discovering the deep features of the target concept before instruction on the correct solution is provided (Kapur 2016; Loibl et al. 2017). For example, when students realize that their generated solution does not take different sample sizes into account when calculating standard deviation, they discover that they should somehow incorporate this as a component in their next solution attempt. However, students often do not come to this realization spontaneously, but rather, need some implicit or explicit guidance. When students’ attention is guided towards deep features of a concept, they tend to recognize them more often (Holmes et al. 2014), which can lead to better learning from subsequent instruction (Roll et al. 2012). Components that operationalize deep features of a concept (e.g., divide by N to take sample size into account) are called functional components (Roll et al. 2011). When subsequent instruction describes the implementation of each functional component (e.g., dividing by N to account for sample size), students have the opportunity to apply these to earlier discovered deep features (e.g., sample size matters; Roll et al. 2011).

The mechanisms mentioned above might explain why PS-I has a beneficial effect on conceptual understanding compared to I-PS. However, it is difficult to identify what aspects of PS-I are responsible for evoking these mechanisms and which (combination of) mechanisms cause the beneficial effects on learning because PS-I (and the I-PS control condition) has been implemented differently across studies (cf. Loibl et al. 2017).

Different implementations of PS-I studies and their relation to the learning mechanisms

Most PS-I studies come from two areas of research: productive failure (e.g., Kapur 2010; Kapur and Bielaczyc 2012) and invention (e.g., Schwartz and Bransford 1998; Schwartz and Martin 2004). Both approaches activate prior knowledge by engaging students in problem solving first. However, these approaches differ with regard to how they foster an awareness of knowledge gaps and deep features. In most productive failure studies, the problem-solving material incorporates multiple cases, but these cases do not highlight the deep features, as they are not varied systematically. However, students in the PS-I condition have the possibility to become aware of their knowledge gaps and to discover deep features of the target concept by comparing their own solution attempts with typical student solutions discussed at the beginning of the instruction phase (Loibl et al. 2017). This implementation has been shown to improve conceptual understanding compared to an I-PS condition (d = 0.6 to 2.3; Kapur 2010, 2011, 2012, 2014; Kapur and Bielaczyc 2012; Loibl and Rummel 2014b). However, students in the I-PS conditions in these studies typically do not get to compare solution attempts during the instruction phase. It therefore remains unclear, whether the effectiveness of PS-I is caused by implementing problem solving prior to instruction or by the form of instruction (i.e., solution comparison). Loibl and Rummel (2014a) addressed this confound and showed that the order of problem solving and instruction had no impact on conceptual understanding when the instruction did not build on student solutions. Only in combination with instruction that built on student solutions, PS-I was more effective than I-PS. The main effect of form of instruction (with or without building on student solutions) was large (d = 0.9), while the main effect of timing of instruction was only medium (d = 0.6). Similarly, Loibl and Leuders (2019) showed that students do not spontaneously engage in comparing correct and incorrect solution approaches on their own. These findings support the notion that the effectiveness of PS-I results not only from the order of problem solving and instruction, but also from an interplay of several mechanisms, that each needs to be triggered.

Similarly, in invention studies, students are often supported to become aware of their knowledge gaps and discover deep features of the target concept by providing them with problem-solving material that incorporates contrasting cases. Students are asked to generate a method or an index that covers all the presented cases (Loibl et al. 2017). As mentioned earlier, contrasting cases are small examples (here: subsets of data) that each differ on one deep feature of a concept while keeping other features constant between cases (Schwartz and Bransford 1998; Schwartz and Martin 2004). When contrasting cases are provided side-by-side, students can easily discover these deep features (Gibson and Gibson 1955; Schwartz and Bransford 1998), which they may take into account in their solution attempts. Indeed, students incorporate more functional components in their solution attempts when they are presented with contrasting cases than students who engage in problem solving without contrasting cases (Loibl and Rummel 2014bFootnote 1). Moreover, it becomes salient to students when a generated solution attempt did not consider the deep features. Thus, when students are unable to address specific deep features (e.g., different sample sizes), they become aware of their knowledge gaps (Roll et al. 2011, 2012) and thereby are prepared to attend to and benefit from explanations of the functional components (e.g., dividing by the sample size) during the subsequent instruction (Roll et al. 2011).

Positive results of PS-I with contrasting cases have been found on transfer assessments when compared to I-PS (Belenky and Nokes-Malach 2012; Schwartz et al. 2011 with d = 0.33 to 0.66). Because transfer measures the ability to apply conceptual understanding beyond the setting it was acquired in (Mestre 2002), these results could indicate that providing contrasting cases during the problem-solving phase of PS-I might also be beneficial for acquiring conceptual understanding (e.g., Loibl and Rummel 2014b; Roll et al. 2011). However, the aforementioned studies do not allow separating the effects of engaging in problem solving prior to instruction (leading to prior knowledge activation) and of studying contrasting cases during problem solving (leading to awareness of knowledge gaps and discovery of deep features).

In summary, the results from PS-I studies suggest that PS-I can improve conceptual understanding. However, the variations in the design of previous studies make it difficult to identify which mechanisms are responsible for the beneficial effect. Therefore, there is a need for further studies with full-factorial designs that keep manipulations constant between conditions.

Effects of the order of the learning phases on procedural fluency

While productive failure and invention studies show beneficial effects for PS-I on conceptual understanding and transfer, the pattern of results on procedural fluency is less clear (cf. Loibl et al. 2017): Studies comparing PS-I and I-PS, report positive, neutral, and negative effects of PS-I on procedural fluency. These divergent effects may result from different implementations of the learning phases. In studies in which neutral to positive (d = 0.42 to 0.67) effects were found, students in the PS-I condition had the opportunity to practice the learned procedure at the end of the instruction phase (DeCaro and Rittle-Johnson 2012; Kapur 2010, 2011, 2012). Thus, these studies implemented no clear PS-I condition, but rather PS-I-PS (with the second problem-solving phase being shorter than the first one). Thus, it may have been the combination of problem solving prior to instruction and the short practice opportunity at the end of the instruction phase that enhanced procedural fluency (as procedural fluency and conceptual knowledge evolve iteratively; Rittle-Johnson et al. 2001). The initial problem-solving phase triggered conceptual understanding, which prepared students for acquiring procedural fluency during the short practice after instruction.

Studies that did not provide an additional practice opportunity for the PS-I condition, showed neutral to negative (d =  − 0.35 to − 0.63) effects of PS-I on procedural fluency (Loibl and Rummel 2014a, b). However, although these studies might suggest that receiving instruction first is beneficial for procedural fluency, these studies do not allow a clear interpretation regarding the effect of the order of the learning phases as the material used in the problem-solving phase differed across conditions. While students in the PS-I condition were asked to generate several solutions to one problem, students in the I-PS condition were asked to apply the instructed solution on multiple isomorphic problems. Practicing a procedure with multiple problems is known to improve procedural fluency (Klahr and Nigam 2004).

In sum, the effect of the order of instruction and problem solving as such (keeping all else equal) on procedural fluency remains unclear. Therefore, the present study investigates effects on procedural fluency when students in both conditions receive not only the same instruction phase, but also the same task during the problem-solving phase.

Research questions and hypotheses

The present study aims to isolate the effect of order of problem solving and instruction from the effect of incorporating the opportunity for contrasting cases that differ in one feature at a time in the materials of the problem-solving phase: What is the effect of the order of problem solving and instruction on learning outcomes? Does incorporating contrasting cases in the materials of the problem-solving phase foster learning? We therefore implement a 2 × 2 design with the factors order of the learning phases (PS-I vs. I-PS) and problem-solving materials with contrasting cases that differ in one feature at a time (with: PScc vs. without: PS). This design results in four conditions: problem solving with contrasting cases first (PScc-I), problem solving without contrasting cases first (PS-I), problem solving with contrasting cases after instruction (I-PScc), and problem solving without contrasting cases after instruction (I-PS). In order to isolate the effect of the contrasting cases in the problem-solving material from other means that may trigger the mechanisms at play, no typical student solutions are included in the instruction phase in this study.

For conceptual understanding, we expect to replicate prior findings (Loibl and Rummel 2014a; Matlen and Klahr 2013) that merely changing the order of the learning phases (i.e., PS-I or I-PS) will not significantly affect conceptual understanding when there are no contrasting cases (as trigger for becoming aware of knowledge gaps and discovering deep features; Hypothesis 1a). However, given that contrasting cases support the discovery of deep features and that they have proven to be beneficial for transfer (Belenky and Nokes-Malach 2012; Schwartz et al. 2011), we hypothesize that PScc-I will outperform PS-I on the conceptual knowledge posttest (Hypothesis 1b). As we assume that contrasting cases have similar effects as building on student solutions during the instruction (Loibl and Rummel 2014a; i.e., both trigger the awareness of knowledge gaps and the discovery of deep features when instruction is delayed), we further hypothesize that PScc-I will outperform I-PScc on conceptual understanding (Hypothesis 1c). We have no directed hypothesis regarding the main effect of contrasting cases, as they may or may not be beneficial in an I-PS setting.

Previous studies investigating the effects of the order of problem solving and instruction show mixed results regarding procedural fluency. However, these studies not only varied the order but also the implementation of the learning phases. Keeping the implementation equal, we would expect that generating solutions to a problem after having received instruction would foster procedural fluency as it allows for practicing the instructed procedure (Klahr and Nigam 2004). Thus, we hypothesize a main effect of the order of the learning phases: I-PS and I-PScc will outperform PS-I and PScc-I on procedural fluency (Hypothesis 2). As prior research did not show a moderating effect of contrasting cases on procedural fluency (Glogger-Frey et al. 2015; Schwartz et al. 2011), we have no hypotheses regarding the effects of contrasting cases.

To gain more insights into the learning mechanisms, we also studied students’ solution attempts during problem solving. We hypothesize that I-PS and I-PScc students will generate fewer (Hypothesis 3a), but higher-quality (Hypothesis 3b) solution attempts than PS-I and PScc-I students, as the former have learned the solution procedure during instruction which they can easily apply during subsequent problem solving. We further expect to replicate the findings by Loibl and Rummel (2014b) that contrasting cases will increase the quality of solution attempts (Hypothesis 3c). We have no directed hypotheses regarding the effect of contrasting cases on the quantity of solution attempts.

Methods

Participants and design

Participants were 222 students from 9 classrooms of 5 different schools, who were in their third year of Dutch secondary education (cf. US ninth grade, age 14–15). Of these, 178 followed general secondary education (the second highest track in the Netherlands) and 44 pre-university education (the highest track). Previous studies found medium to large effect sizes (from d = 0.6 to 2.3 for the productive failure effect and d = 0.9 for building on student solutions which should trigger similar mechanisms as including contrasting cases). A g-power analysis (Faul et al. 2009) for ANCOVA (with α = 0.05, power = 0.95, df = 3, number of groups = 4) showed that a sample size of 195 would allow to identify effects of at least d = 0.6 (corresponding to f = 0.3).

The target concept of this study (i.e., the concept of variance) had not yet been covered in the curriculum, which was verified with each teacher before conducting the experiment. Students participated as part of their regular mathematics class. However, active consent was obtained from students (and passive consent from their parents) for use of the data; on the consent form, they could indicate if they did not want their (child’s) data to be used for research purposes, in which case these were deleted (n = 2). Students who were absent during any part of the experiment were excluded from the analyses (n = 9). Due to unforeseen circumstances, one class (general secondary education) had to stop the posttest prematurely and therefore had to be excluded from the analyses (n = 29). A sensitivity analysis with g-power (see above) indicated that the remaining sample of 182 students still allowed for detecting effect sizes of d = 0.62 (corresponding to f = 0.31). The mean age was 14.53 (SD = 0.67). 93 of the final sample were female and 89 male.

Students were randomly assigned to one of the four conditions resulting from the 2 × 2 design with between-subject factors order of learning phases (PS-I vs. I-PS) and contrasting cases during problem solving (with: PScc vs. without: PS).

Procedure

The experiment consisted of a pretest, two learning phases, and a posttest and had an overall duration of approximately 55 min. The experiment took place at students’ schools. In each class, students were randomly assigned to one of the four conditions. Students participated individually throughout the entire experiment. After a short introduction by the teacher, the experimenter (i.e., one of the authors) gave a brief explanation of the study and answered any questions that remained after reading the informed consent form. After giving consent, students had 10 min to finish the pretest. Depending on the teachers’ lesson plans, the first learning phase followed right away (four classes) or in the next mathematics lesson three days later (four classes, all from general secondary education).Footnote 2 The first learning phase consisted of instruction or problem solving, depending on the condition. Students who started with problem solving were instructed to generate as many methods as possible to compare the three soccer players on consistency. The remaining students accessed an instructional video online and were instructed to wait in silence if they finished before the end of the learning phase. After 15 min, the second learning phase started and students switched from problem solving to instruction and vice versa. After another 15 min, the second learning phase ended and students immediately received the posttest, for which they had 15 min to complete.

Materials and scoring

Like in most PS-I studies, the learning materials in this study addressed the concept of variance (Kapur 2012) and were adapted from Loibl and Rummel (2014a). The target method was the mean absolute deviation, which can be used to calculate mathematical consistency of a dataset. All materials were paper-based, with the exception of the video in the instruction phase.

Prior knowledge

Because prior mathematical knowledge might influence students’ ability to generate solutions and their performance on the posttest, students were asked to report their average grade in mathematics tests in this school year and were given a brief pretest on mathematical knowledge. The pretest consisted of four items. One item measured their familiarity with descriptive statistics (mean, median, quartiles; 1 point each, e.g., calculate the average, the median, and the quartiles for the following list of values). Three items measured familiarity with graphical representations (bar graph, line graph, frequency distribution; 1 point each; e.g. here is a time–temperature diagram with the above values. Place the labels “Time” and “Temperature” on the correct axes). Familiarity with descriptive statistics and graphical representations were expected to help students generate methods in the problem-solving phase. Prior knowledge about the concept of variance was not measured for two reasons: first, students were not expected to have any formal prior knowledge (cf. Loibl and Rummel 2014b). Second, a pretest would reduce the difference between the experimental conditions because the pretest could serve as an unguided problem-solving phase by itself (Kapur 2016), which would blur the effect of the order of the learning phases. An independent rater coded approximately 10% of the data (i.e., data of 19 participants). Inter-rater reliability was excellent (ICC = 0.96). However, with Cronbach’s α = 0.26, the internal consistency of the pretest was insufficient, as was to be expected given the low number and diversity of items (Henson 2001).

Instruction phase

The instruction phase consisted of a pre-recorded video, which was identical in all conditions. In this video, a female instructor, supported by a digitally inserted PowerPoint presentation, introduced the concept of mathematical consistency and explained the mean absolute deviation as the method to compare different datasets. This instruction did not include any incorrect solution attempts. The video had a duration of 9 min and 9 s. After finishing the video, students waited in silence until the other students were done with the problem-solving phase. This waiting phase (which is not uncommon for students) did not seem to bother students. They sat in sufficient distance to each other to not disturb each other.

The instructor first explained that reliability in mathematics can be defined as the consistency of a certain dataset. Then, the instructor illustrated that large variance indicates a low reliability and vice versa. Next, the instructor demonstrated how to calculate the mean absolute deviation, emphasizing the functional components of the method (cf. Roll et al. 2011): (1) including all numbers for calculating the deviations to get a precise result, (2) using absolute or squared deviations to avoid that positive and negative deviations cancel out, (3) calculating deviations from a fixed reference point (the mean) to avoid the impact of sequencing, (4) dividing by the number of data points to account for sample size. Finally, the instructor explained how to interpret the calculated mean absolute deviation when comparing two datasets. As can be seen in Fig. 1, the presentation built upon the prerequisites measured by the pretest in two regards: calculating the mean and understanding a frequency distribution. The presentation of the frequency distribution was analog to the presentation in the problem-solving phase (cf. Figure 2).

Fig. 1
figure 1

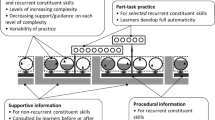
Example slides of the video instruction phase. The instruction introduced the concept of mathematical consistency (i.e., variance), explained the functional components of the method as solution steps (see slide on the left side for component 4), and discussed the interpretation of the result (see slide on the right side)

Full size image
Fig. 2
figure 2

Problem-solving materials without contrasting cases (left) and with contrasting cases (right). The cases on the right side highlight the functional components by systematically varying the relevant features (range, sample size, distribution). The reduced number of data points per case make these differences more salient

Full size image

Problem-solving phase and contrasting cases

During the problem-solving phase, students were instructed to generate as many mathematical methods as they could to compare three datasets on consistency. For the comparison, each method had to be applied to all three datasets. The cover story of the problem was adapted from Kapur (2012): three fictional soccer players are in the race for the title of the best young soccer player. Students received a dataset for each soccer player that represented the number of goals scored during each season over the past years (cf. Figure 2). The task stated that students had to come up with methods to compare the consistency of the three soccer players, using all data. For the comparison, they had to apply each method to all soccer players. The cover story and initial task were the same in all conditions. However, the datasets differed between conditions to operationalize problem solving with and without the opportunity to contrast cases that differ in one feature at a time.

Students in the PS-I and I-PS conditions did not receive contrasting cases during problem solving. In these conditions, all datasets contained the number of goals from each soccer player for the last 10 years. All three subsets of data in these conditions had the same mean and range (see Fig. 2 on the left side). Therefore, in these conditions the datasets did not guide students to any functional components of the mean absolute deviation when students applied their wrong solution attempt to compare the datasets on consistency.

Students in the PScc-I and I-PScc conditions received an opportunity to contrast cases that differed in one feature at a time during problem solving. Their datasets also contained the number of goals from each soccer player per season but differed on range, sample size, and distribution of data (see Fig. 2 on the right side). Furthermore, these differences were made salient to students by only providing them with data from three to six years (Schwartz and Martin 2004). The differences between the cases can focus students’ attention on the deep features, and applying solution attempts to compare these cases helps students to recognize their knowledge gaps (Roll et al. 2011, 2012). For example, students can see that two players have the same range, while one player has a different range. Therefore, they potentially realize that range is insufficient to compare the consistency of the three soccer players, but that it is relevant to consider the extreme values (and not, for instance, only values on the mean) in their solution. Similarly, contrasting the cases highlights the need to consider sample size. The cases were symmetric (as in Roll et al. 2009) for two reasons: first, symmetric cases highlight the fact that positive and negative deviations from the mean should not cancel each other out. Second, symmetric cases are simpler to capture which may increase the likelihood of an intuitive guess. However, in contrast to previous research that implemented contrasting cases during an initial problem-solving phase, we did not ask students for predictions before engaging in problem solving (Roll et al. 2012), nor did we provide any guidance on the use of the contrasting cases (Schwartz and Martin 2004). While this procedure enabled a fair comparison, it may limit the impact of the contrasting cases on learning, as we did not direct students’ attention to using the contrasting cases.

In addition to the datasets, students in all conditions received frequency distributions of the number of goals of each soccer player. Students can use these distributions to make an intuitive prediction about the consistency of each soccer player. They can then compare the result of their generated method to these predictions, which provides implicit feedback on the correctness of their solution (Nathan 1998).

Posttest

The posttest was translated and adapted from Loibl and Rummel (2014a). It consisted of seven items. Two items assessed procedural fluency, requiring students to calculate the mean absolute deviation of a dataset (2 points; e.g., Petra scored 30, 50, 90, and 70. Calculate the consistency.). Five items assessed conceptual understanding: two items required students to recognize a total of three mistakes in fictional incorrect solution attempts and to explain why the wrong solutions cannot measure consistency (3 points; explain in your own words how student A calculated consistency. Explain why the method of student A is suitable or not to calculate consistency). For example, the presented solution attempt took deviations from one value to the next instead of deviations from the mean. In order to obtain the full point, students had to identify this error and to explain that this wrong attempt is sensitive to the sequence of data points as there is no fixed reference point. Two items required students to match functional components of the formula to different graphical representations (4 points; e.g., explain the concept of variance by drawing in the following trend chart). See Loibl and Rummel (2014a) for more details on these items. The last conceptual item asked students to compare two datasets (1 point; compare the results of Petra and Kees—who has the more consistent results?), which requires students to understand the implications of their calculated value (Roll et al. 2011). The experimenter scored the posttest in accordance with the assessment scheme from Loibl and Rummel (2014a), with the exception of one conceptual item: in the original study, points were subtracted when students depicted deviations from the mean with arrows because arrows may be interpreted as directional deviations. In the present study, these points were not subtracted because it was impossible to assess if these arrows were intended as directional or absolute deviations. This different interpretation was caused by the fact that the instruction in Loibl and Rummel (2014a) discussed the representation (including the meaning of arrows), which was not the case in our instruction. An independent rater coded approximately 10% of the data. With ICCprocedural fluency = 0.96 and ICCconceptual understanding = 1.00, inter-rater reliability was excellent (Cicchetti 1994). Internal consistency was good for procedural fluency (Cronbach’s α = 0.83), and lower for conceptual understanding (Cronbach’s α = 0.65).

Quantity and quality of solution attempts

Quantity of solution attempts during the problem-solving phase was determined by counting the number of solution attempts students generated. The quality of those solution attempts was determined by scoring how many of the four functional components ((1) including all numbers for calculating the deviations to get a precise result, (2) using absolute or squared deviations to avoid that positive and negative deviations cancel out, (3) calculating deviations from a fixed reference point (the mean) to avoid the impact of sequencing, (4) dividing by the number of data points to account for sample size) were included in each solution attempt. The quality score consisted of the student’s score on their best solution attempt (Loibl and Rummel 2014a). As discussed by Loibl and Rummel, students usually do not distribute the functional components over several solution attempts. Once they discover a functional component, they are expected to incorporate it in all further attempts. To check this assumption, we also coded which component was included at least once and tested the correlation with the best solution score. Table 1 provides examples for the coding of the solution attempts. An independent rater coded approximately 10% of the data. Inter-rater reliability was excellent (ICCquantity = 0.96, ICCquality = 0.99).

Table 1 Examples for coding quality of solution attempts
Full size table

Results

Means and standard deviations of performance on the pretest, prior mathematics score, conceptual and procedural posttest performance, and quantity and quality of the solution attempts that students generated during the problem-solving phase, are presented in Table 2. There were no significant differences between conditions on pretest score, F(3, 178) = 0.07, p = 0.98, or prior mathematics score, F(3, 178) = 0.81, p = 0.49. One student in the PS-I condition did not report their prior mathematics score. The analyses are therefore based on 181 participants.

Table 2 Means (and SD) of prior knowledge and posttest scores and ratings of quantity and quality of solution attempts
Full size table

Learning outcomes

Students’ pretest score shared no variance with the learning outcomes (procedural fluency, r = 0.09, p = 0.23, conceptual understanding, r =  − 0.02, p = 0.77). Prior mathematics score correlated significantly with procedural fluency (r = 0.31, p < 0.001) and conceptual understanding (r = 0.45, p < 0.001), and was therefore included as a covariate. To investigate our hypotheses on procedural fluency and conceptual understanding, we ran two ANCOVAs with order of the learning phases (PS-I vs. I-PS) and presentation of contrasting cases (with vs. without) as between-subjects factors and prior mathematical skill as covariate. Adding prior mathematics score as an additional factor (using split half coding) instead of using it as covariate, revealed no significant interaction with condition for any of the measures reported below (conceptual understanding p = 0.24, procedural understanding p = 0.06, quantity of solution approaches p = 0.11, and quality of solution approaches p = 0.16).

The ANCOVA on conceptual understanding showed that neither the order of the learning phases, F(1, 176) = 0.74, p = 0.39, η2 < 0.01, nor the presence or absence of contrasting cases during problem solving, F(1, 176) = 2.65, p = 0.11, η2 = 0.02, significantly affected posttest scores. There was no significant interaction, F(1, 176) = 0.76, p = 0.38, η2 < 0.01. To test our hypotheses, we run pair-wise comparisons (LSD)Footnote 3: In support of Hypothesis 1a, that without contrasting cases merely changing the order does not affect conceptual understanding, the difference between PS-I and I-PS was not significant (p = 0.22). As an additional support for Hypothesis 1a (given the hypothesized null-effect, cf. Aberson 2002), the effect size was very small (d = 0.2/η2 = 0.01), the confidence intervals substantially overlapped (PS-I [1.04, 1.93], I-PS [1.44, 2.31]), and the confidence interval for the difference went from negative to positive (− 1.01, 0.23). However, in contrast to Hypothesis 1c, even with contrasting cases the effect of the order of the learning phases was not significant (i.e., PScc-I vs. I-PScc, p = 0.07) and the confidence intervals substantially overlapped (PScc-I [0.85, 1.77], I-PScc [0.87, 1.74]). Moreover, while we hypothesized that contrasting cases would facilitate conceptual understanding (Hypothesis 1b), the analysis showed no significant difference between PScc-I and PS-I (p = 0.60) and again the confidence intervals substantially overlapped (PScc-I [0.85, 1.77], PS-I [1.04, 1.93]). The descriptive results were even contrary to Hypotheses 1b and 1c (cf. Table 2).

In support of Hypothesis 2, the ANCOVA on procedural fluency showed that students performed significantly better on procedural fluency when they received instruction before problem solving (M = 1.34, SD = 0.68), compared to students who engaged in problem solving before receiving instruction (M = 1.02, SD = 0.76), F(1, 176) = 7.92, p = 0.01, η2 = 0.04. Providing students with contrasting cases during the problem-solving phase had no significant effect on procedural fluency, F(1, 176) = 0.45, p = 0.50, η2 < 0.01. There was no significant interaction effect, F(1, 176) = 1.14, p = 0.29, η2 = 0.01.

Quantity and quality of solution attempts during the problem-solving phase

Our coding of which component was included at least once in the solution approaches, revealed similar frequencies for all components: Across all conditions, 38.5% of the students calculated deviations with all numbers, 30.2% used absolute values, 43.4% used a fixed reference point, and 27% accounted for sample size at least once. The coding of the best solution attempt correlated almost perfectly with the sum of the number of components that were included at least once (r = 0.99, p < 0.001). Therefore, only the coding of the best solution was included as measure for the quality of solution attempts in the further analyses (cf. Loibl and Rummel 2014a).

While the pretest score did not correlate with quantity (r = 0.10, p = 0.16) or quality (r =  − 0.04, p = 0.64) of students’ solution attempts during the problem-solving phase, the prior mathematics score did (quantity: r = 0.17, p = 0.02; quality: r = 0.29, p < 0.001) and was therefore included as covariate. To investigate our hypotheses on the quantity and quality of students’ solution attempts, we ran two ANCOVAs with order of learning phases (PS-I vs. I-PS) and presentation of contrasting cases (with vs. without) as between-subjects factors and prior mathematical skill as covariate.

The ANCOVA on the quantity of solution attempts showed a significant main effect for the order of learning phases, F(1, 176) = 32.42, p < 0.001, η2 = 0.16. In line with Hypothesis 3a, students generated more solution attempts when starting with problem solving than when they received instruction first. There was also a significant effect of contrasting cases, F(1, 176) = 3.99, p = 0.05, η2 = 0.02, with students who received contrasting cases generating fewer solution attempts. The interaction effect was not significant, F(1, 176) = 0.22, p = 0.64, η2 < 0.01.

The ANCOVA for the quality of the best solution attempt showed a significant main effect for the order of learning phases, F(1, 176) = 91.18, p < 0.001, η2 = 0.34. In support of Hypothesis 3b, students generated better solution attempts when they received instruction upfront. In contrast to Hypothesis 3c, the effect of contrasting cases, F(1, 176) = 0.53, p = 0.47, η2 < 0.01, and the interaction effect, F(1, 176) = 2.21, p = 0.14, η2 = 0.01, were not significant.

Discussion

The present study aimed to isolate the effect of the order of problem solving and instruction (as trigger for activating prior knowledge) from the effect of the opportunity to contrast cases that differ in one feature at a time in the problem-solving phase (as trigger for becoming aware of knowledge gaps and discovering deep features) on procedural fluency and conceptual understanding in a full-factorial design. The results confirmed our Hypothesis 2: instruction first facilitated procedural fluency more than problem solving first. We also found evidence in support of Hypothesis 1a: the order of the learning phases did not affect conceptual knowledge, when the problem-solving material did not incorporate the opportunity to contrast cases (PS-I = I-PS). However, in contrast to our Hypotheses 1b and 1c, problem solving with contrasting cases prior to instruction did not foster conceptual knowledge in comparison to problem solving without contrasting cases first (PScc-I = PS-I) or instruction first (PScc-I = I-PScc). With regard to students’ solution attempts, our results confirmed Hypotheses 3a and 3b regarding the order of the learning phase: instruction first led to fewer solution attempts with higher quality in comparison to problem solving first. Again, in contrast to Hypothesis 3c, contrasting cases did not increase the quality of the solution attempts.

Practice and procedural fluency

With regard to procedural fluency, previous studies investigating the effects of the order of problem solving and instruction showed mixed results (i.e., no, negative, or positive effects of one order compared to the other; see Loibl et al. 2017). These results are hard to interpret as the studies varied not only the order but also the implementation of the learning phases. We therefore kept the implementation of the instruction phase and the problem-solving phase equal. We hypothesized that in this case, generating possible solutions to a problem after having received instruction would foster procedural fluency as it allows for practicing the instructed procedure (Klahr and Nigam 2004). Indeed, the present study revealed a small to medium effect of receiving instruction prior to engaging in problem solving in comparison to a reversed order of the learning phases on procedural fluency (cf. Hypothesis 2). A similar effect had been found in some previous studies that investigated effects of the order of problem solving and instruction (Loibl and Rummel 2014a, b). However, in these studies participants in the I-PS condition were presented with multiple isomorphic problems on which they could practice by applying the instructed solution procedure. In contrast, in the present study, students in the I-PS condition were given the same task instruction as students in the PS-I condition (i.e., to generate as many solutions as they could to the one problem on consistency), and the only difference was that they had received instruction regarding the underlying concept and the solution procedure. Thus, students who engaged in problem solving after instruction likely focused on applying the learned procedure, which fostered their procedural fluency. Indeed, our process data show that after instruction students generated fewer, but better solution attempts in comparison to those students who started with problem solving (cf. Hypotheses 3a and 3b).

Mechanisms for conceptual knowledge

With regard to conceptual understanding, prior research has shown beneficial effects of attempting to solve problems prior to receiving instruction compared to engaging in problem solving after receiving instruction. So far, it is still unclear which mechanism, or combination of mechanisms, is responsible for this effect because in many studies multiple potentially important features were confounded across conditions. This led to calls for more controlled experiments (Loibl et al. 2017), to which the present study answered by systematically investigating the effect of the order of the learning phases and the opportunity to contrast cases that differ in one feature at a time during problem solving. Regarding conceptual understanding, the finding of this study replicates earlier studies in which no significant effect of delaying instruction until after problem solving was found when no additional measures were taken to enhance the effectiveness of the instruction or problem solving phase (Loibl and Rummel 2014a; Matlen and Klahr 2013). Therefore, our study supports the notion that activating prior knowledge by engaging in problem solving prior to receiving instruction on itself is insufficient to explain beneficial effects on learning (cf. Hypothesis 1a). While non-significant results can only be interpreted with caution, the small effect size and the finding that the confidence interval for the difference ranged from negative to positive, support the notion that the order of the learning phases has no meaningful impact on the acquisition of conceptual knowledge in this context (cf. Aberson 2002). Prior research further found that PS-I was more effective than I-PS when additional measures were taken to help students to become aware of their knowledge gaps and to discover deep features (e.g., by comparisons between students’ solution attempts and the correct solution during instruction: Loibl and Rummel 2014a). However (in contrast to Hypotheses 1b and 1c), in our study, problem solving with the opportunity to contrast cases that differ in one feature at a time did not help students learn more from subsequent instruction (cf. Likourezos and Kalyuga 2017 for similar results).

At a first glance, the absence of the expected moderating effect of contrasting cases seems surprising: students had the possibility to use the provided frequency distributions to make an intuitive prediction about the consistency of each soccer player. Engaging in an active iterative process of generating solution attempts and evaluating the attempts by comparing them to the prior intuitive prediction provides students with grounded feedback on the correctness of their solution attempts (Nathan 1998). This process can make them aware of their knowledge gaps and can help them to discover deep features of the concept (Holmes et al. 2014; Roll et al. 2011, 2012). However, novices often do not use the beneficial opportunities of contrasting cases when they are not explicitly guided to do so (Roll et al. 2012). As we did not implement any explicit guidance on the use of the contrasting cases (in order to keep the task instruction equal across conditions), students probably did not use the frequency distributions to make intuitive predictions prior to generating a solution attempt and therefore missed the opportunity to evaluate their attempts against their predictions. In contrast to our study, Schwartz and Martin (2004) guided students to compare each solution attempt to their initial expectation. This guidance resulted in students in the PScc-I condition performing better on measurements of transfer than students in the I-PScc condition. Against this background, the lack of guidance in the present study might explain the missing moderating effect of contrasting cases on conceptual understanding. The findings of Chin et al. (2016) support this interpretation: they showed that when confronted with contrasting cases students tend to focus on surface features only, unless they are explicitly asked to identify the underlying principle by contrasting all cases. Future research should therefore investigate the effects of drawing students’ attention to the underlying principles of the contrasting cases and support students in utilizing the cases as grounded feedback by explicitly asking for intuitive predictions.

This possible interpretation seems to be supported by our process data: Contrasting cases did not help students in the PScc-I condition to improve their solution attempts more than students in the PS-I condition (in contrast to Hypothesis 3c). Thus, students in the PScc-I condition apparently did not take advantage of the potential feedback provided by the contrasting cases. Therefore, the quality of the solution attempts of students in both conditions that started with problem solving was poor: most students did not include even one functional component in their best attempt (mean 0.34). In contrast, students who received instruction first subsequently included two to three functional components in their solution attempts (mean 2.32). Interestingly, contrasting cases led to fewer solution attempts, both prior to and after instruction. While we had no hypothesis on the effect of contrasting cases on the quantity of solution attempts, it seems that the structure of the contrasting cases limited students’ creativity to generate multiple solution approaches and thereby may have hampered students in differentiating their prior knowledge, one key mechanism of productive failure (cf. Kapur and Bielaczyc 2012).

Another potential reason could relate to students working individually in our study. Kapur and Bielaczyc (2012) argue that collaboration during the problem-solving phase is a key design element of productive failure as it facilitates students’ knowledge activation and differentiation. However, so far, research has failed to demonstrate the advantage of collaborative versus individual problem solving prior to instruction on learning outcomes (e.g., Mazziotti et al. 2019). Against the background of these findings, we hesitate to ascribe the lacking effect in our study to the implementation of an individual problem-solving phase. The short duration of our intervention might be a more likely explanation. While some studies also found effects with similarly short PS-I interventions (e.g., Loibl and Rummel 2014a, b), other researchers have implemented PS-I with much longer phases (e.g., Kapur 2012; Kapur and Bielaczyc 2012) or multiple cycles (Glogger-Frey et al. 2017).

Limitations

The result that even after receiving instruction on the four functional components to measure statistical consistency, students in the I-PS and I-PScc condition included on average only 2.32 of the four functional components, suggest that the effectiveness of the instruction was limited. Our instruction differed from the instruction of other studies (Kapur 2012, 2014; Loibl and Rummel 2014a, b) in two respects: first, our instruction was video-based instead of teacher-led. While this increased the internal validity of the study as it eliminated any variations, it may have reduced students’ motivation, as they could not interact with the instructor. In other studies that refrained from teacher-led instruction, the instruction was given in the form of worked examples (e.g., Glogger-Frey et al. 2015, 2017). In a worked example setting, students also do not interact with the instructor, but they study the material on their own pace and they are prompted to self-explain the example. Thus, teacher-led instruction and worked examples both foster students to engage actively with the content. Second, our instruction was shorter than in the aforementioned studies. While the reduction in time was mostly caused by eliminating student-teacher interactions, students may need this extra time to make sense of the instructed content. Indeed, the overall low posttest scores for conceptual understanding suggest that the relatively brief video instruction was insufficient to provide students with coherent and accurate knowledge of the target concept.

Another limitation is the relatively low internal consistency (Cronbach’s α = 0.65) of the conceptual knowledge test, which may obscure differences between conditions. Our null-results therefore have to be interpreted with caution. However, the highly overlapping confidence intervals of all conditions suggest, that even with a more reliable test, we probably would not have found any significant differences for conceptual understanding.

A general limitation of PS-I studies is the fact that most studies investigate PS-I with a limited set of learning content (usually statistical concepts). While this restriction allows for comparisons between studies, it also limits the generalizability of the found effects. Thus, further studies should extend the replications to different topics and domains.

Conclusion and implications

To conclude, our study replicates the finding that I-PS can foster procedural fluency. Thus, to facilitate procedural fluency, mathematics instruction should include time for practice after the instruction of a new content. Our study further supports the notion that merely delaying instruction is not sufficient to increase conceptual understanding. In our study, the opportunity to contrast cases that differ in one feature at a time, which was intended to trigger an awareness of knowledge gaps and the discovery of deep features, remained ineffective, regarding both the quality of solution attempts and the posttest results. Thus, our study indicates that even when students have all the opportunities to engage in the necessary processes to become susceptible to subsequent instruction, more guidance is needed to elicit an awareness of knowledge gaps and to put emphasis on the deep features of the target concept. In other words, mathematics teachers should support students in engaging in the intended learning processes. Future studies should include guidance for these processes and systematically vary the guidance in ways that allows to further detangle the processes at play.