Human lifetime entropy in a historical perspective (1750–2014)

Abstract

This paper uses Shannon’s entropy index to the base 2 to quantify the risk relative to the age at death in terms of bits (i.e. the amount of information revealed by tossing a fair coin). We first provide a simple decomposition of Shannon’s lifetime entropy index that allows us to analyse the determinants of lifetime entropy (in particular its relation with Wiener’s entropy of the event “death at a particular age conditional on survival to that age”) and to study how the risk about the duration of life is resolved as the individual becomes older. Then, using data on 37 countries from the Human Mortality Database, we show that, over the last two centuries, (period) lifetime entropy at birth has exhibited, in all countries, an inverted-U shape pattern with a maximum in the first half of the twentieth century (at 6 bits), and reaches, in the early twenty-first century, 5.6 bits for men and 5.5 bits for women. It is also shown that the entropy age profile shifted from a non-monotonic profile (in the eighteenth and nineteenth centuries) to a strictly decreasing profile (in the twentieth and twenty-first centuries).

Appendix

1.1 Related entropy indicators

Among indicators of verticalization of survival curves, entropy indexes have also been widely used to measure the variance of the age at death.

The entropy indicator that is the closest to the one studied in this paper is the lifetime entropy index developed by Hill (1993), and which was applied to measure lifetime entropy in Canada in the twentieth century. Hill’s (1993) entropy of the age at death is defined as:

$$\begin{aligned} HI_{k}=-\sum _{i=k}^{115}p_{i,k}\ln (p_{i,k}) \end{aligned}$$

(9)

The unique difference between Shannon’s lifetime entropy index $H_{k}$ and the $HI_{k}$ index lies in the fact that $HI_{k}$ is based on the natural logarithm, and thus consists of an entropy index defined to the base e, whereas Shannon’s entropy index relies on the logarithm defined to the base 2. One can thus rewrite Shannon’s lifetime entropy index in terms of Hill’s entropy index as follows:

$$\begin{aligned} H_{k}=HI_{k}\frac{\sum \nolimits _{i=k}^{115}p_{i,k}\log _{e}\left( p_{i,k}\right) \log _{2}(e)}{\sum \nolimits _{i=k}^{115}p_{i,k}\log _{e}\left( p_{i,k}\right) }=HI_{k}\log _{2}(e) \end{aligned}$$

(10)

This formula shows that Shannon’s entropy index defined to the base 2 can be rewritten in terms of Hill’s entropy index, while rescaling the levels in such a way as to quantify lifetime entropy in terms of bits. This rescaling suggests that, if one focuses only on the growth patterns of lifetime entropy over time, the obtained growth rates are invariant to the measure unit chosen, so that measuring lifetime entropy by means of $H_{k}$ or $HI_{k}$ does not make a difference.

However, focusing on the growth patterns of lifetime entropy is not the only possible use of that measure; one may want to be able to interpret the levels of the measure of life riskiness at a particular point in time or at a particular age. From that perspective, adopting the base 2 rather than the base e allows to quantify risk about the duration of life in a metric that makes life riskiness commensurable with the risk involved in tossing a fair coin. On the contrary, the measurement unit of the $HI_{k}$ index is less easy to connect with common situations of risk. Moreover, relying on the base 2 rather than on the base e allows us also to decompose the lifetime entropy index in terms of Wiener’s entropy of the single event “death at age $k$ conditionally on survival to age $k$”. Wiener’s entropy being defined to the base 2, it is more natural, when constructing a lifetime measure of the risk about the duration of life, to rely also on the base 2, without any re-normalization.

Having compared our indicator with Hill’s entropy indicator, it is also useful to compare Shannon’s lifetime entropy index with Keyfitz’s entropy, which is the most widely used entropy index in demography (see Keyfitz 1977; Demetrius 1976; Nagnur 1986; Noymer and Coleman 2014). Keyfitz’s entropy is:

$$\begin{aligned} K_{k}=-\frac{\sum \nolimits _{i=k}^{115}s_{i,k}\log \left( s_{i,k}\right) }{ \sum \nolimits _{i=k}^{115}s_{i,k}} \end{aligned}$$

(11)

The denominator of Keyfitz’s entropy is merely the life expectancy at age $k$ , whereas the numerator aggregates, along the entire lifecycle, the logarithmic transform of the unconditional survival probabilities to the different ages of life.

It should be stressed that Keyfitz’s life table entropy or population entropy is not, mathematically speaking, an entropy index. It measures the reactivity or elasticity of life expectancy to a proportional change of the strength of age-specific mortality. As such, it differs substantially from the lifetime entropy index that we propose in this paper. Actually, Shannon’s lifetime entropy index can be rewritten in terms of Keyfitz’s entropy as:

$$\begin{aligned} H_{k}=K_{k}L_{k}\frac{\sum \nolimits _{i=k}^{115}\left( s_{i,k}d_{i}\right) \log _{2}\left( s_{i,k}d_{i}\right) }{\sum \nolimits _{i=k}^{115}s_{i,k}\log \left( s_{i,k}\right) } \end{aligned}$$

(12)

where $L_{k}$ is the life expectancy at age $k$. Given the important difference between Shannon’s lifetime entropy and Keyfitz’s population entropy, it is not surprising that these two indicators exhibit quite different patterns over time.

To illustrate those differences, Fig. 8 below compares, for the period life tables for France (males), the pattern of Shannon’s lifetime entropy index to the base 2 (left scale) with Keyfitz’s entropy index (right scale). The comparison of those two curves is made difficult by the fact that these indicators have completely different scales. Whereas the Keyfitz entropy index relies, over the period, between 0.15 and 0.6, the Shannon entropy index varies between 5.4 and 6.2. Having stressed this difficulty, one can nonetheless make some observations regarding those two patterns. First, if we focus on the second part of the twentieth century, the two entropy indexes exhibit both a declining trend. However, if we focus on the period between 1890 and the Second World War, we can see that the two indicators show completely different patterns. Whereas Keyfitz’s entropy exhibits a declining trend, Shannon’s entropy exhibits an increasing trend. Thus the two indicators exhibit quite different patterns, which is not surprising given that these indicators measure two different things.

Fig. 8

Shannon’s lifetime entropy and Keyfitz’s entropy, for France, males, 1816–2014

1.2 Additional material

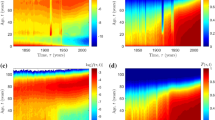
See Figs. 9, 10, 11, 12, 13, 14, 15, 16, 17 and, 18.

Fig. 9

Ranges of period lifetables (left) and cohort lifetables (right) per country in the Human Mortality Database

Fig. 10

Lifetime entropy at birth (period) in Belgium (BEL), Switzerland (CHE), Denmark (DNK) and Finland (FIN), for women (f) and men (m)

Fig. 11

Lifetime entropy at birth (period) in Italy (ITA), Netherlands (NLD) and Norway (NOR), for women (f) and men (m)

Fig. 12

Lifetime entropy at birth (period) in Switzerland (CHE), Denmark (DNK), Finland (FIN) and France (FRATNP), for women (f) and men (m) and corresponding moving averages (arithmetic mean, 20 years)

Fig. 13

Lifetime entropy at birth (period) in Great Britain and Scotland (GBR SCO), Iceland (ISL), Italy (ITA) and The Netherlands (NLD), for women (f) and men (m) and corresponding moving averages (arithmetic mean, 20 years)

Fig. 14

Lifetime entropy at birth (period) in Norway (NOR) and Sweden (SWE), for women (f) and men (m) and corresponding moving averages (arithmetic mean, 20 years)

Fig. 15

Lifetime entropy at birth (cohort) in England and Wales (GBRTENW), France (FRATNP), Italy (ITA) and Sweden (SWE), for women (f) and men (m)

Fig. 16

Period and cohort lifetime entropy at birth in France (FRATNP), England and Wales (GBRTENW), Iceland (ISL) and Sweden (SWE) for women

Fig. 17

Lifetime entropy at birth (cohort) in Denmark, England and Wales, Finland, France, Iceland, Italy, Netherlands, Norway, Scotland, Sweden and Switzerland and associated standard deviation by year, for women (f) and men (m)

Fig. 18

Cohort versus period lifetime entropy along the life cycle in France (FRATNP), England and Wales (GBRTENW), Iceland (ISL) and Sweden (SWE) for men, first and last available years