Mapping regularities in the solar irradiance data using complementary complexity measures

Abstract

Solar irradiance represents one of the principal phenomena of interest in geophysics and recent research, especially which concerned with renewable energy, suggests that the complexity of solar irradiance time series offers important insights into the dynamics of different geophysical systems. We examined the complexity of the daily cumulative global horizontal irradiance (kWh/m²; dGHI in further text) recorded by satellite for 32 stations on the island of La Réunion over a 35-month period (2004–2006) using Kolmogorov complexity (KC) and a recently introduced measure—Aksentijevic–Gibson complexity (AG) which is capable of quantifying the complexity of both long and short strings. Previous examinations of physical data suggest that AG could represent a useful addition to the geophysical analysis toolkit. Our results demonstrate for the first time that running KC is capable of capturing periodic patterns in data and that AG is sensitive to both global/long-scale spatial and temporal structure and local/short-range complexity fluctuations. Importantly, we report a putative weekly periodicity which might be related to environmental factors and human activity. In conclusion, we suggest that AG could represent a useful tool in the study of solar irradiation time series but also with other types of geophysical data.

1 Introduction

Solar irradiation received by Earth fundamentally depends on astronomical factors. The presence of atmosphere as well as the randomness of physical processes (multiple reflection, isotropic and anisotropic diffusion, absorption and multiple scattering) that take place in free atmosphere and within the boundary layer (Boucher 2015) make solar irradiation data highly complex. Synoptic and mesoscale atmospheric circulations in the atmosphere transport heat and mometum insuring the energy balance through turbulence cascades, tropical-extratropical interactions and large-scale connnections in the troposphere. In addition, water vapor and aerosol exert a major influence on the cloudiness which in turn has an important impact on the radiative properties of the atmosphere (Boucher 2015; Trent et al. 2018). All of these processes contribute to the variability of solar irradiation reaching the ground which in turn makes prediction difficult for atmospheric models of different scales. More specifically, the analysis of solar irradiation time series, obtained either by measurement or by prediction is difficult since their dynamics are almost always chaotic or just on the edge of chaos. However, the knowledge of their chaotic behaviour is useful in assessment of the predictability via the Lyapunov time (which is inversely proportional to the Lyapunov exponent)as well as the Kolmogorov time (Mihailović et al. 2019).

The most salient characteristic of solar irradiation is periodic seasonal variation which does not requir e additional analyses since its causes are well-known and predictable (Bessafi et al. 2018). At the same time, a great deal of information resides within daily, weekly and site-specific fluctuations which have not been studied thus far due to the lack of appropriate tools. Here, the accent is on the patterning of the complexity ofsolar irradiation which can expose local regularities and these in turn offer potentially important evidence about its effects and impact on the environment.

Many methods have been applied to solar irradiance time series analysis ranging from wavelet analysis and multifractal approaches to neural networks. Since the performance of existing short-term forecasting methods is far from satisfactory due to a lack of reliable and fast time–frequency models for continuous-time solar irradiance data, Huang et al. (2019) proposed a new method, Elman Neural Network (ENN) driven Wavelet Transform (WT-ENN), for hourly solar irradiance forecasting. Solanki and Unruh (2013) suggested that solar surface features (sunspots, faculae and the magnetic network) are responsible for almost all the variance and are therefore the best explanatory factor. Bessafi et al. (2015) analysed solar radiation measurements collected in Reunion Island from December 2008 to March 2012, in one-minute intervals. Before the forecast modelling they applied two clustering strategies for the analysis of the data base of 951 days.

Cluster analysis, Principal Components Analysis and related techniques represent useful “first responders” of time series analysis which shed light on the large-scale features and reslationships in the data. The next step is to examine the amount of information present in the series. A well-known information measure, namely Shannon’s entropy (Shannon 1948), measures the unpredictability of a specific output and this in turn depends on the capacity of the messagesource. Roughly, the smaller the probability of a particular output, the larger its informational value. Entropy-based measures are widely used in physics, especially in the situations where information quantity rather than its structure is of relevance (e.g. Wackerbauer et al. 1994). Entropy-based measures have been used prolifically in the study of solar radiation primarily because of their ability to detect gross differences in disorder. These include Permutation and weighted permutation entropy (Fadlallah et al. 2013; Xia et al. 2016), Multiscale Weighted Permutation Entropy (Yang and Wang 2016), Multiscale and Composite Multiscale Entropy (Costa et al. 2002; Wu et al. 2013, respectively) and others. Although useful in providing large-scale estimates of randomness, these measures are insensitive to information structure and consequently crude as indexes of complexity.

Kolmogorov complexity (KC; Kolmogorov 1965) represents a general measure of randomness in a sequence and is widely used in science for probing the complexity in data. KC is underpinned by the idea of algorithmic compressibility which gives it access to patterning and makes it more sensitive to pattern regularities relative to uncertainty-based measures. Although compressibility is important for entropy, KC uses it directly to measure pattern randomness (or absence thereof).The complexity of a string is defined as the length of the shortest algorithm capable of encoding it.For example, KC has been applied to geophysical time series such as UV irradiation (Mihailović et al. 2013), radon concentration (Aksentijevic et al. 2020a, b; Mihailović et al. 2015) and solar irradiation (Bessafi et al. 2018; Mihailović et al. 2018). Although KC is an important measure of the complexity of atmospheric processes and the climatic impact of sunlight, its ability to capture regularities in solar activity, atmospheric processes and their interactions has not been examined thus far.

In contrast to KC, AG is a relatively new complexity measure that is based on a distinct premise. Unlike its predecessors, it defines complexity directly—as the quantity of change contained in a pattern. Importantly, it considers relationships between levels (substring lengths) and this hierarchical aspect makes it particularly sensitive to regularities, that is, symmetries and periodicities. Superficially, such sensitivity is advantageous in certain fields (e.g. psychology; Aksentijevic et al. 2020b) but is not necessarily useful in those areas of research which deal with physical data encoded into long time series. Ostensibly, one of such areas is the study of solar irradiation. On short time-scales, solar irradiation data appear random—there is no way of predicting the pattern of irradiance within a day. And yet, at larger time scales (weeks, months, years, decades), effects of Earth rotation and consequently climate should leave a periodic signature on the irradiance time series. While this indeed is the case, what about complexity? If the complexity of the irradiance time series follow some regular pattern, this would bring us one step closer to describing and hopefully understanding the multifaceted effects and interactions of relevant factors.¹ To our knowledge, no paper thus far has examined the possibility that the complexity of solar irradiation data changes lawfully—in synchrony with the grand rhythms of nature.

The aim of the current paper is to study the complexity of solar irradiation data on La Réunion using two complementary information measures in order to examine their ability to capture any spatial or temporal regularities. In the context of climate change, islands such as those located in the southwest Indian Ocean (La Réunion, Mauritius, Comores, Mayotte, Seychelles and Madagascar) are facing the urgent challenge of increasing the production and use of renewable energy where solar energy plays a significant role. This calls for improving our understanding of this complex dynamic and designing solar irradiation-related predictive tools. The advent of the satellite era and the advances in ground-based solar irradiation measurement have given scientists access to a plethora of rich data, ushering the era of intensive study of this important issue.Given the complex atmospheric and aquatic environment and the fragility of its ecosystem, La Réunion demands intensive study of the principal driver of its biological and meteorological processes, namely, solar irradiation. Equally, its rich flora and versatile microclimate represent an excellent platform for the study of atmospheric complexity in general.

To this end, we examined the solar irradiation time series obtained by satellite for the La Réunion Island over nearly a three-year period using KC and AG complexity measures. While KC has been used for a long time, AG is a fairly new perceptually motivated measure originally designed to tackle psychologically relevant short patterns(string size less than 10). Recently, it was shown that AG can successfully quantify the complexity of long time series obtained by measurement of physical processes (Aksentijevic et al. 2020a). Consequently, we employed runningKC to study complexity changes which might reveal new facts about the climatic dynamics of La Réunion. We then performed the same analyses using running AG and compared the results obtained by the two measures. As demonstrated in the above paper, KC and AG are largely complimentary, that is, they focus on different aspects of information. Although they give similar estimates of overall complexity, AG is capable of zooming in on the fine structure in the data—an important requirement for both theory construction and climatic problem solving.

The structure of the paper is as follows. Section 2 presents a description of measurement sites and an overview of satellite data. In Sect. 3 we provide the main mathematical features of the KC and AG complexities. Section 4 (results and discussion) contains two subsections devoted to spatial and temporal analyses, respectively. Concluding remarks are summarized in Sect. 5.

2 Site and satellite data overview

La Réunion is a small tropical island (~ 2512 km²) located in the Southwest Indian Ocean (21° S–55° E) with a maximum elevation of 3069 m a.s.l. (meters above sea level) with two seasons—the dry (June–October) and the wet season (November – April). For the former, the most salient weather feature is the presence of a persistent large-scale southeastern trade wind. For the latter, the weather is mostly governed by the Intertropical Convergence Zone (ITCZ) with low-level convergence of moistened atmospheric flow with vertical instability leading to a strong convective activity. Note that La Réunion is a young volcanic island whose topography is very complex with two volcanoes (one active) and three geological depressions (Cirques). Finally, the island exhibits very sharp geomorphological slopes which set-up a natural orographic upslope forcing flow (Jumaux et al. 2011).

The weather and especially precipitating and non-precipitating clouds observed at La Réunion are influenced by the above-mentioned factors. The complex dynamic of the air flow is caused by a trade wind splitting around the island along the east and west coast with the accelerating Venturi effect, upslope flow over the volcano anda trapped circulation within the Cirques (Fig. 1a; Lesouëf et al. 2011). Additionally, these atmospheric circulations can be capped by the boundary layer during the austral winter when La Réunion is under the influence of the large-scale southern subsident Hadley cell branch which inhibits the atmospheric vertical motion within the first few kilometers above the sea level (Emanuel 1994; Taupin et al. 1999). This results in both a temperature inversion around 1.5 km and a wind inversion around 2.5 km which only allows the formation of shallow-layer stratiform clouds such as cumulus, stratus or stratocumulus. These cloud-topped boundary layers are maintained by a set of feedback processes which involve condensation within clouds, radiative cooling, sensible and latent surface fluxes, precipitation and entrainment of air above the boundary layer (Ghate et al. 2015, 2016; Manninen et al. 2018; Smith 1997). Conversely, during the austral summer, the island is under the influence of the southern ascendant Hadley cell branch (ITCZ) when the air is highly buoyant and deep convection often prevails. In the case of La Réunion, orographic forcing as well as differential thermal heating beetwen sea and land generate instability and excite precipitating and convective clouds such as cumulus and cumulonimbus over and around the island, resulting in strong precipitation episodes.

Fig.1

Spatial distribution of relevant parameters on La Réunion for the period 1. 2. 2004 to 31. 12. 2006: a normalized AG complexity of dGHI. Red ellipses indicate high-complexity regions whereas blue wavy lines show the main circulations on the island (for names of the 32 measuring stations see Table 1). Maximum complexity is at station 12 (Le Tampon) and minimum complexity is at station 26 (Point-Mathurin); b cloud fraction cover average over the island. Arrows indicate the elevation gradient of the terrain; c locations of the 32 measuring stations; d normalized AG complexity of dGHI visualised by black disks whose size is proportional to AG complexity values

For example, La Réunion holds world precipitation records for periods of 12 h (1144 mm) and 15 days (6083 mm; Galmarini et al. 2004; NWS 2013).The cloud formation over La Réunion is closely related to overlapping physical interactions between dynamic, thermodynamic, thermal, micro-physical and radiative processes (Fig. 1b; Kirshbaum et al. 2018). For example, during the day, some areas of the island face the sunlight in the morning while others are in the shade with the opposite happening in the afternoon. This contrast is particularly pronounced in the Cirques but also over east and west slopes of the island. Absorption of solar irradiation by the sloping ground leads to warmer air near the slope which in turn triggers ascent slope wind via a bouyancy process. This geophysical configuration is characterised by an ascending flow along the valley and a subsiding flow in the center of the Cirque. This double circulation inside the Cirque is favorable to the formation of clouds which persist on its ridge top while the center is in the sunlight during the morning and midday. In the afternoon when the west side is in the shadow, differential cooling triggers secondary circulations. There are formations of clouds at the top of each secondary circulation. During the ascendence of the moist air along the slopes of the Cirque, precipitating clouds can be formed if thermodynamical conditions are favorable to the rainfall process (Jumaux et al. 2011). Sea-land breeze circulation is an additional thermally induced circulation which competes with the orographic upslope/downslope and trade winds.

In summary, cloud development is pronounced over La Réunion, especially over the volcano Piton de la Fournaise and along the east coast as shown in Fig. 1b. The west and northwest coasts exhibit lower cloud fraction cover because, in addition to the Venturi effect, the leeward side (west coast) is exposed to a dryer air flow (foehn effect) which originates inland (downstream from the volcano).

As mentioned previously, moist and unstable air that flows over and around a mountainous terrain can significantly affect the cloud formation during the day. Typically, the cloud types are stratiform during winter and cumuliform during summer. The former is usually embedded in the marine boundary layer and the latter has tops that can extend to the tropopause and produce large amounts of rain. Thus, the variability of solar irradiation observed on the ground is highly related to the cloudiness variability. The weather over La Réunion can change drastically within a short time and day-to-day solar irradiation changes are complex due to orography and dynamical forcing (Bessafi et al. 2018; Zheng et al. 2018).

In this study, we used daily cumulative GHI (global horizontal irradiance in kWh/m²; dGHI in further text) measurements recorded during the 2004–2006 period over 32 stations (Table 1) that are freely available in the form of satellite-derived HC3 archives from the website Solar Radiation Data (http://www.soda-pro.com) with an approximate spatial resolution of 3 × 3 km. The daily cloud products used in this study are from the EUMETSAT Satellite Application Facility on Climate Monitoring (CM SAF). The 2004–2006 daily Cloud Fractional Cover (CFC) dataset is also used in this study with a 0.05° × 0.05° spatial resolution which corresponds to roughly 5 × 5 km and is freely available on the site https://www.cmsaf.eu.

Table 1 Names, coordinates and complexity values for the relevant stations

3 Method of analysis

3.1 Kolmogorov complexity

The Kolmogorov complexity can be defined as complexity of an object, such as a piece of text, to be a measure of the computability resources needed to specify the object. This complexity in existing terms is the minimum piece of code/program that one can write to generate a particular string. This measure is non-computable. Therefore, for a given time series, $x_{i} , i = 1,2,3,4, \ldots ,N$ it is calculated approximately using the Lempel–Ziv algorithm (LZA) or some of its variants. This algorithm includes the following steps: (1) Encode the time series by constructing a sequence $S$ of the characters $0$ and $1$ written as $s\left( i \right),\,i = 1,2, \ldots ,N$ according to the rule $s\left( i \right) = 0,x_{i} < x_{m}$ or $1$ if $x_{i} > x_{m}$, where $x_{m}$ is the mean value of the time series samples, selected as the threshold (Mihailović et al. 2015). Other encoding schemes are also used, depending on the application (Radhakrishnan et al. (2000). (2) Calculate the complexity counter $C\left( N \right)$. The $C\left( N \right)$ is defined as the minimum number of distinct patterns contained in a given character sequence. The complexity counter $C\left( N \right)$ is a function of the length of the sequence $N$. The value of $C\left( N \right)$ is approaching an ultimate value $b\left( N \right)$ as $N$ is approaching infinity, i.e., $C\left( N \right) = O\left( {b\left( N \right)} \right)$ and $b\left( N \right) = N/\log_{2} N$. (3) Calculate the normalized information measure $C_{k} \left( N \right)$ which is defined as $C_{k} \left( N \right) = C\left( N \right)/b\left( L \right) = C\left( N \right)\log_{2} N/N$. The parameter $C_{k} \left( L \right)$ represents the information quantity contained in a time series, and it varies from $0$ to $1$, although the values of KC can exceed value 1.

Binarization of time series is commonly performed using a measure of central tendency (mean or median). Consequently, some information about the structure of the time series is lost. The Kolmogorov complexity spectrum takes this problem into account, since it calculates the complexity by treating each element of the series as a threshold (Mihailović et al. 2015). Ultimately, this relates the probability distribution with compressibility.

3.2 Running complexity

In statistical geophysics, a running mean is often calculated to analyze data by creating the series of averages of different subsets of the full data set that is a type of finite impulse response filter. This procedure was used to calculate the running AG and KC complexities. For a given series of solar irradiance values a fixed window (of sizes 64, 128 and 256) is extracted and AG and KC complexities are computed. After that, the window is moved one step forward and the AG or KC algorithm is applied again until the end of the time series is reached.

3.3 Aksentijevic–Gibson complexity

Aksentijevic–Gibson or change complexity (AG) has been formally defined and described by Aksentijevic and Gibson (2012a, b). Nevertheless, a brief overview of the measure is given here. Every time we scan from a “0” to a “1” or vice versa, we encounter a change. The shift from symbols/objects to their relationships reflects a deeper shift in thinking about information. We use the binary version of the measure and all time series are binarized using mean thresholding.

Let $S$ be a binary string of length $L\ge 2$. If we scan the string and note a change whenever we encounter a pair “01” or “10”, the sum of changes over all pairs would represent a crude index of complexity/entropy. Therefore, we scan $j$ symbols at a time, $j=2, 3, \dots , L$ and ask which substring of length j of S should register a change. Suppose we encounter the substring $X$ of $\mathrm{S}$. Then, X will register a change if the two overlapping pairs (01 and 10) differ in the amount of change. We define a change function on binary strings that determines when a substring of should register a change, and then use it to construct the change profile $P=\left({p}_{2},{p}_{3},\dots , {p}_{L}\right)$ of S where ${p}_{j}$ is the number of substrings of length $j$ of $S$ that register a change. Two strings are considered different (the measure registers a change) if they are not a mirror inversion, complement or a mirror complement of each other. The original string and the three transformations represent a pattern class. Let ${p}_{j}$ be the number of substrings of S of length j which have change, j = 2 to L. Therefore,${p}_{j}=\sum_{j=1}^{L-j+1}{X}_{ij}$. The change matrix of $S$ is matrix $A$ (Aksentijevic et al. 2020a) whose entry in row $i$ and column $j$ is $X_{ij}$.

$$A = \left[ {\begin{array}{*{20}c} {X_{{12}} } & {X_{{13}} } & \cdots & {X_{{1L}} } \\ {X_{{22}} } & {X_{{23}} } & \cdots & * \\ \vdots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots \\ \cdot & {X_{{L - 23}} } & \cdots & * \\ {X_{{L - 12}} } & * & \cdots & * \\ \end{array} } \right]$$

The change profile of S is the array $P = (p_{2} ,p_{3} , \ldots ,p_{L} )$. The complexity C of $S$ is defined to be equal to ${\sum }_{j=2}^{L}{p}_{j}{w}_{j}$ where ${w}_{j}=1/(L-j+1)$. We can use weights ${w}_{j}$ to regulate the contribution of different lengths of substrings of So the overall complexity of $S$, and this allows the modelling of different levels of structure. This particular weighting is chosen because it produces a large number of complexity values and gives prominence to the higher levels of structure. For $0 \le {p}_{j}\le L-j+1$ the complexity C lies within the interval $0 \le C\le L-1$. We define the normalized complexity N $of\; S$ to be $C/(L-1)$, so $0\le N\le 1$. Where necessary, we refer to C as the unnormalized complexity of S. The upper bounds for C and N are never attained, but as $L$ becomes large both mean and maximum values of $N$ approach 1. The code for calculating this measure in the R language is given in Aksentijevic et al. (2020b). A detailed demonstration of how AG complexity of solar irradiance time series is computed is given in the Online Appendix.

4 Results and discussion

4.1 Spatial analysis

Figure 1a displays normalized average Aksentijevic–Gibson complexity mapping for the island of La Réunion obtained from 32 stations (Fig. 1c). The complexity was computed on the mean dGHI data for the period 1. 2. 2004 to 31. 12. 2006 and the computations were performed as described in Sect. 3. In this kind of analysis, it is advisable to make a comparison with another information measure which quantifies complexity in a time series. As a referent, we have used Kolmogorov complexity (KC) which has already been compared with AG (Aksentijevic et al. 2020a, b) Mihailović et al. (2018). and Bessafi et al. (2018) obtained spatial distribution of KC of the solar irradiation on La Réunion and explained this primarily in terms of cloud formation and their movement over the island. Table 1 shows the spatial distribution of KC complexity for the same spatiotemporal parameters as those used with AG.

The values for the two measures over the 32 stations correlate almost perfectly, ${r}_{S}$ = 0.96, p < 0.001. This is much higher than in the previous studies and indicates that the observed differences in spatial complexity are not artifacts of measure design. Two circumscribed regions possess overall high AG complexity and the topography of the island (Fig. 1d) suggests a positive relationship between complexity and altitude. Specifically, high-complexity inland regions appear to coincide with high altitudes and the opposite is true of the low-complexity strip on the western coast. The highest complexity was registered at Le Tampon (station 12) which lies at 860 m a.s.l. between the volcano and the Cirques, and the lowest at Point-Mathurin (station 26) located on the coast, whose altitude is only 20 m a.s.l. This impression was confirmed by means of a nonparametric correlation, ${r}_{S}$ = 0.66, $p$ < 0.001 (an identical correlation was obtained using KC). As suggested by the above cited research, cloud cover could also be expected to influence solar irradiation complexity. Inspection of Fig. 1b shows that both high-complexity regions have a higher cloud cover than the surrounding areas but the difference is subtle (10–15%). Again, this was confirmed in that both AG and KC correlated positively with cloud cover, ${r}_{S}$ = 0.59, $p$ < 0.001 and ${r}_{S}$ = 0.54, $p$  = 0.001, respectively. Thus, even with a small sample of stations, AG and KC appear closely yoked to the two fundamental geophysical variables.

Both measures outline two inland regions of high complexity (secondary inland circulation and high variability of cloud cover) and a low-complexity coastal strip. These two high-complexity zones are marked in red in Fig. 1a (they are almost identical with KC) and the coastal low-complexity region (blue) is common to both the measures. KC and AG correlate equally with altitude and both measures see Le Tampon (station 12) as the locus of maximum complexity. The only salient (if not very important) difference is in the location of the minimum complexity measurement. For AG, this is station 26 (Point-Mathurin) and for KC it is station 25 (Pointe des Trois bassins). If this is ignored however, we see that both measure tell the same story. The most salient is the effect of altitude followed by that of cloud cover. The two factors jointly describe up to 50% of the overall variance (${r}^{2}$ = 0.49, $p$  < 0.001). The observed spatial distribution of irradiation complexity can be explained by the effects of inland cloud cover and dynamcs of air circulation—disturbances in the irradiation exposure and cloud cover generated by winds and currents (Badosa et al 2015), namely: (i) the advection of trade cumuli and large-scale cloud systems; (ii) local formation by convection as a result of the interaction between synoptic wind, local thermal winds and the orography and (iii) acceleration of trade winds, along the island coasts parallel to the synoptic wind direction, due to the Venturi effect when clouds tend to be blown away. Thus, the local drop in dGHI complexity (captured by both measures) can be accounted for by the lower cloudiness associated with the Venturi effect [see condition (iii)].

From the above, we can see that AG captures the spatial distribution of complexity well (as confirmed by KC). This is quite surprising given that its original remit are very short 1D patterns (L < 10; Aksentijevic and Gibson 2012a), whereas by contrast, KC was designed to capture the degree of randomness of large data sets. Since the data examined above were averages of long time series, it is notable that AG is capable of preserving large-scale information. Based on the findings of a recent study (Aksentijevic et al 2020a), we expected the measure to perform even better in pinpointing short-term/localized changes in complexity.

4.2 Temporal analysis

Solar radiation data possess a specific signature structure which distinguishes them from other types of physical datain that it consists of two principal rhythms—daily and yearly. The diurnal and annual courses of solar radiation are strictly conditioned by astronomical factors which are regular and visible to the naked eye. However, the analysis of solar irradiance may indicate the appearance of periodicity on some other time scales that could be ascribed to specific environmental factors and human activity. In regard to that we note two things: (i) as stated in Footnote 1, we define regularity (also rhythm) as a recurrence of a condition or a set of conditions at equal intervals and (ii) occurrence of the periodicity on other time scales does not necessarily mean that it will be maintained over long periods.

Next, we examined changes in complexity of dGHI as a function of time over the considered period. To accomplish this, we computed running KC complexities for each of the 32 sites over three window sizes (256, 128 and 64)in order to provide a reference as outlined in Sect. 1. The period under analysis comprised 1065 days (1. 2. 2004 to 31. 12. 2006). The analysis was carried out on the dGHI time series converted into binary form via mean thresholding. Window 256 roughly corresponds to an 8-month interval and window 64 to a two-month period. As can be seen in Fig. 2, solar irradiation maxima coincide with the beginning of the calendar year and follow the onset of the wet season (October / November). By contrast, KC complexity maxima occur in August—past the annual midpoint which is also the height of the dry season. In terms of complexity, most stations capture the seasonal periodicity with all window sizes. KC complexity functions are well defined and demonstrate unambiguously a periodic annual function. In other words, exposure is proportional to complexity on the macro-level and the high-complexity season starts in April. Given some lag between different windows, further analysis is needed in order to qualify this (e.g. some low-level cycles might start at different points). It is worth noting that the KCfunction anticipates the variation in dGHI by about 120 days, suggesting a highly regular relationshipbut also the need for additional study since the complexity of the irradiance is not explainable in terms of its quantity but possibly as a signature of the geophysical “turmoil” which accompanies the changing of the seasons.

Fig. 2

The average of dGHI over the 32 stations (top) and running KC complexity for all stations across three window sizes (256, 128 and 64). Dash lines represent the start of the year and dash dot lines the midpoint

Following this, we examined the picture provided by the running AG complexity. Visual inspection of Fig. 3 shows very clearly that AG captures the same periodicities that KC does—only with less noise. This is especially visible in the maxima which are perfectly delineated at all window sizes. The onset of maximum complexity is somewhat earlier (by about 20–30 days) relative to KC. Otherwise the two pictures are very similar. The correlation between the KC and AG time series means for window 256 is ${r}_{S}$  = 0.74, $p$ < 0.001 (they share about 50–60% of variance at this magnification).

Fig. 3

The original time series showing the average of dGHI over the 32 stations (top) and running normalized AG complexity for all stations across three window sizes (256, 128 and 64). Dash lines represent the start of the year and dash-dot lines, the midpoint

The station least sensitive to seasonal variation is Le Tampon (station 12). This is the station mentioned in Sect. 4.1 as possessing the highest complexity for both measures. While it would be premature to speculate on the nature of this relationship, it is likely that a combination of a relatively high altitude (860 m) and turbulence facilitates a consistently highly complex solar irradiation regimen. The local meteorological conditions create a ceiling effect/saturation which attenuates the seasonal periodicity.

An interesting detail becomes apparent as we zoom in on the 4-month windows. Three stations (6, 25 and 30—Etang St-Leu, Pointe des Trois bassins and St-Leu, respectively) show a non-seasonal drop in complexity at a time at which other stations are at their maxima. As shown in Fig. 1c, the stations are adjacent and located on the southwestern coast of La Réunion. Coastal regions are generally associated with a low complexity. The drop becomes even more pronounced when the time series is scanned using window 64 (2-month period) confirming the presence of a highly localized low-complexity trough formed during a high-complexity summer period. Note that a similar trough is detected by KC but is fuzzy and poorly-defined. Future studies will examine the possibility hinted at in Fig. 3 that such local low-complexity pockets re-occur and reflect a hitherto unacknowledged secondary periodicity.

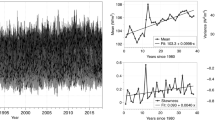
To demonstrate more clearly potential advantages of AG in pinpointing regions of interest, we examined more closely the two stations which recorded the maximum and minimum AG complexity values [stations 12 and 26, Le Tampon (LT) and Point-Mathurin (PM), respectively]. By averaging the running complexity series over the sites for the period 1.2. 2004 to 31. 12. 2006, we are able to locate the global minima and maxima and connect these to physical processes. The AG values were 0.995 and 0.969 respectively. Inspection of the dGHI time series (Fig. 4 top) reveals two variability components—a nearly periodic function caused by the seasonal waxing and waning of irradiance, as well as random-like diurnal variability component.

Fig. 4

Running normalized AG complexity for the Le Tampon (LT) and Point-Mathurin (PM) stations for windows 256, 128 and 64. Areas highlighted in red show the absolute complexity maximum and minimum outside of the regular cycle, respectively. The original time series represents the average dGHI over the considered period (top). Insets are vertical stretch magnifications which highlight the preservation of seasonal periodicity by AG even within a severely compressed range

A similar trend is observed at PM which recorded lowest AG complexity (Fig. 4 right). The difference in variability between LT and PM is visible by naked eye. The complexity curve is smoother but the periodic structure is replicated exactly. The second peak is higher than the first in agreement with LT data. Two things are of note. First, at window 64, the minima possess zero complexity because they correspond to periods of sub-threshold activity. Second, as marked in the figure, a low-complexity trough disrupts a global maximum between steps 255 and 266. This corresponds to a 10-day period in October 2004 and reflects the local complexity trough shown in Fig. 3.

The dGHI series for the two stations (Fig. 4 top) correlate quite highly, ${r}_{S}$ = 0.70, $p$ < 0.001. PM received significantly more solar irradiance compared with LT (0.563 vs 0.478), $t$(1064) = 23.97, $p$ < 0.001. At the same time, the complexity at LT was significantly higher relative to PM (0.979 vs. 0.900) $t$(809) = 55.63, $p$ < 0.001. This was confirmed by means of running KC (window 256), $t$(809) = 71.55, $p$ < 0.001.

Figure 4 (left) gives running normalized AG complexity values for the LT station employing windows 256, 128 and 64 and shows that AG preserves the periodic variation in complexity. In order to locate the absolute maximum more precisely, we note that complexity plateaus around step 520 for all three window sizes. This roughly corresponds to the beginning of June 2005 and the plateau lasts approximately 100 days (mid-September 2005). A similar periodic peak coincides with the beginning of summer 2004. Serendipitously, the contrast between the two stations illustrates the ways in which AG “zooms in” on the structure of interest. In the case of LT, the large-scale regularity (seasonal periodicity) becomes more visible and in the case of PM, a localized drop in complexity not apparent at longer window sizes, is revealed once a sufficiently short window (in this case 64; Fig. 4 bottom right) is employed. In other words, reducing window size is equivalent to zooming in on the temporal structure of the data. The correlation between LT and PM AG time series (window 256) was high, r_S = 0.87, p < 0.001.

Visual inspection of the spatiotemporal KC values indicates a high degree of agreement between the two measures. In other words, while it was expected that AG would capture any significant periodicities, it is worth noting that running KC too was sensitive to the yearly periodicity in the complexity function even with short windows (i.e. 128 and 64; see Fig. 3). KC reliably registers the annual waxing and waning of complexity which is in sync with the regular oscillation in the amount of irradiation. To our knowledge, this is the first time that KC has been shown to be sensitive to periodic structure to this extent. Although on first sight both measures perceive the same dynamic, it would be interesting to compare them on temporal variability.

In any 2D matrix, the variability of data can be measured in terms of rows, columns and their interactions. In our case, the matrix consists of spatial and temporal measurement points (stations and steps, respectively). Examining the spatial component allows us to gauge a measure’s ability to discriminate local changes in complexity. By contrast, by studying temporal variance (variability of complexity changes over time), we can infer something about the stability of a measure overtime. Since the two requirements are mutually conflicted, a temporal advantage implies a spatial deficiency and vice versa.

We computed the sample variance for every time step collapsed over stations. Then, we averaged that to produce a variability function of window size (see Fig. 5). We examined the behavior of both measures via a 2-way repeated-measures Analysis of variance (ANOVA). As expected, there was a highly significant main effect of window size, $F$(1.44, 1165.19) = 399.78, $p$ < 0.001 (Greenhouse–Geisser correction for degrees of freedom was applied where appropriate).This is caused by the tradeoff between window size and number. The fewer the windows, the smaller the variability in the signal. In addition, AG is more sensitive than KC to window size (measure by window size interaction), $F$(1.36, 1096.92) = 35.62, $p$  < 0.001, but the most relevant finding was that it was also significantly more stable than KC, irrespective of window length (main effect of measure), $F$(1, 809) = 439.53, $p$< 0.01. In other words, AG provides a sharper, more focused picture of complexity change. Further research is needed to establish if and when focus trumps variability—either can be advantageous or otherwise—depending on the requirements of the analysis.

Fig. 5

Mean temporal variance (± 2 standard errors of the mean) for KC and AG over three window sizes

A pressing question concerning solar radiation is—are there any small-scale rhythms in GHI data that could be discovered by AG and to which other measures are blind? As noted in the text, solar radiation data possess a specific “grain”, namely, a clear separation between scales. Long periods of consistently sub-threshold activity (low-radiation) are succeeded by relatively hectic periods in which sub- and supra-threshold activity rapidly succeed one another in an ostensibly chaotic manner. This information is potentially important because it shows that the two phases of a solar year are qualitatively different (see Fig. 6a). We have seen that both AG and KC can detect annual periodicities. In the following section, we demonstrate how AG can extract meaningful meteorological information from data that appear disordered or invisible to other measures.

Fig. 6

Zooming in on the low-level structure. a Binarized time series for S26 (Point Mathurin). b Radiation segment L = 128 shows the variability of the sub threshold activity between steps 80 and 208. Two days were added at each end of the 124-step zero run. See text for details

Out of 32 stations covered in this study, the lowest AG complexity was observed at stations 26 (Point Mathurin). Figure 6a shows the binarized time series for the station and the most salient is the presence of three highly regular zero-troughs which signal a long uninterrupted run of sub-threshold emission (124 days). It should be noted that similar runs are present at most stations and we are focusing on Point Mathurin for the purposes of illustration. Although both measures captured the grand seasonal rhythm, its salience renders all other regularities hard to detect and evaluate. To demonstrate the sensitivity of AG to small-scale regularities, we zoomed in on the first zero troughs which consists of 124 zeroes—meaning 124 days of zero AG complexity. A complexity of zero does not mean that a trough (or a peak) does not contain information but simply that under the rules of binarization all the variability is  lower than the threshold/mean. However, if we reanalyze the radiation data inside the trough, the new lower mean emerges and ensures that more information becomes accessible (Fig. 6b).

The first thing to notice is the specific (double-concave) shape of the data within the trough (red shading in Fig. 6b). This potentially interesting detail suggests a dampening of even the subthreshold oscillations at the center of the trough that could be labeled a two- or three week zone of “dead calm” with very little variability. A systematic analysis of zero troughs and the maxima will be presented in our next paper. Here, we focus on the specific segment and demonstrate that AG is capable of extracting information that is out of reach of other measures.

From the above analyses it would seem that the two measures are well matched and cover the same grounds scale-wise. However, this is not quite true. Unlike KC, AG was designed to analyze very short strings ($L$ < 10) and as such it provides a conceptual continuum between different complexity domains—from perception to cosmic radiation. Thus, AG should be favored just on the grounds of parsimony. However, AG also satisfies an important epistemological principle—it facilitates the natural progress of questioning and analysis from the very large towards the very small (and then vice versa). Whichever direction is preferred though, a continuum should exist between the levels of explanation. In the following example we demonstrate how AG covers time scales from several years to days and lower. In other words, the only constraint on the grain of analysis is the sampling rate. Figure 7 shows a structure map of the zero-complexity trough highlighted in Fig. 6. The radiation data for this segment show a specific shape which might or might not be of interest. However, drawing a structure map of the string allows us to examine it for the presence of low-level periodicities which might signal small-scale cyclic processes.

Fig. 7

Putative low-level structure in a time series segment described in Fig. 6. a Structure map covering 128 steps and 128 levels shows some low-level drops in complexity (highlighted). b 7-day periodicity revealed by AG structure mapping within a low-level segment of the map (levels 3–32). Some of the lines in the “comb” are partly white in order to enhance contrast

Figure 7a contains a structure map for 128 steps (abscissa) and 128 levels (ordinate). While most of the map is homogeneous (expected amount of change) we have highlighted a region of low complexity at the bottom which encompasses levels up to $L$ = 32. Here, some short zero-complexity areas (1–14 days long) show up in the form of right-angled triangles, the highest of which propagates up to level 20. The presence of such low-level regularities in solar radiation has not been reported before. A vertical magnification of the bottom portion of the map suggests that these possess a rhythmic structure with a period of approximately seven days (Fig. 7b). Further analyses are necessary to corroborate this but in the first instance; the regularity might reflect the weekly rhythm of human activity. In addition, we are currently working on designing a novel fast spectrum tool for extracting periodicities from AG structural maps. The above example demonstrates the ability of AG complexity to detect stable small-scale periodicities without the need for preparatory detrending.

5 Concluding remarks

The study of the variability/complexity of solar irradiance holds the promise of enhancing our understanding of geophysical processes as well as our preparedness to tackle adverse effects of human activity on the environment. Traditional tools used by scientists to investigate effects of solar irradiance have been statistical (e.g. Shannon’s entropy) but these are not well suited to discovering patterns. Although more sensitive to structure, Kolmogorov complexity was designed as a global estimate of randomness. To examine the ability of KC to detect structure, we employed it in the analysis of solar radiation data and compared it with a pattern-focused measure—Aksentijevic–Gibson complexity—which allows us to focus on short regions/periods (e.g. $L$ = 1–50) and link changes in pattern complexity to specific physical causes. We examined the spatiotemporal satellite record for 32 stations of daily cumulative solar irradiance (dGHI) on the island of La Réunion over 1065 days (2004–2006) and found that AG captured both seasonal and topological/geographical changes in the complexity of this variable. As predicted, KC performed well with spatial differences in complexity but less expectedly, showed sensitivity to large-scale periodicities as well. To our knowledge, this is the first time that KC has been used in this capacity.

In conclusion, it is worth briefly pondering the meaning of complexity and its measurement. It is clear that “objective” measurement of the complexity of a process is not possible because complexity itself is complex and opaque. There is no single solution to the problem and a large number of complexity measures remain in use. Yet, we do seem to possess an intuitive sense of the meaning of this difficult concept and the only way in tackling complexity is to give a solid quantitative basis to this intuition. Shannon’s approach reminds us that the value of information depends on how rare or improbable it is. While useful, this realization tells us little (if more than nothing) about the quality of the information—its structure. In some situations, this can present a problem—for instance when the source cannot be estimated/understood and when all we have to go on is the pattern itself. Here, regularities in the data are the only clues and this necessitates paying more attention to informational structure—which was achieved by Kolmogorov complexity—a non-probabilistic index of pattern compressibility. Compressibility depends on regularities, that is, periodicities and symmetries. We have shown, to our knowledge for the first time, that KC functions well when tasked with detecting large-scale regularities. Given the focus of KC on overall complexity/randomness estimates, this was not a foregone conclusion.

AG complexity takes this to the next level by focusing on the interrelatedness of different structure levels which makes it sensitive to periodicities and symmetries. How does this translate to the examined data? In terms of spatial/geographical and temporal differences in complexity, KC and AG largely agree. This is useful insofar as it connects the intuitive understanding of complexity with its measurement. In addition, this kind of agreement shows that AG is capable of indexing the complexity of data whose generators are far removed from psychology. Where AG seems to excel however, is in providing clear and focused record offline/local variations in complexity. This is not surprising given previous results but encourages us further in employing AG to study geophysical time series.

One interesting finding concerns the strong relationship between the dGHI and complexity data. We can report for the first time that the complexity of solar irradiation generally follows the seasonal waxing and waning of the irradiation itself although the latter lags the former by about four months. Consequently, peak irradiation lags behind peak complexity. Although we are not in the position to speculate on the causes of this lag, the changing of the seasons (as opposed to seasons themselves which appear static by comparison) provides a rich dynamic geophysical background which is captured by both complexity measures.

However, the most important finding concerns the low-level periodicity within a sub-threshold segment recorded at Point Mathurin. To our knowledge, this is the first time such a pattern has been described which pending further investigation promises to open up a new level of meteorological analysis. Consequently, we recommend AG complexity to our colleagues in the hope that its analytical power can help provide pointers for a new approach to studying the Sun’s gift to our world.