Abstract
An exact representation of the Baker–Campbell–Hausdorff formula as a power series in just one of the two variables is constructed. Closed form coefficients of this series are found in terms of hyperbolic functions, which contain all of the dependence on the second variable. It is argued that this exact series may then be truncated and be expected to give a good approximation to the full expansion if only the perturbative variable is small. This improves upon existing formulae, which require both to be small. Several different representations are provided and emphasis is given to the situation where one of the matrices is diagonal, where a particularly easy to use formula is obtained.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In physics and mathematics [1–7] it is often useful to write the product eX
eY
as eZ
, for some Z. When the objects X and Y do not commute, as is often the case when dealing with matrices, it may not be simple to find such a Z. Many authors [5, 8–15] attempted to deal with this problem by targeting 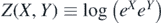 . Such attempts resulted in the Baker–Campbell–Hausdorff formula,
. Such attempts resulted in the Baker–Campbell–Hausdorff formula,

Dynkin [16] found this formula explicitly in terms of commutators for every order, where order means combined powers of X and Y. Unfortunately, this means that if a truncation of the series is to give a good approximation to the full expansion, both X and Y must be sufficiently close to zero. More recently, work has been done to represent this formula in more convenient ways for specific algebras [2–4, 17–22].
There exists an alternative representation to all orders in X but linear in Y. Letting LX Y ≡ [X, Y] denote commutator operators, it is given (in, say, [23]) by
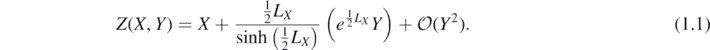
The aim of this work will be to extend this representation to all powers of Y. That is, express Z(X, Y) as
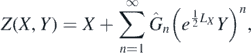
finding explicitly the operators  , which will depend non-trivially on commutator operators LX
. This series may be truncated and give a good approximation to the full expansion if only Y is small, as opposed to both X and Y in the previous. A discussion of what is meant by small is given in appendix
, which will depend non-trivially on commutator operators LX
. This series may be truncated and give a good approximation to the full expansion if only Y is small, as opposed to both X and Y in the previous. A discussion of what is meant by small is given in appendix
The paper is structured as follows. Section 2 contains the derivation of the main result, that is calculating the operators 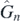 . Section 3 argues, based upon a conjecture, that the result remains a sum of commutators, as would be expected. These sections can be safely ignored by any reader who wishes to avoid mathematical detail. Instead they may prefer to proceed to section 4, where finite examples are given and discussed which provides immediately usable formulae for the
. Section 3 argues, based upon a conjecture, that the result remains a sum of commutators, as would be expected. These sections can be safely ignored by any reader who wishes to avoid mathematical detail. Instead they may prefer to proceed to section 4, where finite examples are given and discussed which provides immediately usable formulae for the 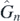 . Section 5 proves an alternative representation for the operators
. Section 5 proves an alternative representation for the operators 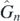 , which is perhaps more practical as it deals with some apparent singularities which shall be encountered. Finally in section 6 it is argued that this result is particularly useful in the basis where the perturbative matrix is diagonal. In this case the operators become merely functions of real numbers and so it is elementary to perform calculations with them.
, which is perhaps more practical as it deals with some apparent singularities which shall be encountered. Finally in section 6 it is argued that this result is particularly useful in the basis where the perturbative matrix is diagonal. In this case the operators become merely functions of real numbers and so it is elementary to perform calculations with them.
2. Derivation of main result
Consider a symmetric version of of the Baker–Campbell–Hausdorff formula,

for two matrices A and B. While this formulation is more natural to work with than (1.1), each may be transformed into the other and so are equivalent. Employing the notation for commutators which shall be used throughout this article, LB ≡ [A, B] and Ln B ≡ [A, [A, ⋯, [A, B], ⋯, ]], the Baker–Hausdorff formula is given by

This then implies

from which it is easily seen that  and additionally
and additionally 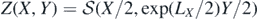 . That is,
. That is,
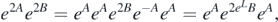
and so all one needs to do is replace any B in the symmetric formula with eL B to obtain the non-symmetric formula. The factors of two have been introduced here in order to simplify the final representation.
The task ahead is to expand equation (2.1). The matrix B will be the focus, with the aim being to write the expansion as a power series in this matrix. Once this is achieved, the coefficients of the power series will be examined in depth and closed form expressions obtained.
The identity
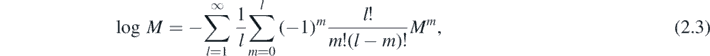
will be employed, setting M = exp(A)exp(2B)exp(A). It will be found that Mm separates into the sum of several parts. Each of these parts will take the form fi exp(2mA)gi , for m-independent quantities fi and gi . The fi and gi may then each be pulled out of the above sums, leaving exp(2mA) in place of Mm . The identity then may be used in reverse to obtain log(M) = ∑i fi 2Agi . This then constitutes the fundamental mathematical approach which shall be taken.
2.1. Expanding Mm in powers of B
The focus will now be on calculating Mm . The Baker–Hausdorff formula (2.2) may be used to symmetrically move exponentials of A to the edges, obtaining
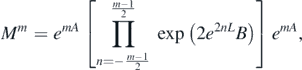
where the product must be taken in the correct order, namely increasing n. The exponentials involving B may then be Taylor expanded

and terms gathered in orders of B,

In the above expression, each term exp(2ni L)B must be thought of as one object—that particular commutator operator L is acting on that particular matrix B and so the two are intrinsically linked. It is helpful to formalise this link, labelling the pair with an index. Then it is understood that the operator Li acts on only the matrix Bi , and no other. Each such pair may then be labelled. This allows the commutation of operators and matrices with different labels, enabling all matrices B in the above expression to be pulled out of each sum. Explicitly,
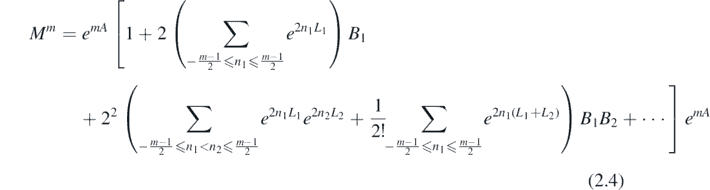
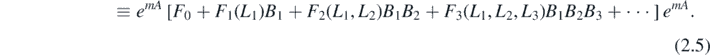
2.2. Rewriting FN in terms of fundamental sums SN
The first aim has thus been achieved; the formula (2.1) has been expanded with a power series in the matrix B. The next is to find closed form expressions for the coefficients FN . First define the sum SN as

then the first few of the coefficients FN are given by

Writing the coefficients FN for an arbitrary order N is a problem in partitioning. As seen in the above examples, the string L1 + L2 + ⋯ + LN is split in all possible ways. The resultant substrings are then used as arguments for the sums Sn . However, each sum is also divided by factorials. These factorials are determined by the length of the substrings used as arguments. For example, the string L1 + L2 + L3 may be split in the following ways giving the following factorials:
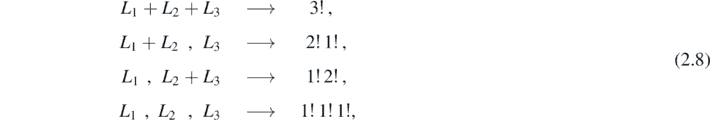
demonstrating how F3 was constructed in equation (2.7).
There are then two major hurdles to finding closed form expressions for each coefficient of the power series. The first is to calculate the explicit sum SN . As the sum SN may be thought of as N finite geometric series, it may be expected to have 2N terms. However, it may be split into N + 1 parts, each of which is a collection of infinite geometric series. This lifting of the constraint is crucial and will be discussed shortly. The second hurdle is then to perform the partition sum, that is to calculate FN given the functions Sr .
2.3. Calculating SN
It is useful at this point to deal with a concrete example. Consider the sum

The summation variables, n1 and n2, are constrained from both above and below. These constraints may be thought of as forming a triangle, as depicted in figure 1. The sum may then be thought of as the combination of three semi-constrained sums, constructed by taking a given vertex of the triangle and extending the constraining lines to form infinite sectors. Explicitly,
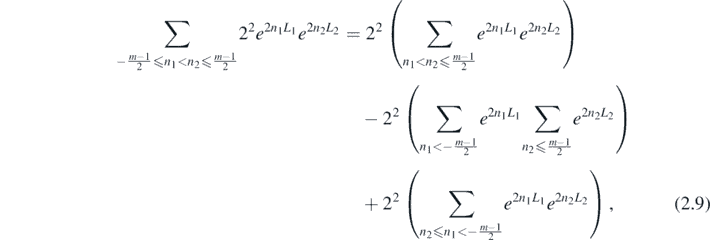
or, using the labels for regions shown in figure 1,

The sums on the right-hand side may then be evaluated to obtain

Figure 1. A depiction of the parameter space of n1 and n2 in equation (2.9). Solid lines imply inclusiveness of that line in a given sum, while dashed imply the line of parameters is excluded. The variables of the original sum are constrained to the triangle formed from the vertices marked with a red circle.
Download figure:
Standard image High-resolution imageGeneralising this idea to the sum SN
involves N + 1 vertices of an N-dimensional tetrahedron. The constraining lines are extended, creating N + 1 sums similar to those in equation (2.9). A careful treatment of this is necessary and is done in appendix
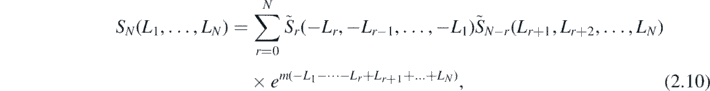
where 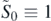 and
and
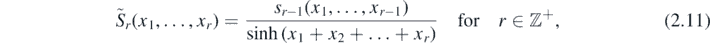
where similarly s0 ≡ 1 and

There are several things to note from this result. Firstly, the N + 1 different forms that the exponential above may take clearly correspond to the vertices of the N-dimensional tetrahedron discussed previously. As mentioned earlier, this exponential, containing all the m-dependence, is crucial in reversing the identity (2.3). Next, note the splitting of each term into  and
and 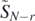 functions. This structure remains for the coefficients FN
, as shall be seen shortly, and appears fundamental to the problem. Furthermore, the representation of the result in hyperbolic functions is perhaps not unexpected; previous results showed that the order B term is best written with a sinh function. Finally, the arguments of the hyperbolic functions only ever contain sums of the commutator operators Li
. As such it is mathematically sensible to think of the active variables not as these commutator operators L1, L2, L3 etc, but rather as strings of such operators, for example L1, L1 + L2, L1 + L2 + L3 etc. More will be said of such strings in later sections, in particular section 6.
functions. This structure remains for the coefficients FN
, as shall be seen shortly, and appears fundamental to the problem. Furthermore, the representation of the result in hyperbolic functions is perhaps not unexpected; previous results showed that the order B term is best written with a sinh function. Finally, the arguments of the hyperbolic functions only ever contain sums of the commutator operators Li
. As such it is mathematically sensible to think of the active variables not as these commutator operators L1, L2, L3 etc, but rather as strings of such operators, for example L1, L1 + L2, L1 + L2 + L3 etc. More will be said of such strings in later sections, in particular section 6.
2.4. Rewriting FN as a partition sum in terms of fr
The next task is to perform the partition sum, or in other words calculate FN given the now known Sr . Once again it is useful to turn to an example. Using the above results, it is simple to read off that
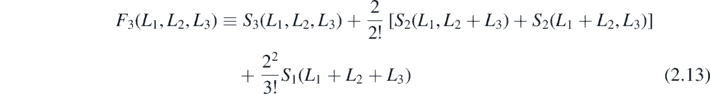
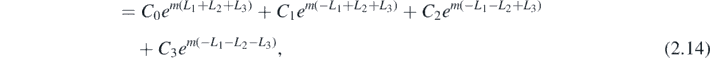
where
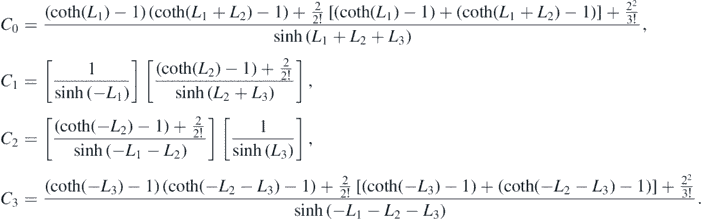
Within this example many of the previous themes are exposed. As in the sums SN , the result splits into N + 1 terms. Each of these terms likewise separate into an m-dependent exponential and an m-independent function (the Ci above). The final similarity is the factorisation of these functions, shown clearly in C1 and C2. More generally, this factorisation arises from partitioning. Any sums which contribute to the coefficient of a given exponential with argument m(−L1 − ⋯ − Lr + Lr+1 + ⋯ + LN ) must contain a partition between Lr and Lr+1. Any other partitioning which occurs to the left of the split affects a given sums contribution to the term independently of any partitioning to the right. More concretely, in the example above the function C1, associated with the exponential with argument m(−L1 + L2 + L3), is contributed to by any sums in equation (2.13) with a partition between L1 and L2. These are S3(L1, L2, L3) and S2(L1, L2 + L3). In the former there is another partition between L2 and L3, giving rise to the coth term in the right factor of C1, while in the latter there is no such extra partition.
These arguments necessitate the partition sum to take the form
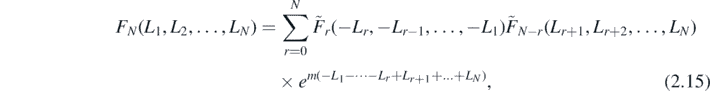
where 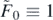 and
and

2.5. A partition formula for fr
The function fr−1(x1, x2, ⋯, xr−1) will be a partition sum of the functions sn which are given from (2.12). For example,

is found in both C0 and C3 above. In general, fr−1(x1, x2, ⋯, xr−1) is a sum of terms, each involving a product of coth functions minus one. As shown for f2, in each of these terms there will be a number of these functions missed out. In a term where m such functions in a row have been missed out, am+1 ≡ 2m /(m + 1)! will be the coefficient. This then implies that

where δi,j is the Kronecker delta. The combinatorial aspect of partitioning expressed in this sum is the next thing to be understood.
While superficially complicated, this sum is actually very simple. In essence, the sum index n counts how many coth functions have not been missed out and the numbers pi give the positions of these. Alternatively, the numbers pi − 1 can be interpreted as counting how many functions have been missed out in a row. As an example, one of the terms in the functions f4 which has two coth functions missing (so n = 2 remain) is

In the function fr−1 there are r − 1 different coth functions; for example, f2(x1, x2) has coth(x1) and coth(x1 + x2). The sum index n indicates the number of coth functions in a given term. If there are only n such functions in a term, that means (r − 1) − n are missing. These missing coth functions determine the numerical coefficient of the term, given by the numbers am+1. However, how each function was missed out is important—if m in a row are missed out then they are replaced with am+1. The indices of the second sum, pi , are designed to convey this information. For example, if p2 is 1 then there has been nothing missed out between the first coth and the second. If, however, it took any other value then p2 − 1 possible coth functions must have been missed out between these two functions. Continuing this logic gives all terms in the above sum.
2.6. Resumming the partition formula
A simpler form of this function may be obtained. The brackets in the sum may be expanded, putting the function into the form

The coefficient 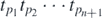 is of course still a product of equivalent numbers
is of course still a product of equivalent numbers 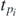 as the same partitioning arguments apply. In other words, the numbers pi
still label the size of gaps in the product of coth functions and each provide a number
as the same partitioning arguments apply. In other words, the numbers pi
still label the size of gaps in the product of coth functions and each provide a number 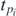 which depends only upon this size, independent of the location of the gap. Comparing the constant term, that is when all coth functions have been missed out, of (2.17) with that of (2.18) gives
which depends only upon this size, independent of the location of the gap. Comparing the constant term, that is when all coth functions have been missed out, of (2.17) with that of (2.18) gives

This sum, once computed for an arbitrary index, will give all numbers 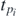 which appear in equation (2.18). The key to computation is to lift the constraint imposed by the Kronecker delta, and as such generating functions may be employed. First multiply both sides by xr
, and sum over r:
which appear in equation (2.18). The key to computation is to lift the constraint imposed by the Kronecker delta, and as such generating functions may be employed. First multiply both sides by xr
, and sum over r:


Now each of the sums over pi can be done freely, resulting in

The above is an expression of a kind of 'partition duality'. It is true for any sequence {ak } and defines a dual sequence {tk } which satisfies equation (2.19). This also implies that equation (2.19) is invertible, that is one can exchange ak and −tk and the equation will still hold. Of course, what has been done here is to replace the (coth(x) − 1) of equation (2.17) with (coth(x) − 0) in equation (2.18). One could instead replace it with a more general (coth(x) − λ), with the analysis being analogous to that which has been performed, though λ = −1, 0, 1 are the only useful cases.
In the present case recall ak ≡ 2k−1/k! and hence it is simple to calculate that
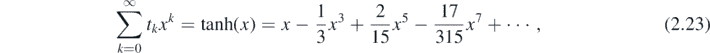
demonstrating the numbers tk are generated by tanh. When combined with equation (2.18), this then gives a clean formula for fr−1 and thus FN . That is, fr−1 is a sum of products of coth functions. In each term of this sum, some even number of these functions in a row will be missed out and replaced with the numbers tk which come from the Taylor expansion of tanh(x). Finite examples of this concept will be given for clarity in section 4.
2.7. Revisiting Mm and implementing the fundamental mathematical approach
Focus will now turned to the exponential in equation (2.15). It is here that the identity (2.3) will be reversed. Equation (2.5) may now be rewritten as

where the arguments of the functions have been suppressed for brevity. Upon repeated application of the Baker–Hausdorff formula (2.2) this can be seen as

The identity (2.3) may then be employed in reverse, obtaining
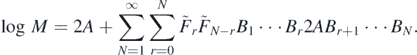
Using the commutator operators Li , the matrix A in the above expression may be moved to either side of the matrices B, via
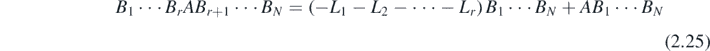

The case m = 0 in equation (2.24) gives
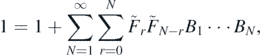
which implies that for all N > 0,

This identity is extremely useful and will appear again later in this work. For now it allows the extraneous final terms in equations (2.25) and (2.26) to be dropped and hence log M to be written in the form

This then gives the promised expansion in powers of the matrix B.
2.8. Final form
To summarise, it has been found that
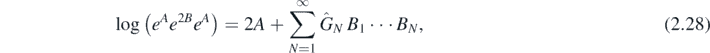
where
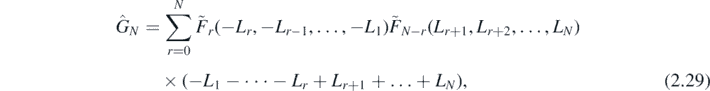

and
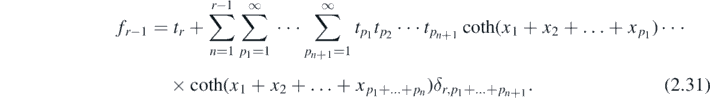
Here the numbers 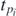 are given from the Taylor expansion of tanh(x).
are given from the Taylor expansion of tanh(x).
3. Representation as a sum of commutators
It is well known that, beyond the initial terms, the Baker–Campbell–Hausdorff formula may be written as the sum of commutators. Unfortunately, for the new representation (2.28) this is not immediately evident. Of course, the commutator operators Li
contained within GN
will be applied to each matrix Bi
to form commutators. However, this would naturally lead to products of commutators when, say, a term like Li
Lj
is applied to Bi
Bj
. In this section a representation will be given for which each term is a single commutator. This representation will rely on unproved identities of the function  , which have been demonstrated for up to N = 10.
, which have been demonstrated for up to N = 10.
The first identity involves picking one argument of  , say L1, then changing its position while preserving the order of the other arguments. Explicitly for
, say L1, then changing its position while preserving the order of the other arguments. Explicitly for 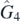 , the following identity is true:
, the following identity is true:

The next identity involves picking two arguments, say L1 and L2. This time the position of both arguments is allowed to change, preserving both their own order and the order of the remaining arguments. Explicitly for 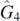 ,
,

In general it is conjectured that identities hold where n < N arguments of  are picked and are dealt with in an analogous way to above. Again, it should be noted that this has been tested successfully up to N = 10 and there is no reason to believe this should fail at any higher order.
are picked and are dealt with in an analogous way to above. Again, it should be noted that this has been tested successfully up to N = 10 and there is no reason to believe this should fail at any higher order.
From these identities it follows, see appendix

and hence that

4. Finite examples
While the general formula has been derived in the preceding sections, it may be helpful to examine several low-order terms explicitly. This section will begin with the functions fr
, for r = 0, ⋯, 5, highlighting the patterns previously discussed. From these the operators 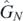 , the targets of this work, may be immediately written down and indeed will be for N = 1, ⋯, 5.
, the targets of this work, may be immediately written down and indeed will be for N = 1, ⋯, 5.
To begin, consider the functions fr . The first few of these functions are given by

where compact notation (c123 = coth(x1 + x2 + x3), for example) has been used. Here the structure previously discussed becomes apparent. In equation (2.31) the term in the sum where n = r − 1 forces each pi to be equal to one, giving the full product of coth functions with none missing. This is the leading term in each of the examples above. To generate the rest of the terms, neighbouring pairs of coth functions in this term are replaced with −1/3, neighbouring quadruplets are replaced with 2/15, and so on. All possible such replacements appear in the above functions, where the replacing numbers are given from

The targets of this work, the operators 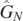 , will now be examined. It was previously mentioned that the leading term
, will now be examined. It was previously mentioned that the leading term  is already well known and while this was calculated for the regular Baker–Campbell–Hausdorff formula Z(X, Y), it is of course trivial to map it to the symmetric version
is already well known and while this was calculated for the regular Baker–Campbell–Hausdorff formula Z(X, Y), it is of course trivial to map it to the symmetric version  considered here. Using the general formulae of the preceding section, it would be natural to write
considered here. Using the general formulae of the preceding section, it would be natural to write

Of course, as both x and sinh(x) are odd functions, the minus signs are irrelevant and there is only really one term.
Next, at second order and third order it is found that

and

With these, some general themes begin to emerge. It is immediately seen that each term factorises into two parts, written above with square brackets. In a given term, all commutator operators with a plus sign gather into one of these parts while those with a minus sign gather into the other. The only question that remains is how the arguments to each coth function are determined.
Consider, for example, the term involving −L1 − L2 − L3 + L4 + L5 + L6 + L7 in  . Pictorially, the arguments for each function can be found from the diagram.
. Pictorially, the arguments for each function can be found from the diagram.

Here, the top red lines highlight the arguments of each sinh function, while the blue lines show the arguments to the coth functions. Combined with the previous discussion on how to write down these coth functions to form the numerators, this says how to write 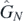 for any order N. Of course equation (2.29) already provides such a formula, but perhaps observing these patterns for finite results may provide a more intuitive understanding.
for any order N. Of course equation (2.29) already provides such a formula, but perhaps observing these patterns for finite results may provide a more intuitive understanding.
For reference, the next two orders in the expansion are given by

and

Here the notation has been made compact by writing, for example, s1 = sinh(L1) and 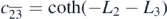 .
.
5. Apparent singularities and an alternative representation
One may, upon reading section 4 and the examples therein, be concerned that the operators 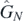 appear divergent. Both coth(x) and 1/ sinh(x) have simple poles when their argument is zero. This section, however, will provide the framework for removing these apparent singularities at will. While this can be done using the operators as given in the preceding section, it is better to rewrite and potentially simplify using hyperbolic identities, creating alternative representations. In this section one such alternative shall be discussed and used as the basis for an algorithmic approach to removing singularities, which is performed in detail in appendix
appear divergent. Both coth(x) and 1/ sinh(x) have simple poles when their argument is zero. This section, however, will provide the framework for removing these apparent singularities at will. While this can be done using the operators as given in the preceding section, it is better to rewrite and potentially simplify using hyperbolic identities, creating alternative representations. In this section one such alternative shall be discussed and used as the basis for an algorithmic approach to removing singularities, which is performed in detail in appendix 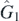 ,
, 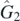 ,
, 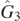 , and
, and 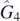 , and the result of removing them. A general approach, rather than the algorithmic method we demonstrate on low order examples, is an open problem worthy of study.
, and the result of removing them. A general approach, rather than the algorithmic method we demonstrate on low order examples, is an open problem worthy of study.
The starting point for obtaining this alternative representation is the m = 0 identity (2.27),

The two outer terms, that is r = 0, N, can be extracted to give

The key to this representation is to eliminate all sinh functions. To that end, the hyperbolic identity
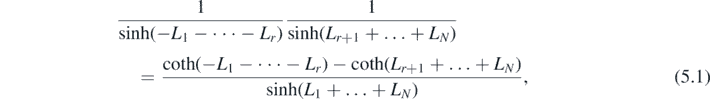
may be used to rewrite the right-hand side of the above equation, and the sinh function is thus eliminated. At this point there is a clear divide, with half of the terms containing the variable L1 but not LN and the other half containing LN but not L1. The equation can be reorganised to separate each half by the equals sign which, along with linear independence of the functions involving L1 and LN , implies that each half separately must be equal to some constant. That is, for the L1 dependent half,

One of the striking features of this representation is the factorisation structure which has been ubiquitous in this work. Its presence here gives reassurance that this formula is natural. Secondly, outside of the fN−1, all dependence on the variable L1 appears only in the outer coth terms. These terms can be thought of as a linearly independent basis functions, with the fr−1
fN−r−1 terms cast as coefficients. This then gives a more controlled way of dealing with these formulae. This equation will be used to rewrite the overall operator 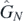 , but first the constant must be found.
, but first the constant must be found.
Finding this constant term may be done by taking the limit L1 → ±∞ in fN−1, which has the effect of setting each coth to one or minus one. Adapting equation (2.17) then,

and so taking the same limits on equation (5.2) gives
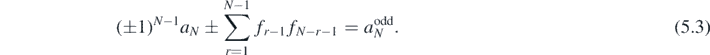
The two equations contained in (5.3) can then be summed to find the constant

with generating function

Similarly the equation (5.3) may be subtracted, giving a set of identities which will prove useful when dealing with apparent singularities,
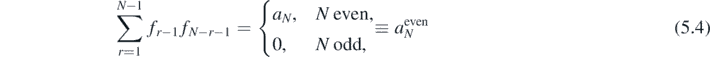
where

Returning to the alternative representation, the overall operators  may now be rewritten. Using the hyperbolic identity (5.1) to combine all sinh functions and the recursion relation (5.2) to eliminate both instances of fN−1, it can be seen that
may now be rewritten. Using the hyperbolic identity (5.1) to combine all sinh functions and the recursion relation (5.2) to eliminate both instances of fN−1, it can be seen that

where

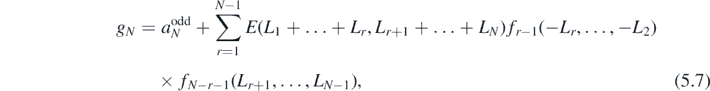
and

For reference, the first few terms in this representation are given by

and

As with the previous representation and the example given in section 4, the patterns demonstrated in these early examples continue. In  , for example, the variables L2 and L3 move from one argument of the E function to the other. When they do so they similarly move from one multiplying f function to another, recalling that f0 ≡ 1 and so is not written above. As they move between these f functions, they incur a minus sign. These patters allow one to write all later functions
, for example, the variables L2 and L3 move from one argument of the E function to the other. When they do so they similarly move from one multiplying f function to another, recalling that f0 ≡ 1 and so is not written above. As they move between these f functions, they incur a minus sign. These patters allow one to write all later functions 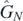 . In appendix
. In appendix 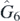 is written explicitly, if one wishes to test their understanding.
is written explicitly, if one wishes to test their understanding.
It is fairly clear that both s(x) and E(x, y) are regular and infinitely differentiable and as such any apparent singularity involving L1 or LN
is automatically safe in this representation. Demonstrating that any other limits are safe involves the identities just introduced in equation (5.4). This is done carefully for a particular example in appendix  ,
, 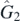 ,
, 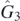 , and
, and  . It should be noted that in applications it is usual, rather than unusual, that such singularities are relevant. As such, the representation presented in this section should be considered as the starting point for practical use of the new formula.
. It should be noted that in applications it is usual, rather than unusual, that such singularities are relevant. As such, the representation presented in this section should be considered as the starting point for practical use of the new formula.
6. Choice of basis
In this section the sums of commutator operators, that is strings like L1 + L2 + ⋯ + Lr , will be discussed. It was previously suggested that these were mathematically natural to use as arguments to various functions. It turns out that in the basis where the matrix A is diagonal, if such a basis exists, these sums result in the difference between two eigenvalues of A. As shall be seen, this drastically reduces the complexity of using the new representation.
First consider the matrix elements of LB ≡ [A, B]:

where summation over repeated indices is assumed. If A is a diagonal matrix then its matrix elements are given in terms of its eigenvalues as Anm = an δnm , where δnm is the Kronecker delta. Hence in the basis A is diagonal the above is given by

More generally, for any Taylor expandable function f, it can be seen that

This is a simple yet powerful result. If the function f is replaced with sinh or coth functions, then 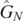 may be determined without difficulty. This would allow calculations to be done numerically with relative ease as all the strings of commutator operators are replaced by real numbers. It is this choice of basis, then, which gives the results of this paper a practical raison d'être.
may be determined without difficulty. This would allow calculations to be done numerically with relative ease as all the strings of commutator operators are replaced by real numbers. It is this choice of basis, then, which gives the results of this paper a practical raison d'être.
A few words ought to be said about the full expansion in this basis. Using the notation of section 5, note that an overall factor of s(L1 + L2 + ⋯ + LN ) may be extracted as, at each order, the argument of this function is the same difference of eigenvalues. That is,

where again summation over repeated indices is assumed. The function s can be interpreted as a Boltzmann suppression factor, appropriately named when one considers potential applications in quantum and statistical mechanics, which reduces the weight of any matrix element for whom the difference in eigenvalues an − an' is sufficiently large. It is plotted in figure 2(a), for reference.
Figure 2. (a) The Boltzmann suppression factor as a function of the difference of eigenvalues. (b) The function g2. Note it appears to limit to ±1 as the eigenvalue difference tends to infinity, and is bounded.
Download figure:
Standard image High-resolution imageThe reduced functions gN , then, are what remains. Figure 2(b) displays g2, which has several features generic to these functions. Firstly, it appears to be bounded and its extrema occur as its arguments diverge. It can be proved, though it will not be done here, that under such limits the relatively complicated gN and the comparatively simple fN−1 coincide. Then finding these extrema is elementary as each constituent coth function within fN−1 takes values ±1. That these limits do in fact correspond to the extrema of gN is not proved, but has been numerically verified up to g8 and the results displayed in table 1. Furthermore, a generating function for the outermost of these bounds can be obtained and is given by

This series is absolutely convergent when |x| < π/4, which can easily be seen performing the rotation x → ix in the equation above. It is entirely possible for the series to converge outside of this region, however. This provides reassurance that the series (6.1) converges for sufficiently small B.
Table 1. Bounds of the functions gN , obtained using the procedure outlined in the text and numerically verified.
| Function | Lower bound | Upper bound |
|---|---|---|
| g2 | −1 | 1 |
| g3 | −4/3 | 2/3 |
| g4 | −5/3 | 5/3 |
| g5 | −6/5 | 32/15 |
| g6 | −122/45 | 122/45 |
| g7 | −1088/315 | 676/315 |
| g8 | −227/63 | 227/63 |
7. Conclusion
A new representation for the Baker–Campbell–Hausdorff formula has been found. This representation is a perturbative expansion in just one of two matrices, as opposed to both in the original representation. The series may then be truncated and give a good approximation to the full expansion for situations where only this second object is small. For physical problems this then would give access to a much larger parameter space than is currently available. Additionally, new problems for which the original representation was unusable may now be tackled. Transfer matrices in statistical mechanics is an example of one such problem, which is under active consideration. Appendix
A final note should be made on practical use of this new formula. First, the representation discussed in section 5 and defined in equation (5.5) is perhaps the best starting point. It is simple to work with and automatically deals with several apparent singularities. Next, appendix
Appendix A.: Future use of the formula
In this appendix the potential future applications of the formula proven in this paper will be discussed. This work is the subject of ongoing research and is presented to aid comprehension as to the practical purpose of some of the formulae.
Simply put, in a quantum mechanical scenario it is common to have a Hamiltonian split into a dominant and perturbative part, say

Here the notation is designed to draw parallels with the objects within this paper, with A typically being a diagonal matrix and B being considered perturbatively small. A physicist would then turn to perturbation theory to progress, writing

where E0 is the groundstate of H, an the eigenvalues of A, and Bnm the matrix elements of B.
In a statistical mechanics scenario one would instead have the equation

when considering transfer matrices, with H = −βF where F is a free-energy operator. At low temperature A is a diagonal matrix and B is small, in the same sense one uses in a quantum mechanical context, and so the formulae derived in this paper are relevant. One can then use perturbation theory on these formulae to obtain the equivalent formula as in quantum mechanics

This E0 contains the free-energy of the model in question and hence the partition function. Note, as mentioned previously, this is the subject of ongoing research and a full derivation will appear in a subsequent paper, up to at least sixth order. This amounts to an improved form of the well-known high-temperature expansion technique, leading to much more powerful and accurate results for both high- and low-temperature expansions. It is presented here purely as a guide to help understand the context in which this paper operates.
Appendix B.: Calculation of the sums
Presented here is a direct method of calculating the sum (2.6). As described in the main text, the key is to split the starting constrained sum into N + 1 semi-constrained sums (that is, one of the limits of the sum may be made infinite). To that end, note

which is demonstrated by the diagram below. In this, circles represent the variables of the sum and their position along the line indicates the value said variables take, while rectangles represent the bounds of the sums. Open rectangles and circles allow equality, while filled do not.
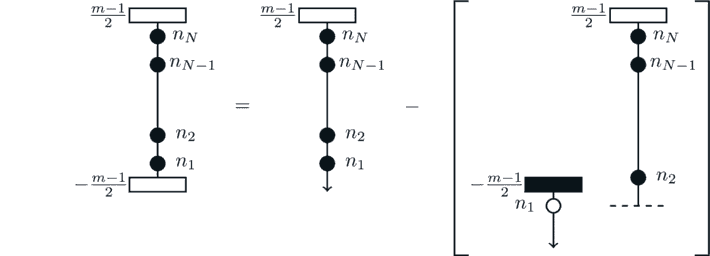
This identity has transformed the constrained sum on the left into two sums. One of these is semi-constrained, as was targeted, while the other has one semi-constrained and N − 1 constrained variables. Applying this idea again gives

or pictorially,

The number of constrained variables on the right-hand side is now reduced to N − 2. This can then be continued until there are no such variables remaining, resulting in an identity relating a sum with N constrained variables to N + 1 sums with only semi-constrained variables.
A generic term in this identity for the particular sum in the main text is given by

that is,

A simple change of variables, indicated on the picture above, gives

which may be trivially calculated. Using the identities

and

provides the result required in the main text.
Appendix C.: Proof of commutator representation
In this appendix it will be proven that, subject to the identities described in section 3,

To begin, the commutator on the right-hand side of the above equation may be written in terms of permutations of the string B1, ⋯, BN . That is,

where 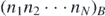 represents a permutation of the string B1, ⋯, BN
. Next the indices in each term may be relabeled, keeping the order B1, ⋯, BN
and instead permuting the arguments of the function
represents a permutation of the string B1, ⋯, BN
. Next the indices in each term may be relabeled, keeping the order B1, ⋯, BN
and instead permuting the arguments of the function 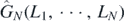 . For example,
. For example,

In general, for any permutation P,

and so equation (C.2) may be rewritten in terms of permutations on 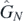 as
as

The identities of the function  may also be written in this permutation style. Most relevantly, choosing the arguments Lm
, Lm−1, ..., L1 and changing their position with respect to the remaining arguments Lm+1, Lm+2, ..., LN
while keeping the two sets internally ordered may be written as
may also be written in this permutation style. Most relevantly, choosing the arguments Lm
, Lm−1, ..., L1 and changing their position with respect to the remaining arguments Lm+1, Lm+2, ..., LN
while keeping the two sets internally ordered may be written as

As an example, for m = 2 and N = 4 the above reads

The sum in the identity can be split into two cases: nm = 1 and nm ≠ 1. This gives

where the argument to the function 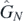 have been suppressed for brevity. This leads naturally to recursion. Using lower order identities, that is starting at m − 1 not m and so on, it can been seen that
have been suppressed for brevity. This leads naturally to recursion. Using lower order identities, that is starting at m − 1 not m and so on, it can been seen that

The left-hand side of the above is exactly what is obtained when expanding equation (C.3), collecting all terms involving m permutations multiplied together. Exactly N copies of this occur, thus proving equation (C.1).
Appendix D.: Algorithmically removing apparent singularities
This appendix will provide an algorithmic approach to removing any apparent singularities in the operator  , using the representation and identities provided in section 5. For immediate use, the first four operators
, using the representation and identities provided in section 5. For immediate use, the first four operators 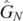 have formulae provided for all possible singularities are provided towards the end of this appendix. However, first the general trends shall be discussed via a single larger example, namely
have formulae provided for all possible singularities are provided towards the end of this appendix. However, first the general trends shall be discussed via a single larger example, namely  when all of L2, L3, L4, and L5 are simultaneously zero.
when all of L2, L3, L4, and L5 are simultaneously zero.
In the language of section 5, that is equation (5.5), the relevant part of  without any singularities may be written as
without any singularities may be written as

There are five limits to be taken and the order in which they should be performed is crucial. For the approach which will be laid out in this section, it is best to work from the outside in. That is, it is best to take the limit L2 + L3 + L4 + L5 → 0 first, followed by L3 + L4 + L5 → 0, and so on. The reason for this will become apparent shortly. For now, under the first limit, both the first and last lines appear singular while the rest are regular. The identity, associated with 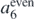 in equation (5.4),
in equation (5.4),

allows one to replace the f4 in the first line. The singular part then becomes

where

In the limit L2 → −L3 − L4 − L5 note, using equation (5.2),

This is the first of four direct limits that will be taken during this example and is the most simple; more will be said later of the general form of these expressions. For now, when L2 → −L3 − L4 − L5, it has been found that

The next limit to consider is when L3 + L4 + L5 → 0. In this case both lines one and two appear singular, and again an identity should be used to rewrite one of them. The identity now is associated with  and states
and states

This then can be used to replace the f3 in the first line. One may wonder about the choice of how to use this identity; should the f3 in the first line or the opposing f3 in the second line be replaced? The generic answer to this is to replace the function multiplying the highest E(n), in order to form a simple expression to be limited. With this the singular part becomes

This is the second direct limit which shall be taken in this example and contains features that appear in all that remain. First note that Taylor expansion gives
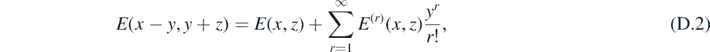
as the denominator of E is unchanged. This then is the reason to take the limits from outside to in as described before, as all subsequent expansions will necessarily be of this form. In general, after n limits have been taken, the singular parts of gN will take the form
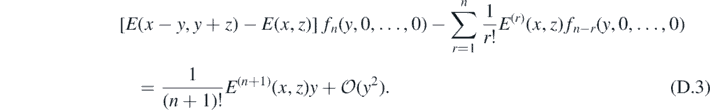
This is proved using a generating function for fn (y, 0, ⋯, 0) in appendix E. Using this knowledge for the current example, the second limit L3 → −L4 − L5 may be taken to leave

The third limit to take is that when L4 + L5 → 0, with lines one and two appearing singular. The approach now is hopefully becoming familiar. First use the identity, associated with  ,
,
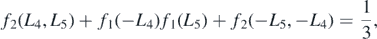
to replace the f2 in the first line. The relevant term is then

and hence in the limit L4 → −L5,

The final limit in this example is when L5 → 0. Now a rather trivial identity may be used,

to replace the f1 in the first line. The relevant term under this limit then is

leaving

This then concludes the example for this appendix. The lessons to draw from it are as follows. First, take sequential limits from out to in; this allows the expansion (D.2) to be used as the denominator of E is untouched. Second, using this approach all relevant terms under a limit will be of the form defined in equation (D.3). The limit then can be easily taken and the regular formula found.
More complicated situations than those discussed in this appendix can occur, for example if there are gaps in the set of variables tending to zero. Having L2, L3 → 0 while simultaneously taking the limit L5 → 0 is one such example, as there is a gap between variables due to L4 ≠ 0. These can be dealt with in an analogous fashion to those of this appendix, but it requires more complicated identities and careful handling. Part of this is discussed in appendix E, but otherwise this will not be dealt with here.
What follows is concrete and usable formulae for the first four operators, in all possible cases. The first two operators are trivial, as

are clearly regular. The first non-trivial example then is 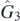 . This has six apparent singularities, of which five involve either L1 or L3 and thus are already resolved. What remains then is the limit L2 → 0. In this case,
. This has six apparent singularities, of which five involve either L1 or L3 and thus are already resolved. What remains then is the limit L2 → 0. In this case,

where E(n) is defined by equation (D.1).
Next,  has ten apparent singularities with three of these being independent of L1 or L4. Explicitly these are when L2 → 0, L3 → 0, L2 + L3 → 0. There is also a double singularity when two of these are taken simultaneously.
has ten apparent singularities with three of these being independent of L1 or L4. Explicitly these are when L2 → 0, L3 → 0, L2 + L3 → 0. There is also a double singularity when two of these are taken simultaneously.
For the first limit, it can be found that

The second limit can be easily found using the identity  . The third limit yields
. The third limit yields

Finally, the fourth, double singularity, limit gives

Appendix E.: Generating functions
In this section a generating function for the operators fr−1, defined in equation (2.31), will be given. This generating function will be perhaps the simplest way of generating these operators in practice. Additionally, it will be used to provide results needed in appendix D to remove apparent singularities in the operators 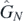 .
.
Starting from equation (2.31), by multiplying by xr , summing over r, and using this sum to eliminate the Kronecker delta on the right-hand side, it can be seen that

where the compact notation ci = coth(x1 + ⋯ + xi ) has been used. Next the sum over p1 can be relabelled to a sum over some index m, and pulled out the front. Relabelling the rest of the variables leaves

Next, inspired by the structure of the above, define
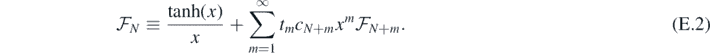
Then clearly, reading off from equation (E.1),

giving a generating function for the operators fr−1. In order to find a given operator, then, one would iteratively substitute in

and so on, then Taylor expand the resulting 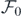 . It should be noted that as substituting in an
. It should be noted that as substituting in an 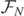 only affects the generating function at
only affects the generating function at  , if one only cared about finding operators up to and including fr
then all subsequent
, if one only cared about finding operators up to and including fr
then all subsequent  , M > r, may be set to zero with no adverse effect.
, M > r, may be set to zero with no adverse effect.
The next task for this appendix is to prove some results required for removing apparent singularities in the operators 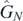 . In particular, equation (D.3) shall be proved. That equation deals with the operator fn
(y, 0, ⋯, 0), which in the language of this appendix implies c1 = c2 = ⋯. In this special case, equation (E.2) simplifies to
. In particular, equation (D.3) shall be proved. That equation deals with the operator fn
(y, 0, ⋯, 0), which in the language of this appendix implies c1 = c2 = ⋯. In this special case, equation (E.2) simplifies to

with all N equations being identical. Subsequent rearrangement and hyperbolic manipulations provide

where the x of this section has been replaced with α in order to distinguish it from the x within equation (D.3). Next take equation (D.3), multiply by αn and sum over n to find

Next note

hence proving the result required.
Similar results are required for more complicated singularities than those observed in appendix D, for example having gaps in the set of variables which tend to zero. That is, having L2, L3 → 0 while also simultaneously having L5 → 0, for instance, leaving a non-zero gap via L4. In that case identities would have to be used which require a generating function for fr (x, y, 0, ⋯, 0), though this fact will not be proved. This appendix will close with the case c2 = c3 = ⋯, while c1 is distinct, providing such a generating function. In this case, equation (E.2) gives two distinct functions,

which can then be rearranged to provide the required generating function. Ever more complicated sets of singularities will require ever more complicated generating functions, but it should be straightforward to see from what has been done here how this can be generalised.


