Validation of an Eulerian Stochastic Fields Solver Coupled with Reaction–Diffusion Manifolds on LES of Methane/Air Non-premixed Flames

Abstract

The Eulerian stochastic fields (ESF) combustion model can be used in LES in order to evaluate the filtered density function to describe the process of turbulence–chemistry interaction. The method is typically computationally expensive, especially if detailed chemistry mechanisms involving hydrocarbons are used. In this work, expensive computations are avoided by coupling the ESF solver with a reduced chemistry model. The reaction–diffusion manifold (REDIM) is chosen for this purpose, consisting of a passive scalar and a suitable reaction progress variable. The latter allows the use of a constant parametrization matrix when projecting the ESF equations onto the manifold. The piloted flames Sandia D–E were selected for validation using a 2D-REDIM. The results show that the combined solver is able to correctly capture the flame behavior in the investigated sections, although local extinction is underestimated by the ESF close to the injection plate. Hydrogen concentrations are strongly influenced by the transport model selected within the REDIM tabulation. A total solver performance increase by a factor of 81% is observed, compared to a full chemistry ESF simulation with 19 species. An accurate prediction of flame F instead required the extension of the REDIM table to a third variable, the scalar dissipation rate.

1 Introduction

Numerical simulations of turbulent reactive flows using detailed chemistry mechanisms tend to be computationally expensive. This is particularly true for combustion of hydrocarbons. Not only the number of species and reactions involved increases with the fuel complexity, but the chemistry time scales also span a broader range. By increasing the mechanism’s complexity, the presence of species in quasi-steady state and reactions almost at the chemical equilibrium would require a smaller time step (of the order of 10$^{-12}$) for the resolution of the chemistry Ordinary Differential Equation (ODE). The share of the ODE resolution within a time step can grow up to 90% of the total simulation time (Echekki and Mastorakos 2011). To overcome this bottleneck, reduced chemistry models are often the best choice. In contrast to the tabulated chemistry techniques based on the flamelet assumption (Oijen and de Goey 1992; Peters 1984; Pierce and Monin 2004), mathematically reduced chemistry models are derived from the analysis of the local chemistry time scales, allowing to reduce the full thermochemical state to a low-dimensional attracting surface. The original formulation of the Intrinsic Low Dimensional Manifold (ILDM), based on the dynamic perturbation of a homogeneous isobaric reactor (Maas and Pope 1992), was further improved (Eggels and de Goey 1995; Wang et al. 2008) until molecular transport was introduced by Bykov and Maas (2007). The latter resulted in a low-dimensional space accounting for physical transport, known as REaction DIffusion Manifold (REDIM). Similar manifolds accounting for molecular transport and based on premixed flame structures developed from the pioneer work of Bradley et al. (1988) and Bradley and Lau (1990), like the Flamelet Generated Manifold (FGM) (Oijen and de Goey 1992) and the Flame Prolongation of the ILDM (FPI) (Fiorina et al. 2003, 2005b; Gicquel et al. 2000). When applied to non-premixed or partially premixed regimes however, they revealed some deficiencies [cf. Ramaekers et al. (2010) and Fiorina et al. (2005a)]. The choice of a counterflow diffusion flame database [REDIM, non-premixed-FGM (Ramaekers et al. 2010) or Flamelet Progress Variable (FPV) (Pierce and Monin 2004)] instead of a premixed-based database (ILDM or FPI) improves the prediction of the major species concentrations in partially premixed configurations like the Sandia flames (Barlow and Frank 2007), as previously shown in Ramaekers et al. (2010). As the REDIM showed promising results (Yu et al. 2019, 2018) when applied to the Sandia flame series D–E–F (Barlow and Frank 2007), this reduced chemistry model is used in this work, combined with a filtered density function model for LES.

In LES of turbulent reacting flows, the rate controlling processes like molecular transport and chemical reactions occur at the smallest scales, which are usually modelled (Pope 2000). As a consequence, the effects of the sub-grid scale (sgs) fluctuations of local filtered reaction rates must be taken into account by the filtered Probability Density Function (PDF). Choosing to solve a transport equation for the PDF instead of assuming its shape a-priori ($\beta$-PDF) has the advantage of presenting the chemical source term in closed form already in the filtered equations. Due to its high dimensionality however, this equation is impracticable to be solved in a deterministic way on computational grids (Haworth 2010). Although Lagrangian Monte Carlo particle methods have been the dominant approaches to solve such equation in both LES and RANS context (Jenny et al. 2001; Muradoglu et al. 1999; Pope 1985, 2000), an Eulerian approach can be used too (Sabel’nikov and Soulard 2005; Soulard 2005; Valiño 1998; Valiño et al. 2016). In the Lagrangian approach, the one-point, one-time joint PDF (or FDF for LES) is constructed from stochastic particles subjected to convection, molecular mixing, turbulent diffusion and chemical reactions. This method has the advantage that any PDF shape can be transported. However, coupling algorithms between the particle method and the Eulerian mesh must be developed to guarantee consistency (Muradoglu et al. 2001; Raman and Pitsch 2007). Moreover, the overall number of particles can be two orders of magnitude larger than the number of mesh elements, in order to achieve statistical convergence. The fact that LES require a 3D computational domain for their validity implies that a higher number of particles shall be transported, which can lead to massive computational costs if detailed chemistry is involved. A recent alternative based on the Multiple-Mapping Conditioning (MMC) model allows the use of a “sparse-Lagrangian” approach (Cleary and Klimenko 2011; Cleary et al. 2009; Cleary and Klimenko 2009). In this way the number of overall particles becomes lower than the number of mesh elements. This is possible in MMC since the micro-mixing is performed in a reference space, enforcing locality in the composition and position spaces.

Alternatively, the LES solver can be combined with a conditional RANS-PDF method to evaluate the composition joint-PDF on coarser meshes, as proposed by Brandl (2010) and Ferraro et al. (2019). However, caution has to be taken when transferring the information from the Lagrangian particles to the Eulerian mesh to ensure mass consistency, usually adopting a density coupling feedback (Cleary and Klimenko 2011; Muradoglu et al. 2001).

The Eulerian approach is followed in this work instead. In fact, such approach allows an easier implementation of the FDF modelled equations using the mesh-based Eulerian solvers available in OpenFOAM (Weller et al. 1998). The FDF is decomposed into N stochastic fields, resulting in N Stochastic Partially Differential Equations (SPDE) (Sabel’nikov and Soulard 2005; Valiño 1998). The increased computational time of about + 50%, observed by Jaishree and Haworth (2012) when applying the stochastic fields to the RANS context instead of Lagrangian particles, is not encountered in the LES implementation. In fact, the number of stochastic fields required for approximate statistical convergence is considerably reduced, from N = 40 (Jaishree and Haworth 2012) to N = 8 (Jones and Prasad 2010; Mustata et al. 2006). An ESF solver was previously implemented in the in-house OpenFOAM code, based on detailed chemistry (Müller 2016). It was further validated for non-premixed (Müller 2016; Zips et al. 2019) and partially premixed flames (Hansinger et al. 2020). Since the target of this investigation is further reducing the computational cost required by the transport of the ESF based on a full chemistry state, the ESF transport equations were coupled with a reduced chemistry model. Recently, ESF solvers combined with pre-tabulated chemistry deriving from the FPV (Pierce and Monin 2004) or the FGM (Oijen and de Goey 1992) combustion models were proposed by several groups (Avdic et al. 2017; Collonval 2015; Duan et al. 2019; Kulkarni and Polifke 2013; Mahmoud et al. 2019) for OpenFOAM applications. In this work, the ESF solver retrieves the thermo-chemical state from REDIM tables instead. The use of the REDIM method has the advantage that it involves projection of the diffusion term onto the slow manifold (Bykov and Maas 2007; Golda et al. 2019; Strassacker et al. 2019). In turbulent flows, where models for diffusion tend to move the states off the manifold, a back-projection is needed (Bender et al. 2000). In order to simplify the treatment a constant back-projection is typically used, although a certain dependence on the progress variable was observed when using a constant matrix projection (Yu et al. 2020). However, an optimal choice of the REDIM progress variables can be determined a-priori, as reported in Yu et al. (2019). The validity of the new ESF-REDIM solver is first assessed on the Sandia flames D–E, presenting a moderate degree of extinction, using a 2-dimensional chemistry table. The REDIM itself was tested for flames D–E by Minuzzi et al. (2019) and Yu et al. (2019) and does not need further validation. Simulations of flame F, characterized by severe extinction, required the extension of the REDIM tables to a third dimension, in order to correctly describe local unsteadiness. Due to its strong dependence on the flow and chemistry parameters (Cao and Pope 2005; Xu and Pope 2000) the Sandia flame F is very challenging in terms of modelling. Here, we present results for flame F which show that the coupled ESF-REDIM model can indeed describe this challenging flame. A detailed analysis and a comparison with ESF-ILDM and FPV-based simulations is object of a future publication.

The manuscript is structured as follows. The governing equations for the CFD simulations are treated in Sect. 2. The numerical implementation of the ESF-REDIM solver in OpenFOAM and the Sandia test case are presented in Sect. 3. A parametric study on the model settings and the results for flame D and E are discussed in Sect. 4, followed by the discussion of the main results for flame F. Finally, Sect. 5 draws the conclusions and provides an outlook for further improvement.

2 Governing Equations

The LES approach allows to capture unsteady features of turbulent flows, while reducing the required model assumptions. Only the small structures larger than a cut-off filter are modeled. By applying the LES cut-off filter $\mathcal {G}$(x − x$^{'}$), variable g becomes

$$\begin{aligned} {\bar{g}}(x)=\int _{}^{} g(x^{'})\,\mathcal {G}(x-x^{'})\,dx^{'}\, \end{aligned}$$

(1)

where $\mathcal {G}$ corresponds to the process of averaging over a box, evaluated from the computational cell size $\varDelta = \root 3 \of {V_{cell}}$. A mass-weighted Favre filtering is further applied on the variable as ${\tilde{g}}= \overline{g\rho }$/${\bar{\rho }}$. With this, the filtered transported equations can be written as reported by Sagaut (2001):

$$\begin{aligned}&\frac{\partial {\bar{\rho }}}{\partial t} + \frac{\partial {\bar{\rho }}{\tilde{u}}_i}{\partial x_i} = 0 \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial {\bar{\rho }}{\tilde{u}}_i}{\partial t} + \frac{\partial {\bar{\rho }}{\tilde{u}}_i{\tilde{u}}_j}{\partial x_j} = -\frac{\partial {\bar{p}}}{\partial x_i} + \frac{\partial }{\partial x_i} \left( {\bar{\tau }}_{ij}-{\bar{\rho }}(\widetilde{u_iu_j}-{\widetilde{u}}_i{\widetilde{u}}_j)\right) \end{aligned}$$

(3)

with ${\widetilde{u}}_i$ the i-th component of the filtered velocity, ${\bar{\rho }}$ and ${\bar{p}}$ the averaged fluid density and pressure. The shear-stress tensor in Eq. 3 for Newtonian fluids is approximated by the gradient diffusion hypothesis (Pope 2000)

$$\begin{aligned} {\bar{\tau }}_{ij}= & {} 2{\bar{\mu }}\left( S_{ij} -\frac{1}{3}\delta _{ij} S_{kk}\right) \end{aligned}$$

(4)

$$\begin{aligned} S_{ij}= & {} \frac{1}{2}\left( \frac{\partial \tilde{u_i}}{\partial x_j}+\frac{\partial \tilde{u_j}}{\partial x_i} \right) \end{aligned}$$

(5)

with ${\bar{\mu }}$ the filtered dynamic viscosity, S$_{ij}$ the components of the rate-of-strain tensor, $\delta _{ij}$ the Kronecker delta. The Boussinesq hypothesis for the unresolved Reynolds stresses yields

$$\begin{aligned} \bar{\rho} (\widetilde{u_iu_j}-{\widetilde{u}}_i{\widetilde{u}}_j) =\tau _{sgs, ij} =-2\,\mu_{sgs} \left( S_{ij} -\frac{1}{3} \delta _{ij} S_{kk}\right) . \end{aligned}$$

(6)

The Wall-Adapting Local Eddy-viscosity (WALE) model was applied in this work to close the sub-grid stresses as

$$\begin{aligned} \mu _{sgs}= \bar{\rho} (C_w\varDelta )^2 \frac{(s_{ij}^d\,s_{ij}^d)^{2/3}}{(S_{ij}\,S_{ij})^{5/2}+(s_{ij}^d\,s_{ij}^d)^{5/4}}. \end{aligned}$$

(7)

The reader is pointed to the original paper for a detailed explanation of the model coefficients (Nicoud and Ducros 1999).

2.1 Filtered Density Function

The stochastic evolution of the temperature and the species mass fractions in LES can be described by a composition FDF. The term ’FDF’ is widely used in the literature to describe the conventional PDF, convoluted with the LES filter kernel [see for example (Pope 1990) or (Haworth 2010)]. To avoid confusion, it should be mentioned the fact that the original PDF formulation for LES was labelled as ’LES-PDF’ by Gao and O’Brien (1993), so that both terms are found in the literature. Here, the $\alpha =1, \ldots ,\textit{n}$ scalar quantities are represented by $\phi _{\alpha }$, their sample spaces are denoted as $\psi _{\alpha }$. Defining the fine-grained composition PDF as $\mathcal {P}_{sgs}(\varvec{\psi })=\prod _{\alpha =1}^{n} \delta (\psi _{\alpha }-\phi _{\alpha })$ and applying the LES filter of Eq. 1, one gets the probability of $\varvec{\phi }= \varvec{\psi }$ localized on the filtered volume. The derived FDF, namely $\widetilde{\mathcal {P}}_{sgs}$, can be transported as

$$\begin{aligned} \begin{aligned}&\frac{\partial {\bar{\rho }}\widetilde{\mathcal {P}}_{sgs}}{\partial t} + \frac{\partial {\bar{\rho }}{\tilde{u}}_j\widetilde{\mathcal {P}}_{sgs}}{\partial x_j}+ \sum _{\alpha =1}^{n}\frac{\partial }{\partial \psi _{\alpha }}({\bar{\rho }}{\dot{\omega }}_{\alpha }\widetilde{\mathcal {P}}_{sgs}) \\&\quad = \frac{\partial }{\partial x_j}\left[ {\bar{\rho }}\left( \frac{{\bar{\nu }}}{Sc}+\frac{\nu _{sgs}}{Sc_{sgs}}\right) \frac{\partial \widetilde{\mathcal {P}}_{sgs}}{\partial x_j}\right] - \sum _{\alpha =1}^{n}\sum _{\beta =1}^{n} \frac{\partial ^2}{\partial \psi _{\alpha }\partial \psi _{\beta }} \left( {\bar{\rho }}\frac{{\bar{\nu }}}{Sc}\overline{\frac{\partial \phi _{\alpha }}{\partial x_i}\dfrac{\partial \phi _{\beta }}{\partial x_i}\bigg |_{\varvec{\phi }\,=\,\varvec{\psi }}}\,\mathcal {P}_{sgs}\right) \end{aligned} \end{aligned}$$

(8)

The reader is referred to Haworth (2010) for a complete derivation of the transport equation. The LHS of Eq. 8 contains the temporal evolution of $\widetilde{\mathcal {P}}_{sgs}$, the convective transport term and the variation due to chemical reactions. Here the advantage of using a transported PDF model is clear, since the chemical source terms appear in closed form. When using tabulated chemistry, this allows to directly look-up ${\dot{\omega }}_{\alpha }$ from the database. On the RHS of the equation, the scalar conditioned velocity fluctuations on the sub-grid level have been modelled using the gradient flux hypothesis. The Schmidt numbers Sc, Sc$_{sgs}$ have been assigned equal to 0.7 according to previous investigations (Breda et al. 2020; Hansinger et al. 2020). Equal diffusivities have been assumed, using unity Lewis numbers. The last term represents the molecular mixing (or micro-mixing) which requires further modelling. Equation 8 can be solved by using a Lagrangian particle method (Pope 1990, 2000). In this work, the equation is solved using an Eulerian approach using the ESF formulation of Valiño (Valiño et al. 2016). There, the micro-mixing term is modelled using the Interaction by Exchange with the Mean (IEM) (Villermaux and Devillon 1972), alternatively known as Linear Mean Square Estimate (LMSE) from the work of Dopazo and O’Brien (1974). Other mixing models are often used in combination with Lagrangian particle methods and the reader is pointed to Mitarai et al. (2005) and Subramaniam and Pope (1998) for further details. Using the IEM model, the last term of Eq. 8 can be written as

$$\begin{aligned} \frac{{\bar{\rho }}}{\tau _{sgs}}\sum _{\alpha =1}^{n_s} \frac{\partial }{\partial \psi _{\alpha }}\left[ \left( \psi _{\alpha }-{\widetilde{\phi }}_{\alpha }\right) \widetilde{\mathcal {P}}_{sgs}\right] . \end{aligned}$$

(9)

By setting C$_d$ = 2 according to previous LES applications (Jones and Prasad 2010; Mustata et al. 2006), the sub-grid time scale $\tau _{sgs}$ is defined as

$$\begin{aligned} \frac{1}{\tau _{sgs}}=C_d\frac{\nu _{sgs}}{\varDelta ^2}. \end{aligned}$$

(10)

2.2 Eulerian Stochastic Fields

In the ESF method the filtered $\widetilde{\mathcal {P}}_{sgs}$ is decomposed into N stochastic fields, with $\zeta _{\alpha }^n$ being the n-th realization of the scalar having index $\alpha$

$$\begin{aligned} \widetilde{\mathcal {P}}_{sgs}(\varvec{\psi })=\frac{1}{N}\sum _{n=1}^{N}\prod _{\alpha =1}^{n}\delta (\psi _{\alpha }-\zeta _{\alpha }^n) . \end{aligned}$$

(11)

Each field $\zeta _{\alpha }^n$ evolves according to the latest ESF method proposed by Valiño et al. (2016):

$$\begin{aligned} \begin{aligned}&d{\bar{\rho }}\zeta _{\alpha }^n + \frac{\partial ({\bar{\rho }}{\tilde{u}}_i\zeta _{\alpha }^n)}{\partial x_j}dt -\frac{\partial }{\partial x_j} \left( \left( \frac{{\bar{\mu }}}{Sc}+\frac{\mu _{sgs}}{Sc_{sgs}} \right) \frac{\partial \zeta _{\alpha }^n}{\partial x_j}\right) dt \\&\quad = {\bar{\rho }}\left( \frac{2\mu _{sgs}}{{\bar{\rho }}Sc_{sgs}} \right) ^{1/2}\frac{\partial \zeta _{\alpha }^n}{\partial x_j}\,dW_j^n - \frac{{\bar{\rho }}}{2\tau _{sgs}}(\zeta _{\alpha }^n-{\widetilde{\phi }}_{\alpha })\,dt -{\bar{\rho }}{\dot{\omega }}_{\alpha }^n(\zeta ^n)\,dt. \end{aligned} \end{aligned}$$

(12)

The solution of each stochastic field must satisfy mass conservation and the boundary conditions for Eq. 8. In fact, the solution of each field is not a physical realization of the real field, but rather an equivalent stochastic system to Eq. 8. Although the two systems can have instantaneously different states, the same one-point statistics is achieved. The filtered ${\tilde{\phi }}_{\alpha }$ required by the IEM model are computed from the average over the fields as

$$\begin{aligned} {\widetilde{\phi }}_{\alpha }=\frac{1}{N} \sum _{n=1}^{N} \zeta _{\alpha }^n. \end{aligned}$$

(13)

The laminar diffusivity was originally included in the stochastic term of Eq. 12 (first on the RHS) by Valiño (1998). Hereby the latest formulation is used (Valiño et al. 2016), which only includes the sub-grid contribution. This prevents unphysical fluctuations of the scalar gradients due to the stochastic term in purely laminar regions of the flow field. Equation 12 was derived by Valiño using the Itô integration for the SPDE, resulting in a Wiener process dW$^{n}$ independent from the diffusion matrix. The random process can be therefore evaluated at the beginning of each time step t$_k$. The alternative ESF formulation of Sabel’nikov and Soulard (2005) is based on the Stratonovich integration instead, which requires the evaluation of the random process at the mid-point of the time step (t$_{k+1/2}$). A detailed comparison between the Itô and Stratonovich integrals for the solution of the SPDE is provided by Gardiner (2009). The Wiener term is hereby approximated by the time-step increment as dW$_j^{n}= \gamma _j\,\sqrt{dt}$, with $\gamma _j=\{-1, 1\}$ being a random dichotomic vector with zero mean (Valiño 1998).

The source terms ${\dot{\omega }}_{\alpha }^n$ appear in closed form and are direct solutions of the chemistry ODE system for the n-th field. An analytically reduced mechanism (Lu and Law 2005) derived from the GRI-3.0 (Frenklach 1995) is used in this work, whenever full chemistry computations of the ESF are attempted. As it consists of 19 species, the mechanism is labelled as Lu19 in this manuscript. The reactive scalars $\phi _{\alpha }$ transported by the stochastic fields of Eq. 12 are therefore 19 species and the specific enthalpy h.

2.3 Reduced Chemistry Model

A reaction–diffusion system can be described by the state vector $\varvec{\varPsi }= [h, p, w_1, \dots , w_{n_s}]^T$, with w$_k$ being the specific mole number of species k, n$_s$ the total number of species, h the specific enthalpy and p the system pressure. The partial differential equation characterizing this system can be written as [Bykov and Maas (2007)]

$$\begin{aligned} \frac{\partial \varvec{\varPsi }}{\partial t} = {\varvec{F}} - {\varvec{u}}\,\mathrm {grad}\varvec{\varPsi } + \frac{1}{\rho }div({\varvec{D}}\,\mathrm {grad}\varvec{\varPsi }) . \end{aligned}$$

(14)

The n$_s+2$ reaction rates of the state vector are contained in F, while matrix D of dimensions (n$_s+2$)$\times$(n$_s+2$) contains the transport coefficients. If equal diffusivities are assumed for all species and unity Lewis numbers are assigned, the diffusion matrix becomes ${{{\varvec{D}}}}\,=\hbox {diag}\{\textit{d}_{th}, 0, \textit{d}_1, \dots , \textit{d}_{n_s}\}$, being the mass diffusivities equal to the thermal diffusivity. The matrix is full in case differential diffusion is considered. Whenever the latter applies, the Hirschfelder-Curtiss approximation is used for the diffusion velocites (Hischfelder et al. 1969) and the Soret effect is included. The REDIM validation for differential diffusion is reported by Maas and Bykov (2011). The presence of the convective-diffusive terms in Eq. 14 allows to overcome the issue observed in the low-temperature region when deriving the ILDM (Eggels and de Goey 1995; Maas and Pope 1992), i.e. the overlapping of the slow eigenvectors and the impossibility of separating the slow chemistry time scales from the fast ones. Equation 14 is the starting point for the derivation of the evolution equation for the REDIM, treated in detail by Bykov and Maas (2007). The estimation of the gradient grad$\varvec{\varPsi }$ for the calculation of the manifold is presented in the works of Bykov and Maas (2007), Minuzzi et al. (2019) and Yu et al. (2018) and it is not discussed here.

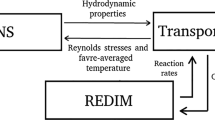
The existence of low-dimensional manifolds ensures that the system dynamics is governed by the m$_s$ slow chemistry modes, once the fast chemistry has relaxed. In other words, the local state space $\varvec{\varPsi }$ will evolve close to or onto an m$_s$-dimensional surface $\mathcal {M}$, defined by generalized coordinates $\varvec{\theta }$. The reader should notice that the generalized coordinates $\varvec{\theta }$ are the local coordinates in the REDIM formulation, which guarantee that the system evolves tangentially to the manifold. Such coordinates differ from the ’physical’ coordinates typically used in flamelet manifolds (FGM or FPV), which are based on a linear combination of the state variables belonging to $\varvec{\varPsi }$. Fig. 1 helps to visualize the representation. The circles denote states on the manifold, the square is a state off the manifold. Due to the stochastic mixing model required by the FDF in turbulent flows, it is possible that a state belonging to the manifold prior mixing ($\varvec{\varPsi }_{pm}$) is pulled off the manifold after mixing ($\varvec{\varPsi }_{am}$). From the theory of the low-dimensional surface attractors, the vector towards the new state can be decomposed into its slow and fast components $\varDelta \varPsi _s$ and $\varDelta \varPsi _f$, the former belonging to the tangential subspace of the generalized coordinates ($\mathcal {T}$ in Fig.1). The projection of the state onto the manifold is performed along the direction of the fast subspace, which can differ depending on the selected projection matrix. The Moore–Penrose pseudo inverse matrix $\varvec{\varPsi _{\theta }^{+}}$ (Golub and van Loan 1989) is usually chosen for this projection [see Bykov and Maas (2007)]. The transformation $\varvec{\theta }\,=\,\varvec{\varPsi _{\theta }^{+}}\,\varvec{\varPsi }$ allows to extract the generalized variables $\varvec{\theta }$ from the state $\varvec{\varPsi }$. For an easier implementation into the ESF solver, the use of a constant parametrization matrix ${\varvec{C}}$ was preferred, in the same way as described by Minuzzi et al. (2019) and Yu et al. (2019). Using this matrix, the fast processes of $\varvec{\varPsi }_{am}$ relax within the ${\varvec{C}}^{\bot }$-subspace. It basically means that the reduced variables $\varvec{\theta }$ shall remain approximately constant while the final state $\varvec{\varPsi }_{p}$ is reached (cfr. Fig.1 for visual representation).

When using the constant parametrization matrix ${\varvec{C}}$ it is convenient to express the REDIM in terms of physical variables as $\varvec{\xi }= {\varvec{C}}\varvec{\varPsi }$. Transforming Eq. 14 into a governing equation for physical variables leads to

$$\begin{aligned} \frac{\partial \varvec{\xi }}{\partial t} = {\varvec{C}}{\varvec{F}} - {\varvec{u}}\,\mathrm {grad}\varvec{\xi } + \frac{1}{\rho }div({\varvec{D}}\,\mathrm {grad}\varvec{\xi }) . \end{aligned}$$

(15)

Fig. 1

Projection of the off-state $\varvec{\varPsi }_{am}$ onto the manifold $\mathcal {M}$ along the direction of constant $\varvec{\theta }$

The physical variables were chosen as $\varvec{\xi } = [Y_{N2}, PV]^T$, where the inert species Y$_{N2}$ represents the degree of mixing, directly proportional to the commonly used mixture fraction f (Peters 1984). The reactive progress variable PV is chosen using a linear combination of species mass fractions. The reader should notice that a Moore–Penrose matrix in physical coordinates $\varvec{\xi }$ can be still retrieved from the constant parametrization matrix as $\varvec{\varPsi _{\xi }^{+}}\,=\,{\varvec{C}}\,\varvec{\varPsi _{\theta }}\,\varvec{\varPsi _{\theta }^{+}}$. A detailed derivation of the variable transformation can be found in the work of Strassacker et al. (2019). There, it was shown that if the REDIM is created with an exact gradient estimation, the physical and the generalized parametrizations ${\varvec{C}}$ and $\varvec{\varPsi _{\theta }^{+}}$ would deliver similar results when applied to quenching flames in laminar regime. The use of a simplified gradient estimation allowed to obtain comparable results (Minuzzi et al. 2019) and the implementation was successfully validated for non-premixed laminar and turbulent flames (Yu et al. 2019). Cross-diffusion is taken into account in the REDIM by the physical gradients of Y$_{N2}$ and PV. The improvement compared to a FPV table neglecting cross-diffusion was previously discussed for a premixed flame subjected to heat-losses (Ganter et al. 2018) and similar observations apply for this work. The scalar dissipation rate is implicitly included in the manifold through the gradient guess on Y$_{N2}$, which is proportional to the mixture fraction gradient.

The linear combination of species for the PV was identified mathematically using a Global Quasi-Linearization (GQL) procedure (Bykov et al. 2008). The GQL approach is similar to the ILDM, where a reduced chemistry is researched for a homogeneous reacting system. In the investigation of flames D–E of Yu et al. (2019), the GQL-reduced chemistry described by the progress variable

$$\begin{aligned} PV = w_{CO_2}+0.5\,w_{H_2O} \end{aligned}$$

(16)

was found to approximate the auto-ignition delay times of CH$_4$/Air reactors within a 5$\%$ error, compared to detailed chemistry calculations. As a consequence, the same PV was used in this work. Although Eq. 16 is expressed in specific mole numbers here the expression in mass fractions Y$_k$ is preferred. Therefore, Eq. 16 becomes PV = Y$_{CO_2}$+0.5 Y$_{H_2O}$. In this way, a direct comparison with an FPV-based simulation (e.g. Ihme and Pitsch 2008) can be performed at any time, using the same progress variable. The selected PV was seen to remain approximately constant while the fast processes relax, which justifies the use of the constant matrix ${\varvec{C}}$. The investigation of flame F required a minor change from this base setup. A third variable was added to the REDIM, the scalar dissipation rate $\chi$, in order to account for local extinction. Moreover, a slightly better prediction of the extinguished states was provided by PV = Y$_{CO_2}$+Y$_{H_2O}$+Y$_{CO}$+Y$_{H_2}$, which was selected accordingly. In the next paragraph, the projection of the ESF equations will be discussed.

2.4 ESF-REDIM Equations

When coupling the transport of the ESF (Eq. 12) with a reduced chemistry model, the number of transported scalars $\phi _{\alpha }$ is considerably reduced. Using the REDIM tabulation, only the reduced coordinates $\varvec{\xi }$ = ($\xi _1$, $\xi _2$) are transported by the N stochastic fields as

$$\begin{aligned} \begin{aligned}&d{\bar{\rho }}\,\xi _k^n + \frac{\partial ({\bar{\rho }}\,{\tilde{u}}_i\,\xi _k^n)}{\partial x_j}dt -\frac{\partial }{\partial x_j} \left( \left( \frac{{\bar{\mu }}}{Sc}+\frac{\mu _{sgs}}{Sc_{sgs}} \right) \frac{\partial \xi _k^n}{\partial x_j}\right) dt \\&\quad ={\bar{\rho }}\left( \frac{2\mu _{sgs}}{{\bar{\rho }}Sc_{sgs}} \right) ^{1/2}\frac{\partial \xi _k^n}{\partial x_j}\,dW_j^n - \frac{{\bar{\rho }}}{2\tau _{sgs}}(\xi _k^n-{\widetilde{\xi }}_k)\,dt -{\bar{\rho }}{\dot{\omega }}_k^n(\xi ^n)\,dt \end{aligned} \end{aligned}$$

(17)

with k = 1,2. The filtered value of each controlling variable is determined by the average over the stochastic fields as from Eq. 13. At run-time, the thermo-chemical state could be bounced off the manifold for two reasons: the stochastic term derived from the Itô formulation could produce unphysical values due to the numerics (Gardiner 2009) and/or the micro-mixing could bring the scalar outside the manifold. In order to guarantee interpolation within the REDIM, the updated value of $\xi _k^n$ is bounded to remain in the realizable space of the table. As explained in section 2.3, a constant parametrization matrix is used to project the state vector back to the manifold, which allows the direct implementation of Eq. 17 into the OpenFOAM routine. According to Bender et al. (2000), it is possible that the fast chemistry space is accessed after applying the IEM mixing. In this case, the state would not be able to relax back to the manifold unless a projection involving the full state is performed. By projecting Eq. (17) with $\varvec{\varPsi _{\xi }^{+}}$, each field n would require the knowledge of its projection matrix, the diffusion matrix $\varvec{\varPsi _{\xi }\,D}\,$ and eventually the source term $\varvec{\varPsi _{\xi }^{+}\,F}$. These variables can be additionally stored in the REDIM table, however the number of interpolation calls per cell at run-time would significantly increase. Although a considerable speed-up compared to a full detailed chemistry simulation is still expected, this solution would be definitely slower than using the constant matrix ${\varvec{C}}$. In this work, it was decided to implement the computationally cheapest solution, which allows to use Eq. 17 directly.

3 Numerical Implementation and Set-Up

The interpolation routine required by the REDIM tables was built over a new combustion class in OpenFOAM, while the ESF equations for the progress variables were implemented directly on the solver level. The starting point is the ESF solver previously implemented by Müller (2016), which is briefly described in the schematics of Fig. 2. For each solver time step t, the momentum and pressure equations are coupled via a PISO loop, where a low-Mach formulation is used. After the momentum equation is solved, the source terms for the stochastic fields equations are calculated (cfr. RHS of Eq. 12). The IEM is applied to the mixing term and the random vector of the Wiener term is generated. The reaction rates ${\dot{\omega }}_k$ are calculated by means of the selected ODE solver. To accelerate the computation, the implementation of Zirwes et al. (2018) was used in this work, which allows to integrate the chemistry ODE system in OpenFOAM using a CVODE Sundials routine. The work of Zirwes et al. (2018) showed a significant speed-up in the integration of the ODE, compared to the conventional solvers available in OpenFOAM. While a detailed investigation of the ODE settings in the same way of Stone and Bisetti (2014) would be out of scope, the reader can refer to Breda et al. (2020) for a comparison between the CVODE-based solver and selected OpenFOAM integrators using Sandia flame D as test case. The use of the accelerated chemistry solver is beneficial for the intensive ESF calculations with finite rate chemistry of this work. Once the construction of the RHS has completed, the N$\cdot$(n$_s$+1) stochastic equations are transported. The reader should notice that the resolution of the ESF equations requires most of the computational share within the solver time step. Previous observations determined an ESF simulation of flame D using detailed-chemistry (30 species) to be about 5 times slower than the same simulation run with the Turbulence–Chemistry Interaction (TCI) sub-grid model disabled (Breda et al. 2020).

Fig. 2

Pressure-based OpenFOAM solver algorithm including the ESF Eq. 12

The 2D-REDIM tables used in this work are built on an uniform equidistant grid of dimensions $200\times 200$ and have a storage size of about 80 Megabytes (MB). The 3D-REDIM for flame F has a third dimension of 6 grid points, for a total storage size of 300 MB. The reader is pointed to Minuzzi et al. (2019) for further details regarding the table generation for these flames. The REDIM chemistry is based on the 30-species mechanisms of Lu and Law (2005). The new ESF-REDIM solver is summarized in Fig. 3. The coupling between the Eulerian transport equations and the REDIM table is one-way: the thermo-chemical state (Y$_k$, T) is retrieved at runtime from the REDIM table, but the table itself is not modified by the solver. The Wiener and the micro-mixing terms are evaluated as from the previous solver. The substantial difference from Fig. 2 is given by the number of transported stochastic equations, which in this case is limited to 2$\cdot$N. Once the fields are transported, a bi-linear interpolation on (N$_2^n$, PV$^n$) (tri-linear for flame F, on (N$_2^n$, PV$^n$, $\chi$)) retrieves the thermo-chemical state in each computational cell, for each stochastic field. The algebraic equation for ${\widetilde{\chi }}$ proposed for LES by Domingo et al. (2008) is additionally solved for the 3D-REDIM. The source terms ${\dot{\omega }}_{PV}^n$ are looked-up from the REDIM table, instead of solving the ODE system for all species. Since N$_2$ is a passive scalar, its source term is null (${\dot{\omega }}_{N2}=0$). The filtered values ${\widetilde{N}}_2$, ${\widetilde{PV}}$, ${\widetilde{T}}$, $\widetilde{{\dot{\omega }}}_{PV}$ are finally calculated from Eq. 13.

Fig. 3

Pressure-based OpenFOAM solver algorithm including the ESF Eq. 17

3.1 Test Case

The experimental data of the non-premixed Sandia flames D–E–F (Barlow and Frank 2007) are used as validation for the ESF-REDIM implementation. A mixture of CH$_4$-Air in volume percentage 25/75 is injected at 294 K into the domain through a pipe of diameter D = 7.2 mm, with a bulk velocity u$_b$ = 49.6 m/s (74.4, 99.2 m/s) for configuration D (E, F). The cold jet is stabilized by a burned lean mixture at 11.4 m/s (17.1, 22.8  m/s) and 1880 K (1860 K for flame F). An air coflow at 291 K embeds the pilot with a velocity of 0.9 m/s in all configurations. An overview of the boundary conditions of flame D is provided in Table 1. The inlet composition does not change for flames E-F, but the new inlet boundary conditions are reported in Table 2. Typical cross-sections for the validations against experimental results are selected at x/D = 7.5, 15, 30. They localize the zones where respectively local extinction, local re-ignition and a diffusion flame behavior are expected.

Table 1 Flame D: inlet conditions

Table 2 Flame E-F: inlet bulk velocities and pilot temperatures

3.2 Solver Set-Up

The Sutherland transport model available in OpenFOAM (Sutherland 1893) is used for all simulations. A total number of 8 stochastic fields is transported, according to Jones and Prasad (2010) and the observations presented in section 4.2. Turbulence was generated at the fuel inlet by means of a separate LES, while a velocity block profile is applied for pilot and coflow. The CFD fields are averaged over 10–15 flow-through times. The calculations use an implicit Euler time integration scheme and a Total Variation Diminishing (TVD) scheme of type van Leer (see van Leer 1974) for the advective terms of the scalar fields. The second order low dissipative scheme filteredLinear is used instead for the velocity field. The conditional means and fluctuations (RMS) of the major species and temperature are calculated a posteriori based on 50 equal-size bins in mixture fraction space. To assess the mixture fraction f on both solvers, the Bilger formula was used (Bilger 1976):

$$\begin{aligned} f = \frac{2(Y_C-Y_{C,0})/W_C+0.5(Y_H-Y_{H,0})/W_H-2(Y_O-Y_{O,0})/W_O}{2(Y_{C,1}-Y_{C,0})/W_C+0.5(Y_{H,1}-Y_{H,0})/W_H-2(Y_{O,1}-Y_{O,0})/W_O} . \end{aligned}$$

(18)

The indices 0 and 1 denote respectively the oxidizer and fuel streams, Y$_e$ and W$_e$ the mass fractions and atomic weights of elements e = C, H, O. The flame Burning Index (BI) based on temperature is evaluated for each flame according to Cao and Pope (2005) and Xu and Pope (2000). It is defined as the ratio between the conditional mean temperature (conditioned on 0.3 < f < 0.4) and a reference value of T = 2023 K obtained from a laminar flame calculation with strain a = 100 s$^{-1}$.

A 3D axially-symmetric mesh consisting of about 2.3 million cells is selected as reference and labelled as R in the plots. Mesh dependency is investigated on two coarser meshes in paragraph 4.1, one having about 1.5 million cells (labelled as C) and one with 0.73 million cells (labelled as SC). The computational domain extends for all meshes to 100 D in axial direction and to 10 D in radial direction.

4 Results

The ESF-REDIM solver is hereby validated against the original ESF solver and the experimental data.

4.1 Mesh and Reduced Chemistry Validation

An ESF simulation using the Lu19 mechanism was compared to an ESF-REDIM simulation for flame E, on the reference mesh R. Flame E was chosen because it introduces a moderate degree of extinction, which could enhance the differences between the two models. Then, the ESF-REDIM simulation was carried out on the coarser meshes C and SC. The configurations investigated in this paragraph are reported in Table 3.

The approximation error given by the ESF-REDIM compared to ESF shall be first discussed. These cases are respectively labelled as ER-R and E-R in Fig. 4-5. The averaged fields and fluctuations in Fig. 4 reveal only minor differences between the two models. Slightly higher ${\widetilde{T}}$ are foreseen by ER-R between the pilot and the co-flow at x/D = 7.5, however the temperature fluctuations are better captured in this section. The mixture fraction ${\widetilde{f}}$ evaluated in the ESF solver within the fuel jet is leaner than then one retrieved by the ESF-REDIM, for sections x/D = 15 and 30. While this calculation better matches the experimental data in ${\widetilde{f}}$ in x/D = 15, it underestimated its value in x/D = 30. In this section, the ${\widetilde{T}}$ predicted by ESF is higher than the ESF-REDIM prediction, since the mixture is shifted towards a leaner composition. A quantitative analysis is given in Fig. 5 for the conditional means of temperature and the major species. The ESF-REDIM predicted higher temperatures and concentrations at stoichiometry and on the fuel-rich side. However, it will be shown in Sects. 4.4-4.5 that the simulation can be further corrected by using a detailed diffusion model while generating the REDIM. Overall, the ESF-REDIM matches the experimental data of flame E with a good agreement.

Table 3 Mesh study and combustion model

Fig. 4

Flame E: LES averaged fields and fluctuations for ${\widetilde{f}}$ and ${\widetilde{T}}$. ESF solver against ESF-REDIM, the latter calculated on three meshes (R, C, SC). Configurations of Table 3

Fig. 5

Flame E: conditional means of T and major species calculated on f. Configurations of Table 3

The behavior of ESF-REDIM on coarser meshes shall now be discussed. The simulations on the intermediate and the coarsest mesh are labelled as ER-C and ER-SC. It is clear from Fig. 4 that the results are influenced only from section x/D = 30. The fuel core extends longer in the domain by decreasing the mesh refinement further downstream. However, the grid resolution close to the injector plate is still enough in ER-SC to guarantee a good match with the ER-R case. The conditional means of Fig. 5 show no significant differences between the three meshes. The use of mesh R for the next paragraphs is therefore justified, as mesh convergence has been reached.

4.2 Number of Stochastic Fields

The number of stochastic fields N used in the ESF-REDIM solver was varied between 1, 2, 4 and 8 on mesh R. The calculation with one stochastic field is achieved by zeroing the Wiener term. A maximum of 8 fields was selected, as this number was seen to be sufficient to capture the sub-grid scalar fluctuations when applied to LES of non-premixed flames (Hansinger et al. 2020; Jones and Prasad 2010; Mustata et al. 2006). All meshes used in this work (SC, C and R) satisfy the Pope criterion requiring the resolution of at least 80 % of the turbulent kinetic energy (Pope 2006), as reported by Breda et al. (2020). Therefore, the sub-grid fluctuations are expected to be small and a low number of stochastic fields should be already sufficient to describe the scalar fluctuations. The response of flame D (not shown hereby) was found to be robust over the variation of N, although the solution sensibly deviated from the case at N = 1, when activating the Wiener term (N = 2). For flame E, the case at N = 2 lead to a premature flame extinction close to the injector plate, using the same solver settings. Removing the low Mach assumption in the transport equations for pressure and momentum helped to restore the solution for 2 stochastic fields. Hereby, the results are discussed for flame E and referenced as ER1, ER2, ER4 and ER8 in the plots. The reader should notice that ER2 is not directly comparable with the other simulations, for the reason previously explained.

Figures 6 and 7 show that the mean fields of flame E remain stable by varying the number of stochastic equations. ER2 presents more diffusive profiles on the fuel-lean side, due to the change in the pressure-momentum equations. The use of a single stochastic field (i.e. neglecting the sgs-TCI) would be already sufficient to capture the flame statistics on the investigated positions. A visible difference appears in the fuel core, at section x/D = 30. Using a single field (ER1), the mixture fraction profile results underestimated and consequently the temperature is higher. Species CO$_2$, H$_2$O and CO also present a higher concentration. Increasing the number of stochastic fields has the benefit of shifting the profiles towards the experimental values in the fuel core. However, further increasing N to 16 or 64 does not seem to improve the accuracy significantly, as observed by Hansinger et al. (2020). While a single field (N = 1) might be the preferred option when using the ESF with finite rate chemistry (Breda et al. 2020; Hansinger et al. 2020), the use of N = 8 in this investigation does not increase significantly the computational cost, since the ESF are coupled with tabulated chemistry. Therefore, a number of 8 ESF is selected to adequately describe the effects of the sgs turbulence on the chemistry.

Fig. 6

Flame E: LES averaged fields and fluctuations for ${\widetilde{f}}$ and ${\widetilde{T}}$ for ESF-REDIM, by varying the number of stochastic fields N

Fig. 7

Flame E: LES averaged fields for major species for ESF-REDIM, by varying the number of stochastic fields N

A brief discussion is also worth for the downstream sections at x/D > 30. By plotting the radial mesh refinement using the LES filter width $\varDelta$, one can see from Fig. 8 that the grid resolution of sections x/D = 45 and 60 is above the spatial resolution estimated from the experiment (Barlow and Frank 1998), i.e. the gray dashed line at 0.75 mm, for the three investigated meshes [for the upstream sections see the Suppl. Material of Breda et al. (2020)]. Where the mesh gets coarser, the modelling of TCI-sgs gains in importance. This explains why at section x/D = 45 the unconditional ${\widetilde{f}}$ and ${\widetilde{T}}$ show a stronger deviation in mean and RMS already on mesh R. The reference simulation of this work is the ESF with 8 fields and the 19-species mechanism. A further mesh refinement on the downstream sections would make this setup exceed the available computational resources. We accept this limitation and contain the investigations within x/D $\le$ 30 instead.

Fig. 8

Flame E: LES filter width $\varDelta$ at sections x/D = 45, 60. LES averaged fields and fluctuations of ${\widetilde{f}}$ and ${\widetilde{T}}$ for ESF-REDIM at x/D = 45 (color legend from Fig. 7)

4.3 Solver Performance

The solver performance is evaluated on a typical configuration exploiting parallel computing on the available cluster. For this purpose, the solver execution time t$_{exe}$ is averaged over three runs on 144 cores, having CPU architecture Intel Xeon E5-2670 v3. A fixed time step of 10$^{-7}$ s is assigned at each run and the solver is advanced for 500 steps. The performance improvement is calculated according to Zirwes et al. (2018) as

$$\begin{aligned} P_{tot} = \frac{t_{exe}-t_{exe,ref}}{t_{exe,ref}}. \end{aligned}$$

(19)

An LES simulation without TCI on the sub-grid level is used as reference case, where the filtered source terms $\widetilde{{\dot{\omega }}}_k$ are directly approximated by the ${\dot{\omega }}_k$. It can be claimed that this assumption is strictly valid for those meshes which allow to capture the Kolmogorov scales (thus for Direct Numerical Simulations). However, similar results were observed for the investigated flames when neglecting the sub-grid TCI, compared to a full chemistry ESF solver (Breda et al. 2020).

Fig. 9 illustrates the performance gain (loss) in percentage, for both ESF solvers. The zero line is the reference case. The results for the full chemistry ESF are given in red, for the reduced chemistry ESF in blue. Each performance was investigated for 8, 4, 2 and 1 stochastic fields, as reported on the x-axis. Each bar is labelled with the correspondent solver performance in percentage. As expected, the ESF-REDIM computations (ER) are always faster than the reference case, since the resolution of the chemistry ODE system is replaced by the table interpolation routine. The chart clearly confirms how the use of a full chemistry ESF solver for LES can easily require massive computational power, in the forecast of N $=$ 16, 32 or 64. Increasing the number of transported stochastic fields in the ESF-REDIM solver reduces its performance gain compared to the reference case. However, the computational time is still reduced of about  11$\%$ using 8 fields. The performance improvement calculated relatively to the full chemistry ESF is 81% when using 8 fields. As a conclusion, the ESF-REDIM solver is the preferable option: a performance gain is still observed when transporting the conventional 8 fields and it accounts for the sub-grid TCI.

Fig. 9

Comparison of solver performance over the number of stochastic fields. Red: ESF solver. Blue: ESF-REDIM solver. Zero line: reference case without TCI on sgs

4.4 Sandia Flame D

The results obtained for flame D are now discussed. In the following plots, E represents the solution for the full chemistry ESF solver, ER-Le1 and ER-DD the solutions for the ESF-REDIM. Although the transport equations were implemented in OpenFOAM by using a unity Lewis number for all species, the REDIM table itself can be generated using different transport models. The REDIM table built using the simplified assumption of unity Lewis numbers is labelled as Le1, while the table generated using differential diffusion is labelled as DD. The simulations presented in the previous paragraphs were all run using the table of ER-Le1. The average and fluctuations of ${\widetilde{f}}$ and ${\widetilde{T}}$ are shown in Fig. 10. ESF and ESF-REDIM provide different predictions in section x/D = 30, as previously observed for flame E (cfr. Sect. 4.1). In this section, E better agrees with the experimental data. A main difference is also given within the ESF-REDIM solver itself, depending whether the REDIM table with simplified transport or detailed transport is used. Due to the preferential diffusion of H$_2$, both ${\widetilde{f}}$ and ${\widetilde{T}}$ profiles in ER-DD are more diffusive on the lean side of the flame, downstream at x/D = 30. This is also confirmed by the H$_2$O profiles shown in Fig. 11. It is worth to notice that in this section CO is overpredicted by both ESF-REDIM simulations in the jet core. Since the REDIM tables were built over a single reactive progress variable, it is possible that the slow chemistry, characteristic of the CO reactions, would need a second reactive progress variable for a correct description. The work of Yu et al. (2020) confirmed this observation.

Fig. 10

Flame D: LES averaged fields and fluctuations for ${\widetilde{f}}$ and ${\widetilde{T}}$

Fig. 11

Flame D: LES averaged fields for major species

Selected conditional values for this flame are shown in Fig. 12. The ESF calculation with reduced chemistry (ER-Le1) approximates very well the ESF with full chemistry (E) in all sections. Major deviations are observed for H$_2$ at x/D = 7.5 and 15, where the full chemistry ESF delivers a better prediction. However, the analysis of the H$_2$ profiles definitely underlines the importance of introducing differential diffusion in the manifold. In fact, the profiles are completely recovered in ER-DD, compared to the cases with unity Lewis numbers. The radical OH is also better represented by this manifold. The unrealistic structures of temperature within 0.8 < f < 0.9 reported by Hinz (2000) and Mahmoud et al. (2019) and attributed to the IEM model are not seen in this work, confirming the validity of the REDIM tabulation method when coupled with the ESF. Due to the low level of local extinction of flame D, the conditional fluctuations are expected to be small. However, the conditional RMS of temperature and CO in Fig. 13 show overall a lower level compared to the experiment, although the conditional means are well captured. Raman and Pitsch (2007) observed a similar behavior for flame E. They partially identified the source of underprediction in the local equilibrium assumption used for the dynamic time scale model ($\tau _{sgs}$ of Eq. 10). The fact that in this work the time scale $\tau _{sgs}$ is not assigned dynamically could enhance the underprediction. Moreover, the mixing model of Raman and Pitsch (2007) was the same as this work, IEM. Differently from RANS, the IEM mixing model for LES is not very sensitive to the choice of the mixing constant (Jones and Prasad 2010), preventing any possible tuning of such parameter to improve the predictions. Interestingly, the conditional RMS of Fig. 13 show less fluctuations for OH and especially H$_2$ when using differential diffusion in the manifold. Section x/D = 30 however reveals that the full chemistry ESF is able to capture the fluctuations of the thermo-chemical state with more accuracy.

Fig. 12

Flame D: conditional means of T and major species calculated on f

Fig. 13

Flame D: conditional fluctuations of T and major species calculated on f

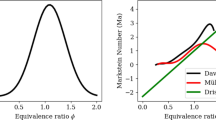
The normalized PDF of temperatures is reported in Fig. 14 for all simulations and for the investigated sections. The temperature sample space is conditioned within 0.3 < f< 0.4 and includes 1000 realizations divided into 50 bins. It can be seen that the PDF of ER-DD is centered on the experimental distribution in sections 7.5 and 15, whereas the PDFs of the simulations with unity Lewis numbers are shifted towards higher temperatures in these sections. Cases E and ER-Le1 however can represent better the statistical distribution in x/D = 30, while the distribution for ER-DD is clustered towards temperatures lower than 2000 K. Overall the CFD simulations show a narrower PDF shape than the experiment in 7.5, meaning that the local extinction is under-predicted in this section. These observations are quantitatively reflected by the burning index profile.

Fig. 14

Flame D: PDF of temperatures for test cases E, ER-Le1, ER-DD compared to the experimental data

The BI(T) index for this flame is shown in Fig. 15. This index shows the level of local extinction: the smaller the value, the stronger is the extinction phenomenon. Flame D is very stable, with BI greater than 0.93 across the domain. An overestimation of BI in sections 7.5 and 15 is seen in the CFD computations, explaining why the PDFs of Fig. 14 present fewer states at low temperature compared to the experiment. According to the BI, the flame at sections 7.5 and 15 is more stable, resulting in a lower amount of extinguished states which are otherwise responsible for the stretch of the PDF distribution towards the left. A possible cause for this behaviour could be the choice of the mixing model, limited to the IEM in the ESF formulation adopted. A detailed discussion about the mixing model is left to Sect. 4.6. Simulation E overestimates the experimental data across the domain, better approaching the experimental data downstream. While ER-DD better represents the BI upstream (x/D = 7.5 and 15), ER-Le1 can well represent the middle locations 15 and 30. The last observation suggests that the assumption of simplified diffusion is not completely justified close to injector. However, including the effects of differential diffusion into the manifold instead of in the CFD solver level is already sufficient to recover the solution. Being the computational time the limiting factor of the ESF simulations, the ESF-REDIM solver with the differential diffusion table (ER-DD) can be identified so far as the best trade-off.

Fig. 15

Flame D: flame burning index based on T

4.5 Sandia Flame E

The results are now discussed for flame E. In the plots, E represents the solution for the full chemistry ESF solver, while ER-Le1 and ER-DD are the solutions for the ESF-REDIM, using respectively the table with unity Lewis numbers and differential diffusion. The analysis of the average and fluctuations of Fig.16 leads to similar observations previously obtained for flame D. The temperature profiles are again more diffusive for ER-DD in all the investigated sections. The fluctuations in ${\widetilde{f}}$ and ${\widetilde{T}}$ however are very well captured. No substantial differences can be observed from Fig. 17 which were not already discussed for flame D. The averaged CO is again better captured by E, for the reason previously explained. The conditional means of Fig. 18 show interesting results. The CO profiles are better represented by the E simulation. As previously explained, in order for the REDIM to capture the slow chemistry involved in the reactions of CO, a second reactive progress variable should be added to the table. The experimental data for OH and H$_2$ are strongly overpredicted by ER-Le1. The full chemistry simulation E can only slightly improve the results obtained in these sections. Once again, the better approximation for these species is given by the manifold including differential diffusion in ER-DD. It is worth to stress the fact that real diffusion is not reproduced by the LES solver itself, but it is contained in the REDIM table. The conditional RMS of Fig. 19 show again that the E can capture better the turbulent fluctuations, especially in section x/D = 30. The reconstructed PDF of temperature is shown in Fig. 20. Compared to flame D, the PDF shape of flame E presents an increased width due to the higher turbulent inflow, which promotes local extinction. The tails of the distributions towards lower temperatures represent the extinguished states, which can be seen for all simulations in sections 7.5 and 15. Simulation ER-DD better captures the extinction phenomenon in these sections. In x/D = 7.5, both distributions for unity Lewis numbers are shifted towards higher temperatures compared to the experiment, resulting in a more stable flame. By moving downstream to x/D = 30 the shape of the PDF decreases in width, meaning that re-ignition processes are more frequent and the flame stabilizes. Here the peak of the ER-DD PDF is shifted towards lower temperatures, with the extinguished states likely to re-ignite further downstream. These observations can be confirmed again by looking at the flame burning index.

Fig. 16

Flame E: LES averaged fields and fluctuations for ${\widetilde{f}}$ and ${\widetilde{T}}$

Fig. 17

Flame E: LES averaged fields for major species

Fig. 18

Flame E: conditional means of T and major species calculated on f

Fig. 19

Flame E: conditional fluctuations of T and major species calculated on f

Fig. 20

Flame E: PDF of temperatures for test cases E, ER-Le1, ER-DD compared to the experimental data

The BI(T) is shown in Fig. 21. The ER-Le1 predicts less extinction across the domain, which better agrees with the experimental data downstream. Upstream instead, the EF-DD is still the best option, although clearly far from the expected extinction degree in the first section (x/D = 7.5), which should be lower than 0.9. In this region however it still works better than case E.

This paragraph showed how the extinction probability of the PDF of temperature could be better reproduced by the ESF simulation in the upstream sections, by including the effect of differential diffusion in the reduced chemistry manifold (ER-DD). However, preferential diffusion does not seem to play a relevant role further downstream, where simplified diffusion ER-Le1 would be sufficient to describe the flame dynamics.

Fig. 21

Flame E: flame burning index based on T

4.6 Influence of the Sub-grid Mixing

Before moving to flame F, a comparison with results previously presented in the literature is shown. In fact, it can be argued that the ESF-REDIM model (and the ESF model itself) might not be suitable to describe these flames. In this work, the micro-mixing term is closed by the IEM model, as originally proposed. It has been argued that using relative simply mixing models like IEM in LES should be sufficient, as only the sgs fluctuations should be described (Haworth 2010). Moreover, LES were seen to be less sensitive to the mixing model parameters compared to RANS (Cao and Pope 2005; Jones and Prasad 2010). It can be useful to compare the BI obtained for the ESF simulations with several RANS simulations available in the literature, all based on the Lagrangian particle method. The compared simulations are listed in Table 4. The empirical constant C$_{\phi }$ is replaced in this work by C$_d$ in Eq. 10 and it can influence the degree of sub-grid mixing applied via the micro-mixing term. It plays an important role especially in RANS, since the species distribution in the composition space is changed only through the influence of chemistry and micro-mixing. The results of Cao and Pope (2005) are chosen as comparison for the ESF-REDIM simulations. There, the influence of C$_{\phi }$ was thoroughly investigated by varying the coefficient between 1.0 and 3.0. In the end, C$_{\phi }$ = 1.5 allowed to better represent flame F, showing severe extinction. This reference case is labelled hereby as PR-ISAT (Particle-RANS using ISAT chemistry). The reader is pointed to the original paper for further details on the ISAT chemistry reduction method (Pope 1997). The second difference with the ESF-REDIM solver of this work is that the Eulerian Minimum Spanning Tree (EMST) was chosen as mixing model instead of the IEM, which delivers better results when applied to RANS (Mitarai et al. 2005). It is a more complicated particle interaction model to mimic the molecular diffusion process, the description of its detailed formulation is left to Subramaniam and Pope (1998). A second simulation is selected for comparison, where a RANS solver was combined with the REDIM (Yu et al. 2019). Similar to PR-ISAT, C$_{\phi }$ = 1.5 was assumed and the EMST model was chosen. This case is labelled as PR-EMST in Table 4. The same simulation was recently run using the IEM model with C$_{\phi }$ = 2 (PR-IEM), for a direct comparison with the ESF-REDIM model of this work. Finally, simulations E and ER of Sect. 4.4 are added to the investigation. Hereby, we only consider the REDIM with unity Lewis numbers, for a direct comparison with the listed simulations.

The BI for flame D is shown in Fig. 22. In section x/D = 7.5 both ESF formulations do not correctly predict the degree of local extinction, which might raise the question whether the ESF are suitable or not to describe the flame under this regime. However, there is an excellent agreement of all models in section x/D = 15, with the ER simulation matching the experimental data in x/D = 30. The solutions are more scattered at x/D = 45. Changing the mixing model in the RANS simulations from EMST to IEM does not seem to affect the results, at least for this flame regime. The BI for flame E is shown in Fig. 23. Since flame E presents more extinction than D, the selection of the mixing model assumes importance. From the plot it is difficult to isolate the best global model. While the ER matches very good sections 30 and 45, the RANS simulations using the EMST model better represent the local extinction in 7.5 and 15. Both ESF models predict again a flame too stable in the first section. Overall however it can be claimed that the ESF-REDIM model used in this work is suitable to correctly describe the global behavior of the flame and the major species. Room for improvement is given by the REDIM tabulation, where a third variable could improve the degree of local extinction.

Table 4 ESF vs RANS-TPDF

Fig. 22

Flame D: BI(T) for test cases of Table 4

Fig. 23

Flame E: BI(T) for test cases of Table 4

4.7 Sandia Flame F

The extension of the REDIM table to a third variable was necessary to correctly capture the degree of extinction of flame F. One can choose between two methods to include the third variable. The first possibility is to generate the REDIM directly for three generalized coordinates. Alternatively, one can build several REDIMs corresponding to a different gradient estimate for two generalized coordinates, using a different value of scalar dissipation rate at each time. For convenience, the second method was chosen for this work. The 2D-REDIM presented in the previous sections was built for different scalar dissipation rates, with $\chi$ becoming the third table parameter. This configuration is referred as 3D-REDIM from now on. A parallel investigation extended the REDIM to a second reaction progress variable instead (Yu et al. 2020). In both cases a significant improvement was obtained for the prediction of the degree of local extinction. Only the major results to confirm the validation of the ESF-REDIM solver are presented in this paragraph.

The REDIM variables Y$_{N2}$ and PV are transported using Eq. 17, while the field ${\widetilde{\chi }}$ is calculated using the formulation of Domingo et al. (2008). The latter includes the effect of the sub-grid fluctuations of the mixture fraction, calculated algebraically as $\widetilde{f^{''2}}= \varDelta ^2$ ($\nabla {\widetilde{f}}$ )$^2$. The lookup of the thermo-chemical state represented in Fig. 3 is therefore performed by parameters (N$_2^n$, PV$_2^n$, ${\widetilde{\chi }}$). The reader should notice that the value of ${\widetilde{\chi }}$ is not averaged from the $\chi ^n$ (see Eq. 13), but it is calculated directly from ${\widetilde{f}}$, and it is therefore kept constant between the $\xi _k^n$ realizations on each cell. This allows to select a single 2D-REDIM for each computational cell, based on a constant piece-wise interpolation of the local value of ${\widetilde{\chi }}$.

Table 5 shows the investigated set-ups. The first two are based on 2D-REDIMs like in the previous sections, in order to compare the effect of the transport (unity Lewis number or differential diffusion) on this flame. They are labelled respectively ER-Le-$\chi _1$ and ER-DD-$\chi _1$. The third configuration is based on six tables (the 3D-REDIM of this work) built for different scalar dissipation rates, using Le = 1 (ER-Le-$\chi _6$). A maximum value of $\chi$ = 504 s$^{-1}$ is included in the tables. Fig. 24 shows the unconditional means and RMS of mixture fraction and temperature in the first two columns, the conditional means of T and OH in the last two columns. It is evident how the predictions in x/D = 7.5, 15 considerably improved for simulation ER-Le-$\chi _6$. Most of the extinct states occur at x/D = 15, which are now correctly described by the 3D-REDIM. This manifold also leads to a better prediction of the temperature fluctuations in the first two sections. Re-ignition is correctly foreseen further downstream in x/D = 30, where all simulations provide a similar profile. The conditional means also report a very good agreement of ER-Le-$\chi _6$ with the experimental data in sections 7.5 and 15. Differential diffusion seems to gain importance at x/D = 30, since ER-DD-$\chi _1$ better describes the OH concentration. The same observation applies to H$_2$, not reported in the plots for the sake of clarity. The extension of ER-Le-$\chi _6$ to include differential diffusion is straightforward but this simulation will be discussed in a separate work.

Table 5 REDIM tables for flame F

Fig. 24

Flame F: unconditional means of f and T in the first two columns. Conditional means of T and OH calculated on f in the last two columns. Test cases from Table 5

Obtaining an accurate representation of flame F is not a trivial task. How well does the ESF-REDIM behave, compared to previous LES simulations of this flame available in the literature? The investigations of Jones and Prasad (2010), Ge et al. (2013) and Ferraro et al. (2019) using respectively a LES-ESF solver with finite rate chemistry, a sparse-Langrangian LES solver and a hybrid LES/RANS conditional transported PDF solver, are selected for comparison. Fig. 25 shows the comparison with ER-Le-$\chi _6$, for the same quantities of Fig. 24. The results taken from the above mentioned references did not always cover the same sections and quantities for a complete comparison. However, the profiles are sufficient to show how the ESF-REDIM can better capture the mean and conditional temperatures (second and third column) compared to the references, for x/D = 7.5 and 15. Overall, a stronger radial diffusion is observed in the sparse-Lagrangian simulation of Ge et al. (2013). At x/D = 30 the ESF-REDIM behaves similarly to the hybrid LES/RANS solver of Ferraro et al. (2019), although the mean ${\widetilde{T}}$ differs from the better prediction provided by the finite rate chemistry ESF simulation of Jones and Prasad (2010). The latter also confirms that the full chemistry ESF tends to produce a too stable flame in the first sections, as observed in Sect. 4.6. The hypothesis is raised, that by including the effect of the scalar dissipation rate in the REDIM table, the predictions could improve in the first sections, compared to using a finite rate chemistry ESF solver. On the other hand, neglecting this effect for flames D and E can still be an acceptable choice due to their low/moderate degree of local extinction, as seen in the previous paragraphs. The CO predictions of flame F show a similar behavior to Fig. 18, since a second reaction progress variable was not introduced in this work. A detailed investigation of the CO predictions is also left to a separate work.

To conclude, the ESF-REDIM solver extended to a third REDIM variable is also capable of correctly represent the degree of local extinction and the hydrogen-based chemistry of flame F, although the C-chemistry predictions shall be further addressed. However, room for improvement is seen on the tabulated chemistry side (REDIM parameters and its coupling with the ESF) rather than on the ESF solver itself. The validation of ESF-REDIM is considered successful for all investigated regimes.

Fig. 25

Flame F: unconditional means of f and T in the first two columns. Conditional means of T and OH calculated on f in the last two columns. ER-Le1-$\chi _6$ compared with previous LES of Ferraro et al. (2019); Ge et al. (2013); Jones and Prasad (2010)

5 Conclusions

This work attempted to considerably reduce the computational cost derived from LES simulations of turbulent reactive flows, which is particularly high if stochastic fields are transported to characterize the filtered PDF. Instead of solving the full chemical system for each stochastic field, a reduced chemistry model was used. The REDIM was chosen as tabulated chemistry table, as it was previously seen to behave well for methane/air turbulent flames in both premixed and non-premixed regime. The table was built on a uniform grid using physical coordinates, the inert species N$_{2}$ and a suitable reactive progress variable as linear combination of species mass fractions. Two tables were tested against the original stochastic fields formulation, one using unity Lewis numbers, the other including differential diffusion. The ESF-REDIM equations were implemented within an in-house OpenFOAM code. A constant parametrization matrix was used to project the ESF equations for the REDIM progress variables into the low-dimensional manifold. The Sandia flames D and E were selected as validation test cases for low and moderate extinction regimes. Two different studies on mesh convergence and number of stochastic fields were first conducted on the ESF-REDIM solver. A number of 8 stochastic fields was found to be the best trade-off between computational cost and solution accuracy, confirming the observations available in the literature. The ESF-REDIM solver was further compared to the original ESF solver with full chemistry. Mean and RMS values of mixture fraction, temperature and major species revealed a minor deviation between the simulations for both flames D and E. The conditional values of OH and H$_2$ however were strongly influenced by the choice of the transport model chosen in the REDIM. Better profiles were obtained when including differential diffusion in the table, although less conditional fluctuations were observed compared to the unity Lewis assumption. Overall, the full chemistry ESF solver provided a better approximation of the RMS values further downstream. A comparison of the BI against RANS simulations using Lagrangian particles showed that, although less extinction is predicted by both ESF solvers in section x/D = 7.5, the stochastic fields were able to capture the overall behaviour of both flames. When coupled with the REDIM reduced chemistry, the solver performance increased of about 81%, compared to a full chemistry ESF simulation. The validation of the solver for flame F, characterized by strong local extinction, required the extension of the REDIM table to a third progress variable, the scalar dissipation rate. The predictions were found to be in very good agreement with previous LES computations available in the literature and the experimental data, although differential diffusion was not included in the 3D manifold. Future work aims to further improve the CO concentrations, where experimental values are overpredicted. A 3D-REDIM with a second reactive progress variable to describe the slow chemistry of CO is currently under investigation. A detailed discussion of both 3D manifolds and the effect of differential diffusion applied to flame F is object of future work.