1 Introduction

Since Khas’minskii [1] used two white noise sources to stabilize a system, a wide range of works have appeared on stochastic stabilization problems. Arnold et al. [2] obtained stabilization results by using noisy terms in Stratonovich sense. Mao [3] presented a general theory on the stabilization by Brownian motion. Huang [4] further developed the general theory by Mao and revealed a more fundamental principle. Zhao et al. [5] established a new type of stability theorem which generalized local Lipschitz and one-sided linear growth conditions. From the considerations of reducing control cost and time, discontinuous controllers have been designed to stabilize a given system, such as discrete-time feedback control [6, 7], pinning control [8], impulsive control [9], adaptive control [10], intermittent control [11], etc. As for intermittent control, the control time is divided into periodic and aperiodic type. Periodically intermittent control has been studied by many authors, especially in synchronization problems. Zhang et al. [11] considered a periodic intermittent Brownian noise perturbation to stabilize and destabilize a given nonlinear system, the obtained criteria are different. Recently, Liu et al. [12] investigated the aperiodically intermittent control which has good performance to quasi-synchronize nonlinear coupled networks [13].

Motivated by the idea of stochastic stabilization via intermittent stochastic noise driven by Brownian motion, we are interested in analyzing whether the presence of intermittent stochastic perturbation driven by G-Brownian motion can stabilize a nonlinear system, since G-Brownian motion has powerful applications in modeling uncertainties. It is necessary to mention the pioneering work by Peng [14] who set up the G-framework. He pointed out that G-Brownian motion has independent increments and can be consistent with the classical Brownian motion in the sense of no volatility uncertainty. Many works have been done on G-Brownian motions [15–20], in particular existence and uniqueness theory for stochastic differential equations driven by G-Brownian motion (G-SDEs), as well as stability behavior and control theory, has been developed. Fei [16] investigated the exponential stability of paths for a G-SDE. Ren [19] designed a feedback control based on discrete-time observations to stabilize a G-SDE system. In [18], the aperiodically intermittent control has been embedded into the drift part, the authors obtained a set of piecewise Lyapunov-type conditions for the moment exponential stability theory.

As far as we know, there is hardly any literature about stochastic stabilization of deterministic systems via aperiodic intermittent stochastic perturbation driven by G-Brownian motion. In the present paper, we add two aperiodic intermittent stochastic perturbations driven by G-Brownian motion into a general deterministic nonlinear system. Those stochastic perturbations can stabilize the nonlinear system. The main contributions are summarized as follows:

  • The control itself is a stochastic perturbation driven by G-Brownian motion, which contains mean and volatility uncertainties, therefore, expands the general deterministic intermittent control and the stochastic intermittent control which is driven by classical Brownian motion.

  • The control time is aperiodically intermittent, which improves flexibility to time nodes and length. The acquired criteria consist of the work and rest width, we can control the steady rate autonomously by adjusting the work and rest width.

In Sect. 2, we establish the aperiodic intermittent stochastically perturbed system (2.2) driven by G-Brownian motion, present four notions, two lemmas, and one definition which will be used in the next section. Stabilization analysis is carried out in Sect. 3. In Sect. 4, we provide an application on stabilizing an SIS epidemic model by adding a special aperiodic intermittent stochastic perturbation driven by G-Brownian motion. This example clearly shows the power of stabilization by aperiodic intermittent stochastic perturbation driven by G-Brownian motion.

2 Preliminaries

Consider a nonlinear system

$$ dx(t)=f\bigl(t,x(t)\bigr)\,dt,\quad t\geq 0, $$
(2.1)

with initial value \(x(t_{0})=x_{0} \in R^{n}\). We add two aperiodic intermittent stochastic perturbations driven by G-Brownian motion to the nonlinear system, then the system becomes

$$ dx(t)=f\bigl(t,x(t)\bigr)\,dt+h\bigl(t,x(t)\bigr)\, d\langle B \rangle (t)+\sigma \bigl(t,x(t)\bigr)\,dB(t), $$
(2.2)

where

$$\begin{aligned}& h(t,x(t))= \textstyle\begin{cases} h_{1}(t,x(t)),& t \in [t_{i}^{h},t_{i}^{h}+c_{i}^{h}), \\ 0,& t \in [t_{i}^{h}+c_{i}^{h},t_{i+1}^{h}), \end{cases}\displaystyle \end{aligned}$$
(2.3)
$$\begin{aligned}& \sigma (t,x(t))= \textstyle\begin{cases} \sigma _{1}(t,x(t)),& t \in [t_{j}^{\sigma },t_{j}^{\sigma }+c_{j}^{ \sigma }), \\ 0,& t \in [t_{j}^{\sigma }+c_{j}^{\sigma },t_{j+1}^{\sigma }), \end{cases}\displaystyle \end{aligned}$$
(2.4)

with \(i ,j \in N\). Here

$$ f,h_{1},\sigma _{1}:[t_{0},\infty )\times R^{n}\rightarrow R^{n}\quad \text{and}\quad f,h_{1},\sigma _{1} \in M_{G}^{2}(0,T). $$

Also \(B(t)\) is a one-dimensional G-Brownian motion with \(G(a)=\frac{1}{2} \hat{\mathbb{E}}[aB_{1}^{2}]=\frac{1}{2}( \bar{\delta }^{2} a^{+}-\underline{\delta }^{2} a^{-})\), where \(\bar{\delta }^{2}=\hat{\mathbb{E}}[B_{1}^{2}]\), \(\underline{\delta }^{2}=- \hat{\mathbb{E}}[-B_{1}^{2}]\); \(\langle B \rangle (t)\) is the quadratic variation process of the G-Brownian motion, which is also a continuous process with independent and stationary distribution, thus can still be regarded as a Brownian motion. Under the perturbation of h type, the time span \([t_{i}^{h},t_{i+1}^{h})\) contains the work time \([t_{i}^{h},t_{i}^{h}+c_{i}^{h})\) and the rest time \([t_{i}^{h}+c_{i}^{h},t_{i+1}^{h})\) as shown in Fig. 1, \(c_{i}^{h}\) denotes the ith h-type noise width. Similarly, the time span \([t_{i}^{\sigma },t_{i+1}^{\sigma })\) contains the work time \([t_{i}^{\sigma },t_{i}^{\sigma }+c_{i}^{\sigma })\) and the rest time \([t_{i}^{ \sigma }+c_{i}^{\sigma },t_{i+1}^{\sigma })\), \(c_{i}^{\sigma }\) denote the ith σ-type noise width. Naturally, those two noise widths satisfy \(0\leq c_{i}^{h} \leq t_{i+1}^{h}- t_{i}^{h}; 0 \leq c_{i}^{\sigma } \leq t_{i+1}^{\sigma }-t_{i}^{\sigma }\). For the aperiodically intermittent perturbation strategy, the start time and the noise width might be different, but the total perturbation time ratio should be fixed in the long term. Mathematically, we assume there exist two positive scalars \(\omega _{h}\), \(\omega _{\sigma }\) such that the above time nodes satisfy the following assumptions:

$$ \begin{aligned} &\frac{\sum_{i=0}^{n}c_{i}^{h}}{t_{n+1}^{h}-t_{0}}=\omega _{h}, \\ &\frac{\sum_{j=0}^{n}c_{j}^{\sigma }}{t_{n+1}^{\sigma }-t_{0}}=\omega _{ \sigma }. \end{aligned} $$
(2.5)

We call \(\omega _{h}\) the h-type perturbation time ratio and \(\omega _{\sigma }\) the σ-type perturbation time ratio.

Figure 1
figure 1

Sketch of the aperiodically intermittent control strategy

Full size image

Throughout this paper, \(f_{1}\), \(h_{1}\), and \(\sigma _{1}\) satisfy the local Lipschitz condition and one-sided growth condition \(x^{T} f(t,x)+x^{T} h_{1}(t,x)+\frac{1}{2}\sigma _{1}^{2}(t,x)\leq K_{0} \| x \|^{2} \), where \(K_{0} >0\). Clearly, \(h(t,x)\) and \(\sigma (t,x)\) also satisfy the local Lipschits condition and one-sided growth condition. Moreover, we assume \(f(t,0)\equiv 0\), \(h(t,0)\equiv 0\), \(\sigma (t,0)\equiv 0\) for stochastic stability analysis, which guarantees the existence of a trivial solution \(x(t;t_{0},0)\equiv 0\).

Letting \(V \in C^{1,2} ([t_{0},\infty )\times R^{n};R^{+})\), we introduce some new notations as follows:

$$\begin{aligned}& F(t,x)=\frac{V_{t}(t,x)+V_{x}(t,x)f(t,x)}{V(t,x)}, \\& H_{1}(t,x)=\frac{\sigma ^{T}(t,x)V_{xx}(t,x)\sigma (t,x)}{2V(t,x)}, \\& H_{2}(t,x)=\frac{V_{x}(t,x)h(t,x)}{V(t,x)}, \\& R(t,x)=\frac{[V_{x}(t,x)\sigma (t,x)]^{2}}{V^{2}(t,x)}. \end{aligned}$$

Definition 2.1

The trivial solution of the intermittent G-stochastic system (2.2) in \(R^{n}\) is said to be quasi-sure exponentially stable, if for any \(x_{0}\neq 0\) and \(t\geq t_{0}\),

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t;t_{0},x_{0}) \bigr\Vert < 0 \quad \text{q.s.} $$

Lemma 2.1

Under the conditions imposed above, system (2.2) has a unique global solution \(x(t;t_{0},x_{0})\). The solution obeys

$$ P\bigl(x(t;t_{0},x_{0}) \neq 0 \textit{ for } t \geq 0 \bigr)=1, \quad \textit{for all } x_{0} \neq 0. $$

Proof

The global existence of a unique solution follows from Theorem 4.5 in Li et al. [21], the nonzero property follows from the same method as in Mao [3] (see Lemma 3.2, p. 120). □

Lemma 2.2

Let \(N(t)\) be G-Ito stochastic integral, \(\tau _{n}\) be a sequence of positive numbers with \(\tau _{n} \rightarrow \infty \). Then for all \(\omega \in \Omega \) there exists a random integer \(n_{0}(\omega )\) such that for all \(n \geq n_{0}\),

$$ N(t)\leq \frac{\gamma _{n}}{2}\bigl\langle N(t)\bigr\rangle + \frac{2}{\gamma _{n}}\log (n) \quad \textit{on } t_{0} \leq t \leq \tau _{n}. $$

Proof

According to Lemma 2.6 in Fei et al. [16],

$$ N(t)\leq \frac{\varepsilon }{2}\bigl\langle N(t)\bigr\rangle + \frac{\theta }{\varepsilon }\log (n), $$

We choose \(\gamma _{n}=\varepsilon \), \(\theta =2\), \(g(n)=n\), and the conclusion of Lemma 2.2 can be obtained naturally. □

Remark 2.1

If \(t_{i+1}-t_{i}=T\), \(c_{i}=\delta \) for all \(i \in N\), and \(\bar{\delta }=\underline{\delta }\), then the system (2.2) becomes a periodic intermittent system. This agrees with system 1 in Zhang et al. [11]. Our results can be regarded as a generalization of Zhang et al. [11].

3 Main results

In this section, we will establish the quasi-sure exponential stability theorem based on aperiodic intermittent stochastic noise driven by G-Brownian motions. Since \(x_{0}=0\) implies \(x(t;t_{0},0)=0\), we only need to concentrate on \(x_{0} \neq 0\).

Theorem 3.1

(Stabilization theorem)

Assume that there exists a function \(V \in C^{1,2} ([t_{0}, \infty )\times R^{n};R^{+})\), and constants \(p>0\), \(c_{1}>0\), \(c_{3} \geq 0\), \(c_{4} \geq 0\), \(c_{5}\geq 0\), \(c_{2}\in R \) such that for \(t \geq t_{0}\),

$$\begin{aligned} (\mathrm{i})&\quad c_{1} \Vert x \Vert ^{p} \leq V(t,x), \\ (\mathrm{ii})&\quad V_{t}(t,x)+V_{x}(t,x)f(t,x) \leq c_{2}V(t,x), \\ (\mathrm{iii})&\quad \sigma _{1}^{T}(t,x)V_{xx}(t,x) \sigma _{1}(t,x) \leq c_{3}V(t,x), \\ (\mathrm{iv})&\quad V_{x}(t,x)h_{1}(t,x) \leq c_{4}V(t,x), \\ (\mathrm{v})&\quad \bigl\Vert V_{x}(t,x)\sigma _{1}(t,x) \bigr\Vert ^{2} \geq c_{5}V^{2}(t,x). \end{aligned}$$

Then the solution \(x(t;t_{0},x_{0})\) satisfies

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t;t_{0},x_{0}) \bigr\Vert \leq - \frac{c_{5} \omega _{\sigma } \underline{\delta }^{2}-c_{3} \omega _{h}\bar{\delta }^{2}-2c_{4} \omega _{\sigma } \bar{\delta }^{2}-2c_{2}}{2p}\quad \textit{q.s.} $$
(3.1)

In particular, if \(c_{5} \omega _{\sigma } \underline{\delta }^{2}-c_{3} \omega _{\sigma } \bar{\delta }^{2}-2c_{4} \omega _{h} \bar{\delta }^{2}-2c_{2}>0\), then the solution \(x(t;t_{0},x_{0})\) of system (2.2) is quasi-sure exponentially stable.

Proof

Fix any \(x_{0}\neq 0\) and write \(x(t;t_{0},x_{0})=x(t)\). By Lemma 2.1, \(x(t)\neq 0\) for all \(t\geq t_{0}\) q.s. Applying Itô’s formula, for \(t\geq t_{0}\), we get

$$\begin{aligned} \begin{aligned} \log V\bigl(t,x(t)\bigr)={}&\log V(t_{0},x_{0})+ \int _{t_{0}}^{t}F\bigl(s,x(s)\bigr)\,ds + \int _{t_{0}}^{t}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ &{}+ \int _{t_{0}}^{t}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) -\frac{1}{2} \int _{t_{0}}^{t}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s)+N(t), \end{aligned} \end{aligned}$$
(3.2)

where

$$ N(t)= \int _{t_{0}}^{t}\frac{V_{x}(s,x(s))\sigma (s,x(s))}{V(s,x(s))}\, d B(s) $$

is a continuous martingale. By Lemma 2.2, taking an arbitrary \(\varepsilon \in (0,1)\), for all \(\omega \in \Omega\) q.s., there exists an integer \(n_{0}(\omega ,P) \) such that if \(n\geq n_{0}\), then

$$ N(t)\leq \frac{2}{\varepsilon }\log (n)+\frac{\varepsilon }{2} \int _{t_{0}}^{t}R\bigl(s,x(s)\bigr)\, d \langle B \rangle (s) $$

holds for all \(t_{0}\leq t\leq t_{0}+n\). Substituting this into (3.2), we have

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+ \int _{t_{0}}^{t}F\bigl(s,x(s)\bigr)\,ds+ \int _{t_{0}}^{t}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ &{}+ \int _{t_{0}}^{t}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s)-\frac{1}{2}(1-\varepsilon ) \int _{t_{0}}^{t}R\bigl(s,x(s)\bigr)\, d\langle B \rangle (s)+\frac{2}{\varepsilon }\log (n). \end{aligned}$$

Then we consider t in a different time interval. Obviously, there exist two positive integers \(n_{1}\), \(n_{2}\) such that \(t \in [t_{n_{1}}^{h},t_{n_{1}+1}^{h}] \cap [t_{n_{2}}^{\sigma },t_{n_{2}+1}^{ \sigma }]\). Depending on h- and σ-type noise widths, there are four possible cases which need to be discussed.

Case 1. For all \(\omega \in \Omega \) and \(n>n_{0}\), \(t\in [t_{n_{1}}^{h},t_{n_{1}}^{h}+c_{n_{1}}^{h}) \cap [t_{n_{2}}^{ \sigma },t_{n_{2}}^{\sigma }+c_{n_{2}}^{\sigma })\), we have

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+ \int _{t_{0}}^{t}F\bigl(s,x(s)\bigr)\,ds \\ & {}+ \int _{t_{0}}^{t_{0}^{\sigma }+c_{0}^{\sigma }}H_{1}\bigl(s,x(s) \bigr)\, d\langle B \rangle (s)+ \int _{t_{0}^{\sigma }+c_{0}^{\sigma }}^{t_{1}^{\sigma }}H_{1}\bigl(s,x(s) \bigr)\, d \langle B\rangle (s) \\ &{}+\cdots + \int _{t_{n_{2}}^{\sigma }}^{t}H_{1}\bigl(s,x(s) \bigr)\, d \langle B\rangle (s) \\ & {}+ \int _{t_{0}}^{t_{0}^{h}+c_{0}^{h}}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s)+ \int _{t_{0}^{h}+c_{0}^{h}}^{t_{1}^{h}}H_{2}\bigl(s,x(s) \bigr)\,d\langle B \rangle (s) \\ &{}+\cdots + \int _{t_{n_{1}}^{h}}^{t}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ & {}-\frac{1}{2}(1-\varepsilon ) \biggl[ \int _{t_{0}}^{t_{0}^{\sigma }+c_{0}^{ \sigma }}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s)+ \int _{t_{0}^{\sigma }+c_{0}^{ \sigma }}^{t_{1}^{\sigma }}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \\ & {}+\cdots + \int _{t_{n_{2}}^{\sigma }}^{t}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \biggr]+\frac{2}{\varepsilon }\log (n). \end{aligned}$$

Substituting conditions (ii), (iii), (iv), and (v) into the above equation, we obtain

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{1}{2}c_{3} \bar{\delta }^{2}\bigl[c_{0}^{\sigma }+0+\cdots + \bigl(t-t_{n_{2}}^{\sigma }\bigr)\bigr] \\ &{}+c_{4} \bar{\delta }^{2}\bigl[c_{0}^{h}+0+ \cdots +\bigl(t-t_{n_{1}}^{h}\bigr)\bigr] \\ &{}- \frac{1}{2}(1-\varepsilon )c_{5} \underline{\delta }^{2} \bigl[c_{0}^{ \sigma }+0+\cdots + \bigl(t-t_{n_{2}}^{\sigma }\bigr)\bigr]+\frac{2}{\varepsilon }\log (n) \\ \leq &\log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{2}{\varepsilon } \log (n) \\ &{}+\frac{1}{2} c_{3} \bar{\delta }^{2} \sum _{i=0}^{n_{2}} c_{i}^{ \sigma }+c_{4} \bar{\delta }^{2}\sum_{i=0}^{n_{1}} c_{i}^{h}- \frac{1}{2}(1-\varepsilon )c_{5} \underline{\delta }^{2}\sum _{i=0}^{n_{2}-1} c_{i}^{\sigma }, \end{aligned}$$

which implies that

$$\begin{aligned} \frac{1}{t}\log V\bigl(t,x(t)\bigr) \leq& \frac{1}{t} \biggl[ \log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{2}{\varepsilon }\log (n) \biggr] \\ &{}+ \frac{c_{3} \bar{\delta }^{2} \sum_{i=0}^{n_{2}} c_{i}^{\sigma }}{2t_{n_{2}}^{\sigma }} + \frac{c_{4} \bar{\delta }^{2}\sum_{i=0}^{n_{1}} c_{i}^{h}}{2t_{n_{1}}^{h}} - \frac{(1-\varepsilon )c_{5} \underline{\delta }^{2}\sum_{i=0}^{n_{2}-1} c_{i}^{\sigma }}{t_{n_{2}+1}}. \end{aligned}$$

By Eq. (2.5), we deduce

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log V\bigl(t,x(t)\bigr) \leq c_{2}+ \frac{c_{3} \omega _{\sigma }\bar{\delta }^{2} }{2} +c_{4} \omega _{h} \bar{\delta }^{2}-\frac{1}{2}(1- \varepsilon )c_{5} \omega _{\sigma } \underline{\delta }^{2}. $$

Using condition (i) and letting \(\varepsilon \rightarrow 0\), it follows that

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t,t_{0},x_{0}) \bigr\Vert \leq - \frac{c_{5} \omega _{\sigma } \underline{\delta }^{2}-c_{3} \omega _{h}\bar{\delta }^{2}-2c_{4} \omega _{\sigma } \bar{\delta }^{2}-2c_{2}}{2p} \quad \text{q.s.} $$

Case 2. For all \(\omega \in \Omega \) and \(n>n_{0}\), \(t\in [t_{n_{1}}^{h},t_{n_{1}}^{h}+c_{n_{1}}^{h}) \cap [t_{n_{2}}^{ \sigma }+c_{n_{2}}^{\sigma },t_{n_{2}+1}^{\sigma })\), the integral interval length of \(\sigma (t,x(t))\) has changed compared to Case 1. Hence we have

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+ \int _{t_{0}}^{t}F\bigl(s,x(s)\bigr)\,ds \\ &{}+ \int _{t_{0}}^{t_{0}^{\sigma }+c_{0}^{h}}H_{1}\bigl(s,x(s) \bigr)\,d\langle B \rangle (s) + \int _{t_{0}^{h}+c_{0}^{\sigma }}^{t_{1}^{\sigma }}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ &{}+\cdots + \int _{t_{n_{2}}^{\sigma }}^{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s)+ \int _{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}^{t}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ &{}+ \int _{t_{0}}^{t_{0}^{h}+c_{0}^{h}}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s)+ \int _{t_{0}^{h}+c_{0}^{h}}^{t_{1}^{\sigma }}H_{2}\bigl(s,x(s) \bigr)\,d\langle B \rangle (s) \\ &{}+\cdots + \int _{t_{n_{1}}^{h}}^{t}H_{2}\bigl(s,x(s) \bigr)\,d\langle B \rangle (s) \\ &{}-\frac{1}{2}(1-\varepsilon ) \biggl[ \int _{t_{0}}^{t_{0}^{\sigma }+c_{0}^{ \sigma }}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s)+ \int _{t_{0}^{\sigma }+c_{0}^{ \sigma }}^{t_{1}^{\sigma }} R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \\ &{}+\cdots + \int _{t_{n_{2}}^{\sigma }}^{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \\ &{}+ \int _{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}^{t}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \biggr]+ \frac{2}{\varepsilon }\log (n). \end{aligned}$$

By conditions (ii), (iii), (iv), and (v), we obtain

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{1}{2}c_{3} \bar{\delta }^{2}\bigl[c_{0}^{\sigma }+0+\cdots +c_{n_{2}}^{ \sigma }\bigr] \\ &{}+c_{4} \bar{\delta }^{2}\bigl[c_{0}^{h}+0+\cdots + \bigl(t-t_{n_{1}}^{h}\bigr)\bigr] \\ &{}-\frac{1}{2}(1-\varepsilon )c_{5} \underline{\delta }^{2} \bigl[c_{0}^{ \sigma }+0+\cdots + \bigl(t-t_{n_{1}}^{h}\bigr)\bigr]+ \frac{2}{\varepsilon }\log (n) \\ \leq &\log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{2}{\varepsilon } \log (n) \\ &{}+\frac{1}{2} c_{3} \bar{\delta }^{2} \sum _{i=0}^{n_{2}} c_{i}^{ \sigma }+c_{4} \bar{\delta }^{2}\sum_{i=0}^{n_{1}} c_{i}^{h}- \frac{1}{2}(1-\varepsilon )c_{5} \underline{\delta }^{2}\sum _{i=0}^{n_{2}} c_{i}^{\sigma }. \end{aligned}$$

Using the same method as in Case 1, we conclude

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t,t_{0},x_{0}) \bigr\Vert \leq - \frac{c_{5} \omega _{\sigma } \underline{\delta }^{2}-c_{3} \omega _{h}\bar{\delta }^{2}-2c_{4} \omega _{\sigma } \bar{\delta }^{2}-2c_{2}}{2p} \quad \text{q.s.} $$

Case 3. For all \(\omega \in \Omega \) and \(n>n_{0}\), \(t\in [t_{n_{1}}^{h}+c_{n_{1}}^{h},t_{n_{1}+1}^{h}) \cap [t_{n_{2}}^{ \sigma },t_{n_{2}}^{\sigma }+c_{n_{2}}^{\sigma })\) for all \(\omega \in \Omega \) and \(n>n_{0}\). This case is similar to Case 1 except for the additional time interval \([t_{n_{1}}^{h}+c_{n_{1}}^{h},t_{n_{1}+1}^{h})\) of \(h(t,x(t))\). Since \(h(t,x(t))=0\), \(t \in [t_{n_{1}}^{h}+c_{n_{1}}^{h},t_{n_{1}+1}^{h})\), \(\log V(t,x(t))\) can be written as

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{1}{2}c_{3} \bar{\delta }^{2}\bigl[c_{0}^{\sigma }+0+\cdots + \bigl(t-t_{n_{2}}^{ \sigma }\bigr)\bigr] \\ &{}+c_{4} \bar{\delta }^{2}\bigl[c_{0}^{h}+0+ \cdots +c_{n_{1}}^{h}\bigr]- \frac{1}{2}(1- \varepsilon )c_{5} \underline{\delta }^{2} \bigl[c_{0}^{ \sigma }+0+\cdots +\bigl(t-t_{n_{2}}^{\sigma } \bigr)\bigr] \\ &{}+ \frac{2}{\varepsilon }\log (n) \\ \leq &\log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{2}{\varepsilon } \log (n) \\ &{}+\frac{1}{2} c_{3} \bar{\delta }^{2} \sum _{i=0}^{n_{2}} c_{i}^{ \sigma }+c_{4} \bar{\delta }^{2}\sum_{i=0}^{n_{1}} c_{i}^{h}- \frac{1}{2}(1-\varepsilon )c_{5} \underline{\delta }^{2}\sum _{i=0}^{n_{2}-1} c_{i}^{\sigma }. \end{aligned}$$

Together with conditions (i)–(v), it follows that

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t,t_{0},x_{0}) \bigr\Vert \leq - \frac{c_{5}(1-\varepsilon ) \omega _{\sigma } \underline{\delta }^{2}-c_{3} \omega _{h}\bar{\delta }^{2}-2c_{4} \omega _{\sigma } \bar{\delta }^{2}-2c_{2}}{2p}\quad \text{q.s.} $$

As \(\varepsilon \rightarrow 0\), the following inequality holds:

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t,t_{0},x_{0}) \bigr\Vert \leq - \frac{c_{5} \omega _{\sigma } \underline{\delta }^{2}-c_{3} \omega _{h}\bar{\delta }^{2}-2c_{4} \omega _{\sigma } \bar{\delta }^{2}-2c_{2}}{2p} \quad \text{q.s.} $$

Case 4. For all \(\omega \in \Omega \) and \(n>n_{0}\), \(t\in [t_{n_{1}}^{h}+c_{n_{1}}^{h},t_{n_{1}+1}^{h}) \cup [t_{n_{2}}^{ \sigma }+c_{n_{2}}^{\sigma },t_{n_{2}+1}^{\sigma })\). This case is similar to Case 2 except for the time interval of \(h(t,x(t))\). This time \(\log V(t,x(t))\) can be divided into

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+ \int _{t_{0}}^{t}F\bigl(s,x(s)\bigr)\,ds \\ &{}+ \int _{t_{0}}^{t_{0}^{\sigma }+c_{0}^{h}}H_{1}\bigl(s,x(s) \bigr)\,d\langle B \rangle (s)+ \int _{t_{0}^{h}+c_{0}^{\sigma }}^{t_{1}^{\sigma }}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ &{}+\cdots + \int _{t_{n_{2}}^{\sigma }}^{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) + \int _{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}^{t}H_{1}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ &{}+ \int _{t_{0}}^{t_{0}^{h}+c_{0}^{h}}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s)+ \int _{t_{0}^{h}+c_{0}^{h}}^{t_{1}^{h}}H_{2}\bigl(s,x(s) \bigr)\,d\langle B \rangle (s) \\ &{}+\cdots + \int _{t_{n_{1}}^{h}}^{t_{n_{1}}^{h}+c_{n_{1}}^{h}}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s)+ \int _{t_{n_{1}}^{h}+c_{n_{1}}^{h}}^{t}H_{2}\bigl(s,x(s) \bigr)\,d\langle B\rangle (s) \\ &{}-\frac{1}{2}(1-\varepsilon ) \biggl[ \int _{t_{0}}^{t_{0}^{\sigma }+c_{0}^{ \sigma }}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s)+ \int _{t_{0}^{\sigma }+c_{0}^{ \sigma }}^{t_{1}^{\sigma }}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \\ &{}+\cdots + \int _{t_{n_{2}}^{\sigma }}^{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \\ &{}+ \int _{t_{n_{2}}^{\sigma }+c_{n_{2}}^{ \sigma }}^{t}R\bigl(s,x(s)\bigr)\,d\langle B \rangle (s) \biggr] + \frac{2}{\varepsilon }\log (n). \end{aligned}$$

The latter implies that

$$\begin{aligned} \log V\bigl(t,x(t)\bigr) =&\log V(t_{0},x_{0})+c_{2} (t-t_{0}) \\ &{}+\frac{1}{2}c_{3} \bar{\delta }^{2} \bigl[c_{0}^{\sigma }+0+\cdots +c_{n_{2}}^{ \sigma }+0 \bigr] \\ &{}+c_{4} \bar{\delta }^{2}\bigl[c_{0}^{h}+0+ \cdots +c_{n_{1}}^{h}+0\bigr] \\ &{}-\frac{1}{2}(1-\varepsilon )c_{5} \underline{\delta }^{2} \bigl[c_{0}^{ \sigma }+0+\cdots +c_{n_{2}}^{\sigma }+0\bigr]+\frac{2}{\varepsilon }\log (n) \\ =&\log V(t_{0},x_{0})+c_{2} (t-t_{0})+\frac{2}{\varepsilon }\log (n) \\ &{}+\frac{1}{2} c_{3} \bar{\delta }^{2} \sum _{i=0}^{n_{2}} c_{i}^{ \sigma }+c_{4} \bar{\delta }^{2}\sum_{i=0}^{n_{1}} c_{i}^{h}- \frac{1}{2}(1-\varepsilon )c_{5} \underline{\delta }^{2}\sum _{i=0}^{n_{2}} c_{i}^{\sigma }. \end{aligned}$$

Thus we claim

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t,t_{0},x_{0}) \bigr\Vert \leq - \frac{c_{5} \omega _{\sigma } \underline{\delta }^{2}-c_{3} \omega _{h}\bar{\delta }^{2}-2c_{4} \omega _{\sigma } \bar{\delta }^{2}-2c_{2}}{2p}\quad \text{q.s.} $$

From the above four cases, for all \(\omega \in \Omega \) and \(t \in [t_{n_{1}}^{h},t_{n_{1}+1}^{h}]\cap [t_{n_{2}}^{\sigma },t_{n_{2}+1}^{ \sigma }]\), the following inequality always holds

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t,t_{0},x_{0}) \bigr\Vert \leq - \frac{c_{5} \omega _{1} \underline{\delta }^{2}-c_{3} \omega _{1}\bar{\delta }^{2}-2c_{4} \omega _{2}\bar{\delta }^{2}-2c_{2}}{2p}\quad \text{q.s.} $$

The proof is complete. □

Remark 3.1

If \(V(t,x)=\|x\|^{2}\), conditions (i)–(v) in Theorem 3.1 become: (i) \(x^{T} f(t, x) \leq s_{1}\|x\|^{2}\); (ii) \(\|\sigma _{1}(t, x) \| \leq s _{2}\|x\|\); (iii) \(x^{T} h_{1}(t, x) \leq s_{3}\|x\|^{2}\); and (iv) \(\|x^{T}\sigma _{1}(t,x)\| \geq s_{4}\|x\|\). Then \(x(t; t_{0},x_{0})\) satisfies

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert x(t; t_{0},x_{0}) \bigr\Vert \leq -\bigl(s_{4}^{2} \omega _{1} \underline{\delta }^{2}-0.5 s_{2} ^{2} \omega _{1}\bar{\delta }^{2}-s_{3} \omega _{2} \bar{\delta }^{2}-s_{1}\bigr)\quad \text{q.s.} $$
(3.3)

In particular, if \(s_{4}^{2} \omega _{1} \underline{\delta }^{2}-0.5 s_{2} ^{2}\omega _{1} \bar{\delta }^{2}-s_{3} \omega _{2} \bar{\delta }^{2}-s_{1}>0\), the solution \(x(t;t_{0},x_{0})\) of system (2.2) is quasi-sure exponentially stale.

Remark 3.2

If \(h_{1}(t,x)=0\), \(\sigma _{1}(t,x)=g_{1}(t,x)\), and \(\bar{\delta }=\underline{\delta }=1\), system (2.2) becomes an intermittently stochastically perturbed system driven by Brownian motion. More specially, if \(t_{j+1}^{\sigma }-t_{j}^{\sigma }=T\) and \(c_{j}^{\sigma }=\delta \) for all \(j \in N\), system (2.2) becomes a periodic intermittent system. Equation (3.1) becomes

$$ \limsup_{t\rightarrow \infty } \frac{1}{t}\log \bigl\Vert x(t; t_{0},x_{0}) \bigr\Vert \leq -\frac{(c_{5} -c_{3} ) \frac{\delta }{T}-2c_{2}}{2p}\quad \text{a.s.} $$

This agrees with Theorem 1 in Zhang et al. [11]. Our results can be regarded as a generalization of Zhang et al. [11].

Remark 3.3

According to Eq. (3.1), the Lyapunov exponential of \(x(t;t_{0},x_{0})\) depends on perturbation time ratios \(\omega _{h}\), \(\omega _{\sigma }\) and volatility uncertainties \(\underline{\delta }\), δ̄. Thus h-type perturbation’s time ratio and volatility uncertainty \(\underline{\delta }\) can speed up exponential convergence, if the control strategy is designed based on our theoretical results.

4 Application to an epidemic system

In this section, we study an application of our theoretical results in Sect. 3 on SIS epidemic model. A classical deterministic SIS epidemic model partitions the host population into the susceptible compartment S and the infectious compartment I. Ordinary differential equations (ODEs) that describe the change of size in compartments S and I can be written as

$$ \begin{aligned} &\frac{{d}S}{{d}t}=A-d S+\mu I - \beta SI, \\ &\frac{{d}I}{{d}t}=\beta SI-d I-\mu I. \end{aligned} $$
(4.1)

Since \(S,I \geq 0\) and \(S+I=\frac{A}{d}\), the above two ODEs can be rewritten as

$$ \frac{{d}I}{{d}t}=\beta \biggl( \frac{A}{d}-I\biggr)I-d I-\mu I. $$

The dynamics of the SIS epidemic model is completely determined by the basic reproduction number

$$ R_{0} =\frac{\beta A}{d(d+\mu )}. $$

If \(R_{0} \leq 1\), the disease-free equilibrium \(P_{0} = (\frac{A}{d},0,0)\) is globally asymptotically stable and the disease always dies out; if \(R_{0} > 1\), then \(P_{0}\) is unstable and an endemic equilibrium exists which means the disease will persist. Now, we aim to control the number of infectious even if \(R_{0}>1\).

Adding two aperiodic intermittently stochastic perturbations \(h SI \, {d}\langle B\rangle (t)\), \(\sigma I \,{d}B(t)\) to SIS epidemic model, it becomes

$$ dI(t)= \biggl[ \beta \biggl(\frac{A}{d}-I\biggr)I-d I-\mu I \biggr]\,dt+h\bigl(t,I(t)\bigr)\, d \langle B\rangle (t)+\sigma \bigl(t,I(t)\bigr)\,dB(t), $$
(4.2)

where

$$\begin{aligned}& h\bigl(t,x(t)\bigr)= \textstyle\begin{cases} h SI,& t \in [t_{i}^{h},t_{i}^{h}+c_{i}^{h}), \\ 0,& t \in [t_{i}^{h}+c_{i}^{h},t_{i+1}^{h}), \end{cases}\displaystyle \\& \sigma \bigl(t,x(t)\bigr)= \textstyle\begin{cases} \sigma I,& t \in [t_{j}^{\sigma },t_{j}^{\sigma }+c_{j}^{\sigma }), \\ 0,& t \in [t_{j}^{\sigma }+c_{j}^{\sigma },t_{j+1}^{\sigma }), \end{cases}\displaystyle \end{aligned}$$

with \(i ,j \in N\). Letting \(V(t,I)=I\) and verifying conditions in Theorem 3.1, we obtain

$$\begin{aligned}& V(t,I)=I\geq \Vert I \Vert ^{1}; \\& V_{I}(t,I)f(t,I)=\beta \biggl(\frac{A}{d}-I\biggr)I-d I-\mu I\leq \biggl( \frac{\beta A}{d} -d-\mu \biggr)I=\biggl( \frac{\beta A}{d} -d-\mu \biggr)V(t,I); \\& \sigma _{1}^{T}(t,I)V_{II}(t,I)\sigma _{1}(t,I)=0\leq 0; \\& V_{I}(t,I)h_{1}(t,I)=h SI \leq \frac{hA}{d}I \leq \frac{hA}{d}V(t,I); \\& \bigl\Vert V_{I}(t,I)\sigma _{1}(t,I) \bigr\Vert ^{2}=\sigma ^{2}I^{2} \geq \sigma ^{2} V^{2}(t,I). \end{aligned}$$

Comparing with conditions (ii)–(v), we obtain \(p=1\), \(c_{1}=1\), \(c_{2}=\frac{\beta A}{d} -d-\mu \), \(c_{3}=0\), \(c_{4}= \frac{hA}{d}\), \(c_{5}=\sigma ^{2}\). Thus the infectious part of the population \(I(t)\) satisfies

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\log \bigl\Vert I(t) \bigr\Vert \leq \frac{\beta A}{d} -d-\mu + \frac{hA\omega _{2} \bar{\delta }^{2}}{d}- \frac{ \omega _{1} \sigma ^{2}\underline{\delta }^{2}}{2}\quad \text{q.s.} $$
(4.3)

If \(R_{0}>1\), which means \(\frac{\beta A}{d} -d-\mu >0\), the Lyapunov exponent of \(I(t)\) would also be lower than 0 by adjusting the perturbation parameter \(\omega _{1}\), σ, \(\underline{\delta }\). This implies that the disease can be stabilized by intermittent stochastic perturbation.

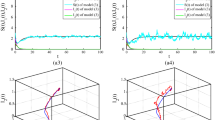
Let us provide a numerical example for the stochastic perturbed SIS epidemic model (4.2) to substantiate the analytic findings. For system (4.2), setting \(A=100\), \(\beta =0.0002\), \(d=0.1\), \(\mu =0.05\) and \(h=0.1\), \(\sigma =0.5\), \(\bar{\delta }=2\), \(\underline{\delta }=1\), \(\omega _{2}=0.1\), we can calculate \(R_{0}=\frac{4}{3}>1\), the endemic equilibrium \(E^{*}\) is \((750,250)\), which means \(I(t)\) tends to 250, the disease will persist. To stabilize the deterministic SIS epidemic model (4.1), we choose different perturbation intensities \(\omega _{1}\) to compare the stabilization effects. Figure 2 shows clearly that the bigger the h-type perturbation intensity \(\omega _{1}\), the faster the steady speed.

Figure 2
figure 2

A single path of the solution

Full size image

5 Conclusions

In this paper, stochastic stabilization of a nonlinear system via aperiodic intermittent stochastic perturbation driven by G-Brownian motion has been investigated. We have derived sufficient conditions for quasi-sure exponential stability for the perturbed system (2.2), the criterion involves intermittent control strength. As an application, we have designed two special aperiodic intermittent stochastic perturbations to a deterministic SIS epidemic model, which would stabilize the epidemic system even though \(R_{0}>1\). Generally, we conclude that an aperiodic intermittent stochastic perturbation driven by G-Brownian motion can stabilize a nonlinear system.

Some interesting topics deserve further investigations. It is also interesting to consider the case that a random perturbation is a real noise and control time is random. We leave these questions for further investigations and look forward to solving them in the near future.