1 Introduction

With recent progress in additive and advanced manufacturing methods, there has been increasing interest in the development of soft and flexible metamaterials [3, 26], which can be subjected to large and tailorable, e.g., auxetic, elastic deformations [2, 4, 12, 23, 34], harness mechanical instabilities and buckling [28], absorb energy or dissipate vibrations [5]. This functional behavior of soft metamaterials is enabled by their microstructural topology [3], whether they consist of truss, beam or shell-like lattice members or multi-phase solids, and their soft material constituents, typically elastomers or polymer hydrogels. Due to their microstructural topology and the soft materials, they are mechanically characterized by nonlinearities, i.e., large elastic deformations and finite strains, as well as mechanical instabilities, such as buckling and snapping, and anisotropy with specific material symmetries.

To efficiently model the mechanical behavior of large scale structures that are constituted of soft metamaterials at a microscopic level, nonlinear multiscale simulation methods are required, for which the effective microstructural behavior must be homogenized, see, e.g., [15, 30]. Concurrent multiscale simulation, e.g., in the framework of the FE2 method, requires the solution and homogenization of a microstructural boundary value problem at each evaluation point of the macroscopic finite element (FE) problem and is thus computationally expensive. In contrast, hierarchical or sequential multiscale simulation requires the formulation of an effective constitutive model, which can then be cheaply evaluated within the macroscale simulation. However, developing such effective constitutive models even for elastic soft metamaterials is difficult, since analytical hyperelastic models based on strain energy potentials must be adapted to include anisotropy and often do not reflect the behaviour of metamaterials well—as will also be shown here. Thus, empirical, data-driven constitutive models are generally developed for nonlinear microstructures by fitting either strain energies or stresses obtained from microstructural simulations as interpolating or approximating response surfaces, e.g., by polynomial database interpolation [19, 36], B-splines [6, 37], or reduced basis models [24].

More recently, the development of data-driven constitutive modeling has gained great momentum. Methods based on artificial neural networks (ANNs) and other machine learning (ML) approaches have shown excellent results in terms of prediction quality, flexibility and performance. In the field of nonlinear elasticity, [25] shows how ANNs can be used in order to calibrate hyperelastic laws, but the approach is limited to small deformations and does not offer strategies for specific material symmetries. In [27] ANNs are used for the identification constitutive relations with known material symmetry for large large deformations. The ansatz is demonstrated for Nickel with cubic material symmetry, where the ANNs are trained on the deformation gradient or specific invariants with structure tensors up to fourth-order for cubic behavior. The approach yields the best results based on the cubic invariants. But since no illustrations of the stress strain behavior are provided, it remains unclear if the ansatz is able to capture highly nonlinear material behavior. In [19] a polynomial approach is presented for the data-driven identification of the constitutive manifold. The approach shows very good results but is limited to small strains and does not cover material symmetry considerations. A data-driven model-free method for nonlinear hyperelasticity at finite strains is developed in [31]. The method demonstrates very good performance but is demonstrated only in one- and two-dimensional problems for isotropic material behavior. The RNEXP approach of [14] offers a highly efficient method for hyperelastic materials, but it is formulated for small deformations and specific material symmetries can only be approximated through patterns in the provided calibration data. In [13] a ANN-based on-the-fly adaptive ansatz is presented for nonlinear hyperelasticity at small strains. The effective material law of the microstructure is replaced by an ANN and used in macroscopic FE simulations. The approach shows also very good results within the training range but does not consider strategies specifically incorporating the material symmetry. In [16] an interesting approach for the data-driven calibration of corrections of given hyperelastic models for finite strain is presented. This approach shows very promising results due to its thermodynamical properties and its application in biomechanics, see [17], but is only demonstrated for isotropic material behavior. The work of [35] introduces efficient sampling strategies and ANN-based models for hyperelasticity at finite deformations for isotorpic material behavior.

Effective constitutive modeling of beam lattices, assumed in this work as hyperelastic systems, is particularly challenging, since they exhibit either stretching- or bending-dominated behavior, which depends on the microarchitecture, and can vary between deformation modes (such as uniaxial, biaxial, shear, etc.) and even between tensile and compressive deformation, see, e.g., [1, 11, 18]. Furthermore, stretching-dominated behavior often results in instabilities and buckling, which makes microstructural simulations and identification of effective material laws challenging. Effective continuum models have so far only been investigated for finite deformations of simpler types of 2D lattices [7, 10, 32]. In [22] a hyperelastic model is proposed, which, however, only performs satisfactory for uniaxial tensile deformation. To the best of the authors’ knowledge, no sensible anisotropic hyperelastic models have been proposed and investigated for typical 3D beam lattices subject to large deformations and instabilities.

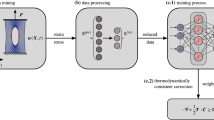
The present work introduces three data-driven models for the homogenized three-dimensional constitutive behavior of anisotropic hyperelastic (meta-) materials at finite deformations. The models are build upon ML methods, more specifically, based on ANNs, and are compared to a highly flexible hyperelastic model incorporating material symmetries proposed by [20]. The structure of the ANN models is designed such that all models fulfill the principle of objectivity and the material symmetry conditions for the known symmetry group of the material. All models are formulated as general as possible, in order to allow for future applications for any hyperelastic material with known material symmetry and alternative ML models. For the investigation of cubic lattice structures, considered as hyperelastic systems, the ANN models are trained based on synthetic data from three-dimensional simulations of two different lattice cells. The calibrated models are then compared to the hyperelastic model of [20] and among themselves in terms of prediction quality, capture of lattice instabilities and generalization behavior.

The outline of the manuscript is as follows. In Sect. 2, first, the basic material theory considerations for anisotropic hyperelastic materials are shortly described. Then, the hyperelastic model of [20] is sketched. This is followed by the development of the three ML models. In Sect. 3 the abilities of all models for the calibration of the effective material behavior of two different lattice cells is demonstrated. The manuscript ends in Sect. 4 with conclusions on the performance of the models.

Notation A symbolic tensor notation is preferred throughout the manuscript. The present work requires only zeroth-, second- and fourth-order tensors. An orthonornmal basis \(\{\varvec{e}_1,\varvec{e}_2,\varvec{e}_3\}\) of the three-dimensional physical space is used to represent all tensors. Scalars (zeroth-order tensors) are denoted by italic letters, e.g., W, a, b. Second- and fourth-order tensors are denoted by bold characters, e.g., \(\varvec{A}, \varvec{B}, \varvec{P}, \varvec{S}\), and blackboard bold characters, e.g., \(\mathbb {C}\), respectively. Einstein’s summation convention is not used in this work. The composition of two second-order tensors is denoted simply by \(\varvec{A}\varvec{B}\) with components \((\varvec{A}\varvec{B})_{ij} = \sum _{k=1} A_{ik}B_{kj}\). The double contraction is simply denoted by a colon, i.e., \(\varvec{A}: \varvec{B}\) is the scalar \(\varvec{A}: \varvec{B}= \sum _{i,j=1}^3 A_{ij} B_{ij}\), \(\varvec{A}: \mathbb {C}\) is a second-order tensor with components \((\varvec{A}: \mathbb {C})_{ij} = \sum _{k,l=1}^3 A_{kl} C_{klij}\) and \(\mathbb {A}: \mathbb {B}\) is a fourth-order tensor with components \((\mathbb {A}: \mathbb {B})_{ijkl} = \sum _{m,n=1}^3 A_{ijmn} B_{mnkl}\). The number of elements in a list or countable finite set L is denoted by \(\#(L)\). The tensor product is denoted by \(\otimes \), while the tensor power is denoted by \(\varvec{A}^{\otimes n}\). Standard variable symbols from continuum mechanics are used, i.e., W is reserved for quantities connected to the strain energy density, \(\varvec{F}\) denotes the deformation gradient, \(\varvec{P}\) and \(\varvec{S}\) are reserved for quantities immediately connected to the first and second Piola-Kirchhoff stress tensors, respectively.

2 Formulation of material models

2.1 Basic material theory considerations

A hyperelastic material model for finite deformations is described by a scalar potential \(W = W(\varvec{F})\), where \(\varvec{F}\) denotes the deformation gradient, which belongs to the set of invertible tensors with positive determinant \(Inv^+\). The potential W represents the strain energy density with respect to the volume in the initial placement. In order to fulfill the principle of material objectivity, see [33], the dependency of the potential is reduced to the right Cauchy-Green tensor \(\varvec{C}= \varvec{F}^T\varvec{F}\), i.e.,

$$\begin{aligned} W = W(\varvec{F}) = {\hat{W}}(\varvec{C}) \ , \end{aligned}$$
(1)

i.e., \({\hat{W}}\) is prescribed and W is determined by (1). In the following, the material model is referred to as objective for short.

The material symmetry of the material is specified by the collection G of all symmetry transformations \(\varvec{Q}\)

$$\begin{aligned} G = \{\varvec{Q}_1,\dots \} \subset SO(3) . \end{aligned}$$
(2)

The collection G is referred to as the material symmetry group. The set of orthogonal second-order tensors in three-dimensional space is denoted by O(3), while the special orthogonal group is denoted as \(SO(3) \subset O(3)\). The present work is restricted to finite symmetry groups. For finite G, \(\#(G)\) is used to denote the number of elements.

The potential satisfies

$$\begin{aligned} W(\varvec{F}) = W(\varvec{F}\varvec{Q}) \quad \forall \varvec{F}\in Inv^+, \varvec{Q}\in G \ , \end{aligned}$$
(3)

which for (1) translates for \({\hat{W}}\) to

$$\begin{aligned} {\hat{W}}(\varvec{C}) = {\hat{W}}(\varvec{Q}^T\varvec{C}\varvec{Q}) \quad \forall \varvec{C}\in Sym^+, \varvec{Q}\in G\ , \end{aligned}$$
(4)

where \(Sym^+\) denotes the set of symmetric positive definite second-order tensors. It is shortly remarked that the present work considers material symmetry groups as subsets of SO(3), and not of O(3), since the potential W is restricted to evaluations of arguments \(\varvec{F}\varvec{Q}\) in (3) with positive determinant.

The first and second Piola–Kirchhoff stress tensors, \(\varvec{P}\) and \(\varvec{S}\), respectively, are defined as follows

$$\begin{aligned} \varvec{P}= \frac{\partial W}{\partial \varvec{F}} \ , \quad \varvec{S}= 2 \frac{\partial {\hat{W}}}{\partial \varvec{C}} \end{aligned}$$
(5)

such that the identity

$$\begin{aligned} \varvec{P}= \varvec{F}\varvec{S}\end{aligned}$$
(6)

and the material symmetry conditions, see, e.g., [8],

$$\begin{aligned} \varvec{P}(\varvec{F})= & {} \varvec{P}(\varvec{F}\varvec{Q})\varvec{Q}^T \quad \forall \varvec{F}\in Inv^+, \varvec{Q}\in G \end{aligned}$$
(7)
$$\begin{aligned} \varvec{S}(\varvec{C})= & {} \varvec{Q}\varvec{S}(\varvec{Q}^T\varvec{C}\varvec{Q})\varvec{Q}^T \quad \forall \varvec{C}\in Sym^+, \varvec{Q}\in G \end{aligned}$$
(8)

are automatically fulfilled if the potential fulfills (1) and (3).

Naturally, the just described properties of constitutive models for hyperelasticity form only a subset of the large set of constraints in material modeling. For instance, ellipticity is an important property in terms of material stability, but it lies beyond the scope of the present work. In the following, only the principle of objectivity, hyperelasticity and material anisotropy are considered for all upcoming constitutive models.

2.2 Material model of [20]

A highly flexible material model was proposed by [20]. It was first proposed for orthotropic hyperelasticity, but it can be easily generalized to arbitrary material symmetry. The potential of [20] will be denoted by \(W^\mathsf {I}\). The core idea of [20] is to define the potential as follows

$$\begin{aligned} W^\mathsf {I}(\varvec{F}) = {\hat{W}}^\mathsf {I}(\varvec{C}) = \frac{1}{2} \sum _{i=1}^N c_i \varvec{E}_i(\varvec{C}) : \mathbb {C}_i : \varvec{E}_i(\varvec{C}) \end{aligned}$$
(9)

with N isotropic tensor-valued functions \(\varvec{E}_i\), i.e.,

$$\begin{aligned} \varvec{E}_i(\varvec{C}) = \varvec{Q}\varvec{E}_i(\varvec{Q}^T\varvec{C}\varvec{Q})\varvec{Q}^T \ \forall \varvec{C}\in Sym^+, \varvec{Q}\in O(3) \end{aligned}$$
(10)

and major-symmetric anisotropic fourth-order tensors fulfilling the associated material symmetry conditions

$$\begin{aligned} \mathbb {C}_i = \varvec{Q}\star \mathbb {C}_i \quad \forall \varvec{Q}\in G, i=\{1,\dots ,N\} \ , \end{aligned}$$
(11)

where \((\varvec{Q}\, \star \, \mathbb {A})_{ijkl} = \sum _{m,n,o,p=1}^3 Q_{im}Q_{jn}Q_{ko}Q_{lp}A_{mnop}\). The ansatz (9) is objective per definition and fulfills the symmetry conditions (3) or (4), respectively. It should be remarked that the ansatz (9) was originally motivated by [20] from the St. Venant material model, which becomes immediately obvious by replacing \(\varvec{E}_i \rightarrow (\varvec{C}-\varvec{I})/2\) and identifying \(\mathbb {C}= \sum _{i=1}^N c_i \mathbb {C}_i\) as the elastic stiffness of the anisotropic material.

In order to formulate a sensible material model, the isotropic functions \(\varvec{E}_i(\varvec{C})\) should fulfill the conditions

$$\begin{aligned}&\varvec{E}_i(\varvec{I}) = \varvec{O}\ , \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial \varvec{E}_i}{\partial \varvec{C}}(\varvec{I}) = \frac{1}{2}\mathbb {I}^S \ , \end{aligned}$$
(13)

where \(\varvec{O}\) and \(\mathbb {I}^S\) denote the zero second-order tensor and the identity on symmetric second-order tensors, respectively. Condition (12) ensures \(W^\mathsf {I}(\varvec{I}) = 0\) and \(W^\mathsf {I}(\varvec{R}) = 0\) for any rigid body rotation \(\varvec{R}\in SO(3)\). Condition (13) ensures that the functions \(\varvec{E}_i(\varvec{C})\) reduce to the infinitesimal strain tensor \(\varvec{\varepsilon }= (\varvec{H}+\varvec{H}^T)/2, \varvec{F}= \varvec{I}+ \varvec{H}\) for small deformations. The gradient

$$\begin{aligned} \frac{\partial {\hat{W}}^\mathsf {I}}{\partial \varvec{C}}(\varvec{C}) = \sum _{i=1}^N c_i \varvec{E}_i(\varvec{C}) : \mathbb {C}_i : \frac{\partial \varvec{E}_i}{\partial \varvec{C}}(\varvec{C}) \end{aligned}$$
(14)

immediately shows, that condition (12) also ensures \(\varvec{S}^\mathsf {I}(\varvec{I}) = \varvec{O}= \varvec{P}^\mathsf {I}(\varvec{R})\) for any \(\varvec{R}\in SO(3)\) for the correspondingly derived stresses.

In [20], the isotropic functions \(\varvec{E}_i\) are chosen as analytic. More specifically, based on the spectral decomposition of \(\varvec{C}\)

$$\begin{aligned} \varvec{C}= \sum _{\alpha =1}^M \varLambda _\alpha \varvec{P}_\alpha \end{aligned}$$
(15)

with M distinct eigenvalues \(\varLambda _\alpha \) and corresponding projectors \(\varvec{P}_\alpha \), the functions \(\varvec{E}_i(\varvec{C})\) are chosen as

$$\begin{aligned} \varvec{E}_i(\varvec{C}) = \sum _{\alpha =1}^M e_i(\varLambda _\alpha ) \varvec{P}_\alpha , \end{aligned}$$
(16)

which is a specific choice of isotropic functions with scalar core functions \(e_i(x)\). In [20], the core function

$$\begin{aligned} e_i(x) = \sum _{r=1}^R \frac{a_{ir}}{b_{ir}}(x^{b_{ir}/2} - 1) \end{aligned}$$
(17)

is used, since it provides a close connection to the Ogden model and related ones. Additionally, the core function (17) can be interpreted from a mechanical point of view as a superposition of R different Seth-strains. The core function (17) fulfills (12). The condition (13) can be reduced to the constraint \(e_i'(1) = 1/2\), which imposes \(\sum _{r=1}^R a_{ir} = 1\). The formulas given in [21] can be used to compute the analytic gradient (14).

We refer to the parametrized potential as \(W^\mathsf {I}= W^\mathsf {I}(\varvec{F};p)\), where p refers to the collection of all model parameters, in this case, \(a_{ir}\) and \(b_{ir}\). The quantities \(c_i\) in (9) could also be considered as free parameters, but in this work, they will be fixed together with \(\mathbb {C}_i\) if the anisotropic stiffness \(\mathbb {C}= \sum _{i=1}^N c_i \mathbb {C}_i\) for the linear behavior is known. For given stiffness \(\mathbb {C}\) of the linear elastic behavior (corresponding to, e.g., triclinic, monoclinic, hexagonal, cubic, etc. material symmetry), one can decompose the stiffness into its spectral representation and use it as \(c_i\) and \(\mathbb {C}_i\), where \(c_i\) correspond to the eigenvalues and \(\mathbb {C}_i\) to the projectors of the decomposed stiffness. This will be discussed later on in more detail in Sect. 3.1.

2.3 Theory-driven non-intrusive ML approaches

Based on available data of a considered material or microstructure, we propose two theory-driven machine learning approaches for building constitutive models that fulfill the objectivity and material symmetry conditions (3):

  1. 1.

    Group symmetrization of the potential: We consider an arbitrary core model for the potential \({\tilde{W}}\) with parameters p, which takes \(\varvec{C}= \varvec{F}^T \varvec{F}\) as input, i.e., \({\tilde{W}} = {\tilde{W}}(\varvec{C};p)\). We assume that the core model \({\tilde{W}}\) is twice continuously differentiable with respect to \(\varvec{C}\). The core model can be any scalar-valued function accepting a six-dimensional input (degrees of freedom of \(\varvec{C}\)) which is twice continuously differentiable. We define the auxiliary quantity \(W_0(\varvec{F};p)={\tilde{W}}(\varvec{C};p)\) and formulate the potential as

    $$\begin{aligned} W^{\mathsf {MLW}}(\varvec{F}; p) = \frac{1}{\#(G)} \sum _{\varvec{Q}\in G} W_0(\varvec{F}\varvec{Q}; p) \ . \end{aligned}$$
    (18)

    This hyperelastic ansatz is objective and, due to the properties of groups, fulfills the symmetry conditions (3) for any choice of its parameters p. A proof of the fulfillment of the group symmetry is given in “Appendix A”. This means that the stresses derived from (18) automatically fulfill (7) and (8). Since the core model \({\tilde{W}}\) is twice continuously differentiable, not only the stress \(\varvec{P}^{\mathsf {MLW}} = \partial W^{\mathsf {MLW}} / \partial \varvec{F}\) is computable, but also the stress tangent tensor. Alternatively, one could define the auxiliary quantities

    $$\begin{aligned} {\tilde{\varvec{G}}}(\varvec{C}; p)= & {} \frac{\partial {\tilde{W}}}{\partial \varvec{C}} (\varvec{C}; p) \ , \nonumber \\ {\hat{W}}_0(\varvec{C}; p)= & {} {\tilde{W}}(\varvec{C}; p) - {\tilde{W}}(\varvec{I}; p) \end{aligned}$$
    (19)
    $$\begin{aligned}&\quad - \tilde{\varvec{G}}(\varvec{I}; p) : (\varvec{C}- \varvec{I}) \ , \end{aligned}$$
    (20)
    $$\begin{aligned} {\check{W}}_0(\varvec{F}; p)= & {} {\hat{W}}_0(\varvec{F}^T\varvec{F}; p) \ , \end{aligned}$$
    (21)

    and use \({\check{W}}_0(\varvec{F};p)\) instead of \(W_0(\varvec{F};p)\) in (18). The usage of \(\tilde{\varvec{G}}(\varvec{I};p)\) in (18) through (20) ensures that the gradient of \({\hat{W}}_0\) vanishes for \(\varvec{C}= \varvec{I}\). This would yield a modified model in (18) which is stress free for any rigid body rotation, see “Appendix A” for a proof. Additionally, \(W^{\mathsf {MLW}}(\varvec{I};p)= 0\) would hold per construction. While these properties are appealing, we do not implement them in the following, since they add computational complexity to the ML model in terms of the parameter dependency with small benefit. Based on a few training points the model (18) can be calibrated to achieve an acceptable approximation of the material state at \(\varvec{C}= \varvec{I}\).

  2. 2.

    Group symmetrization of the stress: We consider a continuously differentiable model \(\tilde{\varvec{S}}\) with parameters p, i.e., \(\tilde{\varvec{S}} = \tilde{\varvec{S}}(\varvec{C};p)\). We define the auxiliary quantity

    $$\begin{aligned} \varvec{P}_0(\varvec{F};p) = \varvec{F}\tilde{\varvec{S}}(\varvec{F}^T\varvec{F};p) \end{aligned}$$
    (22)

    and the corresponding first Piola-Kirchhoff stress as

    $$\begin{aligned} \varvec{P}^{\mathsf {MLP}}(\varvec{F};p) = \frac{1}{\#(G)} \sum _{\varvec{Q}\in G} \varvec{P}_0(\varvec{F}\varvec{Q})\varvec{Q}^T \end{aligned}$$
    (23)

    The ansatz (23) is objective and, due to the properties of groups, fulfills the symmetry conditions (7) for any choice of its parameters. A proof of the fulfillment of the group symmetry is given in “Appendix A”. Since the core model \({\tilde{\varvec{S}}}\) is differentiable, the corresponding stress tangent is computable. Alternatively, the quantity

    $$\begin{aligned} {\check{\varvec{P}}}_0(\varvec{F};p) = \varvec{F}(\tilde{\varvec{S}}(\varvec{F}^T\varvec{F};p) - \tilde{\varvec{S}}(\varvec{I};p)) \end{aligned}$$
    (24)

    could be used in (23) instead of \(\varvec{P}_0\). This would yield a modified model fulfilling \(\varvec{P}^{\mathsf {MLP}}(\varvec{R};p) = \varvec{O}\ \forall \varvec{R}\in SO(3)\). In the following, we do not implement this alternative formulation, since it only adds computational complexity to the model with small benefit. We are further interested in the ability of models in approximating the material state at \(\varvec{C}= \varvec{I}\).

Both proposed approaches offer a highly flexible and non-intrusive form for the usage of arbitrary data-driven ML methods. Here, artificial neural networks (ANNs) will be considered for \({\tilde{W}}\) and \(\tilde{\varvec{S}}\). It should be remarked that the outlined approaches could use any other data-driven model for \({\tilde{W}}\) and \(\tilde{\varvec{S}}\). Further, it should be remarked that the potential model (18) is a hyperelastic model, whereas the stress model (23) is only an elastic model, since no potential for it is known. Still, the model (23) is taken into consideration as a pragmatic model for the stress of an elastic material in view of its practical use for macroscopic FE simulations only requiring \(\varvec{P}\) and its derivative for structural simulations.

As indicated in Sect. 2.1, the present work is restricted to finite material symmetry groups. For material symmetry groups with an infinite number of elements, the approaches (18) and (23) could be reformulated in terms of integrals over the corresponding group. From an implementation point of view, this may be difficult, such that simply using (18) or (23) with a finite subgroup of the infinite group may suffice for the corresponding application. For instance, if transversely isotropic behavior is of interest, then the finite subgroup with 60-degrees rotations around the symmetry axis may provide acceptable results in some situations.

For the current investigation, the material law is path-independent, i.e., solely state-dependent. From the rich pool of data-driven approaches, we consider in this work ANNs due to their enormous flexibility. More specifically, instead of recurrent neural networks for history-dependent processes, we choose feedforward neural networks (FFNNs) for pure state-dependency. Hereby, different number of neurons and hidden layers, as illustrated in detail in “Appendix B” , are considered. In order to ensure (infinite) continuous differentiability, we choose the softplus function \(s(x) = \log (1+\exp (x))\) as activation function in all hidden layers. For a compact reference of the FFNN taken into account, the networks for \({\tilde{W}}\) and \(\tilde{\varvec{S}}\) will be addressed as

$$\begin{aligned} \mathcal {N}[n_1,n_2,\dots ,n_H] \end{aligned}$$
(25)

where \(n_i\), \(i \in \{1,\dots ,H\}\), denote the number of neurons in the H hidden layers. After fixing the number of hidden layers and neurons in each layer, the remaining FFNN parameters are the layer weights and biases, addressed simply by the parameter p. The total number of parameters of each model is described in “Appendix B” and tabulated in Table 3.

2.4 ML-extended theoretical model

Methods from the field of ML can also help (i) to decide, which model from a given collection offers the best quality based on inference criteria, as shown in [29] with a Bayesian approach for a collection of three isotropic hyperelastic models, or (ii) to extend the capabilities of an existing model.

Typically, constitutive models are based on several considerations of material theory, but require manual, human decisions on the choice of representations or ansatz functions at different steps of the model formulation, e.g., here the choice of isotropic functions \(\varvec{E}_i\) in (16) and of the scalar core functions \(e_i\) in (17) for the model of [20]. These human decisions may be, depending on the modeling step, too restrictive with respect to the richness of the theoretical model. Thus, it could be beneficial to combine a motivated material model with ML methods at an appropriate decision point.

The present section aims at this perspective and proposes to extend the model of [20] as follows. The structure of the model of [20] is highly flexible for isotropic \(\varvec{E}_i\). Mainly the choice of \(\varvec{E}_i\) is limited to human imagination and intuition. For a more general approach, one may consider Reiner’s representation theorem which states that any isotropic function \(\tilde{\varvec{E}}_i(\varvec{C})\) of a symmetric tensor \(\varvec{C}\) can be represented as

$$\begin{aligned} \tilde{\varvec{E}}_i(\varvec{C}) = \sum _{j=0}^2 \phi _{ij}(I,II,III) \varvec{C}^j \ , \end{aligned}$$
(26)

with \(\varvec{C}^0 = \varvec{I}\), \(\varvec{C}^1 = \varvec{C}\), \(\varvec{C}^2 = \varvec{C}\varvec{C}\), the invariants

$$\begin{aligned} I = \mathrm {tr}(\varvec{C}) \ , \quad II = \mathrm {tr}(\mathrm {cof}(\varvec{C})) \ , \quad III = \det (\varvec{C}) \end{aligned}$$
(27)

and \(\mathrm {cof}(\varvec{C}) = \det (\varvec{C}) \varvec{C}^{-1}\). The functions \(\phi _{ij}\) in (26) are unknown, which motivates in the current setting the use of FFNNs with parameters \(p_{ij}\) for each function \(\phi _{ij} = \phi _{ij}(I,II,III;p_{ij})\). Usage of (26) in the approach of [20] instead of \(\varvec{E}_i\) given in (16) offers a hybrid model combining some material theory requirements and the power of data-driven ML methods. The ML-extended ansatz based on (26) yields a corresponding potential \(W^{\mathsf {MLI}}\). This ML-extended ansatz inherits from [20] the fulfillment of objectivity, hyperelasticity and material symmetry per construction. The collection of all parameters for the hybrid approach is referred to as p, as for the purely data-driven ones. We denote the corresponding potential as \(W^{\mathsf {MLI}} = W^{\mathsf {MLI}}(\varvec{F};p)\).

Due to linearity, the function

$$\begin{aligned} {\check{\varvec{E}}}_i(\varvec{C}) = \tilde{\varvec{E}}_i(\varvec{C}) - \tilde{\varvec{E}}_i(\varvec{I}) \end{aligned}$$
(28)

is also isotropic. Alternative usage of (28) instead of (26) in the approach of [20] fulfills (12), such that a modified model with vanishing stresses at \(\varvec{C}=\varvec{I}\) can be generated. As for the other ML models, we do not implement this alternative form in order to reduce the complexity of parameter dependency and check the ability to approximate the material state at \(\varvec{C}=\varvec{I}\). Furthermore, the amplifying quantities \(c_i\) in (9) are set to \(c_i=1 \mathrm {\ Pa}\) for the instances of the ML-extended approach \(W^\mathsf {MLI}\), since the output amplification is already carried out by the internal FFNNs.

3 Application to cubic beam-lattice metamaterials

The constitutive models introduced in the previous section are now used to represent the effective material behavior of beam-lattice metamaterials with cubic symmetry. For this purpose, the parameters of the models are fitted to data obtained from numerical homogenization of the respective unit cell models, see “Appendix C” for details.

3.1 Preparations and implementation of considered models for cubic material symmetry

For a clearer identification of the considered models, we refer to them in this section as follows:

  • Theoretical model of [20] (9) with potential \(W^\mathsf {I}\) and derived \(\varvec{P}^\mathsf {I}\):

  • ML model (18) with group symmetrization of the potential \(W^{\mathsf {MLW}}\) and derived \(\varvec{P}^{\mathsf {MLW}}\);

  • ML model (23) with group symmetrization of the stress \(\varvec{P}^{\mathsf {MLP}}\);

  • ML extension of [20] based on (26) with potential \(W^{\mathsf {MLI}}\) and derived \(\varvec{P}^{\mathsf {MLI}}\).

The list of models is referred to as \(\{\mathsf {I},\mathsf {MLW},\mathsf {MLP},\mathsf {MLI}\}\). The preparation of the models for representing cubic material symmetry, their calibration and implementation are discussed in the following.

Pre-calibrated \(c_i\) and \(\mathbb {C}_i\) for [20] model. Calibration of the original approach of [20] requires the determination of the parameters of the core functions \(\varvec{E}_i\) and, eventually, of the quantities \(c_i\) in (9), as well as a decision on which \(\mathbb {C}_i\) are to be used for the cubic material law. Based on linear elasticity, in the present work we choose to decompose a given linear elastic stiffness tensor \(\mathbb {C}\) into its spectral representation, such that \(\mathbb {C}_i\) are the corresponding projectors and \(c_i\) the corresponding eigenvalues. For cubic stiffnesses, the \(N=3\) projectors are known

$$\begin{aligned} \begin{aligned} \mathbb {C}_1&= \frac{1}{3}\varvec{I}\otimes \varvec{I}\ , \qquad \mathbb {C}_2 = \sum _{i=1}^3 \varvec{e}_i^{\otimes 4} - \mathbb {C}_1 \ , \\ \mathbb {C}_3&= \mathbb {I}^S - (\mathbb {C}_1 + \mathbb {C}_2) \ . \end{aligned} \end{aligned}$$
(29)

For the cubic lattice unit cells under consideration, the eigenvalues \(c_i\) are given explicit values, such that \(\mathbb {C}= \sum _{i=1}^3 c_i \mathbb {C}_i\) equals the effective stiffness of the cell for infinitesimal deformations, which can be computed from linear homogenization or nonlinear simulations results around \(\varvec{F}=\varvec{I}\).

Group symmetrization The Schoenflies octahedral groups O and \(O_h\), see, e.g., [9], containing 24 and 48 orthogonal transformations for cubic objects, respectively, are well known. The group \(O_h\) contains transformations including reflections. For the present work, only subsets of SO(3) are acceptable, i.e., \(O \subset SO(3)\) is used for the group symmetrization in the following examples.

Fitting of model parameters Each constitutive model \(\square \in \{\mathsf {I},\mathsf {MLW},\mathsf {MLP},\mathsf {MLI}\}\) has a set of remaining parameters p. These parameters will be calibrated by minimization of the mean squared error (MSE) of the output model, \(W^\square (\varvec{F}; p)\) and \(\varvec{P}^\square (\varvec{F}; p)\), respectively, based on available data. With a given dataset \(D = \{\varvec{F}_1,\dots \}\) with corresponding measured/simulated output \({\check{W}}\) and \(\check{\varvec{P}}\), in J and Pa, respectively, we define the corresponding dimensionless MSE as objective function for the model \(W^\square (\varvec{F}; p)\) as

$$\begin{aligned} MSE_W(p)= & {} \frac{1}{\#(D)} \sum _{\varvec{F}\in D} \Big [ \frac{1}{\mathrm {J^2}} ({\check{W}}(\varvec{F}) - W^\square (\varvec{F}; p))^2 \nonumber \\&+ \frac{1}{9 \ \mathrm {Pa^2}} {\Vert {\check{\varvec{P}}}(\varvec{F}) - \varvec{P}^\square (\varvec{F}; p) \Vert }^2 \Big ] \ . \end{aligned}$$
(30)

The factor 1/9 in the second term of the sum is used to compute the average over the 9 components of \(\varvec{P}\). For the model \(\varvec{P}^{\mathsf {MLP}}(\varvec{F}; p)\) given in (23) we consider only the MSE with respect to the measured/simulated stresses

$$\begin{aligned} MSE_P(p) = \frac{1}{\#(D)} \sum _{\varvec{F}\in D} \frac{1}{9 \ \mathrm {Pa^2}} {\Vert {\check{\varvec{P}}}(\varvec{F}) - \varvec{P}^{\mathsf {MLP}}(\varvec{F}; p) \Vert }^2.\nonumber \\ \end{aligned}$$
(31)

The parameters p of the corresponding models\(\{\mathsf {I},\mathsf {MLW},\mathsf {MLP},\mathsf {MLI}\}\) will be the minimizers of the corresponding MSE, i.e.,

$$\begin{aligned} p_{W/P} = \arg \min _p MSE_{W/P}(p) \ . \end{aligned}$$
(32)

It is shortly remarked, that calibration of material models is usually focused on the stress values. The present approach incorporates the potential values in (30) for the hyperelastic models from the following perspective. Any function being calibrated at given points benefits from information of the function values and of its gradient at those points. In virtual material testing and design, simulation technologies allow for a deeper insight into several state variables. If this information is available, it can enhance the model quality and should, therefore, be used. In real-world experiments many of these state variables are not accessible or only under significant effort. For instance, in lattice structures, if the material of the elastic beams is characterized well, then, in principle, their deformation could be tracked with digital image correlation and the elastic energy density could be computed. Since the current work focuses the simulative investigation of lattice structures, the potential values are at hand and used for the calibration of the hyperelastic models. It should finally be noted, that the gradient error may still dominate (30).

Implementation of models The model \(W^\mathsf {I}\) has been implemented and optimized in Mathematica 12 in order to take advantage of symbolic programming options required due to the usage of the spectral representations in (16). The ML-models \(W^{\mathsf {MLW}}\), \(\varvec{P}^{\mathsf {MLP}}\) and \(W^{\mathsf {MLI}}\) have been implemented and optimized in Python 3.7 with Google’s TensorFlow 2.1 library to use the full extent of efficient optimization of ANNs compatible with the current Anaconda distribution (October 2020).

3.2 Effective constitutive behavior of ”X” cell

3.2.1 Simulation data

We first consider a cubic lattice type with a body-centered micro-architecture, which consists of 8 beams connecting at the center of the cell, see Fig. 1, here denoted as ”X” cell.

Fig. 1
figure 1

Visualization of the beam model of the ”X” cell

Full size image

Synthetic data has been generated in nonlinear simulations with uniaxial, equibiaxial, planar, volumetric and simple shear deformations enforced by periodic boundary conditions. These particular deformation modes were chosen here, since they can also be applied in physical material tests and are thus often used for the experimental characterization of hyperelastic materials. The calibration dataset \(D_C = \{(\varvec{F}_1, {\check{\varvec{P}}}_1, {\check{W}}_1),\dots \}\) contains triples \((\varvec{F}, {\check{\varvec{P}}}, {\check{W}})\) for all simulation steps denoting the effective deformation gradient \(\varvec{F}\) of the cell, the effective first Piola-Kirchhoff stress tensor \(\check{\varvec{P}}\) in Pa and the effective potential (effective strain energy of the cell) \({\check{W}}\) in J. The dataset \(D_C\) will be used for the calibration of models with the objective functions (30) and (31). Additionally, 3 validation tests, to be addressed as the test dataset \(D_T\), were conducted to check the generalization capabilities of the calibrated models. The dataset \(D_T\) consists of 2 biaxial tests with different stretch ratios (test 1 and 2) and a test combining tension and shear (test 3). Further technical details of the conducted simulations are described in “Appendix C” . The dataset \(D_C\) is composed of 905 data points (each with a corresponding triple \((\varvec{F}, {\check{\varvec{P}}}, {\check{W}})\)), while \(D_T\) contains 603 data points. It should be noted that these numbers are relatively low in terms of the dimensionality of the input and output space. Since the input space of deformation tensors is nine-dimensional, an equidistant distribution of only 10 points in each dimension would yield \(10^9\) data points. The current investigation aims at the examination of the proposed models with mechanically sensible design with small amounts of data.

All components of the effective deformation and stress tensors for \(D_C\) and \(D_T\) for the X cell are displayed in Figs. 2 and 3 over the corresponding process parameter, respectively. The data for the potential will not be illustrated, we focus the visualization of the deformation and stress state. In the uniaxial, biaxial, planar and volumetric simulations, the process parameter is \(F_{11}\), where typically \(0.5\le F_{11}\le 1.5\), while in simple shear \(F_{12}\) is used with \(0\le F_{12}\le 0.5\). In the test data \(F_{11}\) is used as process parameter. All plots show the components of the corresponding 3-by-3 matrices for \(\varvec{F}\) (left column in Figs. 2 and 3) and \(\varvec{P}\) (right column in Figs. 2 and 3), denoted by colors in the legends.

Fig. 2
figure 2

Training dataset \(D_C\) of the X cell, showing all components of \(\varvec{F}\) (left column of plots) and \(\varvec{P}\) in Pa (right column of plots) for uniaxial, biaxial, planar, volumetric, and simple shear cases (from top to bottom)

Full size image

The X cell has been chosen as a first benchmark example, since it shows vastly differing stress responses for \(F_{11} > 1\) and \(F_{11} < 1\), as shown in Fig. 2. Furthermore, the stress response in the uniaxial case and biaxial case differ by an order of magnitude. Finally, buckling manifests itself in the volumetric case very early for \(F_{11} < 1\) and the shear case activates several stress components. This very particular and highly nonlinear effective behavior occurs for the X lattice type, since it does not have any beams along the cell edges. The soft responses in compression result from bending of the struts, while the increasingly stiff behaviors in tension result from a combination of bending and stretching of struts. Only in volumetric deformation, all struts are subjected to equal loading, which causes the much stiffer behavior in tension and buckling in compression. Based on these observations, the X cell offers an excellent challenging study case for the proposed anisotropic material models.

Fig. 3
figure 3

Test data of the X cell, showing all components of \(\varvec{F}\) and \(\varvec{P}\) test 1, test 2, test 3. Tests 1 and 2 represent biaxial cases with different stretches, see \(F_{11}\) and \(F_{22}\) components. Test 3 represent a case combining tension and shear, see \(F_{11}\) and \(F_{12}\) components

Full size image

In order to further verify the calibrated material models, the test cases (test 1, 2 and 3) are taken into consideration, see Fig. 3. Test 1 and 2 are biaxial tests with different stretching ratio along the 1 and 2 directions (see \(F_{11}\) and \(F_{22}\) is the left plots of Fig. 3), such that the adaptive properties of the calibrated models solely based on \(D_C\) are to be tested. Test 3 offers a more challenging scenario combining tension and shearing (see \(F_{11}\) and \(F_{12}\) components) and a highly different resulting stress behavior of the non-symmetric \(\varvec{P}\) including instabilities for compression (\(F_{11} < 1\)) and tension (\(F_{11} > 1\)), see \(P_{11}\), \(P_{12}\) and \(P_{21}\) in the bottom right plot of Fig. 3. This behavior is not encountered in any of the cases in \(D_C\). It should, therefore, be stressed that the calibration dataset \(D_C\) contains less complex mechanical scenarios compared to the test dataset \(D_T\). This makes, form the authors’ perspective, the dataset \(D_T\) a good benchmark dataset to evaluate the generalization properties of the considered models.

Interlude Before continuing to the advanced models, it should be shortly discussed that the elementary, linear constitutive relation of St. Venant’s law \(\varvec{P}^{{\mathsf {S}}{\mathsf {V}}} = \varvec{F}(\mathbb {C}: (\varvec{F}^T\varvec{F}- \varvec{I})/2)\) with cubic stiffness \(\mathbb {C}= \sum _{i=1}^3 c_i \mathbb {C}_i\) is not at all suitable for the finite-deformation modeling of the considered structures.

For a clear example, consider the uniaxial case of the X cell depicted in Fig. 2. The uniaxial case with diagonal \(\varvec{F}\) imposes \(F_{11}\) values and is carried out with the stress free condition \(P_{22} = P_{33} = 0\), such that \(F_{22} = F_{33}\) are returned based on that condition. Calibration of the eigenvalues of the cubic stiffness based on all simulation cases yields \(c_1 = 10450.3 \text { Pa}\), \(c_2 = 154.3 \text { Pa}\) and \(c_3 = 7343.6 \text { Pa}\). Computing the ideal condition \(P^{{\mathsf {S}}{\mathsf {V}}}_{22} = P^{{\mathsf {S}}{\mathsf {V}}}_{33} = 0\) yields a dependency of \(F^{\mathsf {SV - ideal}}_{22} = F^{\mathsf {SV - ideal}}_{33}\) in terms of \(F_{11}\)

$$\begin{aligned} F^\mathsf {SV - ideal}_{22} = \frac{\sqrt{(c_2-c_1) F_{11}^2+3 c_1}}{\sqrt{2 c_1+c_2}} \ . \end{aligned}$$
(33)
Fig. 4
figure 4

Left plot: Path of deformation gradient components of simulated uniaxial simulation \((F_{11},F_{22})^\mathsf {uni}\) (blue) and fictitious \((F_{11},F_{22})^\mathsf {SV-ideal}\) (orange); Right plot: \(P_{11}\) component corresponding to \((F_{11},F_{22})^\mathsf {uni}\) (blue), \(P^{\mathsf {S}\mathsf {V}}_{11}\) corresponding to \((F_{11},F_{22})^\mathsf {SV - ideal}\) (orange) and corresponding to \((F_{11},F_{22})^\mathsf {uni}\) (green)

Full size image

The \((F_{11}, F_{22})^\mathsf {uni}\) path of the simulated uniaxial case and the fictitious path for \((F_{11}, F_{22})^\mathsf {SV - ideal}\) based on (33) are displayed in Fig. 4 (left plot). It can be seen that the simulation path \((F_{11}, F_{22})^\mathsf {uni}\) (blue curve) does not deviate much from the fictitious one \((F_{11}, F_{22})^\mathsf {SV-ideal}\) (orange curve) yielding \(P^{\mathsf {S}\mathsf {V}}_{22} = 0\). The \(P_{11}\) values corresponding to the simulated \((F_{11}, F_{22})^\mathsf {uni}\) are depicted in blue in Fig. 4 (right plot), while \(P^{\mathsf {S}\mathsf {V}}_{11}\) corresponding to \((F_{11}, F_{22})^\mathsf {SV-ideal}\) is illustrated in orange. It can be seen, that these stress curves agree reasonably in the vicinity of \(F_{11} = 1\). But it should be stressed that \(P^{\mathsf {S}\mathsf {V}}_{11}\) for \((F_{11}, F_{22})^\mathsf {SV-ideal}\) corresponds to a fictitious deformation, it does not correspond to the real deformation \((F_{11}, F_{22})^\mathsf {uni}\) of the cell. Evaluation of the real cell deformation \((F_{11}, F_{22})^\mathsf {uni}\) with St.-Venant’s law yields the green curve shown in Fig. 4 (right plot).

From this comparison, it can be concluded that outside the infinitesimal deformation regime around \(\varvec{F}\approx \varvec{I}\), St. Venant’s law may not be acceptable for modeling the effective constitutive behavior of such a metamaterial, not even for the simple uniaxial case. Naturally, the cells under consideration pose further challenges for a material law, e.g., manifestation of buckling in compression and tension (cf. test 3 in Fig. 3), such that we do not further discuss St. Venant’s law and move on to the comparison of the ML approaches.

3.2.2 Comparison of calibrated models

The four considered constitutive models are calibrated with the dataset \(D_C\). For the model \(W^\mathsf {I}\) \(R=7\) has been chosen. For the FFNNs in the ML models, the following architecture sweep has been conducted. The number of neurons in all hidden layers has been kept constant throughout the hidden layers, but varied in \(\{8, 16, 32, 64\}\), e.g., \(\mathcal {N}[8,8]\), \(\mathcal {N}[16,16,16]\). The number of hidden layers has been varied in \(\{1,2,3,4\}\). This yields a total of 16 FFNN architectures. Each architecture has been initialized three times in order to start with different randomly initialized states of weights and biases, resulting in a total of 48 model instances. Each model instance has been trained with \(D_C\) (905 datapoints) for 20,000 epochs with full batch training and the ADAM optimizer with default settings in TensorFlow 2.1 with Python 3.7 on a GeForce RTX 2080 Ti graphic card in a Windows system. No parameter regularization has been used. The training times for an instance of the \(W^\mathsf {MLW}\) model were 11–14 min depending on the architecture, for \(\varvec{P}^\mathsf {MLP}\) 8–10 min, and for \(W^\mathsf {MLI}\) 4–6 min.

Table 1 List of calibrated models for X cell; columns: model, total number of parameters, evaluation of calibrated model with test dataset \(D_T\) with \(MSE_W\) and \(MSE_P\), analogous evaluation of calibrated model with calibration dataset \(D_C\)
Full size table

In Table 1, the calibrated models are tabulated and grouped with respect to \(W^\mathsf {I}\), \(W^\mathsf {MLW}\), \(\varvec{P}^\mathsf {MLP}\) and \(W^\mathsf {MLI}\). The table shows the model architectures, the number of parameters, the corresponding \(MSE_W\) and \(MSE_P\) for the test dataset \(D_T\) and calibration dataset \(D_C\). Each model group is sorted with respect to the corresponding objective function of the model, but evaluated with the test dataset \(D_T\) (\(MSE_W\) in the third column for \(W^\mathsf {I/MLW/MLI}\) and \(MSE_P\) in the fourth column for \(\varvec{P}^\mathsf {MLP}\)). Only the best 5 of the 48 corresponding instances of each of the ML models in terms of the corresponding objective function evaluated for \(D_T\) are tabulated.

For the \(W^\mathsf {I}\) model it can be seen by the very high \(MSE_W\) for \(D_T\) and for \(D_C\) that it does not perform well, despite the high number of model functions in each of the \(\varvec{E}_i\) functions (\(R=7\)) and the incorporation of the elastic stiffness for small deformations. The \(W^\mathsf {MLW}\) model shows a significantly better performance than the \(W^\mathsf {I}\) approach. Various architectures achieve satisfactory results in the \(MSE_W\) for \(D_C\) (second last column). It can be seen through \(MSE_P\) for \(D_C\) (last column), that the stress errors dominate. The same holds in the evaluations for \(D_T\). No monotonicity with respect to the \(MSE_W\) for \(D_T\) with respect to the size of the FFNNs can be seen. This is well known in the ANN literature, larger networks do not always yield better results and a unique ”best” performing architecture is usually hardly identifiable. The elastic model \(\varvec{P}^\mathsf {MLP}\) shows good results with respect to its objective function (\(MSE_P\) for \(D_C\), last column), but does not achieve the generalization quality of \(W^\mathsf {MLW}\) with respect to \(MSE_P\) for \(D_T\) (fourth column). Finally, the \(W^\mathsf {MLI}\) model shows acceptable results larger than \(W^\mathsf {MLW}\) for \(D_C\), but a dramatic loss of generalization quality with respect to \(D_T\).

In the following, we consider for \(W^\mathsf {MLW}\) the tabulated instance with \(\mathcal {N}[8,8]\), for \(\varvec{P}^\mathsf {MLP}\) the instance with \(\mathcal {N}[8,8,8]\) yielding \(MSE_P = 5.00 \cdot 10^2\) and for \(W^\mathsf {MLI}\) the instance with \(\mathcal {N}[8,8,8]\). This choice is based on pure pragmatism targeting the selection of models yielding comparable and tolerable quality (within the corresponding model groups) with low computational complexity. In terms of evaluation speed of the chosen instances, 100,000 deformation gradients are evaluated in a single forward pass by \(W^\mathsf {MLW}\) in \(0.89 \mathrm {\ s}\) (potential and stress values), by \(\varvec{P}^\mathsf {MLP}\) in \(0.62 \mathrm {\ s}\) (only stress values) and by \(W^\mathsf {MLI}\) in \(0.18 \mathrm {\ s}\) (potential and stress values). This evaluation speed seems acceptable for FE simulations requiring the evaluation of the material model at a corresponding numbers of integration points.

In terms of the approximation of the material state at \(\varvec{F}= \varvec{I}\) and for rigid body rotations, the chosen ML-model instances have been evaluated for 100 random rotations. The corresponding maximum of the stress norm \({\Vert \varvec{P} \Vert }\) over the 100 sampled rotations evaluates to \(1.27\, \mathrm { Pa}\) for \(W^\mathsf {MLW}\), \(1.53\, \mathrm { Pa}\) for \(\varvec{P}^\mathsf {MLP}\) and \(1.72\,\mathrm { Pa}\) for \(W^\mathsf {MLI}\). This is considered, based by the magnitude of stresses throughout the simulation cases, as acceptable.

Fig. 5
figure 5

Evaluation of calibrated models \(W^\mathsf {I}\) (first column), \(W^{\mathsf {MLW}}\) (second col.), \(\varvec{P}^{\mathsf {MLP}}\) (third col.) and \(W^{\mathsf {MLI}}\) (fourth col.) for cubic X cell for uniaxial, biaxial, planar, volumetric and shear cases (from top to bottom). Continuous lines depict the simulation data, while the dashed lines denote the calibrated models

Full size image
Fig. 6
figure 6

Evaluation of calibrated models \(W^\mathsf {I}\) (first column), \(W^{\mathsf {MLW}}\) (second column), \(\varvec{P}^{\mathsf {MLP}}\) (third column) and \(W^{\mathsf {MLI}}\) (fourth column) for cubic X cell for test 1, 2 and 3 (from top to bottom). Continuous lines depict the simulation data, while the dashed lines denote the calibrated models

Full size image
Fig. 7
figure 7

Evaluation of re-calibrated models \(W^{\mathsf {MLW}}\) (first column), \(\varvec{P}^{\mathsf {MLP}}\) (second column) and \(W^{\mathsf {MLI}}\) (third column) of X cell for calibration cases uniaxial, biaxial, planar, volumetric and shear (from top to bottom). Continuous lines depict the simulation data, while the dashed lines denote the re-calibrated models

Full size image
Fig. 8
figure 8

Evaluation of re-calibrated models \(W^{\mathsf {MLW}}\) (first column), \(\varvec{P}^{\mathsf {MLP}}\) (second column) and \(W^{\mathsf {MLI}}\) (third column) of X cell for tests 1, 2 and 3 (from top to bottom). Continuous lines depict the simulation data, while the dashed lines denote the re-calibrated models

Full size image

Examination of calibration cases In the following, the chosen ML-model instances, i.e., \(W^\mathsf {MLW}\) with \(\mathcal {N}[8,8]\), \(\varvec{P}^\mathsf {MLP}\) with \(\mathcal {N}[8,8,8]\) and \(W^\mathsf {MLI}\) with \(\mathcal {N}[8,8,8]\) (see above), are addressed for the sake of brevity simply as \(W^\mathsf {MLW}\), \(\varvec{P}^\mathsf {MLP}\) and \(W^\mathsf {MLI}\), respectively. Evaluation of all stress components of \(\varvec{P}\) of the calibrated models for the \(D_C\) (uniaxial, biaxial, planar, volumetric and shear cases) is depicted in Fig. 5. The simulation data is depicted by the continuous lines, while the model predictions are depicted by the dashed lines. The models \(W^\mathsf {I}\), \(W^{\mathsf {MLW}}\), \(\varvec{P}^{\mathsf {MLP}}\) and \(W^{\mathsf {MLI}}\) are depicted in the first, second, third and fourth column, respectively.

As shown in Fig. 5, the theoretical model for the stresses based on the potential \(W^\mathsf {I}\) is not able to adequately fit the homogenized material behavior of the metamaterial, even though the model of [20] carries the cubic symmetry and uses the stiffness \(\mathbb {C}\) for infinitesimal deformations (extracted from the simulation data), such that the stress tangent matches exactly around \(\varvec{F}\approx \varvec{I}\). The performance of the calibrated model \(W^\mathsf {I}\) is very low, not only with respect to the potential values, cf. Table 1, but also with respect to the derived stresses. The reason for the low performance of the model \(W^\mathsf {I}\) in this example is the choice of the special class of isotropic function in (16) and of core functions in (17). More specifically, the chosen core functions are too smooth to be able to fit the manifestation of the instabilities due to beam buckling in the cell structure. However, as the choice of functions is a human decision, this illustrates the difficulty in manually formulating an anisotropic hyperelastic model.

In the second column of Fig. 5 the stresses derived from the ML model \(W^{\mathsf {MLW}}\) are depicted. As visible in the plots, the stress predictions of this ML model are almost indistinguishable from the simulation data. This remarkable results show that this machine learning-based hyperelastic model fulfilling the principle of objectivity and all anisotropy conditions of the material law is also able to capture manifestation of the instability in the volumetric case.

The evaluation of the stresses for the model \(\varvec{P}^{\mathsf {MLP}}\) is shown in the third column of Fig. 5. This model has been calibrated solely with the stress data of the simulations. It achieves very good results with respect to the calibration data and is able to capture the instability in the volumetric case.

In the last column of Fig. 5 the stresses based on the hybrid model \(W^{\mathsf {MLI}}\) are shown. Compared to \(W^\mathsf {I}\), the hybrid \(W^{\mathsf {MLI}}\) is able to fit the simulation data very well and also to capture the instability in the volumetric case. This is due to the far more general approach using Reiner’s representation theorem (26) and insertion of highly flexible ML functions for \(\phi _{ij}\). This result demonstrates that theory-based models can very well be extended by ML methods at appropriate decision points.

Examination of test cases As done above, the chosen ML-model instances, i.e., \(W^\mathsf {MLW}\) with \(\mathcal {N}[8,8]\), \(\varvec{P}^\mathsf {MLP}\) with \(\mathcal {N}[8,8,8]\) and \(W^\mathsf {MLI}\) with \(\mathcal {N}[8,8,8]\), are addressed for the sake of brevity by \(W^\mathsf {MLW}\), \(\varvec{P}^\mathsf {MLP}\) and \(W^\mathsf {MLI}\), respectively. After calibration, the models have been evaluated with the test data, as shown in Fig. 6. As for the previous figure, the simulation data is depicted by the continuous lines, while the model predictions are depicted by the dashed lines. The models \(W^\mathsf {I}\), \(W^{\mathsf {MLW}}\), \(\varvec{P}^{\mathsf {MLP}}\) and \(W^{\mathsf {MLI}}\) are shown in the first, second, third and fourth column, respectively.

It can be clearly seen that \(W^\mathsf {I}\) does not generalize well in any form, which is expected since it did not yield satisfactory results for \(D_C\). The model \(W^{\mathsf {MLW}}\) in the second column shows excellent generalization properties, which is best seen in the third test. The instability is well predicted in compression (\(F_{11} < 1\)) as well as in tension (\(F_{11} > 1\)). Furthermore, the hyperelastic model \(W^{\mathsf {MLW}}\) shows in the third test better generalization with respect to \(P_{11}\), compared to \(\varvec{P}^{\mathsf {MLP}}\), and far better compared to \(W^{\mathsf {MLI}}\). The model \(W^{\mathsf {MLI}}\) does not generalize well. As in the evaluation of \(W^\mathsf {I}\), the derived stresses of \(W^{\mathsf {MLI}}\) grow too fast and diverge very quickly from the material behavior in the third test. The authors suspect that this behavior may be an intrinsic property of the structure of the model of [20].

Re-calibration with test data If more calibration data is provided, better results can be obtained with the highly flexible ML models proposed in the present work. The models \(W^{\mathsf {MLW}}\), \(\varvec{P}^\mathsf {MLP}\) and \(W^{\mathsf {MLI}}\) have been re-trained with the complete simulation data (i.e., concatenating \(D_C\) and \(D_T\)) for 5,000 additional epochs. The evaluation of the re-calibrated models with \(D_C\) is depicted in Fig. 7. The evaluation of the re-calibrated models with \(D_T\) is displayed in Fig. 8. It can be clearly seen that the ML model \(W^{\mathsf {MLW}}\) not only maintains its excellent performance in the calibration cases but also improves very well in capturing the material behavior in the test cases, cf. Fig. 8. This also holds for the stress model \(\varvec{P}^\mathsf {MLP}\). The re-calibrated model \(W^{\mathsf {MLI}}\) improves its performance in the test cases, cf. Fig. 8. In this example, the ML hyperelastic model \(W^{\mathsf {MLW}}\) shows its excellent performance in terms of (1) capturing the manifestation of instabilities, (2) generalization behavior and (3) maintaining accuracy during re-calibration. The stress model \(\varvec{P}^\mathsf {MLP}\) shows also excellent results, but does not offer, strictly speaking, a hyperelastic model. The ML-extended approach \(W^\mathsf {MLI}\) shows its ability to go beyond [20] and to capture instabilities, but does not achieve the prediction quality of the former ML models.

3.3 Effective constitutive behavior of ”BCC” cell

3.3.1 Simulation data

This second example follows the structure of the previous one, but a different cell topology is examined, the ”BCC” cell, which is displayed in Fig. 9. Hereby, it should be noted that a periodic arrangement of the cell is considered through the periodic boundary conditions in all simulations. The cell consists of a body-centered architecture that has a cubic frame (through periodic extension) added with further beams on all edges of the cell. This stiffens the cell, but makes it also susceptible to instabilities already in uniaxial compression and other simple cases, cf. Fig. 9. Therefore, this second example provides an even more challenging scenario in terms of complex effective material behavior.

As in the previous example, 3D simulations for the computation of the effective constitutive behavior of the cell are conducted. The calibration dataset \(D_C\) (consisted of the uniaxial, biaxial, planar, volumetric cases as in the previous example), is depicted in Fig. 10 by the continuous lines. The test dataset \(D_T\) (composes of the test 1, 2 and 3 as in the previous example) is depicted in Fig. 11 by the continuous lines. All simulation cases of the corresponding datasets are illustrated over the respective process parameter. In the shear case, the process parameter is the \(F_{12}\) component of the effective deformation gradient of the cell, while in all other cases the \(F_{11}\) is taken as the process parameter. It should be noted that the BCC cell, compared to the X cell, exhibits further instabilities in uniaxial, biaxial and planar compression (\(F_{11} < 1\)), cf. Fig. 10.

Fig. 9
figure 9

Elementary unit BCC cell of a periodic arrangement (left), deformation for uniaxial compression (middle), deformation for volumetric compression (right)

Full size image
Table 2 List of calibrated models for BCC cell; columns: model, total number of parameters, evaluation of calibrated model with test dataset \(D_T\) with \(MSE_W\) and \(MSE_P\), analogous evaluation of calibrated model with calibration dataset \(D_C\)
Full size table
Fig. 10
figure 10

Dataset \(D_C\) (uniaxial, biaxial, planar, volumetric and shear in respective rows) for BCC cell with calibrated models; continuous lines denote the data in \(D_C\) while dashed lines denote the model predictions; respective components are depicted as shown by the legend on the right; \(\varvec{F}\) components (first column of pots); stress prediction of \(W^\mathsf {MLW}\) (second column); stress prediction of \(\varvec{P}^\mathsf {MLP}\) (third column); stress prediction of \(W^\mathsf {MLI}\) (fourth column)

Full size image
Fig. 11
figure 11

Dataset \(D_T\) (test 1, 2 and 3 in respective rows) for BCC cell with calibrated models; continuous lines denote the data in \(D_T\) while dashed lines denote the model predictions; respective components are depicted as shown by the legend on the right; \(\varvec{F}\) components (first column of pots); stress prediction of \(W^\mathsf {MLW}\) (second column); stress prediction of \(\varvec{P}^\mathsf {MLP}\) (third column); stress prediction of \(W^\mathsf {MLI}\) (fourth column)

Full size image
Fig. 12
figure 12

Dataset \(D_T\) (test 1, 2 and 3 in respective rows) for BCC cell with recalibrated models; continuous lines denote the data in \(D_T\) while dashed lines denote the model predictions; respective components are depicted as shown by the legend on the right; \(\varvec{F}\) components (first column of pots); stress prediction of \(W^\mathsf {MLW}\) (second column); stress prediction of \(\varvec{P}^\mathsf {MLP}\) (third column); stress prediction of \(W^\mathsf {MLI}\) (fourth column)

Full size image

3.3.2 Comparison of calibrated models

In this second example we compare the performance of the models \(W^{\mathsf {MLW}}\), \(\varvec{P}^\mathsf {MLP}\) and \(W^{\mathsf {MLI}}\). As in the previous example, we conduct the same architecture sweep with the same 48 architecture instances for each ML model. The five best performing instances of each model with respect to \(D_T\) are tabulated in Table 2.

As in the previous example, Table 2 shows that different architectures achieve comparable quality with respect to \(D_T\). The major challenge is still the minimization of the dominant stress errors, which constitute the major part of the \(MSE_W\) in the hyperelastic models. For \(D_T\), with respect to \(MSE_W\) the \(W^\mathsf {MLW}\) achieves better results than \(W^\mathsf {MLI}\). With respect to \(MSE_P\) the \(W^\mathsf {MLW}\) model performs slightly better than \(\varvec{P}^\mathsf {MLP}\) and \(W^\mathsf {MLI}\).

In the following, from Table 2 one instance for each group is selected: for \(W^\mathsf {MLW}\) the instance with \(\mathcal {N}[16,16]\), for \(\varvec{P}^\mathsf {MLP}\) the instance with \(\mathcal {N}[8,8,8,8]\) and for \(W^\mathsf {MLI}\) the instance with \(\mathcal {N}[32]\). These selected instances will be referred to as \(W^\mathsf {MLW}\), \(\varvec{P}^\mathsf {MLP}\) and \(W^\mathsf {MLI}\), for the sake of brevity.

The selected instances have been evaluated with \(D_C\). The corresponding stress values are depicted in Fig. 10 by dashed lines. The second column corresponds to the evaluation of \(W^{\mathsf {MLW}}\). The third column shows the predictions of the stress model \(\varvec{P}^\mathsf {MLP}\). The right column depicts the predictions of \(W^{\mathsf {MLI}}\). All models are able to capture the main features of the BCC cell, where \(W^\mathsf {MLI}\) shows the lowest performance, as also reflected by the \(MSE_P\) for \(D_C\) in Table 2.

Evaluation of the selected instances for \(D_T\) is displayed in Fig. 11. As reflected by the corresponding \(MSE_P\) of Table 2, all models show comparable performance. Recalibration of the selected instances for 5,000 additional epochs with the union of \(D_C\) and \(D_T\) improves the performance of all instances for \(D_T\), as displayed in Fig. 12.

It should be noted that the selected instance \(W^\mathsf {MLW}\) with \(\mathcal {N}[8,8,8]\) has the least number of parameters from the selected ones. Still, it shows an excellent performance, despite the small size of the core FFNN. In view of the relatively low model-complexity of \(W^\mathsf {MLW}\) and the challenging nonlinearities of the present cell, its generalization behavior seen in Fig. 11 is considered as excellent.

4 Conclusions

The present work proposes new anisotropic models for hyperelasticity at finite deformations, which combine material theoretical considerations with machine learning methods. In this way, data-driven approaches are developed that fulfill by construction the principle of objectivity and material symmetry conditions for any given material symmetry group. In particular, a ML-based hyperelastic model \(W^{\mathsf {MLW}}\) through (18), a ML-based stress model \(\varvec{P}^{\mathsf {MLP}}\) through (23), and aML-extended hyperelastic model \(W^{\mathsf {MLI}}\) based on (28), which is motivated from the work of [20], are introduced. In all ML models, any suitable ML approach can be inserted. In the present work, differentiable FFNNs were used in order to ensure the computation of stresses and potential stress tangents.

These ML-based approaches have been compared to the highly flexible theoretical model proposed by [20] and among themselves. As benchmark examples, simulation data of the homogenized constitutive behavior of cubic 3D lattice cells has been gathered. These considered flexible metamaterials exhibit finite deformations with strong instabilities in various loading scenarios depending on the cell topology. In the first example of the X cell, the approaches of the present work manage not only to capture the instability in volumetric compression, but they also forecast the manifestation of instabilities in more complex test scenarios not contained in the calibration data. Thus, they largely outperform the constitutive model of [20]. In the second example of the BCC cell, the ML models are trained with synthetic data of a BCC cell, which even exhibits several instabilities. All instabilities are reproduced by the ML models, at what \(W^{\mathsf {MLW}}\) shows the best performance.

We conclude that the novel approaches proposed in the present work not only offer better results than the approach of [20], but higher flexibility at minor intrusion. Thus, the hyperelastic ML-based model \(W^{\mathsf {MLW}}\) based on (18) showed the best generalization behavior and the best prediction quality in the investigated examples. The model \(W^{\mathsf {MLW}}\) offers an attractive alternative for anisotropic hyperelastic constitutive models, not only for lattice structures, but for other anisotropic hyperelastic cases, with potential application as material law in finite element simulations. For non-hyperelastic problems, the stress model \(\varvec{P}^\mathsf {MLP}\) may be used as an initial structure for future developments of data-driven constitutive laws. The ML-extended approach \(W^\mathsf {MLI}\) does not offer the prediction quality of the former ML models, but shows that mechanical models, as the one of [20], can be extended at key modeling points in order to capture new constitutive behavior, as the instabilities of lattice structures. All models have been calibrated with small amounts of data based on few mechanical simulations. As shown in the re-calibration of all ML models, the more data is provided, the better performance can be achieve due to their flexibility. Finally, it should be remarked that no single best performing architecture has been identified in the provided examples. For the \(W^\mathsf {MLW}\), based on Tables 1 and 2, it appears that the small architecture \(\mathcal {N}[8,8,8]\) yields very good results at low complexity. For the remaining ML models, very different architectures achieve among themselves comparable quality. It is, therefore, recommended to always perform an architecture sweep for new hyperelastic microstructures, if resources are available. This not only helps to obtain a set of high-quality candidates, but also to allow a model selection with a sensible compromise between prediction quality and model complexity based on pragmatic requirements for applications of interest.