Improved second-order unconditionally stable schemes of linear multi-step and equivalent single-step integration methods

Abstract

Second-order unconditionally stable schemes of linear multi-step methods, and their equivalent single-step methods, are developed in this paper. The parameters of the linear two-, three-, and four-step methods are determined for optimal accuracy, unconditional stability and tunable algorithmic dissipation. The linear three- and four-step schemes are presented for the first time. As an alternative, corresponding single-step methods, spectrally equivalent to the multi-step ones, are developed by introducing the required intermediate variables. Their formulations are equivalent to that of the corresponding multi-step methods; their use is more convenient, owing to being self-starting. Compared with existing second-order methods, the proposed ones, especially the linear four-step method and its alternative single-step one, show higher accuracy for a given degree of algorithmic dissipation. The accuracy advantage and other properties of the newly developed schemes are demonstrated by several illustrative examples.

1 Introduction

Direct time integration methods are powerful numerical tools for solving the ordinary differential and differential-algebraic equations arising in structural dynamics, multi-body dynamics and many other fields. A lot of excellent integration methods have been developed and are available in the literature; they are often classified as explicit and implicit methods. Explicit methods are easy to implement, but their intrinsic conditional stability limits the step size. Implicit methods can be designed to be unconditionally stable, so they are suitable when the accuracy requirements are not very strict.

In addition, time integration methods also can be categorized as multi-step and multi-stage techniques. The multi-step methods employ the states of several previous steps to express the current one, whereas the multi-stage utilize the states of selected collocation points. The single-step methods, which only use the information of the last step, may be included in both classes and represent the connecting link between them.

The most representative methods in the multi-stage class belong to the Runge-Kutta family [6], including the explicit [7], the diagonally implicit [19], and the fully implicit Runge–Kutta methods [16]. Based on the Gauss quadrature, the fully implicit s-stage Runge–Kutta methods can reach up to 2sth-order accuracy. However, the improvement in accuracy is realized at a dramatic increase in computational cost, so these higher-order schemes are not very useful in practice. In this family, the explicit and diagonally implicit Runge–Kutta methods are more widely-used.

The composite methods, which can be classified in the multi-stage class, have been greatly developed in recent years. They divide each step into several sub-steps, in which different schemes may be adopted. For example, the combination of the trapezoidal rule and the 3-point Euler backward scheme yields the two-sub-step Bathe method [4]. It has the maximum degree of algorithmic dissipation, while also retaining preferable low-frequency accuracy. Considering this advantage, the Bathe method was found to perform well in many fields [3, 5, 36]. As a extensions of the Bathe method, several two-sub-step implicit methods with tunable algorithmic dissipation, including the Kim and Reddy [25], the Kim and Choi [23], the $\rho _\infty$-Bathe [35] and the simple ones without acceleration vectors [22], were subsequently proposed. All these methods include the standard Bathe method as a special case; they present the same properties with an appropriate choice of the parameters [26]. To achieve higher accuracy, the three- and four-sub-step implicit composite methods [8, 18, 29, 30, 42] were also developed, adopting similar ideas. In addition, many efforts have been devoted to the development of explicit composite methods, producing several good candidates, such as the Noh and Bathe [34], the Soares [37], and many other methods [21, 24, 43].

In the multi-step class, including many existing single-step methods, Dahlquist [11] has revealed that the methods of higher than second-order accuracy cannot achieve unconditionally stable, known as Dahlquist’s second barrier. As a result, for implicit methods in this class, second-order unconditionally stable schemes are of most concern.

Owing to the simplicity, the single-step methods have received a lot of attention after the 1950s, generating many widely-used schemes, including the Newmark method [33], the Wilson-$\theta$ method [39], the HHT-$\alpha$ method proposed by Hilbert, Hughes, and Taylor [15], the WBZ-$\alpha$ method by Wood, Bossak, and Zienkiewicz [40], the generalized-$\alpha$ (G-$\alpha$) method [9, 17], the GSSSS (generalized single-step single-solve) method [45], and others reviewed in [38]. These single-step methods can display the identical spectral characteristics of the corresponding linear multi-step methods [45]. However, the linear two-step method with optimal parameters [31, 44] can provide better accuracy than most existing single-step methods under the same degree of algorithmic dissipation.

Besides, representative multi-step methods also include the explicit Adams–Bashforth methods [2], the implicit Adams–Moulton methods [13] and the backward differentiation formulas (BDFs) [12]. The Adams–Bashforth and Adams–Moulton methods are designed to achieve higher-order accuracy, but most of them have poor stability. In practical applications, the implicit Adams–Moulton methods are usually used in tandem with the Adams–Bashforth methods as predictor-corrector pairs, which are essentially explicit. The BDFs, although unconditionally stable only up to second order, are particularly useful for solving stiff problems and differential-algebraic equations, owing to their strong algorithmic dissipation. One drawback of the multi-step methods is that they are not self-starting, so another method has to be used to solve the first steps, until there are enough to start the multi-step procedure. As a consequence, multi-step methods may not be as convenient to use as single-step ones.

This paper focuses on second-order accurate and unconditionally stable schemes of the linear multi-step methods. To acquire these accuracy and stability properties, the linear two-step method has been originally studied in [31, 32, 44]. Seeking higher accuracy, the linear three-, and four-step methods are discussed in this paper. From linear analysis, their optimal parameters are determined by minimizing the global error, under the constraints of second-order accuracy, unconditional stability and tunable algorithmic dissipation. The resulting optimal schemes present better accuracy than the linear two-step method, the linear four-step scheme being the best among them. Furthermore, to avoid additional start-up procedures, the single-step methods, spectrally equivalent to the linear multi-step ones, are proposed as well. Instead of utilizing the states of previous steps, the single-step methods get additional information by introducing intermediate variables. With proper parameters, they can achieve the same properties as the linear multi-step methods. Finally, the newly developed methods are applied to solve a few illustrative examples, and the solutions are compared with those of some widely-used implicit second-order schemes.

This paper is organised as follows. The formulations of the linear multi-step methods and the corresponding single-step ones are presented in Sect. 2. The optimization of the parameters is implemented in Sect. 3. The detailed properties of the proposed schemes are discussed in Sect. 4. Numerical examples are provided in Sect. 5, and conclusions are drawn in Sect. 6.

2 Formulations

The linear multi-step method for solving the initial-value problem of the generic first-order implicit differential equation ${\varvec{f}}({\varvec{x}},\dot{{\varvec{x}}},t)={\varvec{0}},{\varvec{x}}(t_0)={\varvec{x}}_0$ can be cast as

$$\begin{aligned}&{\varvec{f}}({\varvec{x}}_k,\dot{{\varvec{x}}}_k,t_k)={\varvec{0}} \end{aligned}$$

(1a)

$$\begin{aligned}&{\varvec{x}}_{k}=\sum _{j=1}^{r}\alpha _{j}{\varvec{x}}_{k-j}+\Delta t\sum _{j=0}^{r}\beta _{j}\dot{{\varvec{x}}}_{k-j} \end{aligned}$$

(1b)

where ${\varvec{x}}_k$ and $\dot{{\varvec{x}}}_k$ are the numerical approximations of ${\varvec{x}}(t_k)$ and $\dot{{\varvec{x}}}(t_k)$, respectively, $\Delta t=t_k-t_{k-1}$ is the time step size, assumed as constant for simplicity, $\alpha _j$ and $\beta _j$ are scalar parameters. The initial condition ${\varvec{x}}_0$ is supposed to be given in advance.

Applied to the linear structural dynamics problem, expressed as

$$\begin{aligned} {\varvec{M}}\ddot{{\varvec{q}}}+{\varvec{C}}\dot{{\varvec{q}}}+{\varvec{K}}{\varvec{q}}={\varvec{R}}(t), \, {\varvec{q}}(t_0)={\varvec{q}}_0, \, \dot{{\varvec{q}}}(t_0)={\varvec{v}}_0 \end{aligned}$$

(2)

where ${\varvec{M}}, {\varvec{C}}, {\varvec{K}}$ are the mass matrix, damping matrix, and stiffness matrix, respectively, ${\varvec{R}}(t)$ is the external load, ${\varvec{q}}$, $\dot{{\varvec{q}}}$ and $\ddot{{\varvec{q}}}$ denote the displacement, velocity and acceleration vectors, respectively, ${\varvec{q}}_0$ and ${\varvec{v}}_0$ are the known initial displacement and velocity vectors, this method can be formulated as

$$\begin{aligned}&{\varvec{M}}\ddot{{\varvec{q}}}_k+{\varvec{C}}\dot{{\varvec{q}}}_k+{\varvec{K}}{\varvec{q}}_k={\varvec{R}}_k \end{aligned}$$

(3a)

$$\begin{aligned}&{\varvec{q}}_{k}=\sum _{j=1}^{r}\alpha _{j}{\varvec{q}}_{k-j}+\Delta t \sum _{j=0}^{r}\beta _{j}\dot{{\varvec{q}}}_{k-j}\end{aligned}$$

(3b)

$$\begin{aligned}&\dot{{\varvec{q}}}_{k}=\sum _{j=1}^{r}\alpha _{j}\dot{{\varvec{q}}}_{k-j}+\Delta t\sum _{j=0}^{r}\beta _{j}\ddot{{\varvec{q}}}_{k-j} \end{aligned}$$

(3c)

From Eq. (3), ${\varvec{q}}_k$, $\dot{{\varvec{q}}}_k$ and $\ddot{{\varvec{q}}}_k$ can be solved by combining the linear multi-step scheme and the discrete dynamics equation at $t_k$.

Table 1 provides the step-by-step solution of the linear r-step method for solving the linear structural dynamics problems. To start the procedure of the linear r-step method, the initial $k < r$ steps need to be prepared by another method. The single-step scheme

$$\begin{aligned} {\varvec{x}}_k={\varvec{x}}_{k-1}+\Delta t(\beta _0\dot{{\varvec{x}}}_k+(1-\beta _0)\dot{{\varvec{x}}}_{k-1}) \end{aligned}$$

(4)

which can be obtained by setting $\alpha _1=1$, $\beta _1=1-\beta _0$ and $\alpha _{j}=0, \beta _{j}=0\ (j=2,3,\cdots ,r)$ in Eq. (1b), is adopted in Table 1. Certainly, other methods, such as the trapezoidal rule, and the combination of single-step and multi-step methods, can also be used for solving the first $r-1$ steps. The scheme in Eq. (4) is employed since it shares the same effective stiffness matrix as the linear r-step method. When applied to linear systems, no additional matrix factorization is requested. With the start-up procedure, the linear multi-step method almost does not require additional computational costs compared with the existing single-step methods. The employed single-step scheme is first-order accurate and unconditionally stable when $\beta _0>1/2$, and it becomes the second-order trapezoidal rule when $\beta _0=1/2$. When applied to nonlinear problems, the Newton-Raphson iteration needs to be used to solve the nonlinear equations per step.

Table 1 Step-by-step solution using the linear r-step method for solving the linear structural dynamics problems

To completely save the start-up procedure of initial steps, the single-step method, which can be used as an alternative of the linear r-step method in Eq. (1b), is also proposed as

$$\begin{aligned}&{\varvec{x}}_k={\varvec{x}}_{k-1}+\Delta t[(1-\gamma _0)\dot{{\varvec{x}}}_{k-1}^{r-1}+\gamma _0\dot{{\varvec{x}}}_k^{r-1}]\end{aligned}$$

(5a)

$$\begin{aligned}&(1-\gamma _1)\dot{{\varvec{x}}}_{k-1}^{r-1}+\gamma _1\dot{{\varvec{x}}}_k^{r-1}=(1-\gamma _2)\dot{{\varvec{x}}}_{k-1}^{r-2}+\gamma _2\dot{{\varvec{x}}}_k^{r-2}\end{aligned}$$

(5b)

$$\begin{aligned}&(1-\gamma _3)\dot{{\varvec{x}}}_{k-1}^{r-2}+\gamma _3\dot{{\varvec{x}}}_k^{r-2}=(1-\gamma _4)\dot{{\varvec{x}}}_{k-1}^{r-3}+\gamma _4\dot{{\varvec{x}}}_k^{r-3}\end{aligned}$$

(5c)

$$\begin{aligned}&\ldots \nonumber \end{aligned}$$

(5d)

$$\begin{aligned}&(1-\gamma _{2r-3})\dot{{\varvec{x}}}_{k-1}^{1}+\gamma _{2r-3}\dot{{\varvec{x}}}_k^{1}=(1-\gamma _{2r-2})\dot{{\varvec{x}}}_{k-1}+\gamma _{2r-2}\dot{{\varvec{x}}}_k \end{aligned}$$

(6a)

where $\dot{{\varvec{x}}}_k^{j}\ (j=1,2,\cdots ,r-1)$ are intermediate variables, and $\gamma _j\ (j=0,1,\cdots ,2r-2)$ are scalar parameters. When applied to the linear structural dynamics problem (2), this method yields

$$\begin{aligned}&{\varvec{M}}\ddot{{\varvec{q}}}_k+{\varvec{C}}\dot{{\varvec{q}}}_k+{\varvec{K}}{\varvec{q}}_k={\varvec{R}}_k\end{aligned}$$

(6b)

$$\begin{aligned}&{\varvec{q}}_k={\varvec{q}}_{k-1}+\Delta t[(1-\gamma _0)\dot{{\varvec{q}}}_{k-1}^{r-1}+\gamma _0\dot{{\varvec{q}}}_k^{r-1}]\end{aligned}$$

(6c)

$$\begin{aligned}&\dot{{\varvec{q}}}_k=\dot{{\varvec{q}}}_{k-1}+\Delta t[(1-\gamma _0)\ddot{{\varvec{q}}}_{k-1}^{r-1}+\gamma _0\ddot{{\varvec{q}}}_k^{r-1}]\end{aligned}$$

(6d)

$$\begin{aligned}&(1-\gamma _1)\dot{{\varvec{q}}}_{k-1}^{r-1}+\gamma _1\dot{{\varvec{q}}}_k^{r-1}=(1-\gamma _2)\dot{{\varvec{q}}}_{k-1}^{r-2}+\gamma _2\dot{{\varvec{q}}}_k^{r-2}\end{aligned}$$

(6e)

$$\begin{aligned}&(1-\gamma _1)\ddot{{\varvec{q}}}_{k-1}^{r-1}+\gamma _1\ddot{{\varvec{q}}}_k^{r-1}=(1-\gamma _2)\ddot{{\varvec{q}}}_{k-1}^{r-2}+\gamma _2\ddot{{\varvec{q}}}_k^{r-2}\end{aligned}$$

(6f)

$$\begin{aligned}&\ldots \nonumber \\&(1-\gamma _{2r-3})\dot{{\varvec{q}}}_{k-1}^{1}+\gamma _{2r-3}\dot{{\varvec{q}}}_k^{1}=(1-\gamma _{2r-2})\dot{{\varvec{q}}}_{k-1}+\gamma _{2r-2}\dot{{\varvec{q}}}_k\end{aligned}$$

(6g)

$$\begin{aligned}&(1-\gamma _{2r-3})\ddot{{\varvec{q}}}_{k-1}^{1}+\gamma _{2r-3}\ddot{{\varvec{q}}}_k^{1}=(1-\gamma _{2r-2})\ddot{{\varvec{q}}}_{k-1}+\gamma _{2r-2}\ddot{{\varvec{q}}}_k \end{aligned}$$

(7)

Table 2 Step-by-step solution using the single-step method equivalent to the linear r-step method for solving the linear structural dynamics problems

Clearly, a series of intermediate variables are introduced by this method. These variables are only useful to proceed the current and next step, but do not need to be stored and output. From Eq. (5), they can be seen as the shift approximations of $\dot{{\varvec{x}}}_k$, so $\dot{{\varvec{x}}}_0^{1}=\dot{{\varvec{x}}}_0^{2}=\cdots =\dot{{\varvec{x}}}_0^{r-1}=\dot{{\varvec{x}}}_0$ is assumed at the initial time. By choosing appropriate values for the $\gamma _j$ parameters, the single-step method of Eq. (5) can achieve spectral characteristics identical to those of the linear r-step method of Eq. (1b), which will be demonstrated in Sect. 3.

Table 2 presents the step-by-step solution of the single-step method for solving the linear structural dynamics problems. The intermediate variables of step $k-1$ are useful to update the state vectors of the current step, and after obtaining the intermediate variables of step k, the storage occupied by these variables of step $k-1$ can be released. Therefore, this single-step method only requires to store $2(r-1)$ vectors additionally. The additional storage is negligible compared to the overall storage. In terms of costs, although the single-step methods need to update the intermediate variables additionally, the required efforts of vector addition and subtraction operations are also negligible compared to the matrix operations per step, especially for large finite element systems. Therefore, it is reasonable to say that the proposed single-step methods have equivalent computational costs to the existing single-step methods. Due to being free from the need of additional start-up procedures, the proposed single-step method can be regarded as a more convenient alternative of the linear r-step method for applications.

3 Optimization

In this section, the linear spectral analysis is executed to determine the parameters and optimize the properties. According to Dahlquist’s second barrier [11], only the second-order unconditionally stable schemes are concerned here.

Generally, the test equation for linear analysis is

$$\begin{aligned} \ddot{q}+2\xi \omega {\dot{q}}+\omega ^2q=0 \end{aligned}$$

(8)

where $\xi$ is the damping ratio, and $\omega$ is the natural frequency. It can be equivalently reduced to the first-order equation

$$\begin{aligned} \dot{{\varvec{x}}}=\left[ \begin{array}{cc} 0 &{} 1 \\ -\omega ^2 &{} -2\xi \omega \end{array}\right] {\varvec{x}}, \, {\varvec{x}}=\left[ \begin{array}{cc} q \\ {\dot{q}} \end{array}\right] \end{aligned}$$

(9)

Decomposing the coefficient matrix in Eq. (8) gives the simplified first-order equation

$$\begin{aligned} {\dot{x}}=\lambda x, \, \lambda =(-\xi \pm \text {i}\sqrt{1-\xi ^2})\omega \end{aligned}$$

(10)

where $\text {i}=\sqrt{-1}$. To simplify the analysis, Eq. (9) is used as the test equation here.

Applied to Eq. (9), the recurrence equation of the linear r-step method, shown in Eq. (1b), is

$$\begin{aligned} (1-\beta _0 \Delta t \lambda )x_k-\sum _{j=1}^{r}(\alpha _j+\beta _j \Delta t \lambda )x_{k-j}=0 \end{aligned}$$

(11)

The characteristic polynomial can be written as

$$\begin{aligned} (1-\beta _0 \Delta t \lambda )\mu ^r-\sum _{j=1}^{r}(\alpha _j+\beta _j \Delta t \lambda )\mu ^{r-j}=0 \end{aligned}$$

(12)

where the generic characteristic root is denoted by $\mu$. According to Eq. (11), this polynomial has r characteristic roots $\mu _1, \mu _2, \cdots , \mu _r$. One of them, called the principal root, dominates the quality of numerical solutions; the other roots are spurious.

Similarly, applying the single-step method of Eq. (5) to the test equation (9) yields the compact scheme

$$\begin{aligned} {\varvec{X}}_{k}={\varvec{A}}{\varvec{X}}_{k-1}, {\varvec{X}}_{k}=[x_k,{\dot{x}}_k^{1},{\dot{x}}_k^{2},\cdots ,{\dot{x}}_{k}^{r-1}]^{\text {T}} \end{aligned}$$

(13)

where ${\varvec{A}}\in {\mathbb {C}}^{r\times r}$ is the amplification matrix, which governs the stability and accuracy characteristics of a method. From Eq. (12), the difference scheme only with respect to x can be written as

$$\begin{aligned} x_k-A_1x_{k-1}+A_2x_{k-2}+\cdots +(-1)^{r}A_{r}x_{k-r}=0 \end{aligned}$$

(14)

where $A_j\ (j=1,\cdots ,r)$ is the sum of the jth-order principal minors of ${\varvec{A}}$. The characteristic polynomial of ${\varvec{A}}$ is

$$\begin{aligned} \mu ^r-A_1\mu ^{r-1}+A_2\mu ^{r-2}+\cdots +(-1)^{r}A_{r}=0 \end{aligned}$$

(15)

Equation (14) shows a form similar to that of Eq. (11), and they can be identical by choosing appropriate values for the respective parameters.Then these two methods can be called spectrally equivalent to each other.

As representatives of the proposed formulation, the linear two-, three-, and four-step methods, respectively referred to as LMS2, LMS3 and LMS4 in the following, and the alternative single-step methods, correspondingly named SS2, SS3 and SS4, are discussed here. After determining the parameters of the linear multi-step methods, the parameters of the single-step methods are directly obtained by comparing the respective characteristic polynomials. To our knowledge, apart from LMS2 [31, 44], the second-order unconditionally stable schemes of the higher-step methods have not been proposed yet.

3.1 LMS2 and SS2

Setting $r=2$ in Eq. (1b) yields the formulation of LMS2 as

$$\begin{aligned} {\varvec{x}}_{k}=\alpha _{1}{\varvec{x}}_{k-1}+\alpha _2{\varvec{x}}_{k-2}+\Delta t(\beta _{0}\dot{{\varvec{x}}}_{k}+\beta _{1}\dot{{\varvec{x}}}_{k-1}+\beta _2\dot{{\varvec{x}}}_{k-2}) \end{aligned}$$

(16)

It is second-order accurate and unconditionally stable with the optimal parameters

$$\begin{aligned}&\alpha _1=\frac{4(\rho _\infty -1)}{\rho _\infty -3}, \, \beta _0=-\frac{2}{(\rho _\infty +1)(\rho _\infty -3)} \\ \nonumber&\alpha _2=1-\alpha _1, \, \beta _1=2\rho _\infty \beta _0, \, \beta _2=\rho _\infty ^2\beta _0, \, \rho _\infty \in [0,1] \end{aligned}$$

(17a)

The detailed process of parameter optimization is presented in [44]. In Eq. (16), all parameters are controlled by a single parameter $\rho _\infty$, which is the asymptotic spectral radius, defined as $\max \{|\mu _j|,j=1,2,\cdots ,r\}$ when $|\lambda \Delta t|\rightarrow {+\infty }$. Generally, $\rho _\infty$ is used to denote the degree of algorithmic dissipation. A smaller $\rho _\infty$ means stronger algorithmic dissipation for the high-frequency content.

As shown in Eq. (5), the corresponding single-step scheme SS2 has the form

$$\begin{aligned}&{\varvec{x}}_{k}={\varvec{x}}_{k-1}+\Delta t((1-\gamma _0)\dot{{\varvec{x}}}_{k-1}^1+\gamma _0\dot{{\varvec{x}}}_{k}^1)\end{aligned}$$

(17b)

$$\begin{aligned}&(1-\gamma _1)\dot{{\varvec{x}}}_{k-1}^{1}+\gamma _1\dot{{\varvec{x}}}_k^{1}=(1-\gamma _2)\dot{{\varvec{x}}}_{k-1}+\gamma _2\dot{{\varvec{x}}}_k \end{aligned}$$

(18)

From Eq. (14), SS2’s characteristic polynomial is

$$\begin{aligned} \mu ^2-A_1\mu +A_2=0 \end{aligned}$$

(19a)

where

$$\begin{aligned}&A_1=\frac{2\gamma _1-1+(\gamma _0+\gamma _2-2\gamma _0\gamma _2)\Delta t\lambda }{\gamma _1-\gamma _0\gamma _2\Delta t\lambda }\end{aligned}$$

(19b)

$$\begin{aligned}&A_2=\frac{\gamma _1-1+(\gamma _0+\gamma _2-\gamma _0\gamma _2-1)\Delta t\lambda }{\gamma _1-\gamma _0\gamma _2\Delta t\lambda } \end{aligned}$$

(20)

Meanwhile, the characteristic polynomial of LMS2 can be obtained by Eq. (11) and the parameters in Eq. (16) as

$$\begin{aligned} \mu ^2&+\frac{-4\rho _\infty ^2+4+4\rho _\infty \Delta t\lambda }{\rho _\infty ^2-2\rho _\infty -3+2\Delta t\lambda }\mu \\\nonumber&+\frac{3\rho _\infty ^2+2\rho _\infty -1+2\rho _\infty ^2\Delta t\lambda }{\rho _\infty ^2-2\rho _\infty -3+2\Delta t\lambda }=0 \end{aligned}$$

(21)

Equation (18) is the same as Eq. (20) when the parameters satisfy

$$\begin{aligned} \gamma _0=\gamma _2=\frac{1}{1+\rho _\infty },\gamma _1=\frac{3-\rho _\infty }{2(1+\rho _\infty )},\rho _\infty \in [0,1] \end{aligned}$$

(22)

Therefore, SS2 with the parameters in Eq. (21) is spectrally equivalent to LMS2 with the parameters in Eq. (16), so the single-step method SS2 also has second-order accuracy, unconditional stability and tunable algorithmic dissipation.

3.2 LMS3 and SS3

According to Eq. (1b), LMS3 can be formulated as

$$\begin{aligned} {\varvec{x}}_{k}&=\alpha _{1}{\varvec{x}}_{k-1}+\alpha _2{\varvec{x}}_{k-2}+\alpha _3{\varvec{x}}_{k-3}\\ \nonumber&\quad +\Delta t(\beta _{0}\dot{{\varvec{x}}}_{k}+\beta _{1}\dot{{\varvec{x}}}_{k-1}+\beta _2\dot{{\varvec{x}}}_{k-2}+\beta _3\dot{{\varvec{x}}}_{k-3}) \end{aligned}$$

(23)

This method is also expected to have second-order accuracy, unconditional stability, and to offer tunable algorithmic dissipation. With respect to Eq. (10), the local truncation error is defined as

$$\begin{aligned} \sigma&=(1-\beta _0 \Delta t\lambda )x(t_k)-(\alpha _1+\beta _1 \Delta t \lambda )x(t_{k-1})\\\nonumber&\quad -(\alpha _2+\beta _2 \Delta t \lambda )x(t_{k-2})-(\alpha _3+\beta _3 \Delta t \lambda )x(t_{k-3}) \end{aligned}$$

(24)

Expanding $\sigma$ at $t_k$ gives

$$\begin{aligned} \sigma&=s_0 x(t_k)+s_1 \Delta t{\dot{x}}(t_k)+s_2 \Delta t^2\ddot{x}(t_k)\\\nonumber&\quad +s_3 \Delta t^3x^{(3)}(t_k)+\text {O}(\Delta t^4) \end{aligned}$$

(25a)

where

$$\begin{aligned} s_0&=1-\alpha _1-\alpha _2-\alpha _3\end{aligned}$$

(25b)

$$\begin{aligned} s_1&=\alpha _1+2\alpha _2+3\alpha _3-\beta _0-\beta _1-\beta _2-\beta _3\end{aligned}$$

(25c)

$$\begin{aligned} s_2&=-\frac{\alpha _1}{2}-2\alpha _2-\frac{9\alpha _3}{2}+\beta _1+2\beta _2+3\beta _3\end{aligned}$$

(25d)

$$\begin{aligned} s_3&=\frac{\alpha _1}{6}+\frac{4\alpha _2}{3}+\frac{9\alpha _3}{2}-\frac{\beta _1}{2}-2\beta _2-\frac{9\beta _3}{2} \end{aligned}$$

(26)

so this method is second-order accurate if

$$\begin{aligned} s_0=s_1=s_2=0 \end{aligned}$$

(27)

To maximize the low-frequency accuracy for a given degree of algorithmic dissipation, the characteristic roots of Eq. (11) when $|\lambda \Delta t|\rightarrow {+\infty }$ need to be equal [9], as $-\rho _\infty$, which implies that

$$\begin{aligned} \beta _1=3\rho _\infty \beta _0, \, \beta _2=3\rho _\infty ^2\beta _0, \, \beta _3=\rho _\infty ^3\beta _0 \end{aligned}$$

(28)

Equations (26) and (27) impose six conditions, so only one parameter, e.g. $\beta _0$, is now adjustable.

Table 3 Generalized Routh array for the case of $r=3$

To evaluate the stability, $\mu =(1+z)/(1-z)$ is assumed; the stability condition $|\mu |\le 1$ is equivalent to $\text {Re}(z)\le 1$. With this assumption, the characteristic polynomial of Eq. (11) can be transformed into

$$\begin{aligned} z^r+\sum _{j=1}^{r}(p_j+q_j\text {i})z^{r-j}=0,p_j,q_j\in {\mathbb {R}} \end{aligned}$$

(29)

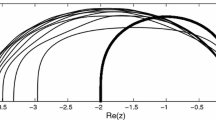
where the real and imaginary parts of the coefficients, denoted by $p_j$ and $q_j$, respectively, are determined by the scalar parameters and $\lambda \Delta t$. When $r=3$, the generalized Routh array [41] with respect to Eq. (28) is listed in Table 3. According to the generalized Routh stability criterion [41], the roots of Eq. (28) satisfy $\text {Re}(z)\le 1$ only when

$$\begin{aligned} p_1\ge 0, \, p_2^{(2)}\ge 0, \, p_3^{(2)}\ge 0 \end{aligned}$$

(30)

Then this method is unconditionally stable if the constraints in Eq. (29) hold for any $\lambda$ in the complex left-half-plane, including the imaginary axis. To simplify the analysis, the undamped case, i.e. $\xi =0$, which implies $\lambda =\pm \omega \text {i}$, is considered first. The desirable range of $\beta _0$ that makes this method unconditionally stable can be obtained as

$$\begin{aligned} \beta _0\in \left[ \frac{6}{(\rho _\infty +1)(\rho _\infty ^2-5\rho _\infty +10)},\frac{2}{(2-\rho _\infty )(\rho _\infty +1)^2}\right] \end{aligned}$$

(31)

To determine $\beta _0$ uniquely, the global error, defined as $E_k=x(t_k)-x_k$, is checked. Subtracting the recursive scheme, as in Eq. (10), from the right-hand side of Eq. (23), yields

$$\begin{aligned}&(1-\beta _0 \Delta t \lambda )E_k-(\alpha _1+\beta _1 \Delta t \lambda )E_{k-1}\\\nonumber&-(\alpha _2+\beta _2 \Delta t \lambda )E_{k-2} -(\alpha _3+\beta _3 \Delta t \lambda )E_{k-3}\\\nonumber&=\sigma =s_3\Delta t^3x^{(3)}(t_k) \end{aligned}$$

(32)

Assuming $E_k\approx E_{k-1}\approx E_{k-2}\approx E_{k-3}$, we can obtain

$$\begin{aligned} E_k=\frac{s_3}{\beta _0+\beta _1+\beta _2+\beta _3}\Delta t^2\ddot{x}(t_k) \end{aligned}$$

(33)

so the global error can be measured by the constant

$$\begin{aligned} \text {EC}&=\left| \frac{s_3}{\beta _0+\beta _1+\beta _2+\beta _3}\right| \\\nonumber&=\left| \frac{1}{(\rho _\infty +1)^3\beta _0}-\frac{2\rho _\infty ^2-5\rho _\infty +11}{6(\rho _\infty +1)^2}\right| \end{aligned}$$

(34)

The optimal $\beta _0$ that minimizes EC is finally obtained as

$$\begin{aligned} \beta _0=\frac{6}{(\rho _\infty +1)(\rho _\infty ^2-5\rho _\infty +10)} \end{aligned}$$

(35)

Then, the other parameters can be obtained from Eqs. (26)–(27).

With the set of parameters obtained above, the characteristic polynomial of Eq. (11) can be written as

$$\begin{aligned} \mu ^3&+\frac{-6\rho _\infty ^3+21\rho _\infty ^2+12\rho _\infty -15-18\rho _\infty \Delta t\lambda }{\rho _\infty ^3-4\rho _\infty ^2+5\rho _\infty +10-6\Delta t\lambda }\mu ^2\\\nonumber&+\frac{15\rho _\infty ^3-12\rho _\infty ^2-21\rho _\infty +6-18\rho _\infty ^2\Delta t\lambda }{\rho _\infty ^3-4\rho _\infty ^2+5\rho _\infty +10-6\Delta t\lambda }\mu \\\nonumber&+\frac{-10\rho _\infty ^3-5\rho _\infty ^2+4\rho _\infty -1-6\rho _\infty ^3 \Delta t\lambda }{\rho _\infty ^3-4\rho _\infty ^2+5\rho _\infty +10-6\Delta t\lambda }=0 \end{aligned}$$

(36a)

The unconditional stability for the damped cases is checked by solving Eq. (35) with different values of $\xi$. As expected, the condition $|\mu |\le 1$ is satisfied for any $\xi >0$ and $\omega \Delta t>0$, so this method is unconditionally stable. For illustration, the absolute values of the characteristic roots $|\mu |$ as a function of $\Delta t/T$, where $T=2\pi /\omega$, for the cases $\xi =0.0$ and $\xi =0.1$ are plotted in Figs. 1 and 2 , respectively.

Consequently, the optimal parameters of LMS3 have been obtained, as shown in Eqs. (26), (27) and (34). The resulting scheme has optimal accuracy, unconditional stability and tunable algorithmic dissipation.

Fig. 1

$|\mu |$ of LMS3 for the case $\xi =0.0$

Fig. 2

$|\mu |$ of LMS3 for the case $\xi =0.1$

According to Eq. (5), the single-step scheme SS3 is

$$\begin{aligned}&{\varvec{x}}_{k}={\varvec{x}}_{k-1}+\Delta t[(1-\gamma _0)\dot{{\varvec{x}}}_{k-1}^2+\gamma _0\dot{{\varvec{x}}}_{k}^2]\end{aligned}$$

(36b)

$$\begin{aligned}&(1-\gamma _1)\dot{{\varvec{x}}}_{k-1}^{2}+\gamma _1\dot{{\varvec{x}}}_k^{2}=(1-\gamma _2)\dot{{\varvec{x}}}_{k-1}^{1}+\gamma _2\dot{{\varvec{x}}}_k^{1}\end{aligned}$$

(36c)

$$\begin{aligned}&(1-\gamma _3)\dot{{\varvec{x}}}_{k-1}^{1}+\gamma _3\dot{{\varvec{x}}}_k^{1}=(1-\gamma _4)\dot{{\varvec{x}}}_{k-1}+\gamma _4\dot{{\varvec{x}}}_k \end{aligned}$$

(37)

Its characteristic polynomial is

$$\begin{aligned} \mu ^3-A_1\mu ^2+A_2\mu -A_3=0 \end{aligned}$$

(38a)

where

$$\begin{aligned} A_1&=\frac{3\gamma _1\gamma _3-\gamma _1-\gamma _3+(\gamma _0\gamma _2+\gamma _0\gamma _4+\gamma _2\gamma _4-3\gamma _0\gamma _2\gamma _4)\Delta t\lambda }{\gamma _1\gamma _3-\gamma _0\gamma _2\gamma _4\Delta t\lambda }\end{aligned}$$

(38b)

$$\begin{aligned} A_2&=\frac{3\gamma _1\gamma _3-2\gamma _1-2\gamma _3+1}{\gamma _1\gamma _3-\gamma _0\gamma _2\gamma _4\Delta t\lambda }\nonumber \\&\quad +\frac{(-\gamma _0-\gamma _2-\gamma _4+2\gamma _0\gamma _2+2\gamma _0\gamma _4+2\gamma _2\gamma _4-3\gamma _0\gamma _2\gamma _4)\Delta t\lambda }{\gamma _1\gamma _3-\gamma _0\gamma _2\gamma _4\Delta t\lambda }\end{aligned}$$

(38c)

$$\begin{aligned} A_3&=\frac{\gamma _1\gamma _3-\gamma _1-\gamma _3+1}{\gamma _1\gamma _3-\gamma _0\gamma _2\gamma _4\Delta t\lambda }\nonumber \\&\quad +\frac{(1-\gamma _0-\gamma _2-\gamma _4+\gamma _0\gamma _2+\gamma _0\gamma _4+\gamma _2\gamma _4-\gamma _0\gamma _2\gamma _4)\Delta t\lambda }{\gamma _1\gamma _3-\gamma _0\gamma _2\gamma _4\Delta t\lambda } \end{aligned}$$

(39)

By comparing Eqs. (37) and (35), SS3 is spectrally equivalent to LMS3 when its parameters are

$$\begin{aligned}&\gamma _0=\gamma _2=\gamma _4=\frac{1}{1+\rho _\infty }\\\nonumber&\gamma _1+\gamma _3=\frac{5-\rho _\infty }{2(1+\rho _\infty )},\gamma _1\gamma _3=\frac{\rho _\infty ^2-5\rho _\infty +10}{6(1+\rho _\infty )^2} \end{aligned}$$

(40a)

where $\gamma _1$ and $\gamma _3$ can be solved from the quadratic equation $y^2-(\gamma _1+\gamma _3)y+\gamma _1\gamma _3=0$. Note that if $\rho _\infty <1$, $\gamma _1$ and $\gamma _3$ are complex conjugate numbers. As such, SS3 yields complex intermediate variables, nonetheless resulting in real-valued ${\varvec{x}}_k$ and $\dot{{\varvec{x}}}_k$, as explained in the following.

As $\dot{{\varvec{x}}}_0^1=\dot{{\varvec{x}}}_0^2=\dot{{\varvec{x}}}_0$ is assumed, the recurrence equations of the first few steps after eliminating the intermediate variables can be written as

$$\begin{aligned}&{\varvec{x}}_1={\varvec{x}}_0+\Delta t\left( a_{10}\dot{{\varvec{x}}}_0+a_{11}\dot{{\varvec{x}}}_1\right) \end{aligned}$$

(40b)

$$\begin{aligned}&{\varvec{x}}_2={\varvec{x}}_1+\Delta t\left( a_{20}\dot{{\varvec{x}}}_0+a_{21}\dot{{\varvec{x}}}_1+a_{22}\dot{{\varvec{x}}}_2\right) \end{aligned}$$

(40c)

$$\begin{aligned}&{\varvec{x}}_3={\varvec{x}}_2+\Delta t\left( a_{30}\dot{{\varvec{x}}}_0+a_{31}\dot{{\varvec{x}}}_1+a_{32}\dot{{\varvec{x}}}_2+a_{33}\dot{{\varvec{x}}}_3\right) \end{aligned}$$

(40d)

$$\begin{aligned}&{\varvec{x}}_4={\varvec{x}}_3+\Delta t\left( a_{40}\dot{{\varvec{x}}}_0+a_{41}\dot{{\varvec{x}}}_1+a_{42}\dot{{\varvec{x}}}_2+a_{43}\dot{{\varvec{x}}}_3+a_{44}\dot{{\varvec{x}}}_4\right) \end{aligned}$$

(41a)

where

$$\begin{aligned} a_{11}&=a_{22}=a_{33}=a_{44} \end{aligned}$$

(41b)

$$\begin{aligned}&=\frac{6}{(\rho _\infty +1)(\rho _\infty ^2-5\rho _\infty +10)}=\beta _0\nonumber \\ a_{21}&=a_{32}=a_{43}\end{aligned}$$

(41c)

$$\begin{aligned}&=\frac{6(3\rho _\infty ^3-10\rho _\infty ^2+8\rho _\infty +5)}{(\rho _\infty +1)(\rho _\infty ^2-5\rho _\infty +10)^2}=\beta _1-(1-\alpha _1)a_{11}\nonumber \\ a_{31}&=a_{42}\end{aligned}$$

(41d)

$$\begin{aligned}&=\frac{18(\rho _\infty -1)^2(\rho _\infty ^3-4\rho _\infty ^2+5)}{(\rho _\infty ^2-5\rho _\infty +10)^3}\nonumber \\&=\beta _2-(1-\alpha _1)a_{21}-(1-\alpha _1-\alpha _2)a_{11}\nonumber \\ a_{41}&=\beta _3-(1-\alpha _1)a_{31}-(1-\alpha _1-\alpha _2)a_{21}\end{aligned}$$

(41e)

$$\begin{aligned} a_{10}&=1-a_{11},a_{20}=1-a_{21}-a_{22}\end{aligned}$$

(41f)

$$\begin{aligned} a_{30}&=1-a_{31}-a_{32}-a_{33}\end{aligned}$$

(41g)

$$\begin{aligned} a_{40}&=1-a_{41}-a_{42}-a_{43}-a_{44} \end{aligned}$$

(42a)

The parameters in Eq. (41) are all real numbers, so the computed state vectors are also real. From Eq. (40), the schemes of the first two steps reduce to first-order accurate, and from the third step on, SS3 shows the same properties of LMS3. Actually, it can be verified that ${\varvec{x}}_3$ and ${\varvec{x}}_4$ in Eq. (40) can be reorganized as

$$\begin{aligned} {\varvec{x}}_3&=\alpha _1{\varvec{x}}_2+\alpha _2{\varvec{x}}_1+\alpha _3{\varvec{x}}_0\nonumber \\&\quad +\Delta t\left( \beta _0\dot{{\varvec{x}}}_3+\beta _1\dot{{\varvec{x}}}_2+\beta _2\dot{{\varvec{x}}}_1+\beta _3\dot{{\varvec{x}}}_0\right) \end{aligned}$$

(42b)

$$\begin{aligned} {\varvec{x}}_4&=\alpha _1{\varvec{x}}_3+\alpha _2{\varvec{x}}_2+\alpha _3{\varvec{x}}_1\nonumber \\&\quad +\Delta t\left( \beta _0\dot{{\varvec{x}}}_4+\beta _1\dot{{\varvec{x}}}_3+\beta _2\dot{{\varvec{x}}}_2+\beta _3\dot{{\varvec{x}}}_1\right) \end{aligned}$$

(43)

The same formulation can also be found in the fifth step, the sixth step and so on, which further validates the equivalence of SS3 and LMS3. In another way, SS3 can be seen as LMS3 with the specific start-up procedure shown in Eq. (40).

3.3 LMS4 and SS4

Similar to LMS2 and LMS3, LMS4 is cast as

$$\begin{aligned} {\varvec{x}}_{k}&=\alpha _{1}{\varvec{x}}_{k-1}+\alpha _2{\varvec{x}}_{k-2}+\alpha _3{\varvec{x}}_{k-3}+\alpha _4{\varvec{x}}_{k-4}\\\nonumber&\quad +\Delta t(\beta _{0}\dot{{\varvec{x}}}_{k}+\beta _{1}\dot{{\varvec{x}}}_{k-1}+\beta _2\dot{{\varvec{x}}}_{k-2}+\beta _3\dot{{\varvec{x}}}_{k-3}+\beta _4\dot{{\varvec{x}}}_{k-4}) \end{aligned}$$

(44)

Its local truncation error is

$$\begin{aligned} \sigma&=(1-\beta _0 \Delta t\lambda )x(t_k)-(\alpha _1+\beta _1 \Delta t \lambda )x(t_{k-1})\\\nonumber&\quad -(\alpha _2+\beta _2 \Delta t \lambda )x(t_{k-2})-(\alpha _3+\beta _3 \Delta t \lambda )x(t_{k-3})\\\nonumber&\quad -(\alpha _4+\beta _4 \Delta t \lambda )x(t_{k-4}) \end{aligned}$$

(45a)

which can be also expanded in the form of Eq. (24) with the coefficients

$$\begin{aligned} s_0&=1-\alpha _1-\alpha _2-\alpha _3-\alpha _4 \end{aligned}$$

(45b)

$$\begin{aligned} s_1&=\alpha _1+2\alpha _2+3\alpha _3+4\alpha _4-\beta _0-\beta _1-\beta _2-\beta _3-\beta _4\end{aligned}$$

(45c)

$$\begin{aligned} s_2&=-\frac{\alpha _1}{2}-2\alpha _2-\frac{9\alpha _3}{2}-8\alpha _4+\beta _1+2\beta _2+3\beta _3+4\beta _4\end{aligned}$$

(45d)

$$\begin{aligned} s_3&=\frac{\alpha _1}{6}+\frac{4\alpha _2}{3}+\frac{9\alpha _3}{2}+\frac{32\alpha _4}{3}-\frac{\beta _1}{2}-2\beta _2-\frac{9\beta _3}{2}-8\beta _4 \end{aligned}$$

(46)

This method is also second-order accurate if

$$\begin{aligned} s_0=s_1=s_2=0 \end{aligned}$$

(47)

Likewise, the requirement of tunable algorithmic dissipation imposes four conditions, as

$$\begin{aligned} \beta _1=4\rho _\infty \beta _0, \, \beta _2=6\rho _\infty ^2\beta _0, \, \beta _3=4\rho _\infty ^3\beta _0, \, \beta _4=\rho _\infty ^4\beta _0 \end{aligned}$$

(48)

Then two parameters remain free, selected as $\beta _0$ and $\alpha _1$.

To investigate the stability, the generalized Routh array for Eq. (28) with $r=4$ is listed in Table 4.

Table 4 Generalized Routh array for the case of $r=4$

This method is unconditionally stable if the constraints

$$\begin{aligned} p_1\ge 0, \, p_2^{(2)}\ge 0, \, p_3^{(2)}\ge 0, \, p_4^{(4)}\ge 0 \end{aligned}$$

(49)

are satisfied for any $\lambda$ in the complex left-half-plane, including the imaginary axis. At the same time, the error constant, defined as

$$\begin{aligned} \text {EC}&=\left| \frac{s_3}{\beta _0+\beta _1+\beta _2+\beta _3+\beta _4}\right| \\\nonumber&=\left| \frac{4-\alpha _1}{(\rho _\infty +1)^4\beta _0}-\frac{\rho _\infty ^2-4\rho _\infty +13}{3(\rho _\infty +1)^2}\right| , \end{aligned}$$

(50a)

needs to be minimized. Under these conditions, the optimal $\beta _0$ and $\alpha _1$ are obtained as

$$\begin{aligned}&\beta _0=\frac{20}{(\rho _\infty +1)(-\rho _\infty ^3+7\rho _\infty ^2-21\rho _\infty +35)}\end{aligned}$$

(50b)

$$\begin{aligned}&\alpha _1=\frac{4(-2\rho _\infty ^3+13\rho _\infty ^2-35\rho _\infty +14)}{-\rho _\infty ^3+7\rho _\infty ^2-21\rho _\infty +35} \end{aligned}$$

(51)

Then other parameters can be obtained from Eqs. (46) and (47). With this set of parameters, the characteristic polynomial of LMS4 can be written as

$$\begin{aligned} \mu ^4&{+}\frac{-8\rho _\infty ^4+44\rho _\infty ^3-88\rho _\infty ^2-84\rho _\infty +56+80\rho _\infty \Delta t \lambda }{\rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-14\rho _\infty -35+20\Delta t\lambda }\mu ^3\\\nonumber&+\frac{28\rho _\infty ^4-136\rho _\infty ^3+136\rho _\infty -28+120\rho _\infty ^2 \Delta t \lambda }{\rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-14\rho _\infty -35+20\Delta t\lambda }\mu ^2\\\nonumber&+\frac{-56\rho _\infty ^4+84\rho _\infty ^3+88\rho _\infty ^2-44\rho _\infty +8+80\rho _\infty ^3\Delta t\lambda }{\rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-14\rho _\infty -35+20\Delta t\lambda }\mu \\\nonumber&+\frac{35\rho _\infty ^4+14\rho _\infty ^3-14\rho _\infty ^2+6\rho _\infty -1+20\rho _\infty ^4 \Delta t \lambda }{\rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-14\rho _\infty -35+20\Delta t\lambda }=0 \end{aligned}$$

(52a)

With $\xi =0.0$ and $\xi =0.1$, the solutions of $|\mu |$ versus $\Delta t/T$ are shown in Figs. 3 and 4 respectively. As can be seen, this method is also unconditionally stable for the damped cases.

Fig. 3

$|\mu |$ of LMS4 for the case $\xi =0.0$

Fig. 4

$|\mu |$ of LMS4 for the case $\xi =0.1$

The alternative single-step scheme SS4 has the form as

$$\begin{aligned}&{\varvec{x}}_{k}={\varvec{x}}_{k-1}+\Delta t[(1-\gamma _0)\dot{{\varvec{x}}}_{k-1}^3+\gamma _0\dot{{\varvec{x}}}_{k}^3]\end{aligned}$$

(52b)

$$\begin{aligned}&(1-\gamma _1)\dot{{\varvec{x}}}_{k-1}^{3}+\gamma _1\dot{{\varvec{x}}}_k^{3}=(1-\gamma _2)\dot{{\varvec{x}}}_{k-1}^{2}+\gamma _2\dot{{\varvec{x}}}_k^{2}\end{aligned}$$

(52c)

$$\begin{aligned}&(1-\gamma _3)\dot{{\varvec{x}}}_{k-1}^{2}+\gamma _3\dot{{\varvec{x}}}_k^{2}=(1-\gamma _4)\dot{{\varvec{x}}}_{k-1}^{1}+\gamma _4\dot{{\varvec{x}}}_k^{1}\end{aligned}$$

(52d)

$$\begin{aligned}&(1-\gamma _5)\dot{{\varvec{x}}}_{k-1}^{1}+\gamma _5\dot{{\varvec{x}}}_k^{1}=(1-\gamma _6)\dot{{\varvec{x}}}_{k-1}+\gamma _6\dot{{\varvec{x}}}_k \end{aligned}$$

(53)

The characteristic polynomial can be written as

$$\begin{aligned} \mu ^4-A_1\mu ^3+A_2\mu ^2-A_3\mu +A_4=0 \end{aligned}$$

(54a)

where

$$\begin{aligned} A_1&=\frac{4\gamma _1\gamma _3\gamma _5-\gamma _1\gamma _3-\gamma _1\gamma _5-\gamma _3\gamma _5}{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(\gamma _0\gamma _2\gamma _4+\gamma _0\gamma _2\gamma _6+\gamma _0\gamma _4\gamma _6+\gamma _2\gamma _4\gamma _6-4\gamma _0\gamma _2\gamma _4\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda } \end{aligned}$$

(54b)

$$\begin{aligned} A_2&=\frac{\gamma _1+\gamma _3+\gamma _5-3\gamma _1\gamma _3-3\gamma _1\gamma _5-3\gamma _3\gamma _5+6\gamma _1\gamma _3\gamma _5}{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(-\gamma _0\gamma _2-\gamma _0\gamma _4-\gamma _0\gamma _6-\gamma _2\gamma _4-\gamma _2\gamma _6-\gamma _4\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(3\gamma _0\gamma _2\gamma _4{+}3\gamma _0\gamma _2\gamma _6{+}3\gamma _0\gamma _4\gamma _6{+}3\gamma _2\gamma _4\gamma _6{-}6\gamma _0\gamma _2\gamma _4\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda } \end{aligned}$$

(54c)

$$\begin{aligned} A_3&=\frac{2\gamma _1+2\gamma _3+2\gamma _5-3\gamma _1\gamma _3-3\gamma _1\gamma _5-3\gamma _3\gamma _5+4\gamma _1\gamma _3\gamma _5-1}{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(\gamma _0+\gamma _2+\gamma _4+\gamma _6-2\gamma _0\gamma _2-2\gamma _0\gamma _4-2\gamma _0\gamma _6-2\gamma _2\gamma _4)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(-2\gamma _2\gamma _6-2\gamma _4\gamma _6+3\gamma _0\gamma _2\gamma _4+3\gamma _0\gamma _2\gamma _6+3\gamma _0\gamma _4\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(3\gamma _2\gamma _4\gamma _6-4\gamma _0\gamma _2\gamma _4\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda } \end{aligned}$$

(54d)

$$\begin{aligned} A_4&=\frac{\gamma _1+\gamma _3+\gamma _5-\gamma _1\gamma _3-\gamma _1\gamma _5-\gamma _3\gamma _5+\gamma _1\gamma _3\gamma _5-1}{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(-1+\gamma _0+\gamma _2+\gamma _4+\gamma _6-\gamma _0\gamma _2-\gamma _0\gamma _4-\gamma _0\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(-\gamma _2\gamma _4-\gamma _2\gamma _6-\gamma _4\gamma _6+\gamma _0\gamma _2\gamma _4+\gamma _0\gamma _2\gamma _6+\gamma _0\gamma _4\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda }\nonumber \\&\quad +\frac{(\gamma _2\gamma _4\gamma _6-\gamma _0\gamma _2\gamma _4\gamma _6)\Delta t\lambda }{\gamma _1\gamma _3\gamma _5-\gamma _0\gamma _2\gamma _4\gamma _6\Delta t\lambda } \end{aligned}$$

(55)

By comparing Eqs. (53) and (51), SS4 is spectrally equivalent to LMS4 when its parameters satisfy

$$\begin{aligned}&\gamma _0=\gamma _2=\gamma _4=\gamma _6=\frac{1}{1+\rho _\infty }\\\nonumber&\gamma _1+\gamma _3+\gamma _5=\frac{7-\rho _\infty }{2(1+\rho _\infty )}\\\nonumber&\gamma _1\gamma _3+\gamma _1\gamma _5+\gamma _3\gamma _5=\frac{\rho _\infty ^2-7\rho _\infty +21}{5(1+\rho _\infty )^2}\\\nonumber&\gamma _1\gamma _3\gamma _5=\frac{-\rho _\infty ^3+7\rho _\infty ^2-21\rho _\infty +35}{20(1+\rho _\infty )^3} \end{aligned}$$

(56a)

where $\gamma _1$,$\gamma _3$ and $\gamma _5$ can be obtained by solving the equation $y^3-(\gamma _1+\gamma _3+\gamma _5)y^2+(\gamma _1\gamma _3+\gamma _1\gamma _5+\gamma _3\gamma _5)y-\gamma _1\gamma _3\gamma _5=0$. If $\rho _\infty <1$, two of $\gamma _1$, $\gamma _3$ and $\gamma _5$ are complex.

By using $\dot{{\varvec{x}}}_0^1=\dot{{\varvec{x}}}_0^2=\dot{{\varvec{x}}}_0^3=\dot{{\varvec{x}}}_0$, the first several steps without the intermediate variables can be also written as

$$\begin{aligned}&{\varvec{x}}_1={\varvec{x}}_0+\Delta t\left( a_{10}\dot{{\varvec{x}}}_0+a_{11}\dot{{\varvec{x}}}_1\right) \end{aligned}$$

(56b)

$$\begin{aligned}&{\varvec{x}}_2={\varvec{x}}_1+\Delta t\left( a_{20}\dot{{\varvec{x}}}_0+a_{21}\dot{{\varvec{x}}}_1+a_{22}\dot{{\varvec{x}}}_2\right) \end{aligned}$$

(56c)

$$\begin{aligned}&{\varvec{x}}_3={\varvec{x}}_2+\Delta t\left( a_{30}\dot{{\varvec{x}}}_0+a_{31}\dot{{\varvec{x}}}_1+a_{32}\dot{{\varvec{x}}}_2+a_{33}\dot{{\varvec{x}}}_3\right) \end{aligned}$$

(56d)

$$\begin{aligned}&{\varvec{x}}_4={\varvec{x}}_3+\Delta t\left( a_{40}\dot{{\varvec{x}}}_0+a_{41}\dot{{\varvec{x}}}_1+a_{42}\dot{{\varvec{x}}}_2+a_{43}\dot{{\varvec{x}}}_3+a_{44}\dot{{\varvec{x}}}_4\right) \end{aligned}$$

(57a)

where

$$\begin{aligned} a_{11}&=a_{22}=a_{33}=a_{44}=\beta _0\end{aligned}$$

(57b)

$$\begin{aligned} a_{21}&=a_{32}=a_{43}=\beta _1-(1-\alpha _1)a_{11}\end{aligned}$$

(57c)

$$\begin{aligned} a_{31}&=a_{42}=\beta _2-(1-\alpha _1)a_{21}-(1-\alpha _1-\alpha _2)a_{11}\end{aligned}$$

(57d)

$$\begin{aligned} a_{41}&=\beta _3-(1-\alpha _1)a_{31}-(1-\alpha _1-\alpha _2)a_{21}\end{aligned}$$

(57e)

$$\begin{aligned}&-(1-\alpha _1-\alpha _2-\alpha _3)a_{11}\nonumber \\ a_{10}&=1-a_{11},a_{20}=1-a_{21}-a_{22}\end{aligned}$$

(57f)

$$\begin{aligned} a_{30}&=1-a_{31}-a_{32}-a_{33}\end{aligned}$$

(57g)

$$\begin{aligned} a_{40}&=1-a_{41}-a_{42}-a_{43}-a_{44} \end{aligned}$$

(58)

One can check that the first three steps only have first-order accuracy, but from the fourth step on, the same formulation as LMS4 can be reproduced. Therefore, SS4 can be also regarded as LMS4 with the specific start-up procedure shown in Eq. (56).

In conclusion, the parameters of LMS2, LMS3, LMS4, SS2, SS3, and SS4 for optimal accuracy, unconditional stability and tunable algorithmic dissipation have been determined in this section. From the parameters of LMS2, LMS3 and LMS4, we can see that when $0\le \rho _\infty <1$, $\beta _0>1/2$ and when $\rho _\infty =1$, $\beta _0=1/2$ , so the single-step scheme used as the start-up procedure in Table 1 is first-order unconditionally stable as $0\le \rho _\infty <1$, and recovers the trapezoidal rule as $\rho _\infty =1$. As opposed to LMS2, other schemes are here presented for the first time. The single-step schemes SS2, SS3 and SS4 can present properties identical to those of the corresponding multi-step method, except for the first few steps.

4 Properties

4.1 Accuracy and stability

Due to the equivalence of single-step and linear multi-step methods, the proposed single-step methods are not considered in this section. Firstly, the error constants (ECs), which are employed to measure the global errors, as in Eqs. (33) and (49), of LMS2, LMS3 and LMS4 are plotted in Fig. 5. As can be seen, LMS4 gives the smallest global error, followed by LMS3, and LMS2, which means that the accuracy can be improved by using the information of more previous steps. As $\rho _\infty$ increases, the gap between them gradually decreases; when $\rho _\infty =1$, these schemes all become the equivalent multi-step expressions of the trapezoidal rule.

Fig. 5

Error constants of the linear multi-step methods

Considering the test equation (9), the exact solution has the form

$$\begin{aligned} x(t)=\text {e}^{\lambda t}x_0,\lambda =(-\xi \pm \text {i}\sqrt{1-\xi ^2})\omega \end{aligned}$$

(59)

Using the linear multi-step method, the numerical solution can be expressed as

$$\begin{aligned} x_k=c_0\mu _p^k+\sum _{j=1}^{r-1}c_j\mu _{s,j}^k \end{aligned}$$

(60)

where $\mu _p$ and $\mu _s$ respectively denote the principal and spurious roots. As shown in Figs. 1, 2, 3 and 4, the one with the largest norm is the principal root when $\rho _\infty <1$, where the effects of spurious roots with smaller norms can be filtered out at the beginning. For the special case of $\rho _\infty =1$, the principal root is $(2+\Delta t\lambda )/(2-\Delta t\lambda )$, and the spurious roots are all equal to $-1$, so the spurious roots have larger norms if $\xi >0$, as shown in Figs. 2 and 4 . However, substituting the recurrence equation of the trapezoidal rule, as

$$\begin{aligned} x_k=\frac{2+\Delta t\lambda }{2-\Delta t\lambda }x_{k-1}, \, k=1,2,\cdots ,r-1 \end{aligned}$$

(61)

to the first $r-1$ steps of the recurrence equation of the linear multi-step method with $\rho _\infty =1$, as shown in Eq. (10), yields that

$$\begin{aligned} x_r=\left( \frac{2+\Delta t\lambda }{2-\Delta t\lambda }\right) ^r x_0, \, x_{r+1}=\left( \frac{2+\Delta t\lambda }{2-\Delta t\lambda }\right) ^{r+1}x_0, \, \cdots \end{aligned}$$

(62)

It follows that, for this case, the large spurious roots do not contribute to the solution, that is $c_1=c_2=\cdots =c_{r-1}=0$ in Eq. (59). Therefore, only the contribution of the principal root $\mu _p$ is considered in the following.

Representing $\mu _p=\text {e}^{\left( -{\overline{\xi }}\pm \text {i}\sqrt{1-{\overline{\xi }}^2}\right) {\overline{\omega }}\Delta t}$, the numerical solution can be expressed in a form similar to that of the exact solution, as

$$\begin{aligned} x_k=\text {e}^{{\overline{\lambda }}t_k}c_0,{\overline{\lambda }}=\left( -{\overline{\xi }}\pm \text {i}\sqrt{1-{\overline{\xi }}^2}\right) {\overline{\omega }} \end{aligned}$$

(63a)

where ${\overline{\xi }}$ and ${\overline{\omega }}$ are the damping ratio and natural frequency of the numerical solution, and they can be obtained from the norm $|\mu _p|$ and phase $\angle \mu _p$ as

$$\begin{aligned}&{\overline{\xi }}=-\frac{\ln {|\mu _p|}}{\sqrt{\left( \angle \mu _p\right) ^2+\left( \ln {|\mu _p|}\right) ^2}} \end{aligned}$$

(63b)

$$\begin{aligned}&{\overline{\omega }}=\frac{\sqrt{\left( \angle \mu _p\right) ^2+\left( \ln {|\mu _p|}\right) ^2}}{\Delta t} \end{aligned}$$

(64a)

By comparing Eqs. (58) and (62), ${\overline{\xi }}$ and $({\overline{T}}-T)/T$ (${\overline{T}}=2\pi /{\overline{\omega }}$), known as the amplitude decay ratio (AD) and period elongation ratio (PE), can be used to measure the amplitude and period accuracy, respectively.

Figures 6, 7 and 8 display the spectral radii (SR=$|\mu _p|$), AD($\%$) and PE($\%$), respectively, of LMS2, LMS3, LMS4 and two representative implicit methods, the generalized-$\alpha$ method and the $\rho _\infty$-Bathe method, referred to as G-$\alpha$ and Bathe respectively, for the undamped case. Because of the two-sub-step scheme, the computational cost required by the Bathe method per step is twice that of other methods approximately, so the abscissa is set as ${\Delta }t/(nT)$ ($n=2$ for Bathe and $n=1$ for other methods) to compare the methods under equivalent computational costs. In addition to $\rho _\infty$, the $\rho _\infty$-Bathe method can also change the spectral characteristics by adjusting the splitting ratio $\gamma$, so three cases of $\gamma =\gamma _0$, $\gamma =\gamma _0-0.2$ and $\gamma =\gamma _0+1$ are considered in these figures, where the value of $\gamma _0$ can refer to [35]. When $\gamma =\gamma _0$, its two sub-steps share the same effective stiffness matrix for linear problems.

Fig. 6

Spectral radii of several implicit second-order methods

As illustrated in Fig. 6, all methods can provide tunable algorithmic dissipation in the high-frequency domain by adjusting the parameter $\rho _\infty$. For a specified $0\le \rho _\infty <1$, LMS4 shows the spectral radius closest to 1 in the low-frequency region, so its dissipation error is the smallest, followed by LMS3, LMS2 and G-$\alpha$. With a small $\rho _\infty$, the Bathe method with $\gamma =\gamma _0$ and $\gamma =\gamma _0-0.2$ have the spectral radii close to that of LMS3 in the low-frequency region, but when $0.6\le \rho _\infty <1$, they have larger dissipation errors than G-$\alpha$. The Bathe method with $\gamma =\gamma _0+1$ shows the largest dissipation error for any $0\le \rho _\infty <1$. When $\rho _\infty =1$, all methods, except the Bathe method with $\gamma =\gamma _0-0.2$ and $\gamma =\gamma _0+1$, present the same properties as the trapezoidal rule.

Figures 7 and 8 focus on the low-frequency behaviour; they display results similar to those of Fig. 6. LMS4 is the most accurate among these methods in terms of both amplitude and period, followed by LMS3, LMS2, and G-$\alpha$. The Bathe method with $\gamma =\gamma _0+1$ shows the largest errors, and when $\rho _\infty$ is close to 1, the Bathe method with $\gamma =\gamma _0$ and $\gamma =\gamma _0-0.2$ are less accurate than G-$\alpha$. From [35], for a given $\rho _\infty$ and $\gamma \in (0,1)$, the Bathe method with $\gamma =\gamma _0$ possesses the largest amplitude decay and the smallest period error, which also can be observed by comparing the cases of $\gamma =\gamma _0$ and $\gamma =\gamma _0-0.2$.

Owing to the higher accuracy, the proposed LMS3 and LMS4 are really better candidates than the existing second-order methods. Since the developed single-step schemes, SS2, SS3 and SS4, are spectrally equivalent to LMS2, LMS3 and LMS4, respectively, SS3 and SS4 also have the same accuracy advantages.

Fig. 7

Amplitude decay ratios of several implicit second-order methods

Fig. 8

Period elongation ratios of several implicit second-order methods

4.2 Overshoot

From [14], the methods of unconditional stability are possible to show pathological growth at the initial steps, that is the so-called “overshoot”. For a convergent method, there is no overshoot as $\omega \Delta t\rightarrow 0$, so generally, only the case of $\omega \Delta t\rightarrow +\infty$ needs to be concerned. With the assumption, the recursive schemes of the linear r-step method, applied to the test model $\ddot{q}+\omega ^2q=0$, can be written as

$$\begin{aligned}&q_k\approx -\sum _{i=1}^{r}\frac{\beta _i}{\beta _0}q_{k-i} \end{aligned}$$

(64b)

$$\begin{aligned}&{\dot{q}}_{k}\approx -\sum _{i=1}^r\frac{\beta _i+\alpha _i\beta _0}{\Delta t\beta _0^2}q_{k-i}-\sum _{i=1}^r\frac{\beta _i}{\beta _0}{\dot{q}}_{k-i}\nonumber \\&r=2,3,4 \end{aligned}$$

(65a)

Since the overshooting phenomenon only occurs at the first few steps, the numerical results of the rth step are considered here. From Eq. (64), they depend on the start-up procedure for computing the first $r-1$ steps. If the single-step method as show in Eq. (4) is employed, that is

$$\begin{aligned}&q_k\approx -\frac{1-\beta _0}{\beta _0}q_{k-1}\\&{\dot{q}}_k\approx -\frac{1}{\Delta t\beta _0^2}q_{k-1}-\frac{1-\beta _0}{\beta _0}{\dot{q}}_{k-1}\\&k=1,2,\cdots ,r-1\nonumber \end{aligned}$$

(65b)

the approximate results at step r of LMS2, LMS3 and LMS4 can be obtained as

$$\begin{aligned} q_2\approx&-\rho _\infty (\rho _\infty ^2-\rho _\infty -1)q_0 \end{aligned}$$

(66a)

$$\begin{aligned} {\dot{q}}_2\approx&\frac{1}{2\Delta t}(\rho _\infty -3)(\rho _\infty +1)^2(2\rho _\infty ^2-3\rho _\infty -1)q_0\nonumber \\&-\rho _\infty (\rho _\infty ^2-\rho _\infty -1){\dot{q}}_0 \end{aligned}$$

(66b)

$$\begin{aligned} q_3\approx&-\frac{\rho _\infty }{12}\left( \rho _\infty ^6-8\rho _\infty ^5+20\rho _\infty ^4-8\rho _\infty ^3-25\rho _\infty ^2\right. \end{aligned}$$

(67a)

$$\begin{aligned}&\left. +16\rho _\infty +16\right) q_0\nonumber \\ {\dot{q}}_3\approx&-\frac{(\rho _\infty +1)^2}{72\Delta t}(\rho _\infty ^2-5\rho _\infty +10)\left( 3\rho _\infty ^6-25\rho _\infty ^5\right. \end{aligned}$$

(67b)

$$\begin{aligned}&\left. +76\rho _\infty ^4-78\rho _\infty ^3-27\rho _\infty ^2+73\rho _\infty +14\right) q_0\nonumber \\&-\frac{\rho _\infty }{12}(\rho _\infty ^6-8\rho _\infty ^5+20\rho _\infty ^4-8\rho _\infty ^3-25\rho _\infty ^2\nonumber \\&+16\rho _\infty +16){\dot{q}}_0 \end{aligned}$$

(67c)

$$\begin{aligned} q_4\approx&-\frac{\rho _\infty }{2000}\left( \rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-4\rho _\infty -15\right) \left( \rho _\infty ^8-\right. \nonumber \\&\left. 12\rho _\infty ^7+64\rho _\infty ^6-176\rho _\infty ^5+214\rho _\infty ^4 +68\rho _\infty ^3-304\rho _\infty ^2\right. \nonumber \\&\left. +120\rho _\infty +225\right) q_0 \end{aligned}$$

(68a)

$$\begin{aligned} {\dot{q}}\approx&\frac{(\rho _\infty +1)^2}{40000\Delta t}(\rho _\infty ^3-7\rho _\infty ^2+21\rho _\infty -35)\left( 4\rho _\infty ^{12}-\right. \nonumber \\&\left. 74\rho _\infty ^{11}+639\rho _\infty ^{10}-3315\rho _\infty ^9+11072\rho _\infty ^8-23430\rho _\infty ^7+\right. \nonumber \\&\left. 26944\rho _\infty ^6-2384\rho _\infty ^5-34890\rho _\infty ^4+32848\rho _\infty ^3+7681\rho _\infty ^2\right. \nonumber \\&\left. -20445\rho _\infty -2650\right) q_0-\frac{\rho _\infty }{2000}\left( \rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-\right. \nonumber \\&\left. 4\rho _\infty -15\right) \left( \rho _\infty ^8-12\rho _\infty ^7+64\rho _\infty ^6-176\rho _\infty ^5+214\rho _\infty ^4+\right. \nonumber \\&\left. 68\rho _\infty ^3-304\rho _\infty ^2+120\rho _\infty +225\right) {\dot{q}}_0 \end{aligned}$$

(68b)

respectively, where the parameters are represented by $\rho _\infty$. The results indicate that LMS2, LMS3 and LMS4 have zero-order overshoot in both displacement and velocity.

If the trapezoidal rule is used to solve the first $r-1$ steps, that is

$$\begin{aligned}&q_k\approx -q_{k-1} \end{aligned}$$

(69a)

$$\begin{aligned}&{\dot{q}}_k\approx -\frac{4}{\Delta t}q_{k-1}-{\dot{q}}_{k-1}\nonumber \\&k=1,2,\cdots ,r-1 \end{aligned}$$

(69b)

the approximate results at step r of LMS2, LMS3 and LMS4 have the form as

$$\begin{aligned} q_2&\approx -\rho _\infty (\rho _\infty -2)q_0 \end{aligned}$$

(70a)

$$\begin{aligned} {\dot{q}}_2&\approx \frac{1}{2\Delta t}(\rho _\infty ^2-5)(\rho _\infty ^2-4\rho _\infty -1)q_0-\rho _\infty (\rho _\infty -2){\dot{q}}_0 \end{aligned}$$

(70b)

$$\begin{aligned} q_3&\approx -\rho _\infty (\rho _\infty ^2-3\rho _\infty +3)q_0 \end{aligned}$$

(71a)

$$\begin{aligned} {\dot{q}}_3&\approx -\frac{1}{6\Delta t}\left( \rho _\infty ^6-7\rho _\infty ^5+20\rho _\infty ^4+14\rho _\infty ^3-115\rho _\infty ^2+\right. \nonumber \\&\left. 137\rho _\infty +22\right) q_0-\rho _\infty (\rho _\infty ^2-3\rho _\infty +3){\dot{q}}_0 \end{aligned}$$

(71b)

$$\begin{aligned} q_4&\approx -\rho _\infty (\rho _\infty -2)(\rho _\infty ^2-2\rho _\infty +2)q_0 \end{aligned}$$

(72a)

$$\begin{aligned} {\dot{q}}_4&\approx \frac{1}{20\Delta t}\left( \rho _\infty ^8-10\rho _\infty ^7+44\rho _\infty ^6-110\rho _\infty ^5+2\rho _\infty ^4\right. \nonumber \\&\left. +570\rho _\infty ^3-1100\rho _\infty ^2+830\rho _\infty +93\right) q_0-\nonumber \\&\rho _\infty (\rho _\infty -2)(\rho _\infty ^2-2\rho _\infty +2){\dot{q}}_0 \end{aligned}$$

(72b)

Also, no overshoot can be observed from the results. Therefore, as long as the method used for the start-up procedure does not have overshoot, the proposed multi-step methods also exhibit no overshoot from the rth step.

For the proposed single-step methods, SS2, SS3 and SS4, the results of the first step, applied to the model $\ddot{q}+\omega ^2q=0$, are checked. With the assumption $\omega \Delta t\rightarrow +\infty$, they can be expressed as

$$\begin{aligned} q_1&\approx \frac{1}{2}(\rho _\infty ^2-2\rho _\infty -1)q_0 \end{aligned}$$

(73a)

$$\begin{aligned} {\dot{q}}_1&\approx -\frac{1}{4\Delta t}(\rho _\infty +1)^2(\rho _\infty -3)^2q_0\nonumber \\&+\frac{1}{2}(\rho _\infty ^2-2\rho _\infty -1){\dot{q}}_0 \end{aligned}$$

(73b)

$$\begin{aligned} q_1&\approx -\frac{1}{6}(\rho _\infty ^3-4\rho _\infty ^2+5\rho _\infty +4)q_0 \end{aligned}$$

(74a)

$$\begin{aligned} {\dot{q}}_1&\approx -\frac{1}{36\Delta t}(\rho _\infty +1)^2(\rho _\infty ^2-5\rho _\infty +10)^2q_0\nonumber \\&-\frac{1}{6}(\rho _\infty ^3-4\rho _\infty ^2+5\rho _\infty +4)q_0 \end{aligned}$$

(74b)

$$\begin{aligned} q_1&\approx \frac{1}{20}(\rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-14\rho _\infty -15)q_0 \end{aligned}$$

(75a)

$$\begin{aligned} {\dot{q}}_1&\approx -\frac{1}{400\Delta t}(\rho _\infty +1)^2(\rho _\infty ^3-7\rho _\infty ^2+21\rho _\infty -35)^2q_0\nonumber \\&+\frac{1}{20}(\rho _\infty ^4-6\rho _\infty ^3+14\rho _\infty ^2-14\rho _\infty -15){\dot{q}}_0 \end{aligned}$$

(75b)

respectively. The numerical results indicate that the proposed single-step methods also have zero-order overshoot in both displacement and velocity.

In addition, the numerical example used in [14] to measure the overshooting behaviour is also considered here, which has the form as

$$\begin{aligned} \ddot{q}+\omega ^2q=0,\omega =2\pi ,q_0=1,v_0=0 \end{aligned}$$

(76)

With $\Delta t/T=10$, the numerical displacements and velocities given by the proposed multi-step methods, single-step methods and the multi-step methods with the trapezoidal rule (TR) as the start-up procedure, are summarized in Figs. 9 and 10 .

From the results, when $\rho _\infty <1$, the displacements show a decaying trend from the beginning; the velocities also begin to decay after the initial disturbance caused by the non-zero initial displacement. When $\rho _\infty =1$, both the displacements and velocities present periodic increases and decreases, since no algorithmic dissipation exists. In all the results, no pathological growth can be observed, which further validates that the proposed methods have no overshoot in both displacement and velocity.

Fig. 9

Displacements given by the proposed methods applied to the equation $\ddot{q}+\omega ^2q=0,\omega =2\pi ,q_0=1,v_0=0$

Fig. 10

Velocities given by the proposed methods applied to the equation $\ddot{q}+\omega ^2q=0,\omega =2\pi ,q_0=1,v_0=0$

5 Illustrative solutions

To check the performance of the proposed LMS2, LMS3, LMS4, SS2, SS3, and SS4, several illustrative examples are simulated in this section, and the G-$\alpha$ and Bathe method are also employed for comparison. In order to compare under the close computational costs, the step size of the two-sub-step Bathe method is set as twice that of the other methods. The G-$\alpha$ developed in [1], which improves the acceleration accuracy to second-order, is used in the computations. Unless otherwise specified, the single-step method in Eq. (4) is used as the start-up procedure for the linear multi-step methods.

Single degree-of-freedom example. The single-degree-of-freedom linear equation [22]

$$\begin{aligned}&\ddot{q}+2\xi \omega {\dot{q}}+\omega ^2q=R_1\sin (\omega _1t)+R_2\cos (\omega _2t) \end{aligned}$$

(77)

where

$$\begin{aligned}&\xi =0.1,\omega =2\pi ,R_1=10,R_2=15,\nonumber \\&\omega _1=3,\omega _2=1,q_0=1, v_0=3 \end{aligned}$$

(78)

is considered to check the convergence rate. The global errors (GE), defined as

$$\begin{aligned} \text {GE}_D=\sqrt{\frac{\sum \left( q_k-q(t_k)\right) ^2}{\sum \left( q(t_k)\right) ^2}} \end{aligned}$$

(79a)

$$\begin{aligned} \text {GE}_V=\sqrt{\frac{\sum \left( {\dot{q}}_k-{\dot{q}}(t_k)\right) ^2}{\sum \left( {\dot{q}}(t_k)\right) ^2}} \end{aligned}$$

(79b)

$$\begin{aligned} \text {GE}_A=\sqrt{\frac{\sum \left( \ddot{q}_k-\ddot{q}(t_k)\right) ^2}{\sum \left( \ddot{q}(t_k)\right) ^2}} \end{aligned}$$

(79c)

Fig. 11

Global errors versus $\Delta t/n$ of several implicit second-order methods with $\rho _\infty =0$

Fig. 12

Absolute errors of several implicit second-order methods with $\rho _\infty =0$

Fig. 13

Absolute errors of several implicit second-order methods with $\rho _\infty =0.6$

Fig. 14

Absolute errors of LMS4 with different start-up procedures

within [0, 10] versus $\Delta t/n$ for these methods using $\rho _\infty =0$ are plotted in Fig. 11. Second-order convergence rate can be clearly observed in all methods. The Bathe method with $\gamma =\gamma _0+1$ shows significantly larger errors than others. Besides, the absolute errors (AE), calculated by

$$\begin{aligned}&\text {AE}_{D}=|q_k-q(t_k)| \end{aligned}$$

(80a)

$$\begin{aligned}&\text {AE}_{V}=|{\dot{q}}_k-{\dot{q}}(t_k)|\end{aligned}$$

(80b)

$$\begin{aligned}&\text {AE}_{A}=|\ddot{q}_k-\ddot{q}(t_k)| \end{aligned}$$

(80c)

with $\Delta t=0.01$ for the case $\rho _\infty =0$ and $\rho _\infty =0.6$ are plotted in Figs. 12 and 13, respectively. In both cases, LMS4 and SS4 predict the most accurate solutions, followed by LMS3 and SS3, LMS2 and SS2, consistent with the discussion in Sec. 4. If the Bathe method with $\gamma =\gamma _0+1$ is excluded, G-$\alpha$ shows the largest errors when $\rho _\infty =0$, and the Bathe method with $\gamma =\gamma _0-0.2$ is the most inaccurate when $\rho _\infty =0.6$. The Bathe method with $\gamma =\gamma _0$ shows higher accuracy than the method with $\gamma =\gamma _0-0.2$, so only this scheme is considered in the following examples.

Fig. 15

Mass-spring oscillator

Fig. 16

Numerical solutions of $m_1$ given by several implicit second-order methods

To exhibit the effect of different start-up procedures on the accuracy, Fig. 14 plots the absolute errors given by LMS4 following the procedure in Table 1, SS4, and LMS4 using the trapezoidal rule for the first three steps with $\Delta t=0.01$. In addition to the trapezoidal rule, the other two start-up procedures are first-order accurate. From the results, the accuracy difference can be observed at the beginning, but gradually disappears over time. The single-step method SS4 has very close accuracy to LMS4 with the trapezoidal rule as the start-up procedure in the whole time. Therefore, the start-up procedure has a very limited impact on the overall accuracy. For linear systems, the procedure shown in Table 1 and the single-step method are more recommended, since they only need one factorization of the effective stiffness matrix.

Stiff-soft mass-spring system. The mass-spring oscillator [5], shown in Fig. 15, is considered as a model problem to test the dissipation ability of a method. The motion of $m_0$ is prescribed as $q_0=\sin (1.2t)$, and other parameters are $k_1=10^7$, $k_2=1$, $m_0=0$, $m_1=m_2=1$. The governing equation of $m_1$ and $m_2$ can be written as

(81)

With zero initial conditions and $\Delta t/n=0.1309$, the numerical solutions of $m_1$ by these methods using $\rho _\infty =0$ are summarized in Fig. 16. The results of $q_1$ are overlapping with each other, and from ${\dot{q}}_1(v_1)$ and $\ddot{q}_1(a_1)$, these methods all can filter out the rigid component in the first several steps. Because the first $r-1$ steps of the linear r-step method and the corresponding single-step method cannot offer the prescribed degree of algorithmic dissipation, the proposed methods need to experience more steps of high-frequency oscillations.

Figure 17 plots the acceleration of $m_1$ given by LMS4 with different start-up procedures. One can see that SS4 shows stronger dissipation in the first three steps, and LMS4 using the trapezoidal rule as the start-up procedure exhibits larger oscillation due to being non-dissipative. At the sixth step, the stiff component has been filtered out in all schemes.

Fig. 17

Acceleration of $m_1$ given by LMS4 with different start-up procedures

Wave propagation in a clamped-free bar. As shown in Fig. 18, the clamped-free bar [18, 35], excited by the load F at the free end, is considered. The system parameters are the elastic modulus $E=3\times 10^7$, cross-sectional area $A=1$, density $\rho =7.3\times 10^{-4}$, length $L=200$, and the step load $F=10^4$. The bar is meshed by 1000 linear two-node finite elements.

With different CFL numbers (the ratio of the propagation length per step $\sqrt{E/\rho }\Delta t$ to the element length L/1000), the velocity at the midpoint $x=100$ given by these methods using $\rho _\infty =0$ are plotted in Figs. 19–23. From the results, the spurious oscillation can be observed in all methods with CFL=1.0 (CFL=2.0 for the Bathe method), and it lasts longer for LMS3, SS3, LMS4 and SS4. However, with a smaller CFL number, which is different for each method, all methods can rapidly filter out the high-frequency oscillation. Among these methods, LMS4 and SS4 provide favorable results with a larger CFL number, so they require fewer steps than other methods.

Fig. 18

Clamped-free bar excited by load F

Fig. 19

Midpoint velocity for the Bathe method

Fig. 20

Midpoint velocity for the G-$\alpha$ method

Fig. 21

Midpoint velocity for LMS2 and SS2

Fig. 22

Midpoint velocity for LMS3 and SS3

Fig. 23

Midpoint velocity for LMS4 and SS4

Fig. 24

Pre-stressed membrane excited by the concentrated load at the center

Fig. 25

Snapshots for displacement at $t\approx 13$ by $70\times 70$ finite element meshes

A two-dimensional wave propagation problem. The two-dimensional wave propagation problem, a pre-stressed membrane excited by the concentrated load at the center [20, 28], as shown in Fig. 24, is considered. Its transverse governing equation can be expressed as

$$\begin{aligned} \frac{1}{c_0^2}\frac{\partial ^2q}{\partial ^2t}-\left( \frac{\partial ^2q}{\partial x^2}+\frac{\partial ^2q}{\partial y^2}\right) =R(0,0,t) \end{aligned}$$

(82)

where the exact wave velocity $c_0$ is assumed as 1. The concentrated load has the form as

$$\begin{aligned} R(0,0,t)=\left\{ \begin{array}{ll} &{}4\left( 1-(2t-1)^2\right) ,0<t<1 \\ &{} 0, t\ge 1 \end{array} \right. \end{aligned}$$

(83)

Because of the symmetry, only the domain $\left[ 0,15\frac{1}{6}\right] \times \left[ 0,15\frac{1}{6}\right]$ needs to be solved. It is meshed regularly by four-node rectangular elements with nodes equally spaced. The consistent mass matrix is used in all solutions.

With zero initial conditions, the displacements at $t\approx 13$ given by these methods with $\rho _\infty =0$ and the CFL number suggested from the last example are shown in Figs. 25–27, where the membrane is meshed by $70\times 70$, $105\times 105$ and $140\times 140$ elements, respectively. By the mesh of $140\times 140$ elements, Fig. 28 plots the obtained displacements and velocities at the angle of $\theta =0$ and $\theta =\pi /4$, where $\theta$ denotes the angle between the wave propagation direction and the x-axis. Except for the trapezoidal rule, other methods all can predict reasonably accurate solutions. The linear multi-step method shows almost identical results to its corresponding single-step method. From the above two examples, the proposed methods perform very well in the wave propagation problems with an appropriate CFL number. A more detailed analysis of the proposed methods for wave propagation problems, such as the optimal CFL numbers for different $\rho _\infty$, other advantages and disadvantages, is still deserved in the future.

Fig. 26

Snapshots for displacement at $t\approx 13$ by $105\times 105$ finite element meshes

Fig. 27

Snapshots for displacement at $t\approx 13$ by $140\times 140$ finite element meshes

Fig. 28

Displacements and velocities at $t\approx 13$ at the angle of $\theta =0$ and $\theta =\pi /4$ (Length=$\sqrt{x^2+y^2}$)

Spring-pendulum model. The spring-pendulum model [10] shown in Fig. 29 is solved. Its motion equation is expressed as

$$\begin{aligned} m\ddot{r}&+kr-m(L_0+r){\dot{\theta }}^2-mg\text {cos}\theta =0 \end{aligned}$$

(84a)

$$\begin{aligned} m\ddot{\theta }&+\frac{m(2{\dot{r}}{\dot{\theta }}+g\text {sin}\theta )}{L_0+r}=0 \end{aligned}$$

(84b)

The system parameters are set as $m=1~\mathrm {kg}$, $L_0=0.5~\mathrm {m}$, $g=9.81~\mathrm {m/s^2}$, $k=98.1~\mathrm {N/m}$ and $98.1\times 10^6~\mathrm {N/m}$ for modelling the compliant and stiff cases, respectively. The initial conditions are

$$\begin{aligned} r_0=0~\mathrm{{m}},\dot{r}_0=1~\mathrm{{m/s}},\theta _0=\frac{\pi }{4}~\mathrm{{rad}},\dot{\theta }_0=0~\mathrm{{rad/s}} \end{aligned}$$

(85)

With $\Delta t/n=0.01~\mathrm {s}$, Figs. 30–31 show the numerical results of r and $\theta$, as well as their absolute errors for the compliant case, where $\rho _\infty =0$ is adopted in all methods, and the reference solution is obtained using the Bathe method with $\Delta t=10^{-5}~\mathrm {s}$. For the nonlinear problem, LMS4 and SS4 still provide the most accurate results, and G-$\alpha$ yields the largest errors. The single-step schemes also show close accuracy to the corresponding multi-step methods.

Figure 32 plots the computed r and $\theta$ for the stiff case by using $\Delta t/n=0.01~\mathrm {s}$ and $\rho _\infty =0$. Since the algorithmic dissipation of the proposed methods works from the rth step, LMS4 and SS4 needs more steps to damp out the stiff component. From about the sixth step, all methods can give reasonable results for r.

Truss element. In this example, the classic pendulum model [27], as shown in Fig. 33, is considered. It is discretized as 1 truss element considering the Green strain. This example is usually used to check the energy-conserving characteristic of a method for nonlinear structural dynamics. The system parameters are the length $L=3.0443~\mathrm {m}$, density per unit length $\rho A=6.57~\mathrm {kg/m}$, axial stiffness $EA=10^4~\mathrm {N}$, and $10^{10}~\mathrm {N}$ for the compliant and stiff cases. The pendulum is excited by the horizontal velocity $v_0=7.72~\mathrm {m/s}$ at the free end. The gravity is not considered, so the pendulum makes continuous rotations in this plane, along with axial straining.

With $\Delta t/n=0.01~\mathrm {s}$ and $\rho _\infty =0$, Figs. 34–35 present the computed results for the compliant and stiff cases, respectively. Figure 34 displays the axial deformation $\Delta L$ and total energy for the compliant case. Significant amplitude and energy decay can be observed with the G-$\alpha$, LMS2 and SS2 methods. LMS4 and SS4 exhibit better energy-conserving properties for the nonlinear system owing to their higher accuracy. Figure 35 gives the axial deformation $\Delta L$ and rotation angle $\theta$ for the stiff case. Plots similar to those of Fig. 32 can be observed. All these methods can effectively filter out the stiff component after a few oscillations.

6 Conclusions

In this paper, second-order unconditionally stable schemes of linear multi-step methods, represented by LMS2, LMS3, and LMS4, are discussed. From linear analysis, the parameters, controlled by $\rho _\infty$, of LMS3 and LMS4 are given for optimal accuracy, unconditional stability and controllable algorithmic dissipation. In addition, single-step methods, spectrally equivalent to the linear multi-step ones, are proposed by using intermediate state variables. The parameters of the latter methods, named SS2, SS3, and SS4, are also obtained by enabling them to have the same characteristic polynomials as LMS2, LMS3, and LMS4, respectively. The resulting schemes show equivalent formulations of the corresponding linear multi-step methods, except for the first few steps, in which the linear multi-step methods require a dedicated start-up procedure. Being self-starting, the equivalent single-step schemes are more convenient to use.

Fig. 29

Spring-pendulum model

Fig. 30

Computed r for the compliant case

Fig. 31

Computed $\theta$ for the compliant case

Fig. 32

Computed r and $\theta$ for the stiff case

Fig. 33

Truss-pendulum model

Fig. 34

Computed $\delta L$ and total energy for the compliant case

Fig. 35

Computed $\delta L$ and $\theta$ for the stiff case

Compared with some representative second-order methods, including LMS2, G-$\alpha$ and the Bathe method, the newly developed LMS3 and LMS4 show higher amplitude and period accuracy for a given degree of algorithmic dissipation. Among them, LMS4 is the most accurate, followed by LMS3, and LMS2, which indicates that employing the states of more past steps helps improving accuracy. The same conclusion can be obtained for SS2, SS3 and SS4. Finally, the above methods mentioned are applied to some illustrative examples. LMS4 and SS4 exhibit accuracy advantage and favorable energy-conserving characteristics in linear and nonlinear examples. The algorithmic dissipation of these methods also perform well in the wave propagation problem and stiff systems.