1 INTRODUCTION

In December, 2019, a pneumonia outbreak was reported in Wuhan, China, during which COVID-2019 virus was identified for the first time by analyzing nucleic acid in a patient with pneumonia. According to data from the Chinese Center for Disease Control and Prevention, the reproduction number is estimated as lying between 2 and 3, which corresponds to the number of new infections from a single infection; so long as it is greater than 1, the epidemic will grow (see Figs. 1, 2).

Fig. 1.
figure 1

Number of COVID-2019 infected (blue), recovered (orange), and died (green) individuals from January 22, 2020 to February 11, 2020 over the territory of China.

Full size image
Fig. 2.
figure 2

Recorded cases of COVID-2019 detected on January 24, 2020 (left) and February 10, 2020 (right) in the territory of China [3, 7].

Full size image

A possible source of COVID-2019 virus is bats, since RNA from COVID-2019 samples was found to coincide up to 96% with virus RNA, which was earlier found in Rhinolophus affinis [1]. Virus replication occurs mainly in the lower respiratory tract, causing cytokine overproduction and an immune response in the organism that reduces the number of Т-lymphocytes in the blood, which are responsible for the protective functions of the organism [2]. As of February 11, 2020, the number of confirmed infected cases was 43 143 people, of which 1018 were deaths and 4347 were recovered people [3]. Genetically, COVID-2019 is 80% identical to severe acute respiratory syndrome (SARS), an outbreak of which was observed in China in 2003 and resulted in more than 5000 infected individuals [4] (see Table 1). However, the rate of spread of COVID-2019 is much higher than that of SARS, since, starting at January 24, the number of recorded cases in Wuhan grew from 549 to 31 728 people over 17 days (see Fig. 2).

Table 1.   Statistical data on spread of SARS (as of July 31, 2003) [4] and COVID-2019 (as February 10, 2020) coronaviruses [7]
Full size table

An additional key epidemiological parameter is the incubation period, which is estimated to be 3–7 days according to WHO data. An optimal incubation period of 5.2 days was obtained in [5, 6].

On January 30, the World Health Organization declared the COVID-2019 disease outbreak a public health emergency of international concern [7].

In the context of the current situation, it is necessary to predict the epidemic evolution in China and the world. An approach to the prediction of COVID-2019 spread is the mathematical modeling of infection transmission in a population with a given infection source, transition rates between groups of people with similar characteristics (symptoms, quarantine, antibodies, strains), death rate, latent period, degree of isolation (population migration between provinces, ban on product import), and statistical data on infected and recovered individuals at fixed times. A mathematical model based on the mass balance law and described by a system of nonlinear ordinary differential equations (ODEs) most accurately describes the spread of infectious diseases in populations divided into groups of individuals with similar characteristics (for example, susceptible, infected, treated, recovered, etc.). Most of the coefficients and initial conditions for the ODEs are not known or can be estimated with a large error. For example, the number of recorder COVID-2019 cases was predicted in [8] based on data for the period of up to January 23, 2020. The predicted number on February 10, 2020, was 75 000 people, although the actual number was 40 645 individuals. Such errors in the predicted evolution of an infectious disease leads to huge costs associated with control measures and result in incorrect conclusions. To identify unknown parameters of mathematical models described by ODE systems, it is necessary to use additional information on the number of infected and recovered individuals on every day. The approach used in this work is classical for inverse problems [9]. In the next sections, we describe existing mathematical models of COVID-2019 spread, present methods for solving the arising inverse problems, and give examples of their solutions.

This paper is organized as follows. In Section 2, we present mathematical models of COVID-2019 spread and formulate inverse problems. The identifiability of a mathematical model is described in Section 3. A classification of optimization methods for solving inverse problems and the domain of their application are addressed in Section 4.

2 MATHEMATICAL MODELS OF COVID-2019 SPREAD

Mathematical epidemiology models based on a compartmental structure are described by systems of nonlinear ODEs

$$\dot {X} = F\left( {X(t),\varphi } \right),~~~X({{t}_{0}}) = {{X}_{0}},\quad t \in \left( {{{t}_{0}},T} \right),$$
(1)

and characterize an isolated spread of infection within a region. An outbreak of a novel infection leads to the development of new mathematical epidemiology models, taking into account its features. One of the first models of a tuberculosis epidemic was constructed in [10] based on mathematical models in meteorology, demography, economy, and epidemiology of acute diseases. It captures the main difference of a tuberculosis epidemic from epidemic processes of acute diseases, namely, the presence of a long latent period. Later, Waaler’s model was developed by Soviet mathematicians Marchuk and his followers [11, 12]. Specifically, a mathematical model of pneumonia transmission was widely used [13].

A mathematical model of COVID-2019 transmission from a supposed source of infection (bats) to humans was developed in [1]. Since the infection source has not been traced thus far, the authors adapted a mathematical model of virus transmission from a seafood market to humans. The model is schematically shown in Fig. 3. It consists of 14 ODEs of type (1) and involves 25 coefficients φ characterizing the transition rates between 14 groups. The groups are identified according to the well-known SEIR model, which describes the dynamics of an infection between susceptible, exposed, infected, and recovered individuals. The problem of identifying unknown coefficients based on available statistical data concerning the number of infected and recovered individuals at fixed days is ill posed, i.e., its solution is neither unique nor stable [14, 15]. To use such a model for predictions, it is necessary to obtain more statistical data.

Fig. 3.
figure 3

Block diagram of the mathematical source–market–people model [1].

Full size image

A more detailed mathematical model of a metapopulation is based on a global network of local population groups connected by edges representing passenger traffic between cities [16]. At each node of the network, the outbreak dynamics is locally modeled using a discrete-time compartmental SEIR model similar in structure to the mathematical model of a tuberculosis epidemic of 1962 [10]. The SEIR parameters are estimated based on a five-day incubation period. It is assumed that initial COVID-2019 cases are present only in Wuhan, and border control is not taken into account.

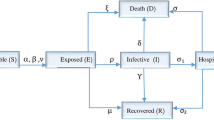
In [17] a deterministic SEIR compartmental model for the dynamics of the novel coronavirus was proposed to estimate the influence exerted by public health care control on the infection (see Fig. 4). According to the model, the outbreak had to reach its maximum on February 7, 2020, with a considerable low peak value. The proposed epidemiology SEIR model is based on eight ODEs with 12 coefficients φ, and parameter values are chosen using the method of interval generation [18]. Note that the prediction was obtained with an error, since the peak value within growth was not reached on February 12, 2020, which requires the development of more accurate methods for parameter identification for ODE systems.

Fig. 4.
figure 4

Diagram of the mathematical model of COVID-2019 spread [17].

Full size image

A new time-delay mathematical model for the COVID-2019 outbreak in China was proposed in [19]. The model consists of four integro-differential equations with three unknown coefficients determined by a local gradient method using additional information on the number of infected and recovered individuals over two weeks. Since the solution of the identification problem is not unique, the reliability of the numerical results is not guaranteed because of the use of local iterative methods [20, 21].

The same approach to the construction of compartmental mathematical models based on systems of nonlinear ODEs was used for other close acute infections, such the SARS outbreak of 2003 in China [22–24], Middle Eastern respiratory syndrome (MERS) in Saudi Arabia and South Korea [25], tuberculosis and HIV in Russia and Kazakhstan [26–28], etc. Despite the genome similarity of COVID-2019 to the SARS and MERS coronavirus, the course of the disease, including the incubation period, differs strongly, which prevents the application of previously developed models to the novel COVID-2019 coronavirus. The presence of a latent period in COVID-2019 is similar to mathematical models of tuberculosis dynamics, which we used to obtain a prediction verified by statistical data [26–28].

2.1 Formulation of the Inverse Problem

In view of the measures taken in China to control the epidemic, including quarantine and isolation, the population in a chosen province is divided into susceptible (S), exposed (E), asymptomatic infected (A), symptomatic infected (I), hospitalized (H), and recovered (R) individuals. Additionally, groups under quarantine are distinguished, namely, susceptible (Sq) and exposed (Eq) [17]. The diagram of the compartmental mathematical model is shown in Fig. 4. Taking into account the mass balance law, the mathematical model for ODE system (1) is written as

$$\begin{gathered} \dot {S} = - \left( {\beta c + cq\left( {1 - \beta } \right)} \right)S\left( {I + \theta A} \right) + \lambda {{S}_{q}}, \\ \dot {E} = \beta c\left( {1 - q} \right)S\left( {I + \theta A} \right) - \sigma E, \\ \dot {I} = \sigma \rho E - \left( {{{\delta }_{I}} + \alpha + {{\gamma }_{I}}} \right)I, \\ \end{gathered} $$
$$\begin{gathered} \dot {A} = \sigma \left( {1 - \rho } \right)E - {{\gamma }_{A}}A, \\ {{{\dot {S}}}_{q}} = \left( {1 - \beta } \right)cqS\left( {I + \theta A} \right) - \lambda {{S}_{q}}, \\ \end{gathered} $$
(2)
$$\begin{gathered} {{{\dot {E}}}_{q}} = \beta cqS\left( {I + \theta A} \right) - {{\delta }_{q}}{{E}_{q}}, \\ \dot {H} = {{\delta }_{I}}I + {{\delta }_{q}}{{E}_{q}} - \left( {\alpha + {{\gamma }_{H}}} \right)H, \\ \dot {R} = {{\gamma }_{I}}I + {{\gamma }_{A}}A + {{\gamma }_{H}}H, \\ \end{gathered} $$

with initial data

$$\begin{gathered} S({{t}_{0}}) = {{S}_{0}},\quad E({{t}_{0}}) = {{E}_{0}},\quad I({{t}_{0}}) = {{I}_{0}},\quad A({{t}_{0}}) = {{A}_{0}}, \\ {{S}_{q}}({{t}_{0}}) = {{S}_{{{{q}_{0}}}}},\quad {{E}_{q}}({{t}_{0}}) = {{E}_{{{{q}_{0}}}}},\quad H({{t}_{0}}) = {{H}_{0}},\quad R({{t}_{0}}) = {{R}_{0}}. \\ \end{gathered} $$
(3)

The parameters of mathematical model (2) and initial data (3) in the case of Wuhan on January 10, 2020, are described in Table 2.

Table 2.   Description of parameters, their approximate values, and initial data for the mathematical model (2), (3) of COVID-2019 spread in China [17]
Full size table

The mathematical model (2), (3) involves 14 unknown parameters \(p = (c,\beta ,q,\rho ,{{\delta }_{I}},{{\delta }_{q}},{{\gamma }_{I}},{{\gamma }_{A}},{{\gamma }_{H}},\alpha ,~{{E}_{0}},{{I}_{0}},{{A}_{0}},{{E}_{{{{q}_{0}}}}}) \in {{\mathbb{R}}^{{14}}}.\) \(p = (c,\beta ,q,\rho ,{{\delta }_{I}},{{\delta }_{q}},{{\gamma }_{I}},{{\gamma }_{A}},{{\gamma }_{H}},\alpha ,~{{E}_{0}},{{I}_{0}},{{A}_{0}},{{E}_{{{{q}_{0}}}}}) \in {{\mathbb{R}}^{{14}}}.\) To identify them, we formulate the inverse problem of determining the parameter vector p from available additional measurements of the number of susceptible individuals at fixed days tk:

$$S({{t}_{k}}) = {{S}_{k}},\quad {{S}_{q}}({{t}_{k}}) = {{S}_{{{{q}_{k}}}}},\quad H({{t}_{k}}) = {{H}_{k}},\quad R({{t}_{k}}) = {{R}_{k}},\quad {{t}_{k}} \in \left( {{{t}_{0}},T} \right),\quad k = 1, \ldots ,K.$$
(4)

In the vector form of (1), \(X = (S,E,I,A,{{S}_{q}},{{E}_{q}},H,R)\) and \(p = (\varphi ,~{{E}_{0}},{{I}_{0}},{{A}_{0}},{{E}_{{{{q}_{0}}}}})\). Data (4) are written as

$${{X}_{i}}({{t}_{k}}) = {{f}_{{ik}}},\quad k = 1, \ldots ,K,\quad i \subset \{ 1, \ldots ,N\} ,$$

where \({{f}_{{ik}}} = ({{S}_{k}},{{S}_{{{{q}_{k}}}}},{{H}_{k}},{{R}_{k}})\) and \(N = 8\).

In operator form, the inverse problem (2)–(4) is written as

$$A(p) = f,$$

where \(A{\kern 1pt} :Q \to F\); \(Q = \{ p \geqslant 0\} \) and F are the Hilbert spaces of feasible parameters and measurements, respectively; \(f = ({{f}_{{i1}}},{{f}_{{i2}}}, \ldots ,{{f}_{{iK}}})\) is the vector of data; and \(i = 1,5,7,8\).

In the general case, inverse problem (2)–(4) is ill posed, i.e., its solution may be nonunique or unstable (the Fréchet derivative \(A{\kern 1pt} '\) of the operator of the inverse problem has no inverse). Based on available data (4), the identifiability analysis performed in Section 3 yields a set of identifiable parameters, which are subsequently determined [14, 15, 29].

Inverse problem (2)–(4) is reduced to the minimization of the objective functional \(J(p) = \left\langle {A(p) - f,A(p) - f} \right\rangle \), which, in our case, has the form

$$J(p) = \frac{1}{K}\mathop \sum \limits_{k = 1}^K \,\mathop \sum \limits_i \,{{({{X}_{i}}({{t}_{k}};p) - {{f}_{{ik}}})}^{2}}$$

and characterizes the standard deviation of the model results from statistical data. Finally, the inverse problem (2)–(4) is written as

$$p\text{*} = \mathop {\operatorname{argmin} }\limits_{p \in Q} J(p).$$
(5)

A classification of methods for solving of problem (5) is given in Section 4.

3 IDENTIFIABILITY OF THE MATHEMATICAL MODEL

In certain cases, the solution of the inverse problem (2)–(4) may be nonunique or unstable with respect to the errors in measurements (4). To determine a unique set of parameters (or their combinations) and the degree of sensitivity of the unknown parameters to errors in the data of the inverse problem, the identifiability of mathematical models for ODE systems was analyzed [14, 30, 31]. Formally, the following three types of identifiability can be distinguished (see the diagram in Fig. 5).

Fig. 5.
figure 5

Classification of identifiability methods [14].

Full size image

1. A priori (structural) identifiability is used to study the structure of a model in the case of continuous data. The methods of structural identifiability include ones of an additional function, differential algebra, series expansions, graph theory, and others [14, 30]. For example, the graph theory method not only determines the identifiability of a model, but also allows one to find a special change of variables that brings the original model to an identifiable form.

2. Practical (a posteriori) identifiability makes it possible to reveal identifiable parameters with respect to noisy data by applying Monte Carlo techniques, the correlation matrix method, and others [14, 29].

3. Sensitivity analysis yields a sequence of parameters sensitive to measurement errors and estimates the degree of this sensitivity [14, 29].

To study the identifiability of the inverse problem (2)–(4), we used the DAISY code [31]. An analysis showed that the problem of identifying 14 parameters \(p\) from measurements (4) has a nonunique solution, i.e., the model is locally unidentifiable. When the parameter vector is reduced to \((\beta ,q,\rho ,{{\delta }_{I}},{{\delta }_{q}},{{E}_{0}},{{I}_{0}},{{A}_{0}},{{E}_{{{{q}_{0}}}}}) \in {{\mathbb{R}}^{9}}\), the mathematical model (2)–(4) becomes locally identifiable.

4 OPTIMIZATION METHODS

Formally, optimization methods can be divided into global, local, and combined ones. The first group consists of nature-like algorithms, including genetic algorithms, simulated annealing, particle swarm optimization, differential evolution, etc., as well as covering methods, for example, Evtushenko’s method of nonuniform coverings [32–34] and tensor decomposition. Global optimization methods localize the domain of an extremum and they are effective in spaces of high dimension. Local optimization methods are subdivided into two groups: order-zero methods, which use only the value of the functional (the Nelder–Mead and Hooke–Jeeves methods) and gradient methods (Gauss–Newton, Levenberg–Marquardt, etc.). A feature of local methods is high efficiency and convergence to a local extremum for gradient methods. The main disadvantage of local methods is the convergence to a local minimum, especially, in spaces of high dimension. Combined methods are based on the following idea: global optimization methods determine the domain of a global extremum, in which local methods start to refine the extremum value [26]. The formal classification of optimization methods is shown as a diagram in Fig. 6. In what follows, we outline the basic methods of three groups: global stochastic methods (Subsection 4.1), covering methods (Subsection 4.2), and local gradient-type methods (Subsection 4.3).

Fig. 6.
figure 6

Classification of optimization methods for solving problem (5).

Full size image

4.1 Global Stochastic Methods

The global stochastic methods include nature-like algorithms modeling natural selection processes (genetic algorithm [28, 35], the method of differential evolution, genetic programming, etc.), as well as algorithms imitating instinctive behavior in nature (particle swarm optimization, the ant algorithm) and processes in physics (simulated annealing [26]). A feature of algorithms of this type is that they solve a simpler problem based on laws of nature and do not take into account the features of the functional to which they are applied. Such algorithms can be naturally extended to parallel architectures. Although these methods are global, i.e., they determine the domain of a global extremum, there are no theoretical estimates for their convergence (only stochastic ones are available). Moreover, the tuning of parameters of nature-like algorithms to ensure statistical convergence is a complicated problem, which is sometimes more complicated than the optimization problem.

4.2 Tensor Decomposition

Covering methods need a priori information about the functional whose extremum is to be found. For example, the basic idea of nonuniform covering method [32] is that the solution space Q is partitioned into subsets covering Q. On each subset, the objective function has certain properties (for example, Lipschitz continuity, convexity, existence of a second derivative, etc.) which are used in solving optimization problems, thus improving the convergence rate.

Tensor decomposition (TD) is a global optimization method that is directly applied to parameter maximization problems [37]. It is based on the properties of the TD [37, 38]

$$\mathcal{T}({{i}_{1}}, \ldots ,{{i}_{d}}) = \mathop \sum \limits_{{{a}_{0}}, \ldots ,{{a}_{d}}} {{G}_{1}}({{a}_{0}},{{i}_{1}},{{a}_{1}}){{G}_{2}}({{a}_{1}},{{i}_{2}},{{a}_{2}}) \ldots {{G}_{d}}({{a}_{{d - 1}}},{{i}_{d}},{{a}_{d}}),$$
(6)

and on the method of TD-cross approximation of the tensor \(\mathcal{T}\) [39], which constructs an approximation based on the largest elements. Here, Gi are called the TD kernels of the tensor \(\mathcal{T}\) and are matrices of size \({{r}_{{i - 1}}} \times {{r}_{i}},\) \({{r}_{0}} = {{r}_{d}} = 1,\) \({{a}_{0}} = {{a}_{d}} = 1.\)

For a large space of admissible parameters, the TD-based optimization method yields optimal parameters. Additionally, some of the computations can be executed in parallel, which makes the method a direct alternative to nature-like algorithms.

4.2.1. TD algorithm for optimization problem. Minimization problem (5) can be reduced to the maximization of the function \(g(J(p)) = \operatorname{arccot} J(p)\). We specify the set of feasible values that can be taken by \({{p}_{k}} \in [{{a}_{k}},{{b}_{k}}]\), i.e., by the components of the vector \(p = ({{p}_{1}}, \ldots ,{{p}_{d}})\), and represent them on a grid, dividing each of the intervals \([{{a}_{k}},{{b}_{k}}]\) by \(n\) nodes.

Let \({{i}_{k}}\) be an arbitrary value taken by the parameter \({{p}_{k}}\). Considering \(g(J(p))\) for all feasible combinations \(p_{k}^{{{{i}_{k}}}}\), taking into account the discrete form of the obtained response, and the representability of the multivariable functional in the form of a tensor, we obtain

$$\mathcal{T}({{i}_{1}}, \ldots ,{{i}_{d}}) = g(p_{1}^{{{{i}_{1}}}}, \ldots ,p_{d}^{{{{i}_{d}}}}).$$

The original problem is reduced to finding the largest component of the tensor \(\mathcal{T}\). Eventually, we obtain the solution of the global minimization problem in the projection onto the grid, and the result can be improved by applying local minimization.

4.3 Gradient-Type Methods

Gradient-type methods as applied to minimization problem (5) consist in successive approximation of the solution p according to the iterative process

$${{p}_{{n + 1}}} = {{p}_{n}} - {{\alpha }_{n}}J{\kern 1pt} '({{p}_{n}}),\quad {{\alpha }_{n}} > 0,\quad {{p}_{0}} \in Q.$$

Here, \({{\alpha }_{n}}\) is the descent parameter, the choice of which is determined by the type of the gradient method (steepest descent method, Landweber iteration, minimum errors, conjugate gradients, etc.) and \(J{\kern 1pt} '({{p}_{n}}) = 2[A{\kern 1pt} '({{p}_{n}})]{\kern 1pt} {\text{*}}(A({{p}_{n}}) - f)\) is the gradient of the objective functional \(J(p)\). The convergence of gradient methods to a normal pseudosolution and convergence acceleration techniques were addressed in [20, 40–43] (see also references therein). The following expression for the objective functional gradient \(J{\kern 1pt} '\) was obtained in [44]:

$$J{\kern 1pt} '(p) = - {{\left( {\mathop \smallint \limits_{{{t}_{0}}}^T F_{\varphi }^{{\text{T}}}(X(t),\varphi ){\Psi }(t)dt,~{{{\Psi }}_{2}}({{t}_{0}}),{{{\Psi }}_{3}}({{t}_{0}}),{{{\Psi }}_{4}}({{t}_{0}}),{{{\Psi }}_{6}}({{t}_{0}})} \right)}^{{\text{T}}}}{\kern 1pt} ,$$

where \({\Psi }(t) = \left( {{{{\Psi }}_{1}}(t), \ldots ,{{{\Psi }}_{8}}(t)} \right)\) is the solution of the adjoint problem

$$\begin{gathered} {\dot {\Psi }} = - F_{X}^{{\text{T}}}(X(t),\varphi )\Psi (t),\quad t \in \bigcup\limits_{k = 0}^K {({{t}_{k}},{{t}_{{k + 1}}})} ,\quad {{t}_{{K + 1}}} = T; \\ \Psi (T) = 0,\quad {{[{{{\Psi }}_{i}}]}_{{t = {{t}_{k}}}}} = \frac{2}{K}({{X}_{i}}({{t}_{k}};p) - {{f}_{{ik}}}),\quad k = 1, \ldots ,K,\quad i \subset \{ 1, \ldots ,N\} . \\ \end{gathered} $$

Here, \({{F}_{\varphi }},~\;{{F}_{X}}\) are the corresponding Jacobian matrices and \({{[{{{\Psi }}_{i}}]}_{{t = {{t}_{k}}}}}\) is the jump in the function \({{{\Psi }}_{i}}\) at the point tk.

5 CONCLUSIONS

Mathematical models for transmission dynamics of COVID-2019, an epidemic of which broke out in Wuhan in December 2019 were presented. The models are described by systems of nonlinear ordinary differential equations, whose coefficients and initial data are unknown or their averaged values are specified. A mathematical model of COVID-2019 spread under quarantine consisting of eight nonlinear ODEs with 10 unknown coefficients and four initial conditions was considered. The identifiability of the model was analyzed using additional measurements of susceptible individuals infected under quarantine and recovered at fixed times. This inverse problem is a priori not identifiable, i.e., its solution is nonunique, but becomes identifiable when some varying parameters of the model are fixed. The problem of identifying model parameters is reduced to the minimization of a quadratic objective functional of the residual. Methods for solving the minimization problem are given based on a combination of global techniques (covering methods, nature-like algorithms, multilevel gradient methods) and local techniques (order-zero methods, gradient methods).

The model under study is similar to the mathematical model for tuberculosis transmission with control programs [26] and for coinfections of tuberculosis and HIV [29]. The combined approaches for functional optimization were found effective as applied to problems of this type. Namely, global optimization methods determine the domain of the global extremum, while local optimization methods refine solutions of the inverse problem, “starting” in the global extremum domain. Specification of parameters in models of tuberculosis transmission in Russian Federation regions allowed us to simulate the situation for several years ahead and to compare the prediction with statistical data (see Fig. 7).

Fig. 7.
figure 7

Number of susceptibles SB (turquoise) under treatment without T (yellow) and with Tm (red) drug-resistant strains in the Sverdlovsk region of the Russian Federation for data over 2010–2013 with a prediction for 2014–2019 as obtained after parameter identification by simulated annealing combined with gradient descent (thin) and by tensor decomposition combined with gradient descent (thick) in thousand people. Circles denote the statistical data used to solve the parameter identification problem (red) and to verify the algorithms (color of the modelled quantity).

Full size image