Thermodynamic modeling and correlations of CH₄, C₂H₆, CO₂, H₂S, and N₂ hydrates with cage occupancies

Abstract

The present work focuses on developing a framework for accurate prediction of thermodynamic conditions for single-component hydrates, namely CH₄, CO₂, N₂, H₂S, and C₂H₆ (coded in MATLAB). For this purpose, an exhaustive approach is adopted by incorporating eight different equations of states, namely Peng–Robinson, van der Waals, Soave–Redlich–Kwong, Virial, Redlich–Kwong, Tsai-Teja, Patel, and Esmaeilzadeh–Roshanfekr, with the well-known van der Waals–Platteeuw model. Overall, for I–H–V phase region, the Virial and van der Waals equation of state gives the most accurate predictions with minimum AAD%. For L_w–H–V phase region, Peng–Robinson equation of state is found to yield the most accurate predictions with overall AAD of 3.36%. Also, genetic programming algorithm is adopted to develop a generalized correlation. Overall, the correlation yields quick estimation with an average deviation of less than 1%. The accurate estimation yields a minimal AAD of 0.32% for CH₄, 1.93% for C₂H₆, 0.77% for CO₂, 0.64% for H₂S, and 0.72% for N₂. The same correlation can be employed for fitting phase equilibrium data for other hydrates too. The tuning parameter, n, is to be used for fine adjustment to the phase equilibrium data. The findings of this study can help for a better understanding of phase equilibrium and cage occupancy behavior of different gas hydrates. The accuracy in phase equilibria is intimately related to industrial applications such as crude oil transportation, solid separation, and gas storage. To date, no single correlation is available in the literature that can accurately predict phase equilibria for multiple hydrate species. The novelty of the present work lies in both the accuracy and generalizability of the proposed correlation in predicting the phase equilibrium data. The genetic programming generalized correlation is convenient for performing quick equilibrium prediction for industrial applications.

Introduction

Gas hydrates are non-stoichiometric, solid ice-like compounds that are formed when gas molecules of a certain size, known as hydrate formers, get trapped within the cavities of hydrogen-bonded H₂O molecules (Sloan and Koh 2007). The hydrates can be formed in a pure water environment in a laboratory (Chaturvedi et al. 2018) as well as in naturally occurring sediments (Ngema et al. 2019a). Moreover, the type of gas hydrate structure (sI, sII, and sH) formed depends upon the thermodynamic (P, T) conditions (Arora et al. 2014, 2015a) and size of guest gas molecules (Sloan Jr 2003) (Fig. 1).

Fig. 1

A general sketch of the present study highlighting investigated aspects

Gas hydrates find a significant scope for applications in energy storage (Makogon 1981; Arora et al. 2015b; Chaturvedi et al. 2018; Sadeq et al. 2018), seawater desalination (Zheng et al. 2017), CO₂ capture, and sequestration (Demirbas 2010; Herslund et al. 2012; Dejam and Hassanzadeh 2018a, b) besides other separation applications (Carroll 2003). However, for the purpose of these applications, thermodynamic conditions of gas hydrate formations should be determined accurately. The importance of thermodynamic modeling (Kazemi et al. 2019; Tan et al. 2019; Qiu et al. 2019) lies in determining the behavior of I–H–V, L_w–H–V (P–T) curves under compositions involving pure component, mixture of gases as well as using inhibitors and promoters (Yan et al. 2019), understanding through cage occupancy analysis (Sun et al. 2018). As such, thermodynamic modeling (Nikpoor et al. 2016; Tan et al. 2019) eliminates the need for carrying out tedious experiments (Ngema et al. 2019b) besides validating experimental findings.

For the prediction of hydrate formation conditions (P, T), van der Waals–Platteeuw (VdW–P) model based on statistical thermodynamics (van der Waals and Platteeuw 1958) is used. The VdW–P model approach requires arbitrary reference parameters, which are obtained from the regression analysis of experimental data. However, this approach was improved upon by Klauda and Sandler (2000), who developed a fugacity-based approach. Their fugacity-based approach eliminated the need for reference parameters, thus minimizing empirical relations. More so, Chen and Guo (1998) also developed a simplified model with an easier approach to calculate Langmuir constants and potentials for both phases (Mohammadi et al. 2016).

Recently, several theoretical studies have employed the VdW–P model used for prediction of hydrate phase equilibria. Recently, Pahlavanzadeh et al. (2019) employed the VdW–P model for predicting phase equilibria of CH₄, CO₂ hydrate with fluid phase as water, SDS using CPA equation of state. de Menezes et al. (2018) used VdW–P model for modeling CH₄, CH₄–C₂H₆ systems using CPA equation of state. Waseem and Alsaifi (2018) employed VdW–P model in conjunction with SAFT-VR Mie equation of state to model C1–C4 hydrate systems with water. Kondori et al. (2018) extended the works of Waseem and Alsaifi to model hydrate systems formed in water in the presence of salts (NaCl, KCl, MgCl₂, and CaCl₂). Other notable using VdW–P model includes Hejrati Lahijani and Xiao (2017) for CH₄, CO₂ hydrates. Ferrari et al. (2016) modeled only CO₂ hydrates with CPA equation of state. A comprehensive review of field-scale testing, techniques, and quantitative analysis is described in detail by Arora et al. (2015c) and Arora and Cameotra (2015). The latest experimental research in gas hydrates is largely driven with a motivation to commercialize the hydrate-based applications. Recently, Rasoolzadeh et al. (2019) performed experimental studies using BMIM-BF₄, BMIM-DCA, and TEACl, on storage capacity, along with kinetics of formation and dissociation. An in-depth review of the latest electromagnetic radiation-induced dissociation techniques can be found here (Khan et al. 2020). Another interesting study was conducted by Abedi-Farizhendi et al. (2019). They investigated the effect of synthesized nanostructures, including graphene oxide, chemically reduced graphene oxide with SDS, chemically reduced graphene oxide with polyvinyl pyrrolidone, and multi-walled carbon nanotubes on induction time and gas storage capacity. The flow choking within pipelines has also been investigated by Kar et al. (2016) and Bbosa et al. (2019). An interesting experimental procedure using motor current for prediction of hydrate formation and dissociation was demonstrated by Sadeq et al. (2017).

From the literature review, it is evident that pure hydrates find tremendous applications concerning separation and storage of gases such as H₂, CH₄, propane, and ethane. Therefore, predicting the correct thermodynamic (T, P) conditions using the right (EOS) becomes imperative. Moreover, high-temperature thermodynamic predictions are one of the least researched areas (T ≥ 295 K). Hence, its accurate estimation (Ɛ ≤ 5–10%) is necessary for successful application under ambient conditions, around T ~ 298 K. Several researchers have tried to establish the performance of EOS for I–H–V and L_w–H–V temperature ranges. Bhawangirkar et al. (2018) predicted thermodynamic data of methane hydrate by applying PRSV, PT, and SRK EOS, with %AAD of 0.55, 0.09, and 0.003, respectively. Sfaxi et al. (2012) predicted the equilibrium temperature of methane hydrate with the CPA-EOS and VdW–P model with an average absolute deviation of 3.2%. Karamoddin and Varaminian (2011) predicted equilibrium pressure of hydrate by applying PR-EOS. Sato et al. (2007) reproduced the phase equilibrium conditions for methane hydrate for the pressure range from 2 to 60 MPa with CSMHYD. Tavasoli et al. (2011) predicted the thermodynamic condition of methane hydrate by ESD–EOS with 9.25% ADD.

To date, there is no generalized correlation available in the literature that can accurately predict phase equilibria accurately for multiple hydrates. Moreover, there are limited studies that report the cage occupancy behavior for hydrates of CH₄, CO₂, N₂, H₂S, and C₂H₆. The present work explores these gaps in the literature. The novelty of the current work lies in the development of a generalized correlation, which yields less than 1% AAD. The VdW–P model has been improved by incorporating the modified UNIFAC model. Accurate phase equilibrium and cage occupancy prediction are achieved using eight different equations of states which have been optimized for I–H–V and L_w–H–V phase regions. Moreover, previous studies involving thermodynamic modeling have shown data prediction only up to 300 K. In the present study, the phase equilibrium prediction and fitting have been extended to T ~ 320 K. The limitations behind the study are that the phase equilibrium prediction is limited to only single-phase components. For mixed hydrates, refer to our previous study here (Kumari et al. 2020). The generalized correlation has not been tested for other pure component and mixed hydrates. These limitations will be addressed in our future studies. The present work is subdivided into several subsections. First, the framework of thermodynamic approach is presented. Next, subsections regarding Langmuir constant calculation, solubility corrections, water activity coefficient, and different equations of states are discussed. The last section entails genetic programming correlation approach. Following the background information, the results and discussion from the thermodynamic modeling and generalized correlation is presented.

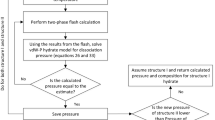
Framework of thermodynamic approach

van der Waals–Platteeuw (VdW–P) model

van der Waals–Platteeuw theory uses the chemical potential of water in the hydrate phase to represent the H–I/L_w–V equilibria and consequently derives an expression. This expression is used for calculating the equilibrium conditions of gas hydrate and the compositions of each of the three components (van der Waals and Platteeuw 1958). The encaged molecules of the gas are assumed to be moving randomly around within the spherical cavity, which contains a single molecule of gas at most. However, the interactions among the guest molecules within the lattice structure are assumed to be adequately small to avert any sort of hydrate lattice disfigurement (Saeedi Dehaghani and Badizad 2016). This suggestion is based on the assumption that internal partition functions for encaged gas molecules and molecules in the ideal gas phase are equal. In the present model, only London forces are considered essential for describing gas–H₂O interaction, because all other polar forces are supposedly incorporated in the hydrate lattice, with hydrogen bonding. This model was further extended for mixed component hydrates (Parrish and Prausnitz 1972; Saeedi Dehaghani 2017). The three phases include solid hydrate (H), vapor (V), and liquid water (L_w), respectively. Hence, for establishing the phase equilibrium, water in (empty hydrate lattice) is taken as a relative common component between the hydrate and liquid water phases as:

$$\Delta \mu_{\text{w}}^{H} = \mu_{\text{w}}^{\beta } - \mu_{\text{w}}^{H} = \mu_{\text{w}}^{\beta } - \mu_{\text{w}}^{{L_{\text{w}} }} = \Delta \mu_{\text{w}}^{{L_{\text{w}} }}$$

(1)

where $\mu_{\text{w}}^{\beta }$ is the chemical potential of water in an imaginary empty hydrate lattice, which represent the reference state. Superscripts L_w and H represent liquid aqueous and hydrate(solid) phase (Valavi and Dehghani 2012). $\beta$ and H represents the hypothetical empty and occupied hydrate lattice. The structures of empty hydrate need a guest for the stabilization of the crystal lattice; hence, the empty hydrate becomes thermodynamically unstable (Talaghat 2009). The following expression can be derived using statistical mechanics for the differences in chemical potential between the metastable empty hydrate and real filled hydrate lattices.

$$\Delta \mu_{\text{w}}^{H} \left( {T,P} \right) = - RT\mathop \sum \limits_{i = 1}^{{N_{\text{cavity}} }} v_{i} \ln \left( {1 - \mathop \sum \limits_{j = 1}^{{N_{\text{species}} }} \theta_{ij} \left( {T,P} \right)} \right)$$

(2)

where $v_{i}$ denote the number of cages of type i per water molecule in the hydrate lattice. $\theta_{ij}$ denotes fractional cage occupancy of species j within cage i; assuming single guest presence per cage, the Langmuir adsorption relation is used for determining the fractional guest cage occupancies.

$$\theta_{ij} \left( {T,P} \right) = \frac{{C_{ij} \left( T \right)f_{i} \left( {T,P} \right)}}{{1 + \mathop \sum \nolimits_{k = 1}^{N} C_{ik} f_{k} \left( {T,P} \right)}}$$

(3)

where $f_{l} \left( {T,P} \right)$ is the fugacity of the guest which can be obtained by a proper equation of state (EOS)

$$f_{j} = y_{j} \varphi_{j} \left( {P,T,y,{\text{EOS}}} \right)P$$

(4)

where $\varphi_{j}$ represents the fugacity coefficient j which is calculated by Saeedi Dehaghani (2017).

$$\ln \varphi_{j} = \ln \left( {\frac{{f_{i} }}{{y_{i} P}}} \right) = \frac{1}{RT}\mathop \int \limits_{0}^{P} \left( {v_{j} - \frac{RT}{P}} \right){\text{d}}P.$$

(5)

Here, $C_{ij}$ represents Langmuir constant, which accounts for all interactions (gas–water particularly).

$$C_{ij} \left( T \right) = \frac{4\pi }{kT}\mathop \int \limits_{0}^{{R_{\text{cav}} }} \exp \left( { - \frac{w\left( r \right)}{kT}} \right)r^{2} {\text{d}}r.$$

(6)

Here, k is the Boltzmann constant, and the guest–water molecule interaction of surrounding cages is represented by w(r), which is known as the (spherically symmetric) cell potential or Kihara cell potential (Sloan and Koh 2007).

This potential equation is acquired by assuming a coating of water molecules over a sphere with a mean radius of cavity $(R_{\text{cav}} )$ (Sloan and Koh 2007). The VdW–P model employs London interactions between water and gas in hydrate with Lenard–Jones potential function (van der Waals and Platteeuw 1958). Interactions in hydrate can be calculated by spherical core Kihara potential function more accurately as (McKoy and Sinanoǧlu 1963)

$$w\left( r \right) = 2z\varepsilon_{k} \left[ {\frac{{\sigma_{k}^{12} }}{{R^{11} r}}\left( {\delta^{10} + \frac{{a_{r} }}{R}\delta^{11} } \right) - \frac{{\sigma_{k}^{6} }}{{R^{5} r}}\left( {\delta^{4} + \frac{{a_{r} }}{R}\delta^{5} } \right)} \right]$$

(7)

$$\delta^{N} = \frac{1}{N}\left[ {\left( {1 - \frac{r}{R} - \frac{{a_{r} }}{R}} \right)^{ - N} - \left( {1 + \frac{r}{R} - \frac{{a_{r} }}{R}} \right)^{ - N} } \right]$$

(8)

where N is equal to 11, 10, 5, and 4, as shown in Eq. (8). z is the coordination number, which represents the number of oxygen atoms along the circumference of the cavity.

Langmuir constant calculation

The phase equilibrium of gas hydrates and cage occupancy can be predicted by Langmuir constant, which is based on accurate intermolecular potential. Various researchers have calculated Langmuir constant using Kihara potential model or an empirical potential model (McKoy and Sinanoǧlu 1963; Ng and Robinson 1976; Robinson and Ng 1985; Lundgaard and Mollerup 1992; Barkan and Sheinin 1993; Englezos 1993; Avlonitis 1994; Anderson et al. 2004). It has been proven that the intermolecular potential between molecules of water and gas can also be calculated by spherical and angle-dependent ab initio potential (Bolis et al. 1983; Novoa and Whangbo 1991; Cao et al. 2001a, b; Finney 2001).

In the present work, two different approaches have been adopted for the calculation of Langmuir constant. First, the Jones and Devonshire cell theory was adopted for determining small and large cavities by employing the regressed Kihara potential parameters (code in MATLAB, LANGS.m, and LANGL.m). This has been more accurate than the correlation available in the literature. It has been used for the prediction of small and large occupancies, which are discussed later in this paper.

Moreover, for the temperature range of 260–300 K (Parrish and Prausnitz 1972) proposed a simpler correlation as a substitute for calculating Langmuir constant. The calculation can be performed using Eq. (3) using the coefficients listed in Table 1 for the different components employed in this study. It must be noticed that units of A are in K/atm, while units of B are 1/K only.

Table 1 Langmuir constant (coefficients of correlation for CH₄ hydrates)

$$C_{ij} = \frac{{A_{ij} }}{T}\exp \left( {\frac{{B_{ij} }}{T}} \right).$$

(9)

The differential chemical potential between empty hydrate lattice, ice phase, or liquid water is presented by,

$$\Delta \mu_{\text{w}}^{\pi } \left( {T,P} \right) = \frac{{\Delta \mu_{\text{w}} \left( {T_{0} ,P_{0} } \right)T}}{{T_{0} }} - T\mathop \int \limits_{{T_{0} }}^{T} \frac{{\Delta h_{\text{w}}^{\pi } \left( T \right)}}{{T^{2} }}{\text{d}}T + \mathop \int \limits_{{P_{0} }}^{P} \Delta V_{\text{w}}^{\pi } {\text{d}}P - RT\ln \left( {\gamma_{\text{w}} X_{\text{w}} } \right)$$

(10)

where $\Delta \mu_{\text{w}} \left( {T_{0} ,P_{0} } \right)$ is the chemical potential of water at the reference temperature and pressure $\left( {T_{0} ,P_{0} } \right)$. The freezing point of water and zero pressure is considered as the reference. The expression for the determination of enthalpy differences is given by Eq. (10). Table 2 lists the relevant parameters used in Eqs. (9), (10), and (11). Equation (10) has been solved using the global adaptive quadrature method by employing integral functions available in MATLAB software. In the first step, $\Delta \mu_{\text{w}} \left( {T_{0} ,P_{0} } \right)$ is used as provided in Table 4, and relevant values of $T, T_{0} , {\text{and}}\;P_{0}$ are used. Next, Eq. (11) is substituted, nested with Eq. (12), and integrated. The overall integral $\Delta \mu_{\text{w}}^{\pi } \left( {T,P} \right)$ is calculated as the sum of three terms in Eq. (10). The second and third terms are also calculated using the adaptive quadrature method employed in integral function.

Table 2 Required thermodynamic parameters for van der Waals model (Parrish and Prausnitz 1972; Mohamadi et al. 2018)

Table 3 (CH₄ hydrate) Kihara parameters for hydrate–gas interaction, obtained from regression

Table 4 Thermodynamic properties of liquid water and empty hydrate at reference conditions (Waseem and Alsaifi 2018)

$$\Delta h_{\text{w}}^{\pi } = \Delta h_{\text{w}}^{0,\pi } + \mathop \int \limits_{{T_{0} }}^{T} \Delta C_{P} {\text{d}}T.$$

(11)

The heat capacity is determined using Eq. (11)

$$\Delta C_{P} = \Delta C_{P}^{0} + \alpha^{\prime}\left( {T - T_{0} } \right).$$

(12)

The Kihara potential parameters and reference parameters for empty hydrate are listed in Tables 3 and 4.

Solubility corrections

As can be seen in Eq. (9), solubility is one of the most important parameters which govern the phase equilibrium modeling of gas hydrates. Some of the hydrate formers, such as CO₂ and H₂S, exhibit high solubility in the water, while other components such as N₂, CH₄, C₂H₆, and other higher members of alkane family exhibit less solubility in water. Moreover, soluble components such as carbon dioxide and hydrogen sulfide exhibit variable solubility for the extreme conditions for pressure and temperature. Hence, a robust formulation presented by Krichevsky–Kasarnovsky was used. The equation is capable of accurately determining the solubility of the gas in aqueous solution. Accordingly, the mole fraction of gas dissolved in the water phase is specified as follows (Carroll and Mather 1992; Klauda and Sandler 2000):

$$X_{\text{g}}^{\text{L}} = \frac{{f_{\text{g}}^{\text{G}} }}{{H_{\text{g-w}} \times {\text{e}}^{{\frac{{v_{\text{g}}^{\infty } \times \left( {P - {\text{Psat}}} \right)}}{RT}}} }}.$$

(13)

Here, $H_{\text{g-w}}$ denotes the Henry’s constant for gas in water, and subscript $\infty$ and G are used for representing infinite dilution and the gas phase, respectively. $f_{\text{g}}^{\text{G}}$ denotes the fugacity of gas in the vapor phase. As mentioned above, the fugacity is calculated using a single EOS for the entire calculation. The procedure is repeated for each equation of state. Also $v_{\text{g}}^{\infty }$ represents the molar volume of the gas at infinite dilution (mol/m³), while Psat denotes the saturated vapor pressure of water which is calculated using the temperature-dependent equation (Klauda and Sandler 2000)

$$P_{\text{w}}^{\text{sat}} = {\text{e}}^{{\left( {4.1539\ln T - \frac{5500.9332}{T} + 7.6537 - 16.1277 \times 10^{ - 3} T} \right)}}$$

(13a)

where T is in (K) and P is in (MPa), respectively.

H_g-w is determined using the temperature-dependent Henry’s constant correlation (Klauda and Sandler 2003; Neto et al. 2018), given by equation:

$$\ln \left( {H_{i} } \right) = - H_{i}^{1} - \frac{{H_{i}^{2} }}{T} - H_{i}^{3} \times \ln T - H_{i}^{4} \times T.$$

(13b)

Activity coefficient of water

Unlike most other thermodynamic hydrate prediction studies where the activity coefficient of water is considered as a unity, we employed the modified UNIFAC model to account for the activity coefficient used in Eq. (9). The modified UNIFAC model calculates the activity coefficient using the combination and residual terms (Zhao et al. 2019). The formulation is described as follows:

$$\ln \gamma_{i} = \ln \gamma_{i}^{\text{c}} + \ln \gamma_{i}^{\text{r}}.$$

(14)

Here, superscripts c and r denote the combinatorial and residual significance, respectively. The combinatorial term accounts mainly for the varying shapes and sizes of molecules. Each of these terms is calculated using Eqs. (14a) and (14b) (Zhao et al. 2019)

$$\ln \gamma_{i}^{\text{c}} = { \ln }\left( {\frac{{\omega_{i} }}{{x_{i} }}} \right) + 1 - \left( {\frac{{\omega_{i} }}{{x_{i} }}} \right)$$

(14a)

$$\omega_{i} = \left( {\frac{{x_{i} r_{i}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}{{\mathop \sum \nolimits_{j} x_{j} r_{j}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}} \right)$$

(14b)

$$r_{i} = \mathop \sum \limits_{k} v_{ki} R_{k}.$$

(14c)

Further, the residual term includes the energetic interactions taking place between the molecules and is represented with Eq. (15) as follows (Zhao et al. 2019):

$$\ln \gamma_{i}^{\text{r}} = \mathop \sum \limits_{k} v_{ki} \left( {\ln \varGamma_{k} - \varGamma_{k}^{i} } \right).$$

(15)

Here, $v_{ki}$ is representative of the number of groups k in given molecule i, in the above equation, $\varGamma_{k}$ denotes the residual activity coefficient for group k, while $\varGamma_{k}^{i}$ represents the individual activity coefficient of each component. The residual activity coefficient (Zhao et al. 2019) is determined as

$$\ln \varGamma_{k} = Q_{k} \left( { - \left[ {\ln \left[ {\mathop \sum \limits_{m} \theta_{m} \theta_{mk} } \right]} \right] + 1 - \mathop \sum \limits_{m} \frac{{\theta_{m} \theta_{mk} }}{{\mathop \sum \nolimits_{n} \theta_{n} \psi_{nk} }}} \right)$$

(15a)

$$\psi_{nm} = {\text{e}}^{{\left( {\frac{{ - A_{nm} }}{T}} \right)}}$$

(15b)

$$A_{nm} = A_{nm,1} + A_{nm,2} \left( {T - T_{0} } \right)$$

(15c)

$$\theta_{m} = \frac{{Q_{m} X_{m} }}{{\mathop \sum \nolimits_{n} Q_{n} X_{n} }}$$

(15d)

$$X_{m} = \frac{{\mathop \sum \nolimits_{j} v_{mj} X_{j} }}{{\mathop \sum \nolimits_{j} \mathop \sum \nolimits_{n} v_{nj} X_{j} }}.$$

(15e)

Different equations of states

The capability of various EOSs in conjunction with the VdW–P model (van der Waals and Platteeuw 1958), Redlich–Kwong (RK) (Redlich and Kwong 1949), modified Soave–Redlich–Kwong (SRK) (Soave 1972), Peng–Robinson (PR) (Peng and Robinson 1976), Patel–Teja (PT) (Patel and Teja 1982), Tsai–Jan (Tsai and Jan 1990), Esmaeilzadeh–Roshanfekr (ER) (Esmaeilzadeh and Roshanfekr 2006) along with Virial is applied for the prediction of stability conditions. Table 5 lists the sources of experimental data. The current work is also validated against CSMHYD (Hashimoto et al. 2008). The following steps were taken in order to solve the different equations of states for obtaining the fugacity and the fugacity coefficient.

Table 5 The values of $H_{i}$ constants for the different guests

• 1. The PV equation form is converted into the cubic form using the compressibility factor definition.

• 2. The equation is expressed into a cubic equation in terms of Z, i.e., compressibility factor with three roots.

• 3. The cubic equation is then solved to obtain the roots using MATLAB. The negative values are discarded, and appropriate root selection is made to obtain Z, compressibility factor.

• 4. The PV equation is also expressed in terms of Z and is used to calculate the fugacity coefficient using Eq. (5). The fugacity coefficient is used for fugacity determination.

• 5. The detailed procedure for each equation of state is explained in Online Appendices B and C.

Correlation for thermodynamic prediction by genetic programming

A new mathematical correlation using genetic programming is developed for the accurate prediction of formation pressure of CH₄, C₂H₆, CO₂, H₂S, and N₂ hydrates. Genetic programming was first introduced by Holland (1984) and extended by Koza (1994) using Darwin’s theory of natural selection. Genetic programming generates a comprehensive set of programs to fit a particular dataset. It randomly generates a population of programs which is depicted using trees. A new population is generated from each tree set, which proceeds with mutation, crossing over with best resulting trees to create a new dataset (population) (Koza 1994; Searson et al. 2010; Abooali and Khamehchi 2017). For the equilibrium prediction of hydrates, pressure, P (MPa), and temperature, T (K), are used as input and output variables. To obtain the relationship, a sequence of steps are followed, namely the initial population of programs, fitness assessment of each program, creating a new population following mutation, crossover, and reproduction, and finally repeating the steps until the termination criterion is satisfied. The initial choice of sets for the population generation is critical to ensure the closure and sufficiency during the course of evaluation. This ensures that the functions are capable of accepting the values, and constants that are obtained from the terminal set. Moreover, it also provides stability to the geometric programming routine as even a failure in evaluation of one of the constituting programs does not invoke error during the execution. The detailed methodology applied in the present study is described in brief as follows:

• 1. The initial population is randomly generated from a pre-defined function set, FS = {+, −, *, %, sin, cos, RLOG, EXP, SQRT}, and termination set, TS = {T, CONSTANTS). The % denotes protected division used to avoid undefined division by zero. The population size was set to 150.

• 2. The programs created using the function and terminal sets evolved using the ramped half and half method, with depth value as 50. This ensures diversity and yields large, full, unbalanced, and small trees.

• 3. The fitness of each program was evaluated using the AAD as defined below. The satisfaction criterion of 2% AAD is used to achieve high accuracy in the developed correlation.

  $${\text{AAD}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {\frac{{Z_{\exp } - Z_{\text{pred}} }}{{Z_{\exp } }}} \right| \times 100\%$$

  .

• 4. Reproduction or copying to the next generation was done in a probabilistic manner. The probability was set as 0.1 for reproduction.

• 5. The crossover events were performed using the standard GP crossover technique, which involves randomly selecting a node and using it as a crossover point. The probability of crossover events was set as 0.80. Moreover, the sub-crossover events, i.e., for internal nodes and overall (internal node plus terminal), the probabilities of 0.9 and 0.1, were used.

• 6. Mutation in the current study was performed using the standard GP mutation. For this purpose, a mutation point is chosen randomly using a uniform probability distribution through a particular program. This is followed by the usual removal and replacement by another tree, the mutation point. The probability for the mutation to occur was set to 0.1.

• 7. The maximum number of generations was set to 500 to achieve the satisfaction criteria of AAD = 2%.

• 8. The steps from 2 to 7 are repeated until the termination criterion is satisfied by the routine.

Hence, using genetic programming tool, a generalized correlation has been developed which provides perfect fitting to all five (CH₄, C₂H₆, CO₂, H₂S, and N₂) different hydrates (with minimal changes in the equation.

In results and discussion section, we discuss the effectiveness and accuracy of the proposed correlation. The correlation includes a tunable parameter (n) with a value ranging between (1–2)* for each of the five different hydrates.

GP tree for new correlation

$$P = A \times T^{B} + C \times T^{D} + E \times T^{F} + G \times {\text{e}}^{{\frac{H}{T}}} + I \times {\text{e}}^{{\frac{J}{{T^{n*} }}}}$$

where P: pressure is in MPa and T: temperature is in K. *represents a tuned value.

The tree structure of the new correlation obtained is shown in Fig. 2. As mentioned previously, the correlation requires temperature, T (K), as the input variable and estimates equilibrium pressure, P (MPa), as the output. The new correlation is generalized as it is capable of predicting equilibrium pressure of hydrate formation for all the five different hydrate species, namely CH₄, C₂H₆, CO₂, H₂S, and N₂. To validate the correlation, non-repetitive datasets were used. The developed correlation applies to a wide range of temperatures 259.2 ≤ T (K) ≤ 320 for the different hydrates. The present correlation, though, a bit long, is easier to implement because of its minimal invoking. Unlike previous correlations, the present correlation does not involve any nested terms. The nesting of terms leads to perquisite background calculations which make them tedious and computationally intensive. The details of proposed correlation, including the respective trees as shown in Fig. 2, are described as follows:

Fig. 2

Tree structure for developed correlation, *represents a tuned value

$$P = P1 + P2$$

(16a)

$$P1 = A \times T^{B} + C \times T^{D}$$

(16b)

$$P2 = P3 + P4$$

(16c)

$$P3 = I \times {\text{e}}^{{\frac{J}{{T^{n*} }}}}$$

(16d)

$$P4 = P5 + P6$$

(16e)

$$P5 = E \times T^{F}$$

(16f)

$$P6 = G \times {\text{e}}^{{\frac{H}{T}}}.$$

(16g)

For the sake of brevity, the depiction of trees, terminal, and individual tree functions are not shown here. The details of the individual trees represented using Eqs. (16a) to (16g) are described in Online Appendix D. Please refer to Online Appendix section for more elaborate descriptions.

The details of all the nested terms used in the correlations compiled in Table 6 are described in Online Appendix B.

Table 6 Equations for different correlations for methane (CH₄) hydrates

In order to exhibit the superiority and accuracy of correlation obtained through genetic programming, a case study for Methane hydrates is carried out in great detail. The phase equilibrium experimental data for methane hydrates are compiled from the available literature. In reference to the plot shown in Fig. 13, it is evident that beyond 300 K, most correlations predict pressure values with significant error. This deviation indicates that most correlations fail to estimate equilibrium pressure values accurately.

Results and discussion

In the current study, the results are divided into three different sections. In the first section, results from thermodynamic phase modeling using VdW–P with the different equations of states are presented. In the following section, evaluation of existing correlations and accuracy of new correlation (based on genetic programming) is performed. The final part entails a discussion on gas hydrate cage occupancies for the different guest components.

Thermodynamic model results

In this study, eight different equations of states, namely Peng–Robinson (PR), Soave–Redlich–Kwong (SRK), Redlich–Kwong (RK), Patel–Teja (PT), Esmaeilzadeh and Roshanfekr (ER), Virial, van der Waals (VDW), and Tsai–Jan (TJ) are used. The calculations are divided into two different temperature ranges, namely below ice point (I–H–V) 260 ≤ T ≤ 273.15, and above ice point, L_w–H–V regime 273.15 ≤ T ≤ Tmax. This is done to identify the EOS, which performs the best in I–H–V and L–H–V region. For determining the best EOS, statistical error AAD has been calculated and is given in Table 7.

Table 7 Statistical error, AAD % for the ice–hydrate–vapor equilibria and liquid hydrate vapor equilibria

Methane hydrates

See Figs. 3 and 4.

Fig. 3

Predicted pressure versus experimental plot for I–H–V phase region, AAD %, [Min/Max] of [1.5/5.4]

Fig. 4

Predicted pressure versus experimental plot for L_w–H–V phase region, AAD % [Min/Max] of [5.5/40.8]

Ethane hydrates

See Figs. 5 and 6.

Fig. 5

Predicted pressure versus experimental plot for I–H–V phase region, AAD %, [Min/Max] of [4.5/7.6]

Fig. 6

Predicted pressure versus experimental plot for L_w–H–V phase region, AAD %, [Min/Max] of [2.1/14]

Carbon dioxide hydrate

See Figs. 7 and 8.

Fig. 7

Predicted pressure versus experimental plot for I–H–V phase region, AAD %, [Min/Max] of [4.2/12.9]

Fig. 8

Predicted pressure versus experimental plot for L_w–H–V phase region, AAD %, [Min/Max] of [2.1/5.1]

Hydrogen sulfide hydrates

See Figs. 9 and 10.

Fig. 9

Predicted pressure versus experimental plot for I–H–V phase region, AAD %, [Min/Max] of [3.1/4.0]

Fig. 10

Predicted pressure versus experimental plot for L_w–H–V phase region, AAD %, [Min/Max] of [4.6/9.1]

Nitrogen hydrates

See Figs. 11 and 12 and Table 8.

Fig. 11

Predicted pressure versus experimental plot for I–H–V phase region, AAD %, [Min/Max] of [2/16.4]

Fig. 12

Predicted pressure versus experimental plot for L_w–H–V phase region, AAD %, [Min/Max] of [1.7/26.2]

Table 8 Statistical errors for temperature range: 260 ≤ T ≤ 320 K

Table 9 The constants determined with n = 1.6

Ice–hydrate–vapor equilibria (I–H–V region)

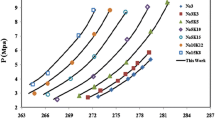
Figures 3, 5, 7, 9, and 11 depict the ice–hydrate–vapor (I–H–V) phase equilibria curves for (1) methane (CH₄), (2) ethane (C₂H₆), (3) carbon dioxide (CO₂), (4) hydrogen sulfide (H₂S), and (5) nitrogen hydrates. Through these figures, it can be stated that decent matching with experimental results is achieved for each hydrate guest. For CH₄ hydrates, as can be observed from Table 7, the minimum average absolute deviation (AAD %) is found to be 1.16 using the van der Waals equation (VDW). The performance of other equations, namely Peng–Robinson (PR), Soave–Redlich–Kwong (SRK), Redlich–Kwong (RK), Patel–Teja (PT), and Esmaeilzadeh–Roshanfekr (ER), also yields excellent matching with experimental results with error values less than 2%. Also, the Virial equation produces a decent approximation with AAD of approximately 5%, which is acceptable. For ethane, C₂H₆ hydrates, the model shows excellent agreement only using the Virial equation of state with AAD of 4.5%. For other equation of states, it is observed that results are the same with similar prediction yielding error values of nearly 7.5%. This can be attributed to the constant values of molar volume, which is assumed to be “constant” in this study. For carbon dioxide hydrates, the model predicts fair results only using the Virial equation of state. The average absolute deviation for CO₂ hydrates is only 4.2%, while other EOSs fail to predict the experimental values correctly with errors over 10%. As can be seen from the tabular data (8), hydrogen sulfide, H₂S, is modeled accurately with an absolute average deviation of less than 4% for all equations of states. The most definitive agreement is achieved using the Virial equation of state, which exhibits minimum AAD of 3.1%. For nitrogen hydrates, the predicted results match closely with those of experimental data with average absolute deviation of only 2%. An excellent agreement is achieved using the van der Waals equation of state. The other equation of states such as RK and PR also yield reasonably accurate results with AAD values of only 4.9 and 5%. Though the values of Langmuir constants are not shown in the paper, from the calculations, it is observed that cage occupancy values for CH₄, CO₂, N₂, and H₂S are found to be considerably higher than those of Ethane, C₂H₆. This is quite understandable since ethane has a larger size in comparison with these gases and only occupies larger cavities. For this purpose, the product of Langmuir constant and fugacity can be computed to observe the trend for understanding this type of behavior. Coming back to the results for the I–H–V region, overall, it can be seen that Virial equation of state and van der Waals equation of state provide the best agreement with experimental results in the I–H–V phase region.

Liquid–hydrate–vapor equilibria (L_w–H–V region)

Figures 4, 6, 8, 10, and 12 depict the overlapping curves for the experimental and results predicted by the model for the L_w–H–V phase region. The same set of gases, namely (1) methane (CH₄), (2) ethane (C₂H₆), (3) carbon dioxide (CO₂), (4) hydrogen sulfide (H₂S), and (5) nitrogen hydrates, have been modeled for the liquid–hydrate–vapor region. It is observable that most equations of states provide excellent agreement with experimental equilibrium pressures of hydrates of C₂H₆, CO₂, H₂S, and nitrogen. For methane hydrates, our model is capable of predicting pressures up to 320 K, which has not been investigated previously. It must be noted that equilibrium data for CH₄ hydrates beyond 295 K are a bit confusing, considering that for the same temperature, different pressure values are reported in the literature.

Moreover, for higher temperatures, hydrate-forming pressure is reported to be decreasing. However, as can be seen from Table 7, the Peng–Robinson equation yields the most accurate predictions with AAD of only 5.5%. However, most other equations of states provide a strong under-predicting trend, thereby producing errors above 40%, while Virial equation diverges for high-temperature values. This behavior is mainly associated with inaccurate calculations concerning fugacity for these temperature ranges. For methane hydrates, the P–T equilibrium curve rises steeply near 298 K, which demands a robust formulation for accurate predictions such as the Peng–Robinson equation. For the case of C₂H₆, ethane hydrates, an excellent agreement is achieved with ER, RK, and SRK EOS with only 2.1% average deviation. The maximum deviation is found to be with Virial equation with AAD of 14%. Other EOS such as Patel–Teja (PT), Peng–Robinson (PR), and van der Waal (VDW) are also found to predict accurately. For CO₂ hydrates, an accurate prediction is made using the Redlich–Kwong equation, which yields an error of only 2.1%. Except for the van der Waal equation, all the other EOS yield excellent agreement with experimental equilibrium pressure with errors less than 5%. For H₂S hydrates, our model is tested for a larger dataset than any other research studies.

Moreover, our model yields excellent agreement with a minimum absolute deviation of 2.65 for the Peng–Robinson equation, while maximum deviation was obtained using the Virial equation of state (9.1%). A similar repetitive trend is observed with ER, TSAI, PATEL, RK, and SRK EOS, which provided decent estimation with an error of approximately 5%. Finally, with N₂ hydrates, our model yields values close to experimental equilibrium pressure values with AAD of 1.7% using the PR-EOS. On the other hand, other equations yield large deviations with such as 26.4% (TSAI) and 14% with (SRK). Additionally, RK EOS yields accurate predictions with AAD of only 4.4%.

Empirical correlations: comparison and new correlation

In the current study, an effort is made to compare the predictive ability of correlations with experimental data taken from Sloan and Koh (2007). Figure 13 shows predictions of different correlations against experimental data for methane hydrates, as shown in Table 6.

Fig. 13

Peq versus T plot showing comparison of experimental data (CH₄ hydrates) for different correlations

For this purpose, correlations of Jager and Sloan (2001), Holder et al. (1988), Makogon (1981), Towler and Mokhatab (2005), Bahadori and Vuthaluru (2009), Hammerschmidt (1934), Zhengquan and Sultan (2008), Ali Ghayyem et al. (2014), Safamirzaei (2016), Sangtam and Kumar Majumder (2018), and Maekawa et al. (1995) are used for computation of equilibrium pressure of hydrate formation.

From the results, it is evident that correlations of Makogon (1981), Zhengquan and Sultan (2008), and Sangtam and Kumar Majumder (2018) provide the most accurate prediction against the experimental data. To establish the accuracy of our correlation, the error estimation for these “best” correlations is calculated below. For details of different error calculations AAD, ARDP, and RMSE, refer to Online Appendix A.

As can be seen from Table 8, the minimum error is associated with Zhengquan and Sultan (2008) correlation. The root mean square error associated with Zhengquan and Sultan (2008) is found to be 20.03334, while absolute average deviation is found to be 12.060%.

Though these correlations provide a reasonable estimation of hydrate formation equilibrium pressure, there is a need for developing a more authentic relationship, which can predict hydrate formation pressure within error bounds of ≤ 10%. The upcoming section addresses this need for developing a far more robust correlation.

Genetic programming (GP)-based generalized correlation

The generalized correlation is:

$$P = A \times T^{B} + C \times T^{D} + E \times T^{F} + G \times {\text{e}}^{{\frac{H}{T}}} + I \times {\text{e}}^{{\frac{J}{{T^{n} *}}}}$$

where P: pressure is in MPa, T: temperature is in K, and n* represents a tuned parameter.

Methane hydrates

As can be noted from Fig. 14, the new correlation provides excellent fitting for the temperature range of 260 ≤ T ≤ 320 K. The error values computed for the above correlation are given in Table 10, in comparison with Zhengquan and Sultan (2008) correlation.

Fig. 14

Peq versus T plot of experimental data (CH₄ hydrates) with “new correlation,” AAD = 0.32%

Table 10 Statistical error for temperature range: 260 ≤ T ≤ 320 K

The small values of AAD, i.e., 0.32 (%), indicate the accuracy of our new proposed correlation and its excellent agreement with experimental data.

Evaluation of correlations using coefficient of determination

To assess how close the predicted pressure values fare against the experimental values, Fig. 15 depicts the scatter plots for three best performing correlations, namely Sangtam and Kumar Majumder (2018), Zhengquan and Sultan (2008), and Makogon et al. (1981). In conjunction, scatter plot of “new correlation” with ${R}^{2} = 0.9999$ is also shown here.

Fig. 15

Comparative scatter plots for “new correlation” and best-fitting correlations of Sangtam and Kumar Majumder (2018), Zhengquan and Sultan (2008), and Makogon (1981)

Ethane hydrates

See Table 11 and Fig. 16.

Table 11 The constants determined with n = 1.46*

Fig. 16

Peq versus T plot of experimental data (C₂H₆ hydrates) with “new correlation,” AAD = 1.93%

Carbon dioxide hydrates

See Table 12 and Fig. 17.

Table 12 The constants determined with n = 1.5*

Fig. 17

Peq versus T plot of experimental data (CO₂ hydrates) with “new correlation,” AAD = 0.77%

Hydrogen sulfide hydrates

See Table 13 and Fig. 18.

Table 13 The constants determined with n = 1.6*

Fig. 18

Peq versus T plot of experimental data (H₂S hydrates) with “new correlation,” AAD = 0.64%

Nitrogen hydrates

See Table 14 and Fig. 19.

Table 14 The constants determined with n = 1.6*

Fig. 19

Peq versus T plot of experimental data (N₂ hydrates) with “new correlation,” AAD = 0.74%

As can be noticed, Figs. 16, 17, 18, and 19 depict the fitting of predicted equilibrium data against experimental data. The values of constants in correlation are given in Tables 9, 11, 12, 13, and 14.

Evaluation of small- and large-cage occupancies

Table 15 depicts the comparison of CH₄ hydrate cage occupancies for the temperature range of 273.65–276.65 K. Data compiled from Sloan (1998), Cao et al. (2001a), and Klauda and Sandler (2002, 2003) are compared to experimental results (Sum et al. 1997) as well as results from the present study.

Table 15 Fractional cage occupancy comparison with results from Klauda and Sandler (2002, 2003), Cao et al. (2001a), and Sloan (1998) and experimental data of Sum et al. (1997)

It must be noted that our model is capable of predicting small- and large-cage occupancies with fair accuracy. It is observed that large-cage occupancies are predicted more accurately. There is an under-prediction trend associated with small cage occupancies for the temperature range of 273.65–274.65 K. However, the trend reverses into over-prediction for higher temperature values of 275.65 and 276.65 K.

In light of the above discussion, the fractional cage occupancies of both small and large cages for the hydrates of methane, ethane, carbon dioxide, hydrogen sulfide, and nitrogen are plotted, as shown in Fig. 20.

Fig. 20

Fractional cage occupancies for the different hydrates, blue line (large), black (small)

Summary and conclusions

The present study aimed at investigating the applicability of different equations of states for the three-phase regions, namely (1) I–H–V and L_w–H–V phase region. (2) Hydrates of CH₄, C₂H₆, N₂, H₂S, and CO₂ were modeled. A separate objective of this research was to develop a generalized correlation that could be used for predicting equilibrium pressure for the various hydrates. For achieving the first two objectives, eight different equations of states, namely Peng–Robinson (PR), Soave–Redlich–Kwong (SRK), Redlich–Kwong (RK), Patel–Teja (PT), Esmaeilzadeh and Roshanfekr (ER), Virial, van der Waals (VDW), and Tsai–Jan (TJ), were incorporated into van der Waals–Platteeuw Model. The applicability of different equations of states for the three-phase region, namely I–H–V, L_w–H–V, was investigated for determining the best-fitting EOS.

The key conclusions and remarks can be summarized in the following points:

• 1. Overall, it was observed that Virial and van der Waals equation could be used for modeling most hydrates accurately in the I–H–V three-phase region.

• 2. In contrast, the Peng–Robinson equation can be used for providing excellent predictions for L_w–H–V three-phase region. The error values reported in this study are much lower in comparison with other relevant studies for the given range of temperatures.

• 3. Using genetic programming algorithms, a robust correlation was developed. As such, the correlation provides excellent agreement with the experimental data with AAD of 0.32%, 1.93%, 0.77%, 0.64%, and 0.74% for CH₄, C₂H₆, CO₂, H₂S, and N₂ respectively.

• 4. The correlation can be used for performing quick calculations based on practical applications for the different hydrates and can be used for fitting other hydrates data as well.

• 5. Overall, AAD and R² for the correlation were found to be less than 1%, and R² was found to be 0.9999, respectively.

• 6. In conjunction with determining equilibrium hydrate formation pressure, fractional small- and large-cage occupancies were determined and compared with those available in the literature. The values were found to be in close agreement with experimental data.