1 Introduction

Sloshing problems in liquid tank have to be considered for the design of cargo ships containing fluids such as OBO, LNG, LPG and VLCC. When the tank is forced to move, the free surface of the liquid in the tank deforms, fluid moves in large amplitudes, and a resultant impact pressure is exerted on the tank walls which may damage the local structure or influence the stability of the ship. Thus, sloshing problems have attracted significant attention. Liquid sloshing leads to high local pressure and large total force, both of which are important to consider in vessel design. The two most prominent causes of severe liquid movement in a cargo tank are the resonance that happens when the sway frequency of the tank is near to or equal to the natural frequency of the liquid movement, and the movement of liquid in a tank with little or no damping. In the case of resonance, the liquid movement in the tank becomes highly magnified. With regard to damping, a rectangular tank with baffles mounted at the bottom is the common engineering remedy applied to loaded liquid containers.

Liquid sloshing can be induced by tank motion. Scholars have carried out a great deal of research on tank sloshing, and most research methods are mature. They can be divided into three approaches, namely numerical, experimental and analytical methods.

There are two main numerical schemes for addressing sloshing problems: one is to apply potential flow theory [1,2,3], the other is to model the viscous Navier–Stokes equations [4,5,6]. Both methods are extensively used to study the weakening effect of the baffles. Popov et al. [7] studied forced turning and braking of the fluid within a tank, obtained the steady-state solutions and analyzed wave height, force and overturning moment by solving continuous Navier–Stokes equations numerically. Wu et al. [8] simulated sloshing waves in a 3D liquid tank by a finite element method based on potential flow theory. The finite element method was adopted by Pal [9] to study the fluid behaviors in a flexible thin-walled cylindrical tank. On the basis of the spatially averaged Navier–Stokes equations, Liu and Lin [10] employed the large eddy simulation approach to model sloshing in a tank with bottom mounted baffles. By using the boundary element method, Wang et al. [11] studied the internal sloshing flow of a tank freely moving in an incident wave by the boundary element method. Zhao et al. [12] investigated sloshing problems in partially filled membrane tank under forced excitations, and viscous effects were considered through validation from experimental tests. Chu et al. [13] focused on mitigating effects of the number and the height of baffles mounted at tank bottom by analyzing the data from large eddy simulation and experiments.

Large displacement of the liquid in a tank produces local high stress on the walls of the vessel. Under these circumstances, the fluid motion has strong nonlinear characteristics, which presents great obstacles to theoretical analysis and numerical calculation. Some assumptions need to be introduced into the analytical or numerical procedure to render the problems solvable, but such assumptions may lead to deviation from the accurate solution. In contrast, experimental studies do not need the artificial assumptions used in numerical or analytical methods, and from this aspect, they are more reliable. Celebi and Akyildiz [14] reported experimental results to show that a shear layer and dissipated energy caused by the viscous term would form in the presence of a baffle inside the tank. They also revealed that the motion of the tank had influence on the nonlinearity of the sloshing phenomena. To analyze the pressure on tank walls and the distorted free surface, a series of experiments were undertaken by Panigrahy et al. [15]. The sway motion of the tank was controlled by a shaking table. The sway frequency of the shaking table was changed, the fill level was altered, the experimental cases with and without baffles were repeated, and the pressure and the free surface elevation were studied.

In both experimental studies and the numerical simulations, one major difficulty is tracking the deformation of the free liquid surface. From the viewpoint of an actual project, quantifying the free surface elevation in the tank is not necessary, as the most important concerns are understanding how large the natural frequencies of the tank are, and taking effective measures to avoid resonance. The resonance that occurs in a liquid cargo tank and effectiveness of mechanisms for suppressing liquid sloshing can be well characterized by analytical methods. Compared with the experimental method and the numerical method, the analytical method can easily give the relationship between physical quantities, and has the advantages of fast calculation speed and small error. Abramson [16] applied linear potential flow theories to analyze the liquid motion in cylindrical and spherical tanks. Evans and Mciver [17] studied the influence of a vertical baffle on the resonant frequency of the fluid in a rectangular container by linear wave theory. The accuracy of the simple approximation is evaluated by comparing it with the exact solution based on eigenfunction expansions. It was found that a surface-piercing baffle can significantly change the resonant frequencies, while the effect of a bottom-mounted baffle is usually negligible. Wu [18] employed velocity potential theory to study the second-order resonance of sloshing. Zhou [19] deduced the analytical solution of the wave radiated by a bottom-opened rectangular body floating in water of finite depth. Zhang et al. [20] found that floating foams can weaken both the sloshing amplitude and the hydrodynamic pressure through observations from experiments and an analytical potential-flow solution.

Recent focus has shifted from studying hydrodynamic behaviors of liquid in a tank to seeking methods of weakening the sloshing phenomena, for which baffles are the most frequently used remedy [21,22,23,24,25]. Although the present topic has been widely researched, most of the previous work has considered fixed baffles, and sloshing was mitigated by changing the baffles’ height, number or altering the baffles’ shape. In the present paper, the baffle is rotating around a bottom-mounted point while the tank is swaying horizontally. The baffle’s motion, including the amplitude and the phase, are adjusted to weaken the sloshing. The mitigating effect is remarkable, and the wave can even be almost eliminated. In this paper, separation of variables is utilized to solve the governing equation, together with all the boundary conditions, to obtain analytical results. The natural frequencies of the tank with the baffle are also computed by fast fourier transform (FFT). Liquid sloshing characteristics in a tank with and without baffles are compared. The effects of the baffle parameters, such as height, on sloshing are examined.

Fig. 1
figure 1

Sketch map

Full size image

2 Governing equation and boundary conditions

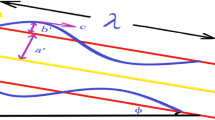
A two-dimensional rectangular tank model is shown in Fig. 1. The tank is undergoing horizontal oscillation with displacement X(t), the total length of the rectangular tank is 2l, the height from the free liquid surface to the bottom of the tank is taken as h, and a rigid baffle with a height of \(h_{1}\) is fixed to the bottom of the tank. The distance from the rigid baffle to the right wall is a, and to the left is b. In the coordinate system, the z-axis is vertical and the x-axis is horizontal and is coincident with the baffle line.

Viscosity and compressibility of the fluid are neglected, rotational behavior of the flow is overlooked, the motion of the tank and the baffle is assumed to be small, and the fluid field satisfies the Laplace equation [17, 21, 23].

$$\begin{aligned} \nabla ^{2}\phi (x,z,t)=0. \end{aligned}$$
(1)

To seek a unique solution, the boundary conditions and initial conditions in the fluid domain are needed. The impermeable bottom condition conforms with

$$\begin{aligned} \left. {\frac{\partial \phi }{\partial z}} \right| _{z=-h} =0. \end{aligned}$$
(2)

On the side wall of the tank, we have

$$\begin{aligned} \frac{\partial \phi }{\partial n}\left| {_{x=-b,x=a} } \right. = {\varvec{U}}\cdot {\varvec{n}}. \end{aligned}$$
(3)

On the baffle,

$$\begin{aligned} \frac{\partial \phi }{\partial n}\left| {_{x=0,-h<z<-h_2 } } \right. =({\varvec{U}}+\Lambda \times {\varvec{r}})\cdot {\varvec{n}}, \end{aligned}$$
(4)

where U denotes the translational velocity of the tank, \({\varvec{\Lambda }}\) represents the rotational speed, and r is the position vector to the hinged point of the baffle. According to the Bernoulli equation, the dynamic free surface condition can be expressed as [18, 26]

$$\begin{aligned} \eta =-\frac{1}{g}\left( \frac{\partial \phi }{\partial t}+\frac{1}{2}\nabla \phi \cdot \nabla \phi \right) , \end{aligned}$$
(5)

where g is the gravity acceleration. Equation (6) is transformed by Taylor expansion, ignoring the higher order term, and the linearized free surface condition is obtained

$$\begin{aligned} \eta =-\frac{1}{g}\frac{\partial \phi }{\partial t},\;\;\;\;\;\;z=0. \end{aligned}$$
(6)

The kinematic condition of the free surface is written as

$$\begin{aligned} \frac{\partial \eta }{\partial t}=\frac{\partial \phi }{\partial z},\;\;\;\;\;\;z=0. \end{aligned}$$
(7)

Substitute Eq. (6) into Eq. (7), and we have

$$\begin{aligned} \frac{\partial ^{2}\phi }{\partial t^{2}}+g\frac{\partial \phi }{\partial z}=0, \;\;z=0. \end{aligned}$$
(8)

Initially the free surface is assumed to be flat

$$\begin{aligned} \eta (x,t)=0, \quad z=0,\;\;t=0, \end{aligned}$$
(9)

and the potential and its time derivative are zero

$$\begin{aligned} \phi (x,z,t)=0 \quad \hbox {and} \quad \frac{\partial \phi }{\partial t}(x,z,t)=0,\;\;\; \quad z=0,\;\;t=0. \end{aligned}$$
(10)

3 Sloshing of a swaying liquid tank with a fixed baffle

3.1 Expressions for potential in the fixed baffle case

We first consider an example of a liquid tank with swaying motion \(U(t)=U_{0} \sin \, \Omega _{0} t\), where the baffle is fixed to the tank. To give the analytical solution, the fluid in the rectangular tank is divided into three sub-domains as shown in Fig. 1, which are \(\hbox {I}\, (-b\le x\le a,\;-h_2 \le z\le 0)\), \(\hbox {II}\, (0\le x\le a,\;-h\le z\le -h_2)\) and \(\hbox {III} \, (-b\le x\le 0,\;-h\le z\le -h_2)\) respectively. Similar work can be seen in Choun and Yun [27] and Zhou, Wu and Zhang [19], who also divided the fluid domain into a few sub-regions, but they focused on the frequency-domain solution. The potentials in each sub-domain are represented by \(\phi _1\), \(\phi _2\) and \(\phi _3\). These potentials satisfy

$$\begin{aligned} \hbox {I}\;\left\{ {\begin{array}{l} \nabla ^{2}\phi _1 =0, \\ \frac{\partial \phi _1 }{\partial x}\left| {_{x=a} } \right. =U(t), \\ \frac{\partial \phi _1 }{\partial x}\left| {_{x=-b} } \right. =U(t), \\ \end{array}} \right. \quad \hbox {II} \left\{ {\begin{array}{l} \nabla ^{2}\phi _2 =0, \\ \frac{\partial \phi _2 }{\partial x}\left| {_{x=a} } \right. =U(t), \\ \frac{\partial \phi _2 }{\partial x}\left| {_{x=0} } \right. =U(t), \\ \frac{\partial \phi _2 }{\partial z}\left| {_{z=-h} } \right. =0, \\ \end{array}} \right. \quad \hbox {III} \left\{ {\begin{array}{l} \nabla ^{2}\phi _3 =0, \\ \frac{\partial \phi _3 }{\partial x}\left| {_{x=-b} } \right. =U(t), \\ \frac{\partial \phi _3 }{\partial x}\left| {_{x=0} } \right. =U(t), \\ \frac{\partial \phi _3 }{\partial z}\left| {_{z=-h} } \right. =0. \\ \end{array}} \right. \end{aligned}$$
(11)

By separating variables, the velocity potential can be written as infinite series [19, 27]

$$\begin{aligned} \phi _1= & {} U(t)x+\sum \limits _{n=1}^\infty {[A_n (t)\cosh k_n (z+h_2 )+B_n (t)\sinh k_n (z+h_2 )]} \cos k_n (x+b), \end{aligned}$$
(12)
$$\begin{aligned} \phi _2= & {} U(t)x+\sum \limits _{n=1}^\infty {C_n } (t)\cos \lambda _n (x-a)\cosh \lambda _n (z+h), \end{aligned}$$
(13)
$$\begin{aligned} \phi _3= & {} U(t)x+\sum \limits _{n=1}^\infty {D_n } (t)\cos \gamma _n (x+b)\cosh \gamma _n (z+h), \end{aligned}$$
(14)

where

$$\begin{aligned} k_n =\frac{n\pi }{a+b}, \quad \lambda _n = \frac{n\pi }{a}\quad \gamma _n =\frac{n\pi }{b},\quad n=1, 2, 3{\ldots } \end{aligned}$$

The unique and unknown coefficients in Eqs. (12)–(14) are to be fixed by continuous conditions between different regions as well as the free surface condition.

3.2 Solution for the unknown coefficients in the fixed baffle case

Along the interfaces between adjacent fluid domains, matching conditions are applied to ensure velocity and pressure continuity [19, 28, 29]. Thus at each interface \(z=-h_2\) and on the free surface \(z =0\), we have

$$\begin{aligned} \begin{aligned}&\displaystyle \phi _{1} =\phi _2 \;(0\le x\le a,z=-h_2 ), \\&\displaystyle \phi _1 =\phi _3 \;(-b\le x\le 0,z=-h_2 ), \\&\displaystyle \frac{\partial \phi _{1} }{\partial z}= \left\{ {\begin{array}{l} \frac{\partial \phi _2 }{\partial z}\;(0\le x\le a,z=-h_2 ),\\ \frac{\partial \phi _3 }{\partial z}\;(-b\le x\le 0,z=-h_2 ), \\ \end{array}} \right. \\&\displaystyle \frac{\partial ^{2}\phi _{1} }{\partial t^{2}}+g\frac{\partial \phi _{1} }{\partial z}=0\;(z=0). \end{aligned} \end{aligned}$$
(15)

At the initial moment, we have

$$\begin{aligned} {\begin{array}{l} \phi _{1} =\phi _2 \;(0\le x\le a,z=-h_2 ,t=0), \\ \phi _1 =\phi _3 \;(-b\le x\le 0,z=-h_2 ,t=0), \\ \frac{\partial \phi _{1} }{\partial z}= \left\{ {\begin{array}{l} \frac{\partial \phi _2 }{\partial z}\;(0\le x\le a,z=-h_2 ,t=0), \\ \frac{\partial \phi _3 }{\partial z}\;(-b\le x\le 0,z=-h_2 ,t=0), \\ \end{array}} \right. \\ \phi _{1} (x,0,0)=0, \\ \end{array}} \quad {\begin{array}{l} \frac{\partial \phi _{1} }{\partial t}=\frac{\partial \phi _2 }{\partial t}\;(0\le x\le a,z=-h_2 ,t=0), \\ \frac{\partial \phi _{1} }{\partial t}=\frac{\partial \phi _3 }{\partial t}\;(-b\le x\le 0,z=-h_2 ,t=0), \\ \frac{\partial ^{2}\phi _{1} }{\partial z\partial t}= \left\{ {\begin{array}{l} \frac{\partial ^{2}\phi _2 }{\partial z\partial t}\;(0\le x\le a,z=-h_2 ,t=0), \\ \frac{\partial ^{2}\phi _3 }{\partial z\partial t}\;(-b\le x\le 0,z=-h_2 ,t=0), \\ \end{array}} \right. \\ \frac{\partial \phi _{1} }{\partial t}(x,0,0)=0. \\ \end{array}} \end{aligned}$$
(16)

Equations (12)–(14) are substituted into Eq. (15), and the orthogonality of the trigonometric function in the eigenfunction method is used [18, 20]; we then have the relationship between the unknown coefficient expressions

$$\begin{aligned} \sum \limits _{j=1}^\infty {A_j (t)} a_{ji}= & {} \frac{a}{2}C_i (t)\cosh \lambda _i h_1, \end{aligned}$$
(17)
$$\begin{aligned} \sum \limits _{j=1}^\infty {A_j (t)} b_{ji}= & {} \frac{b}{2}D_i (t)\cosh \gamma _i h_1, \end{aligned}$$
(18)
$$\begin{aligned} \frac{a+b}{2}k_i B_i (t)= & {} \sum \limits _{j=1}^\infty {\lambda _j C_j } (t)a_{ij} \sinh \lambda _j h_1 +\sum \limits _{j=1}^\infty {\gamma _j D_j } (t)b_{ij} \sinh \gamma _j h_1, \end{aligned}$$
(19)
$$\begin{aligned} {U}^{\prime \prime }(t)c_i +\frac{a+b}{2}[{A}_i^{\prime \prime } (t)\cosh k_i h_2 +{B}_i^{\prime \prime } (t)\sinh k_i h_2 ] +\frac{a+b}{2}gk_i [A_i (t)\sinh k_i h_2 +B_i (t)\cosh k_i h_2 ]=0, \end{aligned}$$
(20)

where

$$\begin{aligned} \begin{array}{l} a_{ji} =\int _0^a {\cos k_j (x+b)\cdot \cos \lambda _i (x-a)} \,\mathrm{d}x, \\ b_{ji} =\int _{-b}^0 {\cos k_j (x+b)\cdot \cos \gamma _i (x+b)} \mathrm{d}x, \\ c_i =\int _{-b}^a {x\cos k_i (x+b)\mathrm{d}x}. \\ \end{array}\quad i=1, 2, 3{\ldots }; \quad j=1, 2, 3{\ldots } \end{aligned}$$

Gaussian elimination method is used. The Laplace transform is performed on Eq. (20) [30], and then we have

$$\begin{aligned} B_i (t)= & {} \frac{2}{(a+b)k_i }\sum \limits _{m=1}^\infty {A_m (t)} \cdot P_{im}, \end{aligned}$$
(21)
$$\begin{aligned} A_i (t)= & {} Q_i (t)+\left( \omega _i \tanh k_i h_2 \;-\frac{gk_i }{\omega _i}\right) \int _0^t {B_i } (\tau )\sin \omega _i (t-\tau )\,\mathrm{d}\tau -B_i (t)\tanh k_i h_2, \end{aligned}$$
(22)

where

$$\begin{aligned} P_{im}= & {} \sum \limits _{j=1}^\infty \left( \frac{2\lambda _j a_{mj} a_{ij} \tanh (\lambda _j h_1 )}{a} +\frac{2\gamma _j b_{mj} b_{ij} \tanh (\gamma _j h_1 )}{b}\right) , \end{aligned}$$
(23)
$$\begin{aligned} \omega _i= & {} \sqrt{gk_i \tanh k_i h_2 }, \end{aligned}$$
(24)
$$\begin{aligned} Q_i (t)= & {} \frac{-2c_i }{(a+b)\omega _i \cosh k_i h_2 }\int _0^t {{U}^{\prime \prime }(\tau )} \sin \omega _i (t-\tau )\,\mathrm{d}\tau +\frac{\sin \omega _i t}{\omega _i }{A}_i^{\prime } (0)+\frac{\tanh k_i h_2 }{\omega _i }B_i^{\prime }(0)\sin \omega _i t \nonumber \\&+A_i (0)\cos \omega _m t+B_i (0)\cos (\omega _i t)\tanh (k_i h_2 ). \end{aligned}$$
(25)

Substitute Eqs. (22) into (21), and finally the expression of the unknown coefficient \(B_i (t)\) is obtained

$$\begin{aligned} \left( \frac{a+b}{2}k_i +P_{ii} \tanh k_i h_2 \right) B_i (t)= & {} \sum \limits _{m=1}^\infty \left[ Q_m (t) +\left( \omega _m \tanh k_m h_2 \;-\frac{gk_m }{\omega _m }\right) \int _0^t {B_m } (\tau )\sin \omega _m (t-\tau )\,\mathrm{d}\tau \right] \cdot P_{im} \nonumber \\&-\sum \limits _{m=1,m\ne i}^\infty B_m (t)\tanh (k_m h_2 )\cdot P_{im}. \end{aligned}$$
(26)

Equation (26), which is to be solved by the iteration method, involves some infinite series, and thus for practical computation, it must be truncated. After \(B_i (t)\) is solved, \(A_i (t)\), \(C_i (t)\) and \(D_i (t)\) can be obtained in turn. Equations (12)–(14) are substituted into Eq. (16), \(A_i (0),{A}_i^{\prime } (0)\), \(B_i (0), {B}_i^{\prime } (0)\), \(C_i (0), {C}_i^{\prime } (0)\), \(D_i (0), {D}_i^{\prime } (0)\) can be also obtained by the above steps.

4 Sloshing of a swaying liquid tank with a rolling baffle

4.1 Expression for the potential in the rolling baffle case

Consider the case in which the tank is swaying with \(U(t)=U_0 \sin \Omega _0 t\), the baffle at the bottom of the tank rotates around the point (\(0, \hbox {-}\) h) under the external excitation of frequency \(\Omega _{\mathrm{p}}\), and does a micro-amplitude roll motion with angular velocity \(\varpi (t) = \varpi _{0} \sin (\Omega _{\mathrm{p}} t + \varphi )\). Then the control equations and boundary conditions satisfied in each sub-domain can be listed as [27]

$$\begin{aligned} \hbox {I}\left\{ {\begin{array}{l} \nabla ^{2}\phi _1 =0, \\ \frac{\partial \phi _1 }{\partial x}\left| {_{x=a} } \right. =U(t), \\ \frac{\partial \phi _1 }{\partial x}\left| {_{x=-b} } \right. =U(t), \\ \end{array}} \right. \quad \hbox {II}\left\{ {\begin{array}{l} \nabla ^{2}\phi _2 =0, \\ \frac{\partial \phi _2 }{\partial x}\left| {_{x=a} } \right. =U(t), \\ \frac{\partial \phi _2 }{\partial x}\left| {_{x=0} } \right. =U(t)+\varpi (t)\cdot (z+h), \\ \frac{\partial \phi _2 }{\partial z}\left| {_{z=-h} } \right. =0, \\ \end{array}} \right. \quad \hbox {III} \left\{ {\begin{array}{l} \nabla ^{2}\phi _3 =0, \\ \frac{\partial \phi _3 }{\partial x}\left| {_{x=-b} } \right. =U(t), \\ \frac{\partial \phi _3 }{\partial x}\left| {_{x=0} } \right. =U(t)+\varpi (t)\cdot (z+h), \\ \frac{\partial \phi _3 }{\partial z}\left| {_{z=-h} } \right. =0. \\ \end{array}} \right. \end{aligned}$$
(27)

Based on a similar procedure in Sect. 3, the potential in each domain is expressed as [19, 27]

$$\begin{aligned} \phi _1= & {} U(t)x+\sum \limits _{n=1}^\infty {[A_n (t)\cosh k_n (z+h_2 )+B_n (t)\sinh k_n (z+h_2 )]} \cos k_n (x+b), \end{aligned}$$
(28)
$$\begin{aligned} \phi _2= & {} U(t)x-\frac{\varpi (t)}{2a}\left[ (z+h)(x-a)^{2}-\frac{(z+h)^{3}}{3}\right] \nonumber \\&+ \sum \limits _{n=1}^\infty {[C_n } (t)\cosh \lambda _n (z+h)+D_n (t)\sinh \lambda _n (z+h)]\cos \lambda _n (x-a), \end{aligned}$$
(29)
$$\begin{aligned} \phi _3= & {} U(t)x+\frac{\varpi (t)}{2b}\left[ (z+h)(x+b)^{2}-\frac{(z+h)^{3}}{3}\right] \nonumber \\&+ \sum \limits _{n=1}^\infty {[E_n } (t)\cosh \gamma _n (z+h)+F_n (t)\sinh \gamma _n (z+h)]\cos \gamma _n (x+b), \end{aligned}$$
(30)

where

$$\begin{aligned} k_n =\frac{n\pi }{a+b},\;\;\lambda _n =\frac{n\pi }{a},\;\;\gamma _n =\frac{n\pi }{b}. \end{aligned}$$

4.2 Solution for the unknown coefficients in the rolling baffle case

Using the continuous condition at \(z = -h_{2}\) [19, 28], the free surface condition \(z =0\) and the bottom boundary conditions \(z = -h\), we have

$$\begin{aligned} \begin{aligned}&\displaystyle \phi _{1} =\phi _2 \;(0\le x\le a,z=-h_2 ),\\&\displaystyle \phi _1 =\phi _3 \;(-b\le x\le 0,z=-h_2 ), \\&\displaystyle \frac{\partial \phi _{1} }{\partial z}= \left\{ {\begin{array}{l} \frac{\partial \phi _2 }{\partial z}\;(0\le x\le a,z=-h_2 ),\\ \frac{\partial \phi _3 }{\partial z}\;(-b\le x\le 0,z=-h_2 ), \\ \end{array}} \right. \\&\displaystyle \frac{\partial ^{2}\phi _{1} }{\partial t^{2}}+g\frac{\partial \phi _{1} }{\partial z}=0\;(z=0), \\&\displaystyle \frac{\partial \phi _2 }{\partial z}=0\;(0\le x\le a,z=-h) ,\\&\displaystyle \frac{\partial \phi _3 }{\partial z}=0\;(-b\le x\le 0,z=-h). \end{aligned} \end{aligned}$$
(31)

Substituting Eqs. (28–30) into Eq. (31) and then using the orthogonality of the trigonometric functions [18, 20], we have

$$\begin{aligned} \begin{aligned}&\displaystyle \sum \limits _{j=1}^\infty {A_j (t)a_{ji} } =-\frac{\varpi (t)}{2a}d_i +\frac{a}{2}[C_i (t)\cosh \lambda _i h_1 +D_i (t)\sinh \lambda _i h_1], \\&\displaystyle \sum \limits _{j=1}^\infty {A_j (t)b_{ji} } =\frac{\varpi (t)}{2b}e_i +\frac{b}{2}\;[E_i (t)\cosh \gamma _i h_1 +F_i (t)\sinh \gamma _i h_1], \\&\displaystyle \frac{(a+b)B_i (t)k_i }{2}=-\frac{\varpi (t)}{2a}f_i +\sum \limits _{j=1}^\infty {[C_j } (t)\lambda _j \sinh \lambda _j h_1 +D_j (t)\lambda _j \cosh \lambda _j h_1 ]a_{ij} \\&\displaystyle \qquad +\frac{\varpi (t)}{2b}g_{ii} +\sum \limits _{j=1}^\infty {[E_j } (t)\gamma _j \sinh \gamma _j h_1 +F_j (t)\gamma _j \cosh \gamma _j h_1 ]b_{ij}, \\&\displaystyle {U}^{\prime \prime } (t)c_i +\frac{a+b}{2}[{A}_i^{\prime \prime } (t)\cosh k_i h_2 +{B}_i^{\prime \prime } (t)\sinh k_i h_2 ] \\&\displaystyle \quad +\frac{a+b}{2}gk_i [A_i (t)\sinh k_i h_2 +B_i (t)\cosh k_i h_2 ]=0 , \\&\displaystyle -\frac{\varpi (t)}{2a}r_i +\frac{aD_i (t)\lambda _i }{2}=0, \\&\displaystyle \frac{\varpi (t)}{2b}s_i +\frac{bF_i (t)\gamma _i }{2}=0, \end{aligned} \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned} a_{ji}&=\int _0^a {\cos k_j (x+b)\cdot \cos \lambda _i (x-a)}\, \mathrm{d}x, \\ b_{ji}&=\int _{-b}^0 {\cos k_j (x+b)\cdot \cos \gamma _i (x+b)}\, \mathrm{d}x, \\ c_i&=\int _{-b}^a {x\cos k_i (x+b)\,\mathrm{d}x}, \\ d_i&=\int _0^a \left[ h_1 (x-a)^{2}-\frac{h_1^{3}}{3}\right] \cos \lambda _i (x-a)\,\mathrm{d}x, \\ e_i&=\int _{-b}^0 \left[ h_1 (x+b)^{2}-\frac{h_1^{3}}{3}\right] \cos \gamma _i (x+b)\,\mathrm{d}x, \\ f_i&=\int _0^a [(x-a)^{2}-h_1^{2}]\cos k_i (x+b)\,\mathrm{d}x, \\ g_i&=\int _{-b}^0 [(x+b)^{2}-h_1^{2}]\cos k_i (x+b)\,\mathrm{d}x, \\ r_i&=\int _0^a (x-a)^{2}\cos \lambda _i (x-a)\,\mathrm{d}x, \\ s_i&=\int _{-b}^0 (x+b)^{2}\cos \gamma _i (x+b)\,\mathrm{d}x. \end{aligned} \end{aligned}$$

Equation (32) is solved by Gaussian elimination, and we have

$$\begin{aligned} \begin{aligned} P_i B_i (t)&=-\frac{\varpi (t)}{2a}f_i +\frac{\varpi (t)}{2b}g_i \\&\quad +\sum \limits _{j=1}^\infty \frac{2\lambda _j a_{ij} \tanh \lambda _j h_1 }{a}D_j (t)a_{ij} \lambda _j \cosh \lambda _j h_1 +\sum \limits _{j=1}^\infty \frac{2\gamma _j b_{ij} \tanh \gamma _j h_1 }{b}F_j (t)b_{ij} \gamma _j \cosh \gamma _j h_1 \\&\quad +\sum \limits _{j=1}^\infty \frac{2\lambda _j a_{ij} \tanh \lambda _j h_1 }{a}\left[ \sum \limits _{m=1}^\infty {(Q_m (t)+\left( \omega _m \tanh k_m h_2 \;-\frac{gk_m }{\omega _m }\right) \int _0^t {B_m } (\tau )\sin \omega _m (t-\tau )\,\mathrm{d}\tau )a_{mj} }\right] \\&\quad -\sum \limits _{j=1}^\infty \frac{2\lambda _j a_{ij} \tanh \lambda _j h_1 }{a}\left[ \sum \limits _{m=1,m\ne i}^\infty B_m (t)a_{mj} \tanh k_m h_2 +\frac{\varpi (t)}{2a}d_{jj} -\frac{a}{2}D_j (t)\sinh \lambda _j h_1 \right] \\&\quad +\sum \limits _{j=1}^\infty \frac{2\gamma _j b_{ij} \tanh \gamma _j h_1 }{b}\left[ \sum \limits _{m=1}^\infty {(Q_m (t)+\left( \omega _m \tanh k_m h_2 \;-\frac{gk_m }{\omega _m }\right) \int _0^t {B_m } (\tau )\sin \omega _m (t-\tau )\,\mathrm{d}\tau )b_{mj} }\right] \\&\quad -\sum \limits _{j=1}^\infty \frac{2\lambda _j a_{ij} \tanh \lambda _j h_1 }{a}\left[ \sum \limits _{m=1,m\ne i}^\infty B_m (t)b_{mj} \tanh k_m h_2 -\frac{\varpi (t)}{2b}e_{jj} -\frac{b}{2}F_j (t)\sinh \gamma _j h_1 \right] , \end{aligned} \end{aligned}$$
(33)

where

$$\begin{aligned} \begin{aligned} P_i&=\frac{(a+b)k_i }{2}+\tanh (k_i h_2 )\sum \limits _{j=1}^\infty \left( \frac{2\lambda _j \tanh \lambda _j h_1 }{a} a_{ij}^{2}+\frac{2\gamma _j \tanh \gamma _j h_1 }{b}b_{ij}^{2}\right) , \\ Q_m (t)&=\frac{-2c_{mm} }{(a+b)\omega _m \cosh k_m h_2 }\int _0^t {{U}^{\prime \prime }(\tau )} \sin \omega _m (t-\tau )\,\mathrm{d}\tau +\frac{\sin \omega _m t}{\omega _m }{A}_m^{\prime } (0)+\frac{\tanh k_m h_2 }{\omega _m }B_m^{\prime }(0)\sin \omega _m t \\&\quad +A_m (0)\cos \omega _m t+B_m (0)\cos (\omega _m t)\tanh (k_m h_2). \end{aligned} \end{aligned}$$

When the Laplace transform is performed on Eq. (32) [30], we have a relational expression as follows:

$$\begin{aligned} A_i (t)=Q_i (t)+\left( \omega _i \tanh k_i h_2 \;-\frac{gk_i }{\omega _i}\right) \int _0^t {B_i } (\tau )\sin \omega _i (t-\tau )\,\mathrm{d}\tau -B_i (t)\tanh k_i h_2 , \end{aligned}$$
(34)

where \(\omega _i =\sqrt{gk_i \tanh k_i h_2}\).

$$\begin{aligned} \begin{aligned} Q_i (t)&=\frac{-2c_i }{(a+b)\omega _i \cosh k_i h_2 }\int _0^t {{U}^{\prime \prime }(\tau )} \sin \omega _i (t-\tau )\,\mathrm{d}\tau +\frac{\sin \omega _i t}{\omega _i }{A}_i^{\prime } (0)+\frac{\tanh k_i h_2 }{\omega _i} B_i^{\prime }(0)\sin \omega _i t \\&\quad +A_i (0)\cos \omega _m t+B_i (0)\cos (\omega _i t)\tanh (k_i h_2 ). \end{aligned} \end{aligned}$$
(35)

We can get the approximate solution of \(B_{i}(t)\) by the iteration algorithm. Then we can get \(A_{i}(t)\) via the relationship of coefficients. The expressions of \(C_{i}(t)\), \(D_{i}(t)\), \(E_{i}(t)\), \(F_{i}(t)\) can be obtained by solving Eq. (32).

$$\begin{aligned} \begin{aligned}&\displaystyle C_i (t)=\frac{2}{a\cosh \lambda _i h_1} \left( \sum \limits _{j=1}^\infty {A_j (t)a_{ji} } +\frac{\varpi (t)}{2a}d_i -\frac{a}{2}D_i (t)\sinh \lambda _i h_1 \right) ,\\&\displaystyle E_i (t)=\frac{2}{b\cosh \gamma _i h_1} \left( \sum \limits _{j=1}^\infty {A_j (t)b_{ji} } -\frac{\varpi (t)}{2b}e_i -\frac{b}{2}F_i (t)\sinh \gamma _i h_1 \right) , \\&\displaystyle D_i (t)=\frac{\varpi (t)r_i }{a^{2}\lambda _i }, \\&\displaystyle F_i (t)=-\frac{\varpi (t)s_i }{b^{2}\gamma _i }.\\ \end{aligned} \end{aligned}$$
(36)

The free surface is undisturbed initially, or \(z = \eta (x,0)=0\). Thus, we can get the initial value of coefficients by solving \(\phi _1 ({x,0,0}) = 0\) and \({\partial \phi _1 ({x, 0, 0})}/{\partial t}= 0\).

5 Analytical results

5.1 Convergence study with the number of the series

The potential expressions are represented by infinite series, and they must be truncated. Convergence analysis with respect to series number N is performed here. The size and parameters of the tank are \(a=b=l=h=0.7\,\hbox {m}\). The motion can be expressed as \(X = -X_{0} \cos \Omega _{0} t\) and the external excitation frequency is \(\Omega _0 =1\,\hbox {rad/s}\). The baffle’s height \(h_{1}/h\) is taken as 0.3, 0.5, 0.7, 0.9, respectively. The results with \(N=15\) and \(N=50\) are presented in Fig. 2, which shows that they are in very good agreement. This means \(N=15\) can provide sufficiently accurate results; therefore, in the following discussion, the potential expressions are truncated with 15 series, unless otherwise stated. When \(h_1 /h\) increases from 0.3 to 0.9, the characteristic frequency \(\omega _1\) in Eq. (24) decreases from 4.2 to 1.85, and they all are much larger than the excitation frequency \(\Omega _0 =1\,\hbox {rad/s}\) and thus no resonance happens. In range of \(\omega _1 /\Omega _0\) changing from 4.2 to 1.85, the influence of the characteristic frequency \(\omega _1\) on the value of free surface elevation is relatively smaller.

Fig. 2
figure 2

Free surface elevation \(\eta \) with different baffle’s height, the sway frequency of the tank \(\Omega _0 =1\,\hbox {rad/s}\)

Full size image

5.2 Verification of the results

The accuracy of the above process in solving the velocity potential coefficients is verified via the identity relationship of equations. Generally, the natural frequency of the sloshing fluid in a rectangular tank without a baffle can be estimated according to the linear theoretical formula derived by Wu [18]:

$$\begin{aligned} \Omega _n =\sqrt{\frac{ng\pi }{a+b}\tanh \left( \frac{n\pi h}{a+b}\right) }. \end{aligned}$$
(37)

The calculation size and parameters of the tank are \(a=b=l=h=0.7\,\hbox {m}\) with no baffle \(h_1 =0\). According to Eq. (37), it can be known that the first natural frequency or the fundamental frequency \(\Omega _1 =4.4910\,\hbox {rad/s}\) under this condition. The external excitation frequency is chosen to be equal to and far from the natural frequency for analysis, or \(\Omega _0 = \Omega _1\), \(\Omega _0 =0.5\Omega _1\). Figure 3 shows the free surface elevation on the left wall of the tank \(x=-b\) with excitation frequency \(\Omega _0 =0.5\Omega _1\) and \(\Omega _1\). In the absence of a baffle, the wave height obtained by the present method completely coincides with that by Wu [18].

Fig. 3
figure 3

Comparison of free surface elevation \(\eta \) between the present result and that by Wu [18] with no baffle

Full size image

Then the case of \(h_1 /h=0.1\) is considered, in which the baffle’s height is very small, and other geometric parameters of the tank are as the above. Theoretically, if the baffle’s height changes a little, the influence of the baffle’s rise on the wave is also small. Here, \(\Omega _0 =0.5\Omega _1\) is used. Figure 4 shows the corresponding free surface elevation. Comparing the present result with a very short baffle and that by Wu [18] with no baffle, they are very close to each other, which conforms with the expectation.

Fig. 4
figure 4

Comparison of free surface elevation \(\eta \) between the present result with a low baffle and that by Wu [18] with no baffle, \(\Omega _0 =0.5\Omega _1\)

Full size image

5.3 Influence of baffle height on wave elevation

When excitation frequency \(\Omega _0 =1.002\Omega _1\), then large amplitude sloshing will happen inside the tank, as shown in Fig. 3b. To analyze the influence of the baffle’s height, \(h_1 /h\) are respectively taken as 0.2, 0.3, 0.4, 0.6, 0.9. Figs. 5 and 6 present the corresponding results. It can be clearly seen that the baffle will inhibit the rise of the disturbed wave. With an increase of the baffle height, the wave becomes lower and the period of the enveloping line shorter. When the baffle’s height reaches 0.3 h, the resonance disappears. For an increase of baffle height from 0.3 to 0.4 h, the maximum wave elevation decreases about \(10X_0\). If the baffle height keeps increasing, the inhibition becomes less evident.

Fig. 5
figure 5

Change of free surface elevation \(\eta \) with time t at \(x=-b\), the baffle height changes from 0.2 to 0.9 h, the sway frequency of the tank \(\Omega _0 =1.002\Omega _1\)

Full size image
Fig. 6
figure 6

The statistics of the disturbed wave with different baffle heights, \(\Omega _0 =1.002\Omega _1\)

Full size image

The case of \(h_1 =0.4\) h is taken as an example to show the shape of the instantaneous free surface, and the period of this enveloping line is 20.992 s as shown in Fig. 7. In one envelope period, six time instants are selected, of which two correspond to crest (a) \(t=4.677\) s, (b) \(t=9.043\) s, two to trough (c) \(t=9.795\) s, (d) \(t=14.114\) s and two to knot (e) \(t=2.896\) s, (f) \(t=9.398\) s respectively. When the wave reaches its peak on the left wall of the tank, the free surface is just lowest on the right, and vice versa. When the free surface elevation on the two sides is very small, the value in the middle is also very small.

Fig. 7
figure 7

Change of free surface elevation with x at different time, a, b crest at left side, c, d trough at left side, e, f knot at left side, with a fixed baffle

Full size image

5.4 Influence of baffle height on fundamental frequency

The symbol \(\sigma _{n}\, (n=1,2,3{\ldots })\) is used to represent a series of natural frequencies of a two-dimensional rectangular tank with a baffle. \(\sigma _{1}\) is the first-order natural frequency, namely the fundamental frequency. According to the formula \(\Omega _{1}=\sqrt{gk_1 \tanh k_1 h}\), the first-order natural frequency of a rectangular liquid tank without a baffle plate can be calculated, or \(\Omega _{1} = 4.4910 \, \hbox {rad/s}\) (\(a = b = h = 0.7 \, m\), \(k_{1} = 2.244\)). For a liquid tank with a baffle, an initial disturbance will be exerted on it and the liquid will move at its natural frequency. Then the time history of the wave elevation is transformed by FFT to obtain the natural frequency. Fig. 8 gives the spectrum of the liquid tank with different baffle heights. Increasing the baffle’s height will make the natural frequency of the system smaller. This explains why a change of the baffle can inhibit sloshing.

Fig. 8
figure 8figure 8

Spectrum of a liquid tank with a fixed baffle, baffle height \(h_{1}\) changes from 0 to 0.8 h

Full size image

5.5 Sloshing of a swaying liquid tank with a rolling baffle

The height of the baffle cannot be easily changed after tank construction is completed. We can achieve the purpose of stabilizing the tank by adjusting the forced movement of the baffle. As linear systems satisfy the superposition principle, the movement of a tank can be decomposed into two kinds of motion. The first is the whole tank moving with velocity \(U(t)=U_{0} \sin \Omega _{0} t\), which has been described in detail in Sect. 5.1 for a fixed baffle relative to the tank. Its translational equation can be set as \(X(t) = -X_{0} \cos \Omega _{0} t\). The second is to point (\(0, \hbox {-}\) h) as the rotating center and make a slight roll at angular velocity \(\varpi (t) = \varpi _{0} \sin (\Omega _{\mathrm{p}} t + \varphi )\) under the external excitation frequency \(\Omega _{\mathrm{p}}\). The symbol \(\varphi \) stands for the initial phase. Suppose the equation of the roll angle with time is \(\theta (\hbox {t}) = - \theta _{0} {\text {cos}}(\Omega _{p} t+ \varphi )\). Here, \(\theta _0\) represents the maximum roll angle that can be reached by the baffle’s movement, \(\theta (t)=0\) corresponds to the vertical position and it is positive that the baffle rotates counter-clockwise.

In this paper, \(\eta _1\) and \(\eta _2\), respectively, represent the wave surface elevation caused by translational motion of the tank and forced oscillation of the baffle. Thus, the total free surface elevation after linear superposition can be expressed as follows:

$$\begin{aligned} \eta =\eta _1 +\eta _2 . \end{aligned}$$
(38)

Tank parameters are still taken as \(a=b=l=h=0.7\,\hbox {m}\) and \(X_0 =2\times {10}^{-4}\,\hbox {m}\). Represented by the two-dimensional rectangular liquid tank with baffle height \(h_1 =0.5\) h, it can be seen from the previous section that the natural frequency of the first-order of the liquid tank at this time is \(\sigma _1 =4.0344\, \hbox {rad/s}\).

This section mainly concentrates on how to control the movement of the baffle in order to suppress the rise of the free surface in the tank and avoid the resonance that occurs the tank does translational motion and the baffle is forced to roll. We adjust the initial phase of baffle movement so that wave height \(\eta _1\) and wave height \(\eta _2\) are opposite, and adjust the maximum roll angle of the baffle’s movement so that the amplitude of \(\eta _2\) is almost equal to that of \(\eta _1\). Finally, the purpose of elimination of waves can be achieved.

The tank’s external excitation frequency is equal to the baffle’s external excitation frequency, namely \(\Omega _{0} =\Omega _{\mathrm{p}}\). Suppose \(\Omega _{0} =\Omega _{\mathrm{p}} = 0.997 \sigma _{1} = 4.0212 \, \hbox {rad/s}\). The free surface elevation at \(x=-b\) is plotted in Fig. 9a. The peak magnitude of the free surface elevation in each period increases with time continuously, and the liquid motion is resonant. Spectral analysis of the wave height is shown in Fig. 9b. The natural frequency \(\sigma _1\) is equal to 4.0212  rad/s.

Fig. 9
figure 9

Spectrum of free surface elevation \(\eta _1\), \(\sigma _1 =4.0212\)

Full size image

Under the above conditions, the amplitude of cosine signal of the time history curve \(\eta _1\) at frequency \(\delta _1\) is calculated by Fourier series.

$$\begin{aligned} a_\omega =\frac{2\int _0^{nT} {\eta \;(t)\cdot \cos \delta _1 t\hbox {d}t}}{nT}, \quad \hbox {where} \, T=\frac{2\pi }{\delta _1}. \end{aligned}$$
(39)

The amplitude of the sinusoidal signal can be calculated as

$$\begin{aligned} b_\omega =\frac{2\int _0^{nT} {\eta \;(t)\cdot \sin \delta _1 t\hbox {d}t}}{nT}, \quad \hbox {where} \, T=\frac{2\pi }{\delta _1}. \end{aligned}$$
(40)

The initial phase of the cosine signal whose frequency \(\omega \) is:

$$\begin{aligned} \varphi _\omega =\arctan \left( -\frac{b_\omega }{a_\omega }\right) . \end{aligned}$$
(41)

Thus, the initial phase of \(\eta _1\) is obtained \(\varphi _{\omega } =85.9023^\circ \). Then the baffle in the tank is forced to roll at a frequency of 4.0212 rad/s. Using a similar procedure for the initial phase of \(\eta _1\), the initial phase of \(\eta _2\) can be calculated \(\varphi _{\omega } =86.7701^\circ \).

After obtaining the initial phase of \(\eta _1\) and \(\eta _2\), the phase of \(\eta _2\) is adjusted to be opposite to that of \(\eta _1\). The initial phase of \(\eta _2 \) will be \(\varphi = 86.7701 + 180-85.9023=180.8678^\circ \). Then adjust the roll range of the baffle so that \(\eta _1 \approx -\eta _2\), and then \(\theta _{0} =6.28 \times 10^{-3} \, \hbox {rad}\). The forced motion equation of baffle plate is \(\theta (t) = -6.28 \times 10^{-3} \cos (4.0212 t + 180.8678{^{\circ }})\). The total wave height \(\eta =\eta _1 + \eta _2\) is obtained by superimposing wave height \(\eta _1\) and wave height \(\eta _2\) after adjustment of initial phase and roll amplitude. As shown in Fig. 10, \(\eta \) tends to be flat with extremely small amplitude, indicating that even in the case of resonance, the wave can also be eliminated by adjusting the motion of the baffle.

Fig. 10
figure 10

Free surface elevation \(\eta \), \(\eta _1\) and \(\eta _2\) by adjusting the baffle’s motion

Full size image

To see if the wave elimination is suitable for the interior part of the tank, the free surface elevation before superimposition \(\eta _1\) and after superimposition \(\eta \) is plotted. According to Fig. 10, six curves are selected which can cover the typical time instants, two of which correspond to the wave crest (a) \(t = 5.073\,\hbox {s}\) (b) \(t =12.894\,\hbox {s}\), two to trough (c) \(t =7.413\,\hbox {s}\) (d) \(t =13.684\,\hbox {s}\), two to knot (e) \(t =7.842\,\hbox {s}\) (f) \(t =15.631\,\hbox {s}\). The free surface elevation \(\eta _1\) is shown in Fig. 11, and it is almost anti-symmetric. The largest amplitude emerges at two sides, no matter whether crest, trough or knot. The eliminated wave surface is shown in Fig. 12. After superposing, the free surface shape becomes more crooked, but the elevation is extremely small. It can be concluded that the wave elevation is effective for all parts of the liquid.

Fig. 11
figure 11

Change of free surface elevation \(\eta _1\) with x at different time, a, b crest at left side, c, d trough at left side, e, f knot at left side, with a hinged rolling baffle

Full size image
Fig. 12
figure 12

Change of free surface elevation \(\eta \) with x at different time, a, b crest at left side, c, d trough at left side, e, f knot at left side, with a hinged rolling baffle

Full size image

The excitation frequency \(\Omega _0 =\Omega _{\mathrm{p}}=1\, \hbox {rad/s}\), which is far from the natural frequency. The spectrum of \(\eta _1 \;(t)\) is analysed in Fig. 13a. It can be seen that the wave amplitude reaches the maximum when \(\sigma _1 =1\,\hbox {rad/s}\). The corresponding phase is \(\varphi _\omega =-0.0388^\circ \), while for \(\eta _2\), \(\varphi _\omega =0.0461^\circ \). With the above procedure, the baffle’s motion is adjusted as \(\theta (t)=-3.79\times 10^{-1}\cos (t+180.0073^\circ )\). The free surface elevation after superimposing is given in Fig. 13b. Whether the excitation frequency is far from or adjacent to the natural frequency, the liquid motion induced by tank and baffle can be roughly balanced to inhibit the total disturbed wave.

Fig. 13
figure 13

Free surface elevation \(\eta \), \(\eta _1\), and \(\eta _2\) by adjusting baffle’s motion

Full size image

6 Conclusions

A baffle was mounted at the tank bottom to inhibit sloshing; it divides the liquid tank into three regions which were solved analytically based on linear potential theory. The potential and its directional directive between different regions were continuous. Firstly, the baffle was fixed to the tank and the tank was in sway motion. The analytical method was verified by comparing the present result with published data. When the excitation frequency is close to the first natural frequency of the unbaffled tank, resonance will happen. Increase of the baffle’s height can inhibit the resonance, as it can make the natural frequency of the tank smaller. Then the baffle was set to roll around a hinged point. According to the superposition principle of linear systems, the movement of the liquid tank can be divided into the sway motion of the liquid tank and the roll motion of the baffle. The disturbed sloshing waves produced by two kinds of motion are summed up to obtain the total wave surface. By changing the initial phase of the forced motion of the baffle and the maximum roll angle of the baffle, the elevation of the sloshing waves generated by sway of the tank and roll of the baffle can be adjusted to be equal, and the phase to be opposite. Through this adjustment, the purpose of wave elimination can be achieved whether the frequency of sway motion is close to or far away from the resonant frequency. Under linear theory, the maximum free surface elevation is prone to emerge at two sides of the tank. Wave elimination method in the present paper is effective both for two sides as well as for the interior part of the tank.