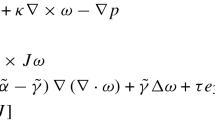Analysis of Micropolar Fluids: Existence of Potential Microflow Solutions, Nearby Global Well-Posedness, and Asymptotic Stability

Abstract

In this paper we concern ourselves with an incompressible, viscous, isotropic, and periodic micropolar fluid. We find that in the absence of forcing and microtorquing there exists an infinite family of well-behaved solutions, which we call potential microflows, in which the fluid velocity vanishes identically, but the angular velocity of the microstructure is conservative and obeys a linear parabolic system. We then prove that nearby each potential microflow, the nonlinear equations of motion are well-posed globally-in-time, and solutions are stable. Finally, we prove that in the absence of force and microtorque, solutions decay exponentially, and in the presence of force and microtorque obeying certain conditions, solutions have quantifiable decay rates.

Appendices

Appendix A: Reduction to Velocity Fields with Vanishing Average

The natural setting for the initial data, force, and microtorque in (1.1) is the space

$$\begin{aligned} &H^{1+s}_{\perp }\left (\mathbb{T}^{3};\mathbb{R}^{3}\right )\times H^{1+s} \left (\mathbb{T}^{3};\mathbb{R}^{3}\right )\times L^{2}\left ( \mathbb{R}^{+};\mathring{H}^{s}\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )\right )\times L^{2}\left (\mathbb{R}^{+};H^{s}\left ( \mathbb{T}^{3};\mathbb{R}^{3}\right )\right ) \\ &\quad \text{ for } s\in \mathbb{R}^{+}\cup \left \{ {0}\right \} . \end{aligned}$$

(A.1)

However, as we will see below, the corresponding solutions are globally integrable in time if and only if $u_{0}$ has vanishing average. It is thus convenient to introduce a change of unknowns that allows us to reduce to studying this case. This is possible due to the invariance of the micropolar equations (1.1) under Galilean transformations.

Lemma 1.1

Let $s\in \mathbb{R}^{+}\cup \left \{ {0}\right \}$. Suppose that $u_{0},\omega _{0}\in H^{1+s}\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )$ are initial data with $\operatorname{div}u_{0}=0$, $f,g\in L^{2}\left (\mathbb{R}^{+};H^{s}\left (\mathbb{T}^{3}; \mathbb{R}^{3}\right )\right )$ are forcing and microtorquing with $\int _{\mathbb{T}^{3}}\!f\!\left (t,x\right )\mathrm{d}x\!=0$ for almost every $t\in \mathbb{R}^{+}$. Suppose that $\left (u,\omega ,p\right )$ are a corresponding strong solution triple to system (1.1). Then the following hold.

• 1. For almost every $t\in \mathbb{R}^{+}$ it holds that $\int _{\mathbb{T}^{3}}u\left (t,x\right )\;\mathrm{d}x=\int _{ \mathbb{T}^{3}}u_{0}\left (x\right )\;\mathrm{d}x$.

• 2. Given any $b\in \mathbb{R}^{3}$, the triple $\left (v,\chi ,q\right ): \mathbb{R}^{+} \times \mathbb{T}^{3} \to \mathbb{R}^{3} \times \mathbb{R}^{3} \times \mathbb{R}$ defined by

  $$ \textstyle\begin{cases} v\left (t,x\right )=-b+u\left (t,x+tb\right ) \\ \chi \left (t,x\right )=\omega \left (t,x+tb\right ) \\ q\left (t,x\right )=p\left (t,x+tb\right ) \\ \varphi \left (t,x\right )=f\left (t,x+tb\right ) \\ \psi \left (t,x\right )=g\left (t,x+tb\right ) \end{cases} $$

  (A.2)

  is a strong solution to system (1.1) with initial data $\left (u_{0}-b,\omega _{0}\right )$ and forcing/microtorquing $\left (\varphi ,\psi \right )$. Moreover, if we posit the space-time regularity of $\left (u,\omega ,p\right )$ to be encoded with the inclusion:

  $$\begin{aligned} &\left (u-\int _{\mathbb{T}^{3}}u_{0},\omega ,p\right )\in \left (L^{2} \left (\mathbb{R}^{+};\mathring{H}^{2+s}_{\perp }\left (\mathbb{T}^{3}; \mathbb{R}^{3}\right )\right )\cap H^{1}\left (\mathbb{R}^{+}; \mathring{H}^{s}_{\perp }\left (\mathbb{T}^{3};\mathbb{R}^{3}\right ) \right )\right ) \\ &\quad {}\times \left (L^{2}\left (\mathbb{R}^{+};H^{2+s}\left (\mathbb{T}^{3}; \mathbb{R}^{3}\right )\right )\cap H^{1}\left (\mathbb{R}^{+};H^{s} \left (\mathbb{T}^{3};\mathbb{R}^{3}\right )\right )\right )\!\times\! \left (L^{2}\left (\mathbb{R}^{+};\mathring{H}^{1+s}\left ( \mathbb{T}^{3};\mathbb{R}^{3}\right )\!\right )\!\right ), \end{aligned}$$

  (A.3)

  then the same inclusion is true for $\left (v-\int _{\mathbb{T}^{3}}\left (u_{0}-b\right ),\chi ,q \right )$. Also, $\left (\varphi ,\psi \right )$ belong to the same space-time regularity class as $\left (f,g\right )$.

As a consequence, to understand the solvability of (1.1) with respect to data and forcing / microtorquing quadruples belonging to the space

$$ H^{1+s}_{\perp }\left (\mathbb{T}^{3};\mathbb{R}^{3}\right )\times H^{1+s} \left (\mathbb{T}^{3};\mathbb{R}^{3}\right )\times L^{2}\left ( \mathbb{R}^{+};\mathring{H}^{s}\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )\right )\times L^{2}\left (\mathbb{R}^{+};H^{s}\left ( \mathbb{T}^{3};\mathbb{R}^{3}\right )\right ), $$

(A.4)

it is sufficient to understand the system’s solvability for data/forcing/microtorquing belonging to the smaller space

$$ \mathring{H}^{1+s}_{\perp }\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )\times H^{1+s}\left (\mathbb{T}^{3};\mathbb{R}^{3}\right ) \times L^{2}\left (\mathbb{R}^{+};\mathring{H}^{s}\left ( \mathbb{T}^{3};\mathbb{R}^{3}\right )\right )\times L^{2}\left ( \mathbb{R}^{+};H^{s}\left (\mathbb{T}^{3};\mathbb{R}^{3}\right ) \right ). $$

(A.5)

Proof

Suppose that we are given a strong solution triple $\left (u,\omega ,p\right )$ corresponding to the data / forcing / microtorquing quadruple $\left (u_{0},\omega _{0},f,g\right )$ as in the hypotheses. Averaging the second equation in (1.1), and then integration by parts yields the identity for almost everywhere on $\mathbb{R}^{+}$:

$$\begin{aligned} 0 =&\int _{\mathbb{T}^{3}}\varrho \left (\partial _{t}u+u\cdot \nabla u \right )-\left (\varepsilon +\frac{\kappa }{2}\right )\Delta u- \kappa \operatorname{curl}\omega +\nabla p \\ =&\varrho \left (\int _{\mathbb{T}^{3}}u \right )'+\int _{\mathbb{T}^{3}}u\operatorname{div}u=\varrho \left (\int _{ \mathbb{T}^{3}}u\right )'. \end{aligned}$$

(A.6)

Thus, the first item now follows from the fundamental theorem of calculus.

Now, if $\mu \in \mathbb{N}^{2}$ is a multi-index with $\left |\mu \right |\le 2$, then for almost every $\left (t,x\right )\in \mathbb{R}^{+}\times \mathbb{T}^{3}$ we have that $\partial ^{\mu }v\left (t,x\right )=\partial ^{\mu }u\left (t,x+tb \right )$ and $\partial ^{\mu }\chi \left (t,x\right )=\partial ^{\mu }\omega \left (t,x+tb \right )$, and $\nabla q\left (t,x\right )=\nabla p\left (t,x+tb\right )$. We next compute the discrepancy in the time derivatives: $\partial _{t}v\left (t,x\right )=\partial _{t}u\left (t,x+tb\right )+b \cdot \nabla u\left (t,x+tb\right )$, and $\partial _{t}\chi \left (t,x\right )=\partial _{t}\omega \left (t,x \right )+b\cdot \nabla \omega \left (t,x+tb\right )$. Finally, using the previous remarks we verify the following equality between the two material derivative terms:

$$ \textstyle\begin{cases} \left (\partial _{t}+v\left (t,x\right )\cdot \nabla \right )v\left (t,x \right )=\partial _{t}u\left (t,x+tb\right )+u\left (t,x+tb\right ) \cdot \nabla u\left (t,x+tb\right ) \\ \left (\partial _{t}+v\left (t,x\right )\cdot \nabla \right )v\left (t,x \right )=\partial _{t}\omega \left (t,x+tb\right )+u\left (t,x+tb \right )\cdot \nabla \omega \left (t,x+tb\right ). \end{cases} $$

(A.7)

Thus, evaluation of the system (1.1) at points $\left (t,x+tb\right )$ for $\left (t,x\right )\in \mathbb{R}^{+}\times \mathbb{T}^{3}$ yields that the triple $\left (v,\chi ,q\right )$ is a strong solution to (1.1) with data $\left (u_{0}-b,\omega _{0}\right )$ and forcing/microtorquing $\left (\varphi ,\psi \right )$. The space-time regularity assertions in the latter part of the second item are now a trivial verification given that the first item shows that the velocity’s average is constant in time. The consequence follows by: changing coordinates and unknowns, taking $b$ equal to the spatial average of $u_{0}$; solving the new system using the hypothesized solvability of (1.1) in the average-zero spaces; and finally transforming back with $b$ equal to the negative of the average of $u_{0}$ and citing the conclusion of the second item. □

Appendix B: Tools from Analysis

In this section we record a number of analysis results used throughout the paper.

2.1 B.1 Real-Valued Distributions and Fourier Coefficients

The following lemma characterizes when a distribution $T \in \mathcal{D}^{\ast }\left (\mathbb{T}^{d};\mathbb{C}^{\ell }\right )$ is actually $\mathbb{R}^{\ell }$-valued. To state the result we recall a few definitions. First, for a sequence $z: \mathbb{Z}^{d} \to \mathbb{C}^{\ell }$ we define its reflection $Rz : \mathbb{Z}^{d} \to \mathbb{C}^{\ell }$ via $Rz(k) = z(-k)$ for $k\in \mathbb{Z}^{d}$. Second, for a distribution $T \in \mathcal{D}^{\ast }\left (\mathbb{T}^{d};\mathbb{C}^{\ell }\right )$ we define its complex conjugate as the distribution $\overline{T}\in \mathcal{D}^{\ast }\left (\mathbb{T}^{d}; \mathbb{C}^{\ell }\right )$ given by $\left \langle {\overline{T}, \psi }\right \rangle = \overline{\left \langle {T,\overline{\psi }}\right \rangle }$ for each $\psi \in \mathcal{D}(\mathbb{T}^{d};\mathbb{C})$.

Lemma B.1

Let $\ell ,d \in \mathbb{N}^{+}$ The following hold.

• 1. If $f \in L^{2}(\mathbb{T}^{d};\mathbb{C}^{\ell })$, then $f$ is $\mathbb{R}^{\ell }$-valued, i.e. $f = \overline{f}$, if and only if $\hat{f} \in \ell ^{2}(\mathbb{Z}^{d};\mathbb{C}^{\ell })$ satisfies $\overline{\hat{f}} = R \hat{f}$.

• 2. If $T \in \mathcal{D}^{\ast }\left (\mathbb{T}^{d};\mathbb{C}^{\ell }\right )$, then $T$ is $\mathbb{R}^{\ell }$-valued, i.e. $T = \overline{T}$, if and only if $\overline{\hat{T}} = R \hat{T}$ holds on the lattice $\mathbb{Z}^{d}$.

Proof

If $f = \overline{f}$, then we have that

$$ \overline{\hat{f}(k)} = \int _{\mathbb{T}^{d}} \overline{f(x)} \mathbf{e}_{k}\left (x\right )\;\mathrm{d}x = \int _{\mathbb{T}^{d}} f(x) \mathbf{e}_{k}\left (x\right )\mathrm{d}x = \hat{f}(-k), $$

(B.1)

and if $\overline{\hat{f}} = R \hat{f}$, then for almost every $x\in \mathbb{T}^{d}$

$$ \overline{f(x)} = \sum _{k \in \mathbb{Z}^{d}} \overline{\hat{f}(k)} \mathbf{e}_{-k}\left (x\right ) = \sum _{k \in \mathbb{Z}^{d}} \hat{f}(-k)\mathbf{e}_{-k}\left (x\right ) = \sum _{k \in \mathbb{Z}^{d}} \hat{f}(k)\mathbf{e}_{k} = f(x). $$

(B.2)

This proves the first item.

We now turn to the proof of the second item. If $\psi \in \mathcal{D}\left (\mathbb{T}^{d};\mathbb{C}\right )$, then the series $\sum _{k\in \mathbb{Z}^{d}}\hat{\psi }\left (k\right )\mathbf{e}_{k}$ converges absolutely in the topology of $H^{s}\left (\mathbb{T}^{3};\mathbb{C}^{\ell }\right )$ for all $s\in \mathbb{R}$. In particular, for each $m\in \mathbb{N}$ we have the convergence:

$$ \lim _{K\to \infty }\left [{\psi -\sum _{ \substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\psi } \left (k\right )\mathbf{e}_{k}}\right ]_{m}=0, $$

(B.3)

where $\left [{\cdot }\right ]_{m}$ is the seminorm from Definition 1.1. Thus, given $T\in \mathcal{D}^{\ast }\left (\mathbb{T}^{d};\mathbb{C}^{\ell }\right )$ such that $\overline{\hat{T}}=R\hat{T}$, we can compute its action on $\psi$ via the series:

$$\begin{aligned} &\left \langle {T,\psi }\right \rangle \\ &\quad =\lim _{K\to \infty }\sum _{ \substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\psi } \left (k\right )\left \langle {T,\mathbf{e}_{k}}\right \rangle = \lim _{K\to \infty }\sum _{ \substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\psi } \left (k\right )\hat{T}\left (-k\right ) \\ &\quad =\lim _{K\to \infty }\sum _{ \substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\psi } \left (k\right ) R\hat{T}\left (k\right )=\lim _{K\to \infty }\sum _{ \substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\psi } \left (k\right ) \overline{\hat{T}\left (k\right )} \\ &\quad =\lim _{K\to \infty } \overline{\sum _{\substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\overline{\psi }}\left (-k\right )\hat{T}\left (k\right )}= \lim _{K\to \infty } \overline{\sum _{\substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\overline{\psi }}\left (-k\right )\left \langle {T,\mathbf{e}_{-k}}\right \rangle }= \overline{\left \langle {T,\lim _{K\to \infty }\sum _{\substack{k\in \mathbb{Z}^{d}\\\left |k\right |\le K}}\hat{\overline{\psi }}\left (k\right )\mathbf{e}_{k}}\right \rangle } \\ &\quad = \overline{\left \langle {T,\overline{\psi }}\right \rangle } =\left \langle {\overline{T},\psi }\right \rangle . \end{aligned}$$

(B.4)

This gives the sufficient condition for the second item. To see that it is also necessary, suppose now that we have $T\in \mathcal{D}^{\ast }\left (\mathbb{T}^{d};\mathbb{C}^{\ell }\right )$ satisfying $T=\overline{T}$. We compute for $k\in \mathbb{Z}^{d}$:

$$ \overline{\hat{T}\left (k\right )}= \overline{\left \langle {T,\mathbf{e}_{-k}}\right \rangle }= \overline{\left \langle {T,\overline{\mathbf{e}_{k}}}\right \rangle }= \left \langle {\overline{T},\mathbf{e}_{k}}\right \rangle =\left \langle {T,\mathbf{e}_{k}}\right \rangle =\hat{T}\left (-k\right )=R \hat{T}\left (k\right ). $$

(B.5)

 □

2.2 B.2 Fractional Sobolev Spaces

Here we record some results in fractional Sobolev spaces, as defined in Definition 1.3.

Proposition B.2

Let $s \in \mathbb{R}$. Then the map $\Pi : H^{s}_{\|} \left (\mathbb{T}^{3};\mathbb{R}^{3}\right ) \to \mathring{H}^{1+s}\left (\mathbb{T}^{3};\mathbb{R}\right )$ defined by

$$ \Pi f = \sum _{k\in \mathbb{Z}^{3} \backslash \{0\}} \left ( \frac{k \cdot \hat{f}(k)}{2\pi i \left |k\right |^{2}} \right ) \mathbf{e}_{k} $$

(B.6)

is well-defined, bounded, and linear, and $\nabla \Pi f = f$ for all $f \in H^{s}_{\|} \left (\mathbb{T}^{3};\mathbb{R}^{3}\right )$. Moreover, $\Pi$ extends to a bounded linear map from $L^{2}\left (\mathbb{R}^{+};H^{s}_{\|} \left (\mathbb{T}^{3}; \mathbb{R}^{3}\right )\right )$ to $L^{2}\left (\mathbb{R}^{+};\mathring{H}^{1+s}\left (\mathbb{T}^{3}; \mathbb{R}\right )\right )$ with the same properties.

Proof

First we compute

$$ \left \lVert \Pi f\right \rVert _{\mathring{H}^{1+s}}^{2} = \sum _{k \in \mathbb{Z}^{3} \backslash \{0\}} \left |k\right |^{2+ 2s} \left | \frac{k \cdot \hat{f}(k)}{2\pi i \left |k\right |^{2}} \right |^{2} \le \frac{1}{4\pi ^{2}} \sum _{k \in \mathbb{Z}^{3} \backslash \{0\}} \left |k\right |^{2s} \left | \hat{f}(k) \right |^{2} = \frac{1}{4\pi ^{2}} \left \lVert f\right \rVert _{\mathring{H}^{s}}^{2}, $$

(B.7)

and then we use Lemma B.1 to see that

$$ \overline{\widehat{\Pi f}(k)} = \frac{-k \cdot \overline{\hat{f}(k) } }{2\pi i \left |k\right |^{2} } = \frac{-k \cdot \hat{f}(-k) }{2\pi i \left |-k\right |^{2} } = \widehat{\Pi f}(-k), $$

(B.8)

which then implies that $\Pi f$ is a real-valued distribution. From this we deduce that $\Pi$ is a well-defined bounded linear map. Then for $f \in H^{s}_{\|} \left (\mathbb{T}^{3};\mathbb{R}^{3}\right )$ we compute

$$ \widehat{\nabla \Pi f}(k) = 2\pi i k \frac{k \cdot \hat{f}(k)}{2\pi i \left |k\right |^{2}} = \frac{k \otimes k}{\left |k\right |^{2}} \hat{f}(k), $$

(B.9)

to deduce that $\nabla \Pi f = (I- \mathbb{P}) f =f$. The extension result then follows trivially. □

Next we record a useful product estimate in fractional Sobolev spaces.

Proposition B.3

Let $d\in \mathbb{N}^{+}$, and suppose that $s,t\in \mathbb{R}^{+}\cup \left \{ {0}\right \}$ satisfy $s>\frac{d}{2}$ and $s\ge t$. Then there exists a constant $C >0$, depending on $s$ and $t$, such that if $f\in H^{s}\left (\mathbb{T}^{d}\right )$ and $h\in H^{t}\left (\mathbb{T}^{d}\right )$, then $fh\in H^{t}\left (\mathbb{T}^{d}\right )$ and

$$ \left \lVert fh\right \rVert _{H^{t}}\le C\left \lVert f\right \rVert _{H^{s}}\left \lVert h\right \rVert _{H^{t}}. $$

(B.10)

Proof

Since $s > d/2$ we have that $H^{s}(\mathbb{T}^{d})$ is an algebra and that $H^{s}(\mathbb{T}^{d}) \hookrightarrow C^{0}_{b}(\mathbb{T}^{d})$. Consequently, for a fixed $f \in H^{s}(\mathbb{T}^{d})$, if we define the linear operator $T_{f}$ via $T_{f} g = fg$, then $T_{f}$ is bounded linear map from $L^{2}\left (\mathbb{T}^{d}\right )$ to $L^{2}\left (\mathbb{T}^{d}\right )$ and from $H^{s}\left (\mathbb{T}^{d}\right )$ to $H^{s}\left (\mathbb{T}^{d}\right )$ satisfying

$$ \left \lVert T_{f}\right \rVert _{\mathcal{L}(L^{2})} \le \left \lVert f\right \rVert _{C^{0}_{b}} \lesssim \left \lVert f\right \rVert _{H^{s}} \text{ and } \left \lVert T_{f}\right \rVert _{ \mathcal{L}(H^{s})} \lesssim \left \lVert f\right \rVert _{H^{s}}. $$

(B.11)

If $s=t$, then we’re done. Otherwise $0 < t < s$, and so the theory of complex interpolation (see, for instance, Theorem 6.23 in [9]) implies that $T_{f}$ is a bounded linear map from $H^{t}(\mathbb{T}^{d})$ to $H^{t}(\mathbb{T}^{d})$ and that there exists $\theta \in (0,1)$, depending on $t$, $s$, such that

$$ \left \lVert T_{f}\right \rVert _{\mathcal{L}(H^{t})} \le C \left \lVert T_{f}\right \rVert _{\mathcal{L}(L^{2})}^{\theta } \left \lVert T_{f}\right \rVert _{\mathcal{L}(H^{s})}^{1-\theta } \le C \left \lVert f\right \rVert _{H^{s}} $$

(B.12)

for a constant $C>0$ depending only on $s$, $t$. Then for $h \in H^{t}(\mathbb{T}^{d})$ we have that $fh = T_{f} h \in H^{t}(\mathbb{T}^{d})$ with the stated estimate. □

2.3 B.3 Space-Time Sobolev Spaces

Here we consider some useful embedding properties of the space-time Sobolev spaced defined in Definition 1.6.

Proposition B.4

Suppose that $r\in \mathbb{R}$, $n\in \mathbb{N}$, and $I= (0,T)$ for $T \in (0,\infty ]$. Then following hold.

• 1. For every $\mathbb{N}\ni k\le n$ and for all $f\in L^{2}\left (I;H^{2+r}\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )\right )\cap H^{n+1}\left (I;H^{r-2n}\left (\mathbb{T}^{3}; \mathbb{R}^{3}\right )\right )$ we have that $f\in H^{k}\left (I;H^{2+r-2k}\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )\right )$. Moreover, there exists a constant $C$ independent of $f$ such that

  $$ \left \lVert f\right \rVert _{H^{k}H^{2+r-2k}}\le C\left (\left \lVert f\right \rVert _{L^{2}H^{2+r}}+\left \lVert f\right \rVert _{H^{n+1}H^{r-2n}} \right ). $$

  (B.13)

• 2. If $\mathbb{N}\ni k\le n$, then for every $f\in L^{2}\left (I;H^{2+r}\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )\right )\cap H^{n+1}\left (I;H^{r-2n}\left (\mathbb{T}^{3}; \mathbb{R}^{3}\right )\right )$ we may redefine $f$ on a null set to arrive at the inclusion $f\in UC^{k}_{b}\left (I;H^{r-2k+1}\left (\mathbb{T}^{3};\mathbb{R}^{3} \right )\right )$. Moreover, there exists a constant $C$ depending on only $k$ such that

  $$ \left \lVert f\right \rVert _{C^{k}_{b}H^{r-2k+1}}\le C\left (\left \lVert f\right \rVert _{L^{2}H^{2+r}}+\left \lVert f\right \rVert _{H^{n+1}H^{r-2n}} \right ). $$

  (B.14)

  Finally, if $T=\infty$, then we have $\lim _{t\to \infty }\left \lVert f(t)\right \rVert _{H^{r-2k+1}}=0$.

Proof

This is proved in Theorem 2.3 and 3.1 of [13]. □