1 Introduction

Today, many efforts are being devoted to developing passive and active graphene devices [1,2,3]. These include interconnects, antennas, attenuators, transistors [4, 5], and nonlinear devices [6]. Many techniques are used to realize these and other prospective components, such as chemical doping [7], integration of graphene with other materials [3], and graphene nanoribbon or nanodot elements [8]. Some problems of active and passive components are solved by staking the graphene nanosheets or using the quantum–mechanical interaction of graphene layers [9]. An analysis of the current state of graphene and other one-atom materials is given in [3], where the industrial mass production of 2-D materials and components is predicted for the next 30 years of this century.

The development of new components, with their analytical and semi-analytical models, will necessarily make these efforts easier. For instance, to avoid the lengthy ab initio computation of graphene components, the semiclassical scalar and dyadic models of conductivity of graphene are known based on the approach described by Kubo [10,11,12,13]. A theory based on a non-Kubo technique is discussed in Ref. [14]. In recent years, much attention has been paid to the experimental verification of conductivity models [15,16,17] and theories of guided plasmons in a multi-strip environment [18]. For instance, in Ref. [15], a difference between the results provided by a Kubo formula and the measurements is explained with the random microstructural properties of graphene films deposited on a dielectric substrate. A statistical analysis of defects or irregularities of graphene and dielectric layers is performed in Ref. [19]. To reduce this influence, researchers have recommended a high-level polishing of silicon dioxide or the use of complementary-to-graphene boron nitride [20] to avoid the morphological obstacles of graphene covering these materials. The influence of impurities on the atomistic level is considered in Ref. [16], where a modified Drude conductivity formula is given for the few-terahertz range.

Special interest is focused on models of the nonlinear properties of graphene when its chemical potential depends on the applied AC voltage [6]. Here, mixing of signals or their parametric amplification is possible [21]. An analytical model of dynamic graphene conductivity was developed in Ref. [10], where it was shown that this material biased by a pumping light demonstrated negative conductivity, and terahertz signal amplification was possible. This effect is discovered and described numerically and in experiments in Refs. [12, 22,23,24,25]. Most papers from this field are on the planar designs when graphene films and conductor strips are placed on a surface of a dielectric substrate, and diffraction of the EM waves is studied in numerical simulation or by measurements. An increase in amplification has been demonstrated with the use of multiple layers of graphene, and formulas for calculating the effective conductivity are given in Ref. [26]. Traveling wave amplification is studied numerically in a conductor-backed slot-waveguide in Ref. [27]. A detailed review of the research on optically pumped terahertz amplifiers and lasers is provided in Ref. [9].

In this paper, we propose a novel design for graphene loaded waveguides illuminated by light. In these waveguides, there are no sharp-edged conductors and graphene strips causing current crowding effect. The wall loss is decreased using the transverse-electric modes with the electric field parallel to the conductor plates. The modal fields are tightly pressed to the graphene film due to its surface nature, and the evanescent effect is realized by properly chosen cross-section geometry. In addition, the multiple-element effect is excluded, which usually leads to a rather dirty spectrum response. A new result found in this paper is the increased gain with the modal number as a result of the designed waveguide structures. In Sect. 2, the waveguides and their semi-analytical theory are given using the quasi-linear approach. The simulation results for the waveguides are presented in Sect. 3. The obtained results are discussed and conclusions drawn in Sect. 3.

2 Proposed waveguides and their electromagnetic quasi-linear theory

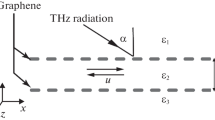
In contrast to planar components proposed previously by other authors, our waveguides have a rectangular enclosure design made of an entirely ideally conducting electric wall \({\mathbf{E}}_{\tau } \left( {x = \pm a,y = 0,b} \right) = 0\) (Fig. 1a) or combined electric \({\mathbf{E}}_{\tau } \left( {y = 0,b} \right)\) and magnetic \({\mathbf{H}}_{\tau } \left( {x = \pm a} \right) = 0\) walls with the cross-section size comparable to several hundred or tens of micrometers depending on the dielectric filling.

Fig. 1
figure 1

Rectangular waveguides with an inserted infinitely-thin graphene film. a Electric wall enclosure, b electric (solid lines) and magnetic (dashed lines) wall enclosure. Modes propagate along the z-axis, which is normal to the picture plane

Full size image

The graphene film shorts the wide-walls, and the low-loss \({\text{TE}}_{\text{y}}\) modes can be employed similarly to the known parallel-plate and the non-radiative dielectric (NRD) waveguides used in the millimeter-wave and terahertz frequency range [28, 29]. The biasing or pumping infra-red light can be launched along the waveguide and illuminates uniformly the graphene film due to reflections from the sidewalls (Fig. 1a). In the case of a magnetic wall (Fig. 1b), the light is directly incident to the graphene film from outside.

The complexity and accuracy of the electromagnetic (EM) theory of these waveguides are highly dependent on the model of graphene conductivity \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\sigma }_{g}\) used here, known as a Kubo formula. For instance, if anisotropy of conductivity should be taken into account at increased terahertz frequencies, then the hybrid modes having all six components of the EM field appear in consideration [11]. It is known that at strong signal fields, the conductivity of graphene shows moderate nonlinearity, and again, this should be treated. Some additional factors involve the substrate influence, impurity of graphene and its doping, quantum discretization of energy for nano-size strips, and edge effect.

Our theory supposes the perfect electric and magnetic walls initially, scalar linear conductivity of graphene σg, and weak signals only. It allows a separate description of the \({\text{TE}}_{\text{y}}\) and \(\text{TM}_{y}\) modes in a quasi-linear manner in the considered waveguides. The subject of our study is the \({\text{TE}}_{\text{y}}\) modes, because other modes \(\left( {{\text{TM}}_{\text{y}} } \right)\) are damped due to the shortening effect of graphene film, although they can propagate if the real part of the conductivity of graphene is negative.

To describe these \({\text{TE}}_{\text{y}}\) modes, the theory presented by Balanis [30] is pertinent, allowing us to write all required field components using one vector potential function F (1,2)m in each subdomain 1, 2 divided from each other by an infinitely thin conducting graphene film (Fig. 1). For the waveguide of the perfect electric wall (Fig. 1a), they are

$$\begin{aligned} & {\mathbf{F}}_{m}^{\left( 1 \right)} \left( {x,y,z} \right) = {\mathbf{y}}_{0} F_{m}^{\left( 1 \right)} = {\mathbf{y}}_{0} A_{m}^{\left( 1 \right)} \sin \left( {k_{y}^{\left( m \right)} y} \right)\cos \left( {k_{x}^{\left( m \right)} \left( {x + a} \right)} \right)e^{{ - jk_{z}^{\left( m \right)} z}} , \\ & {\mathbf{F}}_{m}^{\left( 2 \right)} \left( {x,y,z} \right) = {\mathbf{y}}_{0} F_{m}^{\left( 2 \right)} = {\mathbf{y}}_{0} A_{m}^{\left( 2 \right)} \sin \left( {k_{y}^{\left( m \right)} y} \right)\cos \left( {k_{x}^{\left( m \right)} \left( {a - x} \right)} \right)e^{{ - jk_{z}^{\left( m \right)} z}}, \\ \end{aligned}$$
(1)

where \({\mathbf{y}}_{0}\) is the vector unit, A (1,2)m are the unknown modal amplitudes, \(k_{y}^{\left( m \right)} = m\pi /b, \, m = 1,2, \ldots ,\infty ,\)\(\left( {k_{x}^{\left( m \right)} } \right)^{2} = \kappa^{2} - \left( {k_{y}^{\left( m \right)} } \right)^{2} - \left( {k_{z}^{\left( m \right)} } \right)^{2}\) with  \(\kappa^{2} = k_{0}^{2} \varepsilon_{r} \mu_{r} ,\) \(k_{0} = {\omega \mathord{\left/ {\vphantom {\omega {c,}}} \right. \kern-0pt} {c,}}\) ω = 2πf, f is the driving frequency, ɛr and μr are the relative permittivity and permeability, correspondingly, c is the velocity of light, \(j = \sqrt { - 1}\), and k (m)z is the unknown modal longitudinal propagation constant which should be defined from our treatment.

In the case of electric/magnetic wall enclosure (Fig. 1b), these vector potential functions are

$$\begin{aligned} & {\varvec{\Phi}}_{m}^{\left( 1 \right)} \left( {x,y,z} \right) = {\mathbf{y}}_{0} \varPhi_{m}^{\left( 1 \right)} = {\mathbf{y}}_{0} B_{m}^{\left( 1 \right)} \sin \left( {k_{y}^{\left( m \right)} y} \right)\sin \left( {k_{x}^{\left( m \right)} \left( {x + a} \right)} \right)e^{{ - jk_{z}^{\left( m \right)} z}} , \\ & {\varvec{\Phi}}_{m}^{\left( 2 \right)} \left( {x,y,z} \right) = {\mathbf{y}}_{0} \varPhi_{m}^{\left( 2 \right)} = {\mathbf{y}}_{0} B_{m}^{\left( 2 \right)} \sin \left( {k_{y}^{\left( m \right)} y} \right)\sin \left( {k_{x}^{\left( m \right)} \left( {a - x} \right)} \right)e^{{ - jk_{z}^{\left( m \right)} z}}, \\ \end{aligned}$$
(2)

where B (1,2)m are the unknown modal amplitudes.

The fields are obtained from Ref. [30], p. 275, and they are in the case of Fig. 1a

$$\begin{aligned} & E_{x,m}^{{\left( {1,2} \right)}} = \frac{1}{\varepsilon }\frac{{F_{m}^{{\left( {1,2} \right)}} }}{\partial z},\quad H_{x,m}^{{\left( {1,2} \right)}} = - \frac{j}{\omega \mu \varepsilon }\frac{{\partial^{2} F_{m}^{{\left( {1,2} \right)}} }}{\partial x\partial y}, \\ & E_{y,m}^{{\left( {1,2} \right)}} = 0,\quad H_{y,m}^{{\left( {1,2} \right)}} = - \frac{j}{\omega \mu \varepsilon }\left( {\frac{{\partial^{2} }}{{\partial y^{2} }} + \kappa^{2} } \right)F_{m}^{{\left( {1,2} \right)}} , \\ & E_{z,m}^{{\left( {1,2} \right)}} = - \frac{1}{\varepsilon }\frac{{\partial F_{m}^{{\left( {1,2} \right)}} }}{\partial x},\quad H_{z,m}^{\left( m \right)} = - \frac{j}{\omega \mu \varepsilon }\frac{{\partial^{2} F_{m}^{{\left( {1,2} \right)}} }}{\partial y\partial z} \\ \end{aligned}$$
(3)

where ɛ = ɛ0ɛr and μ = μ0μr are the absolute permittivity and permeability of dielectrics inside waveguides, with ɛ0 and μ0 as the corresponding vacuum constants.

The electric/magnetic wall geometry fields are described in a similar manner using the functions Φ (1,2)m in Ref. (3) instead of F (1,2)m . The chosen functions F (1,2)m and Φ (1,2)m satisfy the boundary conditions for the EM fields everywhere except the graphene film plane x = 0. At this boundary, the following equations are written, valid for both waveguide geometries (Fig. 1a, b)

$$\begin{aligned} & E_{z,m}^{\left( 2 \right)} \left( {x = 0} \right) - E_{z,m}^{\left( 1 \right)} \left( {x = 0} \right) = 0, \\ & H_{y,m}^{\left( 2 \right)} \left( {x = 0} \right) - H_{y,m}^{\left( 1 \right)} \left( {x = 0} \right) = - \sigma_{g} E_{z,m}^{\left( 1 \right)} \left( {x = 0} \right). \\ \end{aligned}$$
(4)

with graphene conductivity according to Ref. [10, 25]

$$\sigma_{g} = \left( {\frac{{e^{2} }}{4\hbar }} \right)\left\{ {\frac{{8k_{B} T\tau }}{{\pi \hbar \left( {1 - j\omega \tau } \right)}}\ln \left[ {1 + \exp \left( {\frac{{E_{F} }}{{k_{B} T}}} \right)} \right] + \tanh \left( {\frac{{\hbar \omega - 2E_{F} }}{{4k_{B} T}}} \right) - \frac{4\hbar \omega }{j\pi }\int_{0}^{\infty } {\frac{{G\left( {E - E_{F} } \right) - G\left( {\frac{\hbar \omega }{2},E_{F} } \right)}}{{\left( {\hbar \omega } \right)^{2} - 4E^{2} }}} {\text{d}}E} \right\},$$
(5)

where e is the electron charge, ℏ is the reduced Planck’s constant, kB is the Boltzmann constant, T is the temperature in Kelvin, τ is the graphene relaxation time, EF is the quasi-Fermi energy, and \(G\left( {E,E^{{\prime }} } \right) = \frac{{\sinh \left( {{E \mathord{\left/ {\vphantom {E {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}} \right)}}{{\cosh \left( {{E \mathord{\left/ {\vphantom {E {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}} \right) + \cosh \left( {{{E^{{\prime }} } \mathord{\left/ {\vphantom {{E^{{\prime }} } {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}} \right)}}.\)

Inserting F (1,2)m and Φ (1,2)m into Eqs. (3) and (4), two sets of linear algebraic homogeneous equations are obtained regarding the unknown amplitudes A (1,2)m and B (1,2)m for the electric and electric/magnetic wall enclosures, correspondingly. Calculating the determinants of these equations at their zero points gives the equations to obtain complex k (m)z . The formulas convenient for an iteration method of the solution are given below.

The propagation constant k (m)z for the electric wall waveguide (Fig. 1a) is found from Eq. (6)

$$\left( {k_{z}^{\left( m \right)} } \right)^{2} = \left( {\kappa^{2} - \left( {k_{y}^{\left( m \right)} } \right)^{2} } \right)\left( {1 + \frac{{4\left( {\kappa^{2} - \left( {k_{y}^{\left( m \right)} } \right)^{2} } \right)}}{{\left( {\omega \mu \sigma_{g} } \right)^{2} }}\cot^{2} \left( {k_{x}^{\left( m \right)} a} \right)} \right).$$
(6)

For the electric/magnetic wall waveguides (Fig. 1b), a similar Eq. (7) is

$$\left( {k_{z}^{\left( m \right)} } \right)^{2} = \left( {\kappa^{2} - \left( {k_{y}^{\left( m \right)} } \right)^{2} } \right)\left( {1 + \frac{{4\left( {\kappa^{2} - \left( {k_{y}^{\left( m \right)} } \right)^{2} } \right)}}{{\left( {\omega \mu \sigma_{g} } \right)^{2} }}\tan^{2} \left( {k_{x}^{\left( m \right)} a} \right)} \right).$$
(7)

Additionally, Eqs. (6) and (7) can be solved using any complex root search algorithm. Still, it has an approximate analytical solution if \(\left| {k_{x}^{\left( m \right)} a} \right| \ll 1\) and \(\left| {\tan^{2} \left( {k_{x}^{\left( m \right)} a} \right)} \right| \approx 1\), and it can be used as an initial value. On the other hand, a = ± ∞ leads to an H-waveguide parallel-plate configuration with an analytical formula (8) for propagation constant

$$\left( {k_{z}^{\left( m \right)} } \right)^{2} = \left( {\kappa^{2} - \left( {k_{y}^{\left( m \right)} } \right)^{2} } \right)\left( {1 - \frac{{4\left( {\kappa^{2} - \left( {k_{y}^{\left( m \right)} } \right)^{2} } \right)}}{{\left( {\omega \mu \sigma_{g} } \right)^{2} }}} \right).$$
(8)

3 Results of simulation and discussion

Initially, let us analyze the waveguides without graphene inserts. Analogously to the non-radiative dielectric waveguides [28], their vertical size b is chosen to provide the condition of non-propagation for the \({\text{TE}}_{y}^{\left( m \right)}\) eigenmodes in the hollow rectangular waveguide. It allows us to study the waves tightly coupled to graphene and reduce the influence of electric or magnetic walls at x = ± a.

Considering the chosen modal propagation constant k (m)z along the z-axis in expressions (1), (2) and satisfying the energy conservation law, then the obtained formulas (6) and (7) describe the backward modes with the phase velocity oriented against the group one k (m)z  = −(β(m) + jα(m)). It follows that if α(m) > 0, then a mode propagates exponentially decreasing along the z-axis according to formulas (1) and (2). The negative sign of α(m) is with the amplification occurring in graphene-based waveguides when \(\text{Re} \left( {\sigma_{g} } \right) < 0 .\)

Before applying formulas (6) and (7) to study these waveguides, the proposed iteration method to calculate the propagation constant should be validated. For this purpose, the parameters of graphene were chosen according to Ref. [27], where these values are properly discussed. It allows some qualitative comparisons with the mentioned paper and other works of the authors from this field.

It has been found that for the geometries a/b > 0.02 from Fig. 1a, b, the propagation constant k (1)z is close to the value provided by the parallel-plate waveguide model (8), and no additional iteration steps are required except one.

At very narrow waveguides, when a/b < 0.02, several iterations are needed to obtain accurate values for the propagation constant. Figures 2 and 3 show the convergence curves for one of the worst-case scenarios when (a/b) = 0.01 (waveguide geometry Fig. 1a). A notable feature of this algorithm is its numerical stability, as seen from Figs. 2 and 3.

Fig. 2
figure 2

Dependence of the normalized loss constant α(1)/k0 versus the iteration number N \(\left( {{\text{TE}}_{\text{y}}^{\left( 1\right)} - {\text{mode}}} \right)\). Waveguide parameters: a/b = 0.01, b = 0.01, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps

Full size image
Fig. 3
figure 3

Dependence of the normalized phase constant β(1)/k0 versus the iteration number N \(\left( {{\text{TE}}_{\text{y}}^{\left( 1\right)} - {\text{mode}}} \right)\). Waveguide parameters: a/b = 0.01, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps

Full size image

Consider the waveguides (Fig. 1a) filled by quartz or boron nitride (ɛr = 3.84) and calculate the frequency dependence of the loss α(m) and phase β(m) constants of the first two modes at two different values of quasi-Fermi energy EF. As an initial value, the propagation constant (8) of an infinite parallel-plate waveguide is chosen. The waveguide sidewalls are far enough from the graphene layers (a/b = 1), and only one iteration is needed to reach a converged value (Figs. 4, 5).

Fig. 4
figure 4

Normalized constants α(m)/k0 of the first two \({\text{TE}}_{\text{y}}^{{\left( {\text{m}} \right)}}\) modes of the studied rectangular waveguide (Fig. 1a) versus frequency. Negative values of this constant indicate the amplification of a mode. Waveguide data: a = b = 0.009 mm, ɛr = 3.84, and μr = 1. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 20,40\,{\text{meV}},\,{\text{and}}\,\tau = 1\,{\text{ps}}.\) Number of iterations N = 1

Full size image
Fig. 5
figure 5

Normalized phase constants β(m)/k0 of the first two \({\text{TE}}_{\text{y}}^{{\left( {\text{m}} \right)}}\) modes of the studied rectangular waveguide (Fig. 1a) versus frequency. Waveguide data: a = b = 0.009 mm, ɛr = 3.84, and μr = 1. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 20,40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image

It is seen that after a specific frequency where \(\text{Re} \left( {\sigma_{g} } \right) = 0\), the loss constant α(m) < 0 (Fig. 4), and its absolute value increases with EF. This effect and frequency is in accord with the results of [27] where the scattering of terahertz waves on multi-strip structures was studied.

At the difference to |α(m)|, the phase constant β(m)/k0 decreases with the value of the quasi-Fermi energy EF (Fig. 5).

The increased gain with the modal number is explained by the increase in the sub-wavelength localization of the field near the graphene film (Fig. 6). It is caused by a non-propagation condition for waves in the ±x-directions of the waveguide. The level of this reflection increases with the modal number, and the localization of the field increases.

Fig. 6
figure 6

\({\text{TE}}_{\text{y}}^{{}}\) normalized |Ex| field component dependence in the x-direction in the right part of the rectangular waveguide (Fig. 1a). Waveguide parameters: a = b = 0.009 mm, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image

Due to the abovementioned effect, the loss α(m) and phase β(m) constants show strong dependence at small values of the waveguide height b (Figs. 7 and 8), and it can be used to obtain a gain of a desired level without tuning EF. On the other hand, a geometry can be chosen, providing stable modal parameters towards manufacturing intolerances at larger b/a.

Fig. 7
figure 7

Normalized α(1)/k0 constant dependence of \({\text{TE}}_{\text{y}}^{\left( 1\right)} - {\text{mode}}\) versus waveguide height b (Fig. 1a). Waveguide parameters: a = b = 0.009 mm, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 20,40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image
Fig. 8
figure 8

Normalized β(1)/k0 constant dependence of \(\left( {{\text{TE}}_{\text{y}}^{\left( 1\right)} - {\text{mode}}} \right)\) versus waveguide height b (Fig. 1a). Waveguide parameters: a = 0.009 mm, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 20,40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image

The abovementioned analysis is confirmed by a study of the field distribution near the graphene film (Fig. 9). At smaller b waveguides, the field is more closely concentrated near graphene, leading to significant amplification. Again, this localization is caused by the substantial reflection of waves from the evanescent waveguide parts in ± x-directions. Thus, varying the height b of the waveguide allows for field localization control in the orthogonal direction.

Fig. 9
figure 9

\({\text{TE}}_{\text{y}}^{\left( 1\right)}\) normalized |Ex| field component dependence in the x-direction in the right part of the rectangular waveguide (Fig. 1a). Waveguide parameters: a = 0.009 mm, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image

In addition to the influence of the waveguide height b, the dependence of the modal parameters on the waveguide width a is simulated. Figure 10 shows an example of these calculations. It is seen that the influence of the sidewalls is strong enough when a/b ≪ 1. It is interesting to note that magnetic walls increase |α(1)/k0|, in contrast to the electric ones. For most practical applications, the sidewalls do not affect the propagation constant of the \({\text{TE}}_{\text{y}}^{\left( 1\right)}\) mode, and this waveguide would be rather stable towards manufacturing inaccuracies.

Fig. 10
figure 10

Loss constant α(1)/k0 dependence versus the normalized waveguide height a/b. Waveguide parameters: b = 0.009 mm, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps in (5). Number of iterations N = 30

Full size image

In addition to the simulation of these ideal waveguides, the dielectric and conductor loss must be considered. The dielectric loss can be calculated using formulas (6), (7), or (8) and complex representation of dielectric permittivity. The use in this paper of quartz (tan δ = 0.007) as waveguide filling shows a negligible loss in comparison to the graphene effect.

The conductor loss constant α (m)c is calculated here with the known perturbation approach where the fields and propagation constant are taken from the ideal waveguide model (3)

$$\alpha_{c}^{\left( m \right)} = \frac{{R_{s} \int\limits_{L} {\left( {{\mathbf{H}}_{\tau ,m} } \right)^{2} {\text{d}}l} }}{{\text{Re} \left( {\int\limits_{S} {E_{x,m} H_{y,m}^{ * } {\text{d}}s} } \right)}},$$
(9)

where Rs is the conductor surface resistance, and integrations are along the waveguide perimeter L and cross-section S, correspondingly.

As the surface resistance Rs, for comparison, two approximations are used. The first is just the conventional skin-effect formulas used to calculate, for instance, micro-strips [31, 32]

$$R_{s} = \text{Re} \left[ { - jZ_{0} \cot \left( {kt} \right)} \right],$$
(10)

where \(Z_{0} = \left( {1 + j} \right)\sqrt {{{\omega \mu_{0} } \mathord{\left/ {\vphantom {{\omega \mu_{0} } {2\sigma }}} \right. \kern-0pt} {2\sigma }}} ,\) \(k = {{\left( {1 - j} \right)} \mathord{\left/ {\vphantom {{\left( {1 - j} \right)} {\sqrt {{{\omega \mu_{0} } \mathord{\left/ {\vphantom {{\omega \mu_{0} } 2}} \right. \kern-0pt} 2}} }}} \right. \kern-0pt} {\sqrt {{{\omega \mu_{0} } \mathord{\left/ {\vphantom {{\omega \mu_{0} } 2}} \right. \kern-0pt} 2}} }}\), σ is the specific conductivity at DC, and t is the thickness of the waveguide walls.

At terahertz frequencies, one can consider the displacement current in conductors [34], and the surface resistance of a thick sheet of metal is

$$R_{s}^{\left( D \right)} = \text{Re} \sqrt {\frac{{j\omega \mu_{0} \mu_{r} }}{{\sigma_{D} + j\omega \varepsilon_{0} }}},$$
(11)

where the Drude conductivity σD is

$$\sigma_{D} = \frac{\sigma }{{1 + j\omega \tau_{c} }},$$
(12)

where τc is the mean free path time of the electrons in the conductors [33].

Figure 11 shows a comparison of calculations α(1)/k0 obtained for an ideal conductor rectangular waveguide and those calculated with the help of formulas (10) and (11). It is seen that loss essentially corrects the calculation results of loss/gain constant, as expected. Nevertheless, the proposed waveguide shows still amplification, but the frequencies where the amplification appears are shifted to higher values. Another conclusion from Fig. 11 is that the Drude and conventional skin-effect formulas show comparable results. Still, the use of the first formula in the terahertz range is preferable due to higher accuracy according to the analysis of Refs. [34, 35].

Fig. 11
figure 11

Loss constants of \({\text{TE}}_{\text{y}}^{\left( 1 \right)}\) mode of studied rectangular waveguide (Fig. 1a) versus frequency. Waveguide data: a = b = 0.009 mm, ɛr = 3.84, μr = 1,  t = 20 μm, \(\sigma = 5.96 \cdot 10^{4} \,{\text{Sim}}/{\text{mm}}\), and \(\tau_{c} = 3.6 \cdot 10^{14} \,{\text{s}}\) are for copper [33]. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image

In full confirmation of the previous theoretical and experimental works cited above, our simulation shows that our proposed optically biased graphene-based waveguides can provide an essential gain for modes propagating in them.

The developed lossy model allowed us to plot more realistic Ex(x, z) field and current Jz(y, z) = -σgEz(y, z) distributions (Figs. 12, 13). The first one is normalized by the value of |Ex(x = a, z = a)|, and the second by |Jz(z = h)|. The figures take into account the corrected values of kx and kz. In Fig. 12, the exponential dependence of the field along the x- and z-directions can be observed.

Fig. 12
figure 12

Normalized |Ex| field-component dependence in the x- and z-directions in the right part of the rectangular waveguide (Fig. 1a) for the \({\text{TE}}_{\text{y}}^{\left( 1\right)}\) mode. Waveguide parameters: a = b = 0.009 mm, ɛr = 3.84, μr = 1, and \(f = 4{\text{ THz}} .\) Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image
Fig. 13
figure 13

Normalized |Jz| current-component dependence in the y- and z-directions in the right part of the rectangular waveguide (Fig. 1a) for the \({\text{TE}}_{\text{y}}^{\left( 1\right)}\) mode. Waveguide parameters: h = a = b = 0.009 mm, ɛr = 3.84, μr = 1, and f = 4 THz. Graphene parameters used for calculations of conductivity (5) are from Ref. [27]: \(E_{F} = 40\,{\text{meV}}\) and τ = 1 ps. Number of iterations N = 1

Full size image

The longitudinal current (Fig. 13) takes into account the Drude model corrections as well, but the y-dependence is taken from the ideal model according to the perturbation technique, and then \(J_{z} \left( {y = 0,h} \right) = 0\). Similarly to the electric field, the current increases exponentially along the z-axis.

4 Conclusions

Novel terahertz graphene-based waveguides and their quasi-linear analytical models have been proposed for light-pumped applications. In these components, at the difference to planar integrated circuits, the following design ideas have been offered:

  1. 1.

    The rectangular waveguides have been proposed evanescent for propagation of the \({\text{TE}}_{\text{y}}^{{\left( {\text{m}} \right)}}\) and \({\text{TM}}_{\text{y}}^{{\left( {\text{m}} \right)}}\) (m > 0) modes for housing the graphene films illuminated by light inducing negative graphene conductivity in the terahertz range

  2. 2.

    These graphene films short two parallel plates of hollow rectangular waveguides while other walls are made of conductors or left open

  3. 3.

    The designs do not employ conductor and graphene strips or micro-strips having sharp edges that cause a current crowding effect

It enables the following to be achieved:

  1. a.

    To decrease the conductor-plate-associated loss in the case of \({\text{TE}}_{\text{y}}^{{\left( {\text{m}} \right)}}\) modes, similarly to the non-radiative dielectric rectangular waveguides

  2. b.

    To exclude the loss caused by sharp edges of conductor and graphene strips, unlike known planar designs

  3. c.

    To provide a better concentration of the field close to the graphene surfaces to gain increase

  4. d.

    To provide enhanced conditions for the integration of many of these waveguides of the increased terahertz power

  5. e.

    To be open using the multilayer graphene films or heterostructures for more effective employment of light power

  6. f.

    To be designed for the current injection lasing configurations in the case of conductor/open wall housing configuration

These proposed waveguides have been modeled using the EM field matching method valid for low-level signal applications when the terahertz field is weak enough so as not to influence the graphene conductivity. Otherwise, the solution of nonlinear Maxwell equations should be employed [21].

The formulas for the iterative calculation of complex propagation constants have been obtained and validated. In these waveguides, similarly to the known planar designs, the negativity of the real part of graphene conductivity caused by infra-red pumping light provides the exponential increase in signals along the longitudinal propagation direction, as shown in the simulation. It revealed a gain increase with the mode number caused by the increasing concentration of high-order modal field to the graphene surface in the considered frequency band. The parameters of modes can be regulated by the level of quasi-Fermi energy EF, dielectric filling ɛr, waveguide height b, and width 2a. The developed model considers the conductor loss according to the Drude theory of metals and dielectric loss at terahertz frequencies.