Abstract
The theoretical cross section for Compton scattering of maximally entangled Bell photons has yet to be rigorously confirmed by experiments. Test cases of Bell states for use in Compton scattering experiments can now be expanded given reports of creating all 4 Bell states in the hard x-ray regime by the process of spontaneous parametric down-conversion. We outline an experiment and apply a matrix method to parameterize Compton scattering theory using the phase matching angles. When the azimuths of two hypothetical photon counters are recorded at angles of 0 degrees and 90 degrees, and the ratio of their counting rates determined, azimuthal ratios are expected to be 600 times larger compared to 511 keV Bell photons.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Simulations show that image quality in Positron Emission Tomography can be improved by exploiting the polarization entanglement of 511 keV photons [1]. These entangled states were also used in Compton scattering experiments [2, 3] to test the kind of entanglement discussed by Einstein, Podolsky and Rosen [4–6]. However, these experiments had to assume theory can predict the angular distributions to a similar accuracy as for non-entangled photons [7]. To this day, this assumption must be invoked because the question concerning the accuracy of Compton scattering theory in the presence of entanglement still remains open [8, 9].
The main contribution of this work is to provide predictions for experiments concerned with closing the question regarding the accuracy of Compton scattering theory for Bell state photons. To date, only the 511 keV cross-polarized Bell state has been available for Compton scattering experiments. Although much research has been conducted using this system, the most accurate measurement of a quantity known as the 'azimuthal ratio' yielded maximum ratio values that are 87% or less than the predicted value [3, 8, 10]. Development of novel x-ray sources [11, 12] which can be used to generate any one of the 4 Bell states in the hard x-ray energy region [13] is appealing, because azimuthal ratios can now, in principle, be measured using controllable incident beams rather than relying solely on positron emitting sources [2, 3, 10].
A fundamental difference between non-entangled photons and Bell state photons is that the former are either polarized or unpolarized, whereas the latter are both polarized and unpolarized. This can be illustrated by first considering the 4 Bell photon state wavefunctions in the linearly polarization basis given by
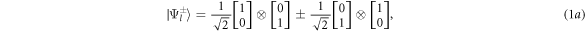
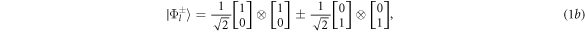
where the cross-polarization entangled states  and
and  only differ by a phase factor, and likewise for the parallel-polarization entangled states
only differ by a phase factor, and likewise for the parallel-polarization entangled states  and
and 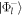 . It will be shown in section 2 that a source of Bell state photons will consist of two photon beams each of which can travel along different trajectories. Each beam in of itself is unpolarized. This dichotomy of Bell photons being both polarized (with respect to each other) and unpolarized (with respect to space-like separated photon detectors) manifests itself in the double differential Compton collision cross section. For example, the cross section for the states
. It will be shown in section 2 that a source of Bell state photons will consist of two photon beams each of which can travel along different trajectories. Each beam in of itself is unpolarized. This dichotomy of Bell photons being both polarized (with respect to each other) and unpolarized (with respect to space-like separated photon detectors) manifests itself in the double differential Compton collision cross section. For example, the cross section for the states 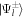 can be expressed as follows [8]
can be expressed as follows [8]

As can be seen, this cross section can be described as the difference of two terms: the term 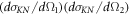 represents the product of Klein-Nishina (KN) cross sections describing Compton scattering by a pair of mutually independent and unpolarized photons. The second term represents the cross section for parallel-polarization entangled states
represents the product of Klein-Nishina (KN) cross sections describing Compton scattering by a pair of mutually independent and unpolarized photons. The second term represents the cross section for parallel-polarization entangled states  .
.
2. Production of hard x-ray Bell states
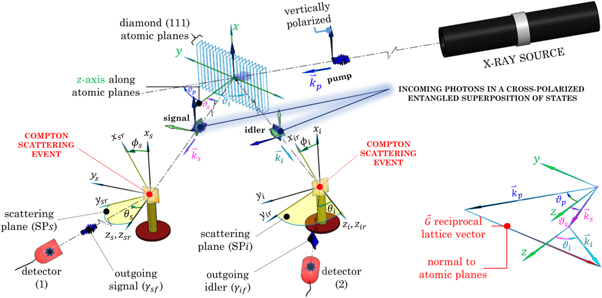
Figure 1 is a sketch of a parametric down-conversion experiment, which assumes diamond as the nonlinear medium for creating Bell states photons. The polarization correlations are analyzed down stream using scattering and photo-absorption based mediums.
Figure 1. Schematic of an experimental setup where the wave vectors  ,
, 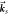 , and
, and  label the wave vectors of the idler, signal, and pump photons, respectively, and these vectors lie in a plane which we define as the 'trajectory plane'.
label the wave vectors of the idler, signal, and pump photons, respectively, and these vectors lie in a plane which we define as the 'trajectory plane'.
Download figure:
Standard image High-resolution imageFigure 1 depicts entangled photons created by a pump photon with wave vector 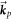 directed towards and impacting on a diamond target. In this example, a pair of maximally entangled signal and idler photon are emitted with wave vectors
directed towards and impacting on a diamond target. In this example, a pair of maximally entangled signal and idler photon are emitted with wave vectors  and
and  , respectively. The vectors
, respectively. The vectors 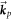 ,
, 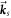 and
and  subtend angles of ϑp
, ϑs
and ϑi
, respectively, with respect to the (111) atomic planes. The pump photon is assumed to be linearly polarized normal to a 'trajectory plane' defined by the three vectors
subtend angles of ϑp
, ϑs
and ϑi
, respectively, with respect to the (111) atomic planes. The pump photon is assumed to be linearly polarized normal to a 'trajectory plane' defined by the three vectors  ,
, 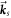 and
and 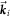 . To generate Bell state photons, these vectors must satisfy the vector condition
. To generate Bell state photons, these vectors must satisfy the vector condition 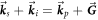 , where
, where 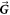 denotes the reciprocal lattice vector. The vector diagram shown near the bottom right of figure 1 visualizes this vector condition.
denotes the reciprocal lattice vector. The vector diagram shown near the bottom right of figure 1 visualizes this vector condition.
Figure 1 visualizes the creation of cross-polarized entangled signal and idler photons described by equation (1a
) wavefunctions. Attached to each photon are two system of coordinates. The first set of coordinate systems are labeled {xs
, ys
, zs
} and {xi
, yi
, zi
}, where the subscript s and i label the coordinate system of the 'signal' and 'idler', respectively. The {ys
, zs
} and {yi
, zi
} axis lie in the trajectory plane and the xs
and xi
axis are perpendicular to it. The photons themselves are represented as wave packets that travel along their respective wave vectors. Prior to a measurement, these photons are in a quantum superposition of cross-polarized states. This is approximated in the sketch by a pair of photons in a superposition of blue and green wave packets, which is to mean that the Bell state wavefunction will collapse to either a pair of blue or green photon states in any given Compton scattering coincidence measurement. The linear polarization state of each photon is represented by arrows which point in the direction of polarization. With respect to their coordinate systems, these arrows point either along the  or
or  directions and represent a vertical and horizontal polarization state, respectively.
directions and represent a vertical and horizontal polarization state, respectively.
The second set of coordinates systems are labeled {xsr
, ysr
, zsr
} and {xir
, yir
, zir
}, where the subscript 'r' denotes 'rotated'. With respect to the first coordinate system, we have the condition  ,
,  , and
, and  , where ϕ denotes the azimuthal angle. The orientation of these rotated system of coordinates are defined only by the Compton scattering process itself, since the Compton scattering planes of the signal and idler photons, labelled SPs and SPi, are defined by the {ysr
, zsr
} and {yir
, zir
} axis, respectively. The angles θi
and θs
are the Compton angles which subtend the incident and scattered wave vectors. Throughout this manuscript we have used the cross-polarized entangled states as a visualization aid to motivate the theoretical analysis of all 4 Bell states given in equation (1).
, where ϕ denotes the azimuthal angle. The orientation of these rotated system of coordinates are defined only by the Compton scattering process itself, since the Compton scattering planes of the signal and idler photons, labelled SPs and SPi, are defined by the {ysr
, zsr
} and {yir
, zir
} axis, respectively. The angles θi
and θs
are the Compton angles which subtend the incident and scattered wave vectors. Throughout this manuscript we have used the cross-polarized entangled states as a visualization aid to motivate the theoretical analysis of all 4 Bell states given in equation (1).
3. Departures from the Klein-Nishina model
The cross section given in equation (2) is based on the Klein-Nishina model which assumes photons Compton scatter off stationary electrons in a zero kelvin temperature environment. Departures from this model occur in situations where the photon incident energy Eo
is comparable with the binding energy Eb
of the inner-shell electron of the target. The incoherent scattering cross sections ∂2
σincoh
/∂Ωi
∂Ωs
for states  and
and  now replaces the Klein-Nishina model in a heuristic way [14] such that
now replaces the Klein-Nishina model in a heuristic way [14] such that
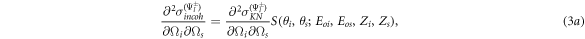
and
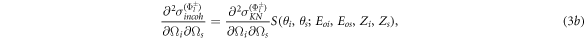
where it has been shown by Ribberfors and Berggren that the factorization on the right of the equal sign appears naturally out of the direct integration of the relativistic formulation of the Compton profiles [14], and where

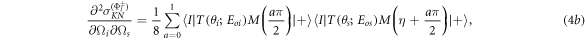
are the matrix representation of the cross sections derived using the pioneering work of Wightman [15], Fano [16], and McMaster [17], and the reader is referred to [8] and references therein for more detail. The cross sections have been averaged and summed over the initial and final electron spin states and summed over the final photon polarization states. The Stokes vectors ∣+〉 and ∣−〉 represent a vertical and horizontal polarization state, respectively. The incident photon energies Eoi and Eos are given in units of mc2, the bra vector 〈I∣ represents an insensitive-to-polarization photon counter, T is the Compton transition matrix, M is a matrix which transforms the Stokes vectors from the first to the second system of coordinates, and η is the relative angle between the two scattering planes such that

where Δϑis = ϑi − ϑs is the difference in phase-matching angles of the idler and signal photons.
The scattering function S(θi , θs ; Eoi , Eos , Zi , Zs ), in equation (3a ) and (3b ), takes into account deviations from the Klein-Nishina model when the idler and signal photons each scatter off an electron bound to atoms with atomic number Zi and Zs , respectively. If the scattering medium of the idler and signal photons are space-like separated and are composed of identical elements with atomic number Z, then S(θi , θs ; Eoi , Eos , Zi , Zs ) is assumed to be factorizable such that
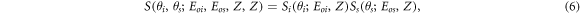
and equation (3a ) and (3b ) can be expressed as
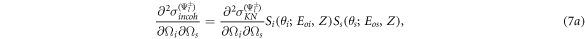
and

In the analysis that follows, theoretical results are obtained using the work by Shwartz and Harris who found phase-matching angles in the case of degenerate 12.5 keV and non-degenerate 10 and 15 keV Bell pairs [13].
To make accurate theoretical Compton scattering predictions in the hard x-ray regime, it is important to select a scattering medium that satisfies the condition Eb ≪ Eo . For photons in the 10−2 MeV range, we have selected neutral helium (Z = 2), since Eb = 0.0547 keV and Compton scattering is the dominant reaction channel at this energy range when Z < 5 (See figure (18) in [18]). We use the values of S for helium calculated by Brown [19], since the total ground state energy of the wave functions used to derive S only differ by 0.02% from the most accurate ground state energy values.
For incident energies above the K-shell ionization threshold, around 90 percent of scattering occurs from K-shell electrons [18]. If both electrons of each scatterer is ejected from the K-shell, it is reported that the dependence of their angular distribution on the relative azimuth η is proportional to  , which is maximum for perpendicular azimuths and zero for coplanar azimuths. Therefore, it is expected that some 65 percent of coincidences will correspond to both electrons originating in the K-shell. One may therefore expect to also observe these azimuthal correlations in Compton scattering experiments [20].
, which is maximum for perpendicular azimuths and zero for coplanar azimuths. Therefore, it is expected that some 65 percent of coincidences will correspond to both electrons originating in the K-shell. One may therefore expect to also observe these azimuthal correlations in Compton scattering experiments [20].
4. Theoretical precision of angular distributions of hard x-rays
The scattering function S is based on the impulse approximation (IA) model [21]. In this model, bound electrons are replaced by free electrons with a momentum distribution determined by the bound electron wave functions [18]. The validity of the IA approximation can be understood in terms of the uncertainty relation in which it is difficult to distinguish between bound and free electrons due to the short time scale of a Compton interaction, which is no greater than 10−11 seconds [18, 22].
The electron binding energy Eb
of an electronic shell is included in the IA model only insofar that the binding energy places a kinematic limit on the lowest incident photon energy that can inelastically scatter from a bound electron [18]. The binding energy Eb
also places a limit on the highest scattered photon energy Emax
that can be observed for a given photon incident energy Eo
. This limit is 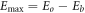 [18, 23]. Taking into account electron binding energy, the scattered photon energy E is defined by the Compton formula
[18, 23]. Taking into account electron binding energy, the scattered photon energy E is defined by the Compton formula

where all energies are defined in units of 511 keV (i.e., mc2).
For a single photon beam scattering off electrons from a many electron system, it has been shown that the IA model is accurate to order of ![${[{E}_{b}/({E}_{o}-E)]}^{2}$](https://content.cld.iop.org/journals/2399-6528/4/11/115011/revision2/jpcoabcb45ieqn31.gif) [23, 24]. The fractional precision of the theoretical incoherent cross section, defined here as A(Eoi
, Eos
, Ei
, Es
, Eb
), is derived using the rules of error propagation, such that the fractional precision
[23, 24]. The fractional precision of the theoretical incoherent cross section, defined here as A(Eoi
, Eos
, Ei
, Es
, Eb
), is derived using the rules of error propagation, such that the fractional precision ![${[{E}_{b}/({E}_{{oi}}-{E}_{i})]}^{2}$](https://content.cld.iop.org/journals/2399-6528/4/11/115011/revision2/jpcoabcb45ieqn32.gif) associated with the incoherent scattering of the idler, and
associated with the incoherent scattering of the idler, and ![${[{E}_{b}/({E}_{{os}}-{E}_{s})]}^{2}$](https://content.cld.iop.org/journals/2399-6528/4/11/115011/revision2/jpcoabcb45ieqn33.gif) associated with the signal, add in quadrature such that
associated with the signal, add in quadrature such that

where the energies of the scattered photons Ei and Es are defined using equation (8) such that

Therefore, the incoherent cross sections for 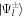 and
and 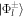 which takes into account the theoretical precision are expressed as follows
which takes into account the theoretical precision are expressed as follows
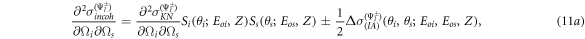
and
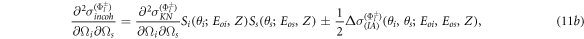
where the theoretical uncertainty of the cross section Δσ(IA) for the states 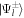 and
and  are defined, respectively, as
are defined, respectively, as

and

The theoretical precision is improved as Δσ(IA) ↦ 0, which can happen in one of two ways: If one is constrained to use a particular scattering medium, then the incident photon energy is chosen such that Eo ≫ Eb . Or, if one is constrained to a given photon energy Eo , then a scattering medium with sufficiently low binding energy is chosen such that Eb ≪ Eo .
5. The counting rates N⊥ and N∥
Compton scattering of polarization entangled photons has been studied in the past by measuring a quantity known as the azimuthal ratio. This involves a coincidence measurement of both photons scattered through the same angle, i.e., θs = θi = θ [20, 25]. The geometrical arrangement to measure the ratio of cross-polarized Bell states when the wave vectors are not colinear is illustrated schematically in figure 2. In this arrangement, the photon counter of the scattered idler is fixed at ϕi = 0°, such that only idler photons scattered in the trajectory plane are detected. Using equation (5), this implies η = ϕs .
Figure 2. The geometrical arrangement of an energy parameterized azimuthal ratio measurement. The measurement assumes the counter of the idler photon remains fixed at an azimuthal angle of ϕi
= 0° and the counter of the signal photon is placed at values of  (ϕs
= 0°) and
(ϕs
= 0°) and 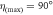 (ϕs
= 90°).
(ϕs
= 90°).
Download figure:
Standard image High-resolution imageThe quantity N⊥ is defined as the coincidence count rate when the photon counter of the signal is set at ϕs
= 90°, such that  . The quantity N∥ is the coincidence count rate when the signal photon counter is set to ϕs
= 0°, and therefore
. The quantity N∥ is the coincidence count rate when the signal photon counter is set to ϕs
= 0°, and therefore 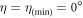 , and the ratio of these quantities is then determined. The count rates N⊥ and N∥ are proportional to the incoherent cross sections, which can be expressed as follows
, and the ratio of these quantities is then determined. The count rates N⊥ and N∥ are proportional to the incoherent cross sections, which can be expressed as follows
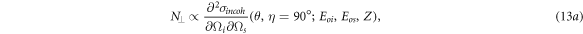
and
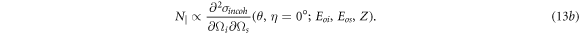
Before evaluating the ratios, which is done in the next two sections, it is instructive to plot equations (13a
) and (13b
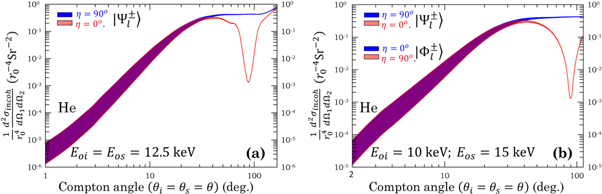
) and examine both their structure and the theoretical precision as a function of θ. These cross sections, normalized over the classical electron radius ( ), have been evaluated and plotted in figure 3(a) for degenerate 12.5 keV photons in the
), have been evaluated and plotted in figure 3(a) for degenerate 12.5 keV photons in the 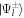 states. As can be seen, there is a significant deviation between the cross sections in the angular range 80° ≤ θ ≤ 100°, where the cross section evaluated at η = 0° drops by around three orders of magnitude relative to the cross section evaluated at η = 90°. The shaded area gives the estimated theoretical precision. Within the angular range 80° ≤ θ ≤ 100°, the estimated theoretical precision is around 8% for both cross sections.
states. As can be seen, there is a significant deviation between the cross sections in the angular range 80° ≤ θ ≤ 100°, where the cross section evaluated at η = 0° drops by around three orders of magnitude relative to the cross section evaluated at η = 90°. The shaded area gives the estimated theoretical precision. Within the angular range 80° ≤ θ ≤ 100°, the estimated theoretical precision is around 8% for both cross sections.
Figure 3. Log-log plot of the incoherent differential cross sections for degenerate (a) and nondegenerate (b) states evaluated at η =0° (ϕs = 0°) and η = 90° (ϕs = 90°), when ϕi = 0°. The shaded area is a first order estimate of the uncertainty in the theoretical cross section when helium is used as a scattering medium. For this case, the uncertainty in the cross section is around 8% between 80° ≤ θ ≤ 100°. (Photon energies and phase-matching angles are obtained from reference [13].)
Download figure:
Standard image High-resolution imageFor the particular case that 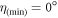 and
and  , an equality is found in the cross sections for Compton scattering of cross- and parallel-polarization entangled Bell states. Using equations given in (4) and (11) it can be shown that
, an equality is found in the cross sections for Compton scattering of cross- and parallel-polarization entangled Bell states. Using equations given in (4) and (11) it can be shown that
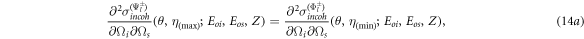
and

Figure 3(b) gives a plot of the cross sections for nondegenerate 10 and 15 keV cross- and parallel-polarization entangled states.
6. Energy parameterized azimuthal ratios
The angle Δϑis
= ϑi
− ϑs
is the difference in phase-matching angles, which were introduced in section 2. As shown in figure 2, Δϑis
is the angle subtended between  and
and  . An energy only parameterized azimuthal ratio is defined for coincidence measurements in which η is independent of Δϑis
. The setup shown in figure 2 satisfies this definition. Therefore, the expected count rates N⊥ and N∥ as a function of θ will be invariant to changes in Δϑis
, which implies that the ratio of these quantities will be invariant as well.
. An energy only parameterized azimuthal ratio is defined for coincidence measurements in which η is independent of Δϑis
. The setup shown in figure 2 satisfies this definition. Therefore, the expected count rates N⊥ and N∥ as a function of θ will be invariant to changes in Δϑis
, which implies that the ratio of these quantities will be invariant as well.
The expected energy only dependent ratio for cross-polarization entangled states that takes into account the theoretical precision is defined as follows
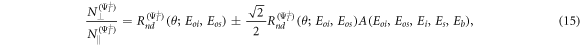
where we have applied error propagation methods to determine the theoretical precision. The subscript nd in R denotes 'nondegenerate' energies. Using equations (3a
) and (4a
) evaluated at 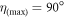 and
and 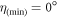 , Rnd
is given by
, Rnd
is given by
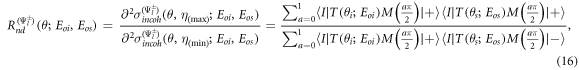
where the scattering function S cancels due to the definition of the incoherent cross section given in equation (3).
In the case for degenerate energies, i.e., Eos = Eoi = Eo , equation (16) simplifies to
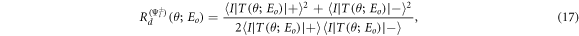
where the subscript 'd' denotes 'degenerate' energy.
Using equations of (14), the energy dependent ratios for parallel-polarization entangled Bell states are related to the ratios for cross polarization entangled states as follows

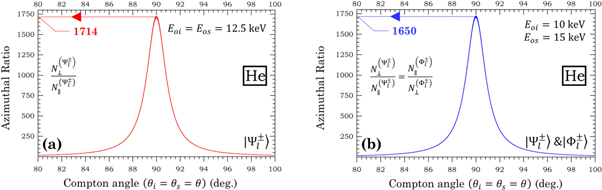
The ratio 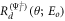 for Eo
= (12.5 keV)/(511 keV) = 0.0245 has been calculated and is shown in figure 4(a). The thickness of the curve gives an estimate of the theoretical precision. The ratios
for Eo
= (12.5 keV)/(511 keV) = 0.0245 has been calculated and is shown in figure 4(a). The thickness of the curve gives an estimate of the theoretical precision. The ratios  and
and  have also been calculated for the case when Eos
= 1.2Eo
(i.e., Eos
= 15 keV) and Eoi
= 0.8Eo
(i.e., Eoi
= 10 keV), and are shown in figure 4(b). As can be seen, both figures 4(a) and (b) show a significant asymmetry in the coincidence counting rates at θ ≈ 89.98 degrees, where the degenerate and non-degenerate ratios reach a peak value of 1713.04 and 1650.26, respectively. These peak values are approximately 600 times larger compared to the value of 2.85 predicted for 511 keV cross-polarized Bell states [20, 25].
have also been calculated for the case when Eos
= 1.2Eo
(i.e., Eos
= 15 keV) and Eoi
= 0.8Eo
(i.e., Eoi
= 10 keV), and are shown in figure 4(b). As can be seen, both figures 4(a) and (b) show a significant asymmetry in the coincidence counting rates at θ ≈ 89.98 degrees, where the degenerate and non-degenerate ratios reach a peak value of 1713.04 and 1650.26, respectively. These peak values are approximately 600 times larger compared to the value of 2.85 predicted for 511 keV cross-polarized Bell states [20, 25].
Figure 4. Energy parameterized azimuthal ratios. (a): The expected azimuthal ratio in the case of  states having degenerate incident energies of Eoi
= Eos
= Eo
= (12.5 keV)/(511 keV) = 0.0245. (b): The azimuthal ratio of
states having degenerate incident energies of Eoi
= Eos
= Eo
= (12.5 keV)/(511 keV) = 0.0245. (b): The azimuthal ratio of  and
and  in the case of non-degenerate incident energies Eos
= 1.2Eo
and Eoi
= 0.8Eo
. (Photon energies and phase-matching angles are obtained from reference [13].)
in the case of non-degenerate incident energies Eos
= 1.2Eo
and Eoi
= 0.8Eo
. (Photon energies and phase-matching angles are obtained from reference [13].)
Download figure:
Standard image High-resolution image7. Azimuthal ratios parameterized by the incident energies and phase-matching angles
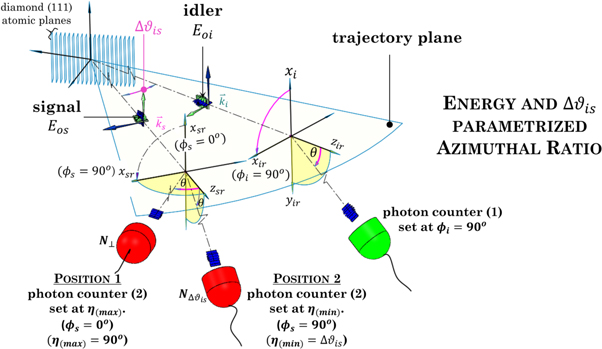
We now propose a coincidence measurement of the azimuthal ratio parameterized in terms of incident energies Eos and Eoi , and the difference in phase matching angles Δϑis = ϑi − ϑs . (The phase matching angles used here are obtained from [13]). The geometrical arrangement is illustrated schematically in figure 5. As can be seen, the photon counter measuring the scattered signal photons is set at the same two positions as in figure 2.
Figure 5. The geometrical arrangement of an energy and Δϑis
parameterized azimuthal ratio measurement. The measurement assumes the counter of the idler photon remains fixed at an azimuthal angle ϕi
= 90°, and the counter of the signal photon is placed at values of  (ϕs
= 90°) and
(ϕs
= 90°) and  (ϕs
= 0°). Refer to equation (
5
).
(ϕs
= 0°). Refer to equation (
5
).
Download figure:
Standard image High-resolution imageHowever, in this scheme, photon counter (1) is now fixed at right angles to the trajectory plane (i.e., ϕi
= 90°), rather than parallel to it, which was the case for energy parameterized ratios discussed in section 6. Using equation (5), we find that  . When photon counter (2) is at position (1), (ϕs
= 0°), the two scattering planes of the signal is perpendicular to that of the idler, and therefore, (
. When photon counter (2) is at position (1), (ϕs
= 0°), the two scattering planes of the signal is perpendicular to that of the idler, and therefore, (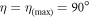 ). When the photon counter (2) is set at position (2), (ϕs
= 90°), it can be shown that
). When the photon counter (2) is set at position (2), (ϕs
= 90°), it can be shown that  .
.
We now define ρnd
(θ; Eoi
, Eos
, Δϑis
) as the energy and phase-matching parameterized azimuthal ratio for the state 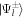 , such that
, such that
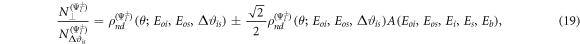
where
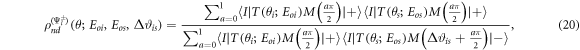
and applying the equalities found in equations (14), we can define the ratio for the state  as
as
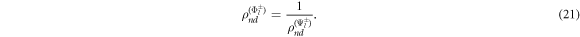
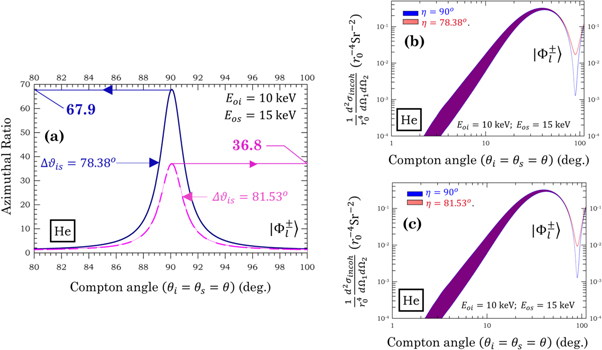
Equations (19) has been calculated and plotted in figure 6, when Δϑis
= 78.38°, 81.53° for the  states with non-degenerate energies Eos
= 1.2Eo
and Eoi
= 0.8Eo
.
states with non-degenerate energies Eos
= 1.2Eo
and Eoi
= 0.8Eo
.
Figure 6. (a): Energy and Δϑis parameterized azimuthal ratios. The ratio for parallel-polarization entangled Bell states in the case of nondegenerate incident energies Eos = 1.2Eo and Eoi = 0.8Eo , with phase-matching angle Δϑis = 78.38° and Δϑis = 81.53°. (b) and (c): Log-log plot of the inchorent differential cross sections used to calcuate the ratios in figure (a). (Photon energies and phase-matching angles are obtained from reference [13].)
Download figure:
Standard image High-resolution image8. Conclusion
Technology can now produce all 4 Bell states with sufficient incident energies required for Compton scattering experiments. Relative to 511 keV cross-polarized photons, hard x-ray Bell states with degenerate or non-degenerate incident energies show a significant amplification in polarization correlations, making them amenable to experimental verification, provided a suitable scattering medium is selected.
When all 4 Bell states are considered, relationships in the cross sections and ratios are found between cross- and parallel-polarization entangled states. In addition, the azimuthal ratio can be further parameterized in terms of the phase matching angles of Bell state photons generated in parametric down-conversion processes. In principle, these mathematical relationships and phase-matching constraints each provide a stringent test of Compton scattering theory itself. Therefore, the present study may be useful for future testing of fundamental laws of quantum mechanics.
Conducting a systematic investigation of this type could validate conclusions of past fundamental and practical research activities. Furthermore, if future experiments confirm theory, then Compton scattering could be used, aside from polarization filters, as a tool to verify the production of high energy polarization-entangled states emitted at specific phase-matching angles.
In future works, we will investigate more practical applications of these polarization-entangled states in the form of signal communication and extracting information in the field of medical imaging. On a fundamental level, since the matrix formalism presented here can also incorporate the dynamics of polarized Compton electrons, a study will be conducted on how entanglement is shared between the Bell state photons and the Compton electrons.
Acknowledgments
I would like to thank Tadayuki Takahashi for his helpful discussions. This research was supported by JSPS KAKENHI Grant Number JP19K23436, the Grant-in-Aid for Scientific Research on Innovative Areas 'Toward new frontiers: Encounter and synergy of state-of-the-art astronomical detectors and exotic quantum beams' and from JSPS KAKENHI grant numbers JP16H02170, JP18H05457 and JP18H02700, and the Grant-in-Aid for Scientific Research (A), Grant Number JP20H00153.