Normal stress differences in the consolidation of strong colloidal gels

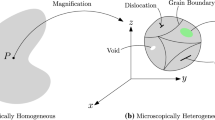
Abstract

Macroscopic models for the uniaxial consolidation of strong colloidal gels typically characterise the compressive strength of the particulate network in terms of the compressive yield stress P_y(ϕ) or uniaxial elastic modulus K ′ (ϕ). Almost all industrial applications involve multi-dimensional (MD) configurations with arbitrary tensorial stress states, and it is unclear how to generalise these 1D constitutive models to MD consolidation. Several studies have attempted to extend these 1D constitutive models to MD by assuming either isotropic consolidation or zero Poisson’s ratio, but the validity of these assumptions is currently unknown. Lacking is a validated tensorial rheology for the consolidation of strong colloidal gels that is capable of predicting the consolidation of these materials. One step toward the development of such tensorial rheology is the consideration of normal stress differences (NSDs) during uniaxial consolidation. Thus, a tensorial constitutive model for the consolidation of colloidal gels cannot be developed without accounting for these NSDs. We address this problem by performing discrete element model (DEM) simulations of the uniaxial consolidation of a two-dimensional (2D) strong colloidal gel and investigate evolution of the tensorial stress state during consolidation. We show that during consolidation, the Poisson ratio increases from zero near the gel point to almost unity near close-packing and uncover the particle-scale mechanisms that underpin these observations. These results provide the first steps toward a complete tensorial rheology of colloidal gels that is capable of resolving the evolution of these complex materials under superposed differential compression and shear.

Graphical abstract

Appendix 1: Extension of particle-scale theory to non-uniform particle contact angle distributions

To explore whether the assumption of uniform contact angle distribution used in the RT theory is responsible for this failure, we consider the evolving force-weighted contact angle distribution E_f(θ, ϕ) that evolves with solids concentration shown in Fig. 6. We approximate this distribution of contact angles by the exponential decay function:

$$ {E}_{\mathrm{f}}\left(\theta, \phi \right)=\left\{\begin{array}{c}\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\kern2em 0\le \theta <\lambda \left(\phi \right),\kern1.25em \\ {}0\kern4.25em \lambda \left(\phi \right)\le \theta \le \pi /2,\kern0.75em \end{array}\right. $$

(19)

where the characteristic contact angle λ(ϕ) evolves linearly with solids concentration as:

$$ \lambda \left(\phi \right)=\left({\theta}_g+{\theta}_{cp}\left(\frac{\phi -{\phi}_g}{\phi_{cp}-{\phi}_g}\right)\right) $$

(20)

where θ_g = 0.005 and θ_cp = 2.00 respectively are the characteristic contact angles at the gel point (Fig. 6a) and close-packing (Fig. 6b) concentrations.

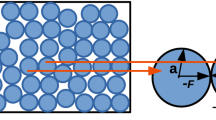
We extend the particle-scale theory of Roy and Tirumkudulu (RT) (Roy and Tirumkudulu 2016c) to non-uniform particle contact angle distributions. RT derive the following expression for the components of the particle-scale average stress tensor by considering the pressure and traction forces acting between two particles as shown in Fig. 1.

$$ {\sigma}_{\mathrm{i}\mathrm{i}}=-\frac{2}{\pi}\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{D}{\int}_0^{\frac{\pi }{2}}E\left[\theta, \phi \right]\left(-P{n}_{\mathrm{i}}+{T}_{\mathrm{i}}\right){n}_{\mathrm{i}} d\theta $$

(21)

where E[θ, ϕ] is the particle contact angle distribution, P is the interparticle pressure, T_i is the interparticle torque, n_i is the normal vector between the particles and 〈z(ϕ)〉 is the mean coordination number. Whilst RT consider a uniform particle distribution E[θ, ϕ] = 2/π, we relax this assumption and consider the evolving force-weighted distribution given by Eqs. (19) and (20). RT divide the integral in Eq. (21) into two regions for the elastic (0 < θ < θ_r) and plastic (θ_r < θ < π/2) components of the sliding friction as:

$$ {\sigma}_{\mathrm{i}\mathrm{i}}=-\frac{2}{\pi}\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{D}\left[{\int}_0^{\frac{\pi }{2}}-E\left[\theta, \phi \right]P{n}_{\mathrm{i}}{n}_{\mathrm{i}} d\theta +\left({\int}_0^{\theta_{\mathrm{r}}}E\left[\theta, \phi \right]{T}_{\mathrm{i}}{n}_{\mathrm{i}} d\theta +{\int}_{\uptheta_{\mathrm{r}}}^{\frac{\pi }{2}}E\left[\theta, \phi \right]{T}_{\mathrm{i}}{n}_{\mathrm{i}} d\theta \right)\right] $$

(22)

The total strain σ_ii is then decomposed into the elastic ${\sigma}_{\mathrm{ii}}^e$ and plastic ${\sigma}_{\mathrm{ii}}^p$ components

$$ {\sigma}_{\mathrm{i}\mathrm{i}}^e=-\frac{4}{\pi^2}\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{D}\left[{\int}_0^{\frac{\pi }{2}}-E\left[\theta, \phi \right]P{n}_{\mathrm{i}}{n}_{\mathrm{i}} d\theta +{\int}_0^{\theta_{\mathrm{r}}}E\left[\theta, \phi \right]{T}_{\mathrm{i}}{n}_{\mathrm{i}} d\theta \right] $$

(23)

$$ {\sigma}_{\mathrm{i}\mathrm{i}}^p=-\frac{4}{\pi^2}\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{D}\left[\left({\int}_{\theta_{\mathrm{r}}}^{\frac{\pi }{2}}E\left[\theta, \phi \right]{T}_{\mathrm{i}}{n}_{\mathrm{i}} d\theta \right)\right] $$

(24)

The transition from elastic to plastic deformation occurs when the applied strain e_o exceeds a critical value e_c which RT (Roy and Tirumkudulu 2016c) derive as

$$ {e}_{\mathrm{c}}=\frac{4\mu {F}_0}{k_{\mathrm{t}}D\left(-\overline{\mu}+\sqrt{{\overline{\mu}}^2+1}\right)} $$

(25)

Equations (23–25) then form the basis for the affine and non-affine particle-scale models for consolidation.

Affine model

The affine model of RT assumes affine deformation at the particle scale, where consolidation occurs in the axial 1-direction and the 2-direction is transverse to the consolidation direction. Under the assumption of uniform contact angle distribution (E[θ, ϕ] = 2/π), Eqs. (23–25) yield a constant value for the normalised NSD as given by Eq. (14). To relax this assumption, we inset the model Eq. (19) for the force-weighted particle contact distribution into Eq. (23), yielding the following expressions for the normal stresses:

$$ {\overline{\sigma}}_{11}=\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{\pi}\frac{1}{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}}{\overline{e}}_c\left(\frac{k_n}{k_t}-1\right){\int}_0^{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}} Si{n}^2\left(\theta \right){Cos}^2\left(\theta \right) d\theta \kern0.5em =\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{\pi}\frac{{\overline{e}}_c}{k}\frac{\left(-1+k\right)\left( Sin\left(4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)-4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)}{32\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}} $$

(26)

$$ {\overline{\sigma}}_{22}=\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{\pi}\frac{1}{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}}{\overline{e}}_c\frac{k_n}{k_t}\left[{\int}_0^{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}}{Cos}^4\left(\theta \right) d\theta +\frac{k_t}{k_n}{\int}_0^{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}} Si{n}^2\left(\theta \right){Cos}^2\left(\theta \right) d\theta \right]\kern0.75em =\frac{\phi \left\langle z\left(\phi \right)\right\rangle }{\pi}\frac{{\overline{e}}_c}{k}\frac{8 Sin\left(2\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)+\left(1-k\right) Sin\left(4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)+4\left(k+3\right)\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}}{32\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}} $$

(27)

The normalised NSD ${N}_1^{\ast }$ can then be calculated from these normal stresses as

$$ {N}_1^{\ast }=1+\frac{\left(1-k\right)\left( Sin\left(4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)-4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)}{\left[8 Sin\left(2\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)+\left(1-k\right) Sin\left(4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right)+4\left(k+3\right)\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]} $$

(28)

As shown in Fig. 11a, this model predicts a reduction of the relative NSD with solid concentration; however, this reduction is only very minor for the parameter values of the DEM simulation.

Fig. 11

Prediction of relative NSD for (a) affine and (b) non-affine RT theory subject to non-uniform contact orientation distribution E_f(θ, ϕ) with parameter values d = 2.0, d_f = 1.55, d₁ = 1.0 and k = 0.88

Non-affine model

Similarly, the non-affine RT model may be extended to non-uniform contact angle distributions as follows. The non-affine model of RT has been developed based on the assumption of non-affine deformation at the particle scale. The normalised NSD as given by Eq. (18) yield an increasing behaviour with solids concentration under the assumption of uniform contact angle distribution (E[θ, ϕ] = 2/π). To facilitate the prediction of normalised NSD as observed in Fig. 8b, we reproduce a non-affine model of RT for the force-weighted particle contact distribution into Eq. (23) that yields the following expressions for the normal stresses:

$$ {\overline{\sigma}}_{11}=\frac{4\alpha {z}_c}{\pi^2}{\phi}^{\frac{d-{d}_f+2{d}_1}{d-{d}_f}}\frac{1}{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}}{\overline{e}}_c\frac{k_n}{k_t}\left[{\phi}^{\frac{-2}{d-{d}_f}}{\int}_0^{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}} Si{n}^2\left(\theta \right){Cos}^2\left(\theta \right) d\theta -\frac{k_t}{k_n}{\int}_0^{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}} Si{n}^2\left(\theta \right){Cos}^2\left(\theta \right) d\theta \right]=\frac{4\alpha {z}_c}{\pi^2}{\phi}^{\frac{d-{d}_f+2{d}_1}{d-{d}_f}}\frac{1}{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}}\frac{{\overline{e}}_c}{k}\left[{\phi}^{\frac{-2}{d-{d}_f}}\left(\frac{1}{32}\left(4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}- Sin\left[4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]\right)\right)-\frac{k}{32}\left(4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}- Sin\left[4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]\right)\right] $$

(29)

$$ =\frac{4\alpha {z}_c}{\pi^2}{\phi}^{\frac{d-{d}_f+2{d}_1}{d-{d}_f}}\frac{1}{\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}}\frac{{\overline{e}}_c}{k}\left[{\phi}^{\frac{-2}{d-{d}_f}}\left(\frac{1}{32}\left(12\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}+8\ Sin\left[2\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]+ Sin\left[4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]\right)\right)+\frac{k}{32}\left(4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}- Sin\left[4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]\right)\right] $$

(30)

These normal stresses of Eq. (29) and Eq. (30) then yields the following expression for the normalised NSD as

$$ {N}_1^{\ast }=\frac{8\ Sin\left[2\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]+2\left(1-k{\phi}^{\frac{-2}{d-{d}_f}}\right) Sin\left[4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]+8\left(1+k{\phi}^{\frac{-2}{d-{d}_f}}\right)\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\ }{8\ Sin\left[2\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]+\left(1-k{\phi}^{\frac{-2}{d-{d}_f}}\right) Sin\left[4\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}\right]+4\left(3+k{\phi}^{\frac{-2}{d-{d}_f}}\right)\lambda \left(\phi \right){e}^{-\lambda \left(\phi \right)}} $$

(31)

This model also yields only a minor reduction of the relative NSD with solids concentration for the parameter values of the DEM simulation (in Fig. 11b). These results indicate that even when non-uniform force-weighted contact angle distribution is accounted for, the affine and non-affine variants of the RT theory cannot resolve the evolution of NSDs under uniaxial consolidation. For the affine RT model, the maximum reduction of the relative NSD occurs in the case of negligible transverse elastic modulus (k = 0), such that the contact angle distribution evolves from the Dirichlet function E_f(θ, ϕ_g) = δ(θ) at the gel point to the uniform distribution E_f(θ, ϕ_cp) = 1/2π near close-packing and the relative NSD decays from ${N}_1^{\ast }$=1 at ϕ = ϕ_g to ${N}_1^{\ast }=2/3$ at ϕ = ϕ_cp. As shown by Fig. 8, we observe a decrease of the normalised NSD to ${N}_1^{\ast}\approx 0.27$, well beyond the theoretical limit of 2/3 suggested by the affine theory. Conversely, the normalised NSD always increases with solids concentration in the non-affine RT model due to the nonlinear contribution of the fractal terms in the model (under the geometric constraint d_f < d), regardless of how the contact angle distribution evolves with concentration.

We attribute the inherently affine nature of the micro-mechanical theory (Roy and Tirumkudulu 2016c) to the inability to resolve the evolution of NSDs under uniaxial consolidation. In the “Simulation results” section, we showed that buckling, collapse and strain hardening of columnar structures oriented in the axial direction play a key role in the evolution of the axial and transverse normal stresses, and these dynamics are not resolved by the two-particle affine model.