Abstract
In the article the spectra of plasmon-polariton in a three-dimensional periodic structure of graphene ribbons embedded in a medium were studied at the first time and for a fixed carrier concentration, influences on the spectra from ribbon width, interface distance and period of ribbon were shown. Compared to those in monolayer periodic structure of graphene ribbons, sharp differences occur. Furthermore, there always exist a match point where frequencies of the plasmon-polarition and the electromagnetic radiation are the same. The study improved our basic knowledge on plasmon dynamics in graphene and was important in the design of high efficiency optoelectronic devices.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Recently, plasmon dynamics in graphene has become an emerging subfield, benefitting from the remarkable electrical and optical properties [1–3], such as the relatively low loss compared to customary matals [4, 5] and the tunable ability utilizing electrical gating or chemical doping [6]. For instance, plasmon-polaritons (PP) in graphene were experimentally and theoretically [7–17] studied extensively and were also applied in optical modulators [18], photodectectors [19], biochemical sensors, and so on.
So far the most issues on the plasmon dynamics in graphene mainly focused on planar structures, for instance, on the planar graphene superlattices [14], on the periodic grid of graphene ribbons [3, 6, 20]. To improve the efficiency of photo-detectors or biochemical sensors, or to improve the ability of optical modulation, we performed a preliminary study of the plasmon dynamics based on graphene in a three-dimensional structure at the first time.
Here we study the PP spectra in a three-dimensional periodic structure of graphene ribbons embedded in a medium. For a fixed carrier concentration, the influence on the PP spectra from ribbon width, interface distance and period in the interface were given. Furthermore, we compared our results with those in a planar periodic structure of graphene ribbons and sharp differences were also shown. We believe that the structure may have applications in graphene-based photodetector and sensor.
For practical photodetectors, we always face a challenge, mismatch. For a certain wave vector, the frequency of PP, at least for graphene system, and that of electromagnetic(EM) radiation in the medium can hardly be equal. In fact, frequency of PP is generally lower than that of EM radiation. We argue that in the discussed structure there always exists a match point where the frequencies of plasmon-polarition and electromagnetic radiation are the same.
2. Helmholtz equation and boundary conditions
Consider a three-dimensional periodic structure of graphene ribbons embedded in a medium with relative dielectric constant,  , as shown in figure 1. For simplification, we assume that each graphene ribbon, parallel to the planar defined by z = 0, has infinite length in the y direction and width d in the x direction. The periods in x direction and interface distance along z direction are a and b, respectively.
, as shown in figure 1. For simplification, we assume that each graphene ribbon, parallel to the planar defined by z = 0, has infinite length in the y direction and width d in the x direction. The periods in x direction and interface distance along z direction are a and b, respectively.
Figure 1. The three-dimensional periodic structure of graphene ribbons embedded in the medium with relative dielectric constance  . The period in x direction and interface distance in z direction are a and b respectively. The ribbon width is d.
. The period in x direction and interface distance in z direction are a and b respectively. The ribbon width is d.
Download figure:
Standard image High-resolution imageWe here suppose that the plasmon propagating in xz plane and only consider the transverse magnetic (TM) mode, that is, the magnetic field has only y component and correspondingly the electric field has only x and z components. We also require the time dependence of the fields in the form e−i ω t and the absence of free volume currents and charges for simplification. The Maxwell equations read as
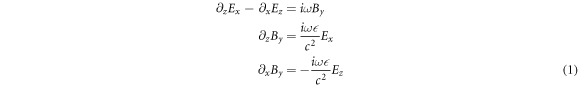
Notice that all the field components are invariant along y direction, that is, ∂y Ex = ∂y Ez = ∂y By = 0.
From above equations one can obtain the Helmholtz equations for each field components. For By , for example, the Helmoholtz equation is,
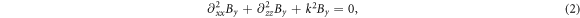
where  is the wave number of electromagnetic (EM) radiation with angle frequencyω in the medium. Equations for Ex
and Ez
are similar.
is the wave number of electromagnetic (EM) radiation with angle frequencyω in the medium. Equations for Ex
and Ez
are similar.
Since the structure is periodic in z direction and there is no volume current and charge, the boundary conditions are
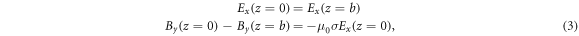
where μ0 is the magnetic permeability and σ the conductivity. One can write them in the form of By ,
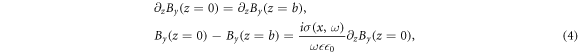
where  0 is the vacuum electric permittivity, and σ(x, ω) is the conductivity in the interface.
0 is the vacuum electric permittivity, and σ(x, ω) is the conductivity in the interface.
Now we assume the wave vector of plasmon is (qx , 0, qz ). From the Fourier-Floquet decomposition, By can be written as
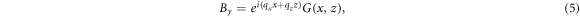
where G(x, z) is a quasiperiodic function. In other words, G(x + a, z) = G(x, z) and G(x, z + b) = G(x, z) almost everywhere except at the interfaces, where G(x, 0) and G(x, b) are not equal but determined by boundary conditions. With the preparations, G(x, z) has the form 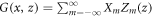 , where
, where  .
.
Instituting above arguments into equation (2) one found that
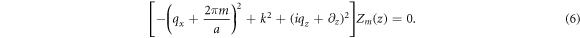
To study the boundary condition, we first deal with the conductivity. In the first period, 0 < x < a, the conductivity can be written as σ(x, ω) = σ(ω)f(x)θ(d − x), where θ(x) denotes the Heaviside step function, σ(ω) is determined by different processes, such as intraband and interband contributions [6, 21], and f(x) is determined by charge contribution in the ribbon. Due to the periodic arrangement in x direction, we have
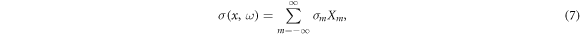
where 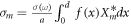 . A simply choice f(x) = 1, leaded to
. A simply choice f(x) = 1, leaded to 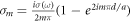 . In the [22], authors used a spatial modulation of conductivity. But their coefficients are twice as the ones obtained here except that the two coefficients at the case of m = 0are the same, σ(ω)d/a. However, such choice does not satisfy the edge condition of each ribbon and furthermore, it takes the coupling between different m'th mode, which will complicate our analysis and make the calculation unstable. The validity of the edge condition [3, 23] assumes that
. In the [22], authors used a spatial modulation of conductivity. But their coefficients are twice as the ones obtained here except that the two coefficients at the case of m = 0are the same, σ(ω)d/a. However, such choice does not satisfy the edge condition of each ribbon and furthermore, it takes the coupling between different m'th mode, which will complicate our analysis and make the calculation unstable. The validity of the edge condition [3, 23] assumes that 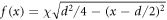 where χ was determined by a lengthy function and also should be adjusted to preserve the stability in calculations. Here, to make calculations stable and simple, and to compare our results with those of monolayer graphene grid, we simply choose
where χ was determined by a lengthy function and also should be adjusted to preserve the stability in calculations. Here, to make calculations stable and simple, and to compare our results with those of monolayer graphene grid, we simply choose  . In the long wavelength approximation, we do not concern the detailed distribution of electromagnetic field and the choice is suitable.
. In the long wavelength approximation, we do not concern the detailed distribution of electromagnetic field and the choice is suitable.
Now boundary conditions change to
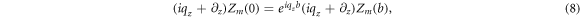
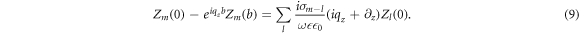
From equation (6), in the first period, one has,
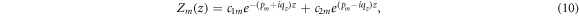
where 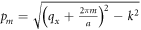 and c1m
and c2m
are constants to be determined. From equation (8), we have
and c1m
and c2m
are constants to be determined. From equation (8), we have 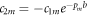 . Therefore, we wrote Zm
(z) in the first period as
. Therefore, we wrote Zm
(z) in the first period as

Above expression guarantees the evanescence of By . In fact, we have Zm (b/2) ≡ 0 and Zm (0) ≡ − Zm (b) for each m.
Then, we have from equation (9),
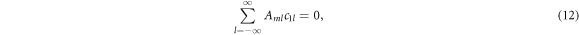
where 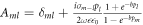 . The requirement that there are nonzero solutions to c1m
means that the ∞ × ∞ matrix A satisfies
. The requirement that there are nonzero solutions to c1m
means that the ∞ × ∞ matrix A satisfies 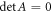 . Therefore,
. Therefore, 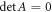 determines the dispersion relation of PP in the periodic structure of graphene ribbons.
determines the dispersion relation of PP in the periodic structure of graphene ribbons.
Since matrix A is independent on qz , the plasmon dispersion only depends on qx . In other words, plasmon frequencies at different qz are the same, as long as qx is at the same. We thus can generate not only PP propagating in x direction, but also degenerate one propagating in xz plane. The interesting result is favourable to manipulate plasmon in the structure.
It seems that the phase factors 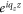 in equation (5) and
in equation (5) and  in equation (11) should be counteracted by each other. Then, there is a puzzle that what role qz
plays. In fact, the factor
in equation (11) should be counteracted by each other. Then, there is a puzzle that what role qz
plays. In fact, the factor 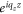 in equation (5) plays its role in the whole z field while
in equation (5) plays its role in the whole z field while  in equation (11) only in the region 0 < z < b, the first period of z. In other word, only in each one period of z, these two factors counteract each other. The phase difference between points (x,z) and (x, z + nb), for instance, is nqz
b, where n is an integer. Therefore, qz
supplies a mechanism of plasmon waveform modulation. Since qz
does not enter in the dispersion relation of plasmon, we simplify assume qz
= 0 in the following.
in equation (11) only in the region 0 < z < b, the first period of z. In other word, only in each one period of z, these two factors counteract each other. The phase difference between points (x,z) and (x, z + nb), for instance, is nqz
b, where n is an integer. Therefore, qz
supplies a mechanism of plasmon waveform modulation. Since qz
does not enter in the dispersion relation of plasmon, we simplify assume qz
= 0 in the following.
3. Results and discussions
Here we consider that the environment temperature T is zero. As for the graphene conductivity σ(ω), it is determined by doping concentrate or Fermi energy (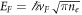 , where vF
∼ 1 × 106 m s−1 is the Fermi velocity of carriers and ne
is electronic density). If a ∼ 10 μm, EF
∼ 0.1 eV and we focus on the THz spectral range (ℏ
ω ∼ 1 meV), the dominant contribution to conductivity is Drude term [6] and the conductivity reads as
, where vF
∼ 1 × 106 m s−1 is the Fermi velocity of carriers and ne
is electronic density). If a ∼ 10 μm, EF
∼ 0.1 eV and we focus on the THz spectral range (ℏ
ω ∼ 1 meV), the dominant contribution to conductivity is Drude term [6] and the conductivity reads as
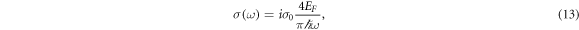
where σ0 = e2/(4ℏ).
To make conclusion more general, we introduce dimensionless quantities, b0 = b/a, q0 = qx
a, d0 = d/a, ω0 = ω
a/c,  ,
, 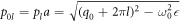 where c is the vacuum light speed. Then, we have
where c is the vacuum light speed. Then, we have
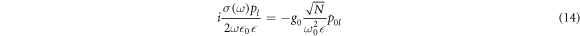
where we have used  and N = ne
a2. We notice that the validity of Drude expression, ℏ
ω/EF
≪ 1, means
and N = ne
a2. We notice that the validity of Drude expression, ℏ
ω/EF
≪ 1, means  .
.
At last, with the notion 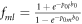 , we have,
, we have,

which determines PP dispersion by 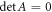 . Notice that if d0 = 1 and p0m
b0 ≫ 1 (leading to fml
→ 1), one shall obtain the famous result of surface PP where there is only one interface [3, 6] from m = l = 0. We thus nominate the fraction fml
as the correction factor due to the periodic arrangement along z direction. If d0 ≠ 1, frequency of PP with only one interface,
. Notice that if d0 = 1 and p0m
b0 ≫ 1 (leading to fml
→ 1), one shall obtain the famous result of surface PP where there is only one interface [3, 6] from m = l = 0. We thus nominate the fraction fml
as the correction factor due to the periodic arrangement along z direction. If d0 ≠ 1, frequency of PP with only one interface, 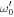 , reads as
, reads as
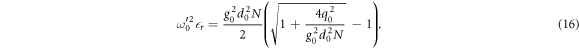
Our choice of σm decouples PP mode with different m and makes the mode with m = 0 the ground one in the first Brillouin zone, ∣q0∣ < π. Such choice therefore simplify our discussions. In the following we focus on the correction to the ground states due to fml .
For the structure the carrier concentration is always fixed and not tunable after the device was fabricated. However, the theoretical study on the effect of different concentration or equivalent N is meaningful. Results of N effect were listed in figure 2. In the figure, 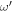 was given by equation (16). We found that, as expected, PP frequency gets larger as N and/or q0 increase . However, there is a coupling between different interface. The smaller the q0, the stronger the coupling. Therefore, ω0 becomes more smoother than
was given by equation (16). We found that, as expected, PP frequency gets larger as N and/or q0 increase . However, there is a coupling between different interface. The smaller the q0, the stronger the coupling. Therefore, ω0 becomes more smoother than  and PP spectrum is lifted. The lifting makes that ω0 does not tend to zero at q0 → 0 although
and PP spectrum is lifted. The lifting makes that ω0 does not tend to zero at q0 → 0 although 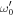 does. p00 is imagine number and Z0 behaves as combination of cosine functions,
does. p00 is imagine number and Z0 behaves as combination of cosine functions,  . In fact,
. In fact, 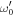 behaves as convex function but ω0 as concave one.
behaves as convex function but ω0 as concave one.
Figure 2. The dispersion of PP at different N. We choose b0 = d0 = 0.5 and  r
= 5. The dotted line, marked as EM, symbols the dispersion of electromagnetic radiation in the medium.
r
= 5. The dotted line, marked as EM, symbols the dispersion of electromagnetic radiation in the medium.
Download figure:
Standard image High-resolution imageTo study the effect of the coupling between different interfaces we also listed our results of PP dispersion at different b0 in figure 3. As expected, the smaller the b0 is, the more obvious the lifting becomes. On the other hand, if b0 ≫ 1, the lifting at larger q0 is neglected and 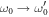 , as shown by the case of b0 = 4 in the figure. However, for small q0 (or larger wavelength), the lifting can not be neglected and we have still no ω0 → 0 when q0 → 0.
, as shown by the case of b0 = 4 in the figure. However, for small q0 (or larger wavelength), the lifting can not be neglected and we have still no ω0 → 0 when q0 → 0.
Figure 3. The dispersion of PP at different b0. We choose d0 = 0.5, N = 106 and  r
= 5. The dotted line is the same as that in figure 2.
r
= 5. The dotted line is the same as that in figure 2.
Download figure:
Standard image High-resolution imageTo study the effect of width of ribbon, d0, we listed PP dispersion at different d0 in figure 4. We found that for a fixing q0, ω0 becomes smaller with decreasing d0. The phenomenon can be understood from equation (15). The equation told us that a smaller d0 is equivalent to a smaller N, which leading to a smaller ω0.
Figure 4. The dispersion of PP at different d0. We choose b0 = 0.5, N = 106 and  r
= 5. The dotted line is the same as that in figure 2.
r
= 5. The dotted line is the same as that in figure 2.
Download figure:
Standard image High-resolution imageIn the section we discussed the PP spectrum in the 3D periodic graphene structure at different ribbon width, interface distance, period in the interface and carrier concentrate. The influences of different parameter were given.
Because of the correction factors, there is always a lifting in the PP spectrum. The smaller q0 becomes, the more obvious the lifting gets. When q0 → 0, we have 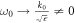 , where k0 is determined by
, where k0 is determined by 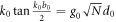 and becomes larger with increasing N, d0 and decreasing b0, as shown in figures 2, 3 and 4. where EM radiation spectra in the medium were also shown. It was found that due to the lifting, there exists an intersection between PP dispersion and EM radiation dispersion, where the two dispersions are the same and a match between PP and EM radiation occurs. To estimate the matching point, we notice that the match always occurs at long wave region, where the frequency of PP hardly changes, therefore, match occurs roughly at the wave vector k0. If
and becomes larger with increasing N, d0 and decreasing b0, as shown in figures 2, 3 and 4. where EM radiation spectra in the medium were also shown. It was found that due to the lifting, there exists an intersection between PP dispersion and EM radiation dispersion, where the two dispersions are the same and a match between PP and EM radiation occurs. To estimate the matching point, we notice that the match always occurs at long wave region, where the frequency of PP hardly changes, therefore, match occurs roughly at the wave vector k0. If 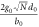 is not large,
is not large, 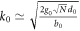 . Therefore, one can easily excite PP in the structure by EM radiation at the match point.
. Therefore, one can easily excite PP in the structure by EM radiation at the match point.
4. Conclusions
In conclusion, to improve the efficiency of photodetectors, we first designed a three-dimensional periodic structure of graphene ribbons embedded in a medium and investigated the dispersion of TM plasmon-polaritons in the structure. It was shown that for a plasmon-polariton propagating in xz-plane, the wave vector of which is, for instance, (qx , qz ), the component of wave vector perpendicular to graphene ribbons, qz , is irrelevant to the PP spectrum but supplies a wave function modulation.
We further considered the spectra of plasmon-polaritons in the structure and compared results with those in monolayer graphene interface embedded in the medium. There are sharp differences between these results. Firstly, wave functions are not exponential decaying but combinations of cosine functions due to the periodic boundary conditions. Secondly, the spectra are lifted and behave as concave functions but not convex ones with respect to qx . The larger the carrier concentration, the more obvious the lifting. Thirdly, although for the case qx b ≫ 1, where b is the interface distance, the two results approximately equal, for the case of qx → 0, the frequencies of plasmon-polaritons in our structure do not tend to zero. The matching condition, where the frequencies of PP and EM radiation are equal, occurs at the wave vector k0. The match makes it easier to excite plasmon polariton with electromagnetic radiations in the three-dimensional period structure than that in a two-dimensional period structure. Thus, the three-dimensional structure supplies a high efficiency of photoelectric detection.
Acknowledgments
The National Natural Science Foundation of China (21773181, 21 573 172) has financially supported this work.





